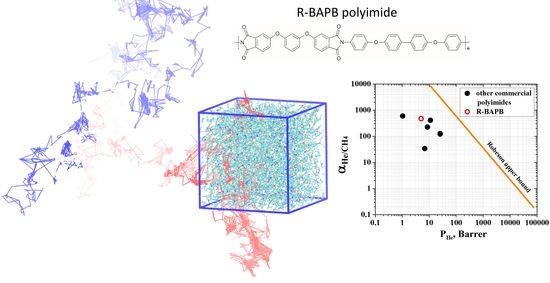
Transport Properties of Thermoplastic R-BAPB Polyimide: Molecular Dynamics Simulations and Experiment
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Methods
2.2. Film Preparation
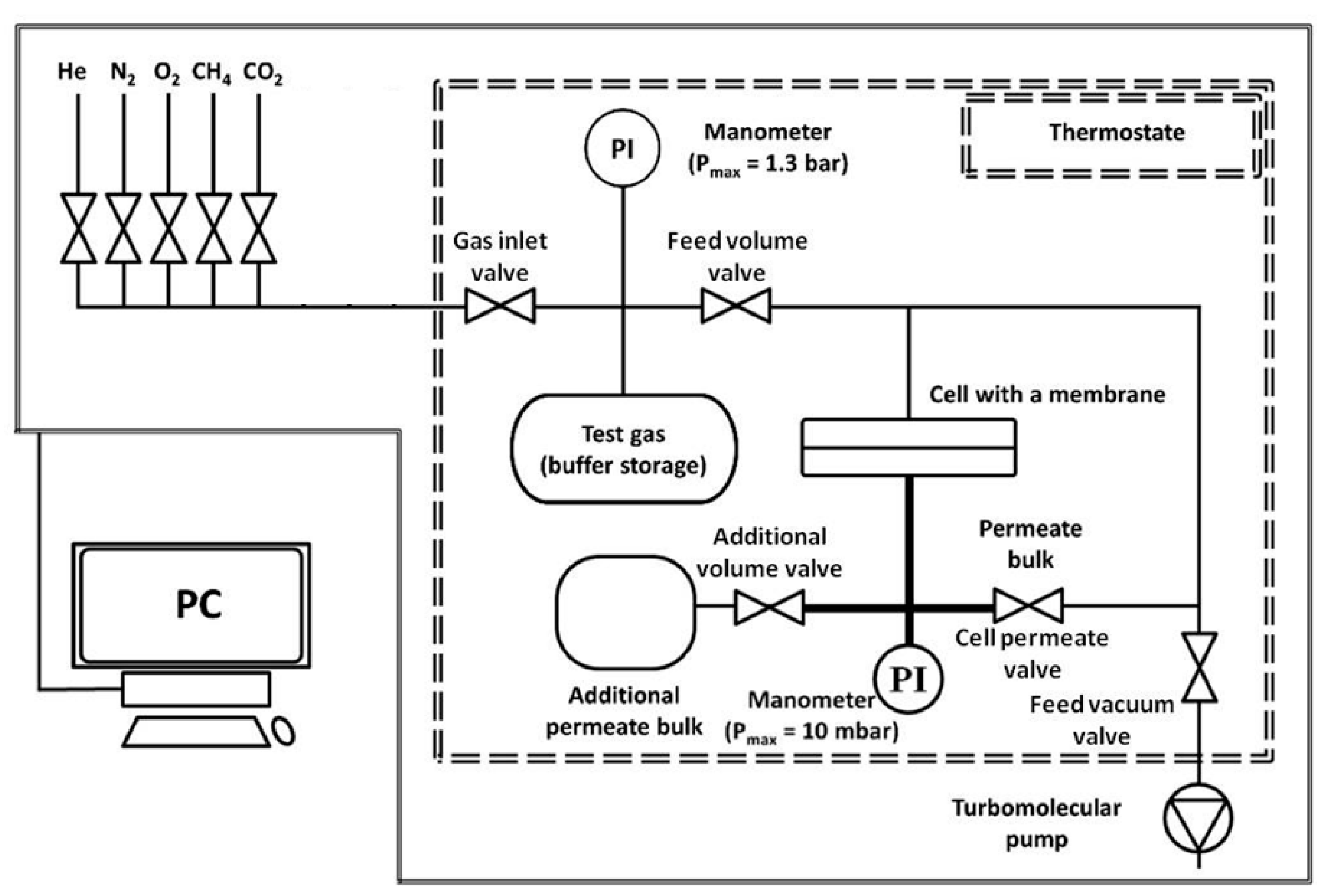
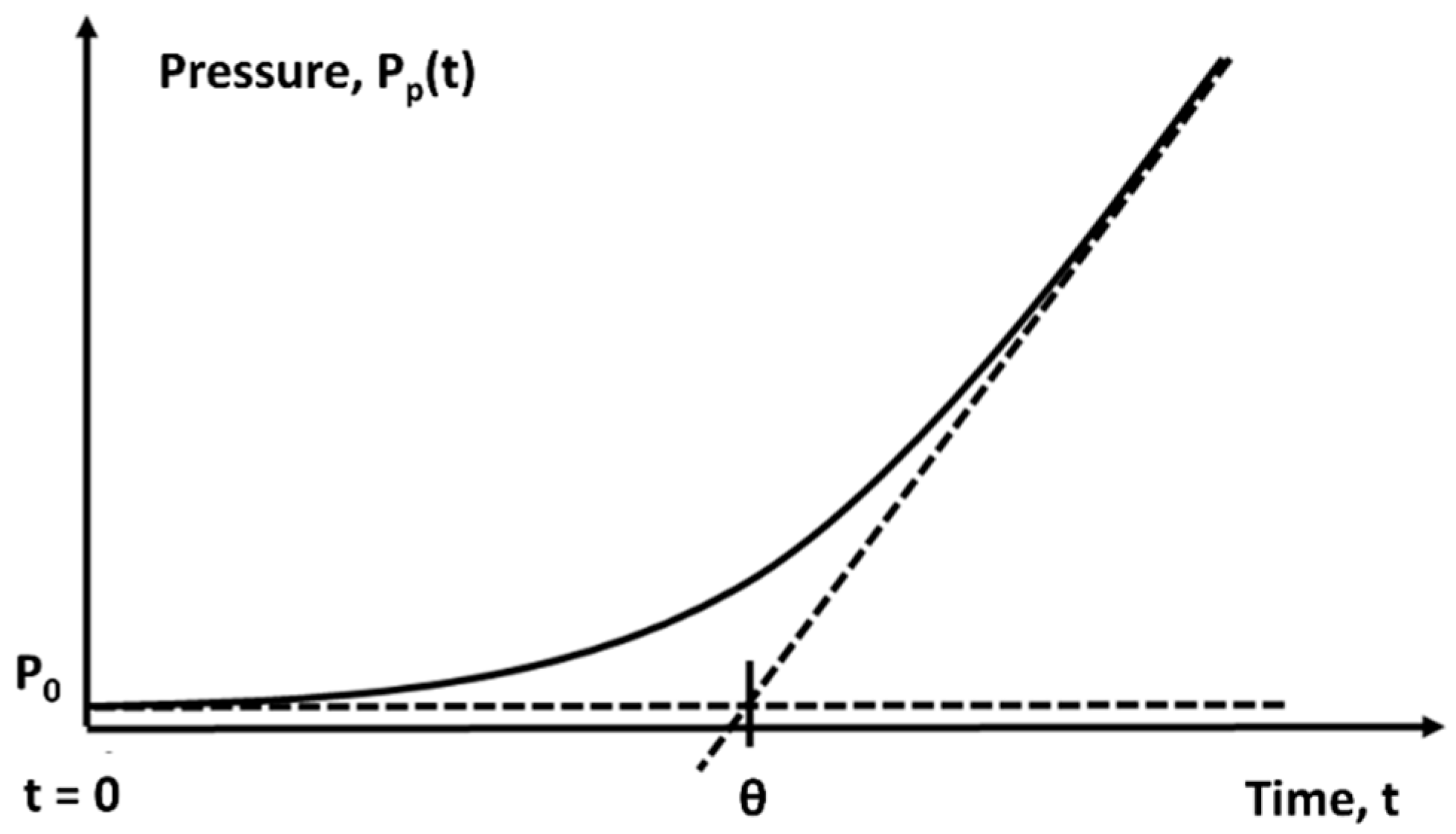
2.3. Characterization of Transport Properties
2.4. Molecular Dynamics Simulations
2.4.1. Simulation Details
2.4.2. Solubility Calculations
2.4.3. Diffusion Coefficient Calculations
3. Results and Discussion
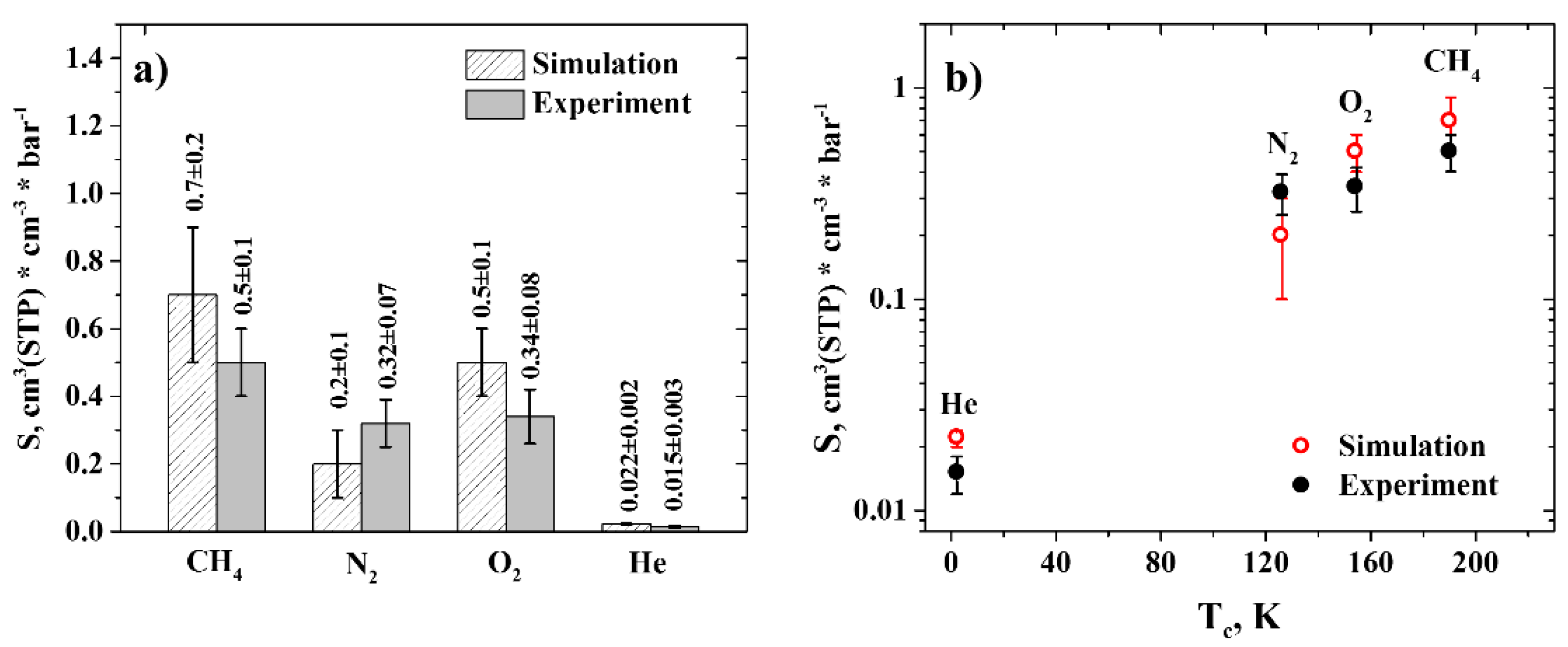
3.1. Solubility
3.2. Diffusion Coefficients
3.3. Permeability and Selectivity
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ravanchi, M.T.; Kaghazchi, T.; Kargari, A. Application of Membrane Separation Processes in Petrochemical Industry: A Review. Desalination 2009, 235, 199–244. [Google Scholar] [CrossRef]
- Yampolskii, Y.; Starannikova, L.; Belov, N.; Bermeshev, M.; Gringolts, M.; Finkelshtein, E. Solubility Controlled Permeation of Hydrocarbons: New Membrane Materials and Results. J. Membr. Sci. 2014, 453, 532–545. [Google Scholar] [CrossRef]
- Scholes, C.A.; Stevens, G.W.; Kentish, S.E. Membrane Gas Separation Applications in Natural Gas Processing. Fuel 2012, 96, 15–28. [Google Scholar] [CrossRef]
- Sridhar, S.; Smitha, B.; Aminabhavi, T.M. Separation of Carbon Dioxide from Natural Gas Mixtures through Polymeric Membranes—A Review. Sep. Purif. Rev. 2007, 36, 113–174. [Google Scholar] [CrossRef]
- Yampolksii, Y.P.; Banerjee, S. Effects of Bulky Substituents on Transport Properties of Membrane Gas Separation Materials. Pet. Chem. 2017, 57, 1195–1206. [Google Scholar] [CrossRef]
- Sanaeepur, H.; Amooghin, A.E.; Bandehali, S.; Moghadassi, A.; Matsuura, T.; Van der Bruggen, B. Polyimides in Membrane Gas Separation: Monomer’s Molecular Design and Structural Engineering. Prog. Polym. Sci. 2019, 91, 80–125. [Google Scholar] [CrossRef]
- Sanders, D.F.; Smith, Z.P.; Guo, R.; Robeson, L.M.; McGrath, J.E.; Paul, D.R.; Freeman, B.D. Energy-Efficient Polymeric Gas Separation Membranes for a Sustainable Future: A Review. Polymer 2013, 54, 4729–4761. [Google Scholar] [CrossRef]
- Robeson, L.M. The Upper Bound Revisited. J. Membr. Sci. 2008, 320, 390–400. [Google Scholar] [CrossRef]
- Liaw, D.J.; Wang, K.L.; Huang, Y.C.; Lee, K.R.; Lai, J.Y.; Ha, C.S. Advanced Polyimide Materials: Syntheses, Physical Properties and Applications. Prog. Polym. Sci. 2012, 37, 907–974. [Google Scholar] [CrossRef]
- Swaidan, R.; Al-Saeedi, M.; Ghanem, B.; Litwiller, E.; Pinnau, I. Rational Design of Intrinsically Ultramicroporous Polyimides Containing Bridgehead-Substituted Triptycene for Highly Selective and Permeable Gas Separation Membranes. Macromolecules 2014, 47, 5104–5114. [Google Scholar] [CrossRef]
- Shamsipur, H.; Dawood, B.A.; Budd, P.M.; Bernardo, P.; Clarizia, G.; Jansen, J.C. Thermally Rearrangeable PIM-Polyimides for Gas Separation Membranes. Macromolecules 2014, 47, 5595–5606. [Google Scholar] [CrossRef]
- Robeson, L.M. Correlation of Separation Factor versus Permeability for Polymeric Membranes. J. Membr. Sci. 1991, 62, 165–185. [Google Scholar] [CrossRef]
- Yang, S.Y. Advanced Polyimide Materials: Synthesis, Characterization, and Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 257–275. [Google Scholar]
- Castro-Muñoz, R.; Martin-Gil, V.; Ahmad, M.Z.; Fíla, V. Matrimid® 5218 in Preparation of Membranes for Gas Separation: Current State-of-the-Art. Chem. Eng. Commun. 2018, 205, 161–196. [Google Scholar] [CrossRef]
- Loloei, M.; Moghadassi, A.; Omidkhah, M.; Amooghin, A.E. Improved CO2 separation performance of Matrimid®5218 membrane by addition of low molecular weight polyethylene glycol. Greenh. Gas Sci. Technol. 2015, 5, 1–15. [Google Scholar] [CrossRef]
- Hosseini, S.S.; Teoh, M.M.; Chung, T.S. Hydrogen Separation and Purification in Membranes of Miscible Polymer Blends with Interpenetration Networks. Polymer 2008, 49, 1594–1603. [Google Scholar] [CrossRef]
- Shen, Y.; Lua, A.C. Structural and Transport Properties of BTDA-TDI/MDI Co-Polyimide (P84)–Silica Nanocomposite Membranes for Gas Separation. Chem. Eng. J. 2012, 188, 199–209. [Google Scholar] [CrossRef]
- Bos, A.; Pünt, I.G.M.; Wessling, M.; Strathmann, H. CO2-Induced Plasticization Phenomena in Glassy Polymers. J. Membr. Sci. 1999, 155, 67–78. [Google Scholar] [CrossRef]
- Lin, W.; Vora, R.H.; Chung, T. Gas Transport Properties of 6FDA-Durene/1,4- Phenylenediamine (PPDA) Copolyimides. J. Appl. Polym. Sci. 2000, 38, 2703–2713. [Google Scholar] [CrossRef]
- Chirkov, S.V.; Kechekyan, A.S.; Belov, N.A.; Antonov, S.V.; Alentiev, A.Y. The influence of uniform deformation of Ultem-1000 polyetherimide films on their mechanical and gas transport characteristics. Pet. Chem. 2016, 56, 1074–1084. [Google Scholar] [CrossRef]
- Laurini, E.; Fermeglia, M.; Pricl, S. Materials by Design: Multiscale Molecular Modelling for the Design of Nanostructured Membranes. In Membrane Engineering for the Treatment of Gases; Drioli, E., Barbieri, G., Brunetti, A., Eds.; Royal Society of Chemistry: Croydon, UK, 2017; Volume 1, pp. 28–49. [Google Scholar] [CrossRef]
- Vergadou, N.; Theodorou, D.N. Molecular Modeling Investigations of Sorption and Diffusion of Small Molecules in Glassy Polymers. Membranes 2019, 9, 98. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Schepers, C.; Böhning, M. Detailed-Atomistic Molecular Modeling of Small Molecule Diffusion and Solution Processes in Polymeric Membrane Materials. Macromol. Theor. Simul. 2000, 9, 293–327. [Google Scholar] [CrossRef]
- Neyertz, S. Tutorial: Molecular Dynamics Simulations of Microstructure and Transport Phenomena in Glassy Polymers. Soft Mater. 2007, 4, 15–83. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D.; Pandiyan, S.; van der Vegt, N.F.A. Carbon Dioxide Diffusion and Plasticization in Fluorinated Polyimides. Macromolecules 2010, 43, 7813–7827. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Air Sorption and Separation by Polymer Films at the Molecular Level. Macromolecules 2018, 51, 7077–7092. [Google Scholar] [CrossRef]
- Tanis, I.; Brown, D.; Neyertz, S.; Heck, R.; Mercier, R.; Vaidya, M.; Ballaguet, J.P. A Comparison of Pure and Mixed-Gas Permeation of Nitrogen and Methane in 6FDA-Based Polyimides as Studied by Molecular Dynamics Simulations. Comput. Mater. Sci. 2018, 141, 243–253. [Google Scholar] [CrossRef]
- Neyertz, S. Molecular Dynamics Simulations of Helium Permeation in Polyimides with a Bulky Dianhydride and a Fluorinated Diamine. Macromol. Theor. Simul. 2007, 16, 513–524. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Oxygen Sorption in Glassy Polymers Studied at the Molecular Level. Macromolecules 2009, 42, 8521–8533. [Google Scholar] [CrossRef]
- Neyertz, S.; Brown, D. Molecular Dynamics Simulations of Oxygen Transport through a Fully Atomistic Polyimide Membrane. Macromolecules 2008, 41, 2711–2721. [Google Scholar] [CrossRef]
- Hofmann, D.; Fritz, L.; Ulbrich, J.; Paul, D. Molecular Simulation of Small Molecule Diffusion and Solution in Dense Amorphous Polysiloxanes and Polyimides. Comput. Theor. Polym. Sci. 2000, 10, 419–436. [Google Scholar] [CrossRef]
- Heuchel, M.; Hofmann, D.; Pullumbi, P. Molecular Modeling of Small-Molecule Permeation in Polyimides and Its Correlation to Free-Volume Distributions. Macromolecules 2004, 37, 201–214. [Google Scholar] [CrossRef]
- Park, C.H.; Tocci, E.; Kim, S.; Kumar, A.; Lee, Y.M.; Drioli, E. A Simulation Study on OH-Containing Polyimide (HPI) and Thermally Rearranged Polybenzoxazoles (TR-PBO): Relationship between Gas Transport Properties and Free Volume Morphology. J. Phys. Chem. B 2014, 118, 2746–2757. [Google Scholar] [CrossRef] [PubMed]
- Chang, K.S.; Tung, C.C.; Wang, K.S.; Tung, K.L. Free Volume Analysis and Gas Transport Mechanisms of Aromatic Polyimide Membranes: A Molecular Simulation Study. J. Phys. Chem. B 2009, 113, 9821–9830. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, R.; Bisoi, S.; Kumar, A.G.; Padmanabhan, V.; Banerjee, S. Polyimides Containing Phosphaphenanthrene Skeleton: Gas-Transport Properties and Molecular Dynamics Simulations. ACS Omega 2018, 3, 13510–13523. [Google Scholar] [CrossRef] [PubMed]
- Yudin, V.E.; Feldman, A.Y.; Svetlichnyi, V.M.; Shumakov, A.N.; Marom, G. Crystallization of R-BAPB Type Polyimide Modified by Carbon Nano-Particles. Compos. Sci. Technol. 2007, 67, 789–794. [Google Scholar] [CrossRef]
- Yudin, V.E.; Svetlichnyi, V.M. Effect of the Structure and Shape of Filler Nanoparticles on the Physical Properties of Polyimide Composites. Russ. J. Gen. Chem. 2010, 80, 2157–2169. [Google Scholar] [CrossRef]
- Yudin, V.E.; Svetlichnyi, V.M.; Shumakov, A.N.; Schechter, R.; Harel, H.; Marom, G. Morphology and Mechanical Properties of Carbon Fiber Reinforced Composites Based on Semicrystalline Polyimides Modified by Carbon Nanofibers. Compos. Part A-Appl. S. Manuf. 2008, 39, 85–90. [Google Scholar] [CrossRef]
- Yudin, V.E.; Svetlichnyi, V.M.; Shumakov, A.N.; Letenko, D.G.; Feldman, A.Y.; Marom, G. The Nucleating Effect of Carbon Nanotubes on Crystallinity in R-BAPB Type Thermoplastic Polyimide. Macromol. Rapid Comm. 2005, 26, 885–888. [Google Scholar] [CrossRef]
- Yudin, V.E.; Otaigbe, J.U.; Drzal, L.T.; Svetlichnyi, V.M. Novel Semicrystalline Thermoplastic R-BAPB Type Polyimide Matrix Reinforced by Graphite Nanoplatelets and Carbon Nanoparticles. Adv. Compos. Lett. 2006, 15, 137–143. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Lyulin, A.V.; Larin, S.V.; Gurtovenko, A.A.; Kenny, J.M.; Lyulin, S.V. Molecular Dynamics Simulations of Uniaxial Deformation of Thermoplastic Polyimides. Soft Matter. 2016, 12, 3972–3981. [Google Scholar] [CrossRef]
- Larin, S.V.; Glova, A.D.; Serebryakov, E.B.; Nazarychev, V.M.; Kenny, J.M.; Lyulin, S.V. Influence of the Carbon Nanotube Surface Modification on the Microstructure of Thermoplastic Binders. RSC Adv. 2015, 5, 51621–51630. [Google Scholar] [CrossRef]
- Lyulin, S.V.; Larin, S.V.; Gurtovenko, A.A.; Lukasheva, N.V.; Yudin, V.E.; Svetlichnyi, V.M.; Lyulin, A.V. Effect of the SO2 Group in the Diamine Fragment of Polyimides on Their Structural, Thermophysical, and Mechanical Properties. Polym. Sci. Ser. A 2012, 54, 631–643. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Larin, S.V.; Yakimansky, A.V.; Lukasheva, N.V.; Gurtovenko, A.A.; Gofman, I.V.; Yudin, V.E.; Svetlichnyi, V.M.; Kenny, J.M.; Lyulin, S.V. Parameterization of Electrostatic Interactions for Molecular Dynamics Simulations of Heterocyclic Polymers. J. Polym. Sci. Pol. Phys. 2015, 53, 912–923. [Google Scholar] [CrossRef]
- Larin, S.V.; Falkovich, S.G.; Nazarychev, V.M.; Gurtovenko, A.A.; Lyulin, A.V.; Lyulin, S.V. Molecular-Dynamics Simulation of Polyimide Matrix Pre-Crystallization near the Surface of a Single-Walled Carbon Nanotube. RSC Adv. 2014, 4, 830–844. [Google Scholar] [CrossRef]
- Falkovich, S.G.; Nazarychev, V.M.; Larin, S.V.; Kenny, J.M.; Lyulin, S.V. Mechanical Properties of a Polymer at the Interface Structurally Ordered by Graphene. J. Phys. Chem. C 2016, 120, 6771–6777. [Google Scholar] [CrossRef]
- Sokolova, M.; Smirnov, M.; Bugrov, A.; Geydt, P.; Popova, E.; Lahderanta, E.; Svetlichnyi, V.; Toikka, A. Structure of Composite Based on Polyheteroarylene Matrix and ZrO2 Nanostars Investigated by Quantitative Nanomechanical Mapping. Polymers 2017, 9, 268. [Google Scholar] [CrossRef]
- Volgin, I.V.; Larin, S.V.; Abad, E.; Lyulin, S.V. Molecular Dynamics Simulations of Fullerene Diffusion in Polymer Melts. Macromolecules 2017, 50, 2207–2218. [Google Scholar] [CrossRef]
- McKeen, L.W. Permeability Properties of Plastics and Elastomers; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Wijmans, J.G.; Baker, R.W. The Solution-Diffusion Model: A Review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Teplyakov, V.; Meares, P. Correlation Aspects of the Selective Gas Permeabilities of Polymeric Materials and Membranes. Gas Sep. Purif. 1990, 4, 66–74. [Google Scholar] [CrossRef]
- Yampolskii, Y.; Pinnau, I.; Freeman, B. Materials Science of Membranes for Gas and Vapor Separation, 1st ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2006; pp. 7–31, 148–151. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Villa, A.; Mark, A.E.; van Gunsteren, W.F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. [Google Scholar] [CrossRef]
- Oostenbrink, C.; Soares, T.A.; van der Vegt, N.F.A.; van Gunsteren, W.F. Validation of the 53A6 GROMOS force field. Eur. Biophys. J. 2005, 34, 273–284. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindah, E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1, 19–25. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Dobrovskiy, A.Y.; Larin, S.V.; Lyulin, A.V.; Lyulin, S.V. Simulating Local Mobility and Mechanical Properties of Thermostable Polyimides with Different Dianhydride Fragments. J. Polym. Sci. Polym. Phys. 2018, 56, 375–382. [Google Scholar] [CrossRef]
- Lyulin, S.V.; Gurtovenko, A.A.; Larin, S.V.; Nazarychev, V.M.; Lyulin, A.V. Microsecond Atomic-Scale Molecular Dynamics Simulations of Polyimides. Macromolecules 2013, 46, 6357–6363. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Larin, S.V.; Lyulin, A.V.; Dingemans, T.; Kenny, J.M.; Lyulin, S.V. Atomistic Molecular Dynamics Simulations of the Initial Crystallization Stage in an SWCNT-Polyetherimide Nanocomposite. Polymers 2017, 9, 548. [Google Scholar] [CrossRef]
- Lyulin, S.V.; Larin, S.V.; Gurtovenko, A.A.; Nazarychev, V.M.; Falkovich, S.G.; Yudin, V.E.; Svetlichnyi, V.M.; Gofman, I.V.; Lyulin, A.V. Thermal Properties of Bulk Polyimides: Insights from Computer Modeling versus Experiment. Soft Matter. 2014, 10, 1224–1232. [Google Scholar] [CrossRef]
- Lee, J.F.; Sears, F.W.; Turcotte, D.L. Equilibrium Statistical Mechanics and Thermodynamics; Entropy Time Evolution Macroscopic Systems; Oxford University Press: Oxford, UK, 1964; pp. 34–58. [Google Scholar] [CrossRef]
- Fischer, J.; Lago, S. Thermodynamic Perturbation Theory for Molecular Liquid Mixtures. J. Chem. Phys. 1983, 78, 5750–5758. [Google Scholar] [CrossRef]
- Cheung, P.S.Y.; Powles, J.G. The Properties of Liquid Nitrogen: IV. A Computer Simulation. Mol. Phys. 1975, 30, 921–949. [Google Scholar] [CrossRef]
- Yin, D.; MacKerell, A.D. Combined ab Initio/Empirical Approach for Optimization of Lennard-Jones Parameters. J. Comput. Chem. 1998, 19, 334–348. [Google Scholar] [CrossRef]
- Falkovich, S.G.; Lyulin, S.V.; Nazarychev, V.M.; Larin, S.V.; Gurtovenko, A.A.; Lukasheva, N.V.; Lyulin, A.V. Influence of the Electrostatic Interactions on the Thermophysical Properties of Polyimides: Molecular-Dynamics Simulations. J. Polym. Sci. Polym. Phys. 2014, 52, 640–646. [Google Scholar] [CrossRef]
- Nazarychev, V.M.; Larin, S.V.; Lukasheva, N.V.; Glova, A.D.; Lyulin, S.V. Evaluation of the Characteristic Equilibration Times of Bulk Polyimides via Full-Atomic Computer Simulation. Polym. Sci. Ser. A 2013, 55, 570–576. [Google Scholar] [CrossRef]
- Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 1984, 52, 255–268. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic Transitions in Single Crystals: A New Molecular Dynamics Method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Taylor, P.; van Gunsteren, W.F.; Berendsen, H.J.C. Algorithms for brownian dynamics. Mol. Phys. 1982, 45, 637–647. [Google Scholar]
- Lyulin, A.V.; Balabaev, N.K.; Michels, M.A.J. Molecular-Weight and Cooling-Rate Dependence of Simulated Tg for Amorphous Polystyrene. Macromolecules 2003, 36, 8574–8575. [Google Scholar] [CrossRef]
- Widom, B. Some Topics in the Theory of Fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Neogi, P. Diffusion in Polymers, 1st ed.; Marcel Dekker, Inc.: New York, NY, USA, 1996; pp. 114–137. [Google Scholar]
- Kotelyanskii, M.; Theodorou, N. Simulation Methods for Polymers, 1st ed.; CRC Press: Boca Raton, FL, USA, 2004; pp. 425–490. [Google Scholar] [CrossRef]
- Hanson, B.; Pryamitsyn, V.; Ganesan, V. Computer Simulations of Gas Diffusion in Polystyrene–C60 Fullerene Nanocomposites Using Trajectory Extending Kinetic Monte Carlo Method. J. Phys. Chem. B 2012, 116, 95–103. [Google Scholar] [CrossRef]
- Yang, Y.; Narayanan Nair, A.K.; Sun, S. Adsorption and Diffusion of Methane and Carbon Dioxide in Amorphous Regions of Cross-Linked Polyethylene: A Molecular Simulation Study. Ind. Eng. Chem. Res. 2019, 58, 8426–8436. [Google Scholar] [CrossRef]
- Dutta, R.C.; Bhatia, S.K. Transport Diffusion of Light Gases in Polyethylene Using Atomistic Simulations. Langmuir 2017, 33, 936–946. [Google Scholar] [CrossRef]
- van der Vegt, N.F.A. Temperature Dependence of Gas Transport in Polymer Melts: Molecular Dynamics Simulations of CO2 in Polyethylene. Macromolecules 2000, 33, 3153–3160. [Google Scholar] [CrossRef]

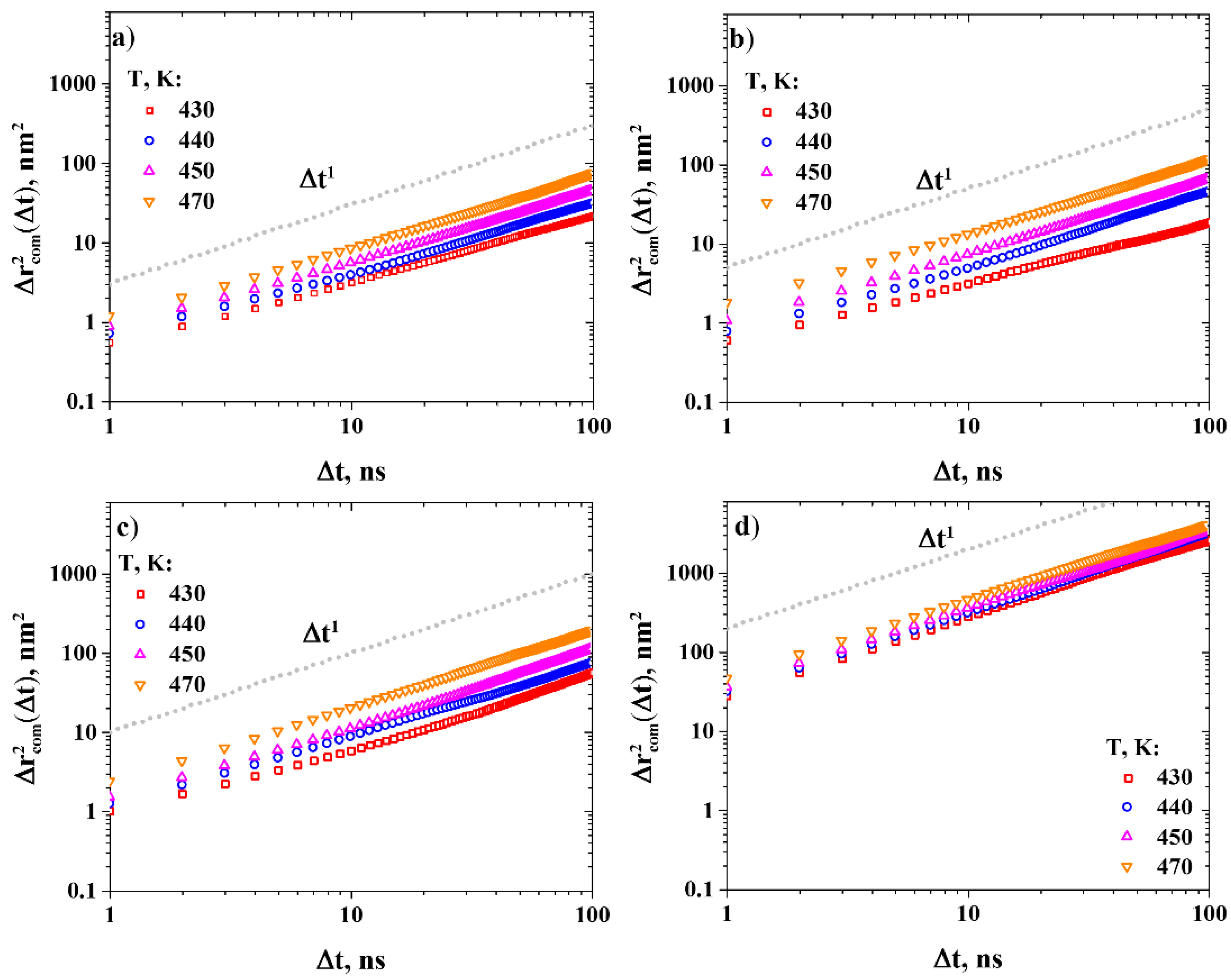
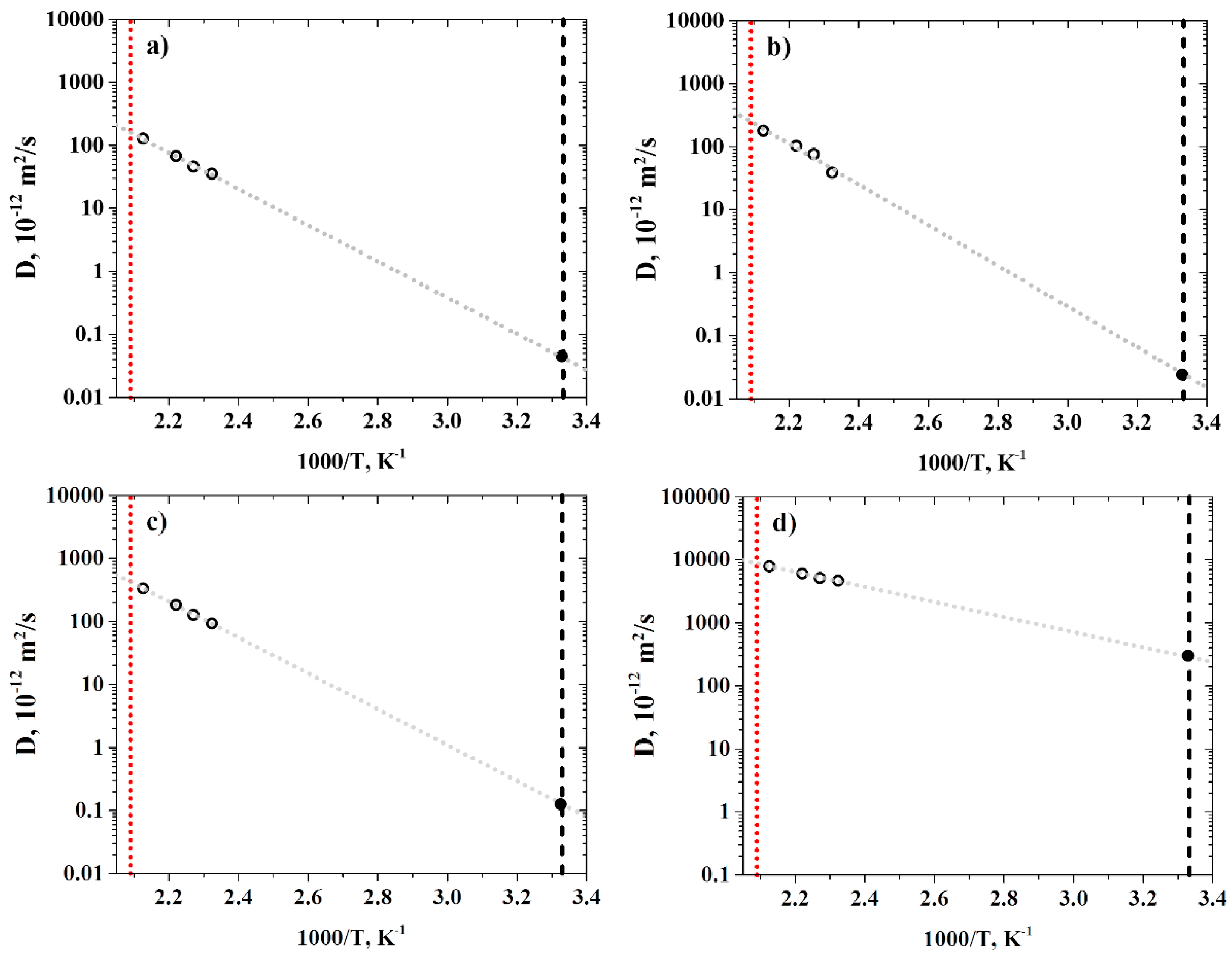
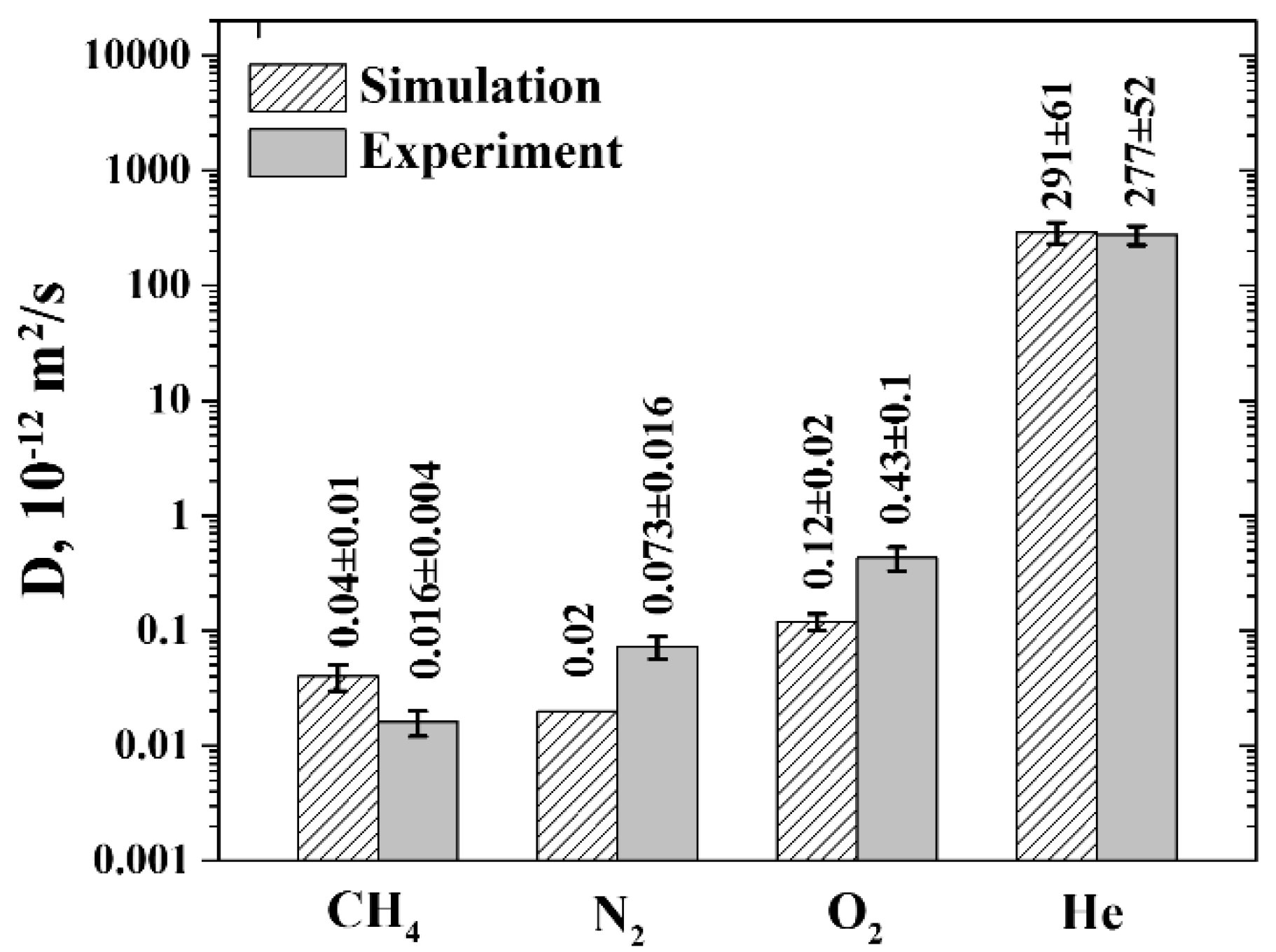
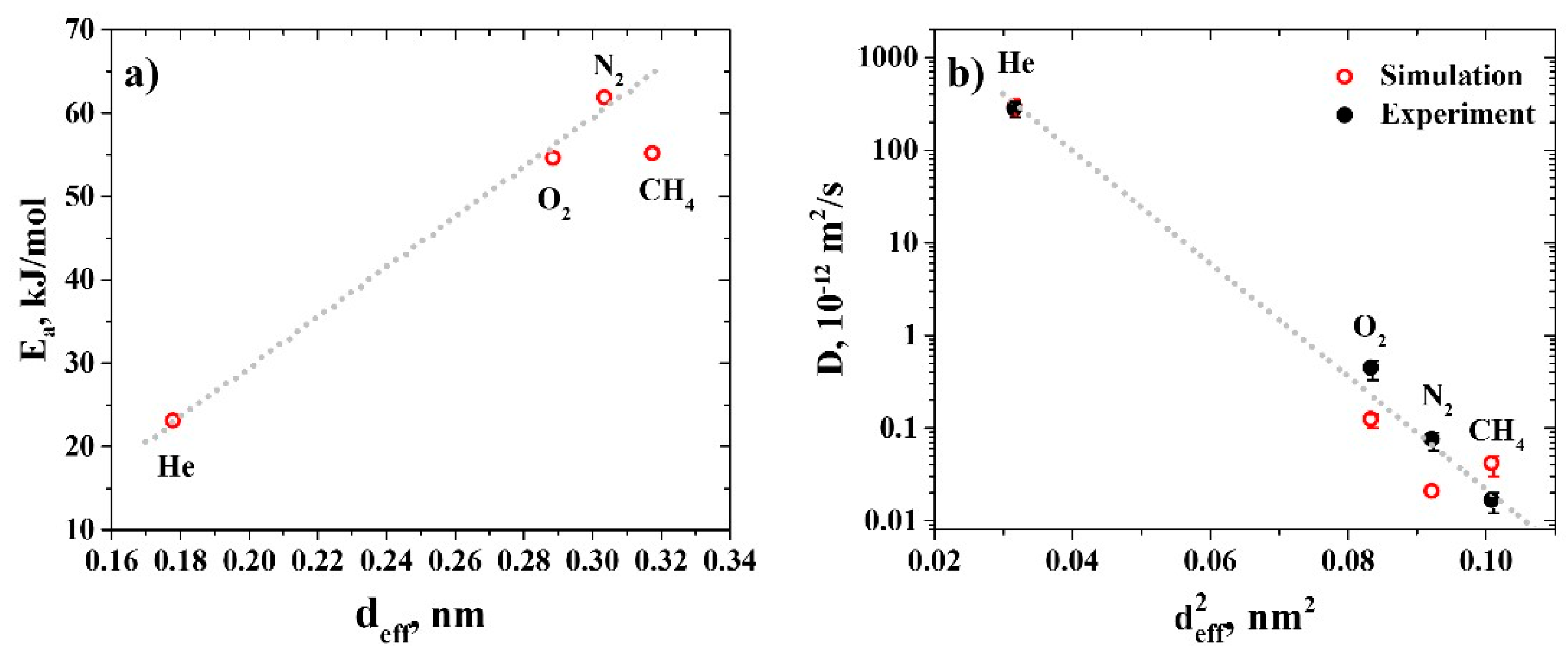
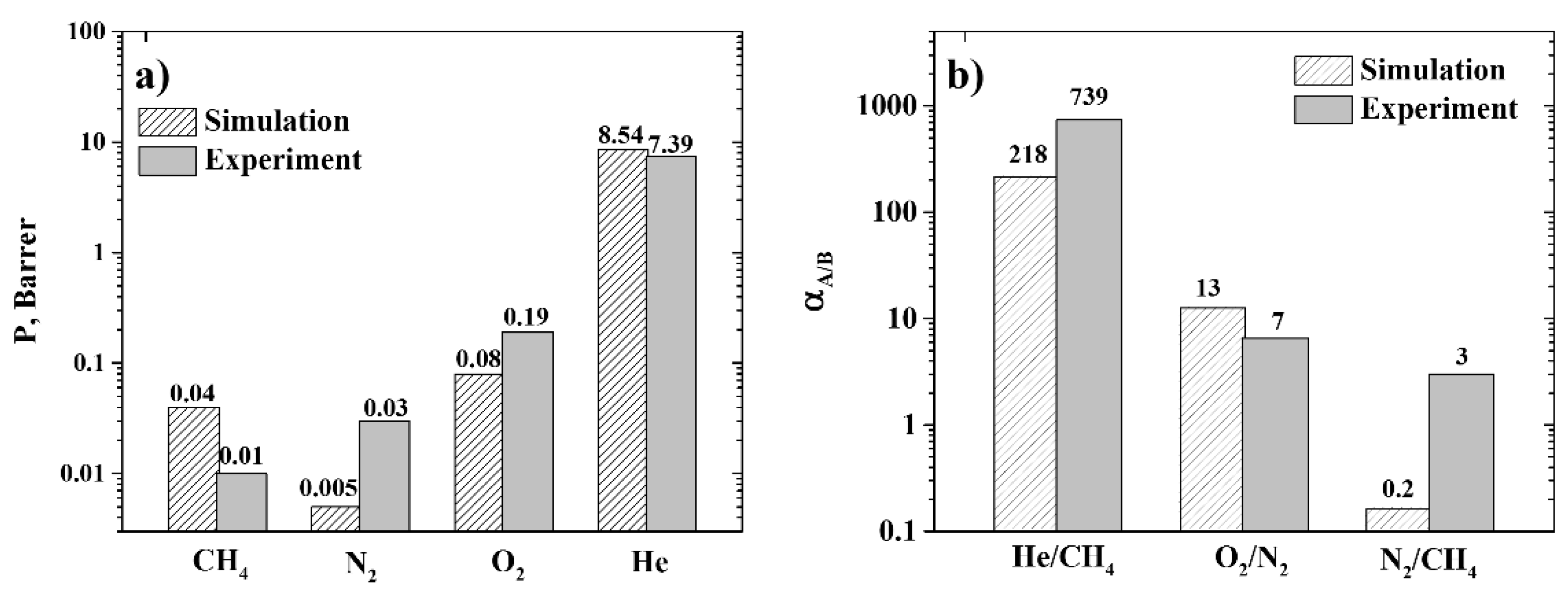
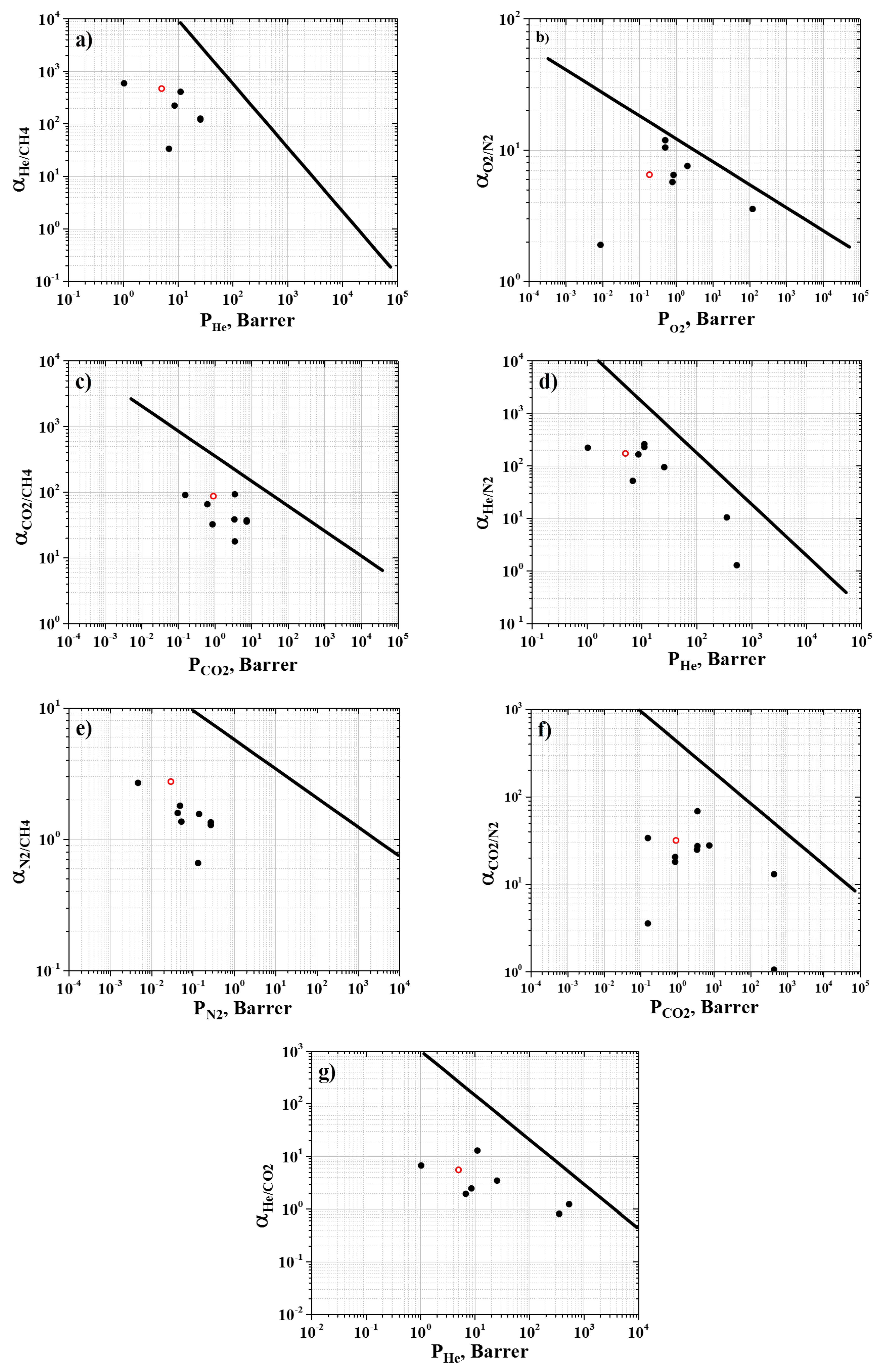
| R-BAPB | Kapton [13] | ULTEM [20] | Upilex-R [13] | Matrimid 5218 [15] | P84 [18] | 6FDA-Durene [19] | PBI [16] | |
|---|---|---|---|---|---|---|---|---|
| Tg, K | 485 | 693 | 488 | 543 | 583 | 573 | 697 | 690 |
| ρ, kg/m3 | 1324 | 1395 | 1280–1300 | 1366 | 1.172 | 1336 | 1333 | 1311 |
| FFV,% | 13.9 | 12.9 | 10.8–11.5 | 12.1 | 26.8 | 20.3 | 18.0 | 11.6 |
| Gas | Atom | Interaction Potential Parameters | Reference | |
|---|---|---|---|---|
| ε/kB, K | σ, Å | |||
| He | He | 6.030 | 2.6282 | [28,60] |
| N2 | N | 37.296 | 3.31 | [61] |
| O2 | O | 44.6 | 3.09 | [62] |
| CH4 | C | 47.8 | 3.7595 | [63] |
| H | 8.5546 | 2.3876 | ||
| Gas | Number of Gas Molecules |
|---|---|
| CH4 | 4 |
| N2 | 1 |
| O2 | 3 |
| He | 0.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volgin, I.V.; Andreeva, M.V.; Larin, S.V.; Didenko, A.L.; Vaganov, G.V.; Borisov, I.L.; Volkov, A.V.; Klushin, L.I.; Lyulin, S.V. Transport Properties of Thermoplastic R-BAPB Polyimide: Molecular Dynamics Simulations and Experiment. Polymers 2019, 11, 1775. https://doi.org/10.3390/polym11111775
Volgin IV, Andreeva MV, Larin SV, Didenko AL, Vaganov GV, Borisov IL, Volkov AV, Klushin LI, Lyulin SV. Transport Properties of Thermoplastic R-BAPB Polyimide: Molecular Dynamics Simulations and Experiment. Polymers. 2019; 11(11):1775. https://doi.org/10.3390/polym11111775
Chicago/Turabian StyleVolgin, Igor V., Maria V. Andreeva, Sergey V. Larin, Andrey L. Didenko, Gleb V. Vaganov, Ilya L. Borisov, Alexey V. Volkov, Leonid I. Klushin, and Sergey V. Lyulin. 2019. "Transport Properties of Thermoplastic R-BAPB Polyimide: Molecular Dynamics Simulations and Experiment" Polymers 11, no. 11: 1775. https://doi.org/10.3390/polym11111775
APA StyleVolgin, I. V., Andreeva, M. V., Larin, S. V., Didenko, A. L., Vaganov, G. V., Borisov, I. L., Volkov, A. V., Klushin, L. I., & Lyulin, S. V. (2019). Transport Properties of Thermoplastic R-BAPB Polyimide: Molecular Dynamics Simulations and Experiment. Polymers, 11(11), 1775. https://doi.org/10.3390/polym11111775