Phase-Field Modeling of Freeze Concentration of Protein Solutions
Abstract
1. Introduction
2. Theoretical Analysis
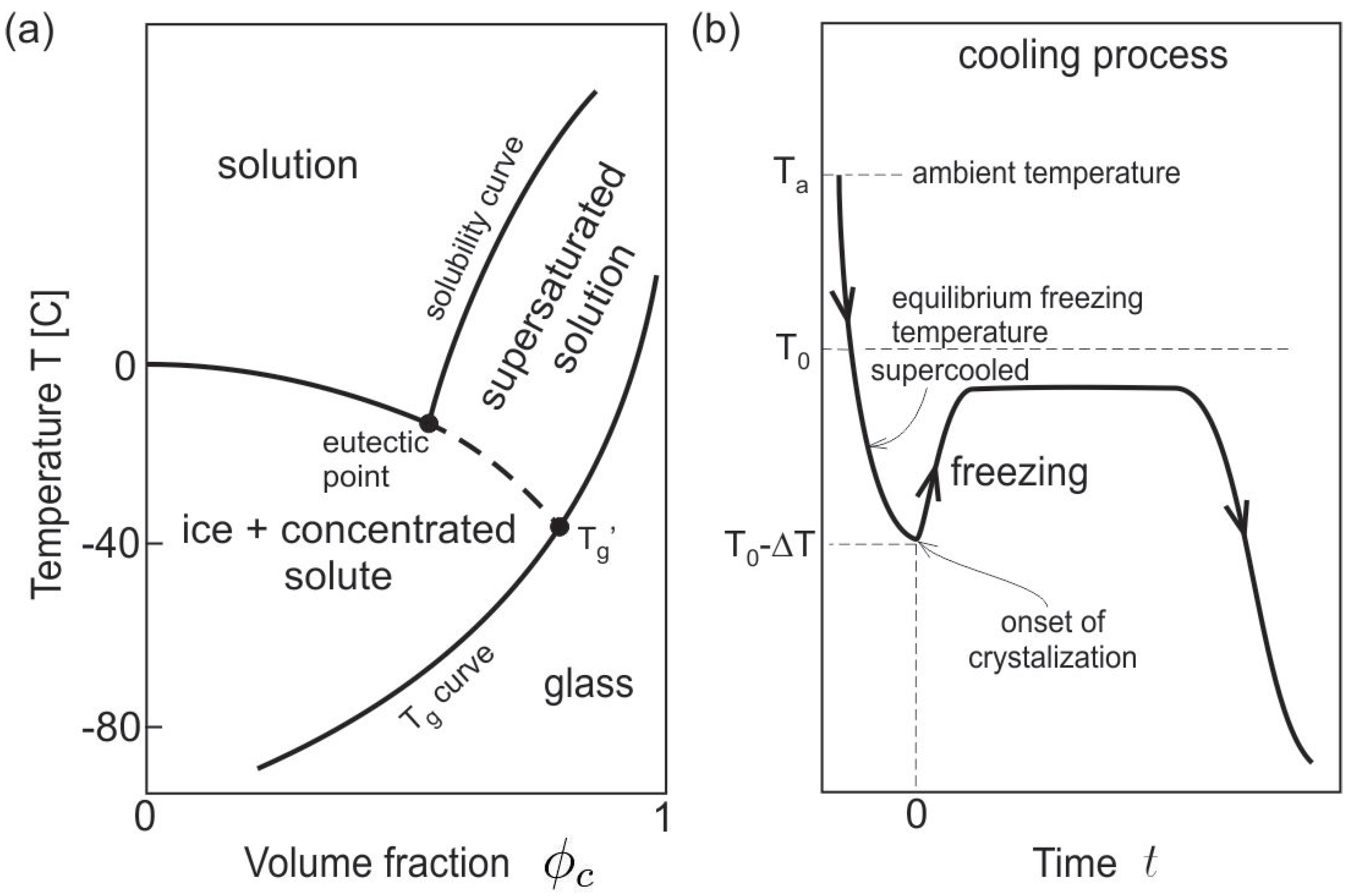
2.1. Thermodynamics Approach
2.2. Internal Energy and Free Energy
2.3. Thermal Energy and Momentum Equations
2.4. Scaling and Computation
3. Material Properties
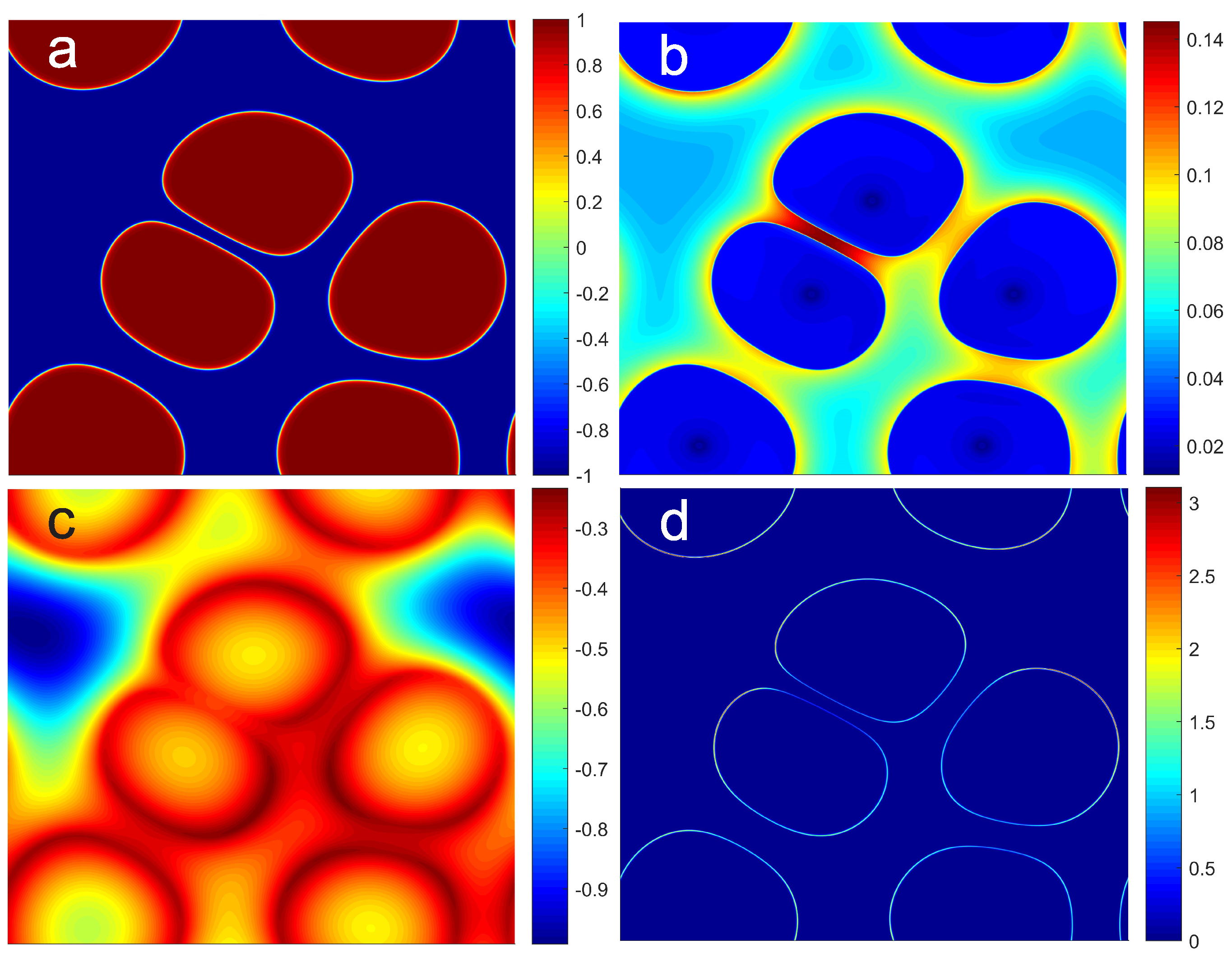
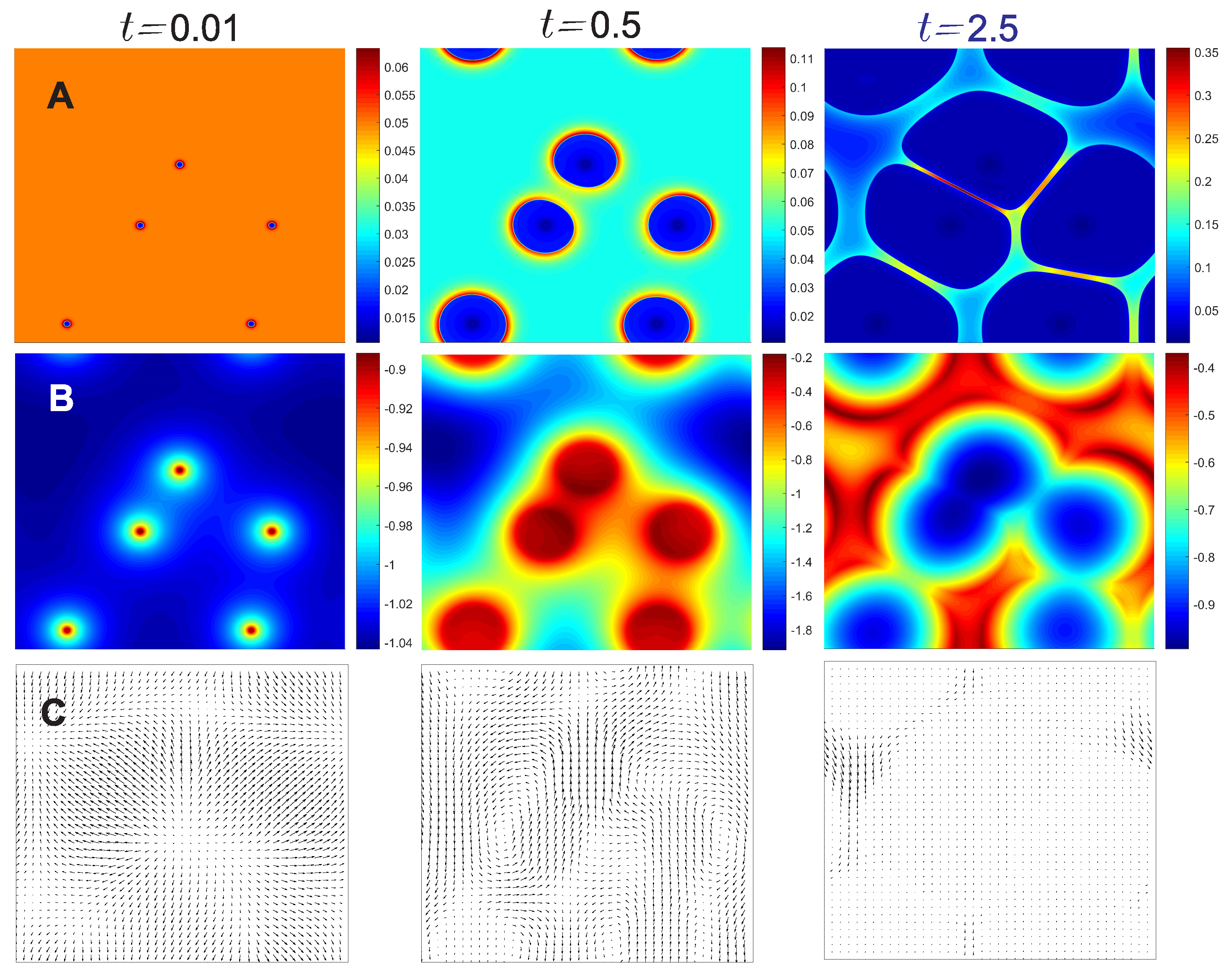
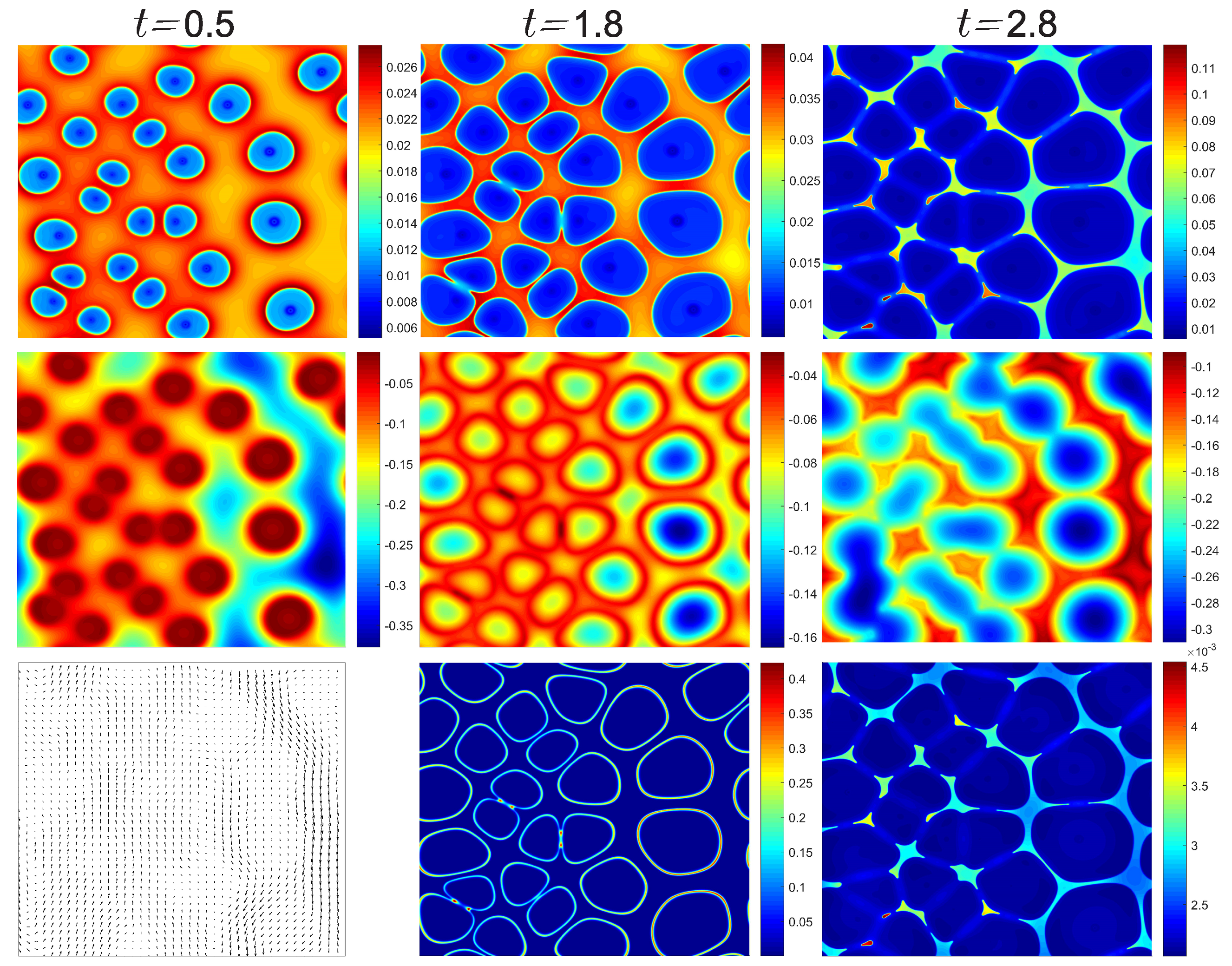
4. Results and Discussion
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Bhatnagar, B.S.; Bogner, R.H.; Pikal, M.J. Protein stability during freezing: Separation of stresses and mechanisms of protein stabilization. Pharm. Dev. Technol. 2007, 12, 505–523. [Google Scholar] [CrossRef] [PubMed]
- Bhatnagar, B.S.; Pikal, M.J.; Bogner, R.H. Study of the individual contributions of ice formation and freeze-concentration on isothermal stability of lactate dehydrogenase during freezing. J. Pharm. Sci. 2008, 97, 798–814. [Google Scholar] [CrossRef] [PubMed]
- Kasper, J.C.; Friess, W. The freezing step in lyophilization: Physico-chemical fundamentals, freezing methods and consequences on process performance and quality attributes of biopharmaceuticals. Eur. J. Pharm. Biopharm. 2011, 78, 248–263. [Google Scholar] [CrossRef] [PubMed]
- Miller, M.A.; Rodrigues, M.A.; Glass, M.A.; Singh, S.K.; Johnston, K.P.; Maynard, J.A. Frozen-state storage stability of a monoclonal antibody: Aggregation is impacted by freezing rate and solute distribution. J. Pharm. Sci. 2013, 102, 1194–1208. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, M.A.; Miller, M.A.; Glass, M.A.; Singh, S.K.; Johnston, K.P. Effect of freezing rate and dendritic ice formation on concentration profiles of proteins frozen in cylindrical vessels. J. Pharm. Sci. 2011, 100, 1316–1329. [Google Scholar] [CrossRef]
- Singh, S.K.; Kolhe, P.; Mehta, A.P.; Chico, S.C.; Lary, A.L.; Huang, M. Frozen state storage instability of a monoclonal antibody: Aggregation as a consequence of trehalose crystallization and protein unfolding. Pharm. Res. 2011, 28, 873–885. [Google Scholar] [CrossRef]
- Kasper, J.C.; Pikal, M.J.; Friess, W. Investigations on polyplex stability during the freezing step of lyophilization using controlled ice nucleation—The importance of residence time in the low-viscosity fluid state. J. Pharm. Sci. 2013, 102, 929–946. [Google Scholar] [CrossRef]
- Rodrigues, M.A.; Balzan, G.; Rosa, M.; Gomes, D.; de Azevedo, E.G.; Singh, S.K.; Matos, H.A.; Geraldes, V. The Importance of heat flow direction for reproducible and homogeneous freezing of bulk protein solutions. AIChE J. 2013, 29, 1212–1221. [Google Scholar] [CrossRef]
- Kobayashi, R. Modeling and numerical simulations of dendritic crystal growth. Physica D 1993, 63, 410–423. [Google Scholar] [CrossRef]
- Warren, J.A.; Boettinger, W.J. Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase-field method. Acta Metall. Mater. 1995, 43, 689–703. [Google Scholar] [CrossRef]
- Murray, B.T.; Wheeler, A.A.; Glicksman, M.E. Simulations of experimentally observed dendritic growth behavior using a phase-field model. J. Cryst. Growth 1995, 154, 386–400. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Phase-field method for computationally efficient modeling of solidification with arbitrary interface kinetics. Phys. Rev. E 1996, 53, R3017–R3020. [Google Scholar] [CrossRef]
- Karma, A.; Rappel, W.J. Quantitative phase-field modeling of dendritic growth in two and three dimensions. Phys. Rev. E 1998, 57, 4323–4349. [Google Scholar] [CrossRef]
- Beckermann, C.; Diepers, H.-J.; Steinbach, I.; Karma, A.; Tong, X. Modeling melt convection in phase-field simulation of solidification. J. Comput. Phys. 1999, 154, 468–496. [Google Scholar] [CrossRef]
- Boettinger, W.J.; Warren, J.A.; Beckermann, C.; Karma, A. Phase-field simulation of solidification. Annu. Rev. Mater. Res. 2002, 32, 163–194. [Google Scholar] [CrossRef]
- Nakagawa, K.; Hottot, A.; Vessot, S.; Andrieu, J. Modeling of freezing step during freeze-drying of drugs in vials. AIChE J. 2007, 53, 1362–1372. [Google Scholar] [CrossRef]
- Radmanovic, N.; Serno, T.; Joerg, S.; Germershaus, O. Understanding the freezing of biopharmaceuticals: First-principle modeling of the process and evaluation of its effect on product quality. J. Pharm. Sci. 2013, 102, 2495–2507. [Google Scholar] [CrossRef]
- Roessl, U.; Jajcevic, D.; Leitgeb, S.; Khinast, J.G.; Nidetzky, B. Characterization of a laboratory-scale container for freezing protein solutions with detailed evaluation of a freezing process simulation. J. Pharm. Sci. 2013, 102, 1194–1208. [Google Scholar] [CrossRef]
- Butler, M.F. Freeze concentration of solutes at the ice/solution interface studied by optical interferometry. Cryst. Growth Des. 2002, 2, 541–548. [Google Scholar] [CrossRef]
- Kaempfer, T.U.; Plapp, M. Phase-field modeling of dry snow metamorphism. Phys. Rev. E 2009, 79, 031502. [Google Scholar] [CrossRef]
- Van der Sman, R.G.M. Phase field simulation of ice crystal growth in sugar solutions. Int. J. Heat Mass Transf. 2016, 95, 153–161. [Google Scholar] [CrossRef]
- Huang, T.-H.; Huang, T.-H.; Lin, Y.-S.; Chang, C.-H.; Chen, P.-Y.; Chang, S.-W.; Chen, C.-S. Phase-field modeling of microstructural evolution by freeze-casting. Adv. Eng. Mater. 2018, 20, 1700343. [Google Scholar] [CrossRef]
- Li, J.-Q.; Fan, T.-H.; Taniguchi, T.; Zhang, B. Phase-field modeling on laser melting of a metallic powder. Int. J. Heat Mass Transf. 2018, 117, 412–424. [Google Scholar] [CrossRef]
- Li, J.-Q.; Fan, T.-H. Phase-field modeling of metallic powder-substrate interaction in laser melting process. Int. J. Heat Mass Transf. 2018. in review. [Google Scholar]
- Van der Waals, J.D. The thermodynamics theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 1979, 20, 200–244. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Hohenberg, P.C.; Halperin, B.I. Theory of dynamic critical phenomena. Rev. Mod. Phys. 1977, 49, 435–479. [Google Scholar] [CrossRef]
- Penrose, O.; Fife, P.C. Thermodynamically consistent models of phase-field type for the kinetics of phase transitions. Physica D 1990, 43, 44–62. [Google Scholar] [CrossRef]
- Wang, S.-L.; Sekerka, R.F.; Wheeler, A.A.; Murray, B.T.; Coriell, S.R.; Braun, R.J.; McFadden, G.B. Thermodynamically-consistent phase-field models for solidification. Physica D 1993, 69, 189–200. [Google Scholar] [CrossRef]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. Diffuse-interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 1998, 30, 139–165. [Google Scholar] [CrossRef]
- Anderson, D.M.; McFadden, G.B.; Wheeler, A.A. A phase-field model of solidification with convection. Physica D 2000, 135, 175–194. [Google Scholar] [CrossRef]
- Bi, Z.; Sekerka, R.F. Phase-field model of solidification of a binary alloy. Physica A 1998, 261, 95–106. [Google Scholar] [CrossRef]
- Yue, P.; Feng, J.J.; Liu, C.; Shen, J. A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 2004, 515, 293–317. [Google Scholar] [CrossRef]
- Takae, K.; Onuki, A. Phase-field model of solid-liquid phase transition with density difference and latent heat in velocity and elastic fields. Phys. Rev. E 2011, 83, 041504. [Google Scholar] [CrossRef] [PubMed]
- Lamorgese, A.G.; Molin, D.; Mauri, R. Phase field approach to multiphase flow modeling. Milan J. Math. 2011, 79, 597–642. [Google Scholar] [CrossRef]
- Roos, Y.H. Glass transition temperature and its relevance in food processing. Annu. Rev. Food Sci. Technol. 2010, 1, 469–496. [Google Scholar] [CrossRef] [PubMed]
- Doi, M. Soft Matter Physics; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Methods in Fluid Dynamics; Springer: New York, NY, USA, 1993. [Google Scholar]
- Zhu, J.; Chen, L.-Q.; Shen, J.; Tikare, V. Coarsening kinetics from a variable-mobility Cahn–Hilliard equation: Application of a semi-implicit Fourier spectral method. Phys. Rev. E 1999, 4, 3564–3572. [Google Scholar] [CrossRef]
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Dehaoui, A.; Issenmann, B.; Caupin, F. Viscosity of deeply supercooled water and its coupling to molecular diffusion. Proc. Natl. Acad. Sci. USA 2015, 112, 12020–12025. [Google Scholar] [CrossRef] [PubMed]
- Swindells, J.F.; Snyder, C.F.; Hardy, B.C.; Golden, P.E. Viscosities of sucrose solutions at various temperatures: Tables of recalculated values. NBS Circ. 1958, 440, 1–7. [Google Scholar]
- Young, F.E.; Jones, F.T. Sucrose Hydrates. The sucrose-water phase diagram. J. Phys. Chem. 1949, 53, 1334–1350. [Google Scholar] [CrossRef]

| Parameters/Characteristic Times/Reference Properties | Value, SI |
|---|---|
| length scale L | m |
| computational domain | |
| interfacial thickness | m |
| reference freezing temperature | 273.15 K |
| characteristic subcooled temperature | 10 K |
| energy barrier coefficient | 0.1456 J/(kg·K) |
| Flory’s parameters , | 2.5, 0.5 |
| solute-to-water ratio of molar volume N | ∼11.5 |
| scaled time step h | |
| latent heat | J/kg |
| interfacial energy | 0.0375 J/m2 |
| cooling rate | 100 K/s |
| initial temperature | 263.15 K |
| characteristic phase transition time | 0.4762 s |
| mass diffusion time | 0.4762 s |
| convective time | 0.4762 s |
| freezing time | 0.1 s |
| thermal diffusion time | s |
| viscous diffusion time | s |
| density | 999.8 |
| specific heat | 2110 |
| thermal conductivity | 2.14 |
| solute diffusivity | |
| dynamic viscosity |
| Dimensionless Groups | Value |
|---|---|
| Peclet number | 1.0 |
| Reynolds number | |
| phase-change number | 312.88 |
| Cahn–Hilliard number | 0.1 |
| interfacial Lewis number | 4830.6 |
| Stefan number | 0.0621 |
| Stefan number | 0.0136 |
| uniform cooling rate | 4.762 |
| Schmidt number | 8620.8 |
| local Grashof number | 25.92 () |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, T.-H.; Li, J.-Q.; Minatovicz, B.; Soha, E.; Sun, L.; Patel, S.; Chaudhuri, B.; Bogner, R. Phase-Field Modeling of Freeze Concentration of Protein Solutions. Polymers 2019, 11, 10. https://doi.org/10.3390/polym11010010
Fan T-H, Li J-Q, Minatovicz B, Soha E, Sun L, Patel S, Chaudhuri B, Bogner R. Phase-Field Modeling of Freeze Concentration of Protein Solutions. Polymers. 2019; 11(1):10. https://doi.org/10.3390/polym11010010
Chicago/Turabian StyleFan, Tai-Hsi, Ji-Qin Li, Bruna Minatovicz, Elizabeth Soha, Li Sun, Sajal Patel, Bodhisattwa Chaudhuri, and Robin Bogner. 2019. "Phase-Field Modeling of Freeze Concentration of Protein Solutions" Polymers 11, no. 1: 10. https://doi.org/10.3390/polym11010010
APA StyleFan, T.-H., Li, J.-Q., Minatovicz, B., Soha, E., Sun, L., Patel, S., Chaudhuri, B., & Bogner, R. (2019). Phase-Field Modeling of Freeze Concentration of Protein Solutions. Polymers, 11(1), 10. https://doi.org/10.3390/polym11010010





