1. Introduction
Our living and working environment has been gradually perplexed by noise pollution due to the rapid developments of modern industries and transportations. Vehicle noise is a major source of noise pollution, which consists of interior noise and exterior noise. Recently, vehicle interior noise is becoming one of the important indices for quality evaluation of vehicles because it not only imposes danger on drivers and passengers’ health, but also decreases the comfort of driving [
1,
2]. Therefore, with the development of social transportation, eliminating vehicle interior noise has involved current and broad interests of automobile manufacturers. The use of acoustic package is an effective method to reduce vehicle interior noise. Thus, the acoustic package design of automotive has become an important research for the automobile industry.
There are mainly two kinds of acoustic package materials: sound absorption materials and sound insulation materials. Sound insulation materials have a high surface density and can reflect sound energy to the incident direction. However, the sound absorption materials are light and have a high porosity, which makes the acoustic wave easily accessible to the interior of the materials [
3]. It means that the sound absorption ability and sound insulation ability of acoustic package materials are hard to get the maximum value simultaneously. Polyurethane (PU) foam is a kind of effective sound absorption material in automobile industry due to the effective sound damping and low-density characteristics. It has been widely applied in interior components, such as seats, inner dash mats, and other acoustic trim parts. The acoustic wave propagation in PU foams mainly dissipates as viscous friction on interconnected pores and thermal heat exchange on solid-fluid boundary [
4]. However, pure PU foam only shows great sound absorption ability in high frequency region due to the special pore morphologies. Previous studies have shown that the acoustic performances of PU foams can be modified by adding functional particles to PU foams or adjusting the chemical compositions of PU foams [
5,
6,
7,
8,
9,
10,
11]. However, it not only cannot get the optimum acoustic performances, but also cause the waste of materials, if the materials are simply mixed together. Thus, this paper improves the acoustic performances of PU foam composites by optimizing the synthetic formula.
Recently, many researchers put their efforts to improve the acoustic performances of acoustic package materials by different optimization methods. Jeon et al. [
12] used particle swarm optimization (PSO) algorithm for optimal bending design of vibrating plate to minimize noise radiation. Chen et al. [
13] applied the grey rational analysis (GRA) with Taguchi method to optimize the acoustic performances of the sound package. Jiang et al. [
14] employed the Taguchi method base on orthogonal arrays to conduct the experiments to improve the acoustic behaviors of PU foams. He et al. [
15] utilized the GRA method and multi-objective particle swarm optimization (MOPSO) algorithm to optimize the acoustic package materials of firewall and floor. Pan et al. [
16] dealt with the optimization of the sound package by using a genetic algorithm to satisfy acoustical targets and packaging requirements in the vehicle design process. Grubeša et al. [
17] applied the genetic algorithm to optimize the acoustic performances and economic feasibility of barrier cross section. The materials and cross section shapes of the barrier are considered in the optimization process. Kim et al. [
18] applied acoustic topology optimization for sound barrier with rigid and porous materials by the finite element method. Considering the sound absorption ability and sound insulation ability are equally important to reduce vehicle interior noise. Both of them should be simultaneously maximized, which is a multi-objective optimization problem inherently. Therefore, this paper applies multi-objective optimization method to optimize the synthetic formula of PU foam composites.
The MOPSO algorithm is one of the evolutionary algorithms that based on the social behavior of flocks of birds that adjust their movement to find the best food position. It has been widely and prevalently applied to solve engineering problems in different fields due to the advantages of relatively fast convergence and good handle continuous, discrete, and integer variables types [
19,
20,
21]. Normally, the analysis models of the acoustic performances of acoustic package materials are complicated, and the normal optimization processes are of extremely low optimization efficiency. In contrast, the surrogate models are more efficient and they can easily bridge the gap among multi-objective optimization. Therefore, it has been widely applied in multi-objective optimization design [
21]. On the other hand, GRA method is a branch of grey system theory, which can be effectively used to analyze the complicated interrelationship among the designated performance characteristics. By combing the entire range of performance criterion values into a quantified value of grey relational grade (GRG). It can be used to identify the major influencing factor and the dominant or subordinate relationship from various factors of multi criteria problems [
22,
23,
24,
25,
26]. Therefore, both the GRA method and MOPSO algorithm are applied in this paper to optimize the formulation of PU foam composites for good acoustic performances. The optimization process of MOPSO algorithm is based on the surrogate model, and the optimization process of GRA method is based on the orthogonal arrays.
A previous study shows that the acoustic performances of PU foam composites are changed when filled with Ethylene Propylene Diene Monomer (EPDM) of different content and hardness. Meanwhile, in the synthesis process of PU foam, modified isocyanate (MDI) is a matrix material and deionized water is used as blowing agent. Both have an impact on the acoustic performances by changing the pore morphologies and the density of PU foams. Moreover, the acoustic performances of PU foam composites can be evaluated by the sound absorption coefficient and sound transmission loss. Therefore, the sound absorption coefficient and sound transmission loss of PU foam composites are investigated in this paper by changing the content of MDI and deionized water, the content and hardness of EPDM. The aim of this paper is to obtain a synthetic formula of a PU foam composite with high sound absorption ability and sound insulation ability under the condition that the sound absorption ability and sound insulation ability are equally important for reducing vehicle interior noise. Therefore, this paper uses the GRA method and MOPSO algorithm to optimize the synthetic formula of PU foam composites, and then the actual samples are prepared according to the optimization results for comparison to determine the optimal synthetic formula. Meanwhile, synthetic formula optimization can improve the utilization rate of PU foam composites preparation materials and reduce environmental pollution that is caused by waste EPDM.
4. Verification
Once the optimal formulation of the PU foam composites is determined, it is important to verify whether the results of the optimization methods are appropriate. The optimum PU foams are not included in the prepared samples. Thus, the validation samples are prepared, according to the optimization results of the GRA method and MOPSO algorithm, respectively. Then, the transmission loss and sound absorption coefficient are measured. After that, the average transmission loss and average sound absorption coefficient are calculated.
Table 8 shows the results of simulation and actual experimental. The rows of “Experiment” and “Simulation” denote the actual experimental results and simulation results, respectively. The row of “Error” denotes the results deviation between the simulation and actual experiments.
It can be seen from
Table 8 that the simulation results of MOPSO algorithm are approximately the same as the experimental results. It indicates that MOPSO algorithm has higher accuracy than the GRA method to guarantee the effectiveness of the acoustic package design. According to the comparison, the optimum values for the content of EPDM and deionized water are different. Because the design variables are discrete values in the GRA method and are continuous values in the MOPSO algorithm. Referring to
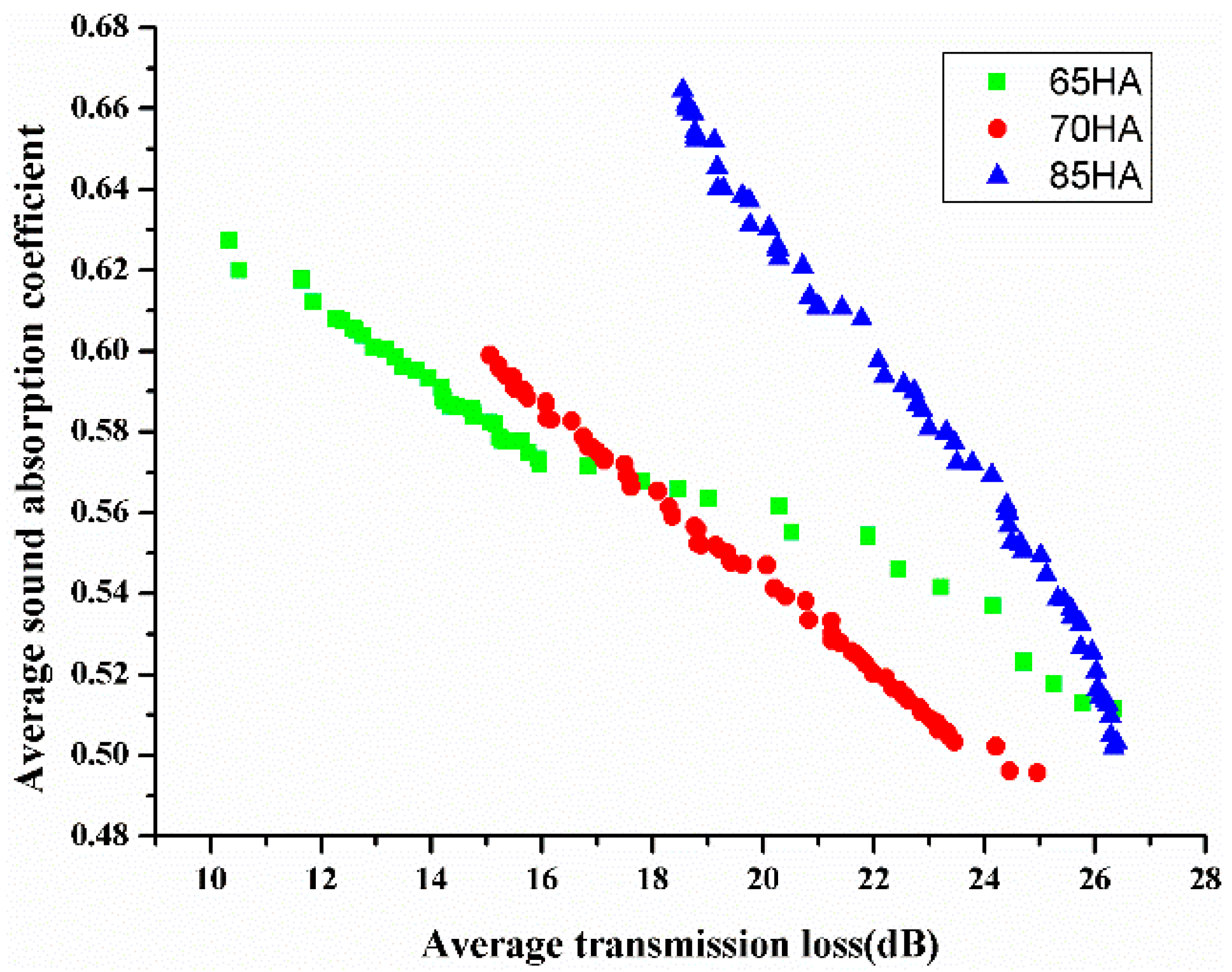
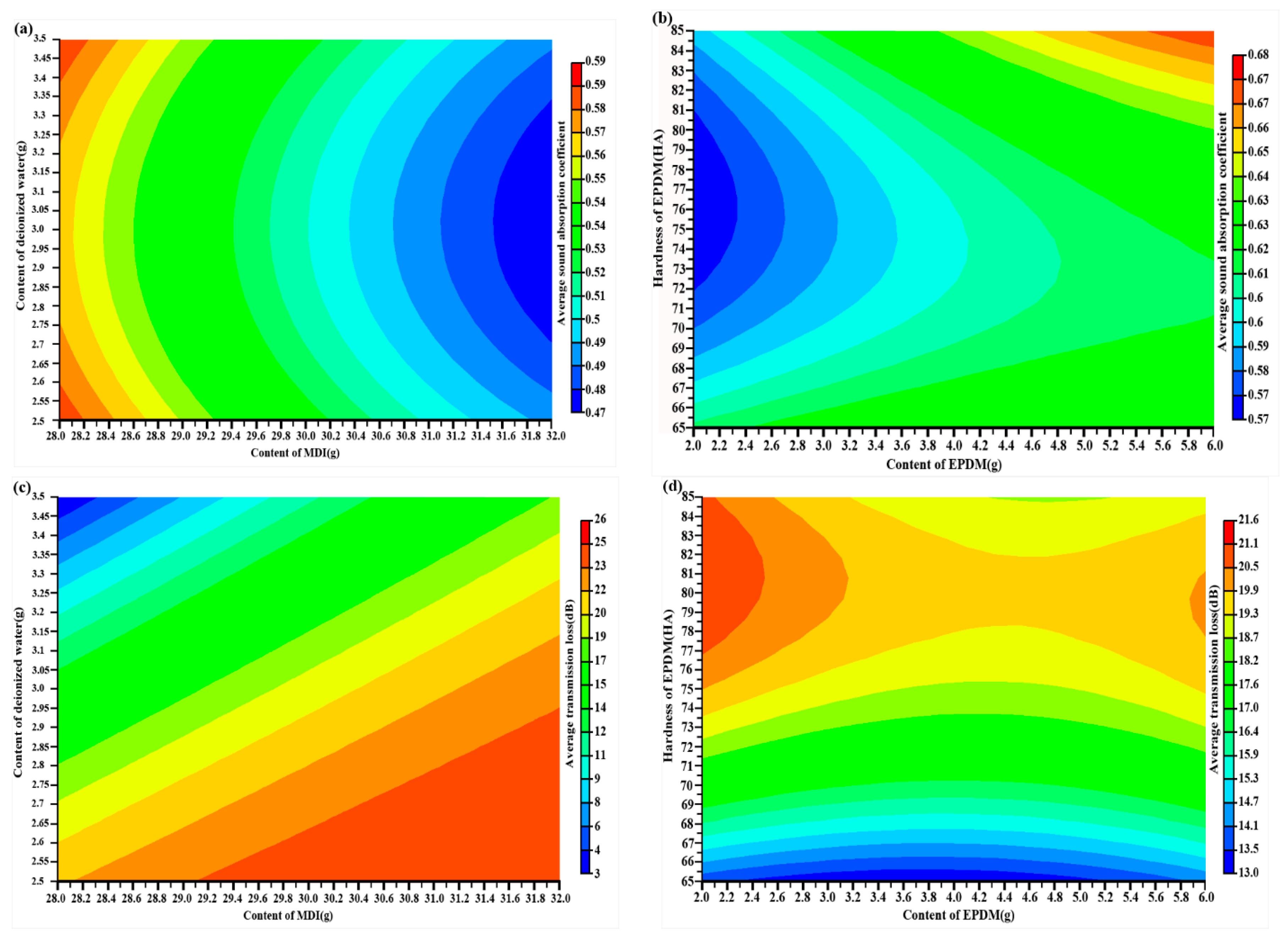
Figure 2, it can be seen that the differences in formulation are responsible for the GRA method having a better sound absorption coefficient and poorer transmission loss than the MOPSO algorithm.
In addition,
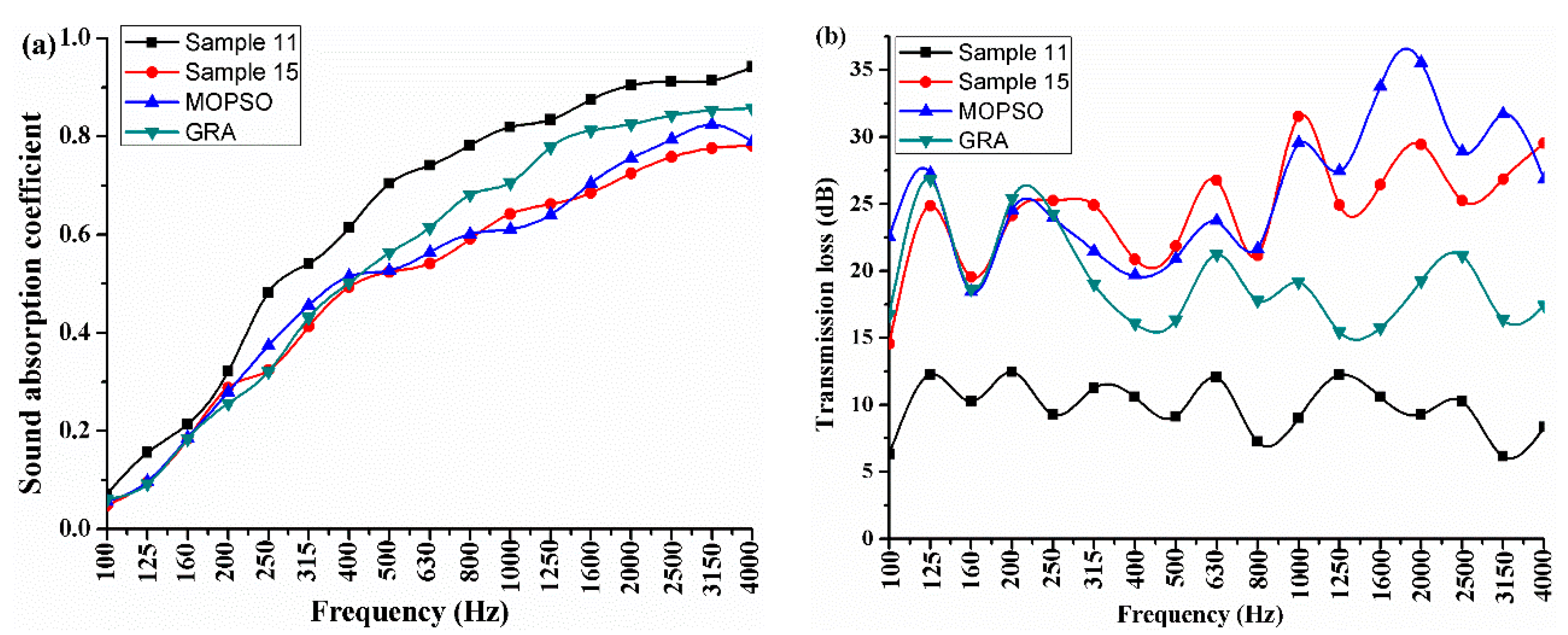
Figure 3 shows the acoustic performances curves of the optimized PU foam composites and two initial samples. In
Figure 3, “MOPSO” means the PU foam composite prepared according to the formulation that was obtained by the MOPSO algorithm, and “GRA” means the PU foam composite prepared according to the formulation as obtained by the GRA method. Sample 11 has the best average sound absorption coefficient and sample 15 has the best average sound transmission loss. The change trends of the sound absorption coefficient and transmission loss are similar. It can be seen from the results comparison between the MOPSO and sample 15, the average sound absorption coefficient of MOPSO is increased by 2.4% and the average transmission loss is increased by 4.86%. This is possibly due to the optimum values for the content of deionized water, the content and hardness of EPDM are different. However, the difference for the content of deionized water is smaller. Referring to
Figure 2, it can be found that the acoustic performances differences of PU foam composites are mainly affected by the content and hardness of EPDM. It agrees with the results that were obtained by GRA method. Moreover, it can be seen that the GRA sample shows better sound absorption coefficient than the MOPSO sample, and the deviation of the sound absorption coefficient of the two samples increase with an increasing frequency. However, the transmission loss of the two samples appears the opposite trend. As shown in
Figure 2, 2 g EPDM and 3.5 g deionized water are advantageous for improving the sound absorption ability, and 5.8 g EPDM and 3.4 g deionized water are good for improving the sound insulation ability. In this paper, in order to find the compromise values for these conflicting objectives, the weight coefficient of the two objectives is set as 0.5. Therefore, the optimum formulation of PU foam composites is obtained by the MOPSO algorithm. The optimum values of the four design variables are MDI of 32 g, deionized water of 3.4 g, EPDM of 5.8 g, and the hardness of EPDM is 65 HA.
5. Conclusions
In this paper, both GRA method and MOPSO algorithm are used to optimize the synthetic formula of PU foam composites to improve the acoustic performances. The average sound absorption coefficient and average transmission loss are selected as the optimization objectives. The content of MDI and deionized water, the content and hardness of EPDM are selected as design variables. The optimization process of GRA method is based on the orthogonal arrays , and the optimization process of MOPSO algorithm is based on the surrogate model. According to the fitting accuracy comparison, the RS surrogate model is adopted in this paper to express the relation between the optimization objectives and design variables. The results show that the acoustic performances of PU foam composites can be improved by optimizing the formulation of PU foam composites. Meanwhile, the results that were obtained by GRA method show the degree of influence of the four design variables on the optimization objectives. The major influence factor on acoustic performances is the content of EPDM, and the hardness of EPDM has the least influence. The results that were obtained by MOPSO algorithm show the specific effects of the design variables on optimization objectives. However, since the GRA method is usually used to search the optimal solution in discrete spaces, it cannot guarantee the solution is globally optimal solution. Therefore, the optimal results that were obtained by the two optimization methods are different. In this paper, the weight coefficient of the optimization objectives is set as 0.5. By confirmation test, the optimum formulation of PU foam composites is obtained by the MOPSO algorithm. The optimal parameters of the four design variables are MDI of 32 g, deionized water of 3.4 g, EPDM of 5.8 g, and the hardness of EPDM is 65 HA. Certainly, the weight coefficients of the sound absorption ability and sound insulation ability can be set as various values in the range of 0 to 1 to meet different operating conditions requirements.