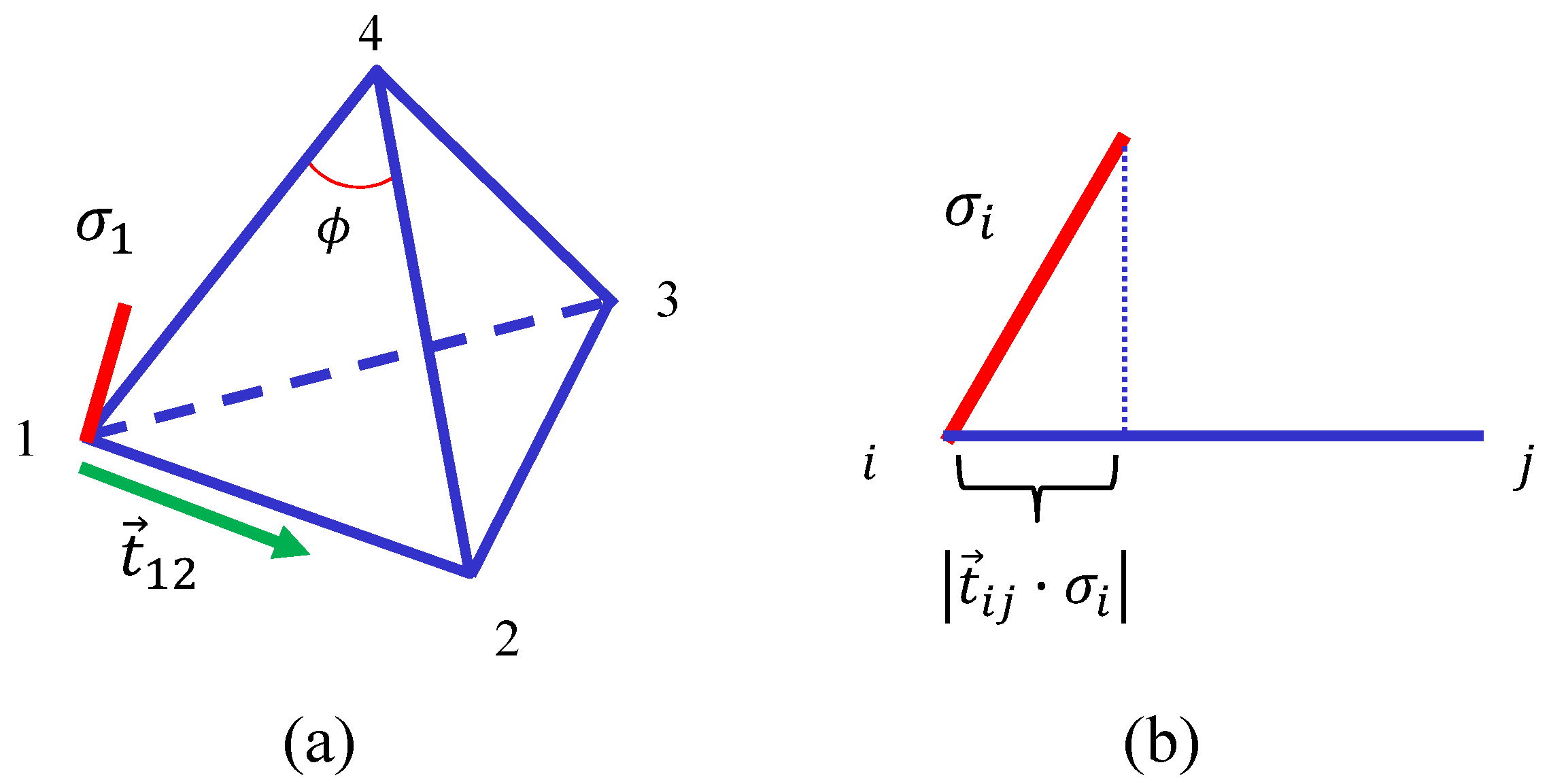1. Introduction
Liquid crystal elastomer (LCE) is a material in which LC molecules are chemically bonded to polymers, and its most remarkable property is that the anisotropy in the direction of nematic ordering of the LC molecules is reflected in the macroscopic shape [
1,
2,
3,
4,
5]. Photoinduced bending of liquid-crystalline gel, which includes azobenzen monomers, shares the same mechanism [
6,
7]. In other words, the macroscopic shape of the LCE is sensitive to the microscopic orientation of the LCs and vice versa. Indeed, LCE elongates into a spontaneously chosen direction at low temperature if no constraint is imposed on the LC molecules, while at high temperatures, the elongation is suppressed due to the phase change from nematic to isotropic. External fields such as electric field and mechanical stresses also elongate the LCEs, and these field-driven elongations have been studied intensively [
8,
9,
10,
11,
12].
Because of these interesting properties, a great deal of attention has been paid to LCEs, and studies of their technological applications, such as artificial muscles, have been conducted [
13,
14,
15]. A polymer-dispersed LCE has recently been proposed as a functional and shape-programmable material for additive manufacturing [
16]. A cellulose liquid crystal motor has also been proposed [
17]. In the statistical mechanical studies of LCEs, the variable
for directors and strains are introduced, and the obtained results successfully describe the experimental data [
2,
3,
4,
5]. However, the strains themselves are not always identical to the LCE shape, so the position vector is better or more straightforward for the analyses of material shape such as polymers [
18,
19].
In Refs. [
20,
21], the interaction between the LC molecules and polymers is coarse-grained and implemented in the 3D Finsler geometry (FG) model, and the elongation phenomenon is successfully explained. The soft elasticity, in which the stress-strain diagram includes a plateau, is also reproduced by the FG model. This soft elasticity arises because the director orientation and the shape of material interact with each other. The so-called J-shaped stress-strain diagrams of soft biological tissues such as animal skin and muscles are also reproduced by the 2D FG model [
22]. In the FG models for the soft-elasticity and J-shaped diagram, we discard the detailed information of the interaction between the LCs and polymers, and instead, we modify the underlying geometry such that the internal metric function of the materials is changed from Euclidean to Finsler. In this sense, the interaction is determined in a more basic and constructive manner from the geometries inside the material and the space
. As a result of this procedure, the interaction between the direction
of the directors and the position
of the polymers is automatically introduced in the model. This is in sharp contrast to the ordinary modeling techniques, in which an interaction energy is explicitly introduced in the Hamiltonian. Therefore, this FG modeling technique is completely new and should hence be checked thoroughly by application it to a variety of experimentally observed phenomena.
In this paper, we apply the 3D FG model to the interesting experimental observation that a thin and small LCE disk moves on the water due to light irradiation [
1]. This phenomenon has attracted a great deal of attention in engineering applications because it is considered a model for a micro robot actuated by a non-mechanical stimulus [
6,
7,
17]. The driving force that moves the disk on the water comes from the shape change. By moving a spot irradiated by light from the center to the radial direction on the disk surface, the position of the bending on the edge of the disk can be controlled. This shape change at the edge moves in the same direction as the spot; at the same time, the water is pushed in the same direction that the bending edge moves, and then, by the action-reaction principle, the disk moves back or swims in the opposite direction on the water. We expect that such a shape change can be studied by using the FG model because the position variable
is directly included as a variable. Therefore, it is worthwhile to study whether the experimentally reported shape change of the disk is consistent with the results of the 3D FG model.
We should comment that the FG modeling technique can also be applied to a deformation of LCE piece in more general situation even for composite materials such as polymer-dispersed LCE [
16]. Such an applicability of FG model is naturally expected because the deformation of the variable
is automatically determined from the variable
, and the deformation of
is independent of the reason for distorting
because of the implemented interaction between
and
.
2. Reported Experiment
We describe the experiment reported in Ref. [
1] and summarize the current understanding of the shape deformation by light irradiation. A dye-doped nematic LCE is used in the experiment; the disk size is 5 mm in diameter and 0.32 mm thick, so the ratio
of thickness
H and diameter
D is approximately
. This small piece of LCE floats nearly motionless on the surface of a water reservoir, which has a depth of 2 cm. The direction of the nematic director, which is the constituent LC molecule, is parallel to the surface.
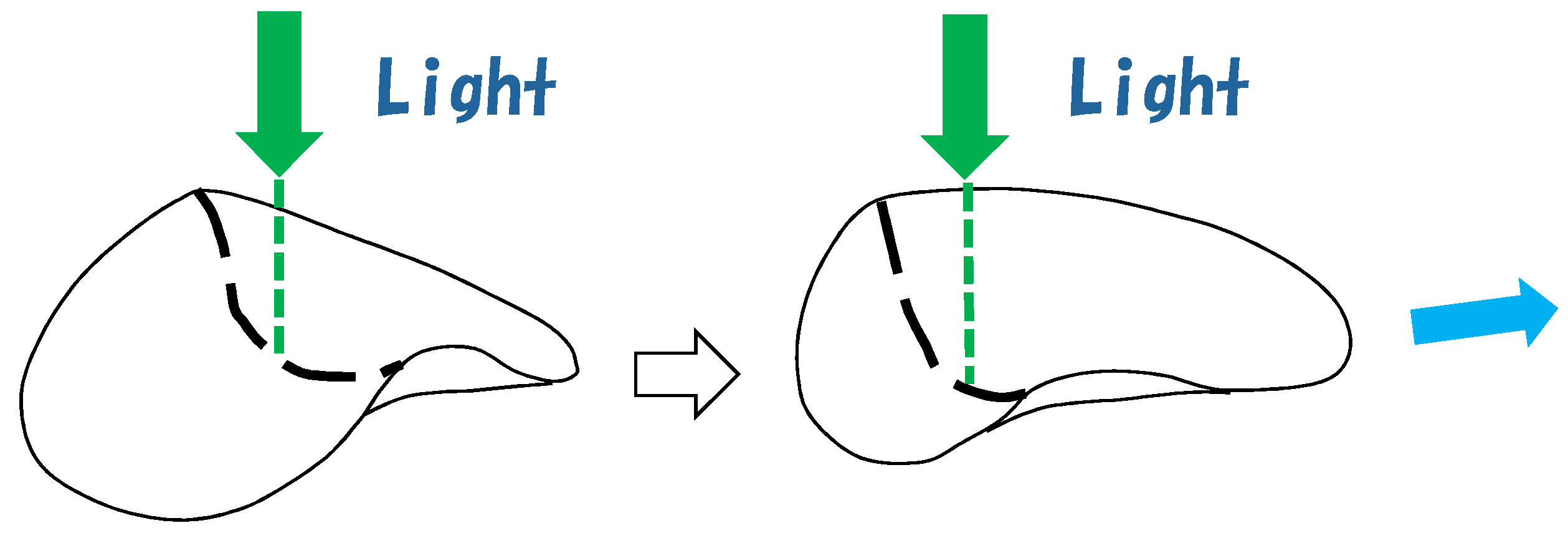
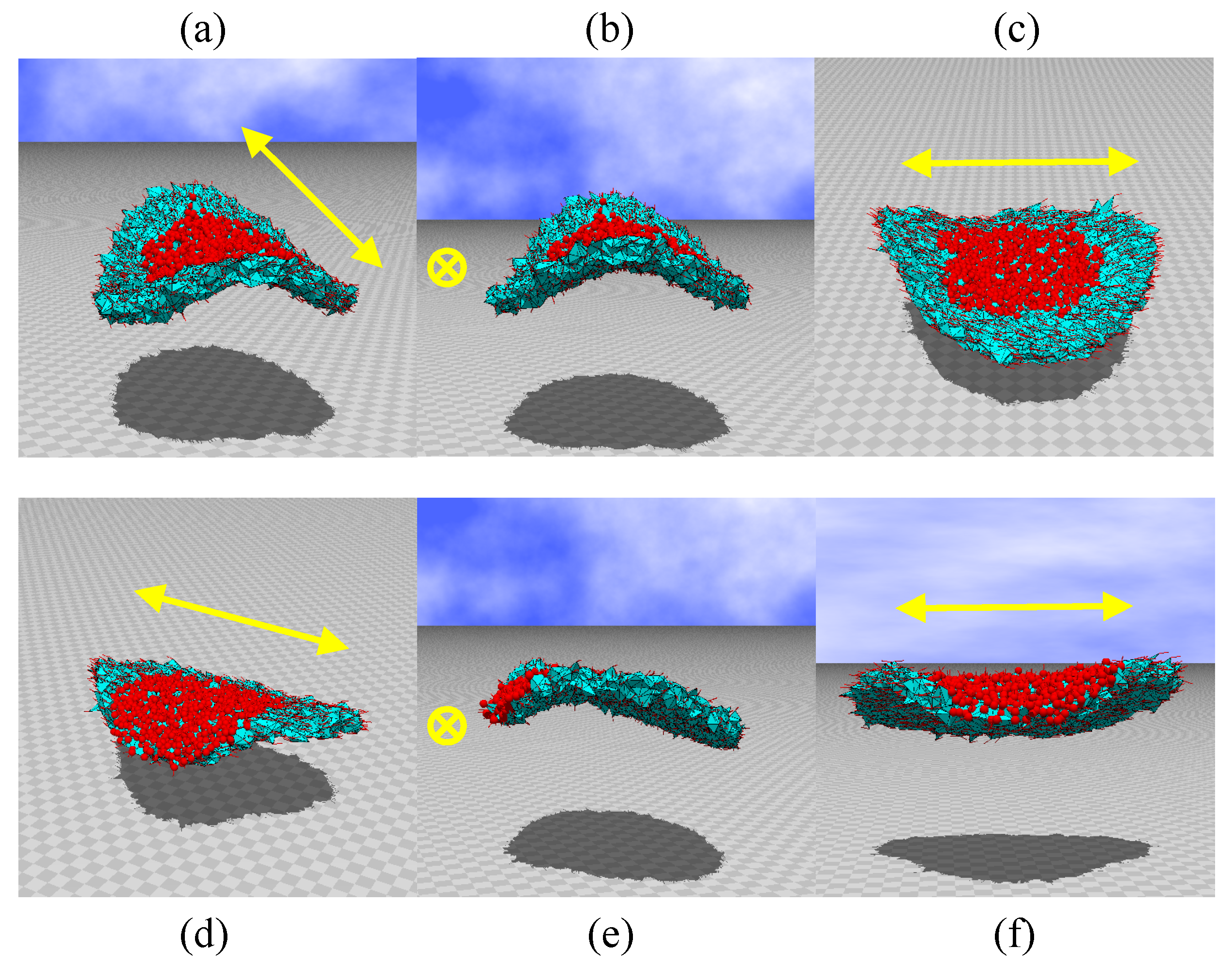
This LCE sample is illuminated from above by an argon-ion laser with a beam width of 3 mm. The light spot is located on the center of the disk in the beginning and is then moved toward an edge along the direction perpendicular to the LC alignment direction. Then, the sample moves opposite to the direction in which the light spot moves (see
Figure 1).
The authors of Ref. [
1] discussed why the LCE sample moves on the water surface. One possible reason that they suggested was the shape deformation, as shown in
Figure 1. A part of sample edge is lifted and strongly deformed compared to the other part of the edge, and this deformed position moves with the movement of the light spot. This deformed edge pushes water in the same direction as the light movement, and by the action-reaction principle, the LCE sample moves in the opposite direction. This is a rough outline of the mechanism of the swimming mentioned in the Introduction.
The effect of light on the dye-doped nematic LCE samples is also discussed in Ref. [
1]. Based on these discussions, there are two possible effects: the first is dye-mediated heating due to the light absorption, with the increase in temperature causing a transition from the nematic ordered phase to the disordered or isotropic phase. The second also reduces the orientation order due to the effect of the photoisomerization of the dissolved dye. The dye-doped LC molecules play the role of an impurity if they change from the trans state to the cis state via irradiation. These two effects are expected to reduce the orientation ordering of directors, and this change in the director orientation leads to a shape change. We should note that these two effects have been throughly investigated and are now well understood [
23,
24,
25,
26,
27,
28].
However, it is unclear why a change in the orientation order causes shape deformation. This is actually very difficult to study from the microscopic perspective because the interaction between the LCs and polymers is unclear. Here, “unclear” means that the corresponding Hamiltonian in the statistical mechanical models remains unknown because the polymer position
is not directly used. One of the reasons for the lack of a Hamiltonian that includes
is that the interaction is very difficult to assume due to the hierarchical structure of polymer, which is composed of monomers and forms a crystalline/non-crystalline structure, with these structures also forming domains. All of these hierarchical structures are connected to the shape deformation; for this reason, a simple interaction energy is not expected as the Hamiltonian [
29,
30,
31].
3. 3D FG Model of LCE
To understand why a dye-doped nematic LCE deforms under light illumination, we employ a model that is completely different from the models utilized in previous statistical mechanical studies of materials, as mentioned in the Introduction. The model in this paper is an FG model and is identical to the model used in Ref. [
21]; however, we describe the model for the readers’ convenience.
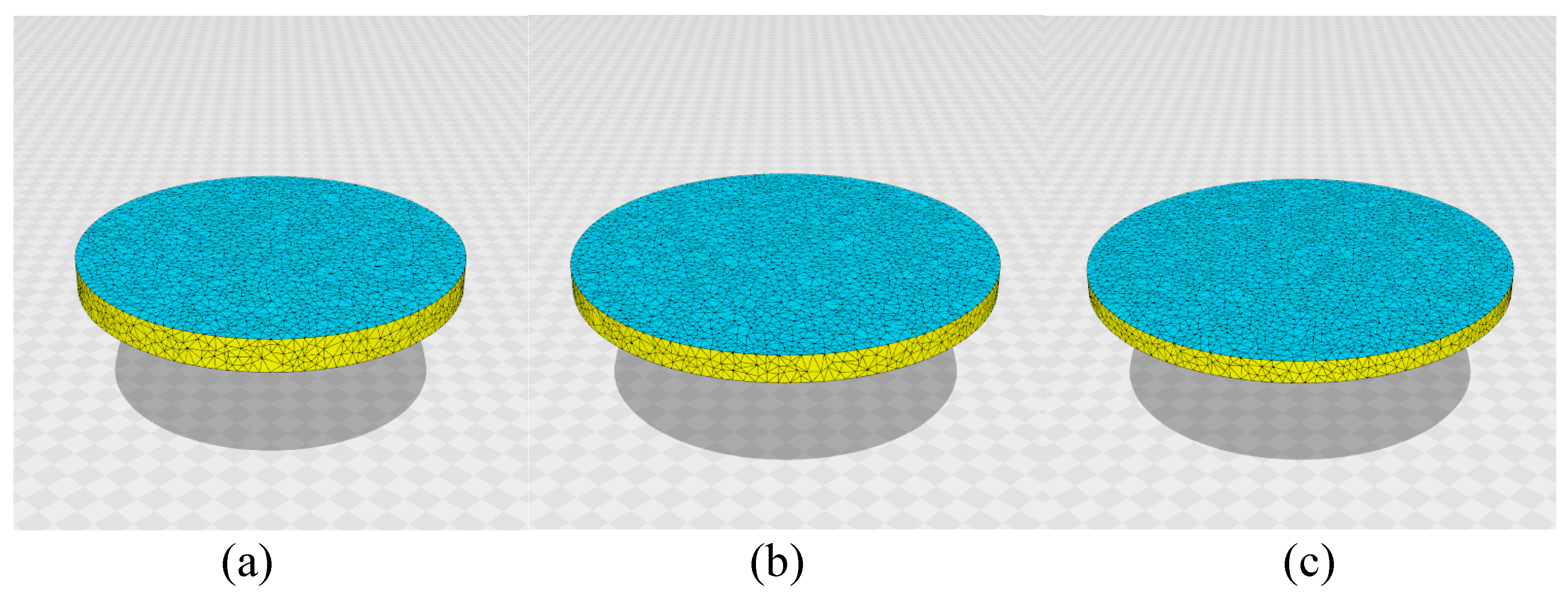
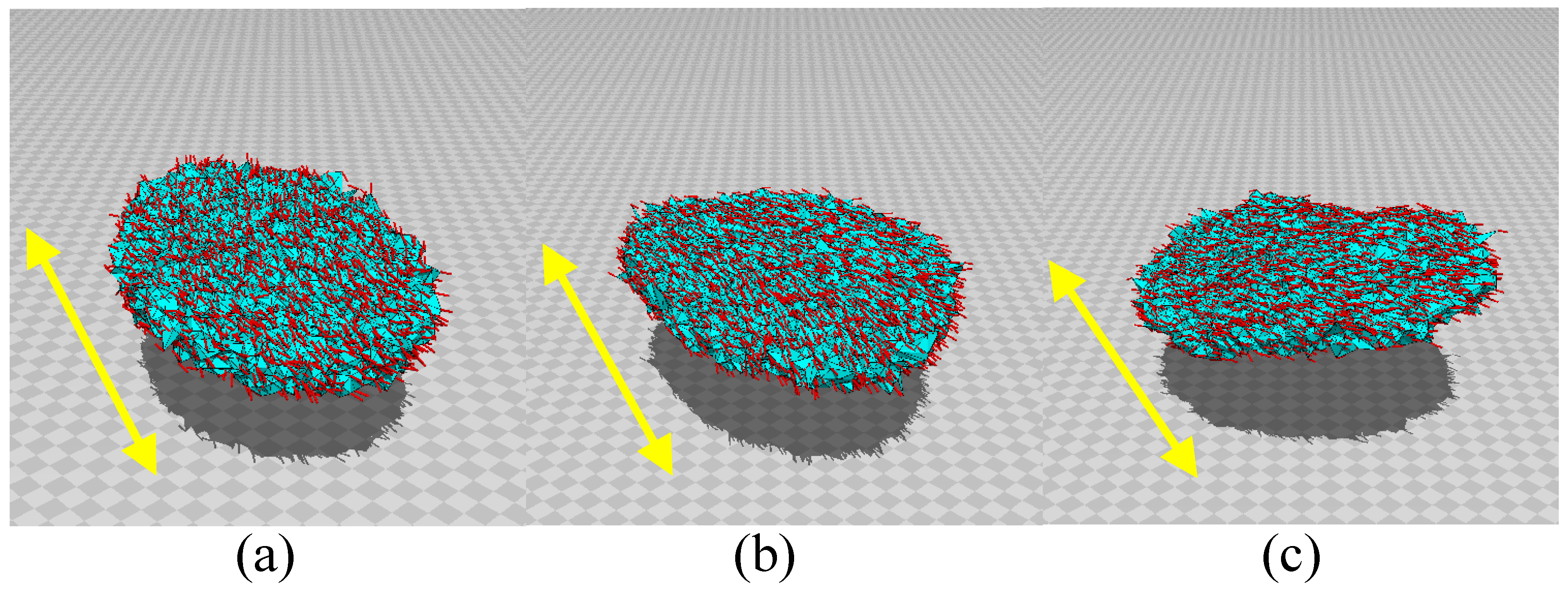
First, the 3D lattices for the simulations are shown in
Figure 2a–c. For the LCE sample in the experiment, the ratio
of height
H and diameter
D is
, as mentioned in the previous section. Thus, we use three different lattices of
,
, and
, as shown in
Figure 2a–c.
We show the data for the lattices, including the lattice of
10,346,
, in
Table 1. The size of the lattice is given by
, where
N,
,
, and
are the total numbers of vertices, edges (or bonds), triangles, and tetrahedrons, respectively. The Euler numbers
of these lattices are identical to those of a tetrahedron, which is characterized by
, because the cylinders are topologically identical to a tetrahedron. The symbols
denote the total number of vertices on the upper and lower surfaces, respectively, and
and
respectively denote the total number of bonds and the total number of triangles on these two-dimensional surfaces. These data also satisfy
because a disk is topologically identical to a sphere with a hole, e.g., a triangle.
To describe the model, we start with the continuous Gaussian bond potential such that
where
is a material position,
is a local coordinate inside the material,
g is the determinant of the Finsler metric
, which is a
matrix, and
is the inverse of
. This continuous
is discretized on 3D lattices such as those in
Figure 2a–c, which are composed of tetrahedra. Please note that this
depends not only on
but also on
, which is a director field corresponding to the directional degrees of freedom of the LC molecule. The dependence of
on
comes from the fact that
depends on
. Note also that this
is a 3D extension of 2D
, which is a model for the membranes [
32,
33,
34,
35,
36,
37,
38], and 2D
is an extension of the 1D model for polymers [
39]. Therefore, this type of Gaussian potential
in Equation (
1) is of fundamental importance in the studies of polymers.
To evaluate the dependence of
on
, we write the discrete 3D Finsler metric
which is obtained by replacing the element 1 of Euclidean metric
with
. This Finsler metric is defined on the tetrahedron in
Figure 3a, where the local coordinate origin is at the vertex 1. In this
,
is given by
where
is the unit tangential vector from the vertex
i to
j (
Figure 3b). This
corresponds to the unit of the Finsler length [
20,
40,
41,
42], and it depends on
; hence,
depends on
. We should note that
in
plays the role of a cut-off because
is divergent if
is vertical to
. We fix
to
in this paper.
A discrete version of
is obtained by replacing the differentials
with differences such as
and the integral
with the sum
. Including several terms, we have the Hamiltonian
such that
This Hamiltonian does not include the energy term for the light irradiation. A detailed description of how to treat this important term is provided in the next section. Here, we describe the terms included in the basic Hamiltonian in more detail.
The first term
is the Lebwohl-Lasher potential, which is always assumed for the nematic transition of LC molecules [
43]. Because of this non-polar interaction of
in
,
is identified as
, and
(
) is expected for sufficiently large (small)
.
The second term is a discrete version of the continuous
in Equation (
1). In the discrete
,
is given by
where
denotes the total number of tetrahedra sharing the bond
, and
is the total number of bonds. The symbol
in
denotes the sum over all bonds
, “tet” in
denotes all tetrahedra connected to the bond
, and
for the tetrahedron in
Figure 3a are given by
We should note that and, hence, for all .
is an energy term that controls the stiffness of the material, and the coefficient
is the stiffness constant. In
,
denotes the sum of internal angles
i of all triangles, and
is the internal angle as shown in
Figure 3a. For sufficiently large
, all internal angles of triangles are expected to be
, and hence the shape of tetrahedra becomes regular. In contrast, for sufficiently small
, the tetrahedra can considerably deviate from the regular shape.
The term is the constraint potential for maintaining the positivity of each tetrahedron volume. The final term is also the constraint potential for maintaining a constant total volume, which is given by . This is determined from the model without . Details of this point are discussed in the next section.
The discrete partition function is given by
where
in
is written to highlight the constraint on the volume.
denotes the sum over all possible values of
, and
denotes the
-dimensional multiple integrations.
4. Monte Carlo Technique and Implementation of Light Irradiation Effect
The standard Metropolis technique is used to update the variables
and
[
44,
45]. A new variable
is accepted with the probability
, where
. The rate of acceptance of
is controlled to be approximately
by the radius
of the sphere containing the three-dimensional random vector
. On the other hand, a new value
is randomly determined on the unit sphere
using three different random numbers, and it is independent of the old value
. To be more precise, three different uniform random numbers
are generated with the constraint
. This constraint makes the point
uniform in the sphere of radius
. Then, the vector
is normalized such that
. Thus, the distribution of this unit vector
is expected to be uniform on the unit sphere.
We should note that
is invariant under
transformation, i.e., that
is degenerate, because of the non-polar interaction in
, as mentioned above. The rate of acceptance of
is uncontrollable and depends on the coefficient
of the energy
in Equation (
3). The total number of iterations called Monte Carlo sweeps (MCS), is typically
to
after
thermalization MCS.
We now describe how to implement “the light irradiation” in the model. As described in the Introduction and in
Section 2, the effect of light irradiation is to reduce the orientation ordering of
[
23,
24,
25,
26,
27,
28]. To focus on this effect, we should remind ourselves that the ordering of
can be controlled by the parameter
in the FG model. Indeed, for a sufficiently large
, the variables
align spontaneously into a single direction, and the system becomes nematic if no external force is applied; on the contrary, for a sufficiently small
,
becomes isotropic under the same conditions for the external forces. Another technique for the implementation of this effect is to introduce temperature into the model as
directly in the Boltzmann factor
in Equation (
6). However, this factor
changes all of the coefficients
,
and
to
,
and
, respectively, where
is the surface tension coefficient and is not included in
S of Equation (
3). If we assume a sufficiently high temperature such as
, then the new factors become
and
. However, this modification is expected to be too strong for the model because
can make the tetrahedron infinitely oblong under the constraint
. Therefore, it is better to use
to change the orientation of
.
The problem is how to modify
to implement the effect of light irradiation. Recalling that the interaction
in
is defined on the bond
, we find that one possible modification of the model is to change the first term
in
S of Equation (
3) as follows:
where the irradiated vertex
i or
j is on the upper surface of the disk. In this definition, the irradiation of bond
is represented by
on this bond. Indeed, it is easy to see that
for
(⇔ bond
is irradiated) is identical to
for
, which corresponds to the disordered phase of
, and that
is identical to
in the case of
(⇔ bond
is not irradiated). In
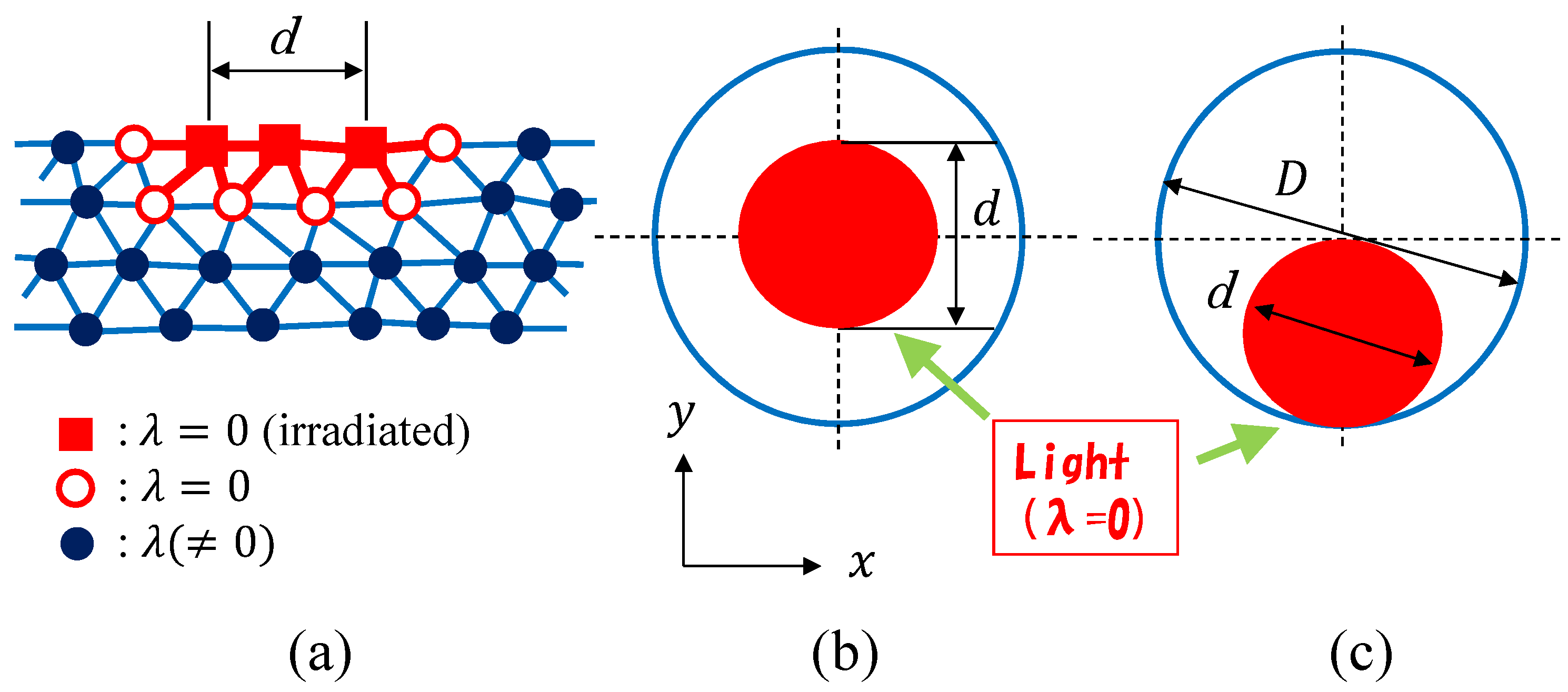
Figure 4a, we illustrate the irradiated (⇔ solid square symbol) and not irradiated (⇔ open and solid circles) vertices. The vertices inside the domain with diameter
d are irradiated. The vertices that are not irradiated are divided into two groups: one contains the vertices that are connected to the irradiated vertices (⇔ open circle), and the other contains the vertices that are not directly connected to the irradiated vertices (⇔ solid circle). The domains for light irradiation are shown in
Figure 4b,c, where the alignment of the nematic director is in the
x-direction.
If we consider
to be the temperature, the definition of the light irradiation in Equation (
7) can be rephrased as follows: the temperature is defined on the bonds through
in Equation (
7) such that
(
) corresponds to a high (low) temperature. This implies that only bond
, one of the vertices of
i and
j is irradiated at least, corresponds to the high temperature (see
Figure 4a) and that all of the remaining bonds correspond to the low temperature characterized by
. Please note that
is identical to
in Equation (
3) if
. Indeed, if
, then all vertices are not irradiated, and hence,
for all bonds
. To summarize, the introduction of
in Equation (
7) is equivalent to introduce a domain of disordered nematic directors.
We should note that the irradiated vertices inside the region of radius
d fluctuate around their original positions and remain irradiated, even when they move outside the region. This point that the irradiated vertices are fixed and independent of their positions is different from the experimental situation, where the irradiated position on the surface is not always identical to the positions of molecules, which also fluctuate thermally. However, our strategy is not so poor because in real LCE samples, the total number of irradiated LC molecules inside the irradiated region is sufficiently large compared to that of the boundary. The light intensity is not always uniform, and the intensity on the boundary is weaker than that of the center of light spot. For these reasons, the modeling for the light irradiation in the FG model in Equation (
7) is sufficiently simple and is considered a good approximation for the experiment.
We comment on how to obtain the constant volume
for the constraint
in Equation (
3). Here, we call the simulation with (without)
a
V-fix (
V-free) simulation. To obtain
, we perform
V-free simulations under the same parameters
and
as in the
V-fix simulations to be performed. In this
V-free simulation, the light is not irradiated (
) because the light irradiation does not change the volume of the sample LCE in the experiment [
1].
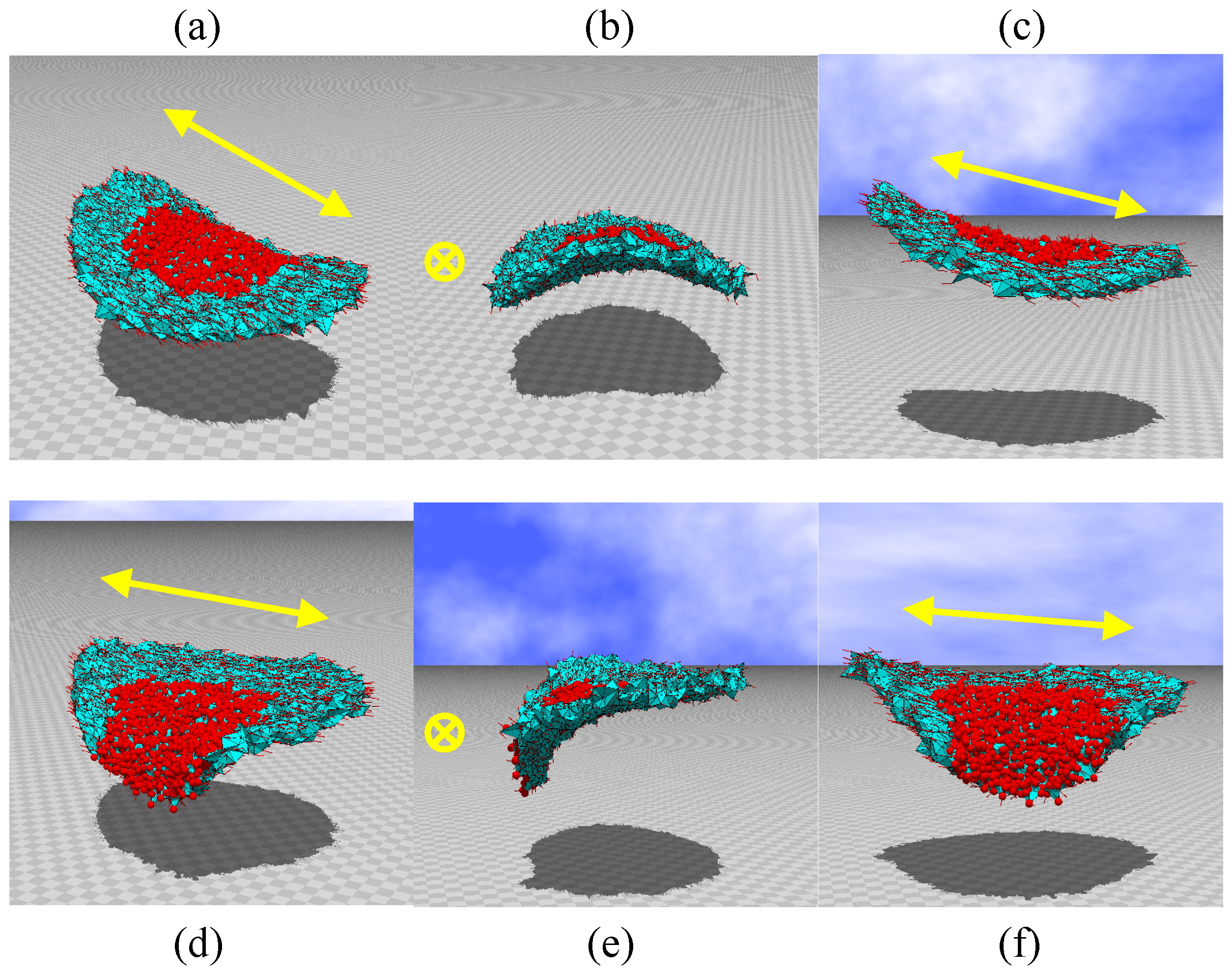
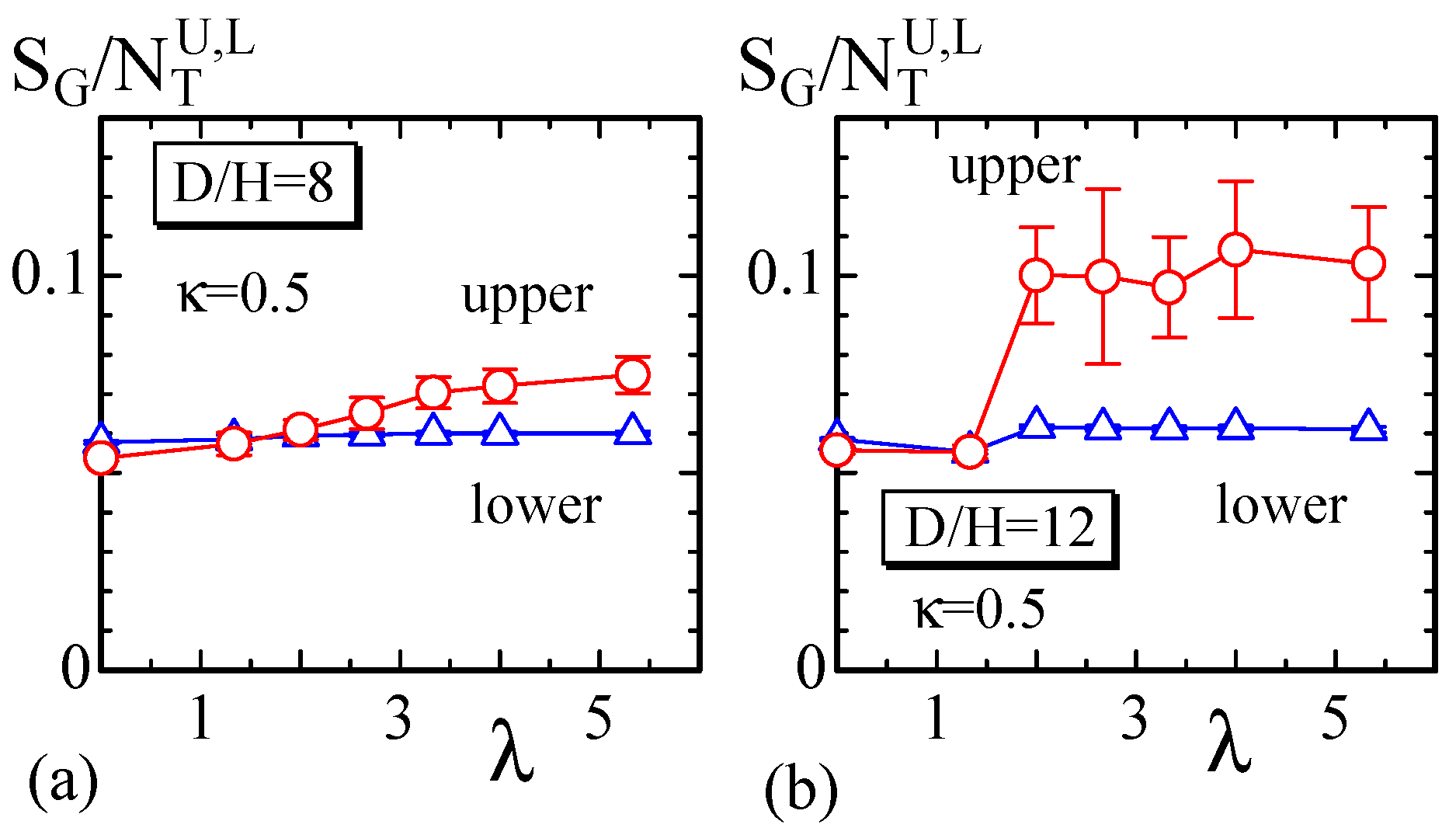
6. Summary and Conclusions
We used MC simulations to demonstrate that the Finsler geometry (FG) model successfully reproduces the experimental results of LCE shape deformation under light irradiation reported in [
1]. In the simulations, the irradiated region is given by a circle on the disk, and the center of the irradiated circle is located at the center of the disk and at the midpoint of the center and edge of the disk. For a sufficiently large
, which is the coefficient of Lebwohl-Lasher potential
, the bending shape of the disk is almost identical to the experimentally observed shapes reported in [
1].
For the FG model, the reason for the bending is simply understood as the orientation becoming disordered (⇔ isotropic) on the irradiated region but ordered (⇔ nematic) on the other parts of the LCE disk. This change in the orientation order of comes from the variation of . The role of is simply to make the orientation of ordered (disordered) if it is sufficiently large (small). On the other hand, in the FG model itself, the ordering of and the macroscopic shape are connected by the interaction between the direction of director and the position of polymer. This interaction is indirectly introduced by a modification of the intrinsic geometry of materials from Euclidian to Finsler. Using the interaction introduced by the FG model technique, we find that (i) the shape of disk is determined only by the change in the director orientation and (ii) the obtained results are consistent with the experimental observations.
We should emphasize that in FG modeling, it is not necessary to delve into the details of the temperature and photoisomerization effects. In this sense, the FG model is a coarse-grained model and, hence, can be applied to many phenomena that are not always elucidated from the microscopic perspective. There is no limitation on the size of sample to which FG modeling is applied, although the sample LCE size targeted in this paper is limited in the range of a few mm.