Flow Behavior of Chain and Star Polymers and Their Mixtures
Abstract
1. Introduction
2. Model and Simulation Method
3. Results and Discussion
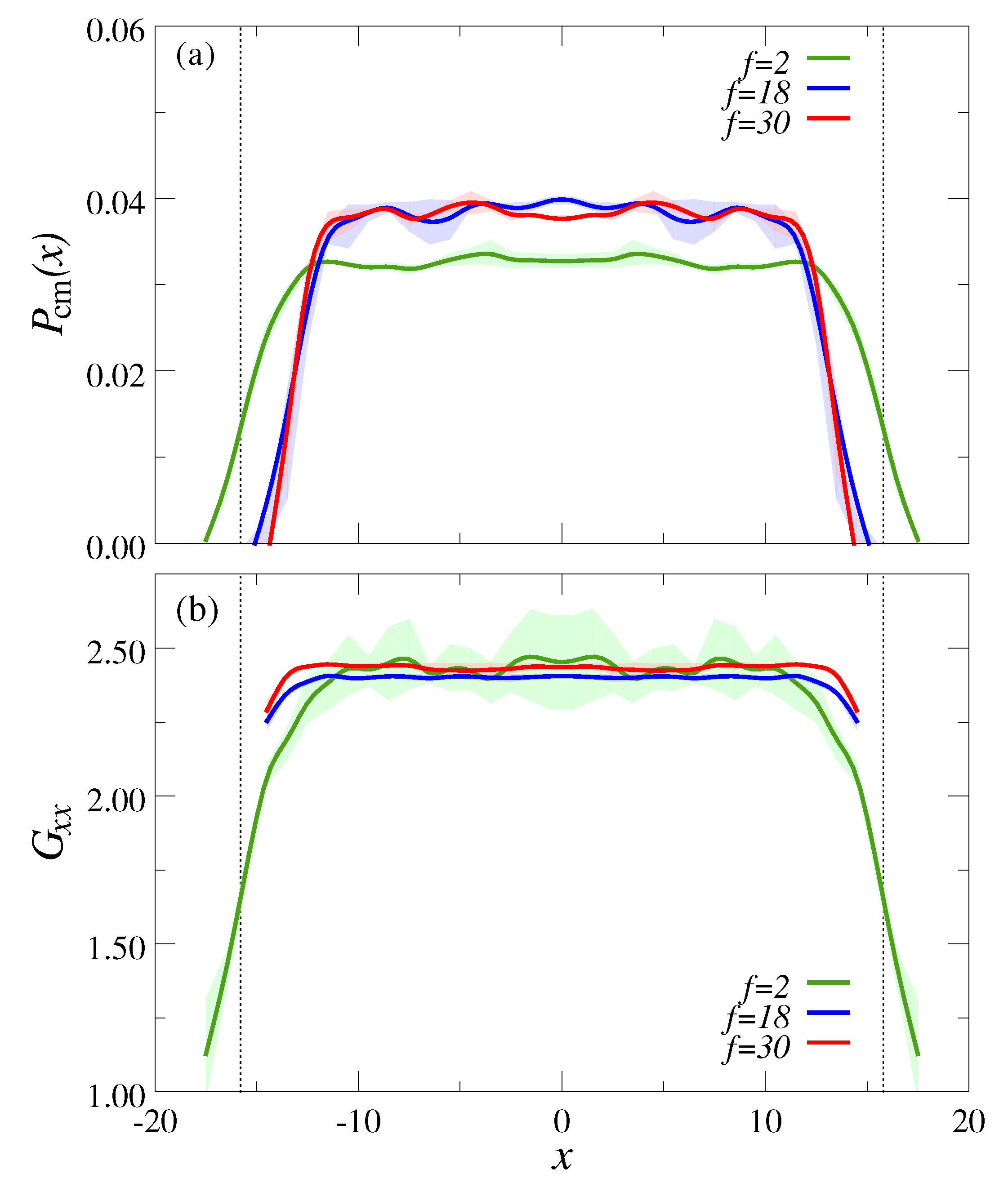
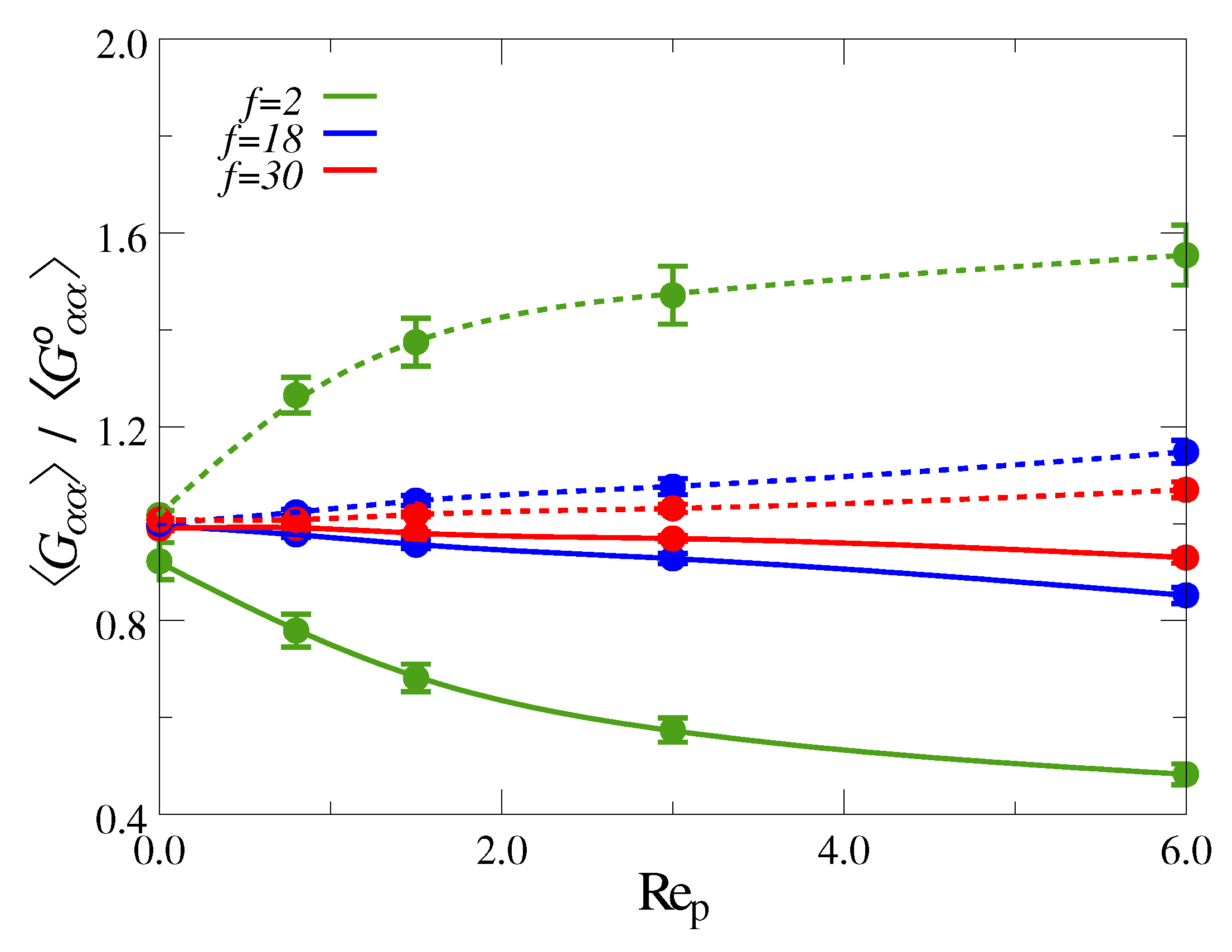
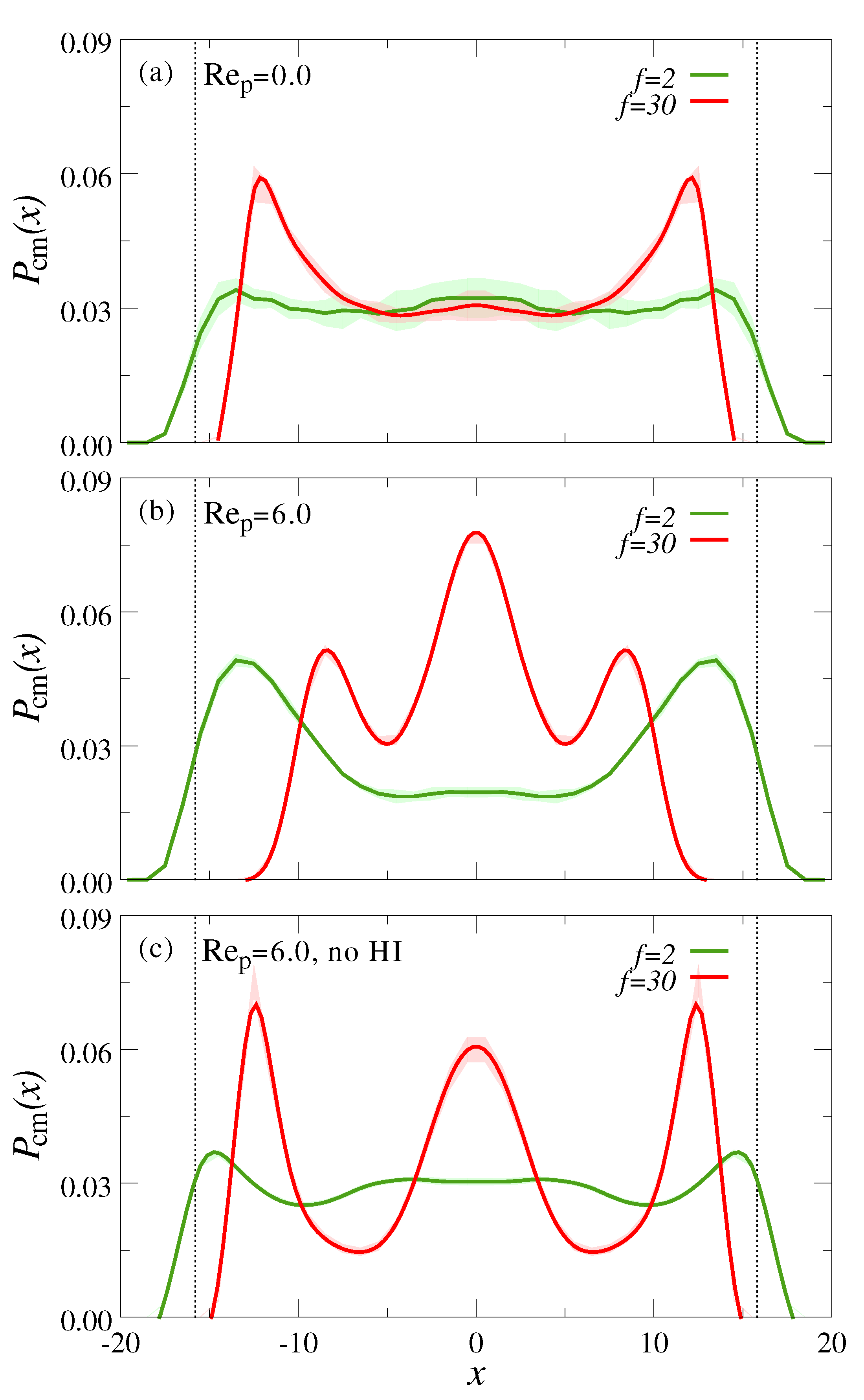
3.1. Ultradiulte Conditions
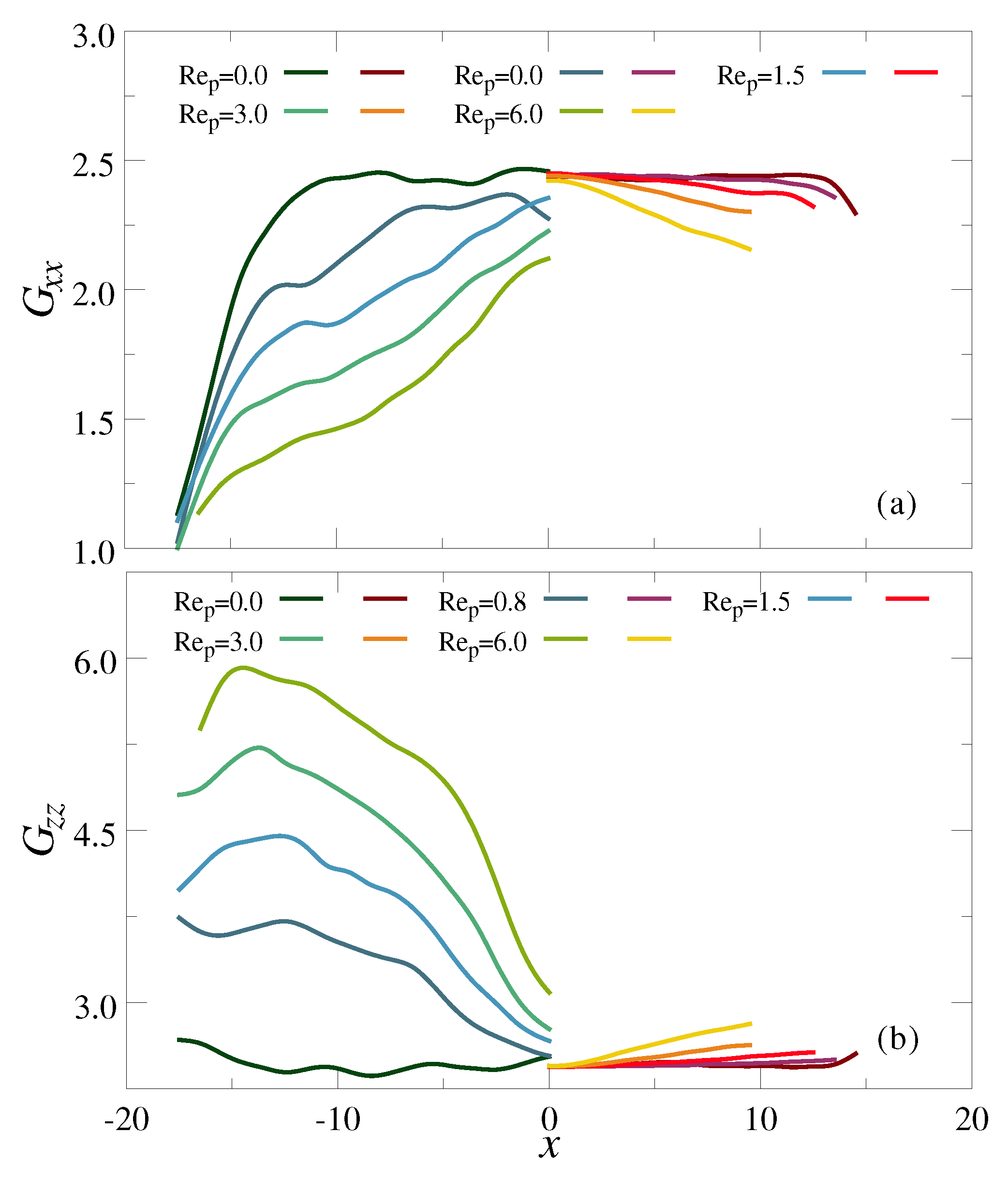
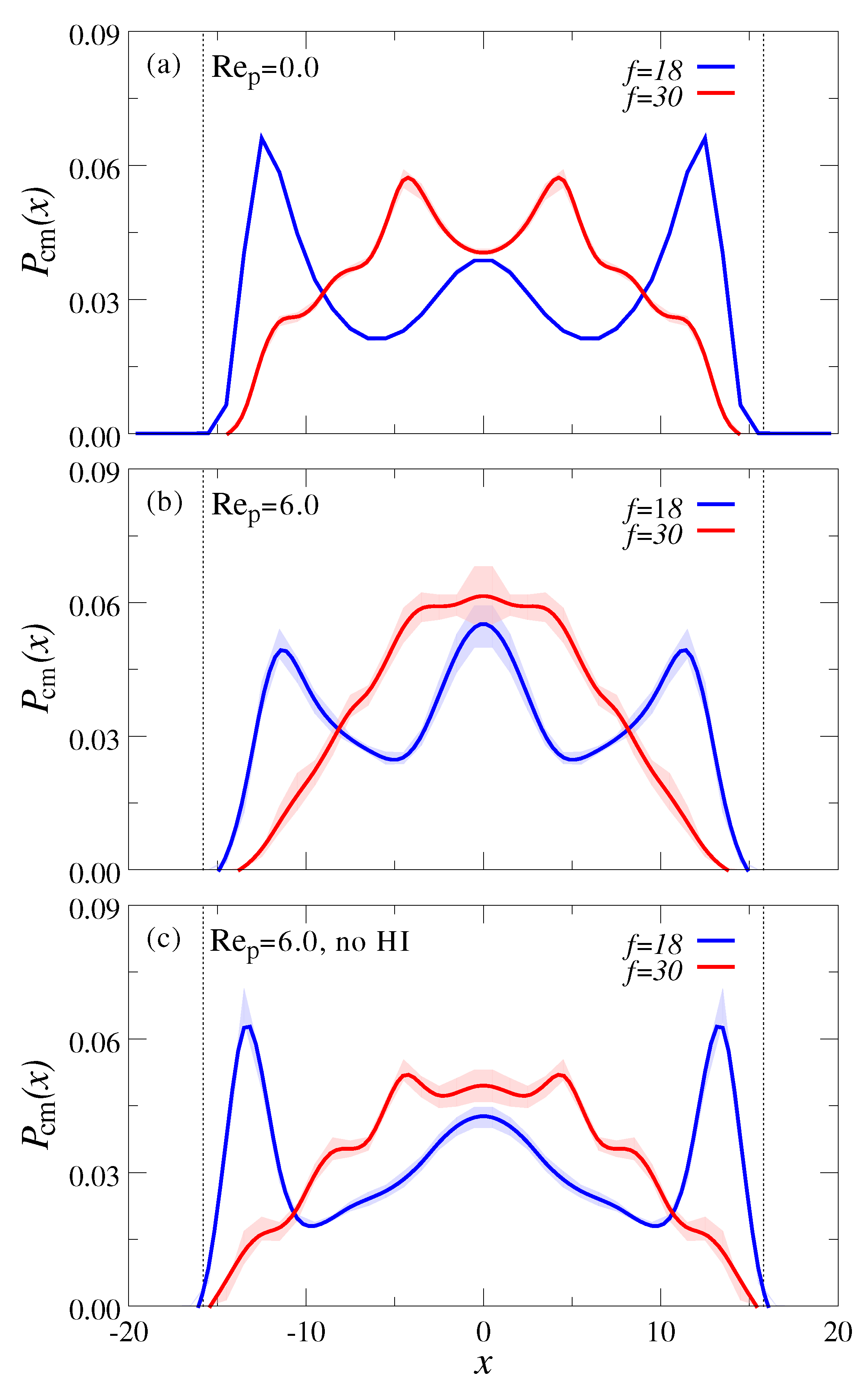
3.2. Polymer Mixtures
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| CM | Center of mass |
| FENE | Finitely extensible nonlinear elastic |
| HI | Hydrodynamic interactions |
| MD | Molecular Dynamics |
| MPCD | Multi-particle collision dynamics |
| PDMS | Polydimethylsiloxane |
| PEO | Poly(ethylene oxide) |
| WCA | Weeks-Chandler-Andersen |
References
- Suresh, S. Biomechanics and biophysics of cancer cells. Acta Biomater. 2007, 3, 413–438. [Google Scholar] [CrossRef] [PubMed]
- Ballas, S.K. Sickle cell anemia with few painful crises is characterized by decreased red cell deformability and increased number of dense cells. Am. J. Hematol. 1991, 36, 122–130. [Google Scholar] [CrossRef] [PubMed]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef]
- Chen, X.; Cui, D.F.; Liu, C.C.; Li, H. Microfluidic chip for blood cell separation and collection based on crossflow filtration. Sens. Actuators B Chem. 2008, 130, 216–221. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Fornleitner, J.; Gompper, G. Margination of White Blood Cells in Microcapillary Flow. Phys. Rev. Lett. 2012, 108, 028104. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.; Lee, S.S.; Ahn, S.W.; Kang, K.; Shim, W.; Lee, G.; Hyun, K.; Kim, J.M. Deformability-selective particle entrainment and separation in a rectangular microchannel using medium viscoelasticity. Soft Matter 2012, 8, 5011. [Google Scholar] [CrossRef]
- D’Avino, G.; Romeo, G.; Villone, M.M.; Greco, F.; Netti, P.A.; Maffettone, P.L. Single line particle focusing induced by viscoelasticity of the suspending liquid: Theory, experiments and simulations to design a micropipe flow-focuser. Lab Chip 2012, 12, 1638. [Google Scholar] [CrossRef] [PubMed]
- Karimi, A.; Yazdi, S.; Ardekani, A.M. Hydrodynamic mechanisms of cell and particle trapping in microfluidics. Biomicrofluidics 2013, 7, 021501. [Google Scholar] [CrossRef] [PubMed]
- McGrath, J.; Jimenez, M.; Birdle, H. Deterministic lateral displacement for particle separation: A review. Lab Chip 2014, 14, 4139. [Google Scholar] [CrossRef] [PubMed]
- Krüger, T.; Holmes, D.; Coveney, P.V. Deformability-based red blood cell separation in deterministic lateral displacement devices—A simulation study. Biomicrofluidics 2014, 8, 054114. [Google Scholar] [CrossRef] [PubMed]
- Zeming, K.K.; Salafi, T.; Chen, C.H.; Zhang, Y. Asymmetrical deterministic lateral displacement gaps for dual functions of enhanced separation and throughput of red blood cells. Sci. Rep. 2016, 6, 22934. [Google Scholar] [CrossRef] [PubMed]
- Sia, S.K.; Whitesides, G.M. Microfluidic devices fabricated in Poly(dimethylsiloxane) for biological studies. Electrophoresis 2003, 24, 3563–3576. [Google Scholar] [CrossRef] [PubMed]
- Segré, G.; Silberberg, A. Radial Particle Displacements in Poiseuille Flow of Suspensions. Nature 1961, 189, 209–210. [Google Scholar] [CrossRef]
- Karnis, K.; Mason, S.G. Particle motions in sheared suspensions. XIX. Viscoelastic media. Trans. Soc. Rheol. 1966, 10, 571. [Google Scholar] [CrossRef]
- Gauthier, F.; Goldsmith, H.L.; Mason, S.G. Particle motions in non-Newtonian media. I. Couette Flow. Rheol. Acta 1971, 10, 344–364. [Google Scholar] [CrossRef]
- Park, S.M.; Liang, X.; Harteneck, B.D.; Pick, T.E.; Hiroshiba, N.; Wu, Y.; Helms, B.A.; Olynick, D.L. Sub-10 nm Nanofabrication via Nanoimprint Directed Self-Assembly of Block Copolymers. ACS Nano 2011, 5, 8523–8531. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.E.; Babcock, H.P.; Chu, S. Single-Polymer Dynamics in Steady Shear Flow. Science 1999, 283, 1724–1727. [Google Scholar] [CrossRef] [PubMed]
- Schroeder, C.M.; Teixeria, R.E.; Shaqfeh, E.S.G.; Chu, S. Characteristic Periodic Motion of Polymers in Shear Flow. Phys. Rev. Lett. 2005, 95, 018301. [Google Scholar] [CrossRef] [PubMed]
- Lagally, E.T.; Medintz, I.; Mathies, R.A. Single-Molecule DNA Amplification and Analysis in an Integrated Microfluidic Device. Anal. Chem. 2001, 73, 565–570. [Google Scholar] [CrossRef] [PubMed]
- Gawad, C.; Koh, W.; Quake, S.R. Single-cell genome sequencing: Current state of the science. Nat. Rev. Genet. 2016, 17, 175–188. [Google Scholar] [CrossRef] [PubMed]
- Nikoubashman, A.; Likos, C.N. Flow-induced polymer translocation through narrow and patterned channels. J. Chem. Phys. 2010, 133, 074901. [Google Scholar] [CrossRef] [PubMed]
- Kim, J.Y.; Ahn, S.W.; Lee, S.S.; Kim, J.M. Lateral migration and focusing of colloidal particles and DNA molecules under viscoelastic flow. Lab Chip 2012, 12, 2807–2814. [Google Scholar] [PubMed]
- Ollila, S.T.T.; Denniston, C.; Karttunen, M.; Ala-Nissila, T. Biopolymer Filtration in Corrugated Nanochannels Santtu. Phys. Rev. Lett. 2014, 112, 118301. [Google Scholar] [CrossRef] [PubMed]
- Weiss, L.B.; Nikoubashman, A.; Likos, C.N. Topology-Sensitive Microfluidic Filter for Polymers of Varying Stiffness. ACS Macro Lett. 2017, 6, 1426–1431. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Polymer Physics; Oxford University Press: Oxford, MS, USA, 2003. [Google Scholar]
- Khare, R.; Graham, M.D.; de Pablo, J.J. Cross-stream migration of flexible molecules in a nanochannel. Phys. Rev. Lett. 2006, 96, 224505. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Ortiz, J.P.; Ma, H.; de Pablo, J.J.; Graham, M.D. Cross-stream-line migration in confined flowing polymer solutions: Theory and simulation. Phys. Fluids 2006, 18, 123101. [Google Scholar] [CrossRef]
- Cannavacciulo, L.; Winkler, R.G.; Gompper, G. Mesoscale simulations of polymer dynamics in microchannel flows. Europhys. Lett. 2008, 83, 34007. [Google Scholar] [CrossRef][Green Version]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Star polymers in shear flow. Phys. Rev. Lett. 2006, 96, 188302. [Google Scholar] [CrossRef] [PubMed]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Hydrodynamic screening of star polymers in shear flow. Eur. Phys. J. E 2007, 23, 349–354. [Google Scholar] [CrossRef] [PubMed]
- Nikoubashman, A.; Likos, C.N. Branched polymers under shear. Macromolecules 2010, 43, 1610–1620. [Google Scholar] [CrossRef][Green Version]
- Vlassopoulos, D. Macromolecular topology and rheology: Beyond the tube model. Rheol. Acta 2016, 55, 613–632. [Google Scholar] [CrossRef]
- Winkler, R.G. Semiflexible polymers in shear flow. Phys. Rev. Lett. 2006, 97, 128301. [Google Scholar] [CrossRef] [PubMed]
- Winkler, R.G. Conformational and Rheological properties of semiflexible polymers in shear flow. J. Chem. Phys. 2010, 133, 164905. [Google Scholar] [CrossRef] [PubMed]
- Chelakkot, R.; Winkler, R.G.; Gompper, G. Migration of semiflexible polymers in microcapillary flow. Europhys. Lett. 2010, 91, 14001. [Google Scholar] [CrossRef]
- Reddig, S.; Stark, H. Cross-streamline migration of a semiflexible polymer in a pressure driven flow. J. Chem. Phys. 2011, 135, 165101. [Google Scholar] [CrossRef] [PubMed]
- Nikoubashman, A.; Howard, M.P. Equilibrium Dynamics and Shear Rheology of Semiflexible Polymers in Solution. Macromolecules 2017, 50, 8279–8289. [Google Scholar] [CrossRef]
- Likos, C.N.; Löwen, H.; Watzlawek, M.; Abbas, B.; Jucknischke, O.; Allgaier, J.; Richter, D. Star polymers viewed as ultrasoft colloidal particles. Phys. Rev. Lett. 1998, 80, 4450–4453. [Google Scholar] [CrossRef]
- Likos, C.N. Effective interactions in soft condensed matter physics. Phys. Rep. 2001, 348, 267–439. [Google Scholar] [CrossRef]
- Vlassopoulos, D.; Fytas, G.; Pakula, T.; Roovers, J. Multiarm star polymers dynamics. J. Phys. Condens. Matter 2001, 13, R855. [Google Scholar] [CrossRef]
- Vlassopoulos, D.; Cloitre, M. Tunable rheology of dense soft deformable colloids. Curr. Opin. Colloid Interface Sci. 2014, 19, 561–574. [Google Scholar] [CrossRef]
- Riest, J.; Athanasopoulou, L.; Egorov, S.A.; Likos, C.N.; Ziherl, P. Elasticity of polymeric nanocolloidal particles. Sci. Rep. 2015, 5, 15854. [Google Scholar] [CrossRef] [PubMed]
- Rodionov, V.; Gao, H.; Scroggins, S.; Unruh, D.A.; Avestro, A.J.; Fréchet, J.M.J. Easy Access to a Family of Polymer Catalysts from Modular Star Polymers. J. Am. Chem. Soc. 2010, 132, 2570. [Google Scholar] [CrossRef] [PubMed]
- Kanibolotsky, A.L.; Perepichka, I.F.; Skabara, P.J. Star-shaped Pi-conjugated oligomers and their applications in organic electronics and photonics. Chem. Soc. Rev. 2010, 39, 2695. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Duong, M.R.; Whittaker, M.R.; Davis, T.P.; Boyer, C. Synthesis of Functional Core, Star Polymers via RAFT Polymerization for Drug Delivery Applications. Macromol. Rapid Commun. 2012, 33, 760–766. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.P.; Chatterji, A.; Gompper, G.; Winkler, R.G. Dynamical and Rheological Properties of Ultrasoft Colloids under Shear Flow. Macromolecules 2013, 46, 8026–8036. [Google Scholar] [CrossRef]
- Ge, H.; Pispas, S.; Wu, C. How does a star chain (nanooctopus) crawl through a nanopore? Polym. Chem. 2011, 2, 1071–1076. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Xiao, M.; Wang, R.; Chen, Y.L. Conformation-dependent translocation of a star polymer through a nanochannel. Biomicrofluidics 2014, 8, 054107. [Google Scholar] [CrossRef] [PubMed]
- Singh, S.P.; Gompper, G.; Winkler, R.G. Steady state sedimentation of ultrasoft colloids. J. Chem. Phys. 2018, 148, 084901. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Bishop, M.; Kalos, M.H.; Frisch, H.L. Molecular dynamics of polymeric systems. J. Chem. Phys. 1979, 70, 1299–1304. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts—A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Malevanets, A.; Kapral, R. Mesoscopic model for solvent dynamics. J. Chem. Phys. 1999, 110, 8605–8613. [Google Scholar] [CrossRef]
- Gompper, G.; Ihle, T.; Kroll, D.; Winkler, R.G. Multi-particle collision dynamics: A particle-based mesoscale simulation approach to the hydrodynamics of complex fluids. Adv. Polym. Sci. 2009, 221, 1–87. [Google Scholar]
- Huang, C.C.; Gompper, G.; Winkler, R.G. Hydrodynamic correlations in multiparticle collision dynamics fluids. Phys. Rev. E 2012, 86, 056711. [Google Scholar] [CrossRef] [PubMed]
- Allahyarov, E.; Gompper, G. Mesoscopic solvent simulations: Multiparticle-collision dynamics of three-dimensional flows. Phys. Rev. E 2002, 66, 036702. [Google Scholar] [CrossRef] [PubMed]
- Ihle, T.; Kroll, D.M. Stochastic rotation dynamics: A Galilean-invariant mesoscopic model for fluid flow. Phys. Rev. E 2001, 63, 020201. [Google Scholar] [CrossRef] [PubMed]
- Lamura, A.; Gompper, G.; Ihle, T.; Kroll, D.M. Multi-particle collision dynamics: Flow around a circular and a square cylinder. Europhys. Lett. 2001, 56, 319. [Google Scholar] [CrossRef]
- Nikoubashman, A.; Mahynski, N.A.; Pirayandeh, A.H.; Panagiotopoulos, A.Z. Flow-induced demixing of polymer-colloid mixtures in microfluidic channels. J. Chem. Phys. 2014, 140, 094903. [Google Scholar] [CrossRef] [PubMed]
- Howard, M.P.; Panagiotopoulos, A.Z.; Nikoubashman, A. Inertial and viscoelastic forces on rigid colloids in microfluidic channels. J. Chem. Phys. 2015, 142, 224908. [Google Scholar] [CrossRef] [PubMed]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Ripoll, M.; Mussawisade, K.; Winkler, R.G.; Gompper, G. Dynamic regimes of fluids simulated by multiparticle-collision dynamics. Phys. Rev. E 2005, 72, 016701. [Google Scholar] [CrossRef] [PubMed]
- Anderson, J.A.; Lorenz, C.D.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comput. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Glaser, J.; Nguyen, T.D.; Anderson, J.A.; Liu, P.; Spiga, F.; Millan, J.A.; Morse, D.C.; Glotzer, S.C. Strong scaling of general-purpose molecular dynamics simulations on GPUs. Comput. Phys. Commun. 2015, 192, 97–107. [Google Scholar] [CrossRef]
- Howard, M.P.; Anderson, J.A.; Nikoubashman, A.; Glotzer, S.C.; Panagiotopoulos, A.Z. Efficient neighbor list calculation for molecular simulation of colloidal systems using graphics processing units. Comput. Phys. Commun. 2016, 203, 45–52. [Google Scholar] [CrossRef]
- Jusufi, A.; Dzubiella, J.; Likos, C.N.; von Ferber, C.; Löwen, H. Effective interactions between star polymers and colloidal particles. J. Phys. Condens. Matter 2001, 13, 6177–6194. [Google Scholar] [CrossRef]
- Marzi, D.; Likos, C.N.; Capone, B. Coarse graining of star-polymer–colloid nanocomposites. J. Chem. Phys. 2012, 137, 014902. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.C.; Winkler, R.G.; Stutmann, G.; Gompper, G. Semidilute Polymer Solutions at Equilibrium and under Shear Flow. Macromolecules 2010, 43, 10107. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. Viscosity of Nanoconfined Polyamide-6,6 Oligomers: Atomistic Reverse Nonequilibrium Molecular Dynamics Simulation. J. Phys. Chem. B 2010, 114, 387–395. [Google Scholar] [CrossRef] [PubMed]
- Zimm, B.H. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K.; Milner, S.T.; Witten, T.A. Relaxation of self-entangled many-arm star polymers. Macromolecules 1989, 22, 1904–1910. [Google Scholar] [CrossRef]
- Wohl, R.P.; Rubinow, S.I. The transverse force on a drop in an unbounded parabolic flow. J. Fluid Mech. 1974, 62, 185–207. [Google Scholar] [CrossRef]
- Chan, P.C.H.; Leal, L.G. The motion of a deformable drop in a second-order fluid. J. Fluid Mech. 1979, 92, 131–170. [Google Scholar] [CrossRef]
- Marson, R.; Huang, Y.; Huang, M.; Fu, T.; Larson, R.G. Inertio-Capillary Cross-Streamline Drift of Droplets in Poiseuille Flow using Dissipative Particle Dynamics Simulations. Soft Matter 2018, 14, 2267–2280. [Google Scholar] [CrossRef] [PubMed]
- Schaaf, C.; Stark, H. Inertial migration and axial control of deformable capsules. Soft Matter 2017, 13, 3544–3555. [Google Scholar] [CrossRef] [PubMed]
- Perram, J.W.; White, L.R. Structure of the liquid/vapour and liquid/solid interfaces. Faraday Discuss. Chem. Soc. 1975, 59, 29–37. [Google Scholar] [CrossRef]
- Henderson, D.; Abraham, F.F.; Barker, J.A. The Ornstein-Zernike equation for a fluid in contact with a surface. Mol. Phys. 1976, 31, 1291–1295. [Google Scholar] [CrossRef]
- Snook, I.K.; Henderson, D. Monte Carlo study of a hard-sphere fluid near a hard wall. J. Chem. Phys. 1978, 68, 2134. [Google Scholar] [CrossRef]
- Howard, M.P.; Gautam, A.; Panagiotopoulos, A.Z.; Nikoubashman, A. Axial dispersion of Brownian colloids in microfluidic channels. Phys. Rev. Fluids 2016, 1, 044203. [Google Scholar] [CrossRef]
- Devanand, K.; Selser, J.C. Asymptotic behavior and long-range interactions in aqueous solutions of poly(ethylene oxide). Macromolecules 1991, 24, 5943–5947. [Google Scholar] [CrossRef]

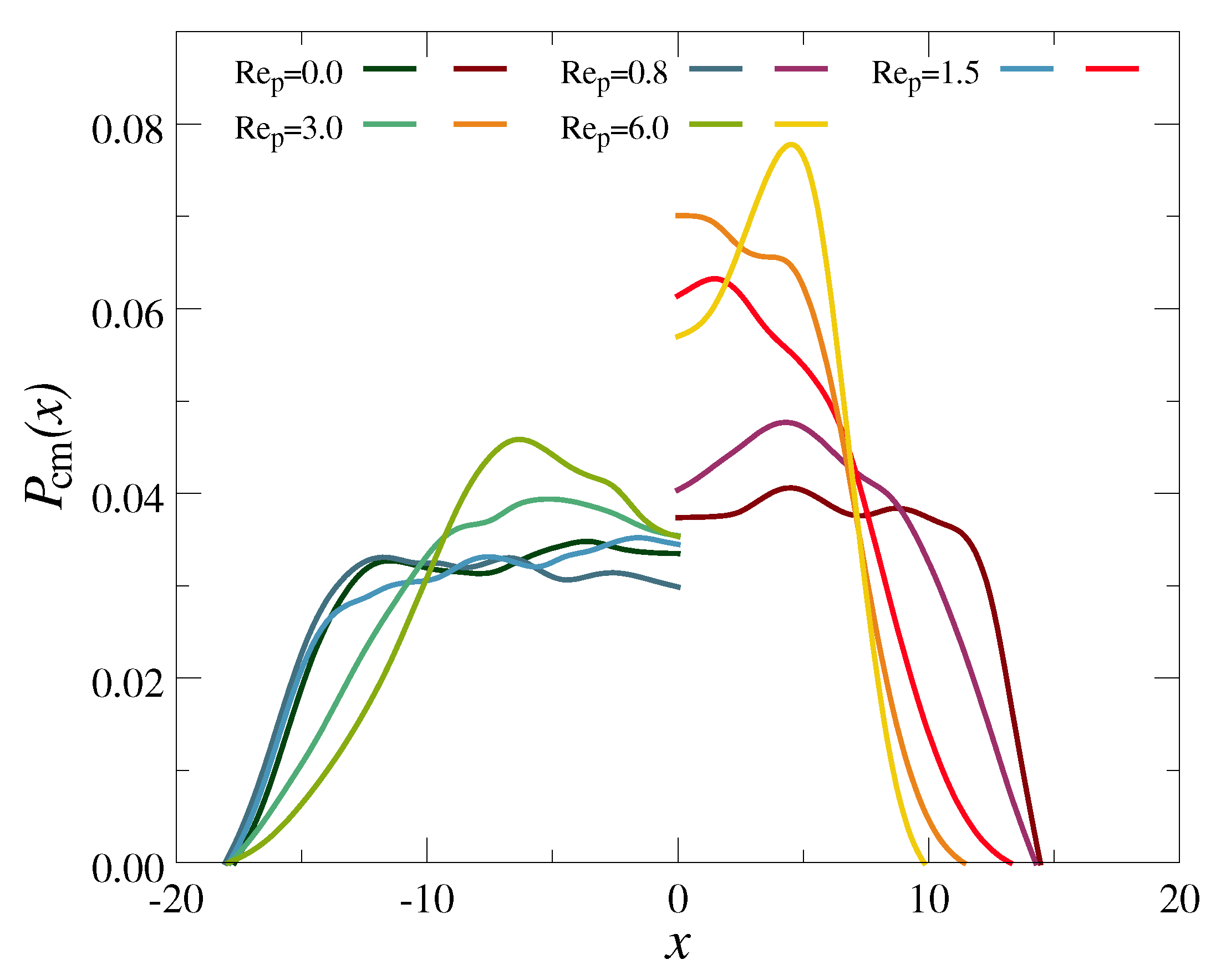
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastva, D.; Nikoubashman, A. Flow Behavior of Chain and Star Polymers and Their Mixtures. Polymers 2018, 10, 599. https://doi.org/10.3390/polym10060599
Srivastva D, Nikoubashman A. Flow Behavior of Chain and Star Polymers and Their Mixtures. Polymers. 2018; 10(6):599. https://doi.org/10.3390/polym10060599
Chicago/Turabian StyleSrivastva, Deepika, and Arash Nikoubashman. 2018. "Flow Behavior of Chain and Star Polymers and Their Mixtures" Polymers 10, no. 6: 599. https://doi.org/10.3390/polym10060599
APA StyleSrivastva, D., & Nikoubashman, A. (2018). Flow Behavior of Chain and Star Polymers and Their Mixtures. Polymers, 10(6), 599. https://doi.org/10.3390/polym10060599