Synthesis and Characterization of a Molecularly Imprinted Polymer of Spermidine and the Exploration of Its Molecular Recognition Properties
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Reagents
2.2. Instruments and Equipment
2.3. Method
2.3.1. Synthesis of Spermidine MIPs
2.3.2. Polymer Elution Treatment
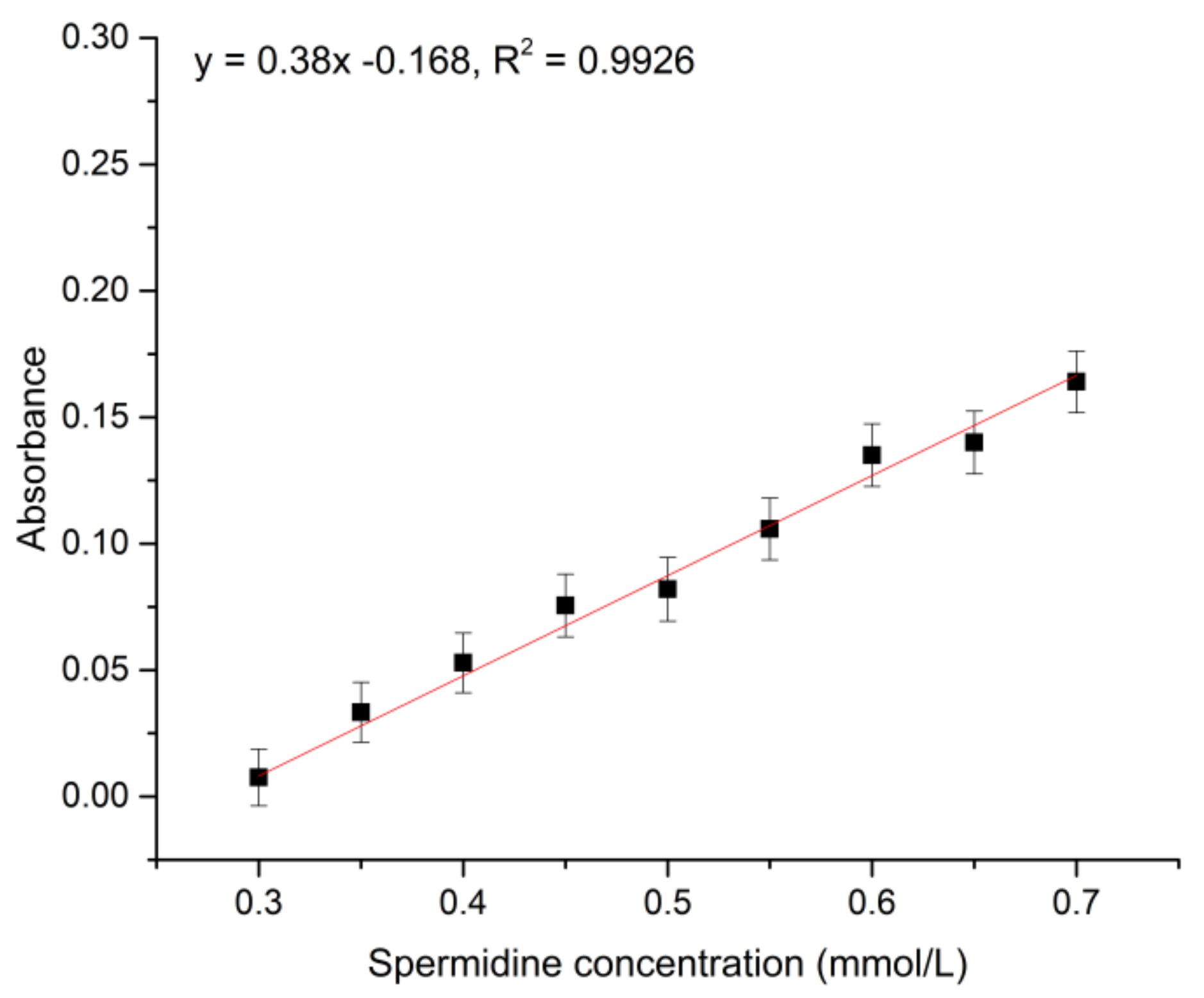
2.3.3. Spermidine Standard Curve Plot
2.3.4. Spermidine MIPs Adsorption Kinetics and Determination of Adsorption Equilibrium Time
2.3.5. Spermidine MIPs Adsorption Kinetics and Adsorption Capacity Determination
2.3.6. Selective Adsorption of Spermidine MIPs
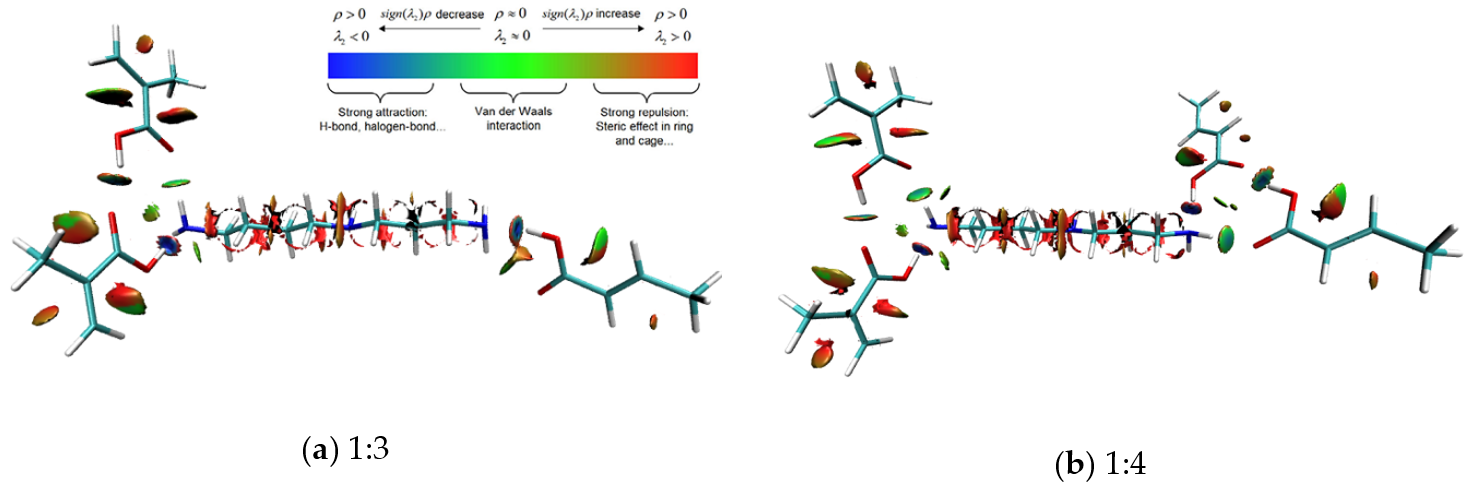
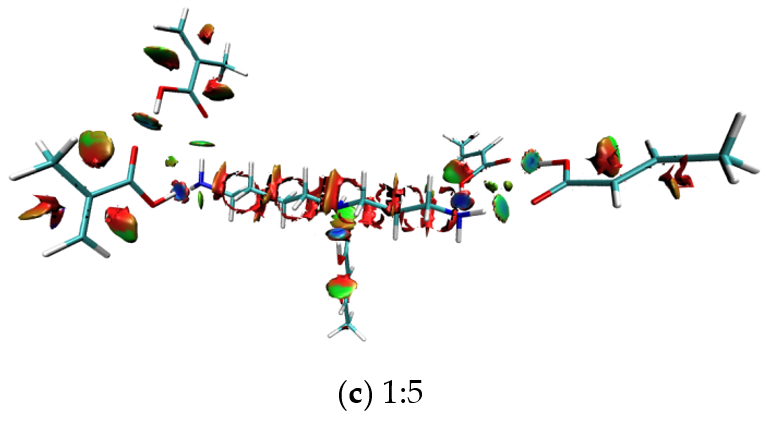
2.3.7. Intermolecular Interaction Analysis
3. Results and Discussion
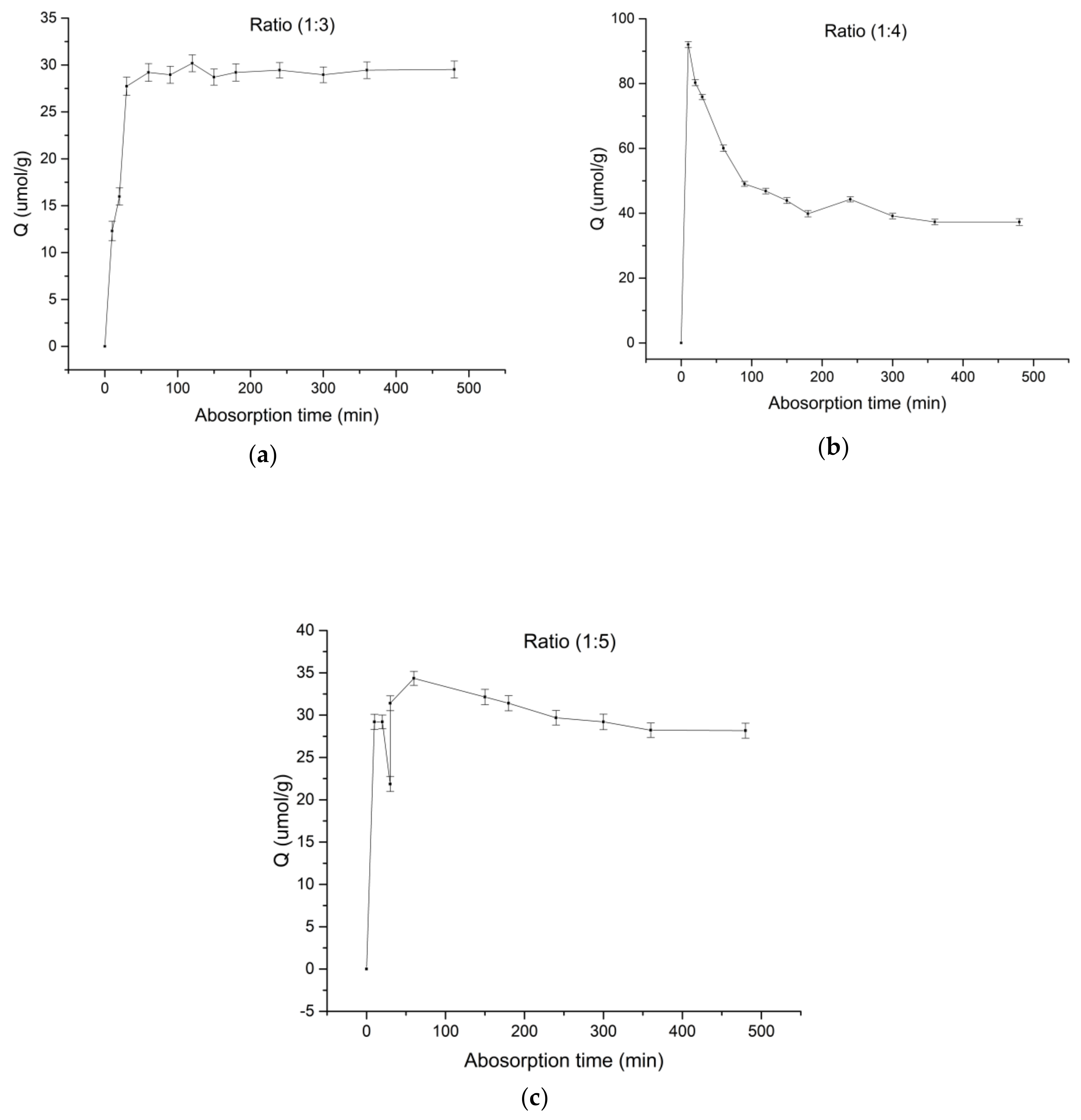
3.1. Adsorption Equilibrium Time of Spermidine MIPs
3.2. Adsorption Equilibrium Time of Spermidine MIPs
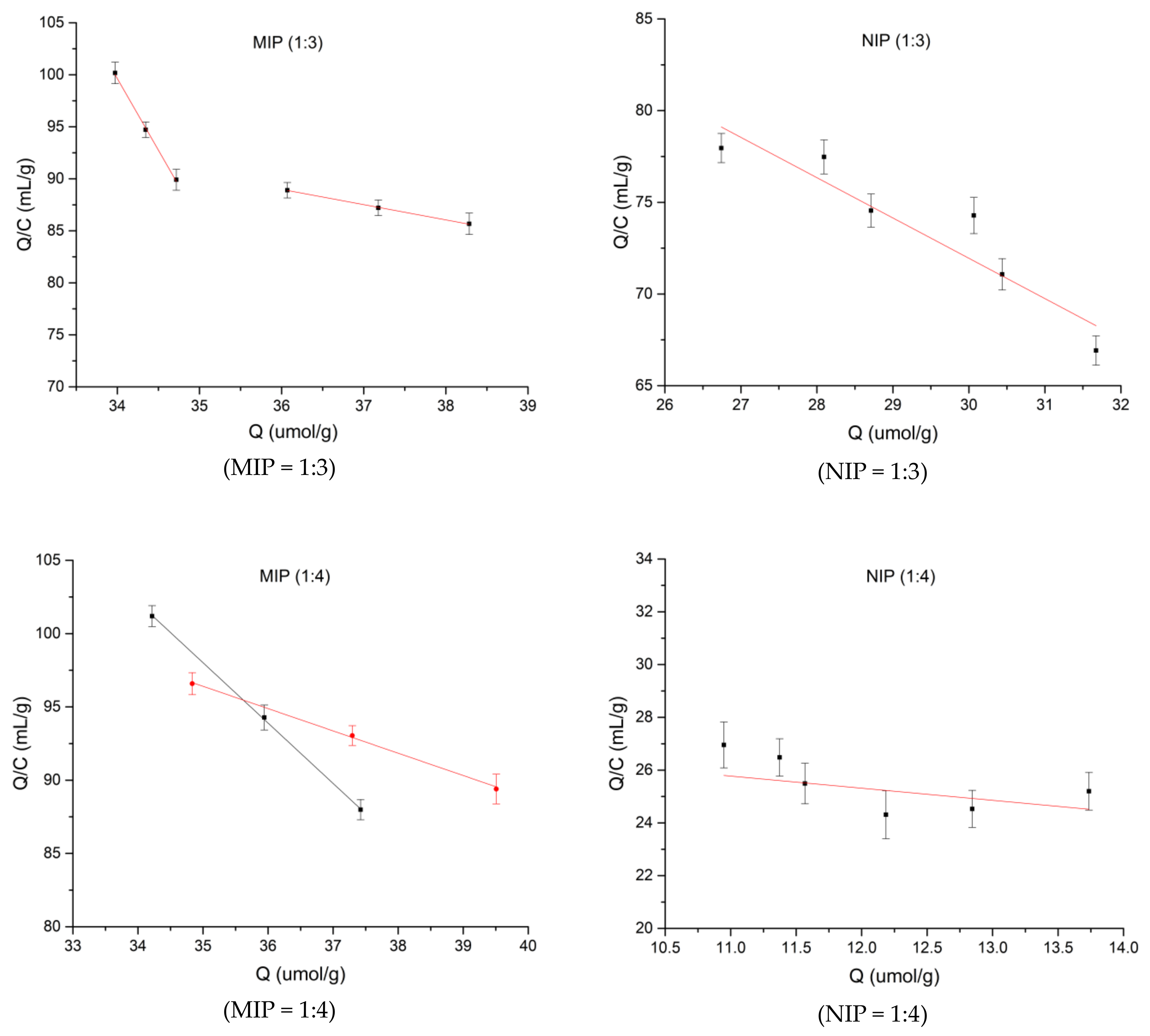
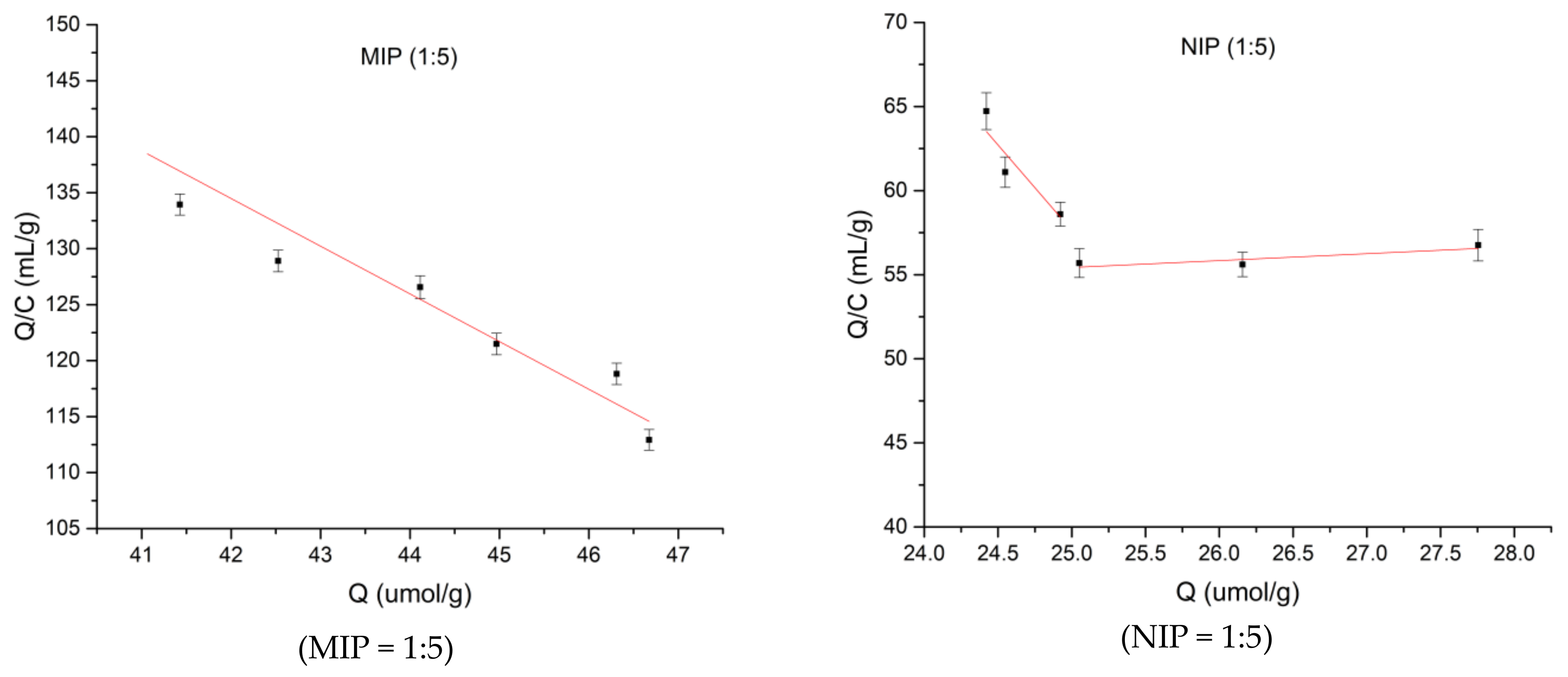
3.3. Adsorption Properties of Three Spermidine MIPs Ratios
3.4. Selective Adsorption Test of Spermidine MIPs
3.5. Intermolecular Interaction Analysis of MIPs
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Banerjee, A.; Bandopadhyay, R. Autophagy: Nobel Prize in Physiology or Medicine’16 to the Intra-Cellular Suicidal Process. Natl. Acad. Sci. Lett. 2017, 40, 461–465. [Google Scholar] [CrossRef]
- Zhou, J.; Farah, B.L.; Sinha, R.A.; Wu, Y.; Singh, B.K.; Bay, B.H.; Yang, C.S.; Yen, P.M. Epigallocatechin-3-gallate (EGCG), a green tea polyphenol, stimulates hepatic autophagy and lipid clearance. PLoS ONE 2014, 9, 87161. [Google Scholar] [CrossRef] [PubMed]
- Sagara, T.; Fiechter, G.; Pachner, M.; Mayer, H.K.; Vollmann, J. Soybean spermidine concentration: Genetic and environmental variation of a potential ‘anti-aging’constituent. J. Food Compos. Anal. 2017, 56, 11–17. [Google Scholar] [CrossRef]
- Eisenberg, T.; Abdellatif, M.; Zimmermann, A.; Schroeder, S.; Pendl, T.; Harger, A.; Stekovic, S.; Schipke, J.; Magnes, C.; Schmidt, A. Dietary spermidine for lowering high blood pressure. Autophagy 2017, 13, 767–769. [Google Scholar] [CrossRef] [PubMed]
- Puyang, X.; An, M.; Han, L.; Zhang, X. Protective effect of spermidine on salt stress induced oxidative damage in two Kentucky bluegrass (Poa pratensis L.) cultivars. Ecotoxicol. Environ. Safe 2015, 117, 96–106. [Google Scholar] [CrossRef] [PubMed]
- Til, H.P.; Falke, H.E.; Prinsen, M.K.; Willems, M.I. Acute and subacute toxicity of tyramine, spermidine, spermine, putrescine and cadaverine in rats. Food Chem. Toxicol. 1997, 35, 337–348. [Google Scholar] [CrossRef]
- Paulsen, P.; Bauer, F. Spermine and spermidine concentrations in pork loin as affected by storage, curing and thermal processing. Eur. Food Res. Technol. 2007, 225, 921–924. [Google Scholar] [CrossRef]
- Chopra, S.; Singh, A.; Venugopalan, P.; Singh, N.; Kaur, N. Organic nanoparticles for visual detection of spermidine and spermine in vapors and aqueous phase. ACS Sustain. Chem. Eng. 2017, 5, 1287–1296. [Google Scholar] [CrossRef]
- Su, H.H.; Chuang, L.Y.; Tseng, W.L.; Lu, C.Y. Micro-scale strategy to detect spermine and spermidine by MALDI–TOF MS in foods and identification of apoptosis-related proteins by nano-flow UPLC–MS/MS after treatment with spermine and spermidine. J. Chromatogr. B 2015, 978, 131–137. [Google Scholar] [CrossRef] [PubMed]
- Pan, J.; Chen, W.; Ma, Y.; Pan, G. Molecularly imprinted polymers as receptor mimics for selective cell recognition. Chem. Soc. Rev. 2018, 47, 5574. [Google Scholar] [CrossRef]
- Ma, X.; Meng, Z.; Qiu, L.; Chen, J.; Guo, Y.S.; Yi, D.; Ji, T.T.; Ji, H.; Xue, M. Solanesol extraction from tobacco leaves by Flash chromatography based on molecularly imprinted polymers. J. Chromatogr. B 2016, 1020, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Vicario, A.; Aragón, L.; Wang, C.C.; Bertolino, F.; Gomez, M.R. A simple and highly selective molecular imprinting polymer-based methodology for propylparaben monitoring in personal care products and industrial waste waters. J. Pharm. Biomed. 2018, 149, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Cieplak, M.; Kutner, W. Artificial biosensors: How can molecular imprinting mimic biorecognition? Trends Biotechnol. 2016, 34, 922–941. [Google Scholar] [CrossRef]
- Kubo, T.; Otsuka, K. Recent progress in molecularly imprinted media by new preparation concepts and methodological approaches for selective separation of targeting compounds. TrAC Trends Anal. Chem. 2016, 81, 102–109. [Google Scholar] [CrossRef]
- Rivero, P.; Goicoechea, J.; Arregui, F. Optical Fiber Sensors Based on Polymeric Sensitive Coatings. Polymers 2018, 10, 280. [Google Scholar] [CrossRef]
- Liu, Y.; Cao, B.; Jia, P.; An, J.H.; Luo, C.; Ma, L.J.; Chang, J.; Pan, K. Layer-by-layer surface molecular imprinting on polyacrylonitrile nanofiber mats. J. Phys. Chem. A 2015, 119, 6661–6667. [Google Scholar] [CrossRef] [PubMed]
- Barahona, F.; Díaz-Álvarez, M.; Turiel, E.; Martín-Esteban, A. Molecularly imprinted polymer-coated hollow fiber membrane for the microextraction of triazines directly from environmental waters. J. Chromatogr. A 2016, 1442, 12–18. [Google Scholar] [CrossRef]
- Hjerten, S.; Liao, J.L.; Nakazato, K.; Nakazato, K.; Wang, Y. Gels mimicking antibodies in their selective recognition of proteins. Chromatographia 1997, 44, 227–234. [Google Scholar] [CrossRef]
- Kavimani, M.; Balachandran, V.; Narayana, B.; Vanasundari, K.; Revathi, B. Topological analysis (BCP) of vibrational spectroscopic studies, docking, RDG, DSSC, Fukui functions and chemical reactivity of 2-methylphenylacetic acid. Spectrochim. Acta A 2018, 190, 47–60. [Google Scholar] [CrossRef]
- Li, H.; Zhou, P.; Zhang, J.; Li, D.; Li, X.; Gao, X. A theoretical guide for screening ionic liquid extractants applied in the separation of a binary alcohol-ester azeotrope through a DFT method. J. Mol. Liq. 2018, 251, 51–60. [Google Scholar] [CrossRef]
- Lande, D.N.; Gejji, S.P. Molecular Recognition, Conformational Behavior, and Spectral Characteristics of Oxatub [4] arene Macrocycle. J. Phys. Chem. A 2018, 122, 714–723. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Dong, X. Preparation of a molecularly imprinted fluorescent chemosensor using quinoline modified vinyl-β-cyclodextrin and acrylamide as monomers for the selective recognition of spermidine. Anal. Methods 2016, 8, 5838–5842. [Google Scholar] [CrossRef]
- Cheng, Y.; Jiang, P.; Dong, X. Molecularly imprinted fluorescent chemosensor synthesized using quinoline-modified-β-cyclodextrin as monomer for spermidine recognition. RSC Adv. 2015, 5, 55066–55074. [Google Scholar] [CrossRef]
- Huang, Y.J.; Zhu, Q. Computational Modeling and Theoretical Calculations on the Interactions between Spermidine and Functional Monomer (Methacrylic Acid) in a Molecularly Imprinted Polymer. J. Chem. NY 2015. [Google Scholar] [CrossRef]
- Yu, C.; Mosbach, K. Molecular imprinting utilizing an amide functional group for hydrogen bonding leading to highly efficient polymers. J. Org. Chem. 1997, 62, 4057–4064. [Google Scholar] [CrossRef]
- Golker, K.; Olsson, G.D.; Nicholls, I.A. The influence of a methyl substituent on molecularly imprinted polymer morphology and recognition–Acrylic acid versus methacrylic acid. Eur. Polym. J. 2017, 92, 137–149. [Google Scholar] [CrossRef]
- Sun, X.; Chiu, Y.Y.; Lee, L.J. Microgel formation in the free radical cross-linking copolymerization of methyl methacrylate (MMA) and ethylene glycol dimethacrylate (EGDMA). Ind. Eng. Chem. Res. 1997, 36, 1343–1351. [Google Scholar] [CrossRef]
- Lorenzo, R.A.; Carro, A.M.; Alvarez-Lorenzo, C.; Concheiro, A. To remove or not to remove? The challenge of extracting the template to make the cavities available in molecularly imprinted polymers (MIPs). Int. J. Mol. Sci. 2011, 12, 4327–4347. [Google Scholar] [CrossRef]
- Nie, D.; Han, Z.; Yu, Y.; Shi, G. Composites of multiwalled carbon nanotubes/polyethyleneimine (MWCNTs/PEI) and molecularly imprinted polymers for dinitrotoluene recognition. Sens. Actuators B Chem. 2016, 224, 584–591. [Google Scholar] [CrossRef]
- Hameed, B.H.; Din, A.T.M.; Ahmad, A.L. Adsorption of methylene blue onto bamboo-based activated carbon: Kinetics and equilibrium studies. J. Hazard. Mater. 2007, 141, 819–825. [Google Scholar] [CrossRef]
- Klotz, I.M. Numbers of receptor sites from Scatchard graphs: Facts and fantasies. Science 1982, 217, 1247–1249. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Su, X.; He, X.; Chen, L.; Zhang, Y. Preparation and characterisation of core–shell CNTs@ MIPs nanocomposites and selective removal of estrone from water samples. Talanta 2011, 83, 757–764. [Google Scholar] [CrossRef] [PubMed]
- Wulff, G. Enzyme-like catalysis by molecularly imprinted polymers. Chem. Rev. 2002, 102, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Kyzas, G.Z.; Bikiaris, D.N.; Lazaridis, N.K. Selective separation of basic and reactive dyes by molecularly imprinted polymers (MIPs). Chem. Eng. J. 2009, 149, 263–272. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef] [PubMed]
- Xantheas, S.S. On the importance of the fragment relaxation energy terms in the estimation of the basis set superposition error correction to the intermolecular interaction energy. J. Chem. Phys. 1996, 104, 8821–8824. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision A 03; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Huang, Z.; Liu, S.; Zhang, B.; Xu, L.; Hu, X. Equilibrium and kinetics studies on the absorption of Cu (II) from the aqueous phase using a β-cyclodextrin-based adsorbent. Carbonhyd. Polym. 2012, 88, 609–617. [Google Scholar] [CrossRef]
- Ho, Y.S.; McKay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Shiomi, T.; Matsui, M.; Mizukami, F.; Sakaguchi, K. A method for the molecular imprinting of hemoglobin on silica surfaces using silanes. Biomaterials 2005, 26, 5564–5571. [Google Scholar] [CrossRef]
- Miura, C.; Li, H.; Matsunaga, H.; Haginaka, J. Molecularly imprinted polymer for chlorogenic acid by modified precipitation polymerization and its application to extraction of chlorogenic acid from Eucommia ulmodies leaves. J. Pharm. Biomed. 2015, 114, 139–144. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Liu, Y.; Tong, H.; Xu, Y.; Liu, S. Preparation of a hollow porous molecularly imprinted polymer using tetrabromobisphenol A as a dummy template and its application as SPE sorbent for determination of bisphenol A. in tap water. Talanta 2013, 117, 281–287. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Gu, L.; Kong, G.; Zheng, Y.L.; Han, Y.; Li, Z.J.; Shi, J.L.; Peng, J. Comparative analysis of atrazine molecularly imprinted polymers using acetonitrile and toluene as solvents. J. Appl. Polym. Sci. 2018, 47190. [Google Scholar] [CrossRef]
- Vlatakis, G.; Andersson, L.I.; Müller, R.; Mosbach, K. Drug assay using antibody mimics made by molecular imprinting. Nature 1993, 361, 645. [Google Scholar] [CrossRef] [PubMed]
- Cao, H.; Xiao, J.B.; Xu, M. Evaluation of new selective molecularly imprinted polymers for the extraction of resveratrol frompolygonum cuspidatum. Macromol. Res. 2006, 14, 324–330. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L. Analysis of malachite green in aquatic products by carbon nanotube-based molecularly imprinted-matrix solid phase dispersion. J. Chromatogr. B 2015, 1002, 98–106. [Google Scholar] [CrossRef]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.P.; Miller, B.J.; Kjaergaard, H.G. Are bond critical points really critical for hydrogen bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef] [PubMed]
- Torshin, I.Y.; Weber, I.T.; Harrison, R.W. Geometric criteria of hydrogen bonds in proteins and identification of bifurcated’hydrogen bond. Protein Eng. Des. Sel. 2002, 15, 359–363. [Google Scholar] [CrossRef]
- Rozas, I.; Alkorta, I.; Elguero, J. Behavior of ylides containing N, O, and C atoms as hydrogen bond acceptors. J. Am. Chem. Soc. 2000, 122, 11154–11161. [Google Scholar] [CrossRef]
- Dauber-Osguthorpe, P.; Hagler, A.T. Biomolecular force fields: Where have we been, where are we now, where do we need to go and how do we get there? J. Comput. Aid. Mol. Des. 2018, 1–71. [Google Scholar] [CrossRef]
- Wang, J.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef]
- Su, P.; Li, H. Energy decomposition analysis of covalent bonds and intermolecular interactions. J. Chem. Phys. 2009, 131, 014102. [Google Scholar] [CrossRef] [PubMed]
- Floris, F.; Tomasi, J. Evaluation of the dispersion contribution to the solvation energy. A simple computational model in the continuum approximation. J. Comput. Chem. 1989, 10, 616–627. [Google Scholar] [CrossRef]
- Johnson, E.R.; Keinan, S.; Mori-Sanchez, P.; Contreras-Garcia, J.; Cohen, A.J.; Yang, W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [PubMed]

| Template molecule: Spermidine (mg) | Functional monomer: Methacrylic acid (mL) | Molar ratio of Template molecule to functional monomer | Initiator AIBN (mg) | Cross-linker EGDMA (mg) |
|---|---|---|---|---|
| 217.5 | 381.60 | 1:3 | 100.00 | 2.00 |
| 217.5 | 510.00 | 1:4 | 100.00 | 2.00 |
| 217.5 | 642.50 | 1:5 | 100.00 | 2.00 |
| Ratio | R2 |
|---|---|
| 1:3 | 0.3372 |
| 1:4 | 0.5662 |
| 1:5 | 0.0233 |
| Ratio | Qe (μmol/g) | Qe caq(μmol/g) | K2 (g/μmoL/min) | R2 | Q% |
|---|---|---|---|---|---|
| 1:3 | 28.95 | 30.04 | 0.004804 | 0.9985 | 3.76 |
| 1:4 | 39.14 | 36.41 | 0.001422 | 0.9949 | 6.99 |
| 1:5 | 29.20 | 28.53 | 0.02328 | 0.9945 | 2.29 |
| Substance | MIP (1:3) | NIP (1:3) | ||||
|---|---|---|---|---|---|---|
| Q (μmol /g) | Ki/j (mL/g) | α | Q (μmol /g) | Ki/j (mL/g) | α | |
| Spermidine | 38.24 | 85.55 | - | 31.67 | 66.96 | - |
| Tyramine | 24.75 | 49.41 | 1.73 | 24.75 | 49.4 | 1.35 |
| Histamine | 26.73 | 54.21 | 1.58 | 26.11 | 52.69 | 1.27 |
| Substance | MIP (1:4) | NIP (1:4) | ||||
| Spermidine | 39.51 | 89.80 | - | 13.74 | 24.98 | - |
| Tyramine | 22.66 | 44.48 | 2.01 | 9.11 | 16.16 | 1.56 |
| Histamine | 25.09 | 50.22 | 1.78 | 10.5 | 18.81 | 1.34 |
| Substance | MIP (1:5) | NIP (1:5) | ||||
| Spermidine | 46.67 | 113.01 | - | 27.75 | 56.74 | - |
| Tyramine | 30.36 | 63.44 | 1.78 | 22.9 | 45.04 | 1.26 |
| Histamine | 32.7 | 69.7 | 1.62 | 20.8 | 40.25 | 1.41 |
| Hydrogen bond | ρ (a.u) | ▽2ρ (a.u) | VBCP (a.u) | GBCP (a.u) | HBCP (a.u) | EBCP (kJ/mol) | Length (Ǻ) |
|---|---|---|---|---|---|---|---|
| Ratio | 1:3 | ||||||
| N1–H2–O63 | 0.0102 | 0.0397 | –0.00807 | 0.0090 | 0.000936 | –10.593 | 3.077 |
| N1–H65–O64 | 0.0307 | 0.215 | –0.0502 | 0.0519 | 0.00174 | –65.920 | 2.734 |
| N27–H27–O53 | 0.0194 | 0.106 | –0.0209 | 0.0237 | 0.00275 | –27.455 | 3.002 |
| O51–H52–O39 | 0.0251 | 0.1861 | –0.0382 | 0.0423 | 0.00417 | –50.117 | 2.707 |
| O40–H41–N27 | 0.0383 | 0.294 | –0.0722 | 0.0729 | 0.000670 | –94.848 | 2.632 |
| Ratio | 1:4 | ||||||
| N10–H40–O21 | 0.0195 | 0.106 | –0.0210 | 0.0237 | 0.00276 | –27.552 | 3.000 |
| O20–H22–O15 | 0.0252 | 0.186 | –0.0382 | 0.0424 | 0.00418 | –50.150 | 2.706 |
| O64–H65–N10 | 0.0385 | 0.296 | –0.0729 | 0.0735 | 0.00610 | –95.657 | 2.629 |
| O62–H63–N1 | 0.0389 | 0.297 | –0.0734 | 0.0739 | 0.000448 | –96.424 | 2.628 |
| O76–H77–O61 | 0.0252 | 0.187 | –0.0385 | 0.0427 | 0.00418 | –50.549 | 2.707 |
| N1–H24–O75 | 0.0202 | 0.113 | –0.0224 | 0.0253 | 0.00288 | –29.476 | 2.978 |
| Ratio | 1:5 | ||||||
| N10–H40–O21 | 0.0195 | 0.106 | –0.0210 | 0.0238 | 0.00276 | –27.590 | 3.001 |
| O15–O20-H22 | 0.0251 | 0.186 | –0.0381 | 0.0423 | 0.00417 | –50.0195 | 2.708 |
| O64–H65–N10 | 0.0386 | 0.297 | –0.0731 | 0.0737 | 0.000606 | –95.969 | 2.629 |
| O62–H63–N1 | 0.0379 | 0.287 | –0.0704 | 0.0711 | 0.000634 | –92.489 | 2.639 |
| O76–H77–O61 | 0.0253 | 0.188 | –0.0386 | 0.0429 | 0.00419 | –50.763 | 2.705 |
| N1–H24–O75 | 0.0203 | 0.113 | –0.0226 | 0.0255 | 0.00288 | –29.661 | 2.975 |
| O88–H89–N5 | 0.0160 | 0.212 | –0.0503 | 0.0517 | 0.00136 | –66.0895 | 2.742 |
| Ratio 1:3 | Electrostatic | Repulsion | Dispersion |
|---|---|---|---|
| SPD-MAA | −54.84 | 64.57 | −49.02 |
| MAA-MAA | −23.62 | 13.94 | −12.18 |
| total | −78.46 | 78.51 | −61.20 |
| Ratio 1:4 | Electrostatic | Repulsion | Dispersion |
| SPD-MAA | −68.67 | 81.15 | −60.83 |
| MAA-MAA | −46.60 | −27.92 | −23.91 |
| total | −115.27 | 109.07 | −84.78 |
| Ratio 1:5 | Electrostatic | Repulsion | Dispersion |
| SPD-MAA | −77.6 | 106.94 | −89.28 |
| MAA-MAA | −46.97 | 27.91 | −24.59 |
| total | −124.57 | 134.85 | −113.87 |
| Compounds | Molecular Structure | Complex Energy (1:4 for MAA) |
|---|---|---|
| Spermidine |  | –1668.207 a.u |
| Tyramine | 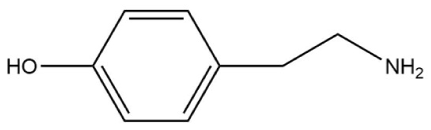 | –1627.883 a.u |
| Histamine | 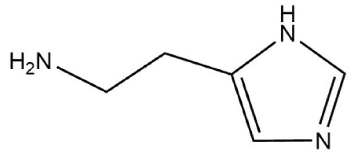 | –1586.008 a.u |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.-J.; Chang, R.; Zhu, Q.-J. Synthesis and Characterization of a Molecularly Imprinted Polymer of Spermidine and the Exploration of Its Molecular Recognition Properties. Polymers 2018, 10, 1389. https://doi.org/10.3390/polym10121389
Huang Y-J, Chang R, Zhu Q-J. Synthesis and Characterization of a Molecularly Imprinted Polymer of Spermidine and the Exploration of Its Molecular Recognition Properties. Polymers. 2018; 10(12):1389. https://doi.org/10.3390/polym10121389
Chicago/Turabian StyleHuang, Yu-Jie, Rui Chang, and Qiu-Jin Zhu. 2018. "Synthesis and Characterization of a Molecularly Imprinted Polymer of Spermidine and the Exploration of Its Molecular Recognition Properties" Polymers 10, no. 12: 1389. https://doi.org/10.3390/polym10121389
APA StyleHuang, Y.-J., Chang, R., & Zhu, Q.-J. (2018). Synthesis and Characterization of a Molecularly Imprinted Polymer of Spermidine and the Exploration of Its Molecular Recognition Properties. Polymers, 10(12), 1389. https://doi.org/10.3390/polym10121389





