Thinning Approximation for Calculating Two-Dimensional Scattering Patterns in Dissipative Particle Dynamics Simulations under Shear Flow
Abstract
1. Introduction
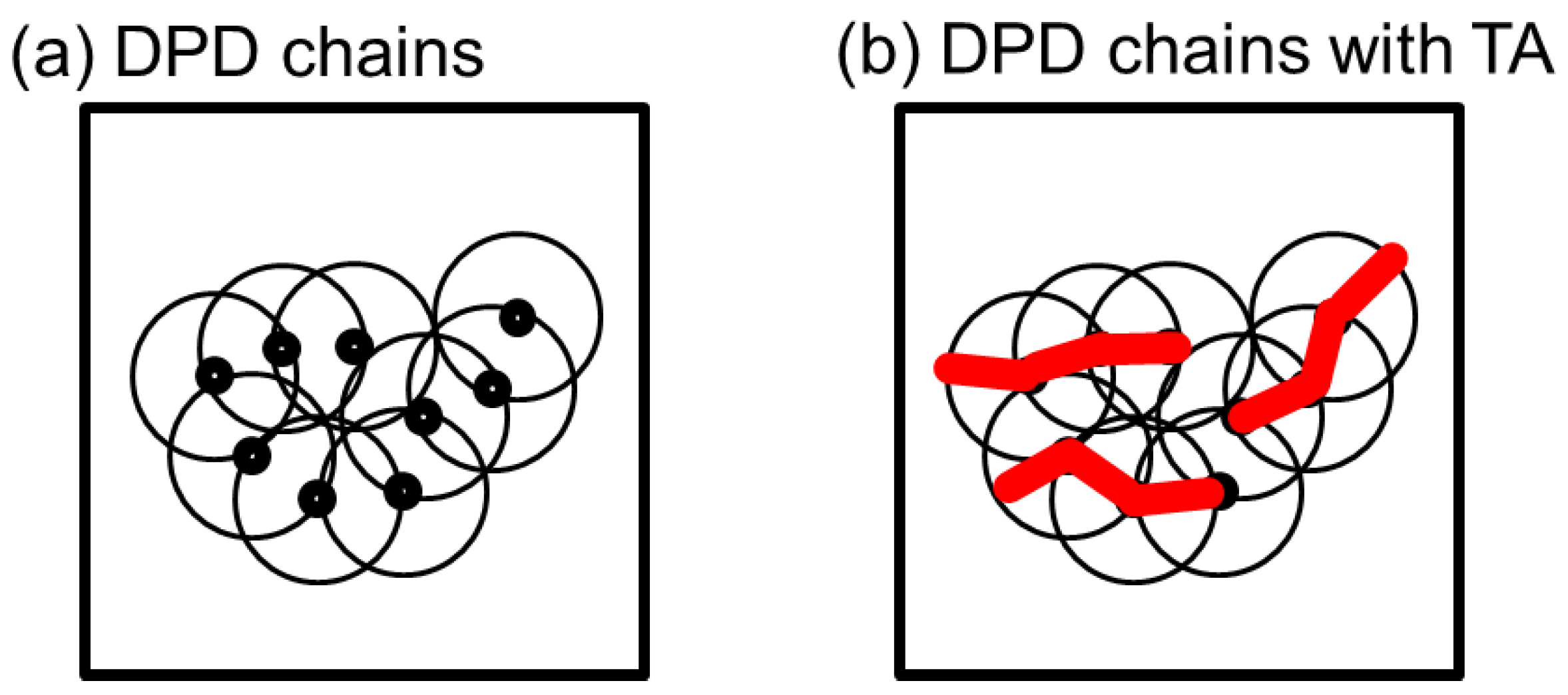
2. Methods and Model
2.1. DPD Simulations
2.2. Two-Dimensional Scattering Patterns
3. Results
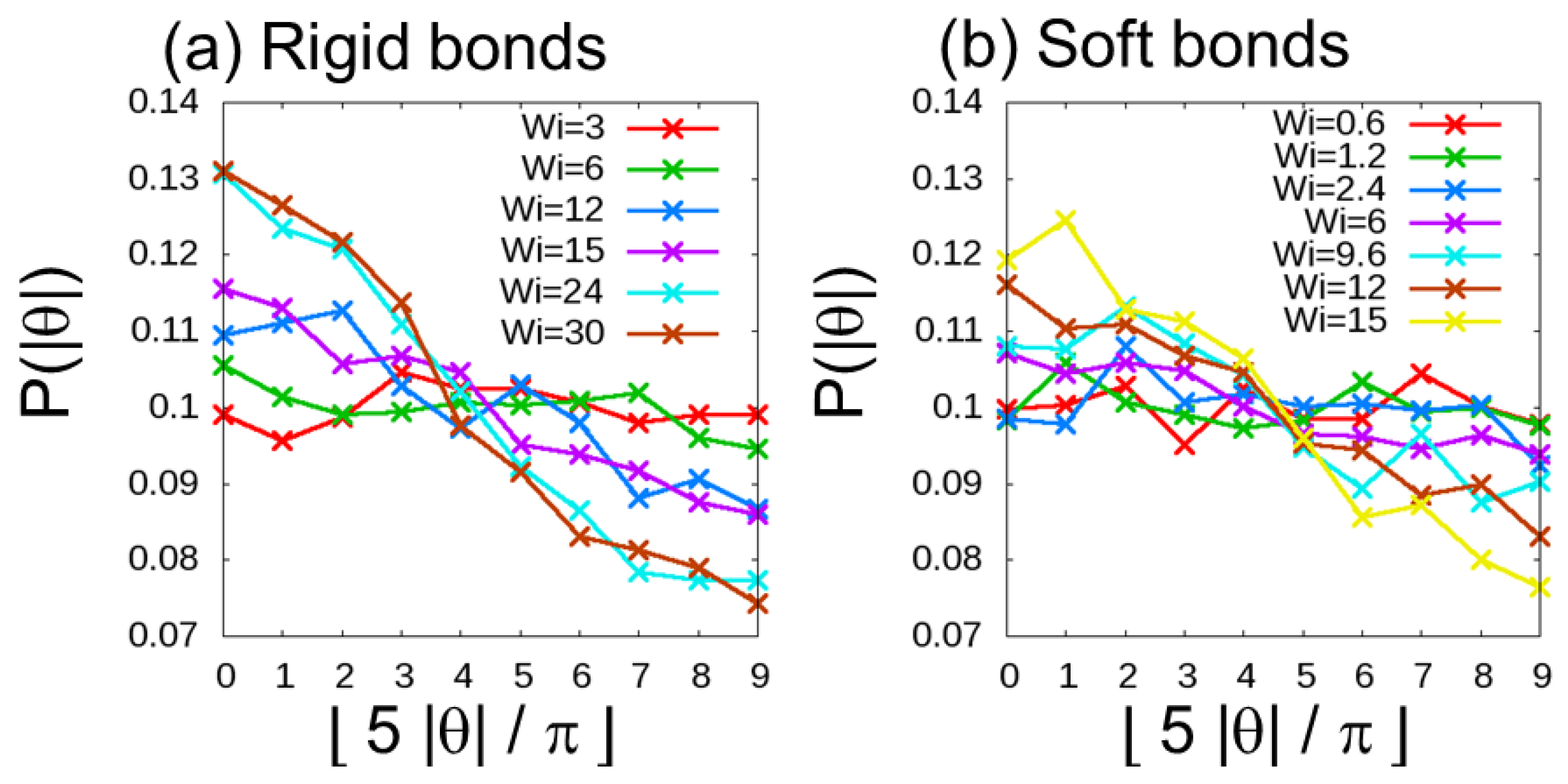
3.1. Weisenberg-Number Dependence of Orientation of Bond Vectors in DPD Simulations under Shear
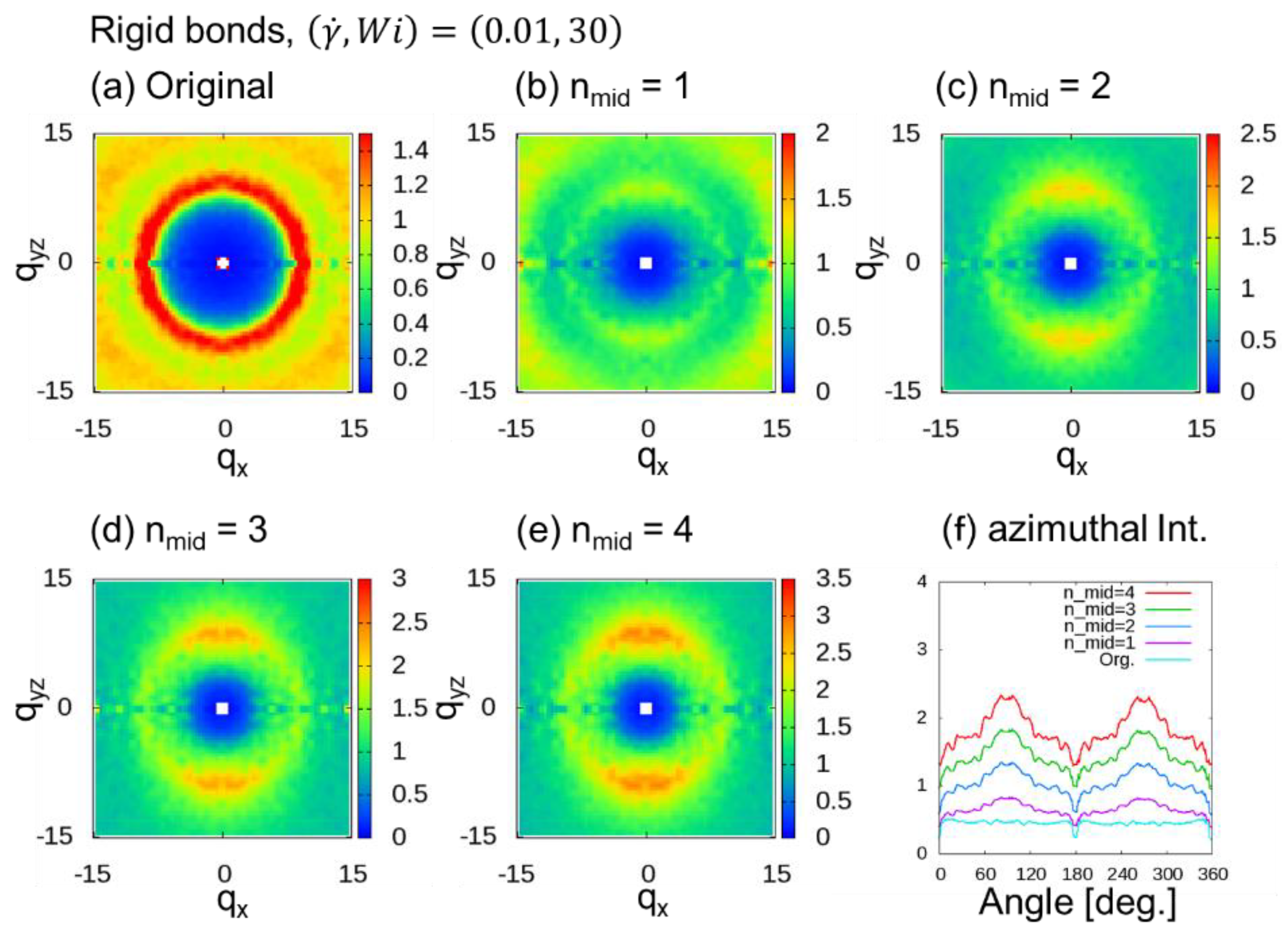
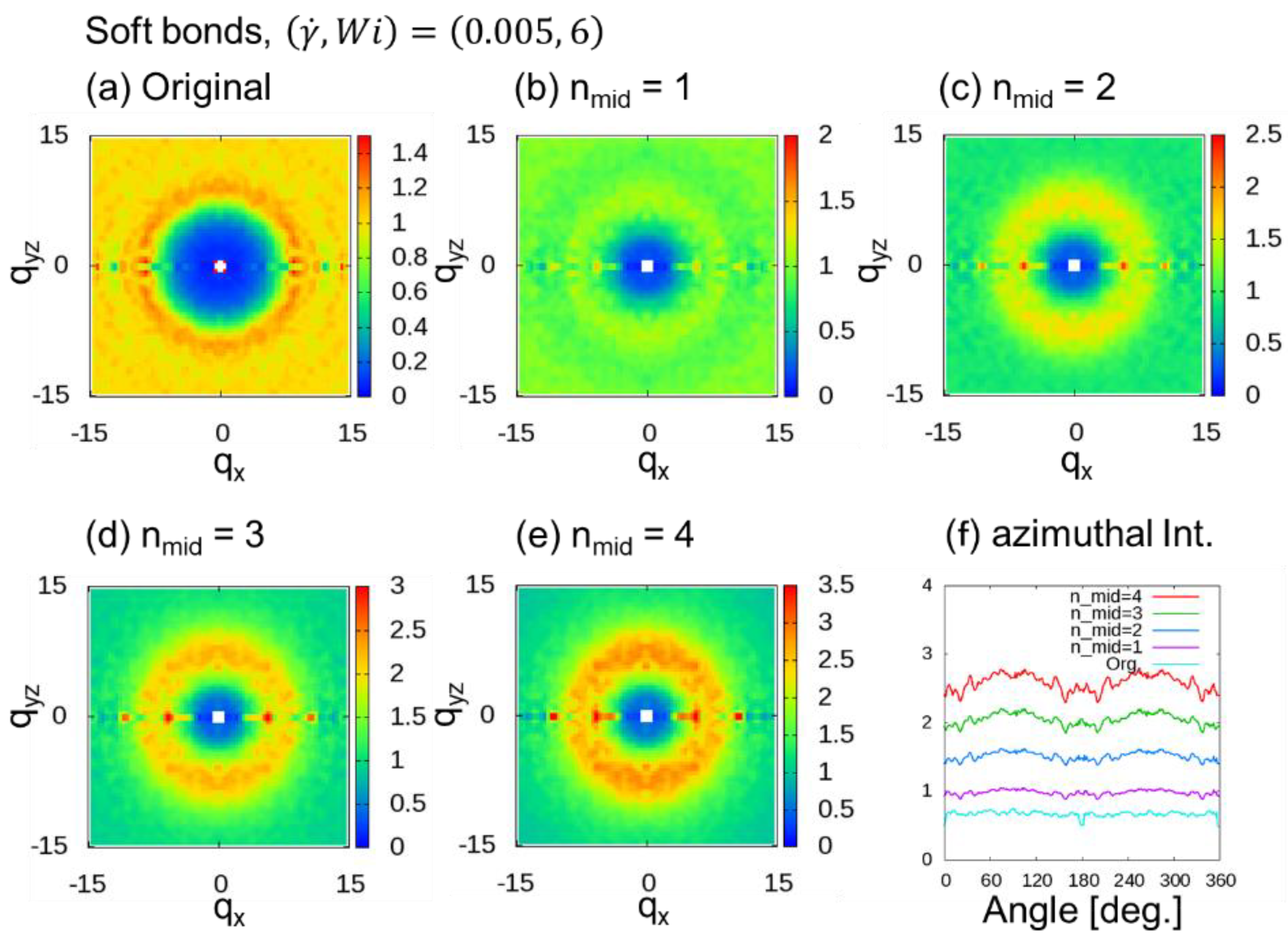
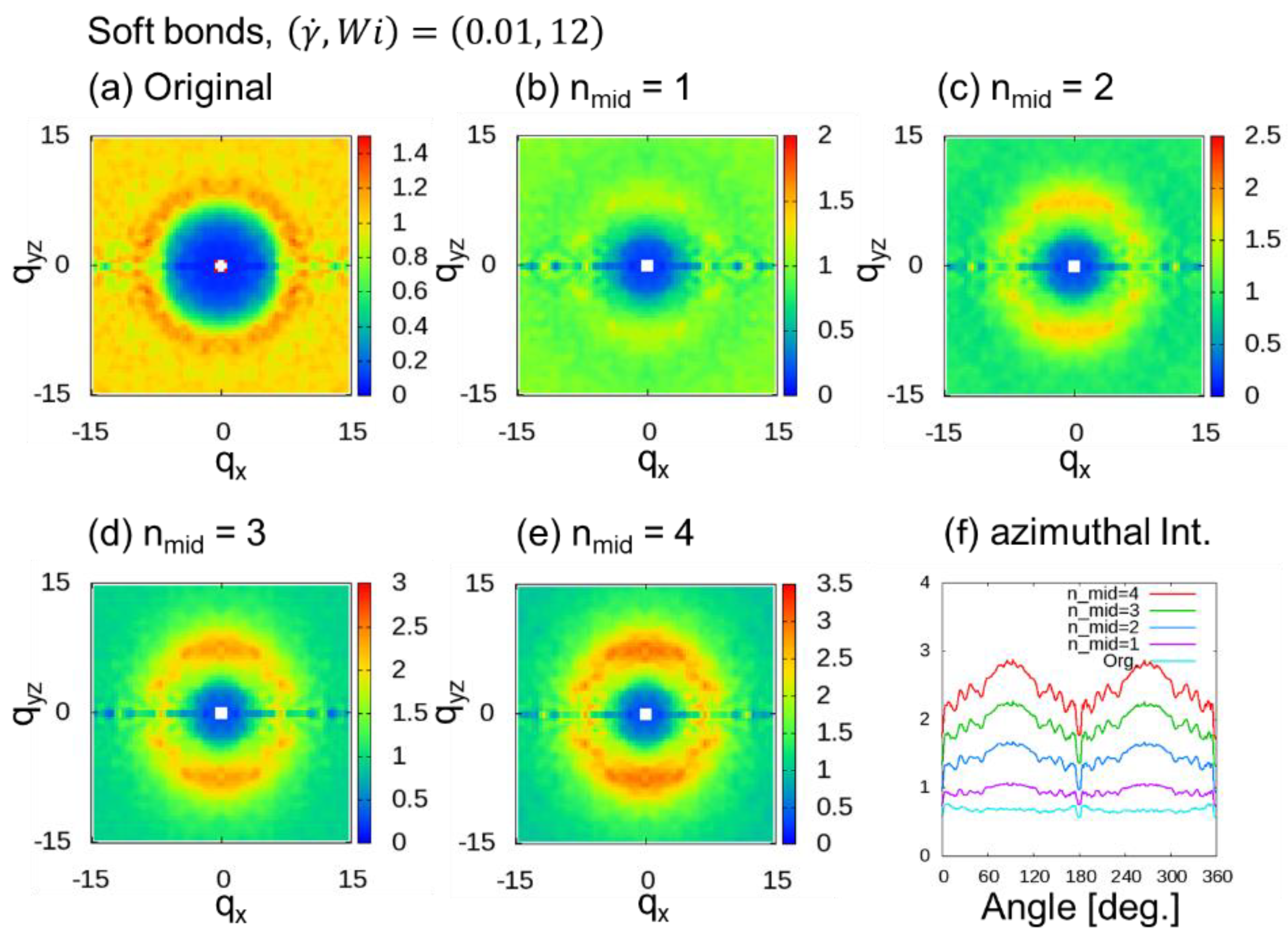
3.2. Thinning Approximation with Fixed Number of Additional Midpoints
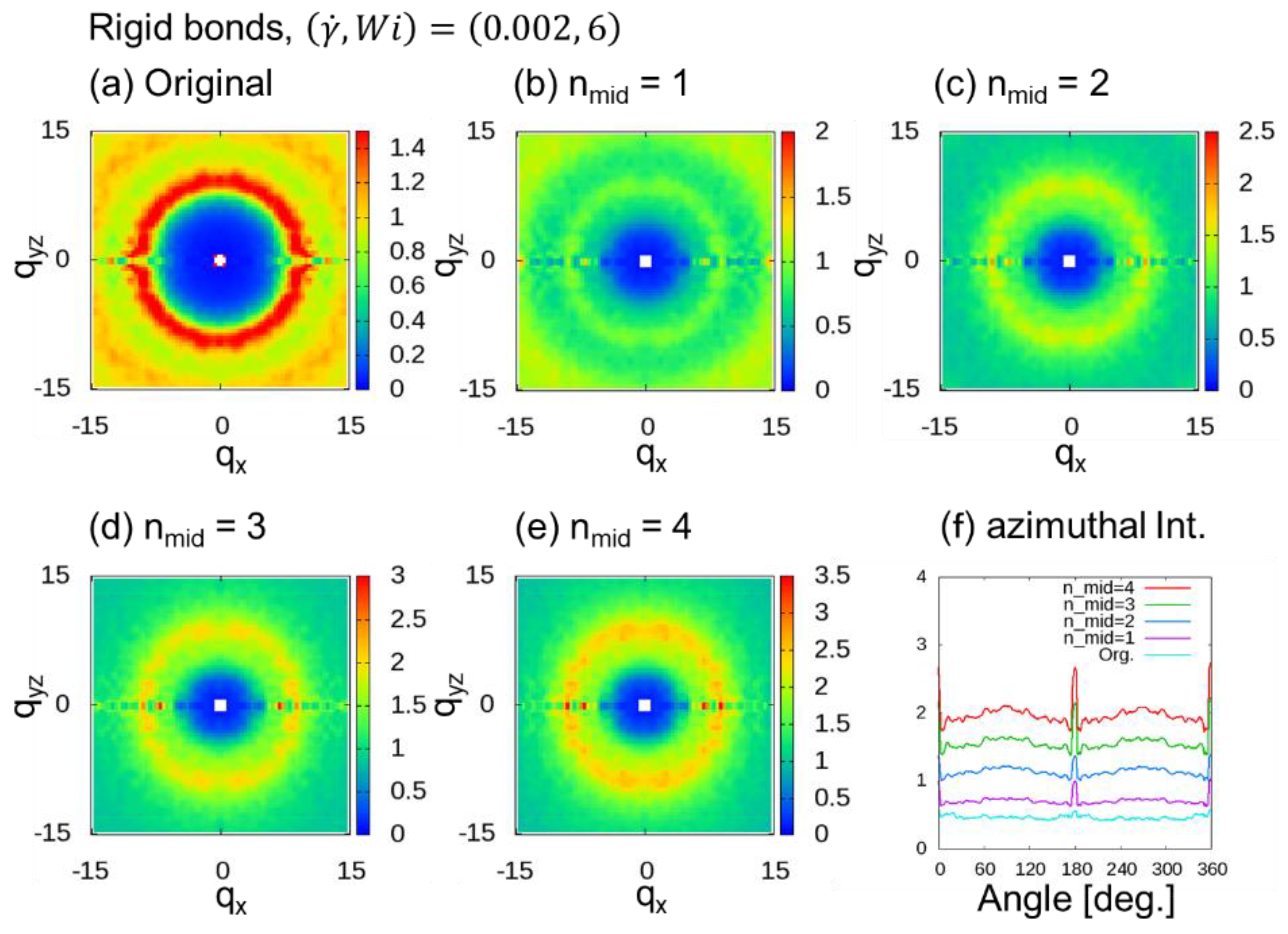
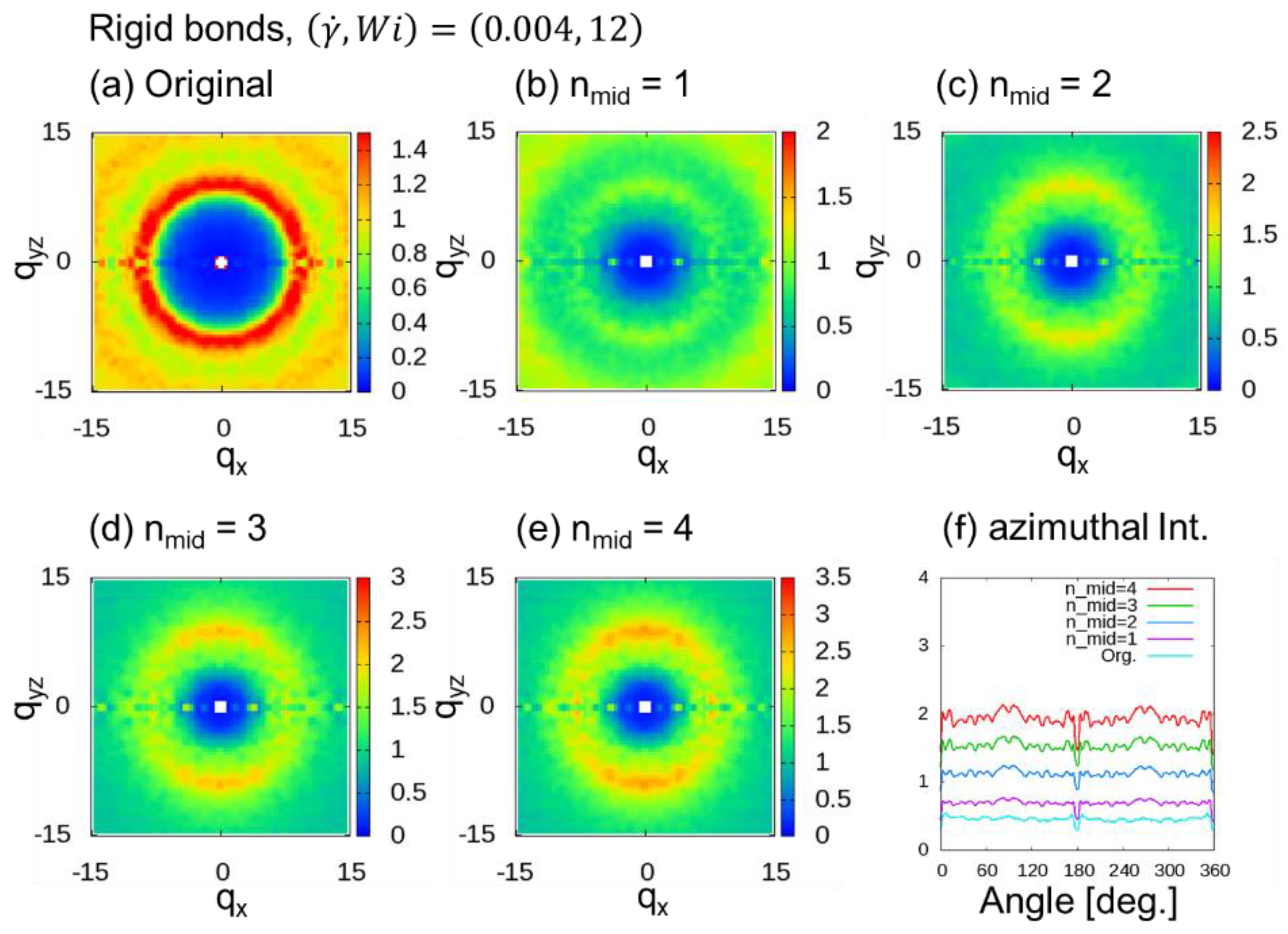
3.2.1. Rigid Bonds
3.2.2. Soft (Groot–Warren) Bonds
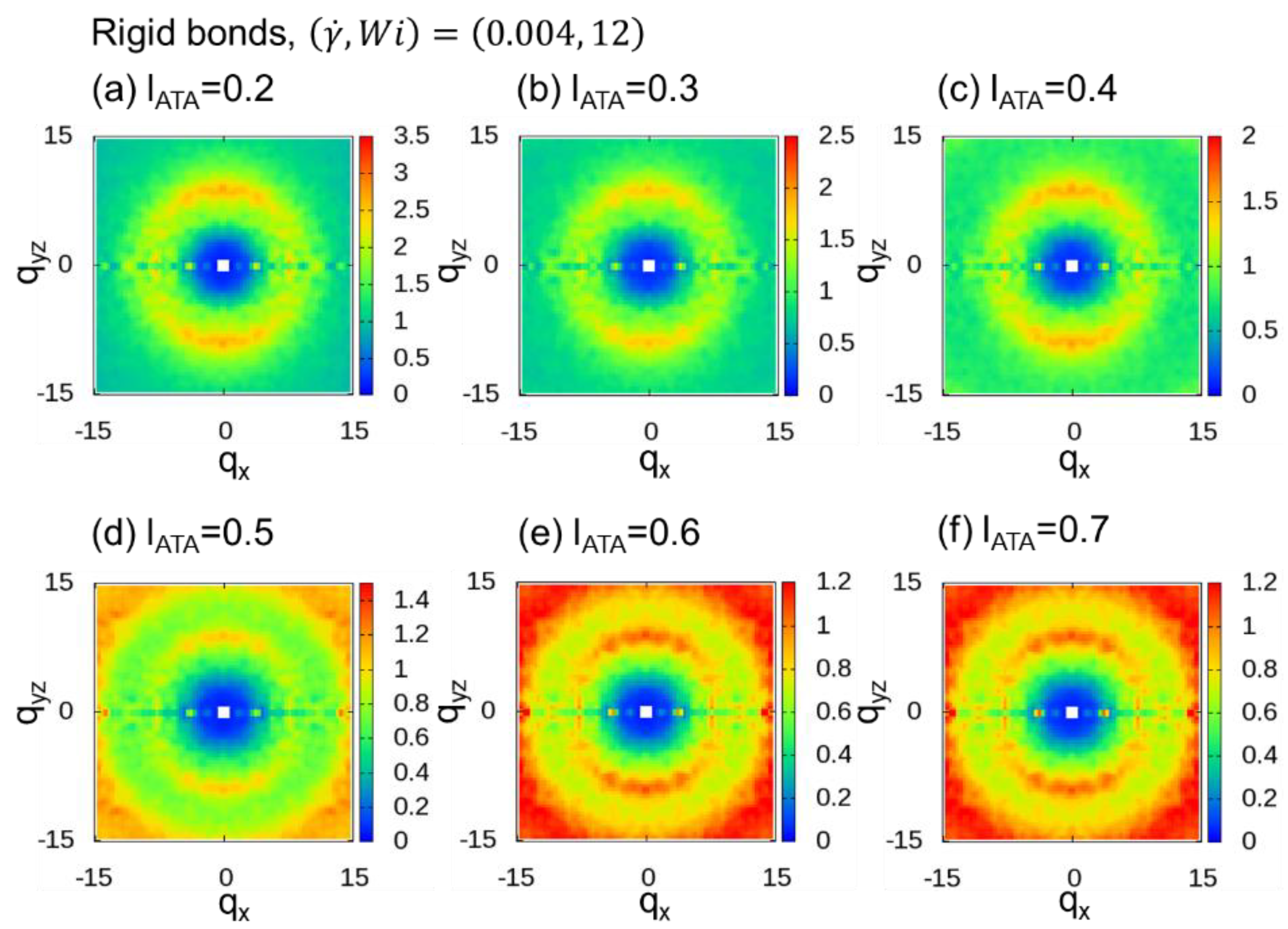
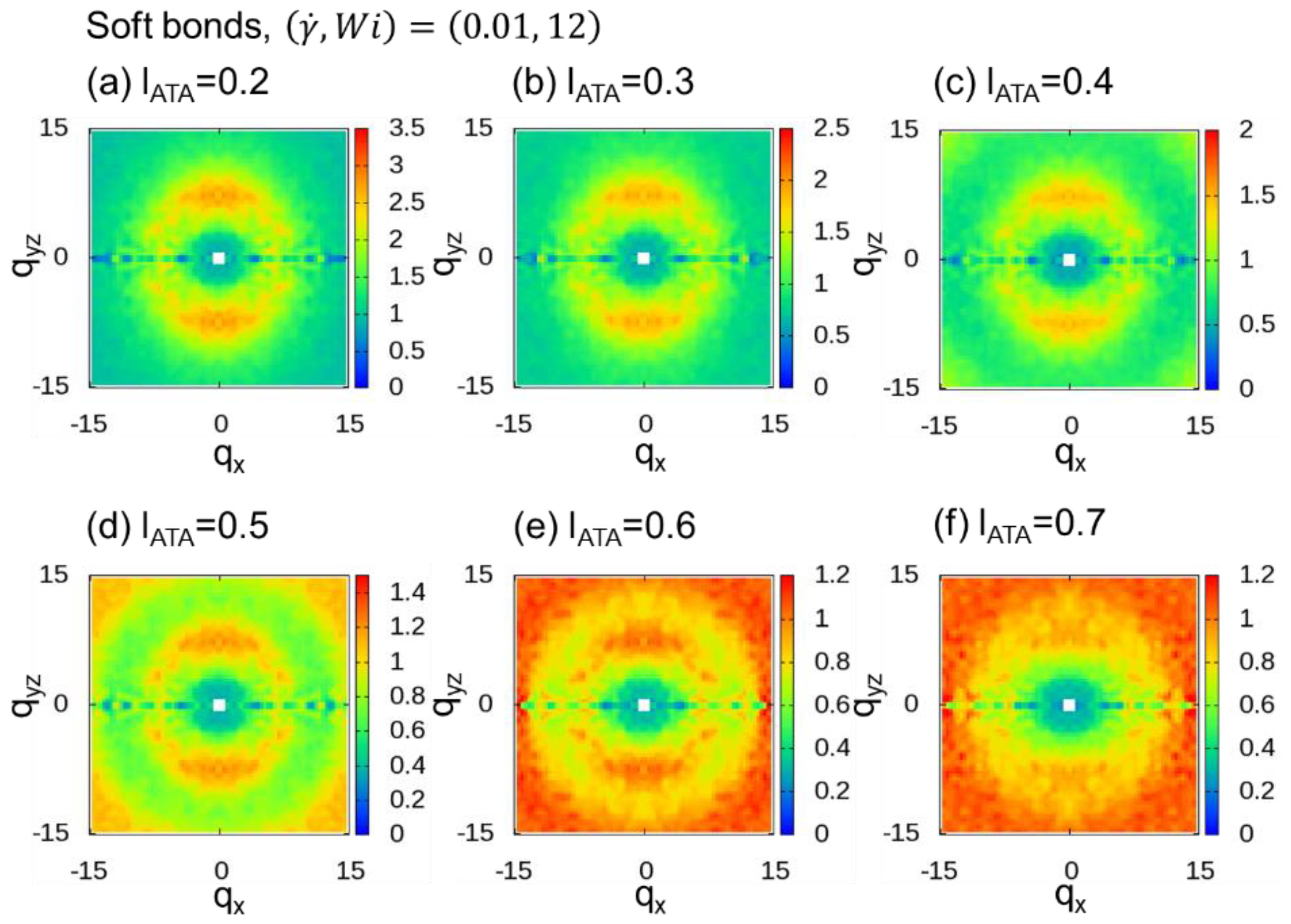
3.3. Adaptive Thinning Approximation (ATA)
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Espanõl, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Jiang, W.; Huang, J.; Wang, Y.; Laradji, M. Hydrodynamic interaction in polymer solutions simulated with dissipative particle dynamics. J. Chem. Phys. 2007, 126, 044901. [Google Scholar] [CrossRef] [PubMed]
- Tzoumanekas, C.; Lahmar, F.; Rousseau, B.; Theodorou, D.N. Onset of entanglements revisited. Topological analysis. Macromolecules 2009, 42, 7474–7484. [Google Scholar] [CrossRef]
- Lahmar, F.; Tzoumanekas, C.; Theodorou, D.N.; Rousseau, B. Topological analysis of linear polymer melts: A statistical approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar]
- Zhao, T.; Wang, X.; Jiang, L.; Larson, R.G. Dissipative particle dynamics simulation of dilute polymer solutions—Inertial effects and hydrodynamic interactions. J. Rheol. 2014, 58, 1039–1058. [Google Scholar] [CrossRef]
- Yong, X. Hydrodynamic interactions and entanglements of polymer solutions in many-body dissipative particle dynamics. Polymers 2016, 8, 426. [Google Scholar] [CrossRef]
- Groot, R.D.; Madden, T.J. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Lisal, M.; Brennan, J.K. Alignment of lamellar diblock copolymer phases under shear: Insight from dissipative particle dynamics Simulations. Langmuir 2007, 23, 4809–4818. [Google Scholar] [CrossRef] [PubMed]
- Soto-Figueroa, C.; Rodríguez-Hidalgo, M.D.R.; Martínez-Magadán, J.-M.; Vicente, L. Dissipative particle dynamics study of order−order phase transition of BCC, HPC, OBDD, and LAM structures of the poly(styrene)−poly(isoprene) diblock copolymer. Macromolecules 2008, 41, 3297–3304. [Google Scholar] [CrossRef]
- Khokhlov, A.R.; Khalatur, P.G. Microphase separation in diblock copolymers with amphiphilic block: Local chemical structure can dictate global morphology. Chem. Phys. Lett. 2008, 461, 58–63. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Kudryavtsev, Y.V.; Khalatur, P.G.; Chertovich, A.V. Microphase separation in regular and random copolymer melts by DPD simulations. Chem. Phys. Lett. 2011, 503, 277–282. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Kudryavtsev, Y.V.; Chertovich, A.V. Phase diagrams of block copolymer melts by dissipative particle dynamics simulations. J. Chem. Phys. 2013, 139, 224901. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qian, H.-J.; Lu, Z.-Y. The influence of one block polydispersity on phase separation of diblock copolymers: The molecular mechanism for domain spacing expansion. Polymer 2013, 54, 3716–3722. [Google Scholar] [CrossRef]
- Shillcock, J.C.; Lipowsky, R. Equilibrium structure and lateral stress distribution of amphiphilic bilayers from dissipative particle dynamics simulations. J. Chem. Phys. 2002, 117, 5048–5061. [Google Scholar] [CrossRef]
- Kranenburg, M.; Venturoli, M.; Smit, B. Phase Behavior and Induced Interdigitation in Bilayers Studied with Dissipative Particle Dynamics. J. Phys. Chem. B 2003, 107, 11491–11501. [Google Scholar] [CrossRef]
- Ganzenmüller, G.C.; Hiermaiera, S.; Steinhauser, M.O. Shock-wave induced damage in lipid bilayers: A dissipative particle dynamics simulation study. Soft Matter 2011, 7, 4307–4317. [Google Scholar] [CrossRef]
- Różycki, B.; Lipowsky, R. Spontaneous curvature of bilayer membranes from molecular simulations: Asymmetric lipid densities and asymmetric adsorption. J. Chem. Phys. 2015, 142, 054101. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, S.; Maruyama, Y.; Hyodo, S. Dissipative particle dynamics study of spontaneous vesicle formation of amphiphilic molecules. J. Chem. Phys. 2002, 116, 5842–5849. [Google Scholar] [CrossRef]
- Hong, B.; Qiu, F.; Zhang, H.; Yang, Y. Dissipative particle dynamics simulations on inversion dynamics of spherical micelles. J. Chem. Phys. 2010, 132, 244901. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.-T.; Vishnyakov, A.; Neimark, A.V. Calculations of critical micelle concentration by dissipative particle dynamics simulations: The role of chain rigidity. J. Phys. Chem. B 2013, 117, 10304–10310. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Kratky, O. Zum deformationsmechanismus der Faserstoffe, I. Colloid Polym. Sci. 1933, 64, 213–222. [Google Scholar] [CrossRef]
- Charlesby, A.; Hancock, N.H. The effect of cross-linking on the elastic modulus of polythene. Proc. R. Soc. Lond. Sec. A 1953, 218, 245–255. [Google Scholar] [CrossRef]
- Katz, J.R. X-ray spectrography of polymers and in particular those having a rubber-like extensibility. Trans. Faraday Soc. 1936, 32, 77–94. [Google Scholar] [CrossRef]
- Murthy, N.S.; Minor, H.; Bednarczyk, C.; Krimm, S. Structure of the amorphous phase in oriented polymers. Macromolecules 1993, 26, 1712–1721. [Google Scholar] [CrossRef]
- Romo-Uribe, A.; Windle, A.H. A flow-orientation transition in a thermotropic random copolyester. Macromolecules 1993, 26, 7100–7102. [Google Scholar] [CrossRef]
- Samon, J.M.; Schultz, J.M.; Hsiao, B.S.; Seifert, S.; Stribeck, N.; Gurke, I.; Collins, G.; Saw, C. Structure development during the melt spinning of polyethylene and poly(vinylidene fluoride) fibers by in situ synchrotron small- and wide-angle X-ray scattering techniques. Macromolecules 1999, 32, 8121–8132. [Google Scholar] [CrossRef]
- Toki, S.; Sics, I.; Ran, S.; Liu, L.; Hsiao, B.S. Molecular orientation and structural development in vulcanized polyisoprene rubbers during uniaxial deformation by in situ synchrotron X-ray diffraction. Polymer 2003, 44, 6003–6011. [Google Scholar] [CrossRef]
- Ogino, Y.; Fukushima, H.; Takahashi, N.; Matsuba, G.; Nishida, K.; Kanaya, T. Crystallization of isotactic polypropylene under shear flow observed in a wide spatial scale. Macromolecules 2006, 39, 7617–7625. [Google Scholar] [CrossRef]
- Bates, F.S.; Koppi, K.A.; Tirrell, M.; Almdal, K.; Mortensen, K. Influence of shear on the hexagonal-to-disorder transition in a diblock copolymer melt. Macromolecules 1994, 27, 5934–5936. [Google Scholar] [CrossRef]
- Okamoto, S.; Saijo, K.; Hashimoto, T. Real-Time SAXS Observations of lamella-forming block copolymers under large oscillatory shear deformation. Macromolecules 1994, 27, 5547–5555. [Google Scholar] [CrossRef]
- Vigild, M.E.; Almdal, K.; Mortensen, K.; Hamley, I.W.; Fairclough, J.P.A.; Ryan, A.J. Transformations to and from the gyroid phase in a diblock copolymer. Macromolecules 1998, 31, 5702–5716. [Google Scholar] [CrossRef]
- Reynders, K.; Mischenko, N.; Mortensen, K.; Overbergh, N.; Reynaers, H. Stretching-induced correlations in triblock copolymer gels as observed by small-angle neutron scattering. Macromolecules 1995, 28, 8699–8701. [Google Scholar] [CrossRef]
- Mortensen, K. Structural properties of self-assembled polymeric micelles. Curr. Opin. Coll. Interface Sci. 1998, 3, 12–19. [Google Scholar] [CrossRef]
- Krishnamoorti, R.; Silva, A.S.; Modi, M.A.; Hammouda, B. Small-angle neutron scattering study of a cylinder-to-sphere order-order transition in block copolymers. Macromolecules 2000, 33, 3803–3809. [Google Scholar] [CrossRef]
- Sakurai, S.; Aida, S.; Okamoto, S.; Sakurai, K.; Nomura, S. Mechanism of thermally induced morphological reorganization and lamellar orientation from the herringbone structure in cross-linked polystyrene-block-polybutadiene-block-polystyrene triblock copolymers. Macromolecules 2003, 36, 1930–1939. [Google Scholar] [CrossRef]
- Tomita, S.; Lei, L.; Urushihara, Y.; Kuwamoto, S.; Matsushita, T.; Sakamoto, N.; Sasaki, S.; Sakurai, S. Strain-induced deformation of glassy spherical microdomains in elastomeric triblock copolymer films: Simultaneous measurements of a stress-strain curve with 2d-SAXS patterns. Macromolecules 2017, 50, 677–686. [Google Scholar] [CrossRef]
- Tomita, S.; Wataoka, I.; Igarashi, N.; Shimizu, N.; Takagi, H.; Sasaki, S.; Sakurai, S. Strain-induced deformation of glassy spherical microdomains in elastomeric triblock copolymer films: Time-resolved 2d-SAXS measurements under stretched state. Macromolecules 2017, 50, 3404–3410. [Google Scholar] [CrossRef]
- Mao, R.; McCready, E.M.; Burghardt, W.R. Structural response of an ordered block copolymer melt to uniaxial extensional flow. Soft Matter 2014, 10, 6198–6207. [Google Scholar] [CrossRef] [PubMed]
- McCready, E.M.; Burghardt, W.R. In situ SAXS studies of structural relaxation of an ordered block copolymer melt following cessation of uniaxial extensional flow. Macromolecules 2014, 48, 264–271. [Google Scholar] [CrossRef]
- Matsushita, Y.; Nomura, M.; Watanabe, J.; Mogi, Y.; Noda, I.; Imai, M. Alternating lamellar structure of triblock copolymers of the ABA type. Macromolecules 1995, 28, 6007–6013. [Google Scholar] [CrossRef]
- Hagita, K.; Murashima, T.; Takano, H.; Kawakatsu, T. Thinning approximation for two-dimensional scattering patterns from coarse-grained polymer melts under shear flow. J. Phys. Soc. Jpn. 2017, 86, 124803. [Google Scholar] [CrossRef]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilibrium Liquids; Cambridge University Press: New York, NY, USA, 1990. [Google Scholar]
- Evans, D.J. The frequency dependent shear viscosity of methane. Mol. Phys. 1979, 37, 1745–1754. [Google Scholar] [CrossRef]
- Hansen, D.P.; Evans, D.J. A parallel algorithm for nonequilibrium molecular dynamics simulation of shear flow on distributed memory machines. Mol. Sim. 1994, 13, 375–393. [Google Scholar] [CrossRef]
- Lees, A.W.; Edwards, S.F. The computer study of transport processes under extreme conditions. J. Phys. C 1972, 5, 1921–1928. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Pan, G.; Manke, C.W. Developments toward Simulation of entangled polymer melts by dissipative particle dynamics (DPD). Int. J. Mod. Phys. B 2003, 17, 231–235. [Google Scholar] [CrossRef]
- Kumar, S.; Larson, R.G. Brownian dynamics simulations of flexible polymers with spring–spring repulsions. J. Chem. Phys. 2001, 114, 6937–6941. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entanglements using dissipative particle dynamics: application to polymer brushes. J. Chem. Phys. 2008, 129, 034902. [Google Scholar] [CrossRef] [PubMed]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entangled polymer brushes under shear: Compression and rheological properties. Macromolecules 2009, 42, 4310–4318. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Interactions between polymer brushes and a polymer solution: mesoscale modelling of the structural and frictional properties. Soft Matter 2010, 6, 3472–3481. [Google Scholar] [CrossRef]
- Sirk, T.W.; Slizoberg, Y.R.; Brennan, J.K.; Lisal, M.; Andzelm, J.W. An enhanced entangled polymer model for dissipative particle dynamics. J. Chem. Phys. 2012, 136, 134903. [Google Scholar] [CrossRef] [PubMed]
- Sliozberg, Y.R.; Sirk, T.W.; Brennan, J.K.; Andzelm, J.W. Bead-spring models of entangled polymer melts: Comparison of hard-core and soft-core potentials. J. Polym. Sci. B 2012, 50, 1694–1698. [Google Scholar] [CrossRef]
- Chantawansri, T.L.; Sirk, T.W.; Sliozberg, Y.R. Entangled triblock copolymer gel: morphological and mechanical properties. J. Chem. Phys. 2013, 138, 024908. [Google Scholar] [CrossRef] [PubMed]
- Chantawansri, T.L.; Sirk, T.W.; Mrozek, R.; Lenhart, J.L.; Kröger, M.; Sliozberg, Y.R. The effect of polymer chain length on the mechanical properties of triblock copolymer gels. Chem. Phys. Lett. 2014, 612, 157–161. [Google Scholar] [CrossRef]
- Iwaoka, N.; Hagita, K.; Takano, H. Multipoint segmental repulsive potential for entangled polymer simulations with dissipative particle dynamics. J. Chem. Phys. 2018, 149, 114901. [Google Scholar] [CrossRef] [PubMed]
- Larson, R.G. The Structure and Rheology of Complex Fluids; Oxford University Press: New York, NY, USA, 1999. [Google Scholar]
- Nicholson, D.A.; Rutledge, G.C. Molecular simulation of flow-enhanced nucleation in n-eicosane melts under steady shear and uniaxial extension. J. Chem. Phys. 2016, 145, 244903. [Google Scholar] [CrossRef] [PubMed]
- Murashima, T.; Hagita, K.; Kawakatsu, T. Elongational viscosity of weakly entangled polymer melt via coarse-grained molecular dynamics simulation. J. Soc. Rheol. Jpn. (Nihon Reoroji Gakkaishi) 2018, 46. in press. [Google Scholar]
- Kraynik, A.M.; Reinelt, D.A. Extensional motions of spatially periodic lattices. Int. J. Mutiphase Flow 1992, 18, 1045–1059. [Google Scholar] [CrossRef]

| Polymer Type | aij | K | r0 | σ |
|---|---|---|---|---|
| Soft bond [3,9,10,11,12,13,14,15] | 25 | 4.0 | 0.0 | 3.0 |
| Rigid bond [52,53,54,55,56,57,58] | 60 | 450 | 0.85 | 3.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hagita, K.; Murashima, T.; Iwaoka, N. Thinning Approximation for Calculating Two-Dimensional Scattering Patterns in Dissipative Particle Dynamics Simulations under Shear Flow. Polymers 2018, 10, 1224. https://doi.org/10.3390/polym10111224
Hagita K, Murashima T, Iwaoka N. Thinning Approximation for Calculating Two-Dimensional Scattering Patterns in Dissipative Particle Dynamics Simulations under Shear Flow. Polymers. 2018; 10(11):1224. https://doi.org/10.3390/polym10111224
Chicago/Turabian StyleHagita, Katsumi, Takahiro Murashima, and Nobuyuki Iwaoka. 2018. "Thinning Approximation for Calculating Two-Dimensional Scattering Patterns in Dissipative Particle Dynamics Simulations under Shear Flow" Polymers 10, no. 11: 1224. https://doi.org/10.3390/polym10111224
APA StyleHagita, K., Murashima, T., & Iwaoka, N. (2018). Thinning Approximation for Calculating Two-Dimensional Scattering Patterns in Dissipative Particle Dynamics Simulations under Shear Flow. Polymers, 10(11), 1224. https://doi.org/10.3390/polym10111224






