Figure 1.
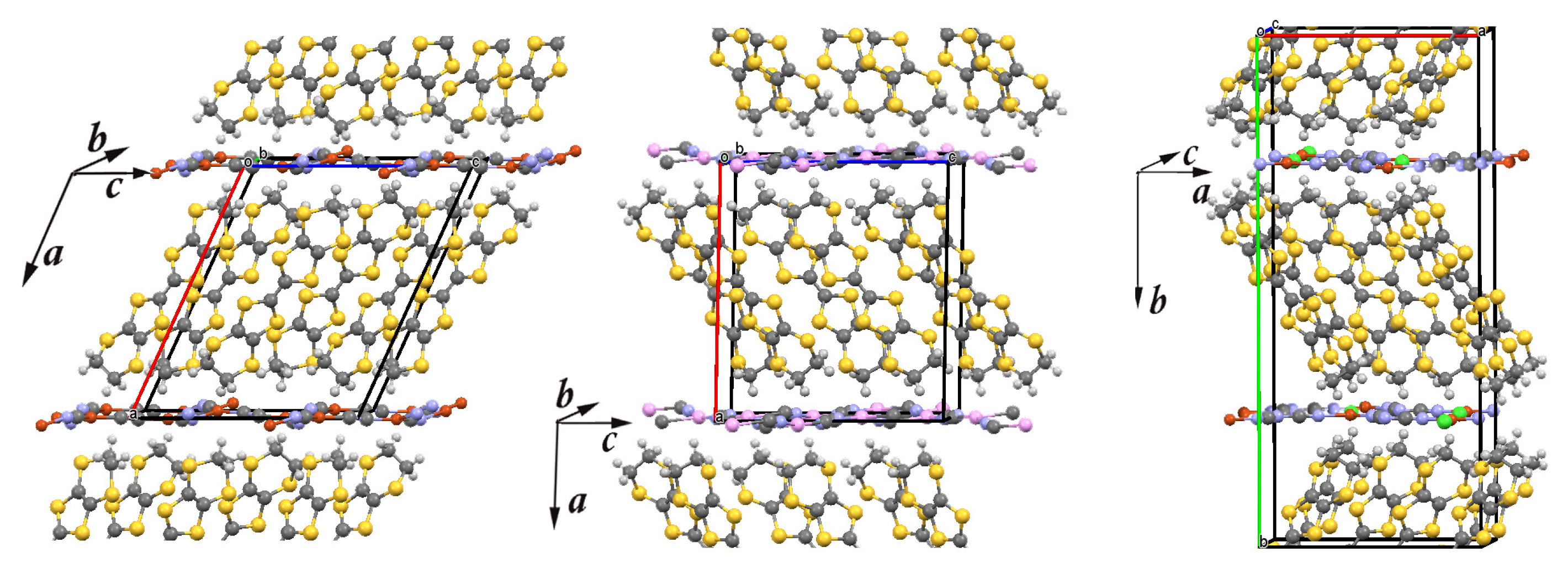
The crystal structure of three layered organic charge-transfer salts -(BEDT-TTF) (X = Cu(CN), Ag(CN), and Cu[N(CN)]Cl). Carbon, sulfur, and hydrogen atoms of the bis(ethylenedithio)tetrathiafulvalene [CH)]CS (BEDT-TTF) molecule are denoted in dark gray, yellow, and light gray, respectively. In the anion (X) network, chlorine, cooper, silver, carbon, and nitrogen are denoted in green, red, pink, dark grey, and violet, respectively. The lines mark the unit cell. Left panel: The unit cell of -CuCN contains 4 BEDT-TTF molecules and 2 Cu(CN) anions. Middle panel: The unit cell of -AgCN contains 4 BEDT-TTF molecules and 2 Ag(CN) anions. Right panel: The unit cell of -Cl contains 8 BEDT-TTF molecules and 4 Cu[N(CN)]Cl anions.
Figure 1.
The crystal structure of three layered organic charge-transfer salts -(BEDT-TTF) (X = Cu(CN), Ag(CN), and Cu[N(CN)]Cl). Carbon, sulfur, and hydrogen atoms of the bis(ethylenedithio)tetrathiafulvalene [CH)]CS (BEDT-TTF) molecule are denoted in dark gray, yellow, and light gray, respectively. In the anion (X) network, chlorine, cooper, silver, carbon, and nitrogen are denoted in green, red, pink, dark grey, and violet, respectively. The lines mark the unit cell. Left panel: The unit cell of -CuCN contains 4 BEDT-TTF molecules and 2 Cu(CN) anions. Middle panel: The unit cell of -AgCN contains 4 BEDT-TTF molecules and 2 Ag(CN) anions. Right panel: The unit cell of -Cl contains 8 BEDT-TTF molecules and 4 Cu[N(CN)]Cl anions.
Figure 2.
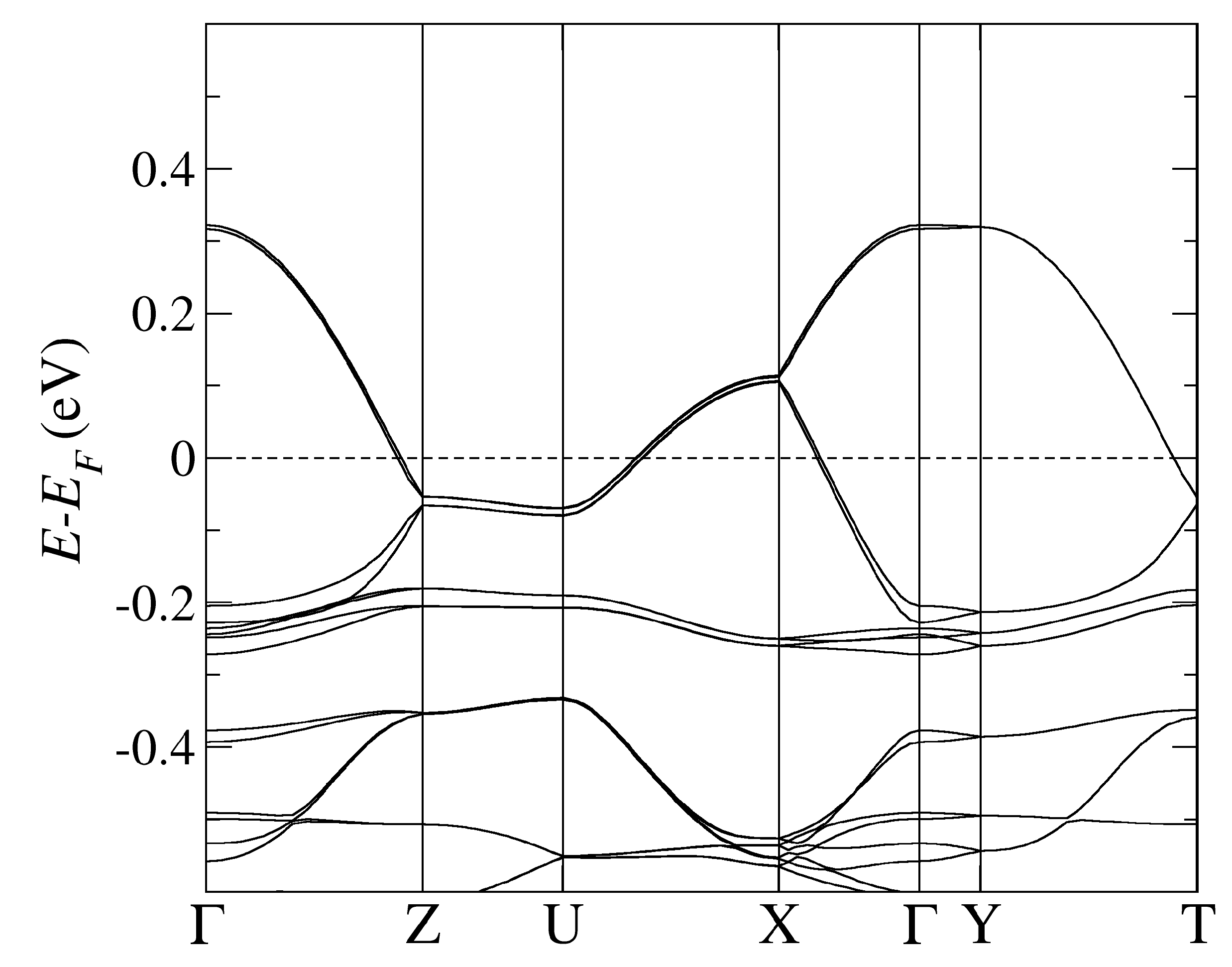
The band structure of -CuCN obtained by using PBE-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (0,0,1/2); Y = (1/2,0,0), Z = (0,1/2,0) in the units of reciprocal lattice vectors.
Figure 2.
The band structure of -CuCN obtained by using PBE-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (0,0,1/2); Y = (1/2,0,0), Z = (0,1/2,0) in the units of reciprocal lattice vectors.
Figure 3.
The band structure of -AgCN obtained by using PBE-vdW and the pseudopotentials C, Ag. = (0,0,0); X = (0,0,1/2); Y = (1/2,0,0), Z = (0,1/2,0) in the units of reciprocal lattice vectors.
Figure 3.
The band structure of -AgCN obtained by using PBE-vdW and the pseudopotentials C, Ag. = (0,0,0); X = (0,0,1/2); Y = (1/2,0,0), Z = (0,1/2,0) in the units of reciprocal lattice vectors.
Figure 4.
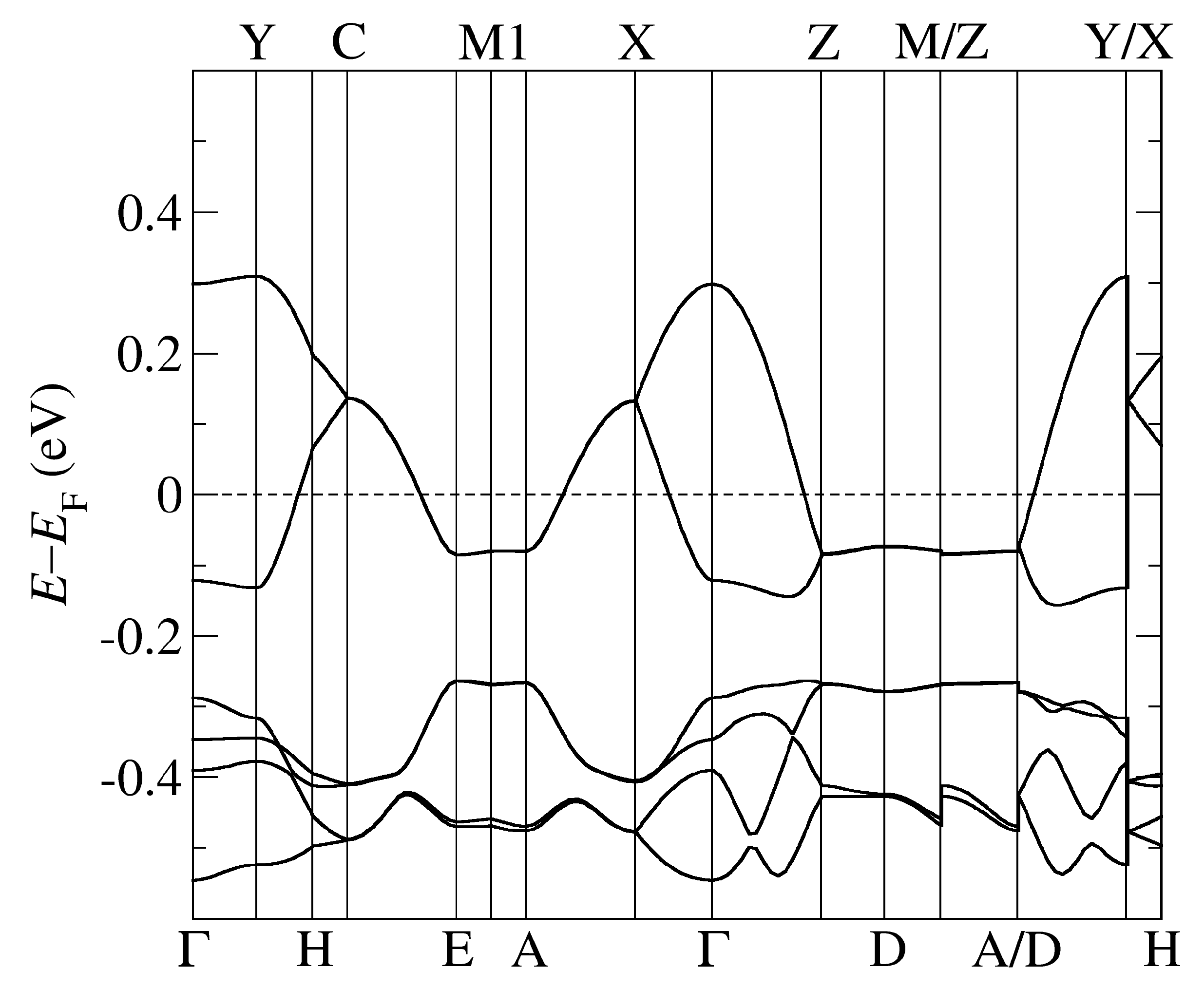
The band structure of -Cl obtained by using PBE-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (1/2,0,0); Y = (0,1/2,0), Z = (0,0,1/2) in the units of reciprocal lattice vectors.
Figure 4.
The band structure of -Cl obtained by using PBE-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (1/2,0,0); Y = (0,1/2,0), Z = (0,0,1/2) in the units of reciprocal lattice vectors.
Figure 5.
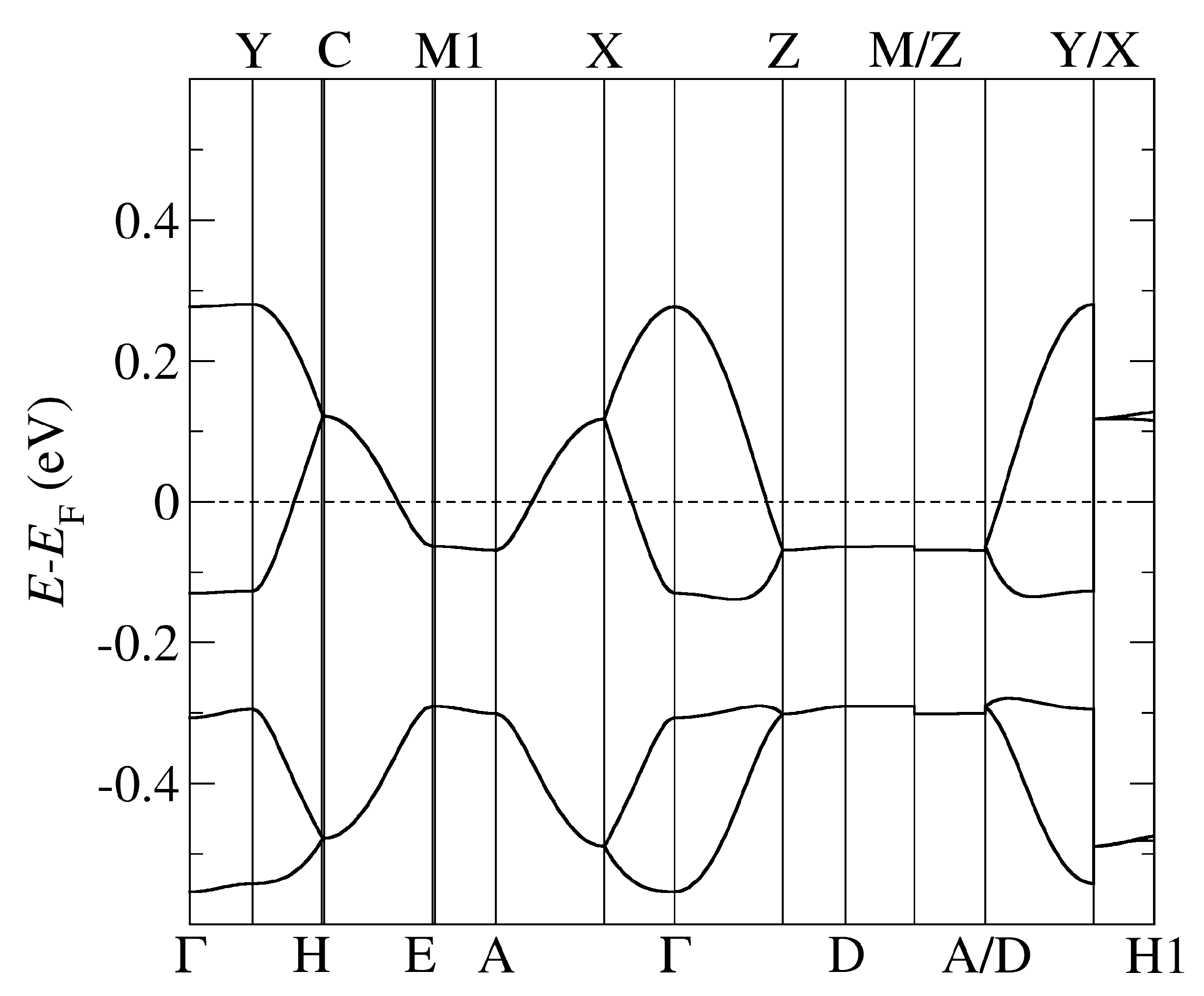
The band structure of -Cl obtained by using optB88-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (1/2,0,0); Y = (0,1/2,0), Z = (0,0,1/2) in the units of reciprocal lattice vectors.
Figure 5.
The band structure of -Cl obtained by using optB88-vdW and the pseudopotentials C, Cu. = (0,0,0); X = (1/2,0,0); Y = (0,1/2,0), Z = (0,0,1/2) in the units of reciprocal lattice vectors.
Table 1.
Unit cell volume enhancement (in %), defined as relative deviation from the experimental value, of -CuCN, -AgCN, and -Cl, obtained from ab initio calculations without van der Waals (vdW, based on PBE functional) and with vdW (based on the PBE-vdW functional). Pseudopotentials used for each system are indicated.
Table 1.
Unit cell volume enhancement (in %), defined as relative deviation from the experimental value, of -CuCN, -AgCN, and -Cl, obtained from ab initio calculations without van der Waals (vdW, based on PBE functional) and with vdW (based on the PBE-vdW functional). Pseudopotentials used for each system are indicated.
| System | -CuCN | -AgCN | -Cl |
|---|
| Pseudopotentials | C, Cu | C, Ag | C, Cu |
| Method: without vdW (PBE) | | | |
| u.c.volume enhancement (%) | 9.7 | 14.1 | 15.3 |
| Method: with vdW (PBE-vdW) | | | |
| u.c.volume enhancement (%) | 2.8 | 2.8 | 2.6 |
Table 2.
Unit cell volume enhancement (in %), defined as relative deviation from the experimental value, of -Cl obtained from ab initio calculations without vdW (based on the PBE functional) and with vdW (based on the optB88-vdW functional), using a different set of pseudopotentials denoted as choices (1), (2), and (3).
Table 2.
Unit cell volume enhancement (in %), defined as relative deviation from the experimental value, of -Cl obtained from ab initio calculations without vdW (based on the PBE functional) and with vdW (based on the optB88-vdW functional), using a different set of pseudopotentials denoted as choices (1), (2), and (3).
| Systems | -Cl | -Cl | -Cl |
|---|
| Pseudopotentials | C, Cu | C, Cu | C, Cu |
| Choice | (1) | (2) | (3) |
| Method: without vdW (PBE) | | | |
| u.c.volume enhancement (%) | 15.3 | 7.0 | 1.4 |
| Method: vdW (optB88-vdW) | | | |
| u.c.volume enhancement (%) | −0.48 | −0.2 | −2.7 |
Table 3.
Unit cell parameters of -Cl obtained from X-ray diffraction measurements at 100 K (left column), ab initio calculations based on the PBE functional (central column) and on the optB88-vdW functional (right column). In both types of calculations, the pseudopotentials denoted as choice (1) were used. Relative deviations from experimental values are given in parentheses.
Table 3.
Unit cell parameters of -Cl obtained from X-ray diffraction measurements at 100 K (left column), ab initio calculations based on the PBE functional (central column) and on the optB88-vdW functional (right column). In both types of calculations, the pseudopotentials denoted as choice (1) were used. Relative deviations from experimental values are given in parentheses.
| Unit Cell Parameters | Exp | Calc:PBE | Calc:optB88-vdW |
|---|
| a | 12.885200 Å | 13.2979 Å (+3.2%) | 12.9192 Å (+0.3%) |
| b | 29.575899 Å | 30.3005 Å (+2.5%) | 29.6463 Å (+0.24%) |
| c | 8.416100 Å | 9.17607 Å (+9.0%) | 8.33348 Å (−0.98%) |
| 90.000000 | 90.0000 | 90.0000 |
| 90.000000 | 90.0000 | 90.0000 |
| 90.000000 | 90.0000 | 90.0000 |
| V | 3207.303 Å | 3697,342 Å (+15.3%) | 3191,777 Å |
Table 4.
Unit cell parameters of -Cl obtained from X-ray diffraction measurements at 100 K (left column), ab initio calculations based on the PBE functional (central column) and on the optB88-vdW functional (right column). In both types of calculations, the pseudopotentials denoted as choice (2) were used. Relative deviations from experimental values are given in parentheses.
Table 4.
Unit cell parameters of -Cl obtained from X-ray diffraction measurements at 100 K (left column), ab initio calculations based on the PBE functional (central column) and on the optB88-vdW functional (right column). In both types of calculations, the pseudopotentials denoted as choice (2) were used. Relative deviations from experimental values are given in parentheses.
| Unit Cell Parameters | Exp | Calc:PBE | Calc:optB88-vdW |
|---|
| a | 12.885200 Å | 13.1036 Å (+1.7%) | 12.7035 Å (−1.4%) |
| b | 29.575899 Å | 30.2876 Å (+2.4%) | 30.0509 Å (+1.6%) |
| c | 8.416100 Å | 8.64857 Å (+2.8%) | 8.38187 Å (−0.4%) |
| 90.000000 | 90.5498 | 90.3761 |
| 90.000000 | 90.0000 | 90.9031 |
| 90.000000 | 90.4393 | 89.2194 |
| V | 3207.303 Å | 3432,415 Å (+7.0%) | 3199,792 Å |
Table 5.
Direct bandwidth of
-CuCN,
-AgCN, and
-Cl, defined as the width of antibonding bands straddling the Fermi level at the
point obtained from ab initio calculations that include vdW interactions (this work) or without them ([
8,
11,
20]). Space groups are also denoted.
Table 5.
Direct bandwidth of
-CuCN,
-AgCN, and
-Cl, defined as the width of antibonding bands straddling the Fermi level at the
point obtained from ab initio calculations that include vdW interactions (this work) or without them ([
8,
11,
20]). Space groups are also denoted.
| System | -CuCN | -AgCN | -Cl | Ref. |
|---|
| Space group | | | | |
| Method: DFT: vdW (PBE-vdW) | | | | this work |
| Bandwidth (meV) | 433 | 406 | 550 | |
| Space group | | | | |
| Method: DFT: vdW (optB88-vdW) | | | | this work |
| Bandwidth (meV) | | | 590 | |
| Space group | | | | |
| Method: DFT: without vdW (PBE) | | | | [20] |
| direct bandwidth (meV) | 400 | | 540 | |
| Space group | P | | | |
| Method: DFT: without vdW (PBE) | | | | [8] |
| Bandwidth (meV) | 390 | | | |
| Space group | | | | |
| Method: Extended Hückel | | | | [11] |
| Bandwidth (meV) | 480 | 458 | 607 | |
Table 6.
Direct antibonding and bonding bandwidths of
-Cl defined as the width at the
point obtained from ab initio calculations that include vdW interactions (this work), or without them ([
20]).
Table 6.
Direct antibonding and bonding bandwidths of
-Cl defined as the width at the
point obtained from ab initio calculations that include vdW interactions (this work), or without them ([
20]).
| System | -Cl | Ref. |
|---|
| Method: DFT: vdW (optB88-vdW) | | this work |
| antibonding bandwidth, outer (meV) | 590 | |
| antibonding bandwidth, inner (meV) | 570 | |
| bonding bandwidth, outer (meV) | 180 | |
| bonding bandwidth, inner (meV) | 150 | |
| Method: DFT: vdW (PBE-vdW) | | this work |
| antibonding bandwidth, outer (meV) | 550 | |
| antibonding bandwidth, inner (meV) | 520 | |
| bonding bandwidth, outer (meV) | 180 | |
| bonding bandwidth, inner (meV) | 140 | |
| Method: DFT: without vdW (PBE) | | [20] |
| antibonding bandwidth, outer (meV) | 540 | |
| antibonding bandwidth, inner (meV) | 490 | |
| bonding bandwidth, outer (meV) | 200 | |
| bonding bandwidth, inner (meV) | 180 | |
Table 7.
Hole () and electron () occupations per unit cell of -CuCN, -AgCN, and -Cl, obtained from ab initio calculations with vdW interactions included via the PBE-vdW functional.
Table 7.
Hole () and electron () occupations per unit cell of -CuCN, -AgCN, and -Cl, obtained from ab initio calculations with vdW interactions included via the PBE-vdW functional.
| Systems | -CuCN | -AgCN | -Cl |
|---|
| / u.c. | 1.93 | 2 | 4 |
| / u.c. | 1.96 | 2 | - |