Charging of Superconducting Layers in Arrays of Coupled Josephson Junctions for Overcritical Currents
Abstract
1. Introduction
2. Model and Method
3. Main Results
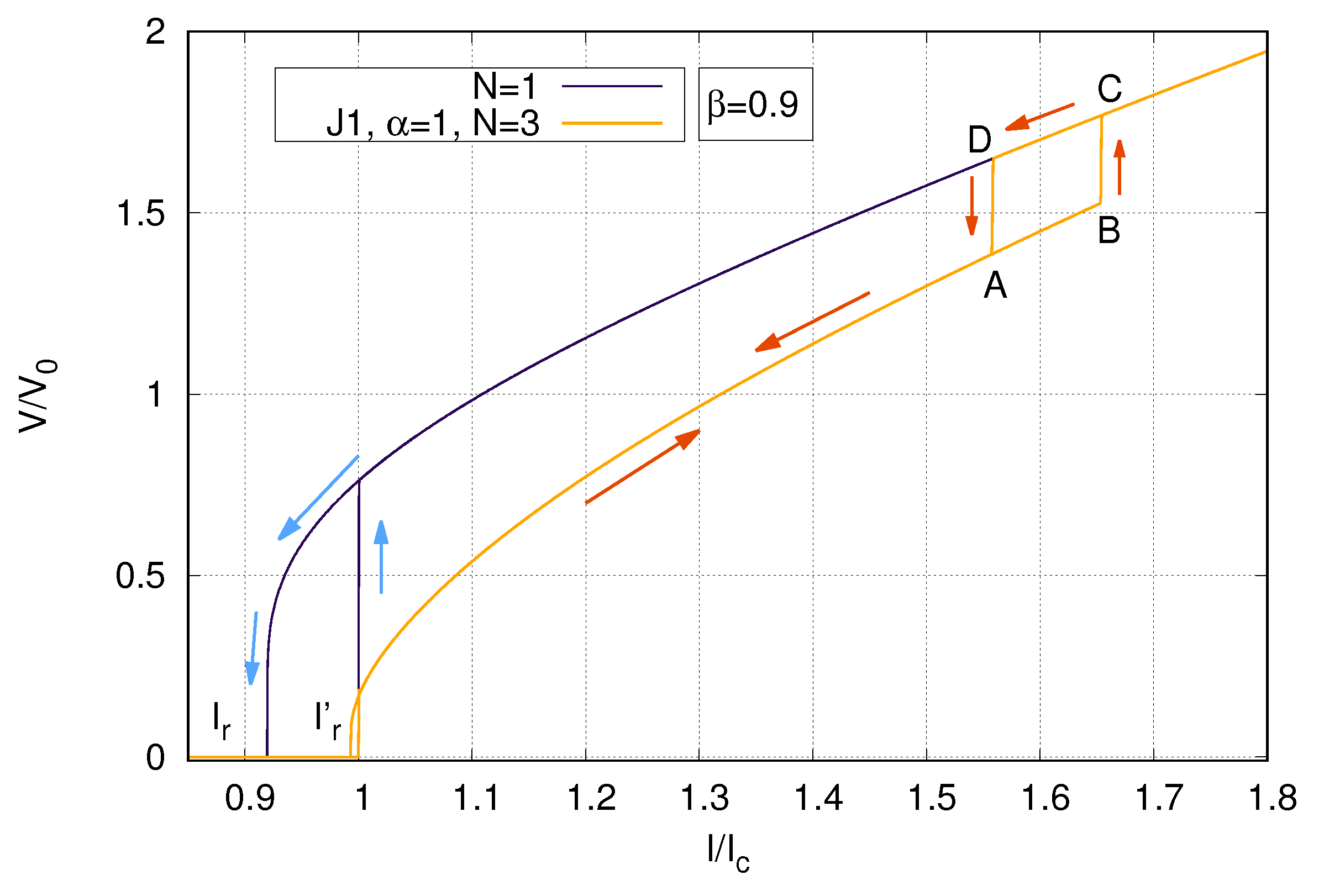
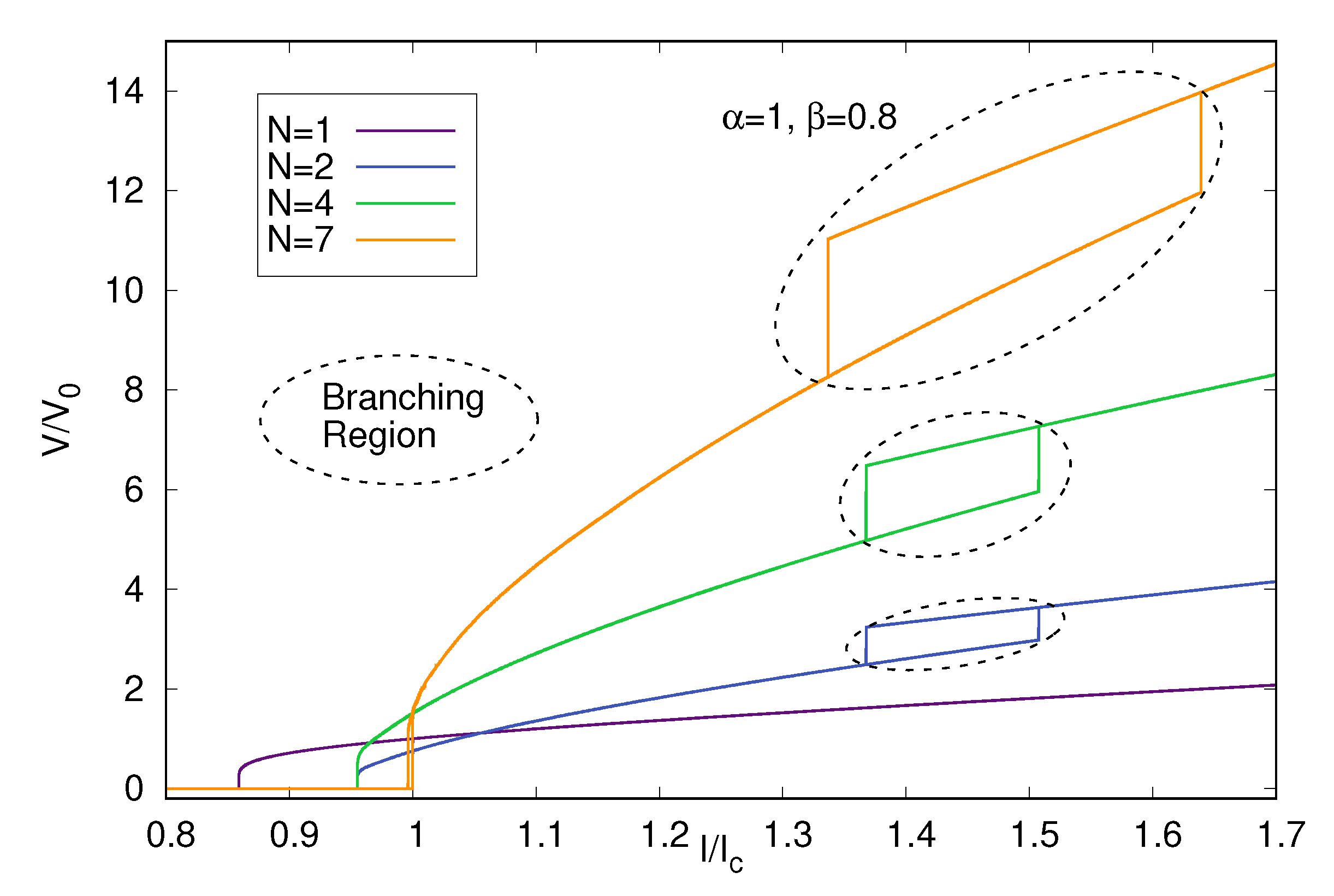
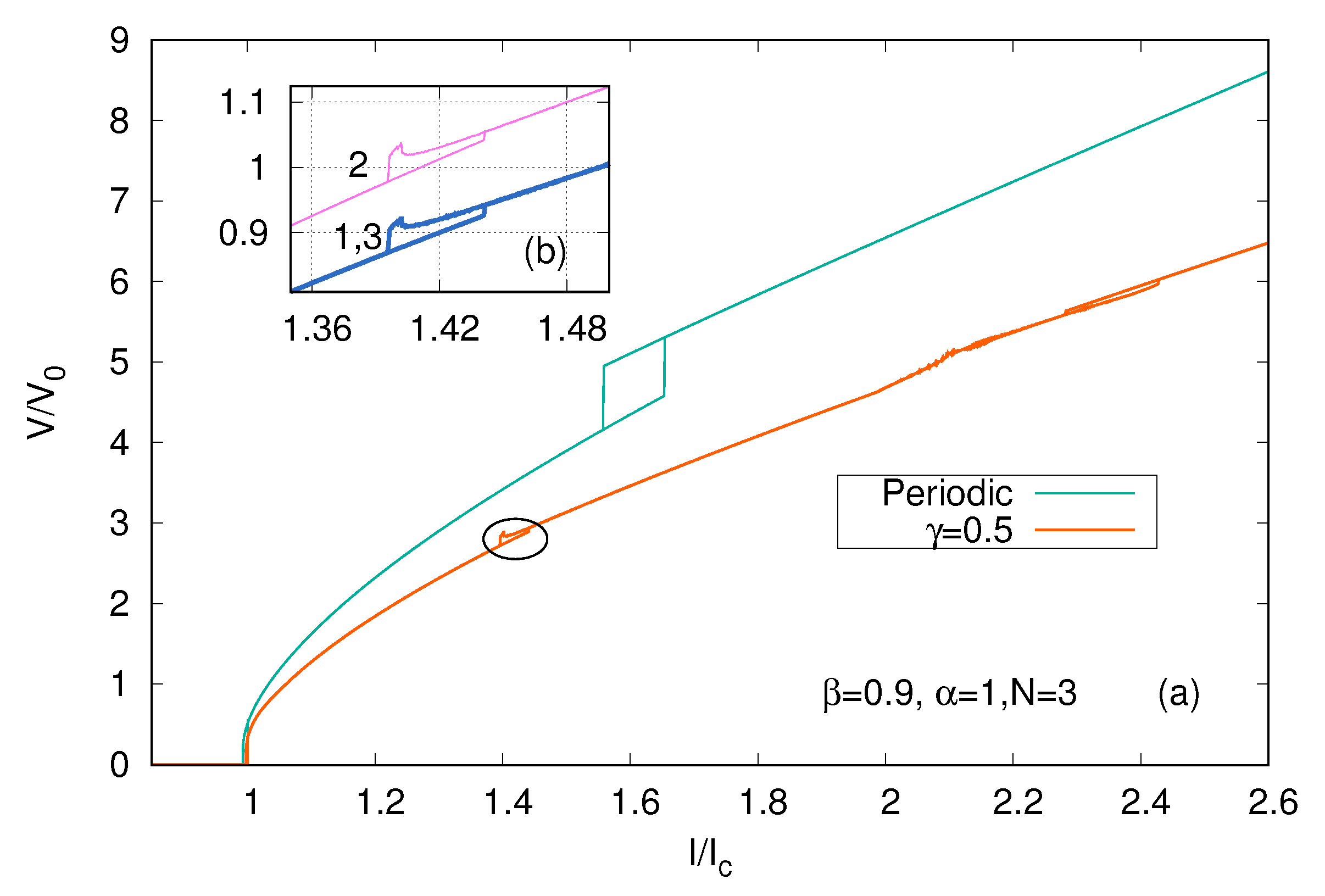
3.1. Appearance of Branching for Overcritical Currents
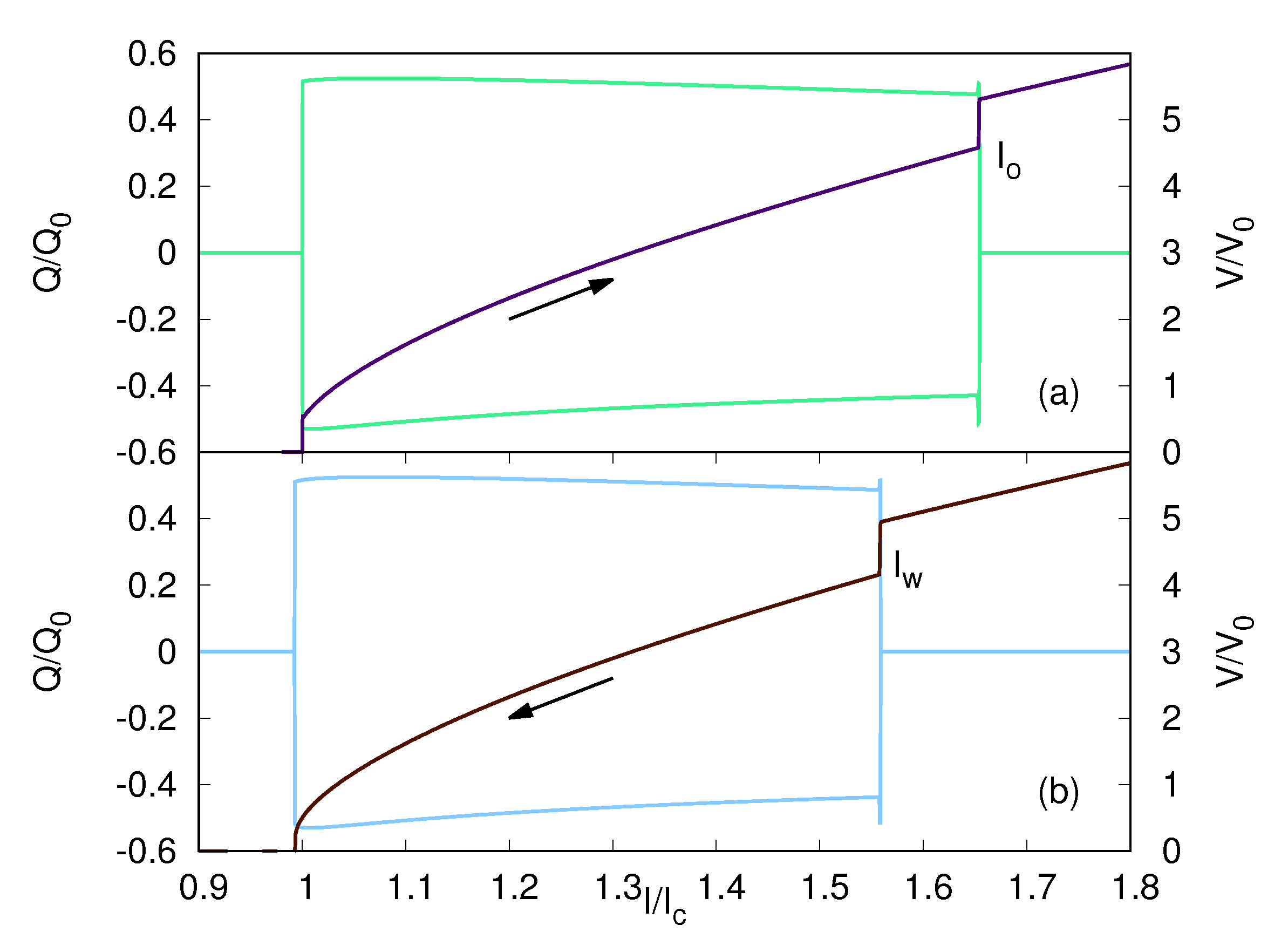
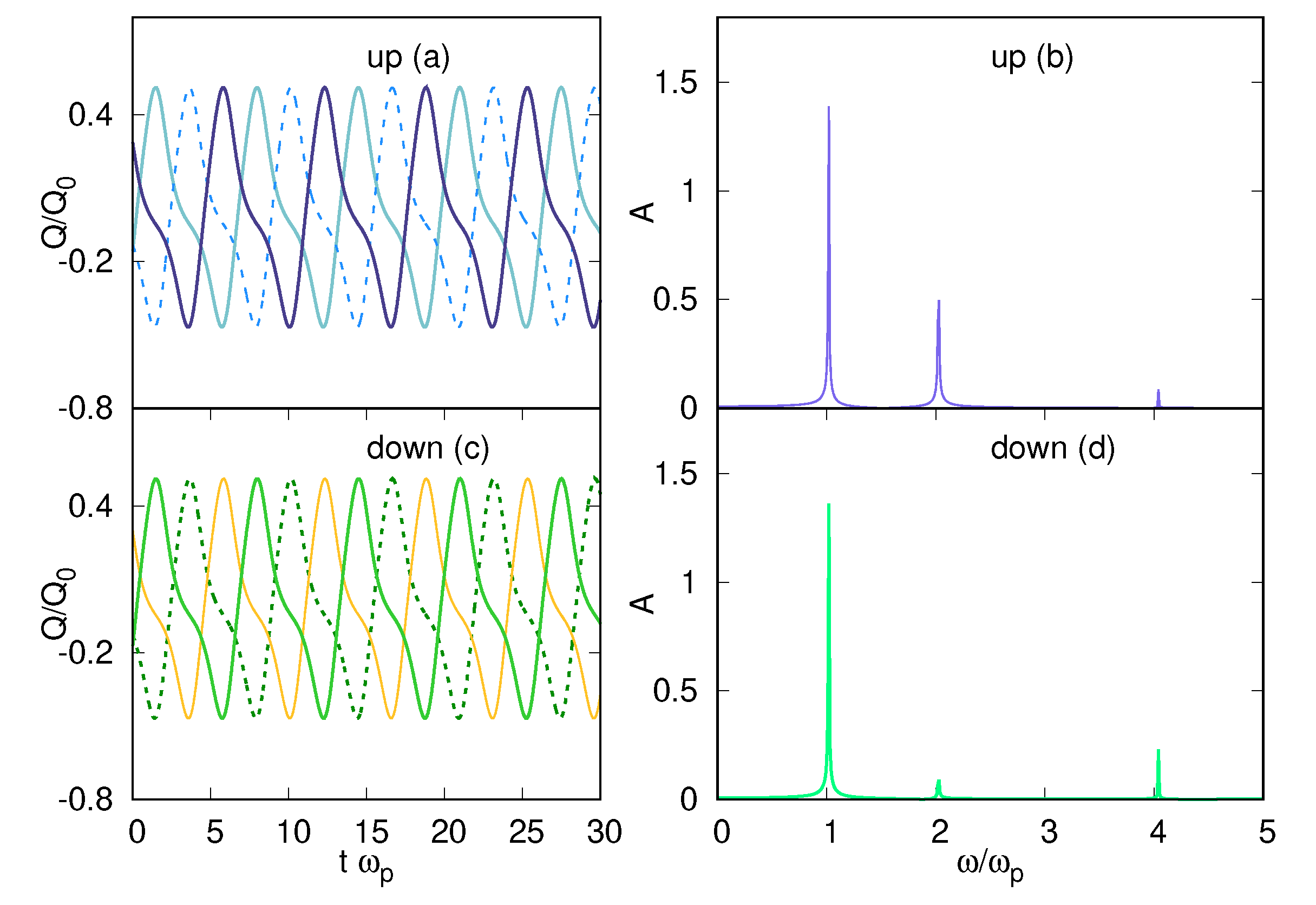
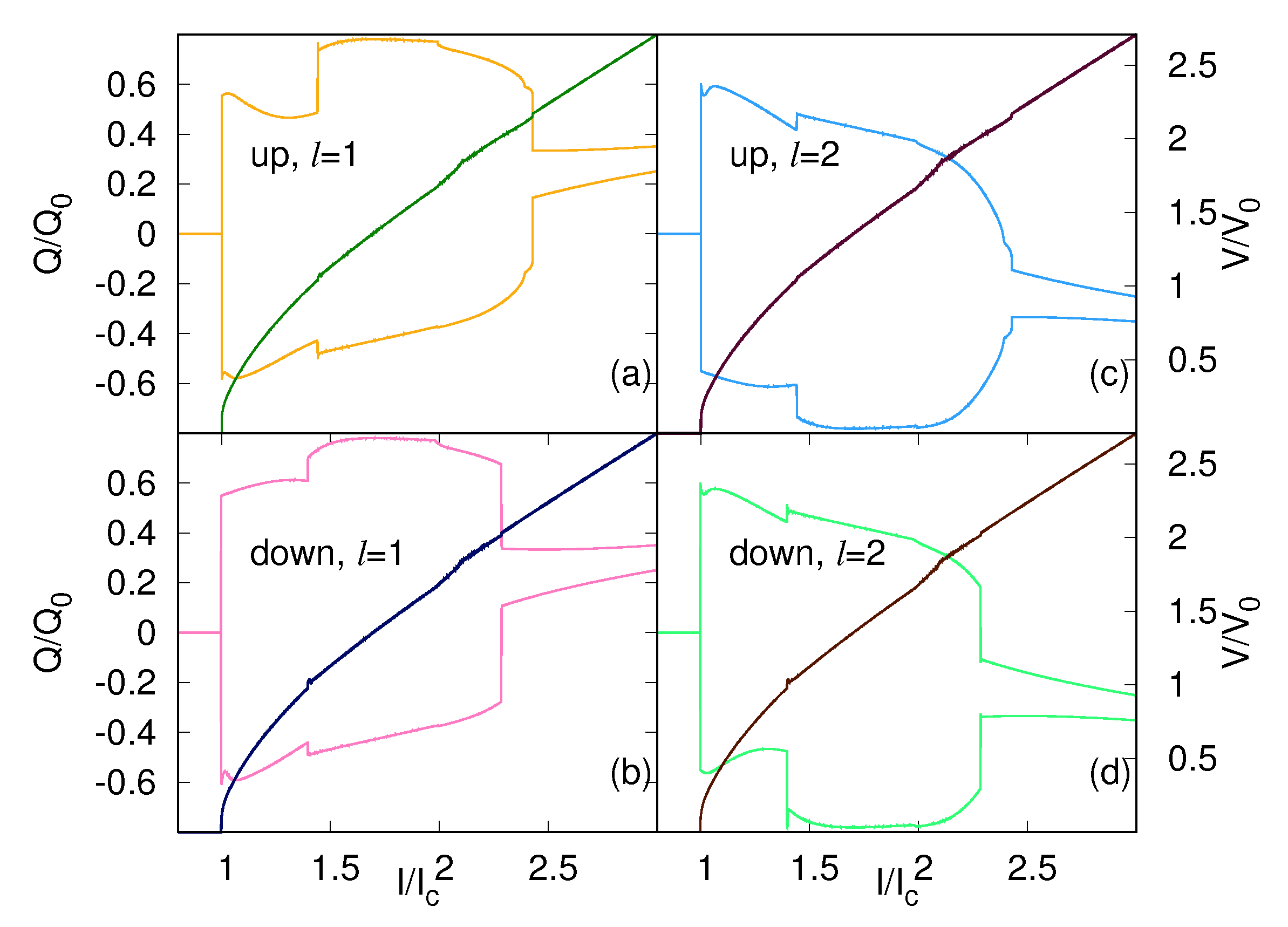
3.2. Charging of the Superconducting Layers
3.3. The Effect of Number o Junctions in the Stack
3.4. Effects of Boundary Conditions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| JJ | Josephson junctions |
| TW | Traveling wave |
| IV-characteristic | Current voltage characteristic |
| FFT | Fast Fourier Transform |
References
- McCumber, D. Effect of ac impedance on dc voltage-current characteristics of superconductor weak-link junctions. J. Appl. Phys. 1968, 39, 3113–3118. [Google Scholar] [CrossRef]
- Weinstock, H.; Nisenoff, M. Superconducting Electronics; Springer Science & Business Media: Berlin, Germany, 2013; Volume 59. [Google Scholar]
- Holmes, D.S.; Ripple, A.L.; Manheimer, M.A. Energy-efficient superconducting computing—Power budgets and requirements. IEEE Trans. Appl. Superconduct. 2013, 23, 1701610. [Google Scholar] [CrossRef]
- Cassidy, M.; Bruno, A.; Rubbert, S.; Irfan, M.; Kammhuber, J.; Schouten, R.; Akhmerov, A.; Kouwenhoven, L. Demonstration of an ac Josephson junction laser. Science 2017, 355, 939–942. [Google Scholar] [CrossRef] [PubMed]
- Clark, T. Experiments on coupled Josephson junctions. Phys. Lett. A 1968, 27, 585–586. [Google Scholar] [CrossRef]
- Tilley, D. Superradiance in arrays of superconducting weak links. Phys. Lett. A 1970, 33, 205–206. [Google Scholar] [CrossRef]
- Welp, U.; Kadowaki, K.; Kleiner, R. Superconducting emitters of THz radiation. Nat. Photonics 2013, 7, 702. [Google Scholar] [CrossRef]
- Ioffe, L.; Feigel’man, M. Possible realization of an ideal quantum computer in Josephson junction array. Phys. Rev. B 2002, 66, 224503. [Google Scholar] [CrossRef]
- Kadigrobov, A.; Shekhter, R.; Jonson, M. Quantum spin fluctuations as a source of long-range proximity effects in diffusive ferromagnet-super conductor structures. EPL Europhys. Lett. 2001, 54, 394. [Google Scholar] [CrossRef]
- Stoutimore, M.J.A. Non-Sinusoidal Current-Phase Relations in Superconductor-Ferromagnet-Superconductor Josephson Junctions; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2009. [Google Scholar]
- Macklin, C.; O’Brien, K.; Hover, D.; Schwartz, M.; Bolkhovsky, V.; Zhang, X.; Oliver, W.; Siddiqi, I. A near-quantum-limited Josephson traveling-wave parametric amplifier. Science 2015, 350, 307–310. [Google Scholar] [CrossRef]
- O’Brien, K.; Macklin, C.; Siddiqi, I.; Zhang, X. Resonant phase matching of Josephson junction traveling wave parametric amplifiers. Phys. Rev. Lett. 2014, 113, 157001. [Google Scholar] [CrossRef]
- Davidson, A. Distributed Array of Josephson Devices with Coherence. U.S. Patent 4,344,052, 10 August 1982. [Google Scholar]
- Kleiner, R.; Müller, P. Intrinsic Josephson effects in high-T c superconductors. Phys. Rev. B 1994, 49, 1327. [Google Scholar] [CrossRef] [PubMed]
- Shimakage, H.; Tamura, Y. Chaotic oscillations in Josephson junctions for random number generation. IEEE Trans. Appl. Superconduct. 2015, 25, 1–4. [Google Scholar] [CrossRef]
- Stewart, W. Current-voltage characteristics of Josephson junctions. Appl. Phys. Lett. 1968, 12, 277. [Google Scholar] [CrossRef]
- Irie, A.; Shukrinov, Y.M.; Oya, G. Experimental manifestation of the breakpoint region in the current-voltage characteristics of intrinsic Josephson junctions. Appl. Phys. Lett. 2008, 93, 152510. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Mahfouzi, F.; Suzuki, M. Structure of the breakpoint region on current-voltage characteristics of intrinsic Josephson junctions. Phys. Rev. B 2008, 78, 134521. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Mahfouzi, F. Branching in current–voltage characteristics of intrinsic Josephson junctions. Superconduct. Sci. Technol. 2006, 20, S38. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Mahfouzi, F.; Pedersen, N.F. Investigation of the breakpoint region in stacks with a finite number of intrinsic Josephson junctions. Phys. Rev. B 2007, 75, 104508. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Hamdipour, M.; Kolahchi, M. Effect of interjunction coupling on superconducting current and charge correlations in intrinsic Josephson junctions. Phys. Rev. B 2009, 80, 014512. [Google Scholar] [CrossRef]
- Du, J.; Hellicar, A.; Leslie, K.; Nikolic, N.; Hanham, S.; Macfarlane, J.; Foley, C. Towards large scale HTS Josephson detector arrays for THz imaging. Superconduct. Sci. Technol. 2013, 26, 115012. [Google Scholar] [CrossRef]
- Holdengreber, E.; Moshe, A.; Mizrahi, M.; Khavkin, V.; Schacham, S.; Farber, E. High sensitivity high Tc superconducting Josephson junction antenna for 200 GHz detection. J. Electromagn. Waves Appl. 2019, 33, 193–203. [Google Scholar] [CrossRef]
- Hamdipour, M. Detailed investigation of the bifurcation diagram of capacitively coupled Josephson junctions in high-Tc superconductors and its self similarity. Phys. C Superconduct. Appl. 2018, 547, 66–68. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Rahmonov, I.; Kulikov, K.; Seidel, P. Effects of LC shunting on the Shapiro steps features of Josephson junction. EPL Europhys. Lett. 2015, 110, 47001. [Google Scholar] [CrossRef]
- Machida, M.; Koyama, T.; Tachiki, M. Dynamical breaking of charge neutrality in intrinsic Josephson junctions: Common origin for microwave resonant absorptions and multiple-branch structures in the I-V characteristics. Phys. Rev. Lett. 1999, 83, 4618. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Gaafar, M. Charging of superconducting layers and resonance-related hysteresis in the current-voltage characteristics of coupled Josephson junctions. Phys. Rev. B 2011, 84, 094514. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Hamdipour, M. Charge creation and nucleation of the longitudinal plasma wave in coupled Josephson junctions. EPL Europhys. Lett. 2010, 92, 37010. [Google Scholar] [CrossRef][Green Version]
- Machida, M.; Sakai, S. Unified theory for magnetic and electric field coupling in multistacked Josephson junctions. Phys. Rev. B 2004, 70, 144520. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Mahfouzi, F. Influence of coupling between junctions on breakpoint current in intrinsic Josephson junctions. Phys. Rev. Lett. 2007, 98, 157001. [Google Scholar] [CrossRef] [PubMed]
- Shukrinov, Y.M.; Hamdipour, M. The c-axis charge traveling wave in a coupled system of Josephson junctions. JETP Lett. 2012, 95, 307–313. [Google Scholar] [CrossRef]
- Lyatti, M.; Wolff, M.; Savenko, A.; Kruth, M.; Ferrari, S.; Poppe, U.; Pernice, W.; Dunin-Borkowski, R.; Schuck, C. Experimental evidence for hotspot and phase-slip mechanisms of voltage switching in ultrathin YBa2Cu3O7−x nanowires. Phys. Rev. B 2018, 98, 054505. [Google Scholar] [CrossRef]
- Lyatti, M.; Savenko, A.; Poppe, U.; Dunin-Borkowski, R. High-quality YBa2Cu3O7−x nanobridges fabricated by FIB etching. arXiv 2016, arXiv:1603.03459. [Google Scholar]
- Shukrinov, Y.M.; Rahmonov, I. Diffusion current in a system of coupled Josephson junctions. J. Exp. Theor. Phys. 2012, 115, 289–302. [Google Scholar] [CrossRef]
- Koyama, T.; Tachiki, M. I-V characteristics of Josephson-coupled layered superconductors with longitudinal plasma excitations. Phys. Rev. B 1996, 54, 16183. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, H.; Sakamoto, S.; Wajima, F.; Koyama, T.; Machida, M. Simulation of I-V hysteresis branches in an intrinsic stack of Josephson junctions in high-T c superconductors. Phys. Rev. B 1999, 60, 3666. [Google Scholar] [CrossRef]
- Shukrinov, Y.M.; Mahfouzi, F.; Seidel, P. Equidistance of branch structure in capacitively coupled Josephson junctions model with diffusion current. Phys. C Superconduct. 2006, 449, 62–66. [Google Scholar] [CrossRef]
- Shukrinov Yu, M.; Rahmonov, I.R.K.K.V. Application of Numerical Methods for the Study of the Josephson Effect: Textbook; JINR: Dubna, Russia, 2016. [Google Scholar]
- Kondepudi, D.; Prigogine, I. Modern Thermodynamics: From Heat Engines to Dissipative Structures; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cuzminschi, M.; Zubarev, A. Charging of Superconducting Layers in Arrays of Coupled Josephson Junctions for Overcritical Currents. Crystals 2019, 9, 327. https://doi.org/10.3390/cryst9070327
Cuzminschi M, Zubarev A. Charging of Superconducting Layers in Arrays of Coupled Josephson Junctions for Overcritical Currents. Crystals. 2019; 9(7):327. https://doi.org/10.3390/cryst9070327
Chicago/Turabian StyleCuzminschi, Marina, and Alexei Zubarev. 2019. "Charging of Superconducting Layers in Arrays of Coupled Josephson Junctions for Overcritical Currents" Crystals 9, no. 7: 327. https://doi.org/10.3390/cryst9070327
APA StyleCuzminschi, M., & Zubarev, A. (2019). Charging of Superconducting Layers in Arrays of Coupled Josephson Junctions for Overcritical Currents. Crystals, 9(7), 327. https://doi.org/10.3390/cryst9070327





