Transformation of the Topological Phase and the Edge Modes of Double-Bilayer Bismuthene with Inter-Bilayer Spacing
Abstract
1. Introduction
2. Calculation Method
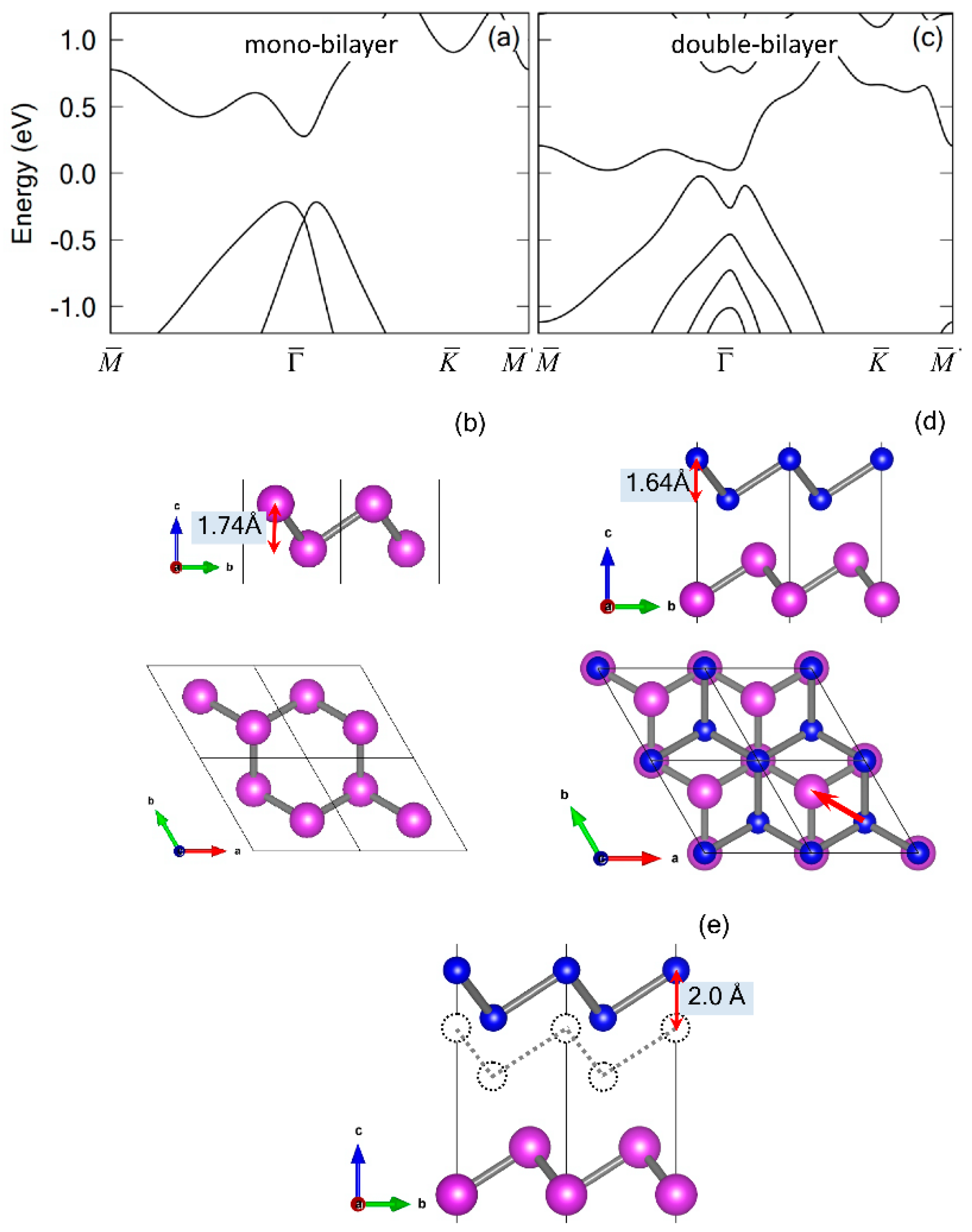
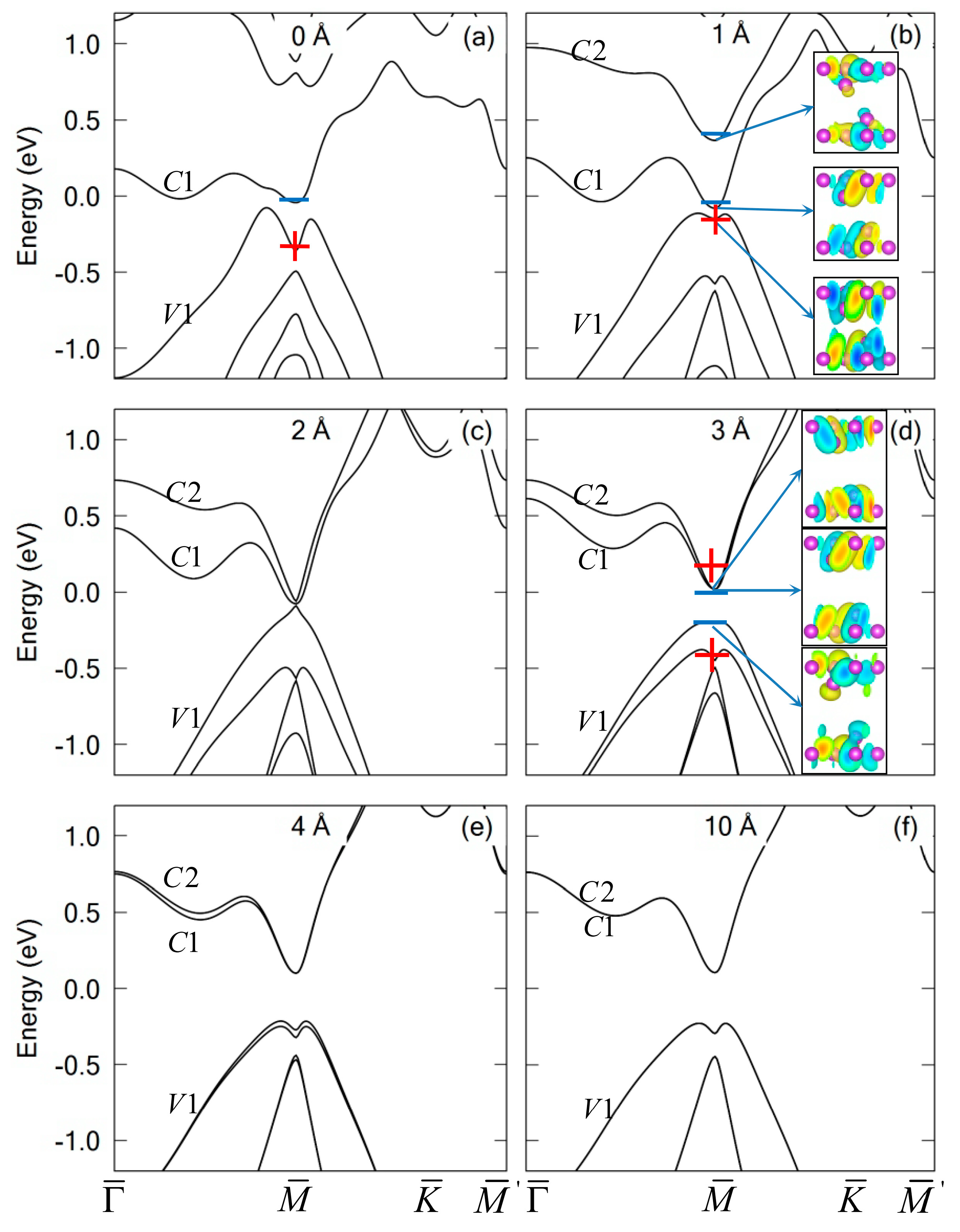
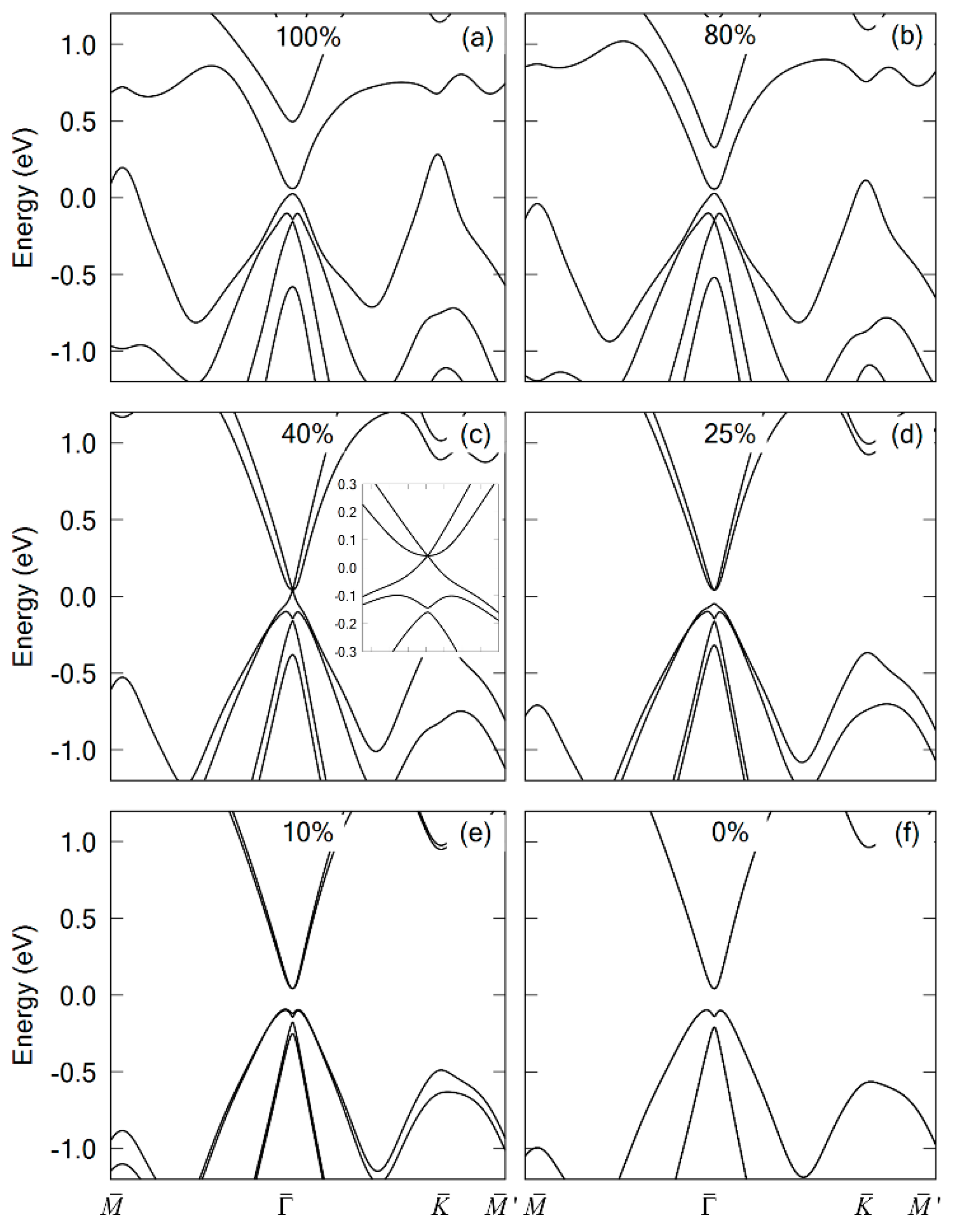
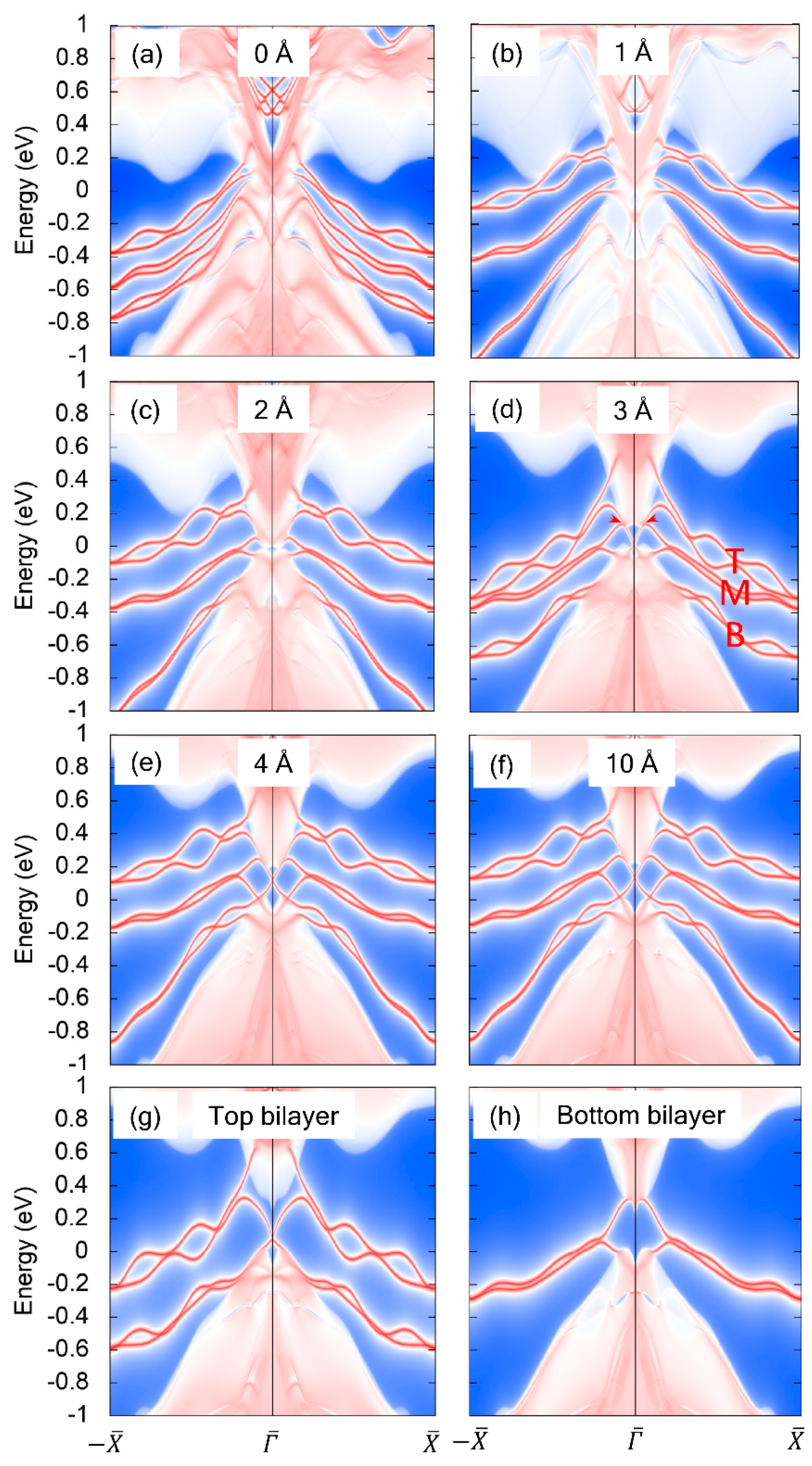
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Niu, Q.; Thouless, D.; Wu, Y.-S. Quantized Hall conductance as a topological invariant. Phys. Rev. B 1985, 31, 3372–3377. [Google Scholar] [CrossRef]
- Roushan, P.; Seo, J.; Parker, C.V.; Hor, Y.S.; Hsieh, D.; Qian, D.; Richardella, A.; Hasan, M.Z.; Cava, R.J.; Yazdani, A. Topological surface states protected from backscattering by chiral spin texture. Nature 2009, 460, 1106–1109. [Google Scholar] [CrossRef] [PubMed]
- Wray, L.A.; Xu, S.-Y.; Xia, Y.; Hsieh, D.; Fedorov, A.V.; San Hor, Y.; Cava, R.J.; Bansil, A.; Lin, H.; Hasan, M.Z. A topological insulator surface under strong Coulomb, magnetic and disorder perturbations. Nat. Phys. 2011, 7, 32–37. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- Pesin, D.; MacDonald, A.H. Spintronics and pseudospintronics in graphene and topological insulators. Nat. Mat. 2012, 11, 409–416. [Google Scholar] [CrossRef]
- Li, S.S.; Ji, W.X.; Li, P.; Hu, S.J.; Cai, L.; Zhang, C.W.; Yan, S.S. Tunability of the Quantum Spin Hall Effect in Bi(110) Films: Effects of Electric Field and Strain Engineering. ACS Appl. Mater. Interfaces 2017, 9, 21515–21523. [Google Scholar] [CrossRef]
- Zhang, R.-W.; Zhang, C.-W.; Ji, W.-X.; Li, P.; Wang, P.-J.; Li, S.-S.; Yan, S.-S. Silicon-based chalcogenide: Unexpected quantum spin Hall insulator with sizable band gap. Appl. Phys. Lett. 2016, 109, 182109. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, L.; Liu, F. Tuning Topological Edge States of Bi(111) Bilayer Film by Edge Adsorption. Nano Lett. 2014, 14, 2879–2883. [Google Scholar] [CrossRef]
- Murakami, S. Quantum spin Hall effect and enhanced magnetic response by spin-orbit coupling. Phys. Rev. Lett. 2006, 97, 236805. [Google Scholar] [CrossRef]
- Yaginuma, S.; Nagaoka, K.; Nagao, T.; Bihlmayer, G.; Koroteev, Y.M.; Chulkov, E.V.; Nakayama, T. Electronic Structure of Ultrathin Bismuth Films with A7 and Black-Phosphorus-like Structures. J. Phys. Soc. Jpn. 2008, 77, 014701. [Google Scholar] [CrossRef]
- Koroteev, Y.; Bihlmayer, G.; Chulkov, E.; Blügel, S. First-principles investigation of structural and electronic properties of ultrathin Bi films. Phys. Rev. B 2008, 77, 045428. [Google Scholar] [CrossRef]
- Hirahara, T.; Bihlmayer, G.; Sakamoto, Y.; Yamada, M.; Miyazaki, H.; Kimura, S.-I.; Blügel, S.; Hasegawa, S. Interfacing 2D and 3D Topological Insulators: Bi(111) Bilayer on Bi2Te3. Phys. Rev. Lett. 2011, 107, 166801. [Google Scholar] [CrossRef] [PubMed]
- Yang, F.; Miao, L.; Wang, Z.; Yao, M.-Y.; Zhu, F.; Song, Y.; Wang, M.-X.; Xu, J.-P.; Fedorov, A.; Sun, Z.; et al. Spatial and Energy Distribution of Topological Edge States in Single Bi(111) Bilayer. Phys. Rev. Lett. 2012, 109, 016801. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, C.-X.; Wu, Y.-S.; Duan, W.-H.; Liu, F.; Wu, J. Stable Nontrivial Z2 Topology in Ultrathin Bi (111) Films: A First-Principles Study. Phys. Rev. Lett. 2011, 107, 136805. [Google Scholar] [CrossRef] [PubMed]
- Hirahara, T.; Fukui, N.; Shirasawa, T.; Yamada, M.; Aitani, M.; Miyazaki, H.; Matsunami, M.; Kimura, S.; Takahashi, T.; Hasegawa, S.; et al. Atomic and Electronic Structure of Ultrathin Bi(111) Films Grown on Bi2Te3(111) Substrates: Evidence for a Strain-Induced Topological Phase Transition. Phys. Rev. Lett. 2012, 109, 227401. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Wang, Z.F.; Liu, F. Robustness of two-dimensional topological insulator states in bilayer bismuth against strain and electrical field. Phys. Rev. B 2013, 87, 235420. [Google Scholar] [CrossRef]
- Zhou, J.-J.; Feng, W.; Liu, C.-C.; Guan, S.; Yao, Y. Large-gap quantum spin Hall insulator in single layer bismuth monobromide Bi4Br4. Nano Lett. 2014, 14, 4767–4771. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Liu, H.; Jiang, H.; Wang, F.; Feng, J. Edge engineering of a topological Bi(111) bilayer. Phys. Rev. B 2014, 90, 165412. [Google Scholar] [CrossRef]
- Aktürk, E.; Aktürk, O.Ü.; Ciraci, S. Single and bilayer bismuthene: Stability at high temperature andmechanical and electronic properties. Phys. Rev. B 2016, 94, 014115. [Google Scholar] [CrossRef]
- Huang, Z.-Q.; Chuang, F.-C.; Hsu, C.-H.; Liu, Y.-T.; Chang, H.-R.; Lin, H.; Bansil, A. Nontrivial topological electronic structures in a single Bi(111) bilayer on different substrates: A first-principles study. Phys. Rev. B 2013, 88, 165301. [Google Scholar] [CrossRef]
- Gonze, X. A brief introduction to the ABINIT software package. Z. Kristallogr. Cryst. Mater. 2005, 220, 558–562. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Comm. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Gøedecker, S.; Hutter, J. Relativistic separable dual-space Gaussian pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3661. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Song, H.-F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405–416. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Liu, C.-X.; Zhang, H.; Yan, B.; Qi, X.-L.; Frauenheim, T.; Dai, X.; Fang, Z.; Zhang, S.-C. Oscillatory crossover from two-dimensional to three-dimensional topological insulators. Phys. Rev. B 2010, 81, 041307(R). [Google Scholar] [CrossRef]
- Zhang, Y.; He, K.; Chang, C.-Z.; Song, C.-L.; Wang, L.-L.; Chen, X.; Jia, J.-F.; Fang, Z.; Dai, X.; Shan, W.-Y.; et al. Crossover of three-dimensional topological insulator of Bi2Se3 to the two-dimensional limit. Nat. Phys. 2010, 6, 584–588. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Moore, J.E.; Louie, S.G. Spin Polarization and Transport of Surface States in the Topological Insulators Bi2Se3 and Bi2Te3 from First Principles. Phys. Rev. Lett. 2010, 105, 266806–266809. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Peng, L.; Xian, J.-J.; Tang, P.; Rubio, A.; Zhang, S.-C.; Zhang, W.; Fu, Y.-S. Visualizing topological edge states of single and double bilayer Bi supported on multibilayer Bi(111) films. Phys. Rev. B 2018, 98, 245108. [Google Scholar] [CrossRef]
| Es | Ep | ΔSOC | ||
| −7.8335 | −0.3665 | 1.5 | ||
| I(NN) | I(SNN) | O(NN) | O(SNN) | |
| Vssσ | −0.720 | −0.086 | −0.375 | −0.225 |
| Vspσ | 1.051 | 0.126 | 0.607 | 0.376 |
| Vppσ | 1.740 | 0.209 | 0.6717 | 0.5022 |
| Vppπ | −0.421 | −0.050 | −0.150 | −0.045 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Shi, Z.; Wang, P.; Zhou, W.; Chiang, T.-C.; Wang, X. Transformation of the Topological Phase and the Edge Modes of Double-Bilayer Bismuthene with Inter-Bilayer Spacing. Crystals 2019, 9, 266. https://doi.org/10.3390/cryst9050266
Hu H, Shi Z, Wang P, Zhou W, Chiang T-C, Wang X. Transformation of the Topological Phase and the Edge Modes of Double-Bilayer Bismuthene with Inter-Bilayer Spacing. Crystals. 2019; 9(5):266. https://doi.org/10.3390/cryst9050266
Chicago/Turabian StyleHu, Huanzhi, Zhibin Shi, Peng Wang, Weiping Zhou, Tai-Chang Chiang, and Xiaoxiong Wang. 2019. "Transformation of the Topological Phase and the Edge Modes of Double-Bilayer Bismuthene with Inter-Bilayer Spacing" Crystals 9, no. 5: 266. https://doi.org/10.3390/cryst9050266
APA StyleHu, H., Shi, Z., Wang, P., Zhou, W., Chiang, T.-C., & Wang, X. (2019). Transformation of the Topological Phase and the Edge Modes of Double-Bilayer Bismuthene with Inter-Bilayer Spacing. Crystals, 9(5), 266. https://doi.org/10.3390/cryst9050266




