Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal
Abstract
1. Introduction
2. Method
3. Results
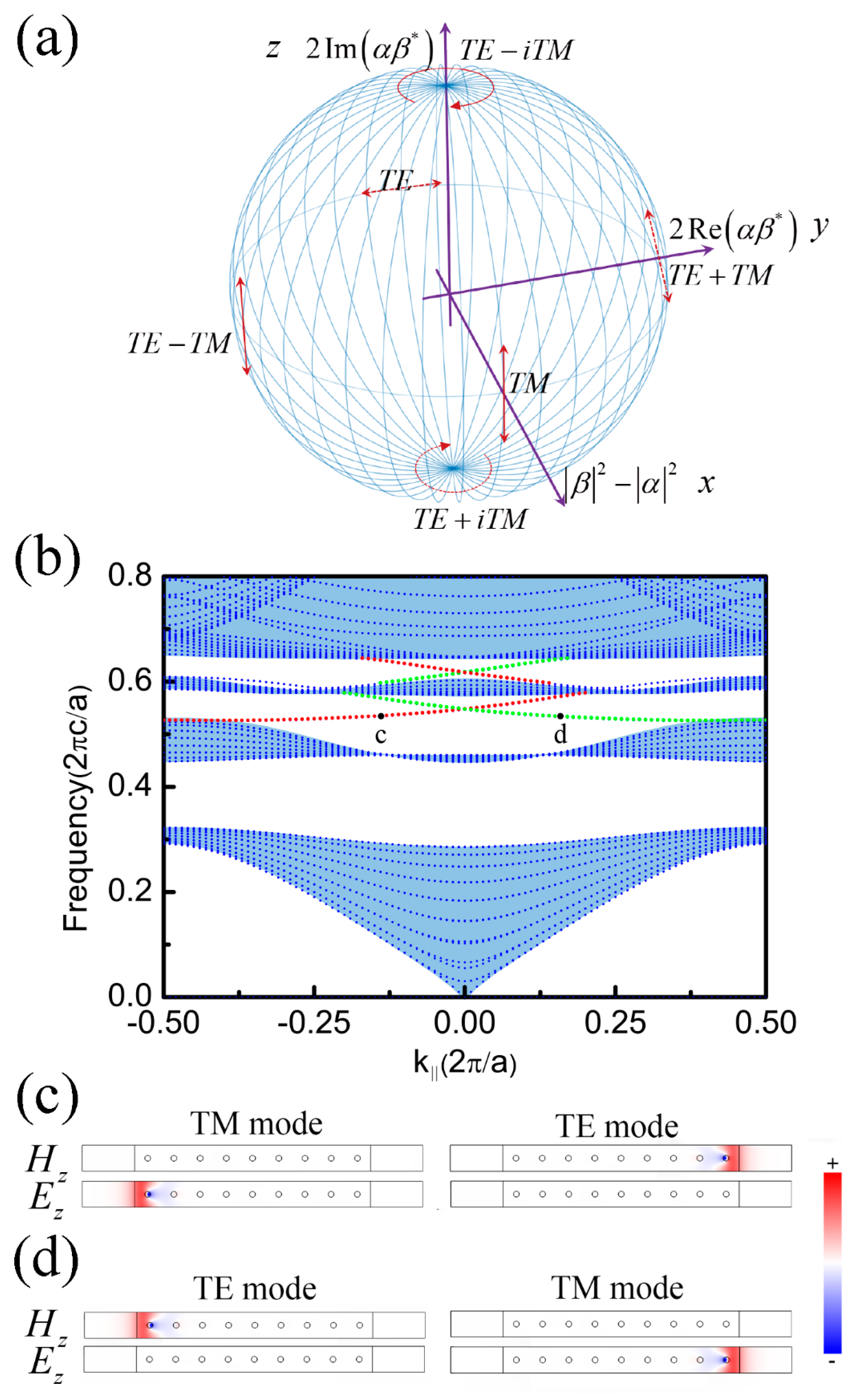
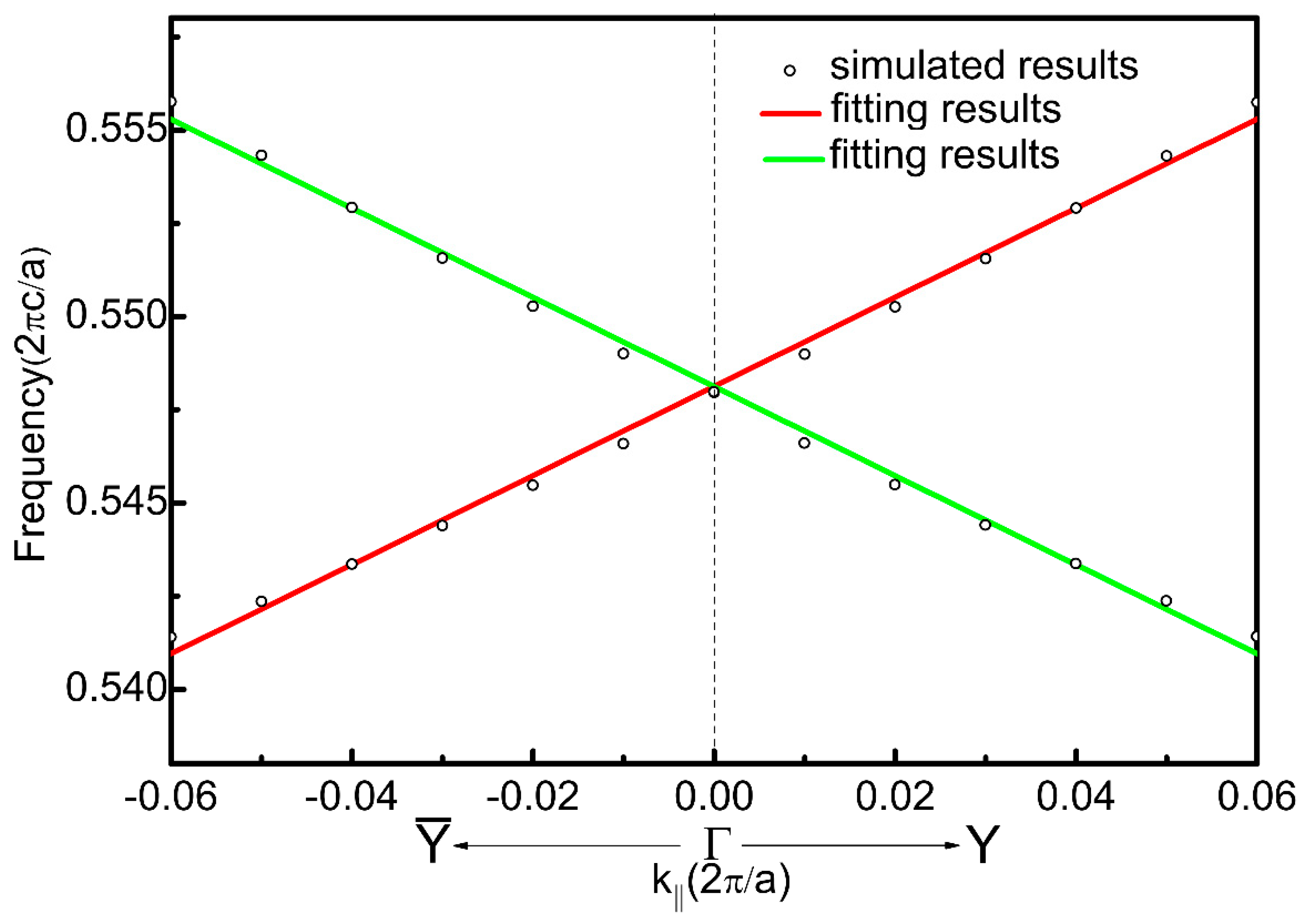
3.1. PTI Model and Gapless Edge States
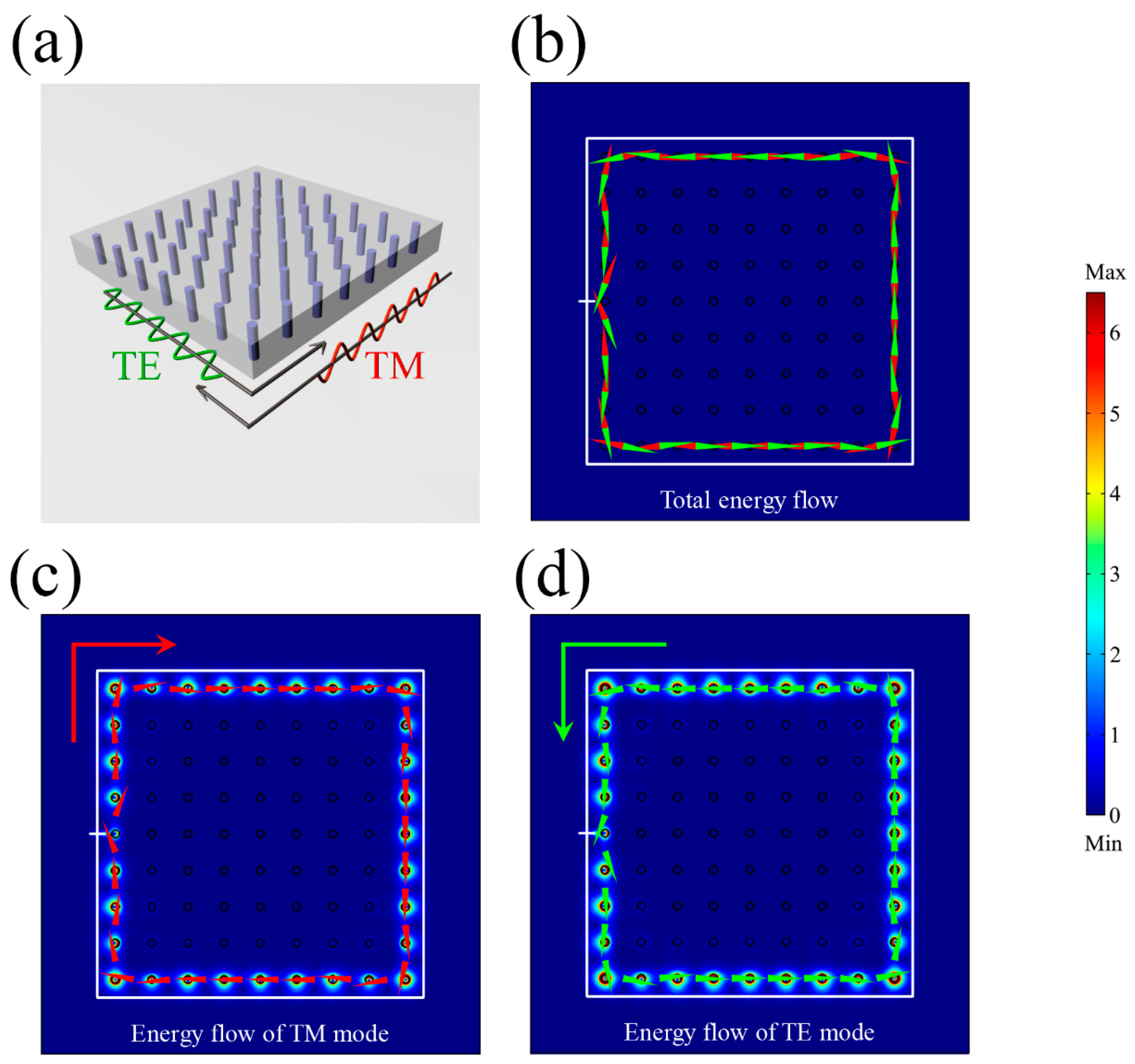
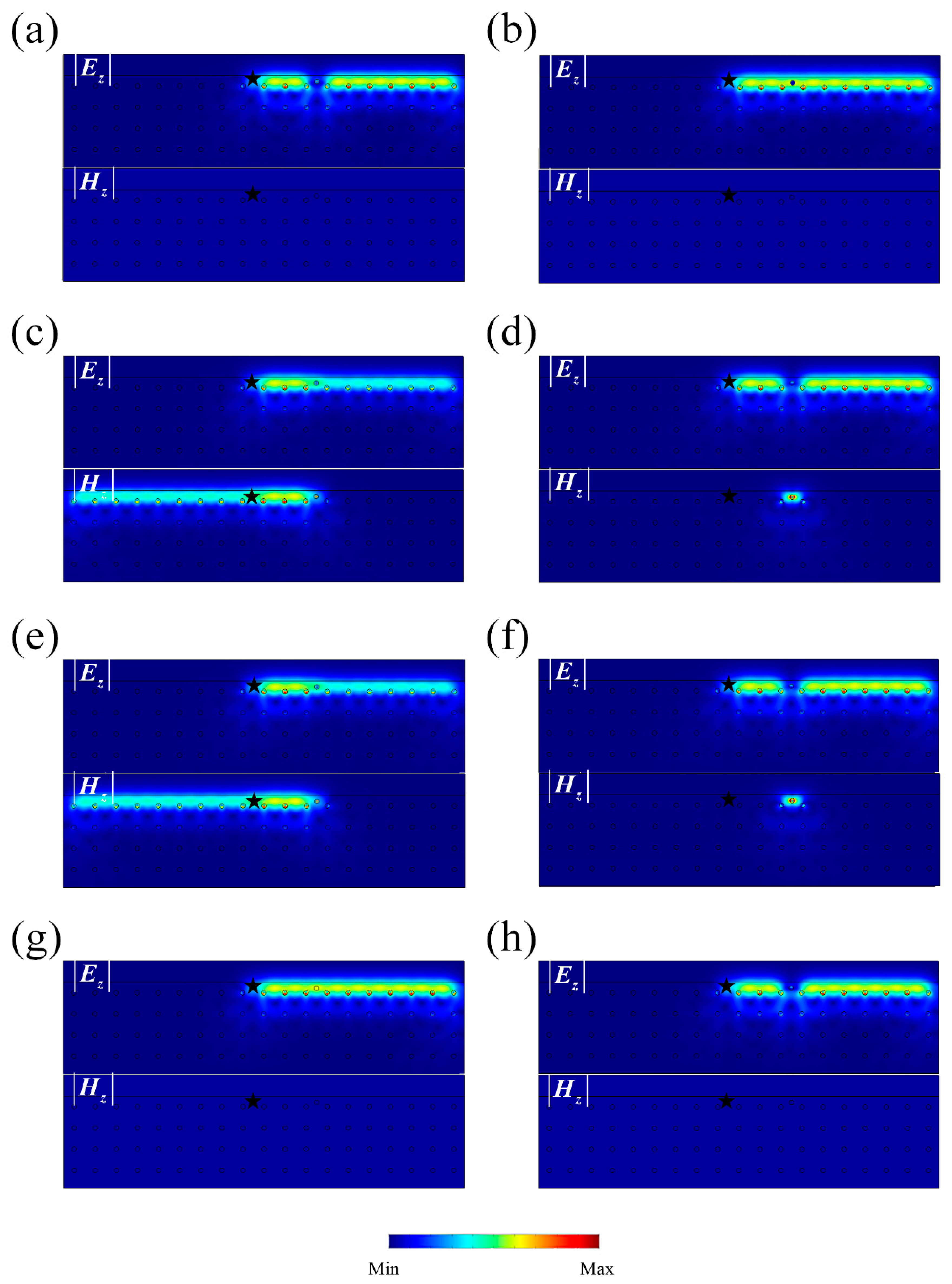
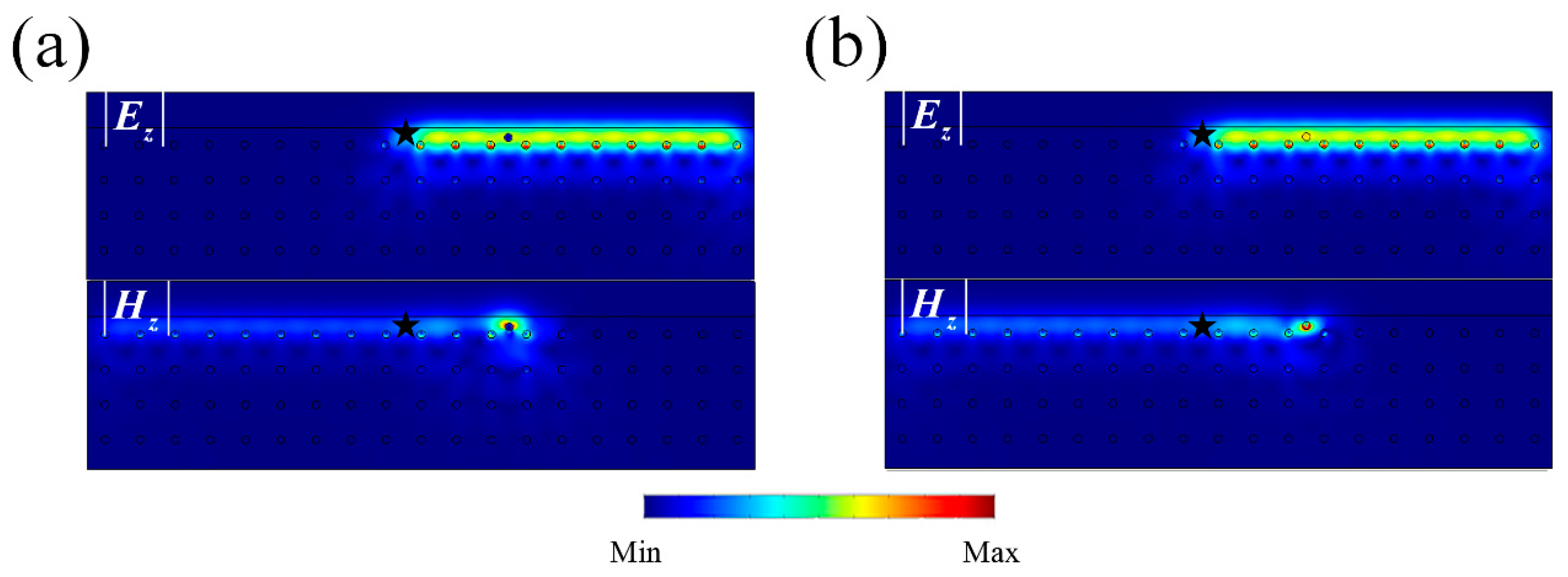
3.2. Pseudo TRS and Robustness of the One-Way Edge State
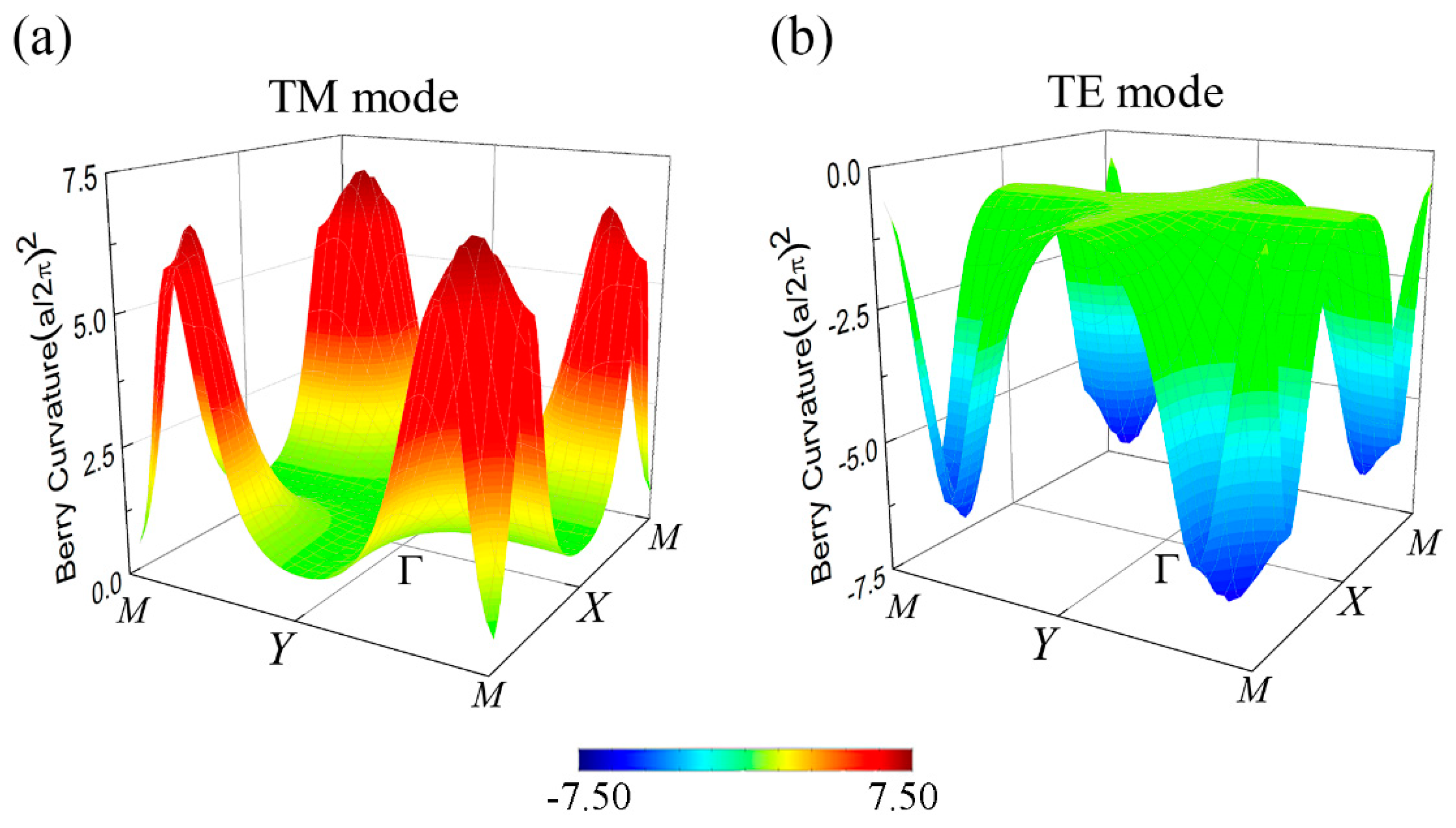
3.3. Theoretical Model of Dirac Degeneracy via Tight Binding Approximation and Spin Chern Number
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Klitzing, K.V.; Dorda, G.; Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 1980, 45, 494–497. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef]
- Tsui, D.C.; Stormer, H.L.; Gossard, A.C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 1982, 48, 1559–1562. [Google Scholar] [CrossRef]
- Hatsugai, Y. Chern number and edge states in the integer quantum Hall effect. Phys. Rev. Lett. 1993, 71, 3697–3700. [Google Scholar] [CrossRef] [PubMed]
- Kane, C.L.; Mele, E.J. Z(2) topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef] [PubMed]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef] [PubMed]
- König, M.; Wiedmann, S.; Brüne, C.; Roth, A.; Buhmann, H.; Molenkamp, L.W.; Qi, X.-L.; Zhang, S.-C. Quantum spin Hall insulator state in HgTe quantum wells. Science 2007, 318, 766–770. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. A topological Dirac insulator in a quantum spin Hall phase. Nature 2008, 452, 970–974. [Google Scholar] [CrossRef] [PubMed]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045–3067. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1110. [Google Scholar] [CrossRef]
- Sheng, L.; Sheng, D.N.; Ting, C.S.; Haldane, F.D.M. Nondissipative spin Hall effect via quantized edge transport. Phys. Rev. Lett. 2005, 95, 136602. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.M.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [PubMed]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljacic, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef] [PubMed]
- Cayssol, J.; Dora, B.; Simon, F.; Moessner, R. Floquet topological insulators. Phys. Status Solidi Rapid Res. Lett. 2013, 7, 101–108. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Khanikaev, A.B.; Mousavi, S.H.; Tse, W.-K.; Kargarian, M.; MacDonald, A.H.; Shvets, G. Photonic topological insulators. Nat. Mater. 2013, 12, 233–239. [Google Scholar] [CrossRef] [PubMed]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photonics 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Ma, T.; Khanikaev, A.B.; Mousavi, S.H.; Shvets, G. Guiding electromagnetic waves around sharp corners: Topologically protected photonic transport in metawaveguides. Phys. Rev. Lett. 2015, 114, 127401. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.-J.; Jiang, S.-J.; Chen, X.-D.; Zhu, B.; Zhou, L.; Dong, J.-W.; Chan, C.T. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 2014, 5, 5782. [Google Scholar] [CrossRef] [PubMed]
- Wu, L.-H.; Hu, X. Scheme for Achieving a Topological Photonic Crystal by Using Dielectric Material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.-X.; Jiang, J.-H.; Hu, X.; Hang, Z.H. Visualization of a Unidirectional Electromagnetic Waveguide Using Topological Photonic Crystals Made of Dielectric Materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Sun, Y.; Zhu, W.; Guo, Z.; Jiang, J.; Kariyado, T.; Chen, H.; Hu, X. Topological LC-circuits based on microstrips and observation of electromagnetic modes with orbital angular momentum. Nat. Commun. 2018, 9, 4598. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Sun, X.-C.; Liu, X.-P.; Lu, M.-H.; Chen, Y.; Feng, L.; Chen, Y.-F. Photonic topological insulator with broken time-reversal symmetry. Proc. Natl. Acad. Sci. USA 2016, 113, 4924–4928. [Google Scholar] [CrossRef] [PubMed]
- Cheng, X.; Jouvaud, C.; Ni, X.; Mousavi, S.H.; Genack, A.Z.; Khanikaev, A.B. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 2016, 15, 542–548. [Google Scholar] [CrossRef] [PubMed]
- Ochiai, T. Time-reversal-violating photonic topological insulators with helical edge states. J. Phys. Soc. Jpn. 2015, 84, 054401. [Google Scholar] [CrossRef]
- Kong, J.A. Theory of Electromagnetic Waves; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1975. [Google Scholar]
- Pozar, D.M. Microwave Engineering, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- He, C.; Lu, M.-H.; Wan, W.-W.; Li, X.-F.; Chen, Y.-F. Influence of boundary conditions on the one-way edge modes in two-dimensional magneto-optical photonic crystals. Solid State Commun. 2010, 150, 1976–1979. [Google Scholar] [CrossRef]
- Ao, X.; Lin, Z.; Chan, C.T. One-way edge mode in a magneto-optical honeycomb photonic crystal. Phys. Rev. B 2009, 80, 033105. [Google Scholar] [CrossRef]
- Poo, Y.; Wu, R.-X.; Lin, Z.; Yang, Y.; Chan, C.T. Experimental realization of self-guiding unidirectional electromagnetic edge states. Phys. Rev. Lett. 2011, 106, 093903. [Google Scholar] [CrossRef] [PubMed]
- Fu, L.; Kane, C.L. Topological insulators with inversion symmetry. Phys. Rev. B 2007, 76, 045302. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.-C. The quantum spin Hall effect and topological insulators. Phys. Today 2010, 63, 33–38. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.-L.; Fegadolli, W.S.; Lu, M.-H.; Oliveira, J.E.B.; Almeida, V.R.; Chen, Y.-F.; Scherer, A. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Cheong, S.-W.; Mostovoy, M. Multiferroics: A magnetic twist for ferroelectricity. Nat. Mater. 2007, 6, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Susstrunk, R.; Huber, S.D. PHYSICS. Observation of phononic helical edge states in a mechanical topological insulator. Science 2015, 349, 47–50. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Shen, R.; Sheng, L.; Wang, B.G.; Xing, D.Y. Electron entanglement detected by quantum spin Hall systems. Phys. Rev. Lett. 2012, 109, 036802. [Google Scholar] [CrossRef] [PubMed]
| ○ | ○ | ○ | ○ | (a) | |||
| ⊗ | ⊗ | ⊗ | ⊗ | (b) | |||
| ⊗ | ○ | ⊗ | ○ | (c) | |||
| ○ | ⊗ | ○ | ⊗ | (d) | |||
| ⊗ | ○ | ○ | ⊗ | (e) | |||
| ○ | ⊗ | ⊗ | ○ | (f) | |||
| ⊗ | ⊗ | ○ | ○ | (g) | |||
| ○ | ○ | ⊗ | ⊗ | (h) | |||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, X.-C.; He, C.; Liu, X.-P.; Zou, Y.; Lu, M.-H.; Hu, X.; Chen, Y.-F. Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal. Crystals 2019, 9, 137. https://doi.org/10.3390/cryst9030137
Sun X-C, He C, Liu X-P, Zou Y, Lu M-H, Hu X, Chen Y-F. Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal. Crystals. 2019; 9(3):137. https://doi.org/10.3390/cryst9030137
Chicago/Turabian StyleSun, Xiao-Chen, Cheng He, Xiao-Ping Liu, Yi Zou, Ming-Hui Lu, Xiao Hu, and Yan-Feng Chen. 2019. "Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal" Crystals 9, no. 3: 137. https://doi.org/10.3390/cryst9030137
APA StyleSun, X.-C., He, C., Liu, X.-P., Zou, Y., Lu, M.-H., Hu, X., & Chen, Y.-F. (2019). Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal. Crystals, 9(3), 137. https://doi.org/10.3390/cryst9030137





