Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal
Abstract
:1. Introduction
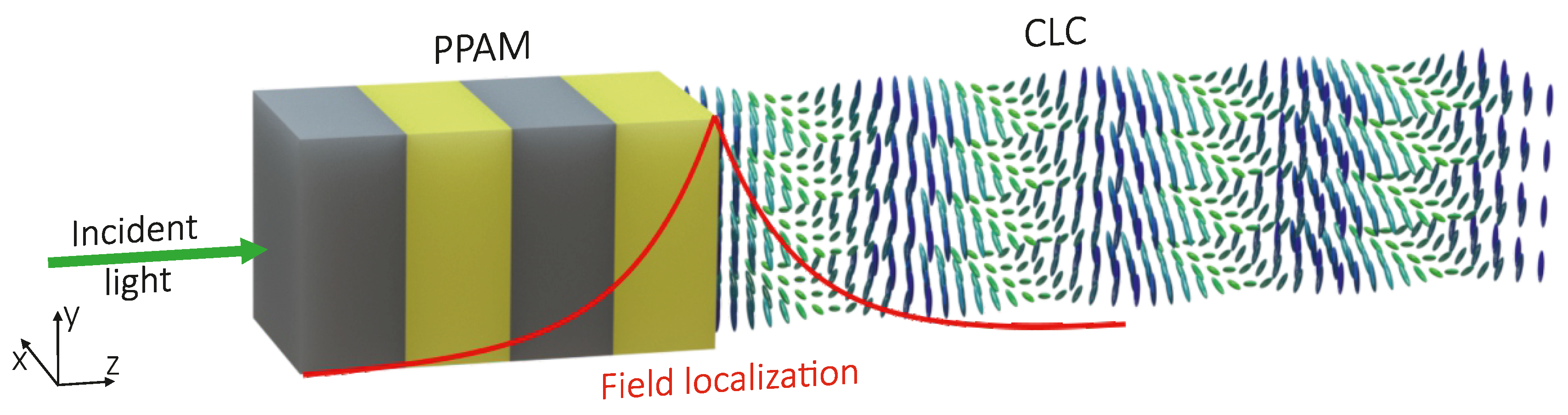
2. Description of the Model
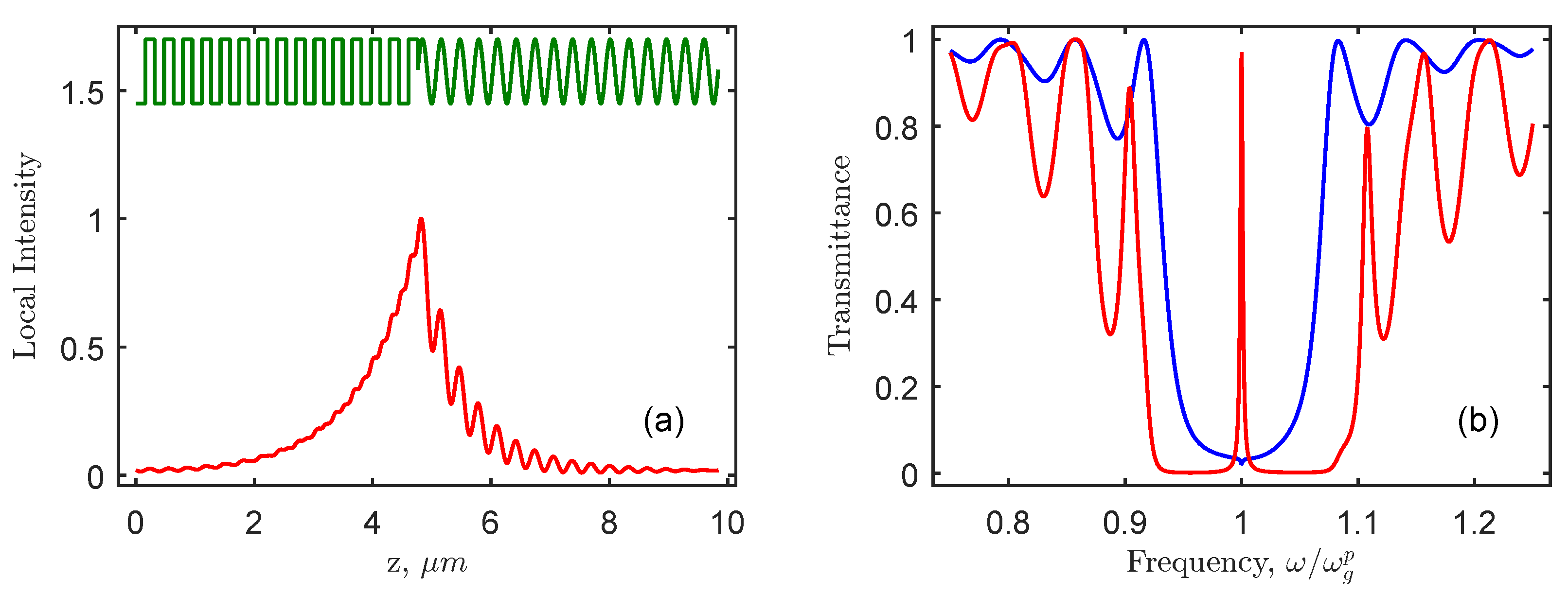
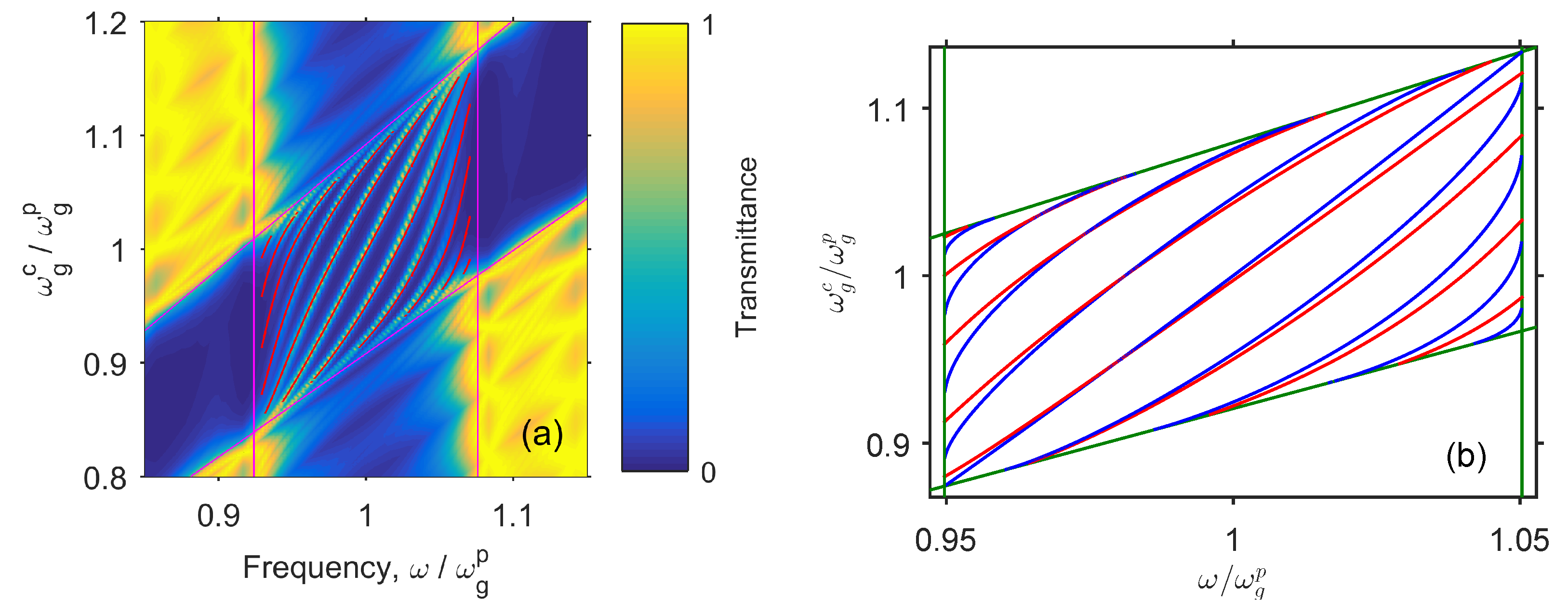
3. Eigenmode Phase Matching Condition
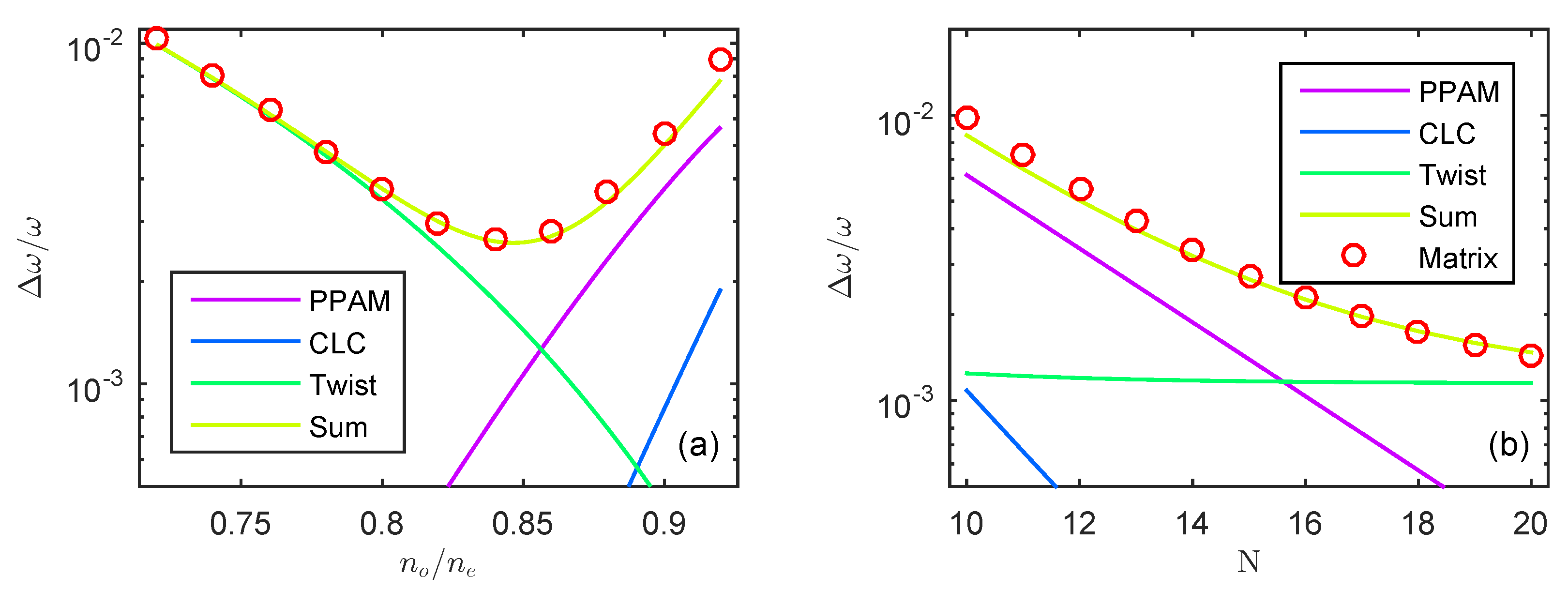
4. Temporal Coupled-Mode Theory
5. Results and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| OTS | Optical Tamm State |
| CLC | Cholesteric Liquid Crystal |
| PPAM | Polarization-Preserving Anisotropic Mirror |
| COTS | Chiral Optical Tamm State |
References
- Kavokin, A.V.; Shelykh, I.A.; Malpuech, G. Lossless interface modes at the boundary between two periodic dielectric structures. Phys. Rev. B 2005, 72, 1–4. [Google Scholar] [CrossRef]
- Kaliteevski, M.A.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef] [Green Version]
- Vinogradov, A.P.; Dorofeenko, A.V.; Merzlikin, A.M.; Lisyansky, A.A. Surface states in photonic crystals. Usp. Fiz. Nauk 2010, 180, 249–263. [Google Scholar] [CrossRef]
- Capaldo, P.; Mezzadrelli, A.; Pozzato, A.; Ruffato, G.; Massari, M.; Romanato, F. Nano-fabrication and characterization of silicon meta-surfaces provided with Pancharatnam-Berry effect. Opt. Mater. Express 2019, 9, 1015–1032. [Google Scholar] [CrossRef]
- Afinogenov, B.I.; Bessonov, V.O.; Soboleva, I.V.; Fedyanin, A.A. Ultrafast all-optical light control with Tamm plasmons in photonic nanostructures. ACS Photonics 2019, 6, 844–850. [Google Scholar] [CrossRef]
- Fedorin, I. Surface electromagnetic waves at the interface between dissipative porous nanocomposite and hypercrystal under different temperatures. Phys. Lett. A 2019, 125863. [Google Scholar] [CrossRef]
- Takayama, O.; Bogdanov, A.; Lavrinenko, A. Photonic surface waves on metamaterial interfaces. J. Phys. Condens. Matter 2017, 29, 463001. [Google Scholar] [CrossRef] [PubMed]
- Takayama, O.; Crasovan, L.C.; Johansen, S.K.; Mihalache, D.; Artigas, D.; Torner, L. Dyakonov surface waves: A review. Electromagnetics 2008, 28, 126–145. [Google Scholar] [CrossRef]
- Takayama, O.; Crasovan, L.; Artigas, D.; Torner, L. Observation of Dyakonov Surface Waves. Phys. Rev. Lett. 2009, 102, 043903. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Sonin, A.S. Optika Kholestericheskikh Zhidkikh Kristallov [Optics of Choltsteric Liquid Crystals]; Nauka Publ.: Moscow, Russia, 1982; p. 360. [Google Scholar]
- Belyakov, V.A. Diffraction Optics of Complex-Structured Periodic Media: Localized Optical Modes of Spiral Media; Springer International Publishing: Cham, Switzerland, 2019; p. 253. [Google Scholar] [CrossRef]
- Schmidtke, J.; Stille, W. Photonic defect modes in cholesteric liquid crystal films. Eur. Phys. J. E Soft Matter 2003, 12, 553–564. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Arkhipkin, V.; Vetrov, S.; Zyryanov, V.; Lee, W. Enhanced light absorption with a cholesteric liquid crystal layer. Opt. Mater. Express 2013, 3. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Pyatnov, M.V.; Timofeev, I.V. Surface modes in “photonic cholesteric liquid crystal–phase plate–metal” structure. Opt. Lett. 2014, 39, 2743–2746. [Google Scholar] [CrossRef] [PubMed]
- Vetrov, S.Y.; Pyatnov, M.; Timofeev, I.V. Spectral and polarization properties of a ’cholesteric liquid crystal–Phase plate–Metal’ structure. J. Opt. 2015, 18. [Google Scholar] [CrossRef]
- Pyatnov, M.; Vetrov, S.Y.; Timofeev, I.V. Localized optical modes in a defect-containing liquid-crystal structure adjacent to the metal. J. Opt. Soc. Am. B Opt. Phys. 2017, 34. [Google Scholar] [CrossRef]
- Isaacs, S.; Placido, F.; Abdulhalim, I. Investigation of liquid crystal Fabry–Pérot tunable filters: Design, fabrication, and polarization independence. Appl. Opt. 2014, 53, H91. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, I.V.; Vetrov, S.Y. Chiral optical Tamm states at the boundary of the medium with helical symmetry of the dielectric tensor. JETP Lett. 2016, 104, 380–383. [Google Scholar] [CrossRef] [Green Version]
- Rudakova, N.V.; Timofeev, I.V.; Vetrov, S.Y.; Lee, W. All-Dielectric polarization-preserving anisotropic mirror. OSA Contin. 2018, 1, 682. [Google Scholar] [CrossRef]
- Plum, E.; Zheludev, N.I. Chiral mirrors. Appl. Phys. Lett. 2015, 106, 221901. [Google Scholar] [CrossRef] [Green Version]
- Rajasekharan, R.; Roberts, A. Optical ’magnetic mirror’ metasurfaces using interference between Fabry–Pérot cavity resonances in coaxial apertures. Sci. Rep. 2015, 5, 10297. [Google Scholar] [CrossRef]
- Fedotov, V.A.; Rogacheva, A.V.; Zheludev, N.I.; Mladyonov, P.L.; Prosvirnin, S.L. Mirror that does not change the phase of reflected waves. Appl. Phys. Lett. 2006, 88, 091119. [Google Scholar] [CrossRef] [Green Version]
- Rudakova, N.V.; Timofeev, I.V.; Pankin, P.S.; Vetrov, S.Y. Polarization-preserving anisotropic mirror on the basis of metal–dielectric nanocomposite. Bull. Russ. Acad. Sci. Phys. 2017, 81, 10–14. [Google Scholar] [CrossRef]
- Reusch, E. Untersuchung über Glimmercombinationen. Ann. Phys. Chem. 1869, 214, 628–638. [Google Scholar] [CrossRef]
- Dixit, M.; Lakhtakia, A. Selection strategy for circular-polarization-sensitive rejection characteristics of electro-optic ambichiral Reusch piles. Opt. Commun. 2008, 281, 4812–4823. [Google Scholar] [CrossRef]
- Voloshinov, V.B.; Porokhovnichenko, D.L.; Dyakonov, E.A. Design of far-infrared acousto-optic tunable filter based on backward collinear interaction. Ultrasonics 2018, 88, 207–212. [Google Scholar] [CrossRef] [PubMed]
- Faryad, M.; Lakhtakia, A. The circular Bragg phenomenon. Adv. Opt. Photonics 2014, 6, 225. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Pankin, P.S.; Vetrov, S.; Arkhipkin, V.; Lee, W.; Zyryanov, V. Chiral optical Tamm states: Temporal coupled-mode theory. Crystals 2017, 7, 113. [Google Scholar] [CrossRef]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: New York, NY, USA, 1984; p. 304. [Google Scholar]
- Belyakov, V.A.; Semenov, S.V. Optical defect modes in chiral liquid crystals. J. Exp. Theor. Phys. 2011, 112, 694–710. [Google Scholar] [CrossRef]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008; p. 304. [Google Scholar]
- Auguié, B.; Bruchhausen, A.; Fainstein, A. Critical coupling to Tamm plasmons. J. Opt. 2015, 17, 035003. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.G.; Pankin, P.S.; Timofeev, I.V.; Nagao, T.; Chen, K.P. Narrowband wavelength selective thermal emitters by confined Tamm plasmon polaritons. ACS Photonics 2017, 4, 2212–2219. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in stratified and anisotropic media: 4×4-matrix formulation. J. Opt. Soc. Am. 1972, 62, 502. [Google Scholar] [CrossRef]
- Palto, S.P. An algorithm for solving the optical problem for stratified anisotropic media. J. Exp. Theor. Phys. 2001, 92, 552–560. [Google Scholar] [CrossRef]
- Symonds, C.; Lheureux, G.; Hugonin, J.P.; Greffet, J.J.; Laverdant, J.; Brucoli, G.; Lemaitre, A.; Senellart, P.; Bellessa, J. Confined Tamm plasmon lasers. Nano Lett. 2013, 13, 3179–3184. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.L.; Feng, J.; Han, X.C.; Liu, Y.F.; Chen, Q.D.; Song, J.F.; Sun, H.B. Hybrid Tamm plasmon-polariton/microcavity modes for white top-emitting organic light-emitting devices. Optica 2015, 2, 579–584. [Google Scholar] [CrossRef]
- Huang, S.G.; Chen, K.P.; Jeng, S.C. Phase sensitive sensor on Tamm plasmon devices. Opt. Mater. Express 2017, 7, 1267–1273. [Google Scholar] [CrossRef]
- Pancharatnam, S. Generalized theory of interference, and its applications. Proc. Indian Acad. Sci. Sect. A 1956, 44, 247–262. [Google Scholar] [CrossRef]
- Timofeev, I.V.; Gunyakov, V.A.; Sutormin, V.S.; Myslivets, S.A.; Arkhipkin, V.G.; Vetrov, S.Y.; Lee, W.; Zyryanov, V.Y. Geometric phase and o-mode blueshift in a chiral anisotropic medium inside a Fabry-Pérot cavity. Phys. Rev. E 2015, 92, 052504. [Google Scholar] [CrossRef] [PubMed]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- Timofeev, I.V.; Maksimov, D.N.; Sadreev, A.F. Optical defect mode with tunable Q factor in a one-dimensional anisotropic photonic crystal. Phys. Rev. B 2018, 97, 024306. [Google Scholar] [CrossRef]
- Avendaño, C.G.; Ponti, S.; Reyes, J.A.; Oldano, C. Multiplet structure of the defect modes in 1D helical photonic crystals with twist defects. J. Phys. A Math. Gen. 2005, 38, 8821–8840. [Google Scholar] [CrossRef]
- Gevorgyan, A.H.; Rafayelyan, M.S. Optics of anisotropic metamaterial based structurally chiral photonic crystals. J. Opt. 2013, 15, 125103. [Google Scholar] [CrossRef]
- Yang, Y.C.; Kee, C.S.; Kim, J.E.; Park, H.Y.; Lee, J.C.; Jeon, Y.J. Photonic defect modes of cholesteric liquid crystals. Phys. Rev. E 1999, 60, 6852–6854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kopp, V.I.; Genack, A.Z. Twist defect in chiral photonic structures. Phys. Rev. Lett. 2002, 89, 033901. [Google Scholar] [CrossRef] [PubMed]
- Belyakov, V.A.; Orlov, V.P.; Shilina, G.I. Surface guided electromagnetic modes in films with periodically modulated characteristics. J. Exp. Theor. Phys. 1992, 75, 189. [Google Scholar]
- Gorlach, M.A.; Ni, X.; Smirnova, D.A.; Korobkin, D.; Zhirihin, D.; Slobozhanyuk, A.P.; Belov, P.A.; Alù, A.; Khanikaev, A.B. Far-Field probing of leaky topological states in all-dielectric metasurfaces. Nat. Commun. 2018, 9, 909. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudakova, N.V.; Timofeev, I.V.; Bikbaev, R.G.; Pyatnov, M.V.; Vetrov, S.Y.; Lee, W. Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal. Crystals 2019, 9, 502. https://doi.org/10.3390/cryst9100502
Rudakova NV, Timofeev IV, Bikbaev RG, Pyatnov MV, Vetrov SY, Lee W. Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal. Crystals. 2019; 9(10):502. https://doi.org/10.3390/cryst9100502
Chicago/Turabian StyleRudakova, Natalya V., Ivan V. Timofeev, Rashid G. Bikbaev, Maxim V. Pyatnov, Stepan Ya. Vetrov, and Wei Lee. 2019. "Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal" Crystals 9, no. 10: 502. https://doi.org/10.3390/cryst9100502
APA StyleRudakova, N. V., Timofeev, I. V., Bikbaev, R. G., Pyatnov, M. V., Vetrov, S. Y., & Lee, W. (2019). Chiral Optical Tamm States at the Interface between an All-Dielectric Polarization-Preserving Anisotropic Mirror and a Cholesteric Liquid Crystal. Crystals, 9(10), 502. https://doi.org/10.3390/cryst9100502







