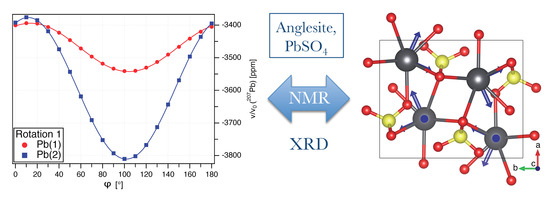
Determination of the Full ²⁰⁷Pb Chemical Shift Tensor of Anglesite, PbSO₄, and Correlation of the Isotropic Shift to Lead–Oxygen Distance in Natural Minerals

Abstract

The full ${}^{207}$Pb chemical shift (CS) tensor of lead in the mineral anglesite, PbSO${}_4$, was determined from orientation-dependent nuclear magnetic resonance (NMR) spectra of a large natural single crystal, using a global fit over two rotation patterns. The resulting tensor is characterised by the reduced anisotropy $\Delta \delta =(-327\pm 4)$ ppm, asymmetry ${\eta }_{CS}=0.529\pm 0.002$, and ${\delta }_{iso}=(-3615\pm 3)$ ppm, with the isotropic chemical shift ${\delta }_{iso}$ also verified by magic-angle spinning NMR on a polycrystalline sample. The initially unknown orientation of the mounted single crystal was included in the global data fit as well, thus obtaining it from NMR data only. By use of internal crystal symmetries, the amount of data acquisition and processing for determination of the CS tensor and crystal orientation was reduced. Furthermore, a linear correlation between the ${}^{207}$Pb isotropic chemical shift and the shortest Pb–O distance in the co-ordination sphere of Pb${}^{2+}$ solely surrounded by oxygen has been established for a large database of lead-bearing natural minerals.

1. Introduction

For the structural characterization of periodic solids, either in single or multicrystalline form, X-ray crystallography is an invaluable tool [1]. As a complementary technique for the elucidation of structure and dynamics in solids, including amorphous ones, nuclear magnetic resonance (NMR) spectroscopy has become an established method [2,3,4], to the extent that, since 2014, a “Commission on NMR Crystallography and Related Methods” exists in the International Union of Crystallography [5]. In the context of NMR crystallography, many questions (e.g., the determination of asymmetric units, assignment of space groups) may already be answered by considering only the isotropic chemical shift ${\delta }_{iso}$ of the NMR-observed nuclide [2]. The deceptively simple scalar ${\delta }_{iso}$ is, however, the result of a contraction (of the isotropic part) of the second-rank chemical shift (CS) tensor:

$${\delta }_{iso}=\frac{1}{3}\left({\delta }_{11}+{\delta }_{22}+{\delta }_{33}\right)$$

(1)

Here, ${\delta }_{11}$, ${\delta }_{22}$, and ${\delta }_{33}$ are the components of the main diagonal of the CS tensor, which are the ’eigenvalues’ in its principal axes system. The full CS tensor $\delta$ reflects the spatial distribution of electrons around the observed nucleus, which ’shield’ it from the external magnetic field to a certain extent. Therefore, a more complete picture becomes available when the full chemical shift tensor is known, which provides possible information on co-ordination, the influence of electron lone pairs, etc. The eigenvalues ${\delta }_{11}$, ${\delta }_{22}$, and ${\delta }_{33}$ may be determined by measuring the NMR spectrum of a multicrystalline (’powder’) sample under static conditions, as exemplified by Reference [6]. It is also possible to derive these eigenvalues from the rotational side-band pattern of magic-angle spinning (MAS) spectra [7] to even higher precision [8]. In unrivalled accuracy, however, the eigenvalues of the CS tensor may be extracted from orientation-dependent measurements of single crystals [9,10]. Furthermore, the orientation of the CS tensor in the crystal structure, expressed by the corresponding eigenvectors, is unequivocally only accessible via single-crystal NMR spectroscopy. (In certain cases, indirect determination might be possible from the relative orientation of the CS tensor to the dipolar coupling tensor [11].) In spite of these obvious advantages, single-crystal NMR is comparatively seldom employed for tensor determination. This may be traced to (at least) three problems with this method:

(i) 

Data acquisition and evaluation is rather time-consuming when compared to static or MAS NMR of polycrystalline samples;

(ii) 

tensor eigenvector determination in the crystal frame requires knowledge of the exact orientation of the crystal on the goniometer axis;

(iii) 

single crystals of sufficient size must be available because of the comparatively poor signal-to-noise ratio of NMR spectroscopy.

One purpose of this paper is to show that, in many cases, these difficulties may be overcome. As for problem (i), the amount of necessary work could be greatly reduced by exploiting internal crystal symmetries, i.e., considering the NMR resonances of symmetry-related atoms in the unit cell as an additional dataset acquired for an independent but virtual rotation axis [12,13,14]. The same concept can be used to address problem (ii) by calculating the exact orientation of the rotation axis from NMR data alone [15,16,17]. Regarding problem (iii), many systems are amenable to crystal growth by methods available in a standard laboratory. In addition, natural minerals offer a great supply of single crystalline material already prepared by nature, often of sufficient size for NMR investigations [16,17,18,19]. To illustrate how to tackle the above listed problems (i)–(iii), here we present the determination of the full ${}^{207}$Pb chemical shift tensor of anglesite, PbSO${}_4$, using a single crystal from a natural mineral deposit, as pictured in Figure 1a. Anglesite crystallises in the orthorhombic space group Pbnm [20], with the location of the ${}^{207}$Pb in the unit cell shown in Figure 1b.

Figure 1. (a) Single crystal of anglesite, PbSO${}_4$, from Monteponi Mine, Iglesias, Sardinia/Italy (Mineralogical State Collection, Munich inventory MSM 6140). (b) Unit cell of anglesite according to Reference [20]. The lead atoms (gray, located at Wyckoff position 4c) are related by glides $\left(a\frac{1}{4}c\right)$, $\left(a\frac{3}{4}c\right)$ and $\left(\frac{1}{4}bc\right)$, $\left(\frac{3}{4}bc\right)$, and are co-ordinated by the ten nearest oxygen atoms (red). The sulfur atoms (yellow) are located in the $\left(ab\frac{1}{4}\right)$ and $\left(ab\frac{3}{4}\right)$ planes, with their covalent bonds to oxygen in tetrahedral co-ordination also shown. (Drawing generated with the Vesta program [21]).

NMR spectroscopy of ${}^{207}$Pb (the only stable lead isotope with a nuclear spin, namely, $I=1/2$) is a valuable analytical tool in solid-state research. As a ‘heavy’ nuclide, lead has a very large chemical shift range, extending over approximately 10,000 ppm, which makes ${}^{207}$Pb a sensitive reporter of the local electronic state [22,23,24]. Recently, there has been intensified interest in ${}^{207}$Pb-NMR to characterise organolead halide perovskites, which have been identified as promising materials in photovoltaics [25,26,27]. Frequently, ${}^{207}$Pb NMR studies are augmented with quantum-mechanical calculations of chemical shifts [16,17,24,27]. While, in general, such calculations have matured to the point where their results are very useful for comparison with experimental data [28], calculations for heavy nuclei are still problematic, even when relativistic effects for the electrons are included [29]. Hence, another purpose of the current work is to add to the comparatively small database of ${}^{207}$Pb CS tensors available in the literature, and to provide more experimental numbers against which calculation methods may be calibrated. Finally, to further advance the use of ${}^{207}$Pb-NMR as an analytical tool for structure characterisation, we examine an earlier attempt to correlate ${}^{207}$Pb isotropic shift ${\delta }_{iso}$ to interatomic distances between lead and the co-ordinating oxygen atoms [22]. In this previous work, a connection was proposed between ${\delta }_{iso}$ and the average distance of all oxygens in a co-ordination sphere, which, however, is not unequivocally defined. Here, we suggest to instead use the shortest distance between lead and oxygen, which is not only a well-defined parameter, but also improves the observed correlation.

Before discussing our results in detail, we briefly outline the basic principles of our main analytical technique, i.e., NMR spectroscopy of spin $I=1/2$ in a single crystal.

2. Single-Crystal NMR of ${}^{\mathbf{207}}$Pb with Spin $\mathit{I}=\mathbf{1}/\mathbf{2}$

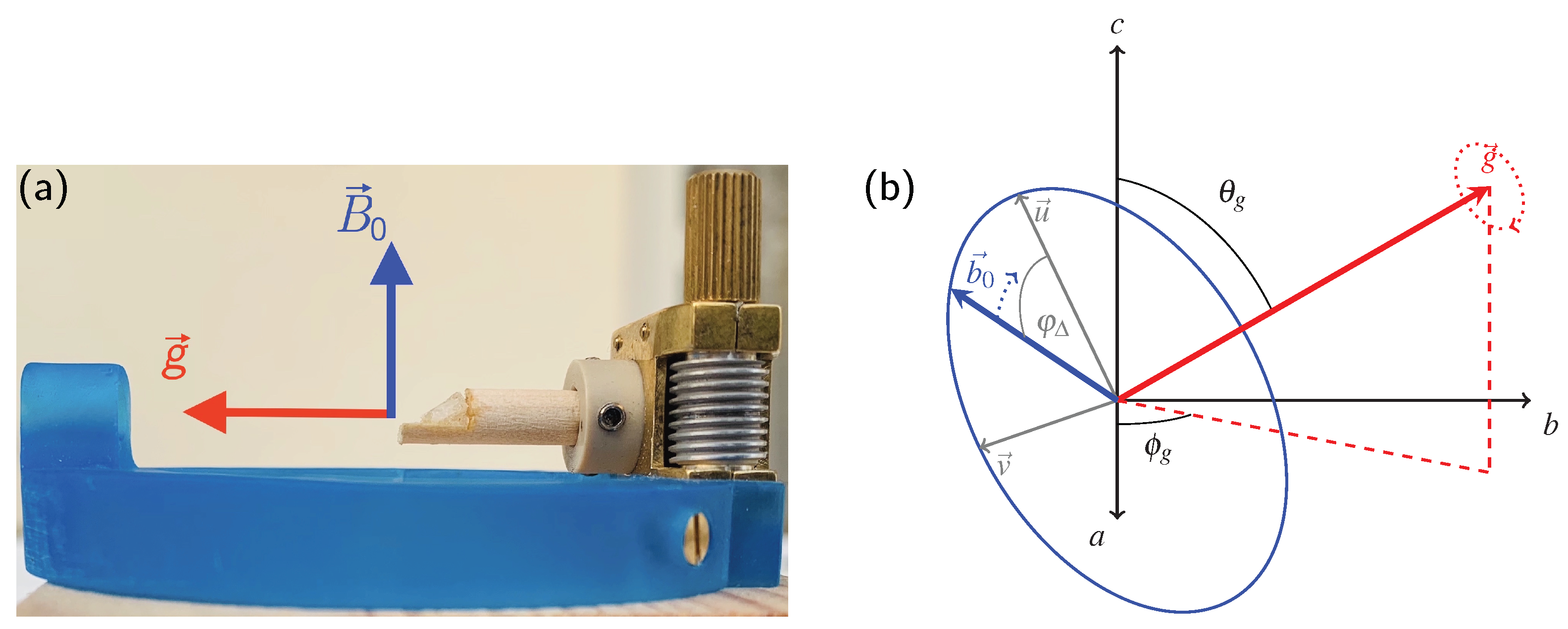
2.1. General Definitions

The energy levels of nuclear spin I in an external magnetic field ${\overrightarrow{B}}_0$ are quantum mechanically described by Hamiltonians $\widehat{H_i}$, with the following general form [30,31,32]:

$${\widehat{H}}_i=C_i\widehat{I}{\mathit{T}}_{\mathit{i}}{\overrightarrow{B}}_0$$

(2)

Here, $C_i$ is a characteristic constant for the i interaction, and $\widehat{I}$ is the spin operator in vector form. ${\overrightarrow{B}}_0$ is the magnetic field vector of an external magnetic field $B_0$. The second-rank tensor ${\mathit{T}}_{\mathit{i}}$, which can be written as a $3\times 3$ matrix, connects the two vector quantities, and therefore encapsulates the orientation dependence of the interaction. For spin–spin interactions, such as direct (dipolar) or indirect (J) couplings, Hamiltonians take a form different from Equation (2). However, for the ${}^{207}$Pb NMR spectroscopy of anglesite, such couplings result only in some unspecified line broadening, and are not evaluated in detail here. Therefore, the NMR behaviour of ${}^{207}$Pb (with spin $I=1/2$, for which no quadrupolar coupling exists) in our anglesite crystal is primarily determined by the Zeeman interaction ${\widehat{H}}_Z$ and its modification by the electron cloud surrounding the nucleus, the chemical shift ${\widehat{H}}_{CS}$ [30,31,32]:

$${\widehat{H}}_{NMR}={\widehat{H}}_Z+{\widehat{H}}_{CS}=-{\gamma }_n{\widehat{I}}_z{B}_0-{\gamma }_n\widehat{I}\delta {\overrightarrow{B}}_0$$

(3)

The nuclear Zeeman interaction determines the resonance (or Larmor) frequency ${\nu }_0$ for a nuclide with gyromagnetic ratio ${\gamma }_n$. The relevant interaction tensor ${\mathit{T}}_Z$ according to Equation 2 is simply the identity matrix, which means that ${\nu }_0$ solely scales with magnetic field strength. In solids, the chemical shift is orientation-dependent, which is reflected by the existence of the CS tensor ${\mathit{T}}_{CS}=\delta$. Since the antisymmetric part of $\delta$ is practically unobservable, only the symmetric part is considered [33]. The CS tensor, thus, takes the following form in the laboratory co-ordinate system ($LAB$), where the ${\overrightarrow{B}}_0$ field vector defines the z axis of a Cartesian co-ordinate system ($xyz$):

$${\delta }^{\mathit{LAB}}=\left(\begin{array}{ccc}{\delta }_{xx}& {\delta }_{xy}& {\delta }_{xz}\\ {\delta }_{xy}& {\delta }_{yy}& {\delta }_{yz}\\ {\delta }_{xz}& {\delta }_{yz}& {\delta }_{zz}\end{array}\right)$$

(4)

For the NMR spectroscopy of single crystals, it is useful to define two other co-ordinate systems, i.e., the frame of the crystal lattice ($CRY$), which here is the $abc$ system of the orthorhombic unit cell of anglesite, and the principal axis system ($PAS$) of the tensor. The CS tensor may be transformed between these three co-ordinate systems using the Euler angles ${\mathsf{\Omega }}_{ij}$ relating one frame to the other [34,35]:

$${\delta }^{\mathit{LAB}}\underset{{\mathsf{\Omega }}_{CL}}{\stackrel{{\mathsf{\Omega }}_{LC}}{\rightleftharpoons }}{\delta }^{\mathit{CRY}}\underset{{\mathsf{\Omega }}_{PC}}{\stackrel{{\mathsf{\Omega }}_{CP}}{\rightleftharpoons }}{\delta }^{\mathit{PAS}}$$

(5)

Symmetric tensors take diagonal form in their own $PAS$, where the tensor eigenvalues (${\delta }_{11},{\delta }_{22},{\delta }_{33}$) are the diagonal tensor elements:

$${\delta }^{\mathit{PAS}}=\left(\begin{array}{ccc}{\delta }_{11}& 0& 0\\ 0& {\delta }_{22}& 0\\ 0& 0& {\delta }_{33}\end{array}\right)=\left(\begin{array}{ccc}{\delta }_{iso}-\frac{\Delta \delta }{2}(1+{\eta }_{CS})& 0& 0\\ 0& {\delta }_{iso}-\frac{\Delta \delta }{2}(1-{\eta }_{CS})& 0\\ 0& 0& \Delta \delta +{\delta }_{iso}\end{array}\right)$$

(6)

In the notation on the right-hand side, we used the definition of the isotropic chemical shift ${\delta }_{iso}$ (Equation (1)), and two alternative tensor parameters according to the Haeberlen convention [31], namely, asymmetry parameter ${\eta }_{CS}$ and reduced anisotropy $\Delta \delta$:

$${\eta }_{CS}=\frac{{\delta }_{22}-{\delta }_{11}}{\Delta \delta };\Delta \delta ={\delta }_{33}-{\delta }_{iso}$$

(7)

For the above definitions to work properly, the eigenvalues of $\delta$ need to be sorted according to:

$$|{\delta }_{33}-{\delta }_{iso}|\ge |{\delta }_{11}-{\delta }_{iso}|\ge |{\delta }_{22}-{\delta }_{iso}|$$

(8)

2.2. Single-Crystal NMR of Anglesite, PbSO${}_4$

When evaluating the single-crystal NMR of anglesite, it is advantageous to determine the CS tensor of ${}^{207}$Pb in the orthorhombic crystal frame $abc$ since the crystallographic symmetry requirements markedly simplify the tensor. The lead atoms occupy Wyckoff position 4c in the crystal structure, which means that they are located on mirror planes parallel to $ab$, and generated by glides parallel to $ac$ and $bc$ (see also Figure 1b). Since translational elements and inversion do not affect NMR spectra, the four symmetry-related lead atoms in the unit cell form two groups of magnetically inequivalent ${}^{207}$Pb, which can be considered to be related by a ${180}^{°}$ rotation about the crystallographic b axis:

$$\underset{(x,\frac{1}{4},z)}{\mathrm{Pb}\left(1\right)}\stackrel{{180}^{°}}{⟷}\underset{(x+\frac{1}{2},\frac{1}{4},\overline{z}+\frac{1}{2})}{\mathrm{Pb}\left(2\right)}$$

(9)

Their respective CS tensors in the $CRY$ frame are described by only four independent tensor components, P, Q, R, and S:

$$\begin{array}{c}{\delta }_{\mathit{Pb}\left(\mathbf{1}\right)}^{\mathit{CRY}}=\left(\begin{array}{ccc}P& Q& 0\\ Q& R& 0\\ 0& 0& S\end{array}\right){\delta }_{\mathit{Pb}\left(\mathbf{2}\right)}^{\mathit{CRY}}=\left(\begin{array}{ccc}P& -Q& 0\\ -Q& R& 0\\ 0& 0& S\end{array}\right)\hfill \end{array}$$

(10)

To determine the tensor components P, Q, R, and S from our NMR experiments, we now consider what happens when a chemical-shift tensor is rotated in the $LAB$ frame around an axis $\overrightarrow{g}$, perpendicular to the external magnetic field ${\overrightarrow{B}}_0$ (described by normal vector ${\overrightarrow{b}}_0$ here), by an angle $\phi$. To this end, a single crystal of anglesite (approximate size 3 × 3 × 2 mm) was fixed on a rod and installed in a goniometer mechanics, as pictured in Figure 2a. The mechanics allows a defined change of rotation angle $\phi$ around the goniometer axis $\overrightarrow{g}$. For such a rotation, the orientation dependence of the resonance frequency (in units of ppm, i.e., scaled by Larmor frequency ${\nu }_0$) is given by Volkoff harmonics [9]:

$${\nu }^n\left(\phi \right)/{\nu }_0={\overrightarrow{b}}_0^T·{\delta }^{\mathit{LAB}}\left(\phi \right)·{\overrightarrow{b}}_0=A^n+B^{n}cos2\phi +C^{n}sin2\phi$$

(11)

Figure 2. (a) ‘Clip-on’ goniometer built by NMR Service GmbH (Erfurt, Germany) for a wide-bore Bruker static NMR probe, with an arbitrary single crystal mounted on a wooden rotation axis with 5 mm diameter. The goniometer axis (red) is perpendicular to the applied magnetic field ${\overrightarrow{B}}_0$ (blue). (b) Co-ordinates used for the interpretation of the rotation patterns (Figure 3b,d); a, b, and c are the unit vectors of the orthorhombic crystal system ($CRY$) of anglesite, $\overrightarrow{g}$ is the unit vector along the goniometer axis, ${\theta }_g$ and ${\varphi }_g$ its polar angles in the $CRY$, ${\overrightarrow{b}}_0$ is the unit vector of the magnetic field, $\phi$ is the rotation angle, and $\overrightarrow{u}$ and $\overrightarrow{v}$ are auxiliary unit vectors necessary to define ${\overrightarrow{b}}_0$ perpendicular to $\overrightarrow{g}$ [15].

Plots of the resonance positions over the rotation interval of ${180}^{°}$, also known as ‘rotation patterns’, are shown in Figure 3. The contribution of each magnetically inequivalent nuclide n in these rotation patterns follows the type of harmonic function shown in Equation (11). The factors $A^n$, $B^n$, and $C^n$ are linear combinations of CS tensor components, their precise form depending on the relative orientation of the $PAS$ frame to the $LAB$ frame. In the general case, three rotation experiments about three nonparallel axes with known orientation are required to derive the full CS tensor [9,10]. However, anglesite is one of the cases where internal crystal symmetry may be exploited [12,13,14] to obtain two rotation patterns from just one rotation experiment, corresponding to the two magnetically inequivalent ${}^{207}$Pb atoms shown in Equation (9). The use of internal symmetry makes the $CRY$ frame the preferred choice for carrying out all calculations needed to determine the CS tensors of Equation (10). In this frame, the magnetic field vector ${\overrightarrow{b}}_0$ has a general orientation depending on the rotation angle $\phi$, and the line position observed for Pb(1) can be expressed as:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\nu }^{Pb\left(1\right)}\left(\phi \right)/{\nu }_0& ={\overrightarrow{b}}_0^T\left(\phi \right)·{\delta }_{\mathit{Pb}\left(\mathbf{1}\right)}^{\mathit{CRY}}·{\overrightarrow{b}}_0\left(\phi \right)\hfill \\ & =P{b}_x^2+R{b}_y^2+S{b}_z^2+Q2b_x{b}_y\hfill \end{array}\end{array}$$

(12)

Figure 3. ${}^{207}$Pb NMR spectra of a single crystal of anglesite, PbSO${}_4$, rotated counterclockwise by the indicated angle $\phi$ around rotation axes ${\overrightarrow{g}}_1$ (a) and ${\overrightarrow{g}}_2$ (c), both perpendicular to the external magnetic field ${\overrightarrow{B}}_0$ (varying signal intensity is due to the limited excitation width of the used spin–echo sequence). Full rotation pattern over ${180}^{°}$ for the two magnetically inequivalent ${}^{207}$Pb at Wyckoff position 4c, acquired by rotating the anglesite crystal stepwise by ${10}^{°}$ around ${\overrightarrow{g}}_1$ (b) and ${\overrightarrow{g}}_2$ (d). Lines represent the fit of the experimental points to the CS tensor elements (see main text for details).

The components of ${\overrightarrow{b}}_0$ in the $CRY$ frame can be described in terms of the (initially unknown) orientation of goniometer axis $\overrightarrow{g}$:

$$\overrightarrow{g}=\left(\begin{array}{c}sin{\theta }_{g}cos{\varphi }_g\\ sin{\theta }_{g}sin{\varphi }_g\\ cos{\theta }_g\end{array}\right)$$

(13)

To describe the stepwise rotation of ${\overrightarrow{b}}_0$ around $\overrightarrow{g}$, it is useful to define two auxiliary unit vectors, $\overrightarrow{v}$ and $\overrightarrow{u}$, in the plane perpendicular to $\overrightarrow{g}$. To unequivocally set $\overrightarrow{v}$ and $\overrightarrow{u}$, a reference vector is needed (that obviously needs to be nonparallel to $\overrightarrow{g}$), the choice of which determines the definition of offset angle ${\phi }_{\Delta }$ in the plane, as shown in Figure 2b. For our data, we chose $(0,0,1)$, i.e., the unit vector along the crystallographic c-axis, so that $\overrightarrow{v}$ and $\overrightarrow{u}$ are given by [15]:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \overrightarrow{v}=\frac{1}{sin{\theta }_g}\left(\overrightarrow{g}\times \overrightarrow{c}\right);\overrightarrow{u}=\overrightarrow{v}\times \overrightarrow{g}& =\frac{1}{sin{\theta }_g}\left(\overrightarrow{g}\times \overrightarrow{c}\right)\times \overrightarrow{g}\hfill \\ & =\frac{1}{sin{\theta }_g}\left(\overrightarrow{c}-\overrightarrow{g}cos{\theta }_g\right)\hfill \end{array}\end{array}$$

(14)

The orientation of ${\overrightarrow{b}}_0$ in the $CRY$ frame may then be written as:

$$\begin{array}{c}\hfill {\overrightarrow{b}}_0\left(\phi \right)=\overrightarrow{v}sin\left(\phi -{\phi }_{\Delta }\right)+\overrightarrow{u}cos\left(\phi -{\phi }_{\Delta }\right)\end{array}$$

(15)

Using this formalism, we can now proceed to determine the chemical shift tensor ${\delta }^{\mathit{CRY}}$ for ${}^{207}$Pb in anglesite, PbSO${}_4$.

3. Results and Discussion

3.1. ${}^{207}$Pb NMR of Anglesite: Single Crystal

From fitting the experimental line positions in Figure 3, we obtained two sets of prefactors ($A^1,B^1,C^1$ and $A^2,B^2,C^2$) from the Volkoff harmonics, see Equation (11). Since the rotation was carried out around one physical goniometer axis $\overrightarrow{g}$, the two harmonics of the magnetically inequivalent lead atoms are linked by one constraint [14], and only five linear independent parameters may be extracted from one rotation pattern. The chemical shift tensor ${\delta }^{\mathit{CRY}}$, which we want to calculate from the rotation pattern, possesses four independent tensor elements (Equation (10)) due to constraints imposed by crystal symmetry. However, there are also two parameters ($\theta$, $\varphi$) describing the unknown orientation of the goniometer axis in the $CRY$ frame, plus the unknown initial orientation of the crystal expressed by offset angle ${\phi }_{\Delta }$, which need to be included into the fit routine. Overall, therefore, our system is underdetermined, with seven fit parameters versus five experimental ones. The obvious solution to this problem is to acquire two rotation patterns about two different rotation axes, ${\overrightarrow{g}}_1$ (Figure 3b) and ${\overrightarrow{g}}_2$ (Figure 3d), yielding enough free parameters to also include the orientations of ${\overrightarrow{g}}_1$ and ${\overrightarrow{g}}_2$ into the fit. Thus, the two rotation patterns were simultaneously fitted according to Equation (12) (and its symmetry-related counterpart), with the motion of field vector ${\overrightarrow{b}}_0$ in the $CRY$ frame described by Equation (15). The fit converged on a global solution with the following values for the ten parameters (the errors reflect the fit residuals):

$$\begin{array}{cccc}{\overrightarrow{g}}_1:& {\theta }_g={(76.8\pm 0.4)}^{°}& {\varphi }_g={(149.8\pm 0.2)}^{°}& {\phi }_{\Delta }={(17.5\pm 0.2)}^{°}\\ {\overrightarrow{g}}_2:& {\theta }_g={(126.6\pm 0.2)}^{°}& {\varphi }_g={(228.3\pm 0.7)}^{°}& {\phi }_{\Delta }={(178.4\pm 0.6)}^{°}\\ P=(-3873\pm 4)\mathrm{ppm}& Q=(152.0\pm 0.5)\mathrm{ppm}& R=(-3607\pm 3)\mathrm{ppm}& S=(-3365\pm 1)\mathrm{ppm}\end{array}$$

(16)

The diagonalization of the CS tensor defined by the $P,Q,R,S$ values listed above transforms it to its own $PAS$ frame, giving the eigenvalues and eigenvectors shown in Table 1. Inspecting the properties of ${\delta }^{\mathit{CRY}}$, we find the anisotropy of the CS tensor ($\Delta \delta =-327$ ppm) to be comparatively small, which indicates that the electron lone pair at the lead atoms has predominantly s-character [36]. The asymmetry parameter ${\eta }_{CS}=0.529$, on the other hand, reflects the comparatively low symmetry of the polyhedron defined by the surrounding oxygens, with the co-ordination number being 10 (see Section 3.3 below). Both derived tensor parameters agree reasonably well with those previously reported from static spectra of a polycrystalline sample: $\Delta \delta =-320$ ppm and ${\eta }_{CS}=0.545$ [6].

Table 1. Chemical shift tensor ${\delta }^{\mathit{CRY}}$ of ${}^{207}$Pb in the anglesite structure. Left: Determined from single-crystal NMR experiments about two rotation axes at room temperature. The orientations of the corresponding eigenvectors are listed in spherical co-ordinates ($\theta ,\phi$) in the orthorhombic $abc$ crystal system $CRY$ and refer to the atom closest to the origin, i.e., Pb(1). Error values are derived from the fit residuals. Right: Determined from a Herzfeld–Berger analysis [7] of the rotational side-band pattern at ${\nu }_r=+12.5$ kHz magic-angle spinning (MAS) (i.e., at slightly elevated temperature), with $I_{-1}/I_0=0.52$, $I_{-2}/I_0=0.24$, and $I_{-3}/I_0=0.054$, leading to $\rho =-0.3\pm 0.04$ and $\mu =4.5\pm 0.3$. The error values of the tensor components are derived from those of $\rho$ and $\mu$.

	Single-Crystal NMR	MAS NMR
${\delta }_{11}^{PAS}$	$(-3365\pm 3)$ ppm	$(-3369\pm 15)$ ppm
${\delta }_{22}^{PAS}$	$(-3538\pm 3)$ ppm	$(-3557\pm 10)$ ppm
${\delta }_{33}^{PAS}$	$(-3942\pm 4)$ ppm	$(-3907\pm 30)$ ppm
${\overrightarrow{d}}_{11}$	0.00${}^{\circ }$, 0.00${}^{\circ }$
${\overrightarrow{d}}_{22}$	90.00${}^{\circ }$, 65.59${}^{\circ }$
${\overrightarrow{d}}_{33}$	90.00${}^{\circ }$, 155.59${}^{\circ }$
$\Delta \delta$	$(-327\pm 4)$ ppm	$(-296\pm 30)$ ppm
${\eta }_{CS}$	$0.529\pm 0.002$	$0.64\pm 0.06$
${\delta }_{iso}$		$(-3611\pm 4)$ ppm
	$(-3615\pm 3)$ ppm	$(-3614\pm 3)$ ppm ${}^a$

${}^a$ From extrapolation of MAS spectra to zero spinning, see Figure 5b.

The orientation of the scaled eigenvectors of the CS tensor in the unit cell of anglesite, as listed in Table 1, may be visualised from Figure 4. These orientations are in agreement with the crystal symmetry, with the eigenvector of one of the lesser tensor components (${\delta }_{11}^{PAS}$) aligning exactly along the c axis in the crystal frame. This is a consequence of the symmetry enforced by the mirror plane in the orthorhombic unit cell at Wyckoff position 4c, on which the ${}^{207}$Pb atoms are situated. This generates CS tensors of the shape shown in Equation (10), where the principal component S does not change when transforming from the $CRY$ to the $PAS$ frame. The eigenvectors belonging to the two other principal components are free to orient according to the electronic environment, generated chiefly by the surrounding oxygen atoms. The eigenvector with the second largest corresponding eigenvalue, i.e., ${\overrightarrow{d}}_{22}$, points exactly along the bisector of the next two nearest oxygen atoms with the same Pb–O distance, as may be best seen in the lower-left corner of Figure 4b.

Figure 4. Orientation of the experimentally determined ${}^{207}$Pb chemical-shift eigenvectors (blue) in the unit cell of anglesite, scaled according to the magnitude of the associated eigenvalues, such that an absolute value of 750 ppm corresponds to a length of 1 Å, with the lead atoms (gray) shown with their co-ordination to ten oxygen atoms (red): (a) View down the c axis; (b) view down the b axis. (Drawings generated with the Vesta program [21]).

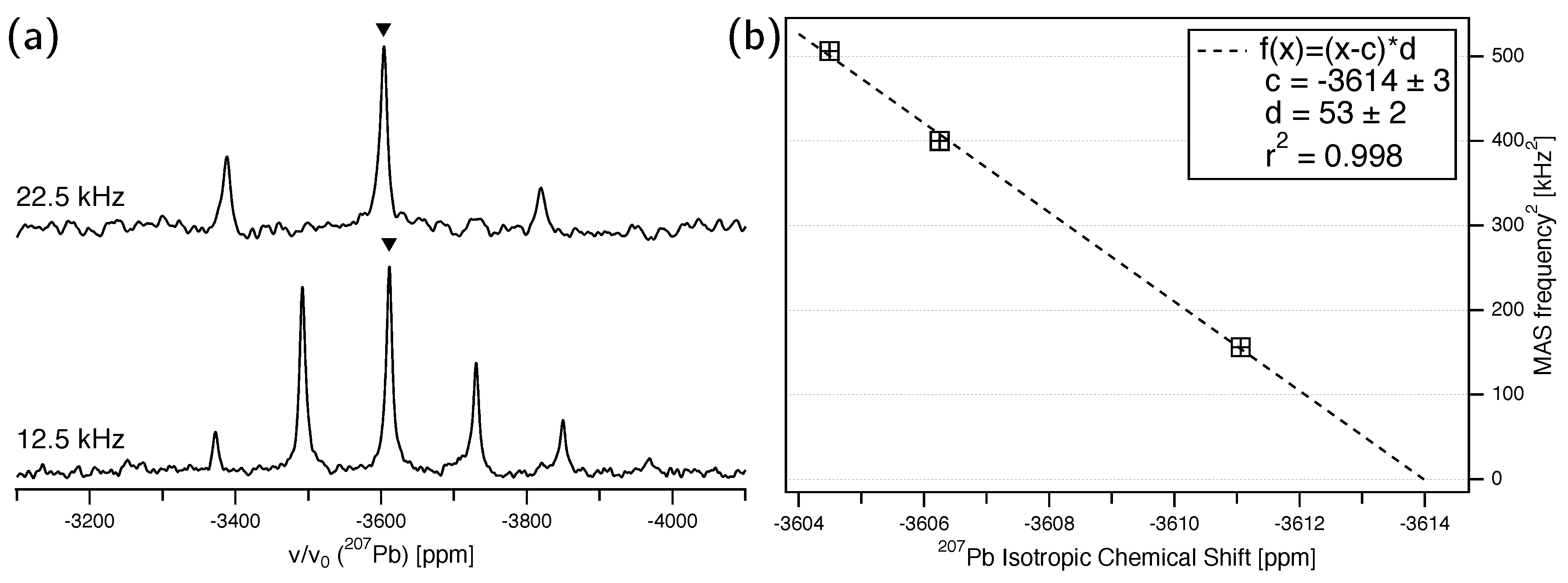
3.2. ${}^{207}$Pb NMR of Anglesite: Magic-Angle Spinning

For the single-crystal NMR experiments, the isotropic chemical shift is computed from the diagonal elements of $\delta$ according to Equation (1), to ${\delta }_{iso}=-3615$ ppm. As a useful comparison, ${\delta }_{iso}$ may also be obtained from MAS NMR spectroscopy. To this end, we acquired the NMR spectra of a polycrystalline sample (prepared by crushing larger anglesite crystals in a mortar) at various spinning speeds, ranging from 22.5 to 12.5 kHz. The ${}^{207}$Pb MAS NMR spectrum at 22.5 kHz spinning speed, shown in Figure 5a, shows the isotropic band at $-3604.5$ ppm, deviating significantly from the single-crystal value. It is, however, well known that for many lead-containing compounds, the ${}^{207}$Pb chemical shift markedly varies with temperature, to the extent that lead nitrate is routinely used for temperature calibration of NMR probes [37,38,39]. Our anglesite sample also already showed a noticeable change in ${\delta }_{iso}$ within the comparatively small temperature deviations produced by friction effects of the MAS technique. In order to be able to compare the isotropic shift derived from our single-crystal experiments at static (and therefore room-temperature) conditions, we extrapolated the temperature dependence of the isotropic shift to zero spinning speed, taking into account that the resonance position quadratically varies with MAS frequency [6]. The fit (see Figure 5b) resulted in an ‘static’ isotropic chemical shift of $-3614\pm 3$ ppm, in near perfect agreement with the single-crystal NMR value. Our ${\delta }_{iso}$ for anglesite is also in good agreement with the value of $-3613$ ppm, published in 1997 [22]. Curiously, the isotropic shift determined from a static polycrystalline sample [6] is significantly different at $-3505$ ppm. All principal tensor components given in that work are about $+110$ ppm off ours, so that ${\delta }_{iso}$ is strongly affected, but derived parameters $\Delta \delta$ and ${\eta }_{CS}$ are not (see above). Since the obvious pitfall of referencing can be ruled out, we currently have no convincing explanation for this large difference in tensor values.

Figure 5. (a) ${}^{207}$Pb magic-angle spinning NMR spectra of polycrystalline anglesite, acquired at the indicated MAS frequencies, with isotropic bands marked by a triangle. (b) Plot of the ${}^{207}$Pb isotropic chemical shift of anglesite versus the squared MAS frequency, with the linear fit given by the dashed line. An extrapolation to zero spinning speed results in an isotropic chemical shift of $-3614\pm 3$ ppm.

As already mentioned in the introduction, it is also possible to extract all three eigenvalues of the CS tensor from the rotational side-band pattern of MAS spectra. We have performed a Herzfeld–Berger analysis [7] on our MAS spectrum measured at the slowest speed ($12.5$ kHz). The results are listed in Table 1, and agree remarkably well with the single-crystal values. The comparatively large errors of the MAS-derived values could be improved by investing extensive amounts of measurement time to acquire spectra at lower spinning speeds and with better signal-to-noise ratio, but that is outside the scope of this work.

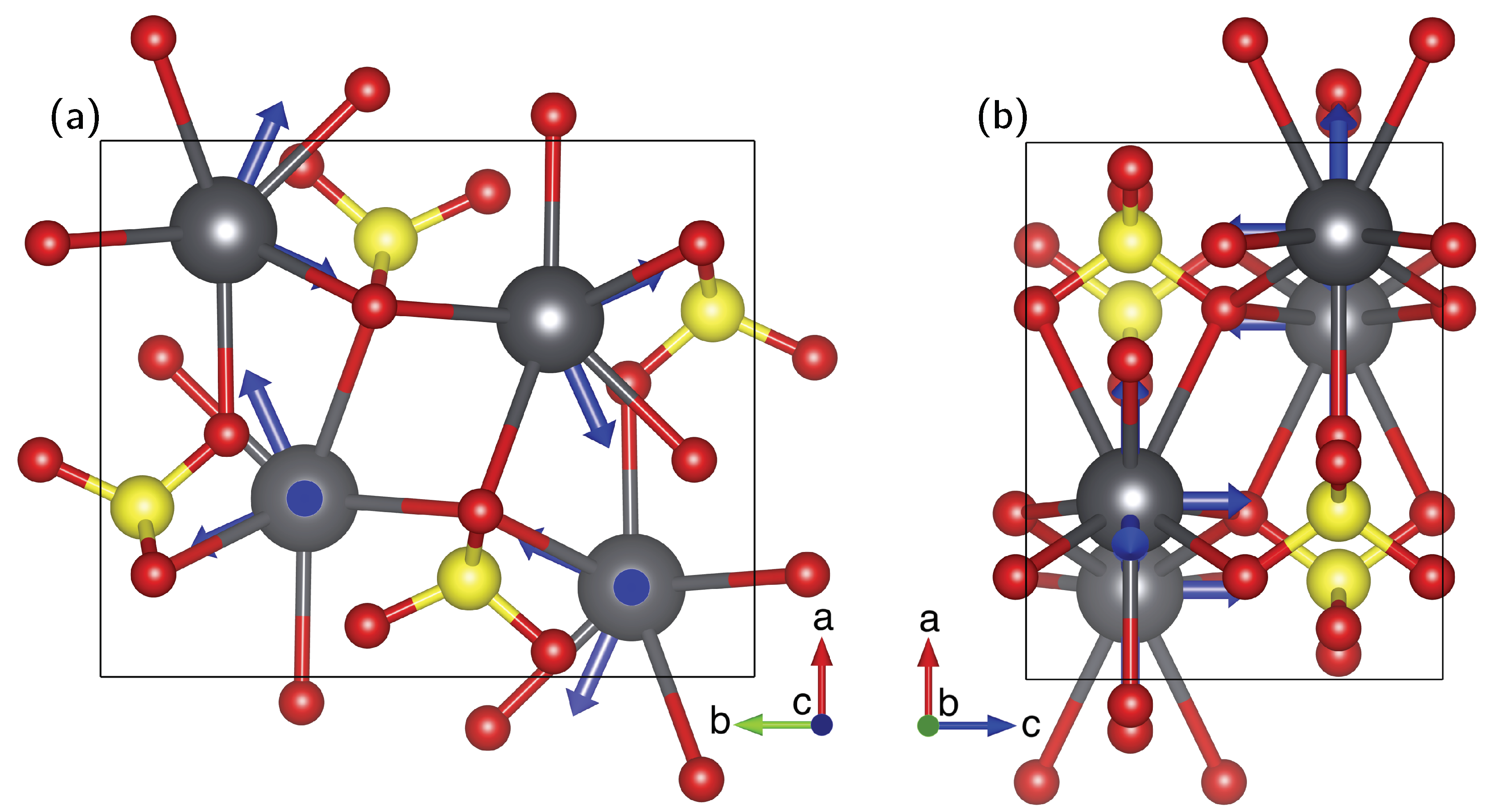
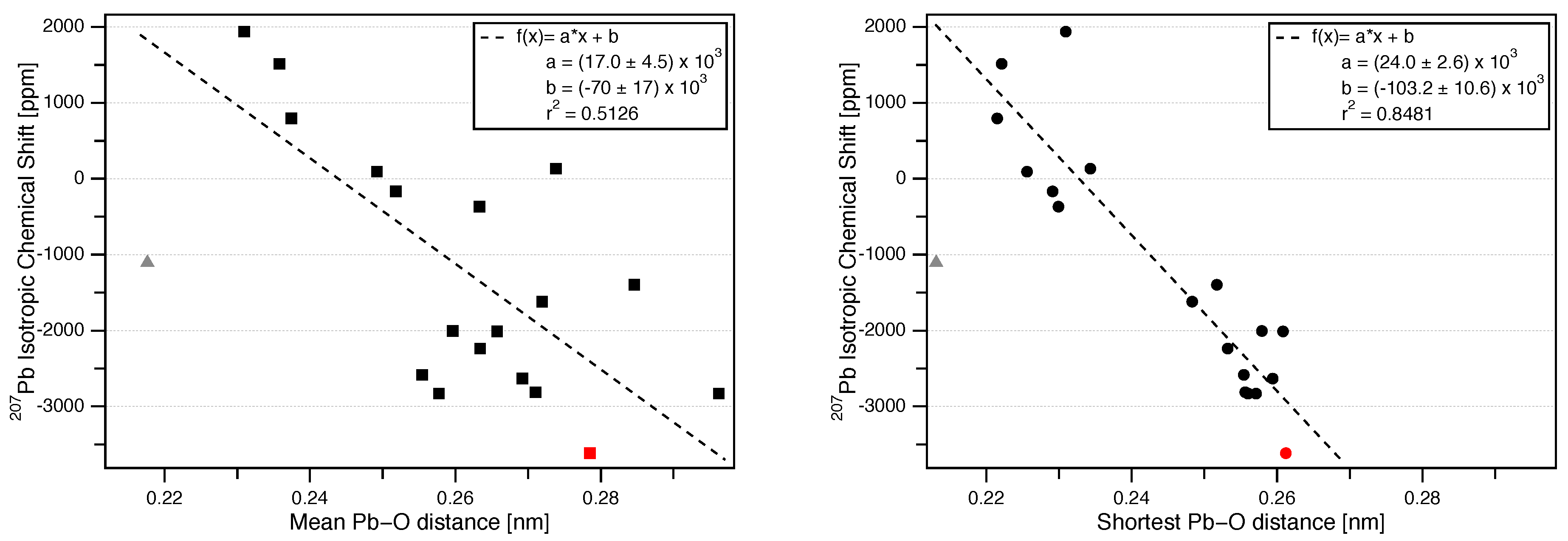
3.3. Correlation of ${}^{207}$Pb Isotropic Shifts and Pb–O Distances

In the context of NMR crystallography, the aspiration is always to find connections between NMR parameters and structural features of the compounds under investigation. As already mentioned in the introduction, it has previously been attempted to correlate the ${}^{207}$Pb isotropic shift ${\delta }_{iso}$ to interatomic distances between lead and oxygen for compounds where lead occurs solely in oxygen co-ordination. In this work by Fayon et al. in 1997 [22], a connection was proposed between ${\delta }_{iso}$ and the mean Pb–O distance in a given co-ordination sphere. However, this average distance is obviously strongly dependent on the chosen co-ordination sphere and the co-ordination number (CN) following from it. In fact, the question of how to define a co-ordination sphere around a given atom in a periodic structure is complex [40], and still a matter of debate among inorganic chemists. When checking the suggested correlation [22] for our anglesite data, classical counting within the co-ordination polyhedra gives $\mathrm{CN}=10$ for ${}^{207}$Pb, whereas the more convoluted concept of effective co-ordination number (eCoN) according to Hoppe [40] produces the almost identical value of 9.8. Thus, for lead in PbSO${}_4$, the co-ordination sphere is comparatively well-defined, and the calculation of a mean Pb–O distance from the atomic co-ordinates is a straightforward task. However, when we tried to reproduce the plot of Reference [22], we encountered many compounds where the definition of the co-ordination sphere was more ambiguous. For a number of those, our best effort at determining the co-ordination number, and the average distance following from it, gave a result that deviated from the earlier work. The CN’s and corresponding Pb–O distances of our assessment are listed in Table 2, where we restricted ourselves to lead compounds that also occur as natural minerals, with the respective mineral names specified. The plot of ${\delta }_{iso}$ versus mean Pb–O distance is shown in Figure 6(left), evidently correlating these two parameters only poorly.

Table 2. Crystallographic data and ${}^{207}$Pb isotropic chemical shifts ${\delta }_{iso}$ of lead-bearing minerals. The first co-ordination sphere of at least one lead side for each compound is solely determined by the next neighbouring oxygen atoms.

Mineral	Space Group (Reference)	Pb Coord. No.	Pb–O Mean Bond Length (nm)	Pb–O Shortest Bond Length (nm)	${\mathit{\delta }}_{\mathit{iso}}$ (ppm)	NMR Reference
red PbO [Litharge]	$P4/nmm$ [41]	4	0.2309	0.2309	1939 ± 5	[22]
yellow PbO [Massicot]	$Pbcm$ [42]	4	0.2358	0.2221	1515 ± 5	[22]
PbSiO${}_3$: Pb(1) [Alamosite] Pb(2) [Alamosite] Pb(3)	$P2/n$ [43]	5 5 6	0.2518 0.2492 0.2633	0.2291 0.2256 0.2299	$-166$± 5 93 ± 5 −366 ± 5	[22] [22] [22]
Pb${}_3$O${}_4$: Pb${}^{4+}$(1) [Minium] Pb(2)	$P{4}_2/mbc$ [44]	6 4	0.2176 0.2374	0.2131 0.2215	−1105 ± 1 795 ± 2	[22] [22]
PbTiO${}_3$ [Macedonite]	$P4mm$ [45]	12 (8+4)	0.2846	0.2517	−1395.1 ± 8.4	[6]
Pb${}_5$(VO${}_4$)${}_3$Cl: Pb(1) [Vanadinite] Pb(2)${}^a$	$P{6}_3/m$ [46]	9 6	0.2719 0.2664	0.2483 0.2324	−1619 ± 2 −1729 ± 9	[17] [17]
PbWO${}_4$ [Stolzite]	$I{4}_1/a$ [47]	8	0.2596	0.2579	−2003	[48]
PbMoO${}_4$ [Wulfenite]	$I{4}_1/a$ [49]	8	0.2657	0.2608	−2009 ± 2	[22]
PbCrO${}_4$ [Crocoite]	$P{2}_1/n$ [50]	8	0.2634	0.2532	−2236.2 ± 2.9	[6]
PbSb${}_2$O${}_6$ [Rosiaite]	$P\overline{3}m$ [51]	6	0.2554	0.2554	−2581 ± 3	[52]
PbCO${}_3$ [Cerussite]	$Pmcn$ [53]	9	0.2692	0.2594	−2630 ± 2	[22]
Pb${}_5$(PO${}_4$)${}_3$Cl: Pb(1) [Pyromorphite] Pb(2) ${}^a$	$P{6}_3/m$ [46]	9 6	0.2710 0.2761	0.2556 0.2353	−2810 ± 14 −2172 ± 11	[16] [16]
PbNb${}_2$O${}_6$: Pb(1) [Changbaiite] Pb(2) [Changbaiite] Pb(3)	$R3m$ [54]	6 6 (3+3) 12 (6+6)	0.2577 0.2962 0.2738	0.2560 0.2571 0.2343	−2829 −2829 134	[55] [55] [55]
PbSO${}_4$ [Anglesite]	$Pbnm$ [20]	10	0.2785	0.2612	−3615 ± 3	this work

${}^a$ Pb(2) is located on Wyckoff position 6h in vanadinite and pyromorphite, and is not included into the Pb–O distance correlation due to chlorine also being in the first co-ordination sphere.

Figure 6. (Left) Evolution of ${}^{207}$Pb isotropic chemical shift (${\delta }_{iso}$) versus mean Pb–O distance for compounds where lead occurs solely in oxygen co-ordination, with anglesite shown in red. (Right) ${\delta }_{iso}$ versus the shortest Pb–O distance. All data given in Table 2. (Dashed lines show the least-squares linear fit, with fit parameters and their errors given in the upper-right corners. The data point for Pb${}^{4+}$(1) in Pb${}_3$O${}_4$ (Minium) is shown as a gray triangle and was not included in the least-square fits, as the correlation was restricted to only Pb${}^{2+}$).

However, we found that using the shortest Pb–O distance, which, in contrast to the mean distance, can be established unequivocally, results in much improved correlation with the ${}^{207}$Pb isotropic chemical shift, as shown in Figure 6(right). Thus, the evolution of ${\delta }_{iso}$ with the shortest Pb–O distance in the co-ordination sphere, $d_{\mathrm{short}}$, may be described by:

$${\delta }_{iso}\left[\mathrm{ppm}\right]=23925-102780·d_{\mathrm{short}}\left[\mathrm{nm}\right]$$

(17)

Here, it should be emphasised that the above correlation only applies to Pb${}^{2+}$. The absence of the lone pair in Pb${}^{4+}$ obviously strongly changes the electronic surrounding of the ${}^{207}$Pb nucleus. As one example, we included the Pb${}^{4+}$ at the Pb(1) site of the mixed-valence oxide Pb${}_3$O${}_4$ (minium), which clearly lies far away from the suggested correlation lines in both plots of Figure 6. Regarding the well-documented temperature dependence of the ${}^{207}$Pb isotropic shift (see above), all ${\delta }_{iso}$ values in Table 2 were reported at ’room temperature’. While this specification is obviously somewhat vague, we note that the possible errors introduced by temperature deviations of a few degrees Celsius are so small that the error bars would be inside the size of the symbols used in the plots of Figure 6.

Furthermore, in the plot using the shortest Pb–O distances, the data points seem to appear in two clusters. Broadly, this clustering follows chemical intuition in the sense that shorter Pb–O distances are possible for the compounds with lower co-ordination number (for higher co-ordination, the ’crowding’ of oxygen around lead makes close contact difficult). There are, however, exceptions to that rule of thumb, in particular for changbaiite, PbNb${}_2$O${}_6$. Compounds with $\mathrm{CN}=6$ also show up in either cluster. It can therefore not be decided from the currently available database whether the observed clustering is a real effect or purely coincidental.

4. Conclusions

In this work, the full ${}^{207}$Pb chemical shift tensor in the orthorhombic crystal structure of anglesite, PbSO${}_4$, has been determined using orientation-dependent NMR measurements on a natural single crystal. With this study, we also attempted to demonstrate that problems usually associated with single-crystal NMR, i.e., problems (i)–(iii) listed in the introduction, may be overcome:

(i) 

The presumed extensive effort for data acquisition and evaluation is clearly manageable for the anglesite system. Despite the relatively low natural abundance of ${}^{207}$Pb of 22.1%, the spectra for the rotation pattern shown in Figure 3b were acquired with only eight scans and 60 s recycle delay, meaning the absolute measurement time was only about 2.5 hours. It can be seen from Figure 3a that the signal-to-noise ratio of the single-crystal spectra is satisfactory under these conditions. In contrast to static spectra of polycrystalline material (see, for example, Reference [6]), spectral intensity is focused on only few resonance lines, making detection less demanding. Our total experimental time was, of course, longer than 2.5 hours, with reorientation of the crystal and especially the subsequent necessary tuning and matching of the probe causing additional delays (the procedure of reorient/tune/match, however, may in principle be automated, considerably lessening the work load of the operator [56]). To further improve the efficiency of both data acquisition and processing, we utilised crystallographic symmetry relations [12,13,14] between two groups of magnetically inequivalent ${}^{207}$Pb atoms, reducing the necessary data for determining the full CS tensor to two rotation patterns, about two nonparallel rotation axes. A generous estimate of the optimised total time for data acquisition would therefore be 7–8 h. It took three hours to record the MAS spectrum of a polycrystalline sample shown in Figure 5a, yet, for ${}^{207}$Pb spectra of systems with large $\Delta \delta$, two such MAS spectra are usually required to unequivocally assign the isotropic peak. In terms of pure experimental time, therefore, single-crystal NMR compares not unfavourably to MAS NMR, although the necessary effort for data processing and evaluation is obviously more extensive. At the end of this process, however, the full CS tensor is gained, and not only the value of ${\delta }_{iso}$ available from fast MAS experiments.

(ii) 

The necessity to know the orientation of the rotation axis in the crystal frame is generally solvable in a number of ways, including optical orientation using well-developed crystal faces. The most precise method is certainly the use of X-ray diffraction on the mounted crystal on which NMR measurements are to be performed. However, the large crystals needed for NMR tend to absorb most of the X-ray beam, in particular when compounds with high lead content, such as anglesite, are being investigated. For these systems, resolving the orientation of the rotation axis by relying only on NMR data is a very useful approach, as shown here and in earlier work [15,16,17].

(iii) 

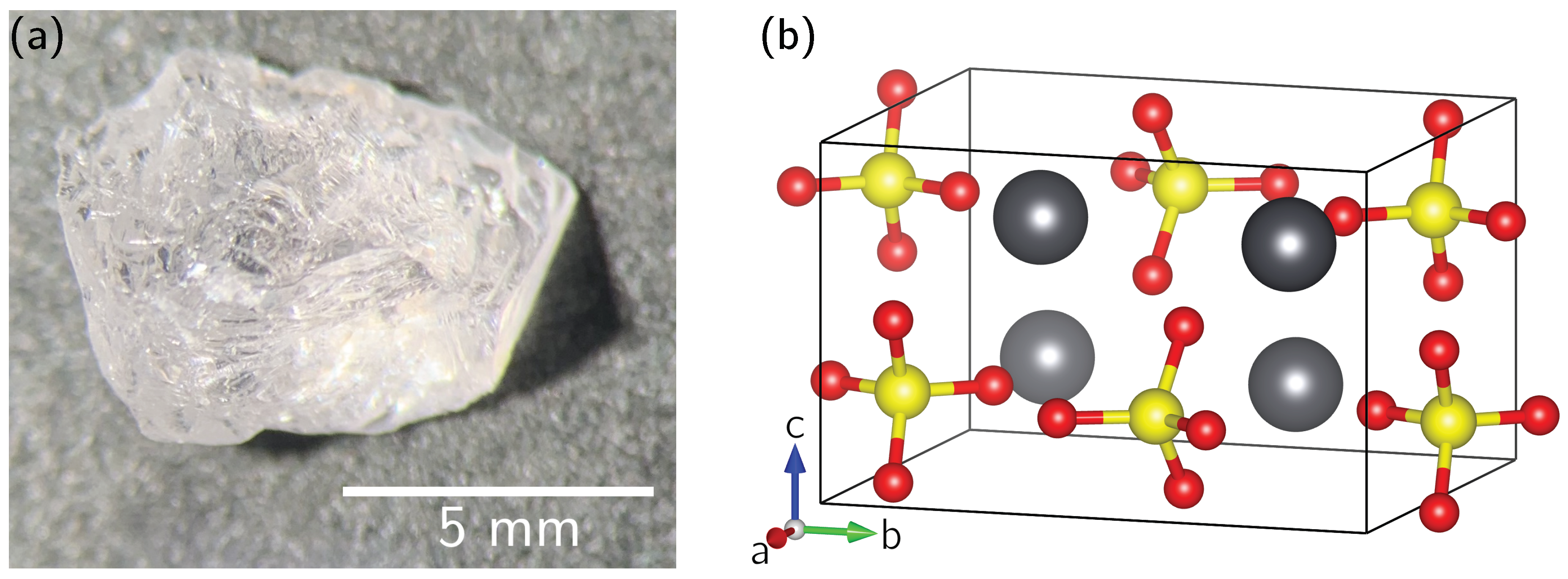
For the scarce availability of single crystals of sufficient size for NMR experiments, no general solution appears to exist. For the area of ${}^{207}$Pb-NMR, however, a considerable number of compounds also occur as natural minerals (see Table 2). For many lead compounds, comparatively large single crystals are therefore available from mineral collections.

Furthermore, in the context of establishing connections between NMR parameters and crystal structure, we here have reported on a linear correlation between ${}^{207}$Pb isotropic chemical shift and the shortest Pb–O distance in the co-ordination sphere, for compounds with Pb${}^{2+}$ solely surrounded by oxygen. This correlation appears to work better than the previously suggested connection between ${\delta }_{iso}$ and an average distance of all oxygens in a co-ordination sphere [22], in particular because the precise definition of this sphere is debatable.

As an outlook, the strategy of deriving full chemical shift tensors from single crystals with an initially unknown rotation axis discussed in this paper may also be extended to crystal systems with lower symmetry. In such systems, two rotation axes are insufficient due to the lack of magnetically independent but crystallographically related atoms. Further work along these lines is in progress in our laboratory with the aim to determine chemical-shift eigenvalues and eigenvectors of nuclei with spin $I=\frac{1}{2}$ with high precision and without the need for additional crystal-alignment techniques, thus bringing NMR spectroscopy and X-ray diffraction crystallography in close relation.

5. Materials and Methods

${}^{207}$Pb NMR spectra were acquired on a Bruker Avance-III 500 (${\overrightarrow{B}}_0=11.7$ T) spectrometer at LMU Munich, with a Larmor frequency of ${\nu }_0$(${}^{207}$Pb) = 104.63 MHz. A spin–echo sequence [57] was employed to minimise baseline roll. A recycle delay of 60 s was used for both single-crystal and MAS spectra. The rotation pattern of Figure 3b was acquired with 8 scans for each spectrum, the pattern in Figure 3d mostly with 16 scans (one exception is the spectrum at 40 degrees shown in Figure 3c, for which 60 scans were added). The orientation change of the single crystal was realised by a goniometer mechanics build by NMR Service GmbH (Erfurt, Germany), which was ’clipped on’ (see Figure 2a) a wide-bore Bruker static NMR probe with a home-built 6 mm solenoid coil. For the MAS spectra, a polycrystalline sample was prepared by crushing single crystals of anglesite with an agate mortar and measured using a 2.5 mm rotor. All spectra were indirectly referenced to ${}^1$H in 100% TMS at $-0.1240$ ppm. According to our measurements, this is equivalent to the commonly used reference of a static Pb(NO${}_3$)${}_2$ powder spectrum at room temperature, with ${\delta }_{iso}=-3492$ ppm, or $-3474$ ppm at the highest point of the line shape, both in good agreement with previously reported values [6]. The global fit of the two rotation patterns was performed with the program Igor Pro 7 from WaveMatrics Inc., which delivers excellent nonlinear fitting performance.