Simultaneous Generation of Two Pairs of Stokes and Terahertz Waves from Coupled Optical Parametric Oscillations with Quasi-Phase-Matching
Abstract
:1. Introduction
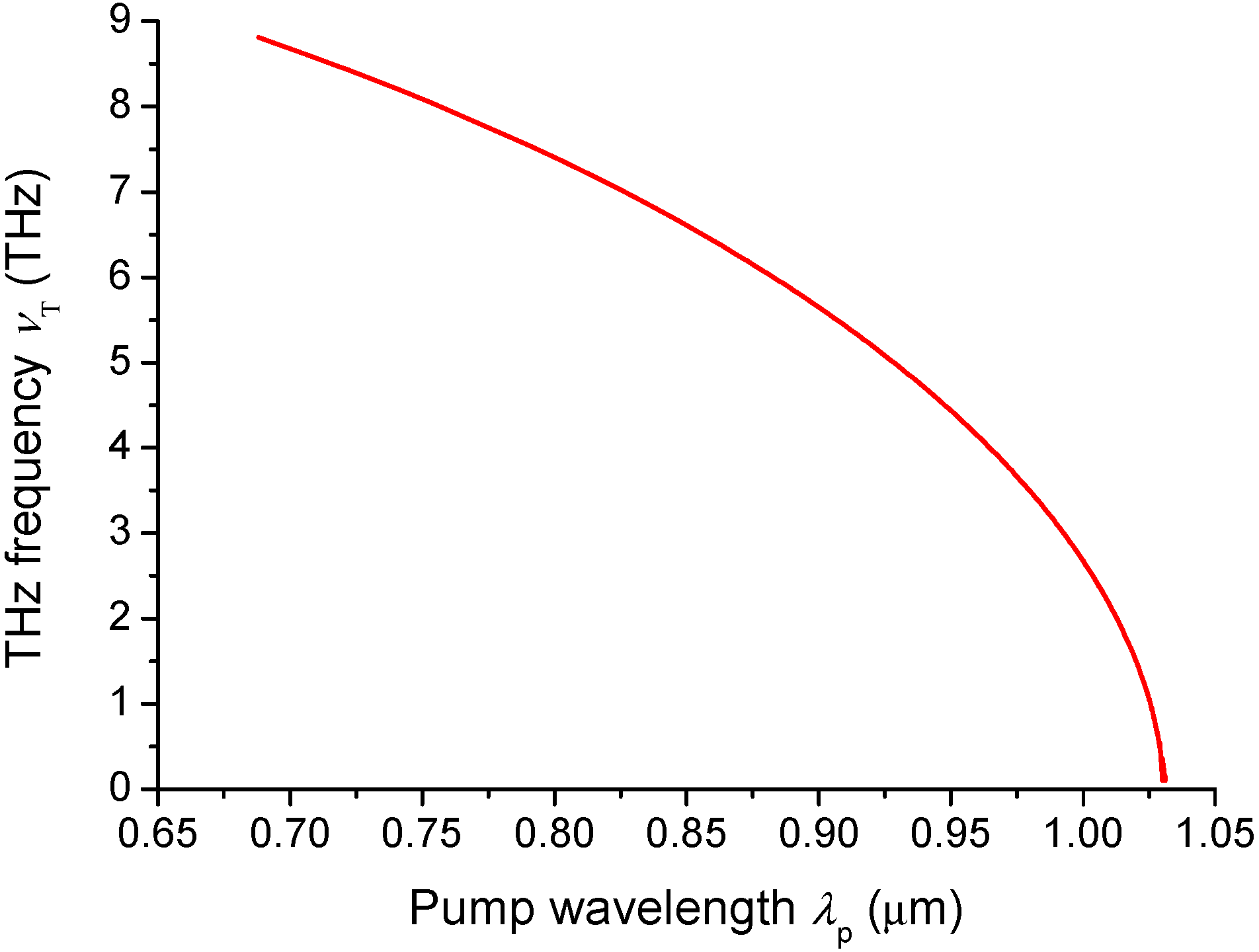
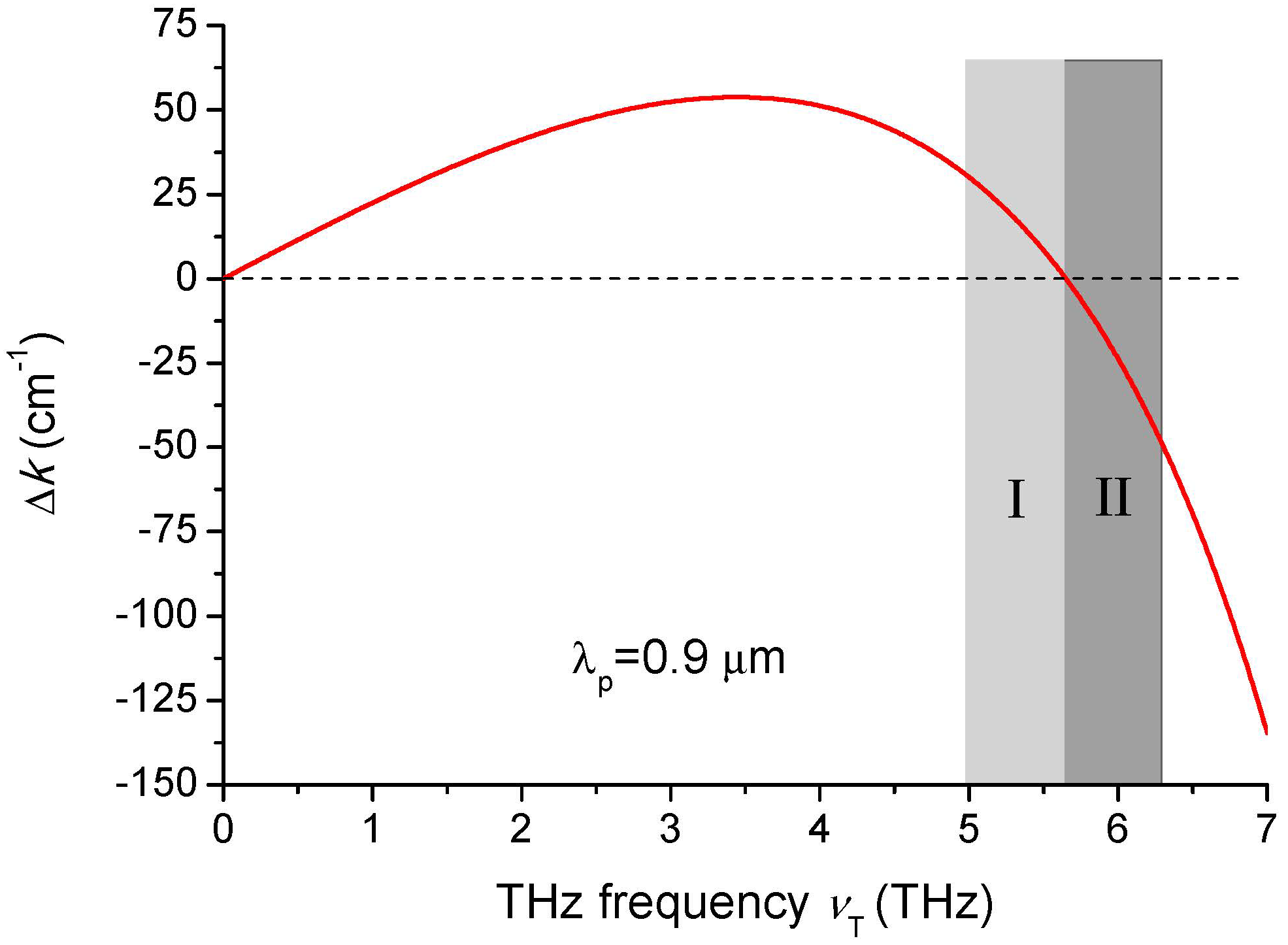
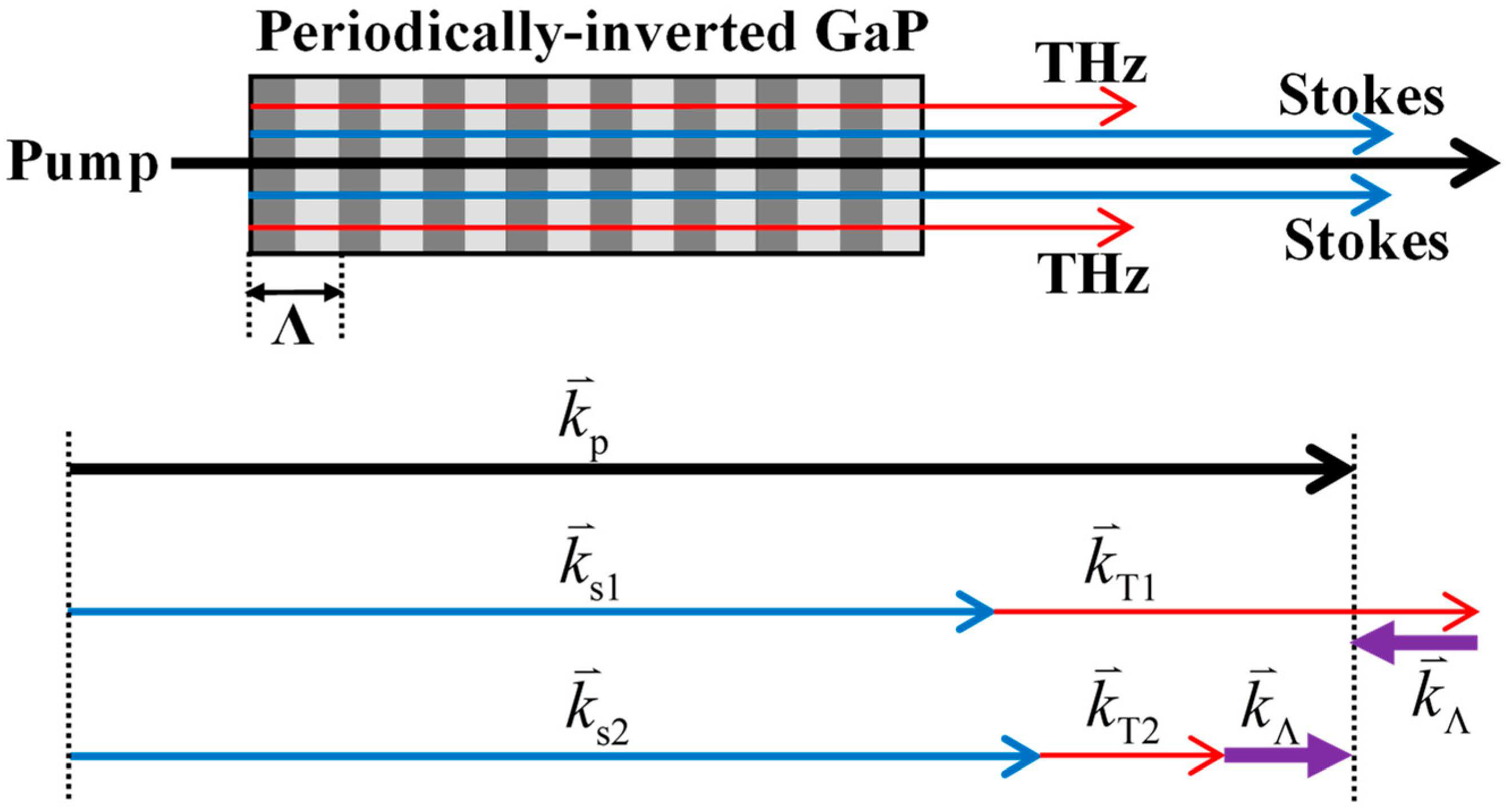
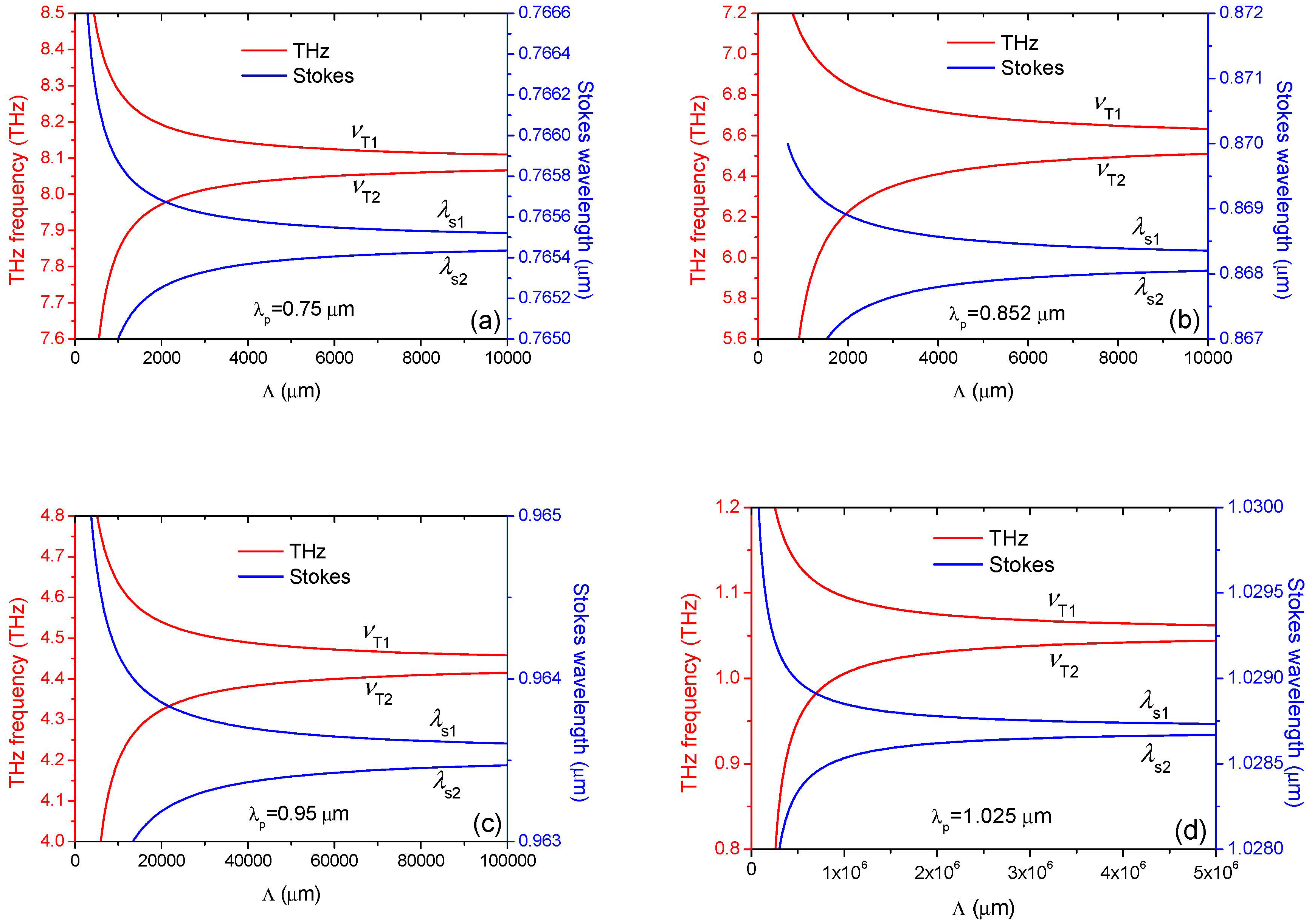
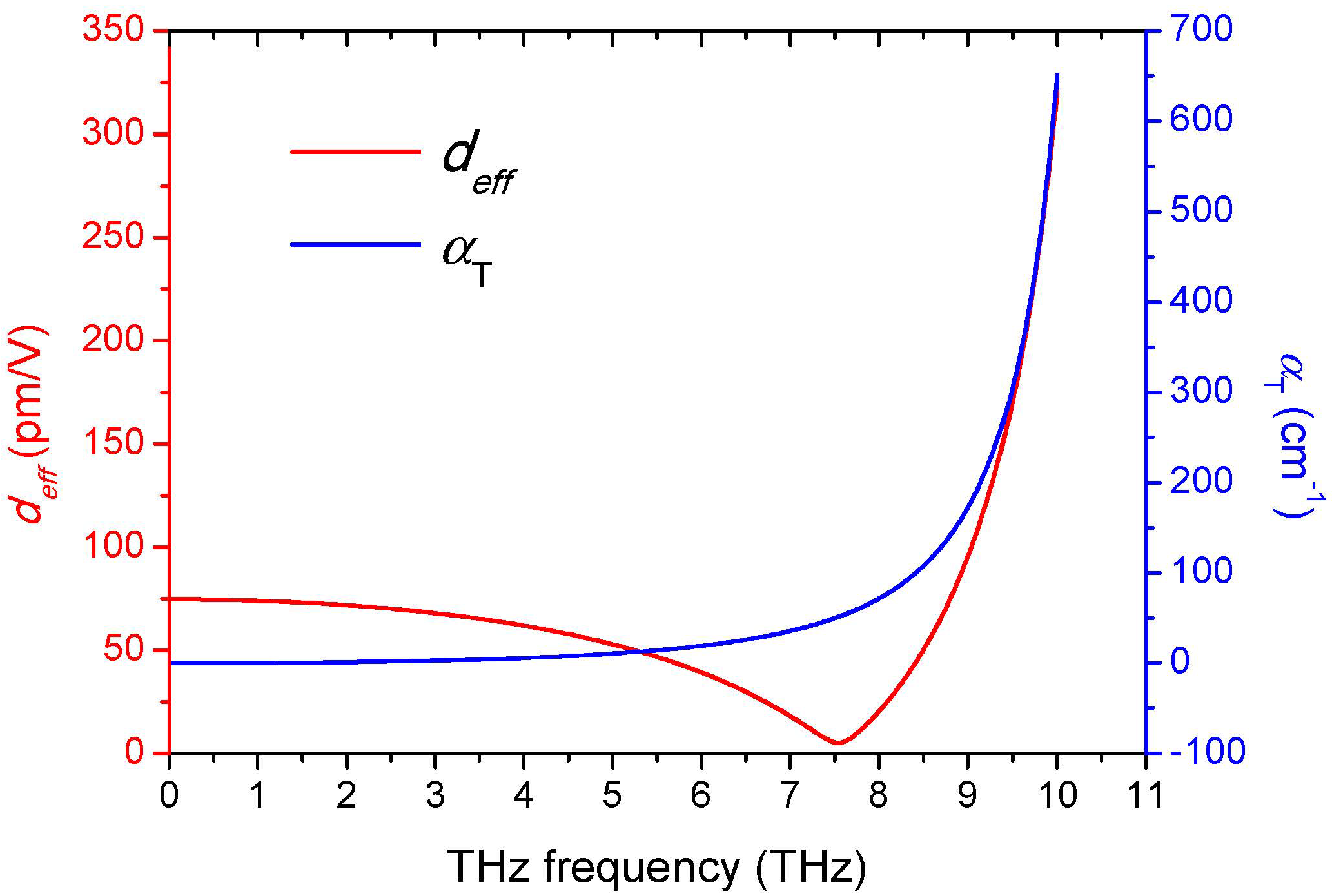
2. Phase-Matching Characteristics
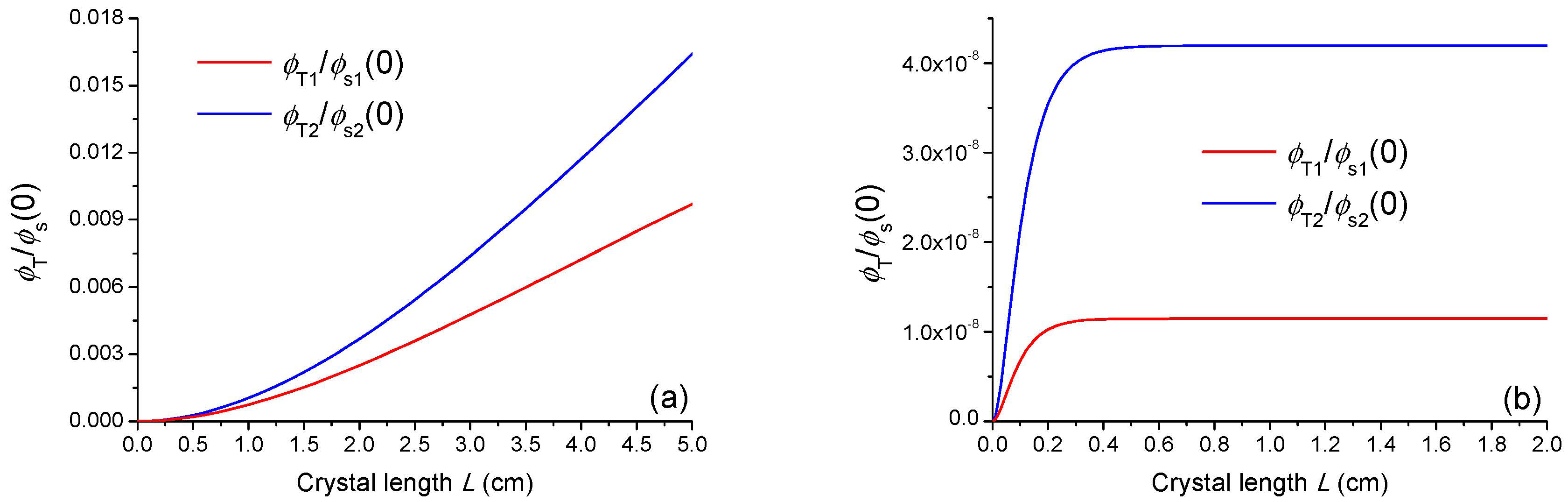
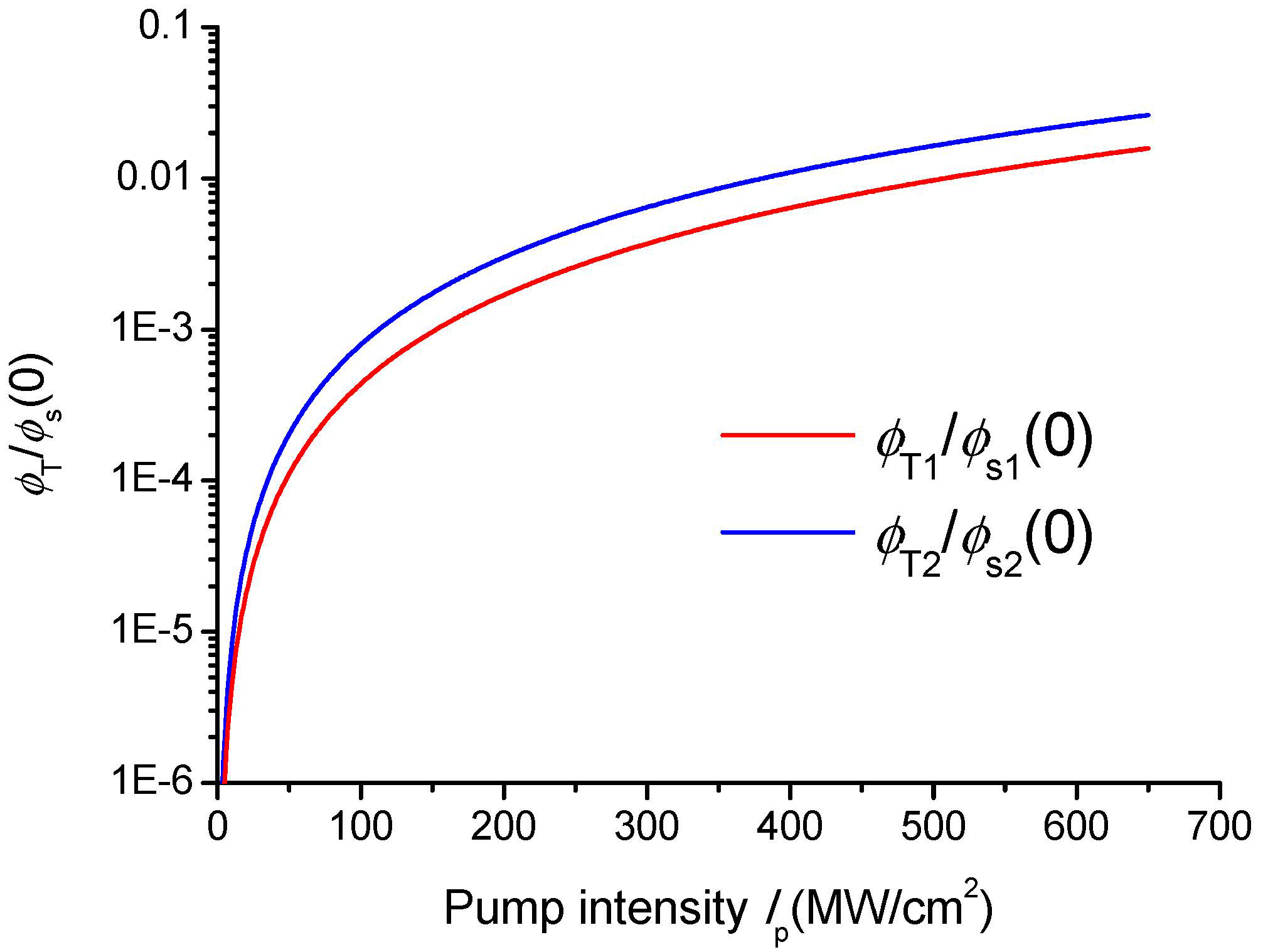
3. THz Wave Photon Flux Density
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mu, X.D.; Meissner, H.; Lee, H.C. Optical parametric oscillations of 2 μm in multiple-layer bonded walk-off compensated KTP stacks. Opt. Lett. 2010, 35, 387–389. [Google Scholar] [CrossRef] [PubMed]
- Zhao, P.; Ragam, S.; Ding, Y.J.; Zotova, I.B.; Mu, X.D.; Lee, H.C.; Meissner, S.K.; Meissner, H. Singly resonant optical parametric oscillator based on adhesive-free-bonded periodically inverted KTiOPO4 plates: Terahertz generation by mixing a pair of idler waves. Opt. Lett. 2012, 37, 1283–1285. [Google Scholar] [CrossRef] [PubMed]
- Valk, N.C.J.; Marel, W.A.M.; Planken, P.C.M. Terahertz polarization imaging. Opt. Lett. 2005, 30, 2802–2804. [Google Scholar] [CrossRef] [PubMed]
- Mathanker, S.K.; Weckler, P.R.; Wang, N. Terahertz (THz) applications in food and agriculture: A review. Trans. ASABE 2013, 56, 1213–1226. [Google Scholar]
- Kawase, K.; Shikata, J.; Ito, H. Terahertz wave parametric source. J. Phys. D Appl. Phys. 2002, 35, R1–R14. [Google Scholar] [CrossRef]
- Ikari, T.; Guo, R.; Minamide, H.; Ito, H. Energy scalable terahertz-wave parametric oscillator using surface-emitted configuration. J. Eur. Opt. Soc. Rapid Publ. 2010, 5, 10054. [Google Scholar]
- Ortega, T.A.; Pask, H.M.; Spence, D.J.; Lee, A.J. THz polariton laser using an intracavity Mg:LiNbO3 crystal with protective Teflon coating. Opt. Express 2017, 25, 3991–3999. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.L.; Qu, Y.C.; Zhao, W.J.; Chen, Z.L. High energy, widely tunable Si-prism-array coupled terahertz-wave parametric oscillator with a deformed pump and optimal crystal location for angle tuning. Appl. Opt. 2017, 56, 2412–2417. [Google Scholar] [CrossRef] [PubMed]
- Molter, D.; Theuer, M.; Beigang, R. Nanosecond terahertz optical parametric oscillator with a novel quasiphase-matching scheme in lithium niobate. Opt. Express 2009, 17, 6623–6628. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.; Strömqvist, G.; Pasiskevicius, V.; Canalias, C. Control of forward stimulated polariton scattering in periodically-poled KTP crystals. Opt. Express 2013, 21, 27277–27283. [Google Scholar] [CrossRef] [PubMed]
- Jang, H.; Viotti, A.L.; Strömqvist, G.; Zukauskas, A.; Canalias, C.; Pasiskevicius, V. Counter-propagating parametric interaction with phonon-polaritons in periodically poled KTiOPO4. Opt. Express 2017, 25, 2677–2686. [Google Scholar] [CrossRef] [PubMed]
- Wu, M.H.; Chiu, Y.C.; Wang, T.D.; Zhao, G.; Zukauskas, A.; Laurell, F.; Huang, Y.C. Terahertz parametric generation and amplification from potassium titanyl phosphate in comparison with lithium niobate and lithium tantalate. Opt. Express 2016, 24, 25964–25973. [Google Scholar] [CrossRef] [PubMed]
- Vodopyanov, K.L. Optical THz-wave generation with periodically-inverted GaAs. Laser Photon. Rev. 2008, 2, 11–25. [Google Scholar] [CrossRef]
- Vodopyanov, K.L. Terahertz-wave generation with periodically inverted gallium arsenide. Laser Phys. 2009, 19, 305–321. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids III; Elsevier: San Diego, CA, USA, 1998; pp. 32–40. [Google Scholar]
- Shoji, I.; Kondo, T.; Ito, R. Second-order nonlinear susceptibilities of various dielectric and semiconductor materials. Opt. Quantum Electron. 2002, 34, 797–833. [Google Scholar] [CrossRef]
- Bahoura, M.; Herman, G.S.; Barnes, N.P.; Bonner, C.E.; Higgins, P.T. Terahertz wave source via difference-frequency mixing using cross-Reststrahlen band dispersion compensation phase matching: A material study. Proc. SPIE 2000, 3928, 132–140. [Google Scholar]
- Faust, W.L.; Henry, C.H. Mixing of visible and near-resonance infrared light in GaP. Phys. Rev. Lett. 1966, 17, 1265–1268. [Google Scholar] [CrossRef]
- Sussman, S.S. Tunable Light Scattering from Transverse Optical Modes in Lithium Niobate; Report No. su-mlr-1851(1970); Microwave Laboratory, Stanford University: Stanford, CA, USA, 1971. [Google Scholar]
- Walsh, D.A. Intracavity Terahertz Optical Parametric Oscillators. Ph.D. Thesis, University of St Andrews, Scotland, UK, 2011. [Google Scholar]
- Kitaeva, G.K.; Penin, A.N. Parametric frequency conversion in layered nonlinear media. J. Exp. Theor. Phys. 2004, 98, 272–286. [Google Scholar] [CrossRef]
- Wang, T.D.; Huang, Y.C.; Chuang, M.Y.; Lin, Y.H.; Lee, C.H.; Lin, Y.Y.; Lin, F.Y.; Kitaeva, G.K. Long range parametric amplification of THz wave with absorption loss exceeding parametric gain. Opt. Express 2013, 21, 2452–2462. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, L.P.; Guha, S.; Trivedi, S. Damage thresholds and nonlinear optical performance of GaP. In Proceedings of the Conference on Lasers and Electro-Optics, San Francisco, CA, USA, 16–21 May 2004. [Google Scholar]
- Takida, Y.; Shikata, J.; Nawata, K.; Tokizane, Y.; Han, Z.L.; Koyama, M.; Notake, T.; Hayashi, S.; Minamide, H. Terahertz-wave parametric gain of stimulated polariton scattering. Phys. Rev. A 2016, 93, 043836. [Google Scholar] [CrossRef]
- Hayashi, S.; Nawata, K.; Taira, T.; Shikata, J.; Kawase, K.; Minamide, H. Ultrabright continuously tunable terahertz-wave generation at room temperature. Sci. Rep. 2014, 4, 5045. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Tan, L.; Li, Y.; Yuan, B.; Wang, S.; Wang, M.; Bing, P.; Yuan, S. Simultaneous Generation of Two Pairs of Stokes and Terahertz Waves from Coupled Optical Parametric Oscillations with Quasi-Phase-Matching. Crystals 2018, 8, 323. https://doi.org/10.3390/cryst8080323
Li Z, Tan L, Li Y, Yuan B, Wang S, Wang M, Bing P, Yuan S. Simultaneous Generation of Two Pairs of Stokes and Terahertz Waves from Coupled Optical Parametric Oscillations with Quasi-Phase-Matching. Crystals. 2018; 8(8):323. https://doi.org/10.3390/cryst8080323
Chicago/Turabian StyleLi, Zhongyang, Lian Tan, Yongjun Li, Bin Yuan, Silei Wang, Mengtao Wang, Pibin Bing, and Sheng Yuan. 2018. "Simultaneous Generation of Two Pairs of Stokes and Terahertz Waves from Coupled Optical Parametric Oscillations with Quasi-Phase-Matching" Crystals 8, no. 8: 323. https://doi.org/10.3390/cryst8080323




