The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations
Abstract
:1. Introduction
2. Computational Methods and Details
3. Results and Discussion
3.1. Lattice Constants
3.2. Elastic Properties
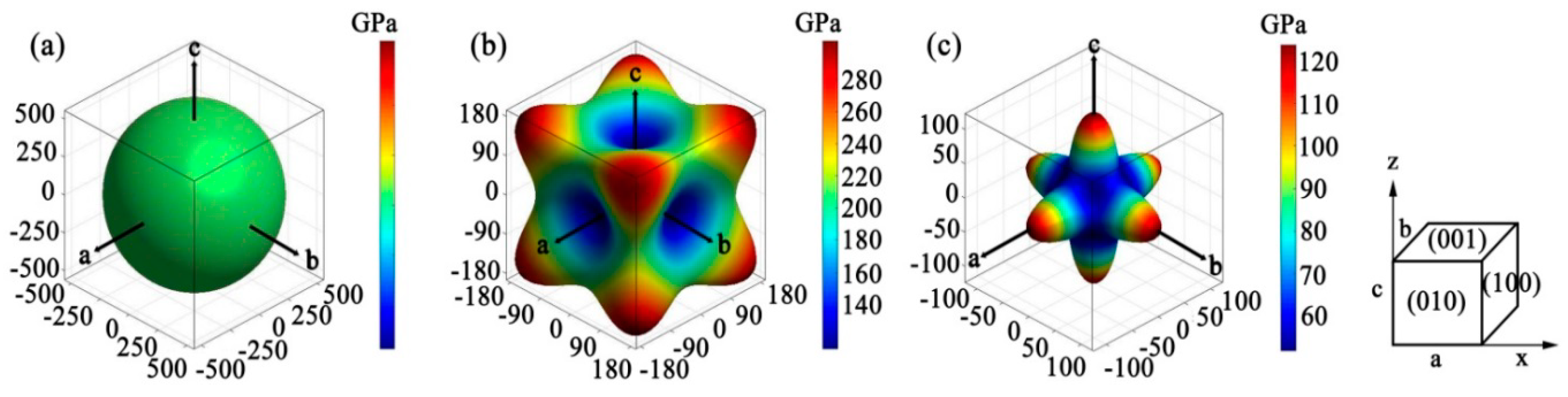
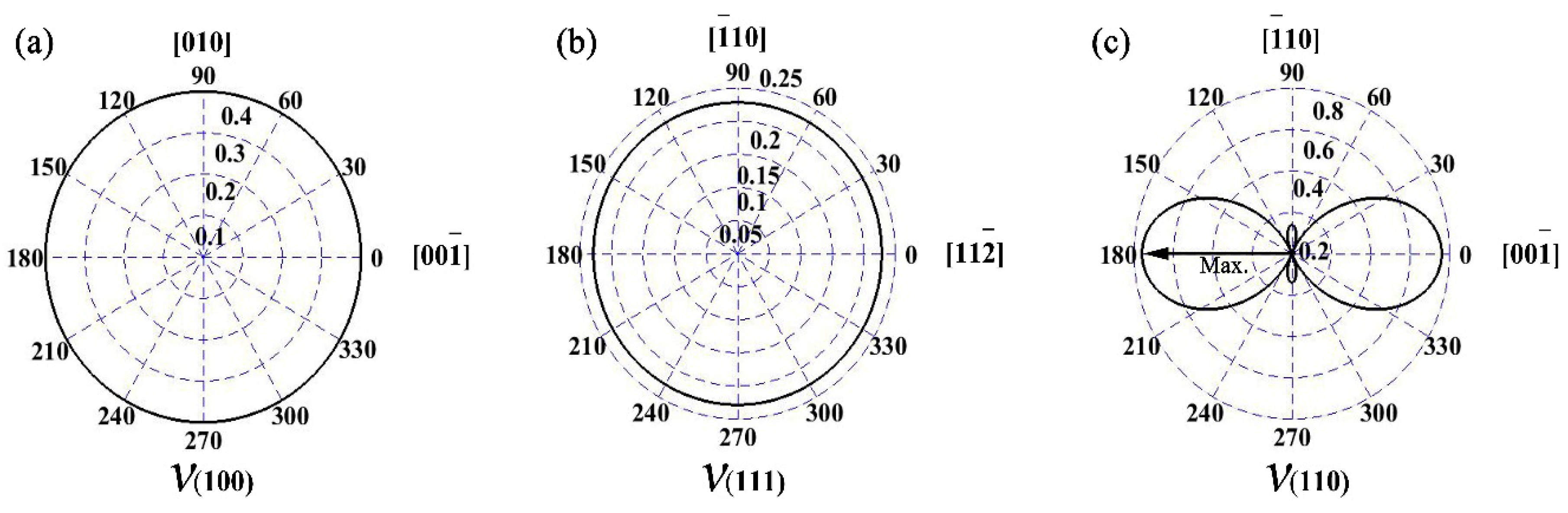
3.3. Elastic Anisotropy
3.4. Thermodynamic Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wen, Z.; Zhao, Y.; Hou, H.; Tian, J.; Han, P. First-principles study of Ni-Al intermetallic compounds under various temperature and pressure. Superlattices Microstruct. 2017, 103, 9–18. [Google Scholar] [CrossRef]
- Wen, M.; Wang, C.Y. Transition-metal alloying of γ′−Ni3Al: Effects on the ideal uniaxial compressive strength from first-principles calculations. Phys. Rev. B 2018, 97, 024101. [Google Scholar] [CrossRef]
- Goiri, J.G.; Ven, A.V.D. Phase and structural stability in Ni-Al systems from first principles. Phys. Rev. B 2016, 94, 094111. [Google Scholar] [CrossRef]
- Jiang, L.; Li, S.; Han, Y. Rotating bending fatigue property of the Ni3Al-based single crystal superalloyIC6SX at 900 °C. Mater. Sci. Eng. 2017, 182, 012058. [Google Scholar]
- Jozwik, P.; Polkowski, W.; Bojar, Z. Applications of Ni3Al based intermetallic alloys γ current stage and potential perceptivities. Materials 2015, 8, 2537–2568. [Google Scholar] [CrossRef]
- Hou, H.; Wen, Z.; Zhao, Y.; Fu, L.; Wang, N.; Han, P. First-principles investigations on structural, elastic, thermodynamic and electronic properties of Ni3X (X=Al, Ga and Ge) under pressure. Intermetallics 2014, 44, 110–115. [Google Scholar] [CrossRef]
- Chen, D.; Luo, F.; Lou, X.; Qing, Y.; Zhou, W.; Zhu, D. Comparison of thermal insulation capability between conventional and nanostructured plasma sprayed ysz coating on Ni3Al substrates. Ceram. Int. 2016, 43, 4324–4329. [Google Scholar] [CrossRef]
- Pearson, W.B.; Raynor, G.V. A Handbook of Lattice Spacings and Structures of Metals and Alloys; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Yasuda, H.; Takasugi, T.; Koiwa, M. Elasticity of Ni-based L12-type intermetallic compounds. Acta Metall. 1992, 40, 381–387. [Google Scholar] [CrossRef]
- Qin, H.; Luan, X.; Feng, C. Mechanical, thermodynamic and electronic properties of wurtzite and zinc-blende gan crystals. Materials 2017, 10, 1419. [Google Scholar] [CrossRef] [PubMed]
- Liu, D.; Zhu, X.; Qin, J.; Wang, A.; Duan, J.; Gu, T. First-principles study of chemical and topological short-range orders in the Mg–Si liquid alloys. Metals 2016, 6, 78. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, C.; Liu, J.; Li, Y.; Fang, X.; Li, J.; Han, P. First-principles study on the structural stability and segregation behavior of γ-Fe/Cr2N interface with alloying additives M (M = Mn, V, Ti, Mo, and Ni). Metals 2016, 6, 156. [Google Scholar] [CrossRef]
- Li, X.; Xia, C.; Wang, M.; Wu, Y.; Chen, D. First-principles investigation of structural, electronic and elastic properties of HFX (X = Os, Ir and Pt) compounds. Metals 2017, 7, 317. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, Y.; Xiao, Z.; Reng, X. Study of adsorption of hydrogen on Al, Cu, Mg, Ti surfaces in al alloy melt via first principles calculation. Metals 2017, 7, 21. [Google Scholar] [CrossRef]
- Kim, D.E.; Shang, S.L.; Liu, Z.K. Effects of alloying elements on elastic properties of NiAl by first-principles calculations. Intermetallics 2010, 18, 1163–1171. [Google Scholar] [CrossRef]
- Huang, M.L. First-principles studies of effects of interstitial boron and carbon on the structural, elastic, and electronic properties of Ni solution and Ni3Al intermetallics. Chin. Phys. B 2016, 25, 107104. [Google Scholar] [CrossRef]
- Ai, C.; Li, S.; Zhao, X.; Zhou, J.; Guo, Y.; Sun, Z.; Song, X.; Gong, S. Influence of solidification history on precipitation behavior of TCP phase in a completely heat-treated Ni3Al based single crystal superalloy during thermal exposure. J. Alloy Compd. 2017, 722, 740–745. [Google Scholar] [CrossRef]
- Jiang, L.; Li, S.; Han, Y. Research on the creep mechanism of a Ni3Al-based single crystal superalloyIC6SX under 980 °C/205MPa. Mater. Sci. Eng. 2017, 182, 012059. [Google Scholar]
- Jiang, L.W.; Wu, M.L.; Li, S.S.; Han, Y.F. Rotating bending fatigue behaviour of a Ni3Al-based single crystal alloy IC6SX at 760 °C. Mater. Res. Innov. 2015, 19, S163–S169. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W. Dependence of stresses and strain energies on grain orientations in FCC metal films. J. Cryst. Growth 2005, 285, 427–435. [Google Scholar] [CrossRef]
- Choi, J.H.; Kang, S.Y.; Dong, N.L. Relationship between deposition and recrystallization textures of copper and chromium electrodeposits. J. Mater. Sci. 2000, 35, 4055–4066. [Google Scholar] [CrossRef]
- Mohan Rao, P.V.; Suryanarayana, S.V.; Satyanarayana Murthy, K.; Nagender Naidu, S.V. The high-temperature thermal expansion of Ni3Al measured by X-ray diffraction and dilation methods. J. Phys. Condens. Matter 1989, 1, 5357. [Google Scholar]
- Lindan, P.J.D.; Probert, M.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.; Clark, S.J.; Payne, M.C. First-principles simulation. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar]
- Monkhorst, H.J. Special points for brillouin-zone integrations. Phys. Rev. B Condens. Matter 1976, 16, 1748–1749. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Martin, R.; Nagathil, A. Stability investigation and thermal behavior of a hypothetical silicon nanotube. J. Mol. Struct. Theochem. 2001, 539, 101–106. [Google Scholar]
- Hammer, B. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerh of functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef] [Green Version]
- Francis, G.P.; Payne, M.C. Finite basis set corrections to total energy pseudopotential calculations. J. Phys. Condens. Matter 1999, 2, 4395. [Google Scholar] [CrossRef]
- Kumar, S.; Jung, J.P. Mechanical and electronic properties of Ag3Sn intermetallic compound in lead free solders using ab initio atomistic calculation. Mater. Sci. Eng. B 2013, 178, 10–21. [Google Scholar] [CrossRef]
- Lee, N.T.S.; Tan, V.B.C.; Lim, K.M. Structural and mechanical properties of Sn-based intermetallics from ab initio calculations. Appl. Phys. Lett. 2006, 89, 353–489. [Google Scholar] [CrossRef]
- Chen, J.; Lai, Y.S. Towards elastic anisotropy and strain-induced void formation in Cu-Sn crystalline phases. Microelectron. Reliab. 2009, 49, 264–268. [Google Scholar] [CrossRef]
- Nguyen-Manh, D.; Pettifor, D.G. Electronic structure, phase stability and elastic moduli of ab transition metal aluminides. Intermetallics 1999, 7, 1095–1106. [Google Scholar] [CrossRef]
- Chen, W.H.; Yu, C.F.; Cheng, H.C.; Lu, S.T. Crystal size and direction dependence of the elastic properties of Cu3Sn through molecular dynamics simulation and nanoindentation testing. Microelectron. Reliab. 2012, 52, 1699–1710. [Google Scholar] [CrossRef]
- Fatmi, M.; Ghebouli, M.A.; Ghebouli, B.; Chihi, T.; Boucetta, S.; Heiba, Z.K. Study of structural, elastic, electronic, optical and thermal properties of Ni3Al. Rom. J. Phys. 2011, 56, 935–951. [Google Scholar]
- Zhao, W.; Sun, Z.; Gong, S. Synergistic effect of co-alloying elements on site preferences and elastic properties of Ni3Al: A first-principles study. Intermetallics 2015, 65, 75–80. [Google Scholar] [CrossRef]
- Kayser, F.X.; Stassis, C. The elastic constants of Ni3Al at 0 and 23.5 °C. Phys. Status Solidi 2010, 64, 335–342. [Google Scholar] [CrossRef]
- Nye, J.F.; Lindsay, R.B. Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK, 1984. [Google Scholar]
- Verma, J.K.D.; Nag, B.D. On the elastic moduli of a crystal and voigt and reuss relations. J. Phys. Soc. Jpn. 2007, 20, 635–636. [Google Scholar] [CrossRef]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. 2002, 65, 349–354. [Google Scholar] [CrossRef]
- Prikhodko, S.V.; Yang, H.; Ardell, A.J.; Carnes, J.D. Temperature and composition dependence of the elastic constants of Ni3Al. Metall. Mater. Trans. A 1999, 30, 2403–2408. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 2009, 45, 823–843. [Google Scholar] [CrossRef]
- Aoki, K.; Izumi, O. On the ductility of the intermetallic compound Ni3Al. Mater. Trans. 2007, 19, 203–210. [Google Scholar]
- Liu, Z.T.Y.; Gall, D.; Khare, S.V. Electronic and bonding analysis of hardness in pyrite-type transition-metal pernitrides. Phys. Rev. B 2014, 90, 134102. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, B.; Zhao, Z. Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 2012, 33, 93–106. [Google Scholar] [CrossRef]
- Ranganathan, S.I.; Ostoja-Starzewski, M. Universal elastic anisotropy index. Phys. Rev. Lett. 2008, 101, 055504. [Google Scholar] [CrossRef] [PubMed]
- Vahldiek, F.W.; Mersol, S.A. Anisotropy in Single-Crystal Refractory Compounds; Springer: New York, NY, USA, 1968. [Google Scholar]
- Ravindran, P.; Fast, L.; Korzhavyi, P.A.; Johansson, B.; Wills, J.; Eriksson, O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2. J. Appl. Phys. 1998, 84, 4891–4904. [Google Scholar] [CrossRef]
- Huang, B.; Duan, Y.H.; Hu, W.C.; Sun, Y.; Chen, S. Structural, anisotropic elastic and thermal properties of Mb (M=Ti, Zr and Hf) monoborides. Ceram. Int. 2015, 41, 6831–6843. [Google Scholar] [CrossRef]
- Zhang, J.M.; Zhang, Y.; Xu, K.W.; Ji, V. Young’s modulus surface and poisson’s ratio curve forcubic metals. J. Phys. Chem. Solids 2007, 68, 503–510. [Google Scholar] [CrossRef]
- Wu, Q.; Li, S. Alloying element additions to Ni3Al: Site preferences and effects on elastic properties from first-principles calculations. Comput. Mater. Sci. 2012, 53, 436–443. [Google Scholar] [CrossRef]
- Anderson, O.L. A simplified method for calculating the debye temperature from elastic constants. J. Phys. Chem. Solids 1963, 24, 909–917. [Google Scholar] [CrossRef]
- Ho, J.C.; Liang, R.C.; Dandekar, D.P. Low temperature heat capacities of Ni3Al. J. Appl. Phys. 1986, 59, 1397–1398. [Google Scholar] [CrossRef]
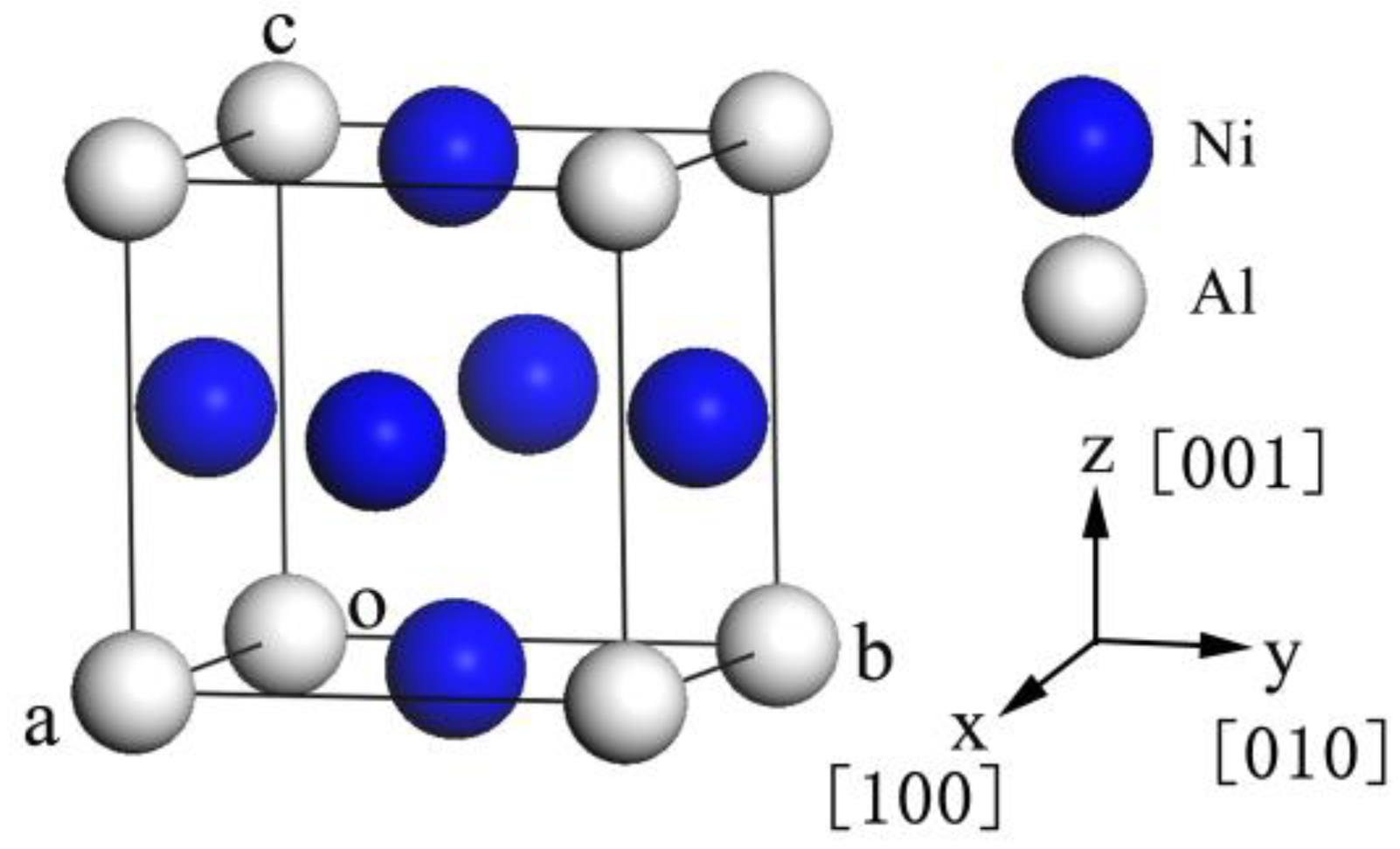
| Lattice Parameters | a(Å) | b(Å) | c(Å) | V(Å3) | ΔV/Ve, % |
|---|---|---|---|---|---|
| Present work (GGA) | 3.577 | 3.577 | 3.577 | 45.757 | +0.397 |
| Present work (LDA) | 3.486 | 3.486 | 3.486 | 42.377 | −7.019 |
| GGA [16] | 3.569 | 3.569 | 3.569 | 45.461 | −0.252 |
| GGA [35] | 3.561 | 3.561 | 3.561 | 45.156 | +0.922 |
| LDA [35] | 3.486 | 3.486 | 3.486 | 42.363 | −7.050 |
| Experiment [22] | 3.572 | 3.572 | 3.572 | 45.576 | -- |
| Elastic Constant | C11 | C12 | C44 |
|---|---|---|---|
| Present work | 240.104 | 160.034 | 123.831 |
| GGA [6] | 225.3 | 157.6 | 121.1 |
| GGA [36] | 232.7 | 154.5 | 123.0 |
| GGA [35] | 230.31 | 162.51 | 124.79 |
| Experiment [37] | 224.3 | 148.6 | 125.8 |
| BV, GPa | BR, GPa | GV, GPa | GR, GPa | B, GPa | G, GPa | E, GPa | v | B/G | Hv | |
|---|---|---|---|---|---|---|---|---|---|---|
| Present Work | 186.724 | 186.724 | 90.313 | 67.401 | 186.724 | 78.857 | 207.378 | 0.315 | 2.368 | 54.004 |
| GGA [6] | -- | -- | -- | -- | 180.2 | 72.9 | -- | -- | -- | -- |
| GGA [36] | -- | -- | -- | -- | 180.6 | 77.8 | 204.0 | -- | -- | -- |
| GGA [35] | -- | -- | -- | -- | 184.49 | 73.05 | 196.65 | 0.320 | -- | -- |
| Exp. [41] | -- | -- | -- | -- | 173.9 | 77.8 | 203.1 | 0.305 | 2.235 | -- |
| Anisotropic Index | AU | AB | AG | A1 | A2 | A3 | ABa | ABc |
|---|---|---|---|---|---|---|---|---|
| Value | 1.670 | 0.000 | 0.145 | 3.093 | 3.093 | 3.093 | 1.000 | 1.000 |
| Planes | {100} | {110} | {111} |
|---|---|---|---|
| Ehkl, GPa | 112.094 | 212.973 | 304.241 |
| Plane | (100) | (110) | (111) | |||
|---|---|---|---|---|---|---|
| Direction | [] | [] | [] | [] | [] | [] |
| Poisson’s ratio | 0.400 | 0.400 | −0.140 | 0.760 | 0.228 | 0.228 |
| Property | ρ, g/cm3 | vt, m/s | vl, m/s | vm, m/s | θD, K |
|---|---|---|---|---|---|
| Value | 7.371 | 3270.809 | 6292.559 | 3660.396 | 475.734 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, X.; Qin, H.; Liu, F.; Dai, Z.; Yi, Y.; Li, Q. The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations. Crystals 2018, 8, 307. https://doi.org/10.3390/cryst8080307
Luan X, Qin H, Liu F, Dai Z, Yi Y, Li Q. The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations. Crystals. 2018; 8(8):307. https://doi.org/10.3390/cryst8080307
Chicago/Turabian StyleLuan, Xinghe, Hongbo Qin, Fengmei Liu, Zongbei Dai, Yaoyong Yi, and Qi Li. 2018. "The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations" Crystals 8, no. 8: 307. https://doi.org/10.3390/cryst8080307
APA StyleLuan, X., Qin, H., Liu, F., Dai, Z., Yi, Y., & Li, Q. (2018). The Mechanical Properties and Elastic Anisotropies of Cubic Ni3Al from First Principles Calculations. Crystals, 8(8), 307. https://doi.org/10.3390/cryst8080307





