Inhomogeneous Superconductivity in Organic and Related Superconductors
Abstract
1. Introduction
- -(BEDT-TTF)Cu(NCS):ET-CuNCS,
- -(BETS)GaCl:BETS-GaCl,
- -(ET)SFCHCFSO:ET-SF5,
- -(ET)Cu[N(CN)]Br:ET-Br.
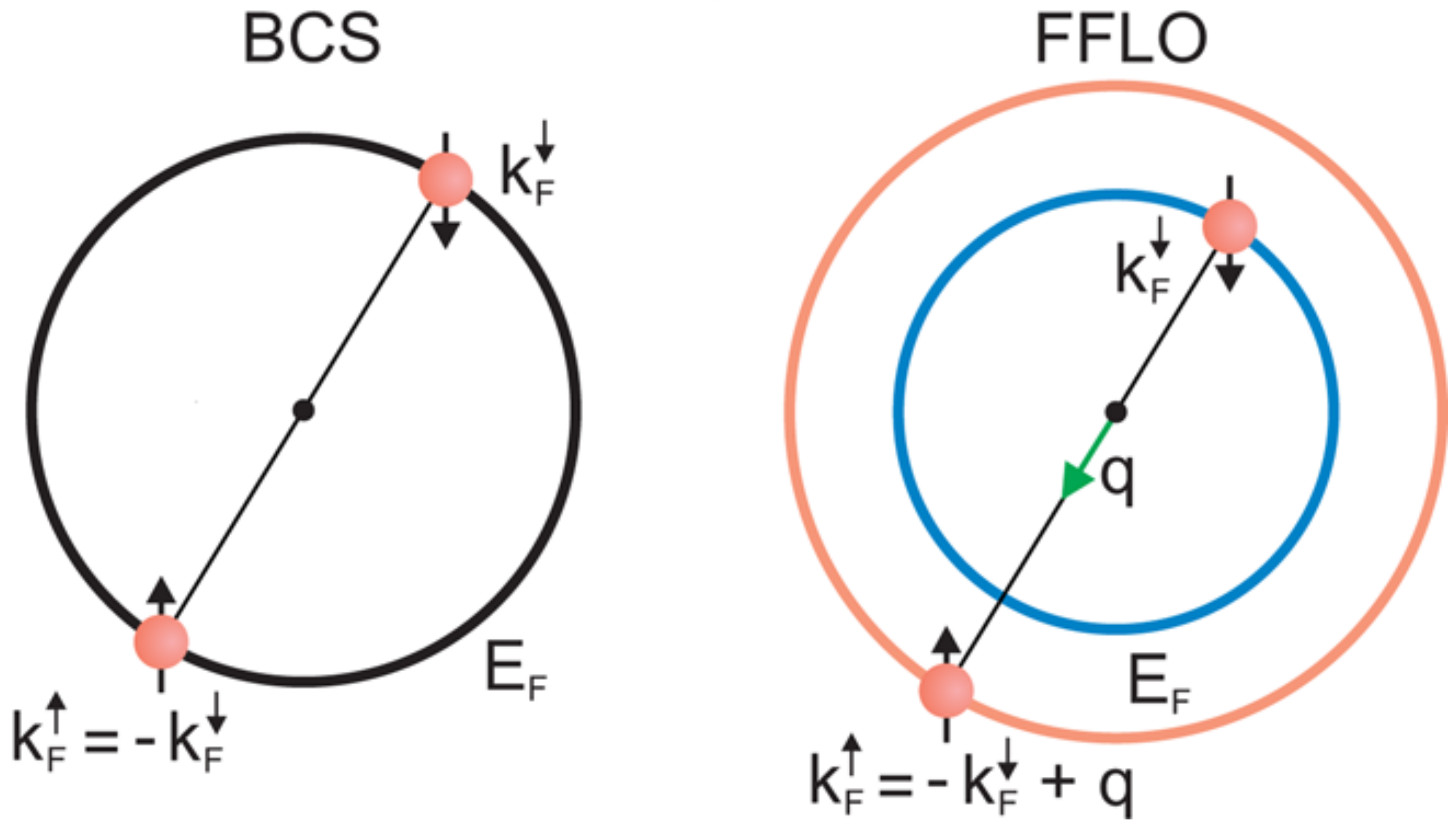
1.1. Inhomogeneous Superconductivity
1.2. Critical Parameters
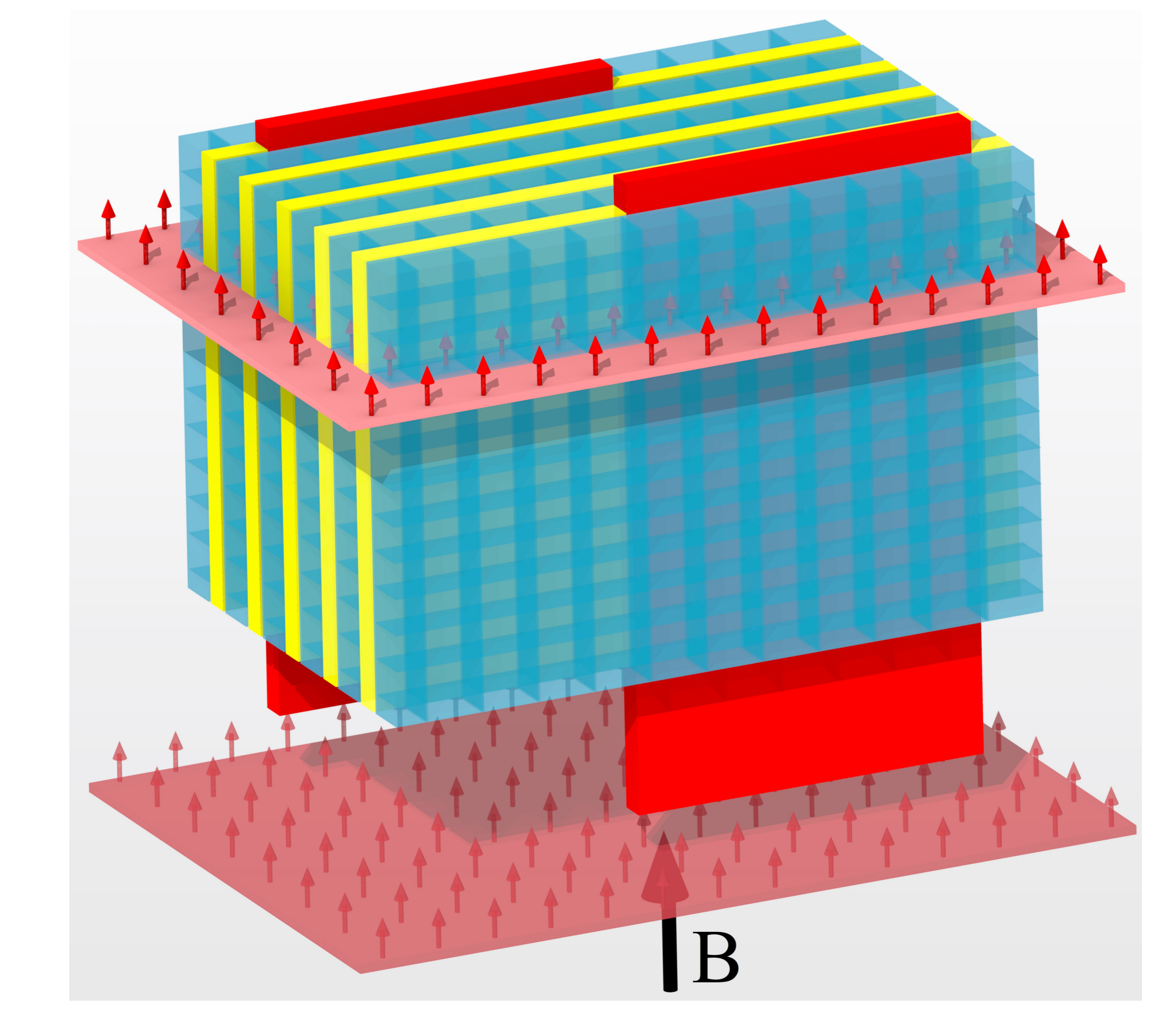
2. Materials and Methods
2.1. The Paramagnetic Limit
2.2. Specific Heat, Energy Gap, and Other Parameters
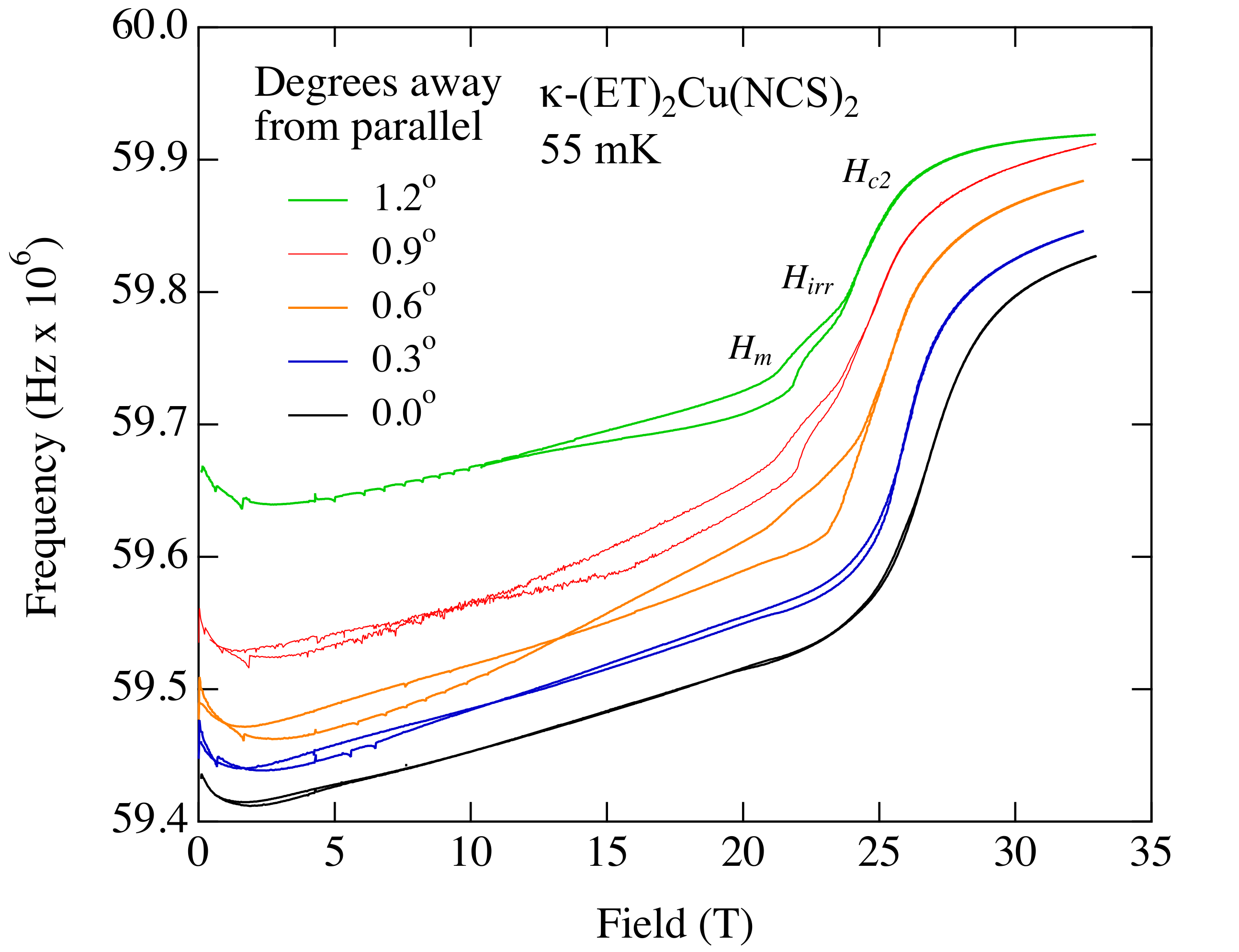
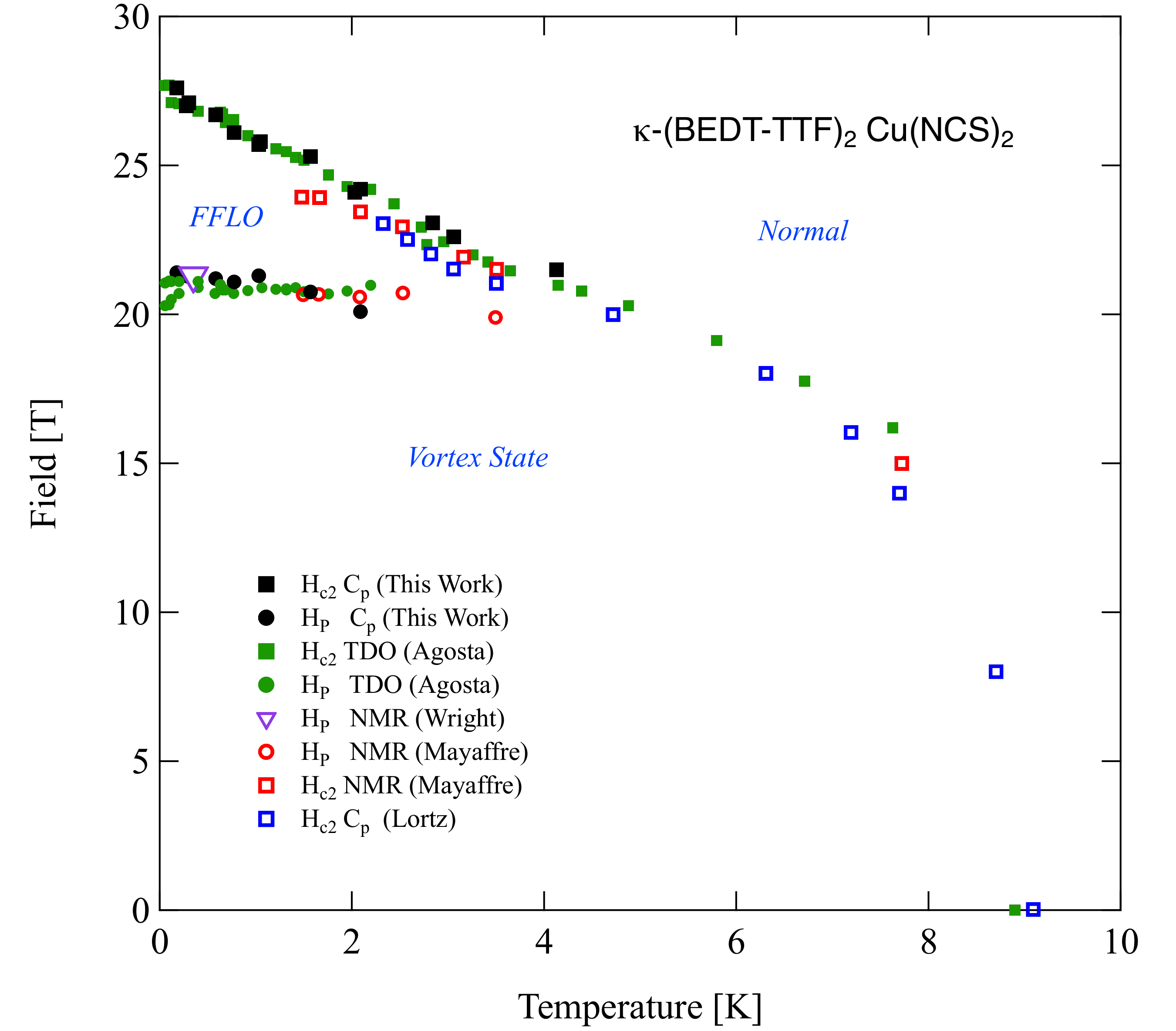
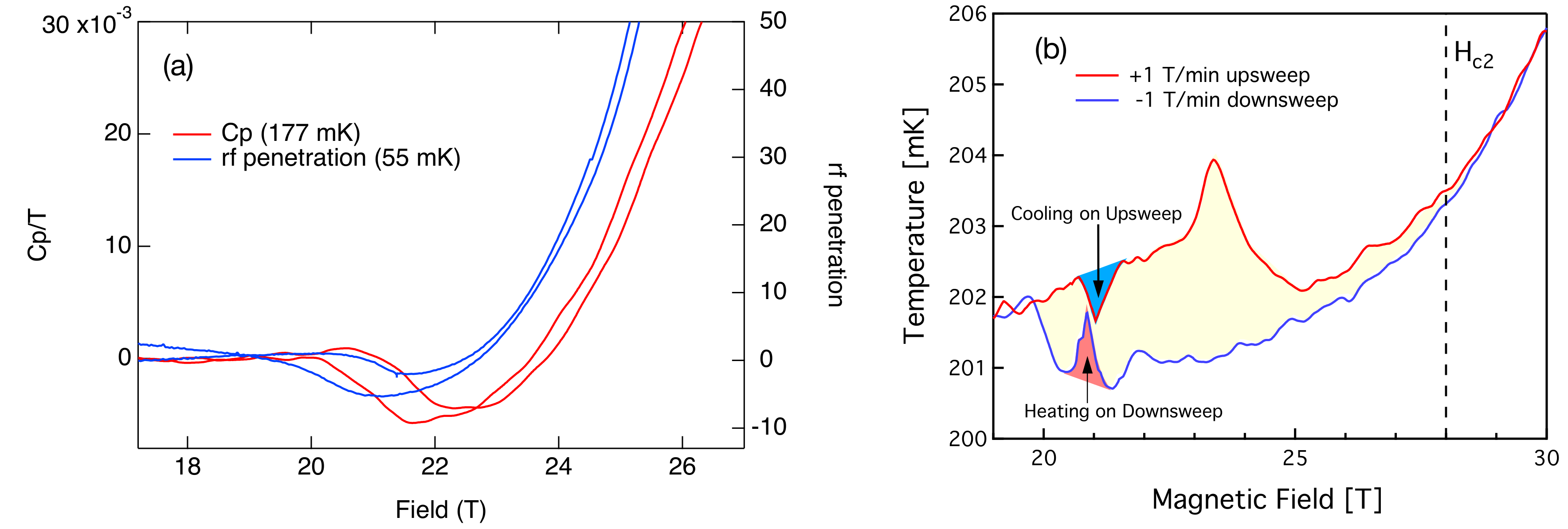
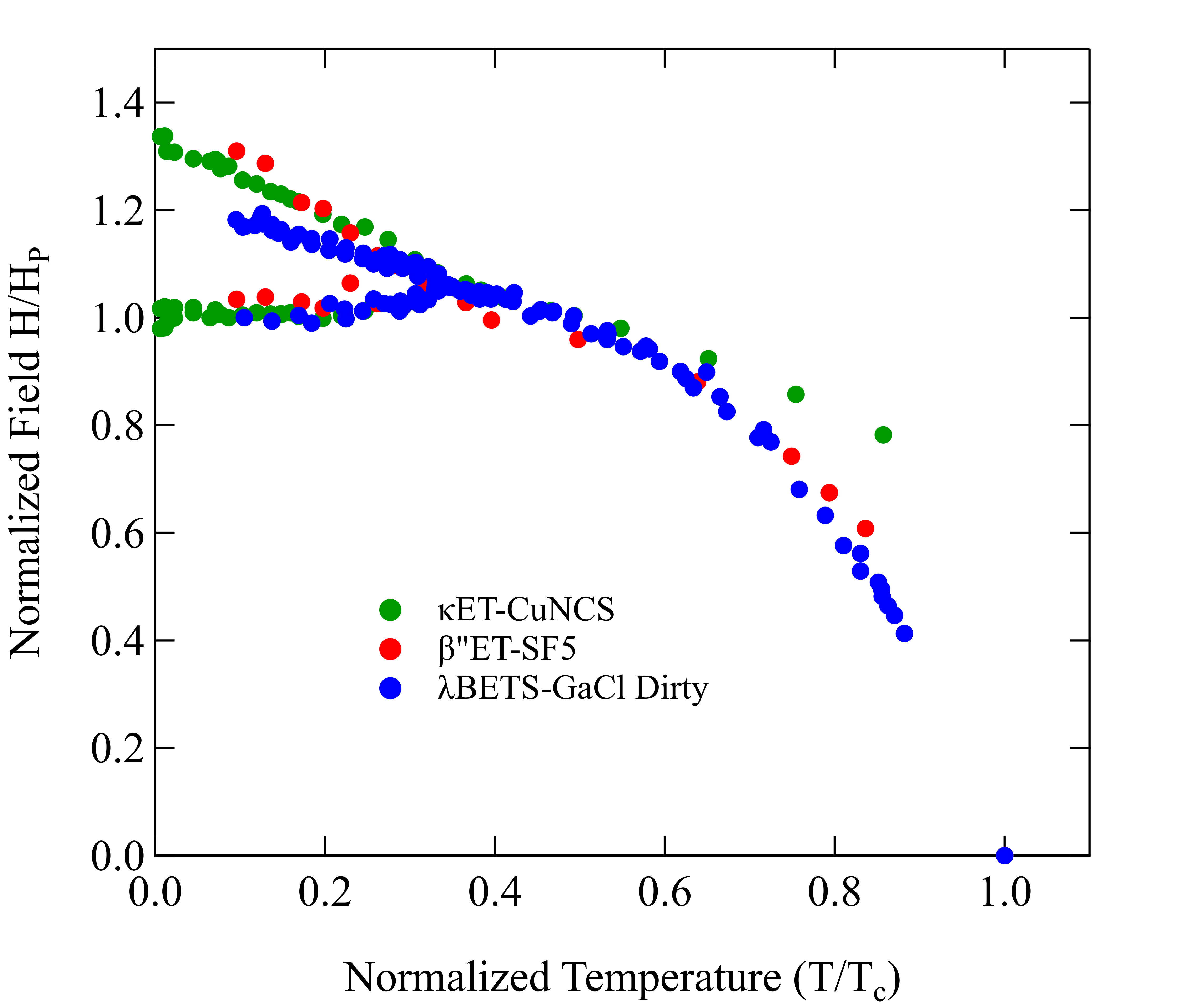
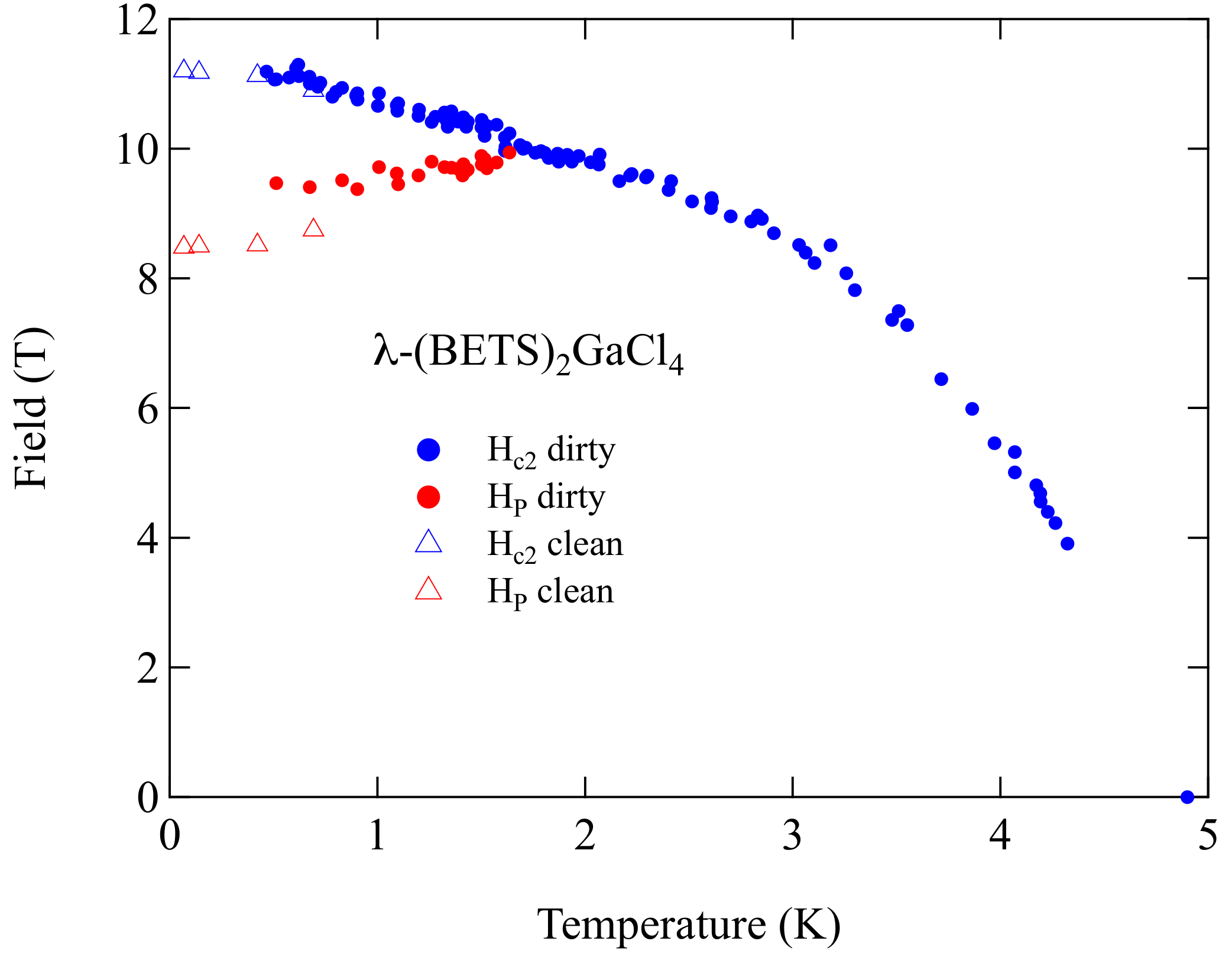
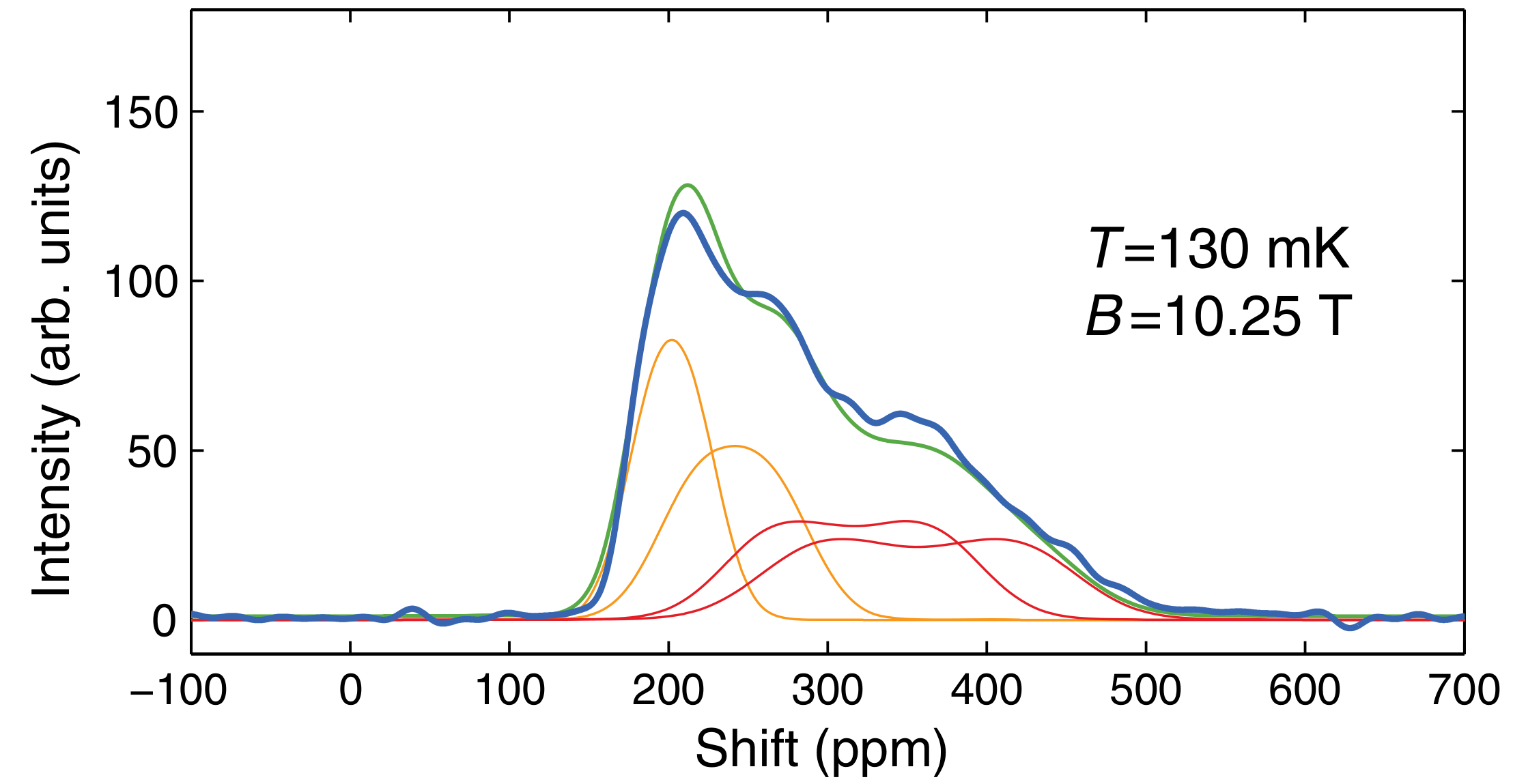
3. Results and Discussion
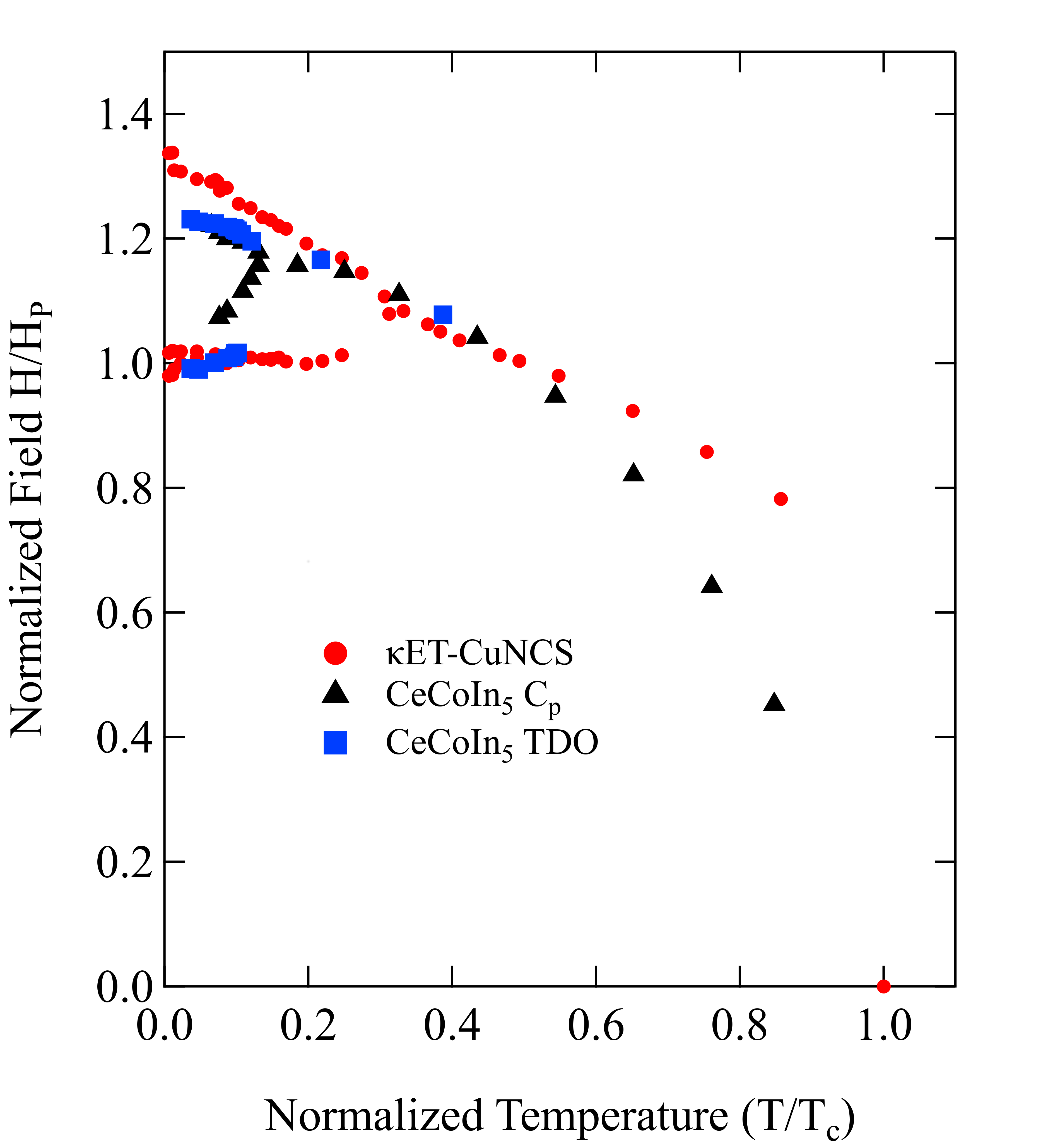
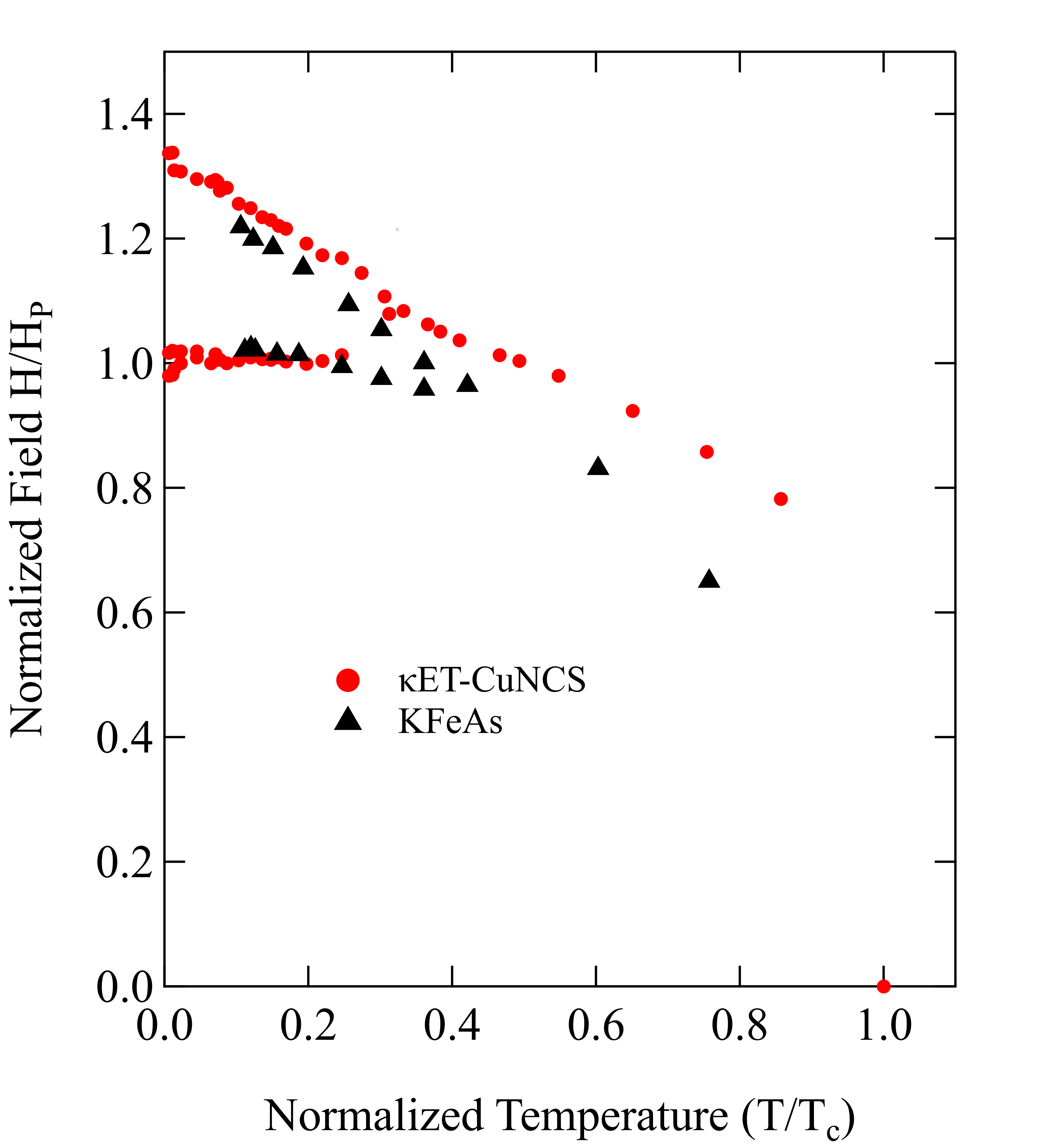
3.1. Other Materials
3.2. New Materials
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Fulde, P.; Ferrell, R.A. Superconductivity in a Strong Spin-Exchange Field. Phys. Rev. 1964, 135, A550–A563. [Google Scholar] [CrossRef]
- Larkin, A.I.; Ovchinnikov, Y.N. Inhomogeneous State of Superconductors. Sov. Phys. JETP 1965, 20, 762–769. [Google Scholar]
- Agosta, C.C.; Fortune, N.A.; Hannahs, S.T.; Gu, S.; Liang, L.; Park, J.H.; Schleuter, J.A. Calorimetric Measurements of Magnetic-Field-Induced Inhomogeneous Superconductivity Above the Paramagnetic Limit. Phys. Rev. Lett. 2017, 118, 267001. [Google Scholar] [CrossRef] [PubMed]
- Bergk, B.; Demuer, A.; Sheikin, I.; Wang, Y.; Wosnitza, J.; Nakazawa, Y.; Lortz, R. Magnetic torque evidence for the Fulde-Ferrell-Larkin-Ovchinnikov state in the layered organic superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 2011, 83, 064506. [Google Scholar] [CrossRef]
- Tsuchiya, S.; Yamada, J.I.; Sugii, K.; Graf, D.; Brooks, J.S.; Terashima, T.; Uji, S. Phase Boundary in a Superconducting State of κ-(BEDT-TTF)2Cu(NCS)2: Evidence of the Fulde-Ferrell-Larkin-Ovchinnikov Phase. J. Phys. Soc. Jpn. 2015, 84, 034703. [Google Scholar] [CrossRef]
- Agosta, C.C.; Jin, J.; Coniglio, W.A.; Smith, B.E.; Cho, K.; Stroe, I.; Martin, C.; Tozer, S.W.; Murphy, T.P.; Palm, E.C.; et al. Experimental and semiempirical method to determine the Pauli-limiting field in quasi-two-dimensional superconductors as applied to κ-(BEDT-TTF)2Cu(NCS)2: Strong evidence of a FFLO state. Phys. Rev. B 2012, 85, 214514. [Google Scholar] [CrossRef]
- Wright, J.A.; Green, E.; Kuhns, P.; Reyes, A.; Brooks, J.; Schlueter, J.; Kato, R.; Yamamoto, H.; Kobayashi, M.; Brown, S.E. Zeeman-Driven Phase Transition within the Superconducting State of κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. Lett. 2011, 107, 087002. [Google Scholar] [CrossRef] [PubMed]
- Mayaffre, H.; Kramer, S.; Horvatić, M.; Berthier, C.; Miyagawa, K.; Kanoda, K.; Mitrović, V.F. Evidence of Andreev bound states as a hallmark of the FFLO phase in κ-(BEDT-TTF)2Cu(NCS)2. Nat. Phys. 2014, 10, 928–932. [Google Scholar] [CrossRef]
- Tanatar, M.A.; Ishiguro, T.; Tanaka, H.; Kobayashi, H. Magnetic field-temperature phase diagram of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 studied via thermal conductivity. Phys. Rev. B 2002, 66, 134503. [Google Scholar] [CrossRef]
- Coniglio, W.A.; Winter, L.E.; Cho, K.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting phase diagram and FFLO signature in λ-(BETS)2GaCl4 from rf penetration depth measurements. Phys. Rev. B 2011, 83, 224507. [Google Scholar] [CrossRef]
- Cho, K.; Smith, B.E.; Coniglio, W.A.; Winter, L.E.; Agosta, C.C.; Schlueter, J.A. Upper critical field in the organic superconductor β′′-(ET)2SF5CH2CF2SO3: Possibility of Fulde-Ferrell-Larkin-Ovchinnikov state. Phys. Rev. B 2009, 79, 220507. [Google Scholar] [CrossRef]
- Koutroulakis, G.; Kuhne, H.; Schlueter, J.A.; Wosnitza, J.; Brown, S.E. Microscopic Study of the Fulde-Ferrell-Larkin-Ovchinnikov State in an All-Organic Superconductor. Phys. Rev. Lett. 2016, 116, 067003. [Google Scholar] [CrossRef] [PubMed]
- Burkhardt, H.; Rainer, D. Fulde-Ferrell-Larkin-Ovchinnikov state in layered superconductors. Ann. Phys. 1994, 506, 181–194. [Google Scholar] [CrossRef]
- Buzdin, A.I.; Kachkachi, H. Generalized Ginzburg-Landau theory for nonuniform FFLO superconductors. Phys. Lett. A 1997, 225, 341–348. [Google Scholar] [CrossRef]
- Houzet, M.; Buzdin, A. Influence of the paramagnetic effect on the vortex lattice in 2D superconductors. EPL (Europhys. Lett.) 2000, 50, 375. [Google Scholar] [CrossRef]
- Klein, U.; Rainer, D.; Shimahara, H. Interplay of Fulde-Ferrell-Larkin-Ovchinnikov and Vortex States in Two-Dimensional Superconductors. J. Low Temp. Phys. 2000, 118, 91–104. [Google Scholar] [CrossRef]
- Shimahara, H. Fulde-Ferrell state in quasi-two-dimensional superconductors. Phys. Rev. B 1994, 50, 12760. [Google Scholar] [CrossRef]
- Agterberg, D.F.; Yang, K. The effect of impurities on Fulde-Ferrell-Larkin-Ovchinnikov superconductors. J. Phys. Cond. Matt. 2001, 13, 9259–9270. [Google Scholar] [CrossRef]
- Houzet, M.; Meurdesoif, Y.; Coste, O.; Buzdin, A. Structure of the non-uniform Fulde-Ferrell-Larkin-Ovchinnikov state in 3D superconductors. Phys. C Superconduct. 1999, 316, 89–96. [Google Scholar] [CrossRef]
- Matsuda, Y.; Shimahara, H. Fulde-Ferrell-Larkin-Ovchinnikov State in Heavy Fermion Superconductors. J. Phys. Soc. Jpn. 2007, 76, 051005. [Google Scholar] [CrossRef]
- Piazza, F.; Zwerger, W.; Strack, P. FFLO strange metal and quantum criticality in two dimensions: Theory and application to organic superconductors. Phys. Rev. B 2016, 93, 085112. [Google Scholar] [CrossRef]
- Kinnunen, J.J.; Baarsma, J.E.; Martikainen, J.P.; Törmä, P. The Fulde-Ferrell-Larkin-Ovchinnikov state for ultracold fermions in lattice and harmonic potentials: A review. Rep. Prog. Phys. 2018, 81, 046401. [Google Scholar] [CrossRef] [PubMed]
- Zwierlein, M.W.; Schirotzek, A.; Schunck, C.H.; Ketterle, W. Fermionic Superfluidity with Imbalanced Spin Populations. Science 2006, 311, 492–496. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.A.; Rittner, A.S.C.; Paprotta, T.; Li, W.; Partridge, G.B.; Hulet, R.G.; Baur, S.K.; Mueller, E.J. Spin-imbalance in a one-dimensional Fermi gas. Nature 2010, 467, 567–569. [Google Scholar] [CrossRef] [PubMed]
- Heidrich-Meisner, F.; Orso, G.; Feiguin, A.E. Phase separation of trapped spin-imbalanced Fermi gases in one-dimensional optical lattices. Phys. Rev. A 2010, 81, 1136–1137. [Google Scholar] [CrossRef]
- Olsen, B.A.; Revelle, M.C.; Fry, J.A.; Sheehy, D.E.; Hulet, R.G. Phase diagram of a strongly interacting spin-imbalanced Fermi gas. Phys. Rev. A 2015, 92, 063616. [Google Scholar] [CrossRef]
- Korolyuk, A.; Massel, F.; Törmä, P. Probing the Fulde-Ferrell-Larkin-Ovchinnikov Phase by Double Occupancy Modulation Spectroscopy. Phys. Rev. Lett. 2010, 104, 236402. [Google Scholar] [CrossRef] [PubMed]
- Paglione, J.; Greene, R.L. High-temperature superconductivity in iron-based materials. Nat. Phys. 2010, 6, 645–658. [Google Scholar] [CrossRef]
- Stewart, G.R. Unconventional superconductivity. Adv. Phys. 2017, 66, 75–196. [Google Scholar] [CrossRef]
- Chandrasekhar, B.S. A Note on the Maximum Critical Field of High-Field Superconductors. Appl. Phys. Lett. 1962, 1, 7. [Google Scholar] [CrossRef]
- Clogston, A.M. Upper Limit for the Critical Field in Hard Superconductors. Phys. Rev. Lett. 1962, 9, 266–267. [Google Scholar] [CrossRef]
- Klemm, R.A.; Luther, A.; Beasley, M.R. Theory of the upper critical field in layered superconductors. Phys. Rev. B 1975, 12, 877–891. [Google Scholar] [CrossRef]
- Saint-James, D.; Sarma, G.; Thomas, E.J. Type II Superconductivity; Saint-James, D., Sarma, G., Thomas, E.J., Eds.; International Series of Monographs on Natural Philosophy; Pergamon Press: Oxford, NY, USA, 1969; Volume 17. [Google Scholar]
- Casalbuoni, R.; Nardulli, G. Inhomogeneous superconductivity in condensed matter and QCD. Rev. Mod. Phys. 2004, 76, 263–320. [Google Scholar] [CrossRef]
- Wosnitza, J. FFLO States in Layered Organic Superconductors. Annalen der Physik 2018, 530, 1700282. [Google Scholar] [CrossRef]
- Zwicknagl, G.; Wosnitza, J. Breaking Translational Invariance By Population Imbalance: The Fulde-Ferrell-Larkin-Ovchinnikov States. Int. J. Mod. Phys. B 2010, 24, 3915–3949. [Google Scholar] [CrossRef]
- Ptok, A.; Kapcia, K.J.; Piekarz, P.; Oleś, A.M. The ab initio study of unconventional superconductivity in CeCoIn5 and FeSe. New J. Phys. 2017, 19, 063039. [Google Scholar] [CrossRef]
- Denisov, D.; Buzdin, A.; Shimahara, H. Types of Fulde-Ferrell-Larkin-Ovchinnikov states induced by anisotropy effects. Phys. Rev. B 2009, 79, 064506. [Google Scholar] [CrossRef]
- Croitoru, M.D.; Buzdin, A.I. Resonance in-plane magnetic field effect as a means to reveal the Fulde-Ferrell-Larkin-Ovchinnikov state in layered superconductors. Phys. Rev. B 2012, 86, 064507. [Google Scholar] [CrossRef]
- Ptok, A. The influence of the dimensionality of the system on the realization of unconventional Fulde-Ferrell-Larkin-Ovchinnikov pairing in ultra-cold Fermi gases. J. Phys. Condens. Matter 2017, 29, 475901. [Google Scholar] [CrossRef] [PubMed]
- Croitoru, M.D.; Houzet, M.; Buzdin, A.I. In-Plane Magnetic Field Anisotropy of the Fulde-Ferrell-Larkin-Ovchinnikov State in Layered Superconductors. Phys. Rev. Lett. 2012, 108, 207005. [Google Scholar] [CrossRef] [PubMed]
- Gurevich, A. Upper critical field and the Fulde-Ferrel-Larkin-Ovchinnikov transition in multiband superconductors. Phys. Rev. B 2010, 82, 184504. [Google Scholar] [CrossRef]
- Bulaevskii, L.N. Inhomogeneous state and the anisotropy of the upper critical field in layered superconductors with Josephson layer interaction. Zhurnal Eksperimentalnoi i Teoreticheskoi Fiziki 1974, 38, 1278–1288. [Google Scholar]
- Mola, M.M.; King, J.T.; McRaven, C.P.; Hill, S.; Qualls, J.S.; Brooks, J.S. Josephson plasma resonance in κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 2000, 62, 5965–5970. [Google Scholar] [CrossRef]
- Hill, S.; Mola, M.M.; Qualls, J.S. Interlayer electrodynamics in the organic superconductor κ-(BEDT-TTF)2Cu(NCS)2 (BEDT-TTF = bis-ethylenedithio-tetrathiafulvalene): Evidence for a transformation within the vortex state. J. Phys. Condens. Matter 2002, 14, 6701. [Google Scholar] [CrossRef]
- Kirtley, J.R.; Moler, K.A.; Schlueter, J.A.; Williams, J.M. Inhomogeneous interlayer Josephson coupling in κ-(BEDT-TTF)2Cu(NCS)2. J. Phys. Condens. Matter 1999, 11, 2007–2016. [Google Scholar] [CrossRef]
- Lebed, A.G. Orbital effect for the Fulde-Ferrell-Larkin-Ovchinnikov phase in a quasi-two-dimensional superconductor in a parallel magnetic field. Phys. Rev. B 2018, 97, 144504. [Google Scholar] [CrossRef]
- Werthamer, N.R.; Helfand, E.; Hohenberg, P.C. Temperature and Purity Dependence of the Superconducting Critical Field, Hc2. III. Electron Spin and Spin-Orbit Effects. Phys. Rev. 1966, 147, 295–302. [Google Scholar] [CrossRef]
- Schneider, T.; Schmidt, A. Dimensional crossover in the upper critical field of layered superconductors. Phys. Rev. B 1993, 47, 5915–5921. [Google Scholar] [CrossRef]
- Ptok, A. The Fulde-Ferrell-Larkin-Ovchinnikov Superconductivity in Disordered Systems. Acta Phys. Pol. A 2010, 118, 420–422. [Google Scholar] [CrossRef]
- Tedrow, P.M.; Meservey, R. Spin-Paramagnetic Effects in Superconducting Aluminum Films. Phys. Rev. B 1973, 8, 5098–5108. [Google Scholar] [CrossRef]
- Gloos, K.; Modler, R.; Schimanski, H.; Bredl, C.D.; Geibel, C.; Steglich, F.; Buzdin, A.I.; Sato, N.; Komatsubara, T. Possible formation of a nonuniform superconducting state in the heavy-fermion compound UPd2Al3. Phys. Rev. Lett. 1993, 70, 501–504. [Google Scholar] [CrossRef] [PubMed]
- Tachiki, M.; Takahashi, S.; Gegenwart, P.; Weiden, M.; Lang, M.; Geibel, C.; Steglich, F.; Modler, R.; Paulsen, C.; Ōnuki, Y. Generalized Fulde-Ferrell-Larkin-Ovchinnikov state in heavy-fermion and intermediate-valence systems. Z. Phys. B Condens. Matter 1997, 100, 369–380. [Google Scholar] [CrossRef]
- Radovan, H.A.; Fortune, N.A.; Murphy, T.P.; Hannahs, S.T.; Palm, E.C.; Tozer, S.W.; Hall, D. Magnetic enhancement of superconductivity from electron spin domains. Nature 2003, 425, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, A.; Movshovich, R.; Capan, C.; Pagliuso, P.G.; Sarrao, J.L. Possible Fulde-Ferrell-Larkin-Ovchinnikov Superconducting State in CeCoIn5. Phys. Rev. Lett. 2003, 91, 187004. [Google Scholar] [CrossRef] [PubMed]
- Mielke, C.; Singleton, J.; Nam, M.S.; Harrison, N.; Agosta, C.C.; Fravel, B.; Montgomery, L.K. Superconducting properties and Fermi-surface topology of the quasi-two-dimensional organic superconductor λ-(BETS)2GaCl4 (BETS=; bis(ethylene-dithio)tetraselenafulvalene). J. Phys. Condens. Matter 2001, 13, 8325–8345. [Google Scholar] [CrossRef]
- Singleton, J.; Goddard, P.; Ardavan, A.; Harrison, N.; Blundell, S.; Schlueter, J.; Kini, A. Test for interlayer coherence in a quasi-two-dimensional superconductor. Phys. Rev. Lett. 2002, 88, 037001. [Google Scholar] [CrossRef] [PubMed]
- Singleton, J.; Goddard, P.A.; Ardavan, A.; Coldea, A.I.; Blundell, S.J.; McDonald, R.D.; Tozer, S.; Schlueter, J.A. Persistence to High Temperatures of Interlayer Coherence in an Organic Superconductor. Phys. Rev. Lett. 2007, 99, 027004. [Google Scholar] [CrossRef] [PubMed]
- Mansky, P.A.; Chaikin, P.M.; Haddon, R.C. Vortex lock-in state in a layered superconductor. Phys. Rev. Lett. 1993, 70, 1323–1326. [Google Scholar] [CrossRef] [PubMed]
- Mansky, P.A.; Chaikin, P.M.; Haddon, R.C. Evidence for Josephson vortices in κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. B 1994, 50, 15929–15944. [Google Scholar] [CrossRef]
- Singleton, J.; Mielke, C. Quasi-two-dimensional organic superconductors: A review. Contemp. Phys. 2002, 43, 63–96. [Google Scholar] [CrossRef]
- Agosta, C.; Martin, C.; Radovan, H.; Palm, E.; Murphy, T.; Tozer, S.; Cooley, J.; Schlueter, J.; Petrovic, C. Penetration depth studies of organic and heavy fermion superconductors in the Pauli paramagnetic limit. J. Phys. Chem. Solids 2006, 67, 586–589. [Google Scholar] [CrossRef]
- Coffey, T.; Bayindir, Z.; DeCarolis, J.F.; Bennett, M.; Esper, G.; Agosta, C.C. Measuring radio frequency properties of materials in pulsed magnetic fields with a tunnel diode oscillator. Rev. Sci. Inst. 2000, 71, 4600–4606. [Google Scholar] [CrossRef]
- Martin, C.; Agosta, C.C.; Tozer, S.W.; Radovan, H.A.; Palm, E.C.; Murphy, T.P.; Sarrao, J.L. Evidence for the Fulde-Ferrell-Larkin-Ovchinnikov state in CeCoIn5 from penetration depth measurements. Phys. Rev. B 2005, 71, 020503. [Google Scholar] [CrossRef]
- Martin, C.; Agosta, C.; Tozer, S.; Radovan, H.; Kinoshota, T.; Tokumoto, M. Critical Field and Shubnikov-de Haas Oscillations of κ-(BEDT-TTF)2Cu(NCS)2 under Pressure. J. Low Temp. Phys. 2005, 138, 1025–1037. [Google Scholar] [CrossRef]
- Orlando, T.P.; McNiff, E.J., Jr.; Foner, S.; Beasley, M.R. Critical fields, Pauli paramagnetic limiting, and material parameters of Nb3 Sn and V3 Si. Phys. Rev. B 1979, 19, 4545–4561. [Google Scholar] [CrossRef]
- Schossmann, M.; Carbotte, J. Pauli limiting of the upper critical magnetic field. Phys. Rev. B 1989, 39, 4210–4216. [Google Scholar] [CrossRef]
- Zuo, F.; Brooks, J.S.; McKenzie, R.H.; Schlueter, J.A.; Williams, J.M. Paramagnetic limiting of the upper critical field of the layered organic superconductor κ-(BEDT-TTF)2Cu(SCN)2. Phys. Rev. B 2000, 61, 750–755. [Google Scholar] [CrossRef]
- McKenzie, R.H. Wilson’s ratio and the spin splitting of magnetic oscillations in quasi-two-dimensional metals. arXiv, 1999; arXiv:9905044. [Google Scholar]
- Padamsee, H.; Neighbor, J.; Shiffman, C. Quasiparticle phenomenology for thermodynamics of strong-coupling superconductors. J. Low Temp. Phys. 1973, 12, 387–411. [Google Scholar] [CrossRef]
- Johnston, D.C. Elaboration of the α-model derived from the BCS theory of superconductivity. Superconduct. Sci. Technol. 2013, 26, 115011. [Google Scholar] [CrossRef]
- Taylor, O.J.; Carrington, A.; Schlueter, J.A. Specific-Heat Measurements of the Gap Structure of the Organic Superconductors κ-(BEDT-TTF)2-Cu[N(CN)2]Br and κ-(ET)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 057001. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, Y.; Kanoda, K. Low-temperature specific heat of κ-(BEDT-TTF)2Cu[N(CN)2]Br in the superconducting state. Phys. Rev. B 1997, 55, R8670–R8673. [Google Scholar] [CrossRef]
- Analytis, J.G.; Ardavan, A.; Blundell, S.J.; Owen, R.L.; Garman, E.F.; Jeynes, C.; Powell, B.J. Effect of Irradiation-Induced Disorder on the Conductivity and Critical Temperature of the Organic Superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. Lett. 2006, 96, 177002. [Google Scholar] [CrossRef] [PubMed]
- Zantout, K.; Altmeyer, M.; Backes, S.; Valentí, R. Superconductivity in correlated BEDT-TTF molecular conductors: Critical temperatures and gap symmetries. Phys. Rev. B 2018, 97, 014530. [Google Scholar] [CrossRef]
- Coffey, T.; Martin, C.; Agosta, C.C.; Kinoshota, T.; Tokumoto, M. Bulk two-dimensional Pauli-limited superconductor. Phys. Rev. B 2010, 82, 212502. [Google Scholar] [CrossRef]
- Mihut, I.; Agosta, C.; Martin, C.; Mielke, C.; Coffey, T. Incoherent Bragg reflection and Fermi-surface hot spots in a quasi-two-dimensional metal. Phys. Rev. B 2006, 73, 125118. [Google Scholar] [CrossRef]
- Wanka, S.; Hagel, J.; Beckmann, D.; Wosnitza, J.; Schlueter, J.A.; Williams, J.M.; Nixon, P.G.; Winter, R.W.; Gard, G.L. Specific heat and critical fields of the organic superconductor β′′-(BEDT-TTF)2SF5CH2CF2SO3. Phys. Rev. B 1998, 57, 3084–3088. [Google Scholar] [CrossRef]
- Elsinger, H.; Wosnitza, J.; Wanka, S.; Hagel, J.; Schweitzer, D.; Strunz, W. κ-(BEDT-TTF)2-Cu[N(CN)2]Br: A Fully Gapped Strong-Coupling Superconductor. Phys. Rev. Lett. 2000, 84, 6098–6101. [Google Scholar] [CrossRef] [PubMed]
- Imajo, S.; Kanda, N.; Yamashita, S.; Akutsu, H.; Nakazawa, Y.; Kumagai, H.; Kobayashi, T.; Kawamoto, A. Thermodynamic Evidence of d-Wave Superconductivity of the Organic Superconductor λ-(BETS)2GaCl4. J. Phys. Soc. Jpn. 2016, 85, 043705. [Google Scholar] [CrossRef]
- Kwok, W.; Welp, U.; Carlson, K.; Crabtree, G.; Vandervoort, K.; Wang, H.; Kini, A.; Williams, J.; Stupka, D.; Montgomery, L. Unusual behavior in the upper critical magnetic fields of the ambient-pressure organic superconductor κ-(BEDT-TTF)2Cu[N(CN)2]Br [where BEDT-TTF represents bis (ethylenedithio) tetrathiofulvalene]. Phys. Rev. B 1990, 42, 8686–8689. [Google Scholar] [CrossRef]
- Mielke, C.; Harrison, N.; Rickel, D.; Lacerda, A.; Vestal, R.; Montgomery, L. Fermi-surface topology of κ-(BEDT-TTF)2Cu [N (CN) 2] Br at ambient pressure. Phys. Rev. B 1997, 56, 4309–4312. [Google Scholar] [CrossRef]
- Petrovic, C.; Pagliuso, P.G.; Hundley, M.F.; Movshovich, R.; Sarrao, J.L.; Thompson, J.D.; Fisk, Z.; Monthoux, P. Heavy-fermion superconductivity in CeCoIn 5 at 2.3 K. J. Phys. Condens. Matter 2001, 13, L337. [Google Scholar] [CrossRef]
- Ikeda, S.; Shishido, H.; Nakashima, M.; Settai, R.; Aoki, D.; Haga, Y.; Harima, H.; Aoki, Y.; Namiki, T.; Sato, H.; et al. Unconventional Superconductivity in CeCoIn5 Studied by the Specific Heat and Magnetization Measurements. J. Phys. Soc. Jpn. 2001, 70, 2248–2251. [Google Scholar] [CrossRef]
- Murphy, T.P.; Hall, D.; Palm, E.C.; Tozer, S.W.; Petrovic, C.; Fisk, Z.; Goodrich, R.G.; Pagliuso, P.G.; Sarrao, J.L.; Thompson, J.D. Anomalous superconductivity and field-induced magnetism in CeCoIn5. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
- Abdel-Hafiez, M.; Aswartham, S.; Wurmehl, S.; Grinenko, V.; Hess, C.; Drechsler, S.L.; Johnston, S.; Wolter, A.U.B.; Büchner, B.; Rosner, H.; et al. Publisher’s Note: Specific heat and upper critical fields in KFe2As2 single crystals. Phys. Rev. B 2012, 85, 179901. [Google Scholar] [CrossRef]
- Hardy, F.; Böhmer, A.E.; Aoki, D.; Burger, P.; Wolf, T.; Schweiss, P.; Heid, R.; Adelmann, P.; Yao, Y.X.; Kotliar, G.; et al. Evidence of Strong Correlations and Coherence-Incoherence Crossover in the Iron Pnictide Superconductor KFe2As2. Phys. Rev. Lett. 2013, 111, 027002. [Google Scholar] [CrossRef] [PubMed]
- Zocco, D.A.; Grube, K.; Eilers, F.; Wolf, T.; Löhneysen, H.v. Pauli-Limited Multiband Superconductivity in KFe2As2. Phys. Rev. Lett. 2013, 111, 057007. [Google Scholar] [CrossRef] [PubMed]
- Kim, H.; Tanatar, M.A.; Song, Y.J.; Kwon, Y.S.; Prozorov, R. Nodeless two-gap superconducting state in single crystals of the stoichiometric iron pnictide LiFeAs. Phys. Rev. B 2011, 83, 100502. [Google Scholar] [CrossRef]
- Cho, K.; Kim, H.; Tanatar, M.; Song, Y.; Kwon, Y.; Coniglio, W.; Agosta, C.; Gurevich, A.; Prozorov, R. Anisotropic upper critical field and possible Fulde-Ferrel-Larkin-Ovchinnikov state in the stoichiometric pnictide superconductor LiFeAs. Phys. Rev. B 2011, 83, 060502. [Google Scholar] [CrossRef]
- Gruenberg, L.W.; Gunther, L. Fulde-Ferrell Effect in Type-II Superconductors. Phys. Rev. Lett. 1966, 16, 996–998. [Google Scholar] [CrossRef]
- Singleton, J.; Symington, J.A.; Nam, M.S.; Ardavan, A.; Kurmoo, M.; Day, P. Observation of the Fulde-Ferrell-Larkin-Ovchinnikov state in the quasi-two-dimensional organic superconductor κ-(BEDT- TTF)2Cu(NCS)2 (BEDT-TTF = bis(ethylene-dithio)tetrathiafulvalene). J Phys. Condens. Matter 2000, 12, L641–L648. [Google Scholar] [CrossRef]
- Lortz, R.; Wang, Y.; Demuer, A.; Böttger, P.H.M.; Bergk, B.; Zwicknagl, G.; Nakazawa, Y.; Wosnitza, J. Calorimetric Evidence for a Fulde-Ferrell-Larkin-Ovchinnikov Superconducting State in the Layered Organic Superconductor κ-(BEDT-TTF)2Cu(NCS)2. Phys. Rev. Lett. 2007, 99, 187002. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Wang, Y.; Wu, C. Stable Fulde-Ferrell-Larkin-Ovchinnikov pairing states in two-dimensional and three-dimensional optical lattices. Phys. Rev. A 2011, 83, 063621. [Google Scholar] [CrossRef]
- Tokiwa, Y.; Bauer, E.D.; Gegenwart, P. Quasiparticle Entropy in the High-Field Superconducting Phase of CeCoIn5. Phys. Rev. Lett. 2012, 109, 116402. [Google Scholar] [CrossRef] [PubMed]
- Young, B.L.; Urbano, R.R.; Curro, N.J.; Thompson, J.D.; Sarrao, J.L.; Vorontsov, A.B.; Graf, M.J. Microscopic Evidence for Field-Induced Magnetism in CeCoIn5. Phys. Rev. Lett. 2007, 98, 036402. [Google Scholar] [CrossRef] [PubMed]
- Kenzelmann, M.; Strässle, T.; Niedermayer, C.; Sigrist, M.; Padmanabhan, B.; Zolliker, M.; Bianchi, A.D.; Movshovich, R.; Bauer, E.D.; Sarrao, J.L.; et al. Coupled Superconducting and Magnetic Order in CeCoIn5. Science 2008, 321, 1652–1654. [Google Scholar] [CrossRef] [PubMed]
- Kenzelmann, M.; Gerber, S.; Egetenmeyer, N.; Gavilano, J.L.; Strässle, T.; Bianchi, A.D.; Ressouche, E.; Movshovich, R.; Bauer, E.D.; Sarrao, J.L.; et al. Evidence for a Magnetically Driven Superconducting Q Phase of CeCoIn5. Phys. Rev. Lett. 2010, 104, 127001. [Google Scholar] [CrossRef] [PubMed]
- Raymond, S.; Ramos, S.M.; Aoki, D.; Knebel, G.; Mineev, V.P.; Lapertot, G. Magnetic Order in Ce 0.95Nd 0.05CoIn 5: The Q-Phase at Zero Magnetic Field. J. Phys. Soc. Jpn. 2014, 83, 013707. [Google Scholar] [CrossRef]
- Koutroulakis, G.; Stewart, M.D.J.; Mitrovic, V.F.; Horvatic, M.; Berthier, C.; Lapertot, G.; Flouquet, J. Field Evolution of Coexisting Superconducting and Magnetic Orders in CeCoIn5. Phys. Rev. Lett. 2010, 104, 087001. [Google Scholar] [CrossRef] [PubMed]
- Kumagai, K.; Shishido, H.; Shibauchi, T.; Matsuda, Y. Evolution of Paramagnetic Quasiparticle Excitations Emerged in the High-Field Superconducting Phase of CeCoIn5. Phys. Rev. Lett. 2011, 106, 137004. [Google Scholar] [CrossRef] [PubMed]
- Hatakeyama, Y.; Ikeda, R. Antiferromagnetic order oriented by Fulde-Ferrell-Larkin-Ovchinnikov superconducting order. Phys. Rev. B 2015, 91, 094504. [Google Scholar] [CrossRef]
- Fortune, N.A.; Hannahs, S.T. Top-loading small-sample calorimeters for measurements as a function of magnetic field angle. J. Phys. Conf. Ser. 2014, 568, 032008. [Google Scholar] [CrossRef]
- Kim, D.Y.; Lin, S.Z.; Weickert, F.; Kenzelmann, M.; Bauer, E.D.; Ronning, F.; Thompson, J.D.; Movshovich, R. Intertwined Orders in Heavy-Fermion Superconductor CeCoIn5. Phys. Rev. X 2016, 6, 041059. [Google Scholar] [CrossRef]
- Ptok, A.; Crivelli, D. The Fulde-Ferrell-Larkin-Ovchinnikov State in Pnictides. J. Low Temp. Phys. 2013, 172, 226–233. [Google Scholar] [CrossRef]
- Ptok, A. Multiple phase transitions in Pauli-limited iron-based superconductors. J. Phys. Condens. Matter 2015, 27, 482001. [Google Scholar] [CrossRef] [PubMed]
- Cho, C.W.; Yang, J.H.; Yuan, N.F.Q.; Shen, J.; Wolf, T.; Lortz, R. Thermodynamic Evidence for the Fulde-Ferrell-Larkin-Ovchinnikov State in the KFe2As2 Superconductor. Phys. Rev. Lett. 2017, 119, 593–595. [Google Scholar] [CrossRef] [PubMed]
- Kittaka, S.; Aoki, Y.; Kase, N.; Sakakibara, T.; Saito, T.; Fukazawa, H.; Kohori, Y.; Kihou, K.; Lee, C.H.; Iyo, A.; et al. Thermodynamic Study of Nodal Structure and Multiband Superconductivity of KFe2As2. J. Phys. Soc. Jpn. 2014, 83, 013704. [Google Scholar] [CrossRef]
- Poole, C.; Farach, H.; Creswick, R.; Prozorov, R. Superconductivity; Elsevier Science: New York, NY, USA, 2014. [Google Scholar]
- Buzdin, A.I.; Fiz, V.T. Phase diagrams of electronic and superconducting transitions to soliton lattice states. Sov. Phys. JETP 1983, 58, 428. [Google Scholar] [CrossRef]
- Lebed, A.G.; Wu, S. Larkin-Ovchinnikov-Fulde-Ferrell phase in the superconductor (TMTSF)2ClO4: Theory versus experiment. Phys. Rev. B 2010, 82, 172504. [Google Scholar] [CrossRef]
- Lee, I.J.; Brown, S.E.; Naughton, M.J. Unconventional Superconductivity in a Quasi-One-Dimensional System (TMTSF) 2X. J. Phys. Soc. Jpn. 2006, 75, 051011. [Google Scholar] [CrossRef]
| Material | (K) | (T) | (T) | (Å) | ℓ(Å) | |||
|---|---|---|---|---|---|---|---|---|
| -(BEDT-TTF)Cu(NCS) | 3.0 [72] | 1.26 [69] | 9.6 | 21.6 | 4.9 | 130 [35] | 13 | 900 [77] |
| -(BEDT-TTF)SFCHCFSO | 1.94 [78] | 1.0 [69] | 4.5 | 9.2 | 3.9 | 75 [35] | 21 | 520 |
| -(ET)NHHg(SCN) | 1.76 [79] | 0.86 [69] | 0.96 | 2.1 | 5.5 | 8.1 [76] | 53 | 681 [76] |
| -(BETS)GaCl | 1.83 [80] | 1.0 [69] | 4.3 | 8.3 | 3.9 | 23.1 [10] | 31.5 | 170 [56] |
| -(ET)Cu[N(CN)]Br | 2.77 [72] | 1.4 [69] | 11.5 | 23.8 | 9.6 | 161 [81] | 12 | 260 [82] |
| CeCoIn | 3.03 [83,84] | 0.73 [83] | 2.16 | 9.44 | 6.5 | 43.5 [85] | 23 | 810 |
| KFeAs | 1.75 [86] | 1.3 [87] | 3.14 | 4.84 | 2.9 | 9.9 | 48 | 1770 [88] |
| LiFeP | 1.89 [89] | 1.0 | 17.6 | 34.9 | 2.1 | 51 [90] | 21 | 5500 [90] |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agosta, C.C. Inhomogeneous Superconductivity in Organic and Related Superconductors. Crystals 2018, 8, 285. https://doi.org/10.3390/cryst8070285
Agosta CC. Inhomogeneous Superconductivity in Organic and Related Superconductors. Crystals. 2018; 8(7):285. https://doi.org/10.3390/cryst8070285
Chicago/Turabian StyleAgosta, Charles C. 2018. "Inhomogeneous Superconductivity in Organic and Related Superconductors" Crystals 8, no. 7: 285. https://doi.org/10.3390/cryst8070285
APA StyleAgosta, C. C. (2018). Inhomogeneous Superconductivity in Organic and Related Superconductors. Crystals, 8(7), 285. https://doi.org/10.3390/cryst8070285





