1. Introduction
Radiation damage in X-ray crystallography has been for a long time an active area of research amongst several groups, but a detailed and general understanding of the physical and chemical mechanisms responsible for the appearance of global or specific damage at a microscopic level is still largely incomplete, even in the case of experiments carried out at cryogenic temperatures. Global damage is characterized by loss of sample diffraction power, indicating reduced crystalline order. Specific damage on the other hand is a local change in the electron density of the crystal constituents around particular atoms of the crystalline structure. In metallo-proteins at 100 K, for instance, it has been shown to involve the reduction of metal ion centres and the formation of radical species at disulphide bonds in the early stages of the experiment [
1,
2,
3,
4]. These phenomena are then followed by various chemical changes involving, for instance, the elongation and eventual breaking of disulphide bonds, the decarboxylation of glutamate and aspartate residues and the breaking of covalent bonds between the protein backbone and the metal centres. Gerstel et al. [
1] provide an exhaustive methodological discussion concerning different susceptibilities empirically observed for all the different types of specific damage described in the literature, while Borek and collaborators recently provided a promising method to discern temperature-dependent changes from other types of change [
5]. On the other hand, combined measurements based on single-crystal X-ray diffraction, small angle scattering and radiolysis experiments have shown that hydrogen gas formed in the sample during irradiation, rather than bond cleavage, is mainly responsible for the loss of high-resolution information [
6].
Dose and
dose rate are key parameters of the process. Dose is the energy absorbed by the material upon irradiation in gray (1 Gy = 1 J/kg) whereas dose rate is the power absorbed by the same mass in grays per second (1 Gy/s = 1 W/kg). It is also important to note that historically it is the X-ray dose and not the dose rate that is understood to determine damage at cryotemperatures [
7], and that, surprisingly, specific damage is observed also in ultra-short (80 fs) X-ray free-electron laser (XFEL) single crystal diffraction experiments [
8], performed at room temperature.
Several attempts at rationalizing the radiation-induced structural changes in a crystalline sample have been proposed (e.g., [
9,
10,
11,
12]), typically—but not only—based on purely mechanistic diffusion models, similar to the well-known processes that dominate radiochemistry in solution at room temperature [
13]. They are excellent ground work and pragmatically allowed experimenters to steer away from global damage and mapped the bulk of the observable specific damage cases. However, the limitation of the approach is that it cannot explain nor model specific damage, apart from broadly indicating the likely affected parts of a structure. In any case, attempting to perform calculations to understand these effects within a quantum mechanical framework has been impracticable until recently [
14].
In this work, we will outline how specific damage events in crystallographic models can be interpreted in terms of local structural deformations caused by the population and depopulation of virtual and occupied electronic states in the close vicinity of the Fermi energy of the perfect crystal. Previous reports in the literature have addressed and quantified the local changes, but unfortunately, due to the lack of a unifying model, a quantification of this effect has proved to be very subjective and system dependent (although procedures for radiation damage corrections have been refined empirically to a point where a systematic and automated assessment is possible [
1,
5,
15]). It is our view that single crystal macromolecular crystallography oscillation datasets are unsuitable for assessing the structural changes caused by specific damage, since they rely on information obtained too long (seconds) after the initial interaction of the X-ray beam with the sample. For long measurement times, the branching of damage events depends both on (1) the type of protein and (2) the actual conditions of the particular samples for each experiment. As we will indicate, over short time-scales (1–10 fs) from the beginning of the experiment, the electronic phenomena mentioned above determine a redistribution of the valence electron density and the appearance of quantum-mechanical forces on the atoms, which, subsequently (>10–20 fs), drive the evolution of the atomic arrangement and determine the appearance of structural defects and a deviation of the crystal structure from its equilibrium configuration. The model that we propose is based on the wealth of evidence available in the literature [
1,
7,
9,
15,
16,
17,
18,
19,
20] complemented by our recent study of X-ray radiation damage in
n-eicosane crystals with quantum-mechanical calculations [
14], in which we have demonstrated that the appearance of structural defects following X-ray irradiation is a consequence of (1) the promotion of electrons to low-lying virtual states; (2) the Coulomb interaction of these excited electrons with localized holes at energies comparable to the Fermi energy (excitonic effects); and (3) the structural rearrangement caused by the quantum-mechanical forces induced by the appearance of localized excitonic states. We have also shown that photoemission events do not necessarily lead to structural rearrangement, at least over time-scales of 10–20 fs. The main implication of these findings is that specific radiation damage in simple macromolecules, like
n-eicosane, occurs at energy scales corresponding to electronic excitations between states very close to the Fermi energy (ca. 0.1–10 eV in semiconducting and insulating crystals) and typical of UV and optical transitions, rather than of photoemission phenomena and core-hole excitations (10
3–10
4 eV). In our model, the electronic and structural changes caused by the interaction of X-rays with a macromolecular crystal structure are therefore akin to typical non-thermal melting phenomena in semiconductors and insulators [
21] and Refs. [1–9] therein. In this communication, we describe a phenomenological model of how different classes of specific damage induced by X-rays can be rationalized in terms of the basic assumptions of this model, and how the appearance of specific damage features in X-ray measurements and sample degradation relate to the timescales of the electronic and nuclear processes described above.
2. A Model of Radiation-Induced Structural Changes
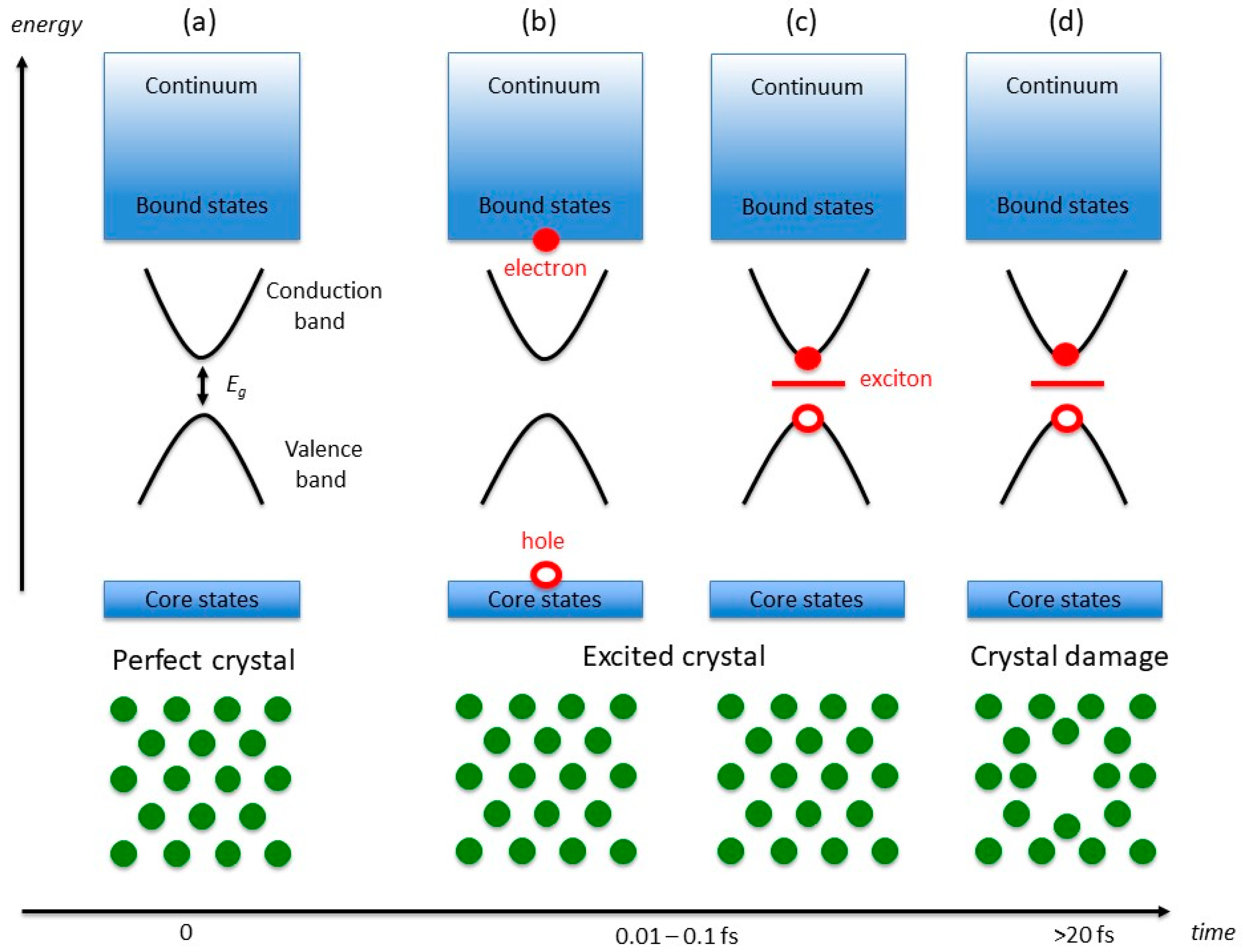
The central assumption of our model is that radiation damage in macromolecular crystals is related to the generation of bound excitonic states in the forbidden gap region of the perfect crystal. The mechanism leading to the formation of these bound electron-hole pairs is however different from the standard generation of excitons in optical spectroscopy [
22], which involves electronic transitions between frontier orbitals (or valence and conduction states) of energies comparable to the band gap of the material (ca. 0.1–10 eV). In typical X-ray experiments, the crystal ground-state electrons (
Figure 1a) interact with photons of energies of the order of 10
4 eV, which can either lead to photoemission or to the population of (semi-)bound high-energy conduction states (X-ray absorption), with the simultaneous generation of core holes (
Figure 1b).
In typical macromolecular crystallography experiments, which use (monochromatic) beams of around 13 keV in energy, X-ray absorption accounts for a total beam loss of ca. 2% for 100 µm thick metal-free crystals, and generates photoelectrons with kinetic energies comparable to the X-ray photons. The photoelectrons undergo a fast series of inelastic scattering events that progressively reduce their energy [
23]. These events can be interpreted as a series of transitions between electronic levels of progressively lower energy, and it can be estimated to occur within 0.01–0.1 fs in typical experimental conditions [
14]. Simultaneously, the energy of the core hole increases, owing to the many-body electronic screening. For our purposes, we will assume that the screening is sufficient to create a quasi-hole in the vicinity of the Fermi energy, which can then form a Coulombically bound pair with the excited electron and give rise to excitonic intra-gap states (
Figure 1c). In consequence to the localised nature of the exciton, strong electron-phonon interactions couple the nuclear lattice dynamics with the electron-hole pair. The relaxation of the lattice, and the consequent formation of a localised defect in the crystal (
Figure 1d), are therefore a consequence of the exciton screening by the crystal phonons and they are promoted by the long lifetimes of excitonic states.
This model is consistent with the results of reference [
14], in which hybrid time-dependent density-functional theory (TD-DFT) calculations were used to study the time evolution of the crystal structure of n-eicosane (C
20H
42) after X-ray irradiation. An important conclusion of this work is that the presence of a localised electron-hole bound pair is the essential factor driving the structural distortion of the crystal lattice. In the case of a photoexcitation process, in which only the (quasi-)hole is present in the system after irradiation, no formation of localised structural defects was observed in excited-state ab initio molecular dynamics (AIMD) simulations (cf. Figure 6 in Ref. [
14]). In turn, the resulting change in the crystal symmetry affects the response of the sample to incoming radiation, which can determine changes in measured X-ray structure factors, as well as in a different response of the sample to polarised radiation impinging on different crystal planes during X-ray experiments.
One of the defining features of this model is the clear time-scale separation for electronic and nuclear dynamics phenomena. Whereas the charge rearrangement leading to the formation of the exciton pair occurs virtually instantaneously following X-ray absorption (0.01–0.1 fs) the nuclear relaxation is a relatively slow phenomenon, which, depending on the stiffness of the macromolecular structure, typically cannot occur before at least ca. 10 fs. In the case of n-eicosane simulations, the vibrational dynamics of the lattice and the clear nucleation of a defect were observed within ca. 3 ps. As we will indicate below, the presence of two well defined time-scales and physical phenomena leads to the appearance of different forms of radiation damage.
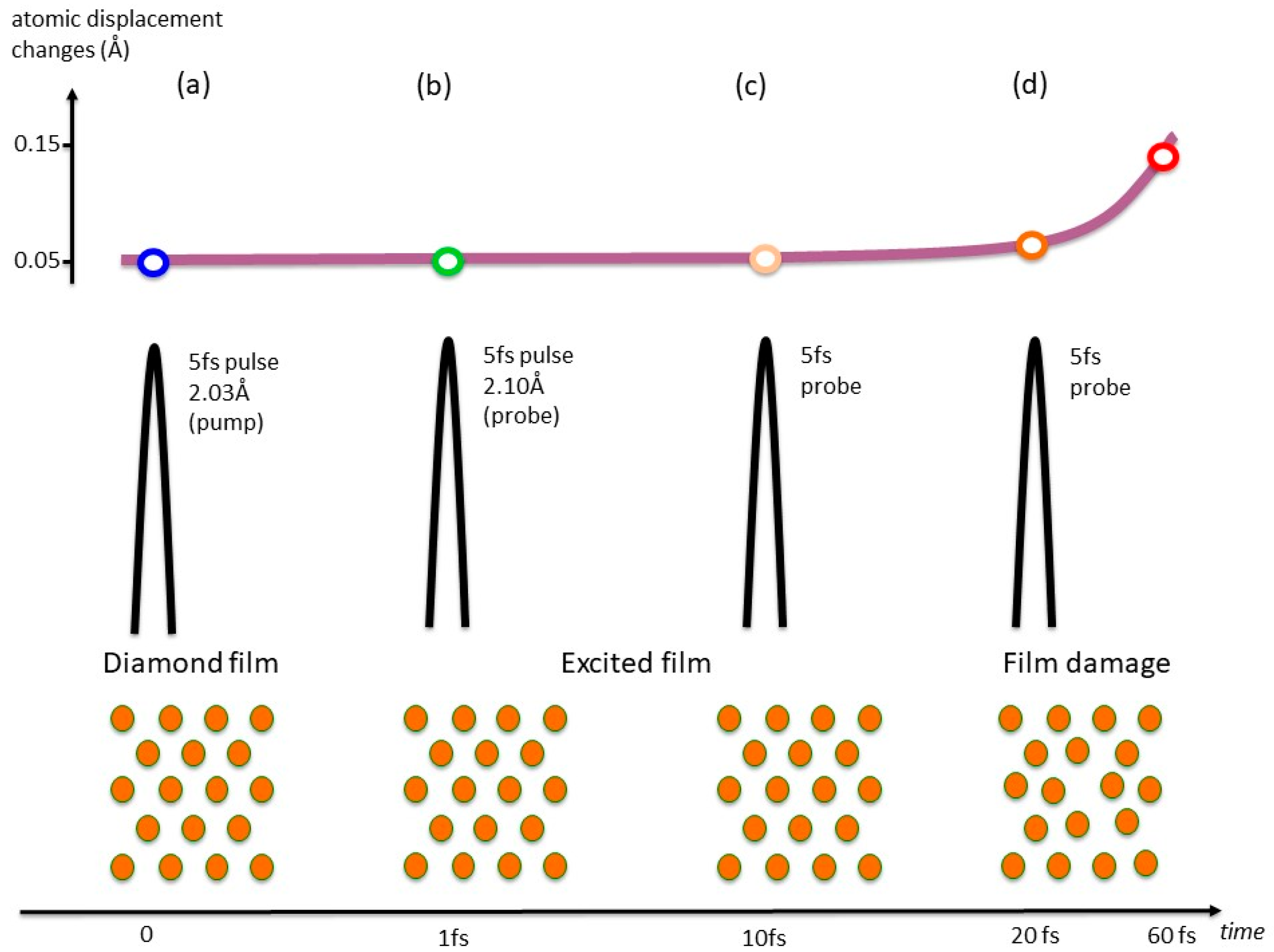
The existence of two well separated time regimes in X-ray induced lattice changes has been demonstrated in an elegant experiment by Inoue and collaborators [
24], in which an XFEL pump-probe arrangement was used to examine the dependence of the damage in a diamond film target as a function of time at room temperature as illustrated in
Figure 2. The pump and probe diffraction intensities were found to be almost constant for at least 20 fs, after which a decrease in the probed intensity was detected. This indicates that sub-10 fs XFEL pulses can effectively be used to explore the regime in which only the electronic relaxation (which, in our model, corresponds to the exciton formation) has occurred. The results presented in Ref. [
14] indicate how these electronic phenomena can be interpreted, and how they subsequently lead to defect formation, crystal symmetry reduction and, potentially, changes in the chemical composition of the system (e.g., bond breaking/formation, evolution of H
2, etc.) [
1,
6,
7,
8,
15,
16,
17,
18,
19,
20].
This model can be used to interpret specific radiation damage effects in a variety of systems. For instance, macromolecular crystals with metal centres are the systems most notoriously affected by X-ray induced damage, and, long before the appearance of third generation X-ray sources, they have demanded careful consideration for the interpretation of crystallographic models, typically requiring complementary spectroscopic investigations to obtain a satisfactory description of the local metal-centre environment. A widely studied example of this class, investigated by crystallography at cryotemperatures, is the ferryl heme group in peroxidases [
4,
18].
For moderate to high X-ray doses, a reduction of electron density is observed in the vicinity of the Fe centre during the early stages of a measurement, which essentially results in the “disappearance” of the Fe atoms from the diffraction maps and/or in a change of their oxidation state. Despite all single crystal samples yielding oscillation diffraction datasets with very good quality statistics (ca. 1.6 Å resolution), only at low total dose (20 kGy) the electron density in the vicinity of the Fe centres did not show a reduction compared to crystallographic models, and a multiple-crystal data collection strategy was required [
18]. According to our model, the key process induced by the absorption of X-ray photons during irradiation is the excitation of one or more electrons from core and/or valence states of Fe to the conduction band of the crystal, which, in the vicinity of the Fe centre, is likely to possess a predominant heme π* character. The electron density initially localised on the metal centre is therefore displaced, through a charge-transfer process, to a state delocalised (by conjugation) over the whole heme group. Effectively, this results in the disappearance of electron density at the Fe position, which is then diluted over a much larger volume. This is the factor responsible for the density changes observed for Fe atoms. The formation of a long-lived exciton pair is, in this case, unlikely, since the excited electron lacks localised character. The atomic structure is therefore likely to largely maintain its initial unperturbed configuration (apart from minor variations in bond orders), consistent with the experimental findings. A detailed quantum-mechanical description of this excitation process will be presented elsewhere. In the case of proteins containing disulphide bonds, X-ray irradiation can induce S-S bond lengthening or cleavage (along with the formation of radical species) [
2]. Early local ab initio calculations showed that the bond elongation presents a value consistent with a single electron trapped in the bond, which has been verified more recently in a thorough multi-technique effort using X-ray crystallography, EPR and optical spectroscopy [
3]. In our model, these findings can be interpreted in terms of the promotion of one electron from the S-S bond (or from S core states) to the local conduction band, which has σ* (antibonding) character. This causes a decrease of the bond order, which leads to bond lengthening and, potentially, cleavage. Similarly, the observed rapid decline of electron density in covalent Hg-S bonds [
16] can also be interpreted as a consequence of the σ* (antibonding) character of the excited state resulting in a Hg-S bond lengthening of ca. 7 Å, in conjunction with the mismatch between the original Hg bond environment and the limitations of the atomic distance models used to constrain the structural refinement against the diffraction data.
Other cases of X-ray induced radiation damage can similarly be interpreted as a radiation-induced charge-depletion effect in bonding regions of the protein. These include the decarboxylation of acidic residues [
17]. A thorough assessment of electron density loss in the crystallographic model at carboxyl acidic residue sites was conducted in a variety of local settings within the structure of Haloarcula marismortui malate dehydrogenase (HmMD) at 100 K. It confirmed that specific damage is most pronounced in acidic side-chains located in the enzymatic active site, followed by acidic residues in the internal cavity formed by the four monomers and those residues involved in crystal contacts. On the other extreme of the scale, HmMD carboxyl bonds mediated by salt bridges are observed to be less sensitive to damage. Similarly, the radiation-induced electron density loss on the −OH group of tyrosine residues [
20] and the cleavage of methylthio groups in methionine can be interpreted as a direct consequence of the electron density rearrangement following excitation to predominantly anti-bonding conduction states, which cannot be interpreted by the a priori crystallographic models used during the refinement.
3. Conclusions
We have described a new model of X-ray induced damage in macromolecular crystals. Our model is based on experimental work concerning various forms of specific radiation damage and on recent quantum-mechanical calculations on macromolecular crystals. The interaction of X-ray radiation with a sample results in the diffraction, inelastic scattering (Compton effect) or absorption of X-ray photons. The X-ray absorption drives either the photoemission of electrons from the sample, or the creation of electron/hole pairs. In the latter case, the electron and the hole can either remain unbound (e.g., if the electron is promoted to a very delocalized state, as in a conjugated heme system) or form bound pairs (excitons), strongly localised in space, which are characterised by long life times (ca. 1–10 ns, [
22]) and whose charge distribution perturbs the atomic arrangement. Over short timescales (up to ca. 10–20 fs), the formation of exciton pairs only involves a redistribution of the electron density, while the nuclear positions remain unchanged relative to their unperturbed geometry. In this situation, localised regions of electronic density depletion can appear (as in the case of peroxidases [
18]), which cannot be matched by the global crystallographic models used to refine the crystal structure. For longer time scales, electron-phonon interaction and atomic relaxation can induce substantial rearrangements of the crystal structure, potentially leading to chemical changes in the sample, including bond breaking and the formation of new chemical species (such as H
2) within the crystal. These phenomena are responsible for the occurrence of global damage. It is important to remark that the persistence of localised electron-hole pairs over long times is a
dose-rate independent phenomenon, in which dose accumulation correlates to the actual atomic displacements within the crystal lattice. Excitons can also act as energy carriers within the macromolecular crystal (e.g., inducing the formation of mobile polaron-like states [
25]), and they can be responsible for the energy redistribution in the lattice. Potentially, these approaches can also be extended to the study of the dependence of damage on the wavelength of the applied X-ray radiation, to address longer wavelength regimes which improve the anomalous diffraction signal from weakly diffracting samples [
12], or to address the other extreme, short wavelengths for reduced global damage [
19]. Computational work on an improved analogue system (crystalline sodium acetate tri-hydrate) is currently in progress, which extends the simple alkane model of Ref. [
14] to include carboxylic groups and water molecules, providing a better approximation to proteins in the crystal state. Although the model present here is largely qualitative, the theoretical and computational tools developed in recent years to address the structural and dynamic properties of excited states of extended systems [
25,
26,
27] are paving the way for the development of a general quantitative quantum-mechanical model of radiation damage in X-ray macromolecular crystallography, along the lines indicated in, e.g., Ref. [
14], which will provide a robust framework for the interpretation of chemical information from XFEL and synchrotron structural research.