Dislocation-Free SiGe/Si Heterostructures
Abstract
1. Introduction
2. Vertical Heterostructures with Constant Composition
2.1. Vertical Growth of Ge/Si by LEPECVD
2.2. Other Deposition Techniques and Other Materials
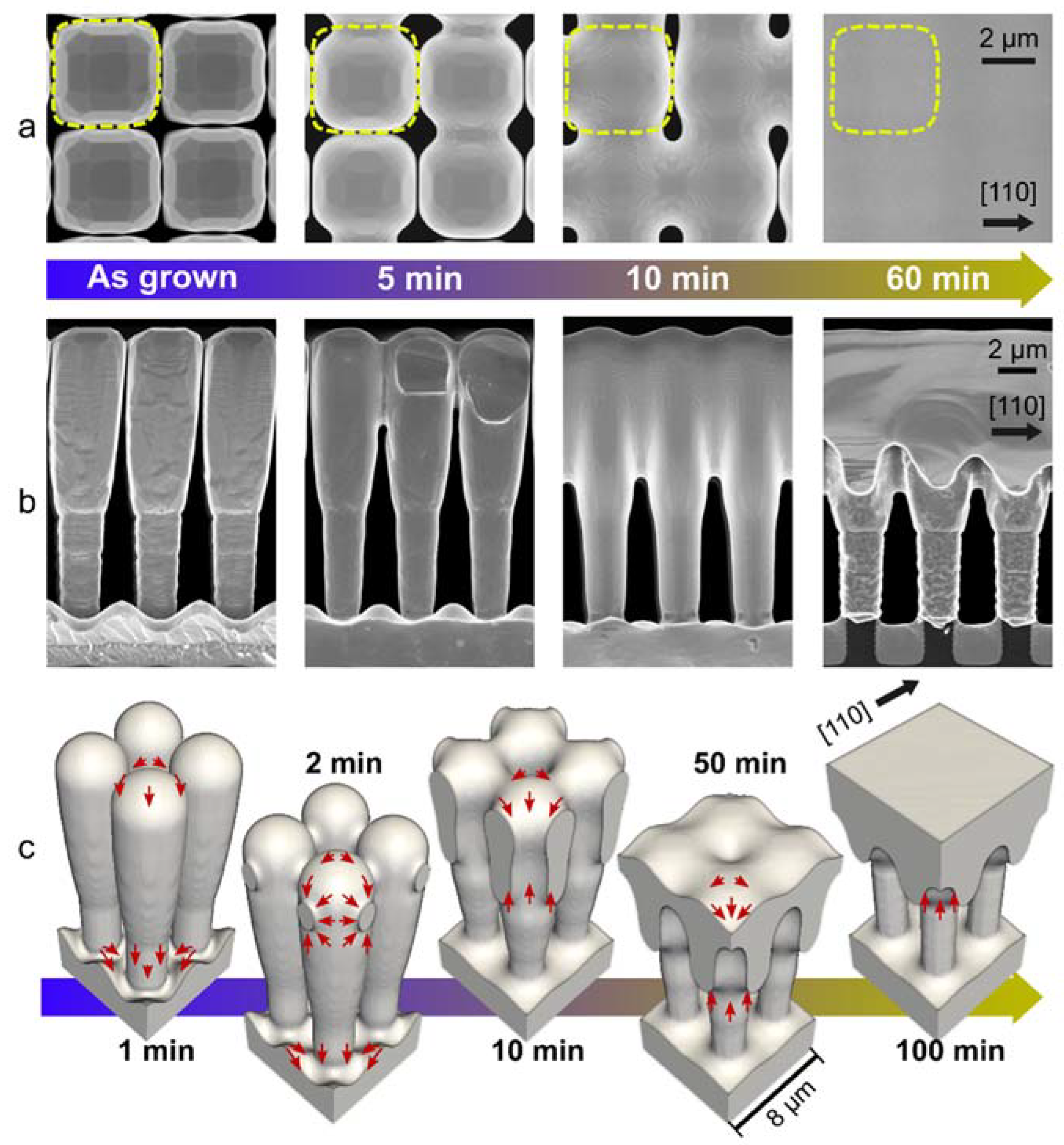
2.3. Suspended Films
3. Graded, Vertical Heterostructures
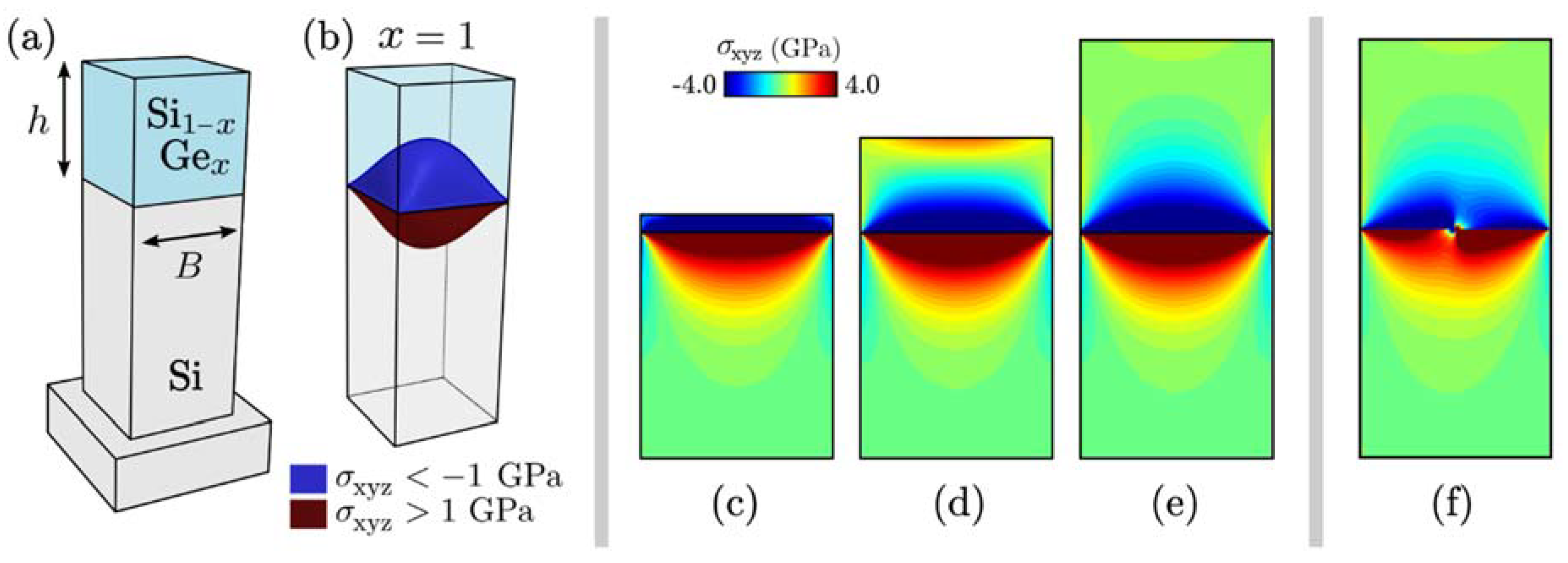
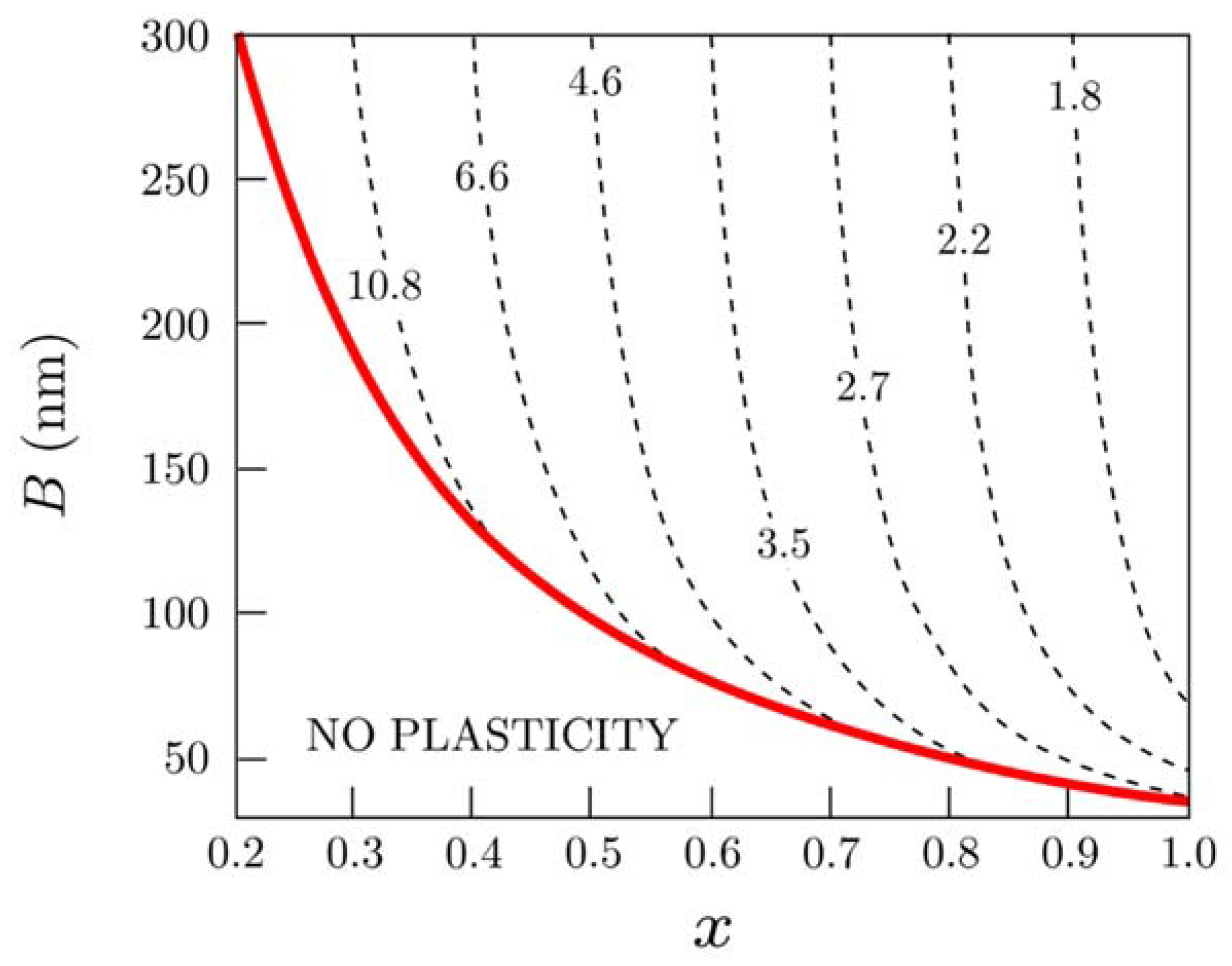
3.1. Elastic vs. Plastic Relaxation: Theory
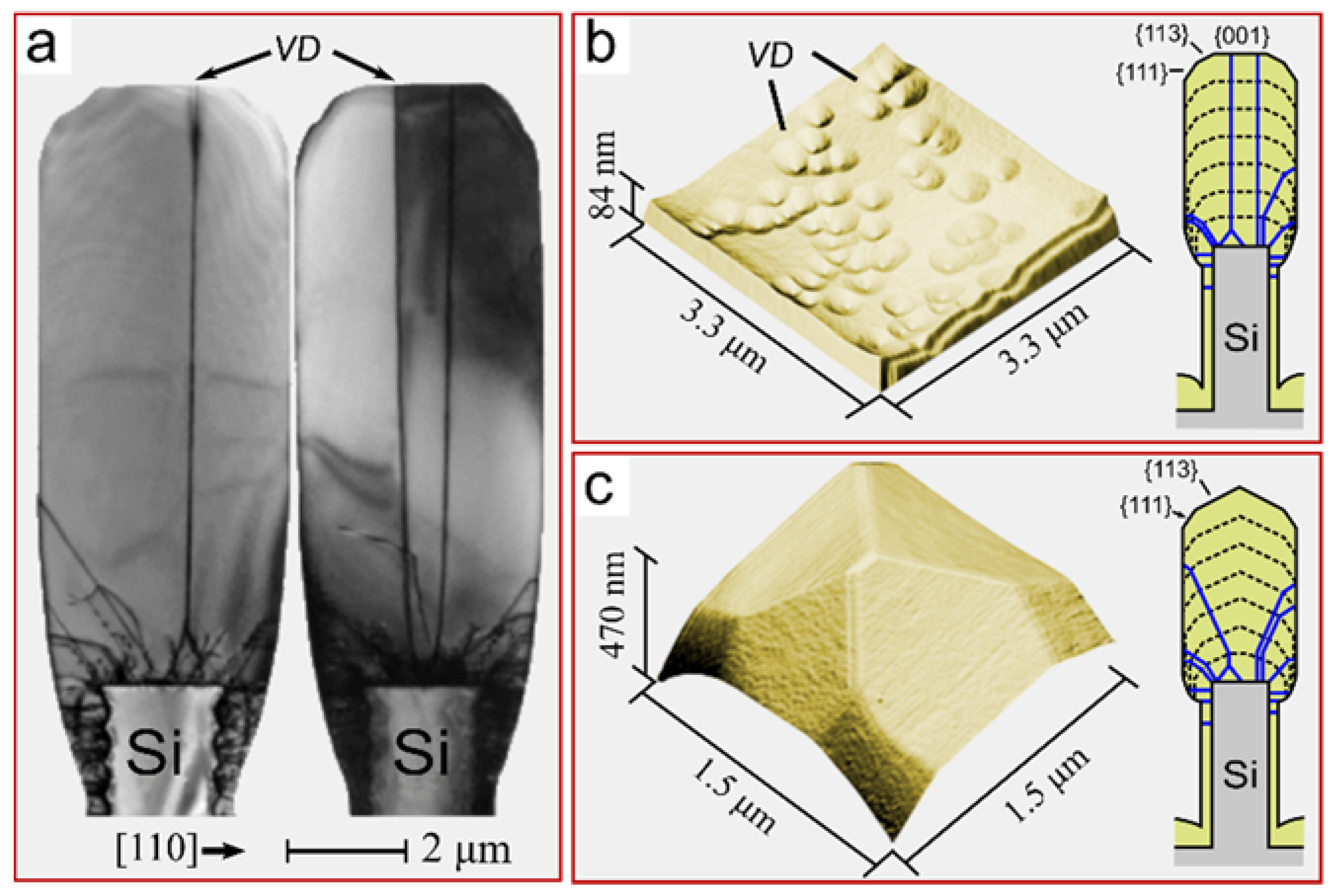
3.2. Dislocation-Free Graded Heterostructures
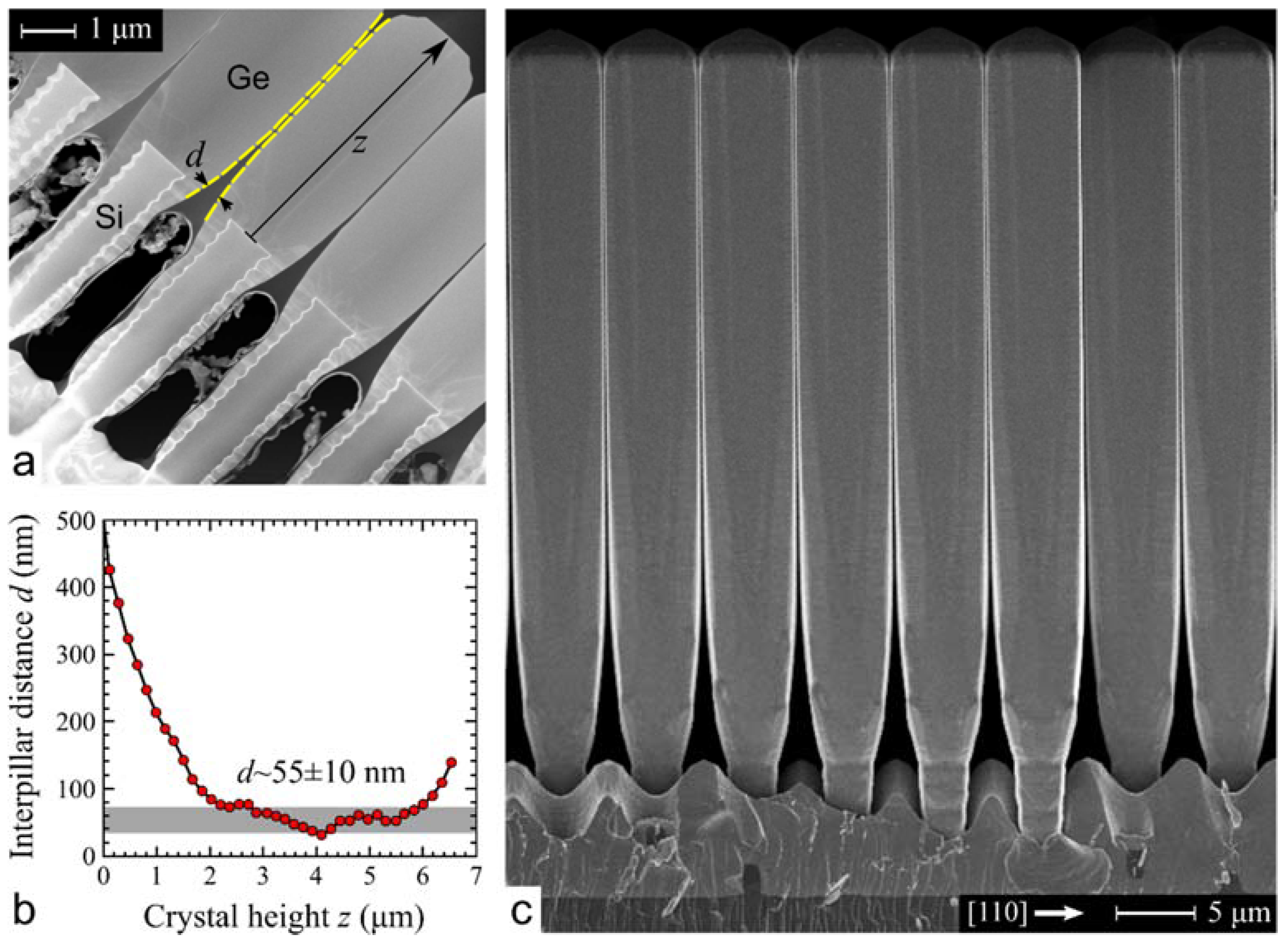
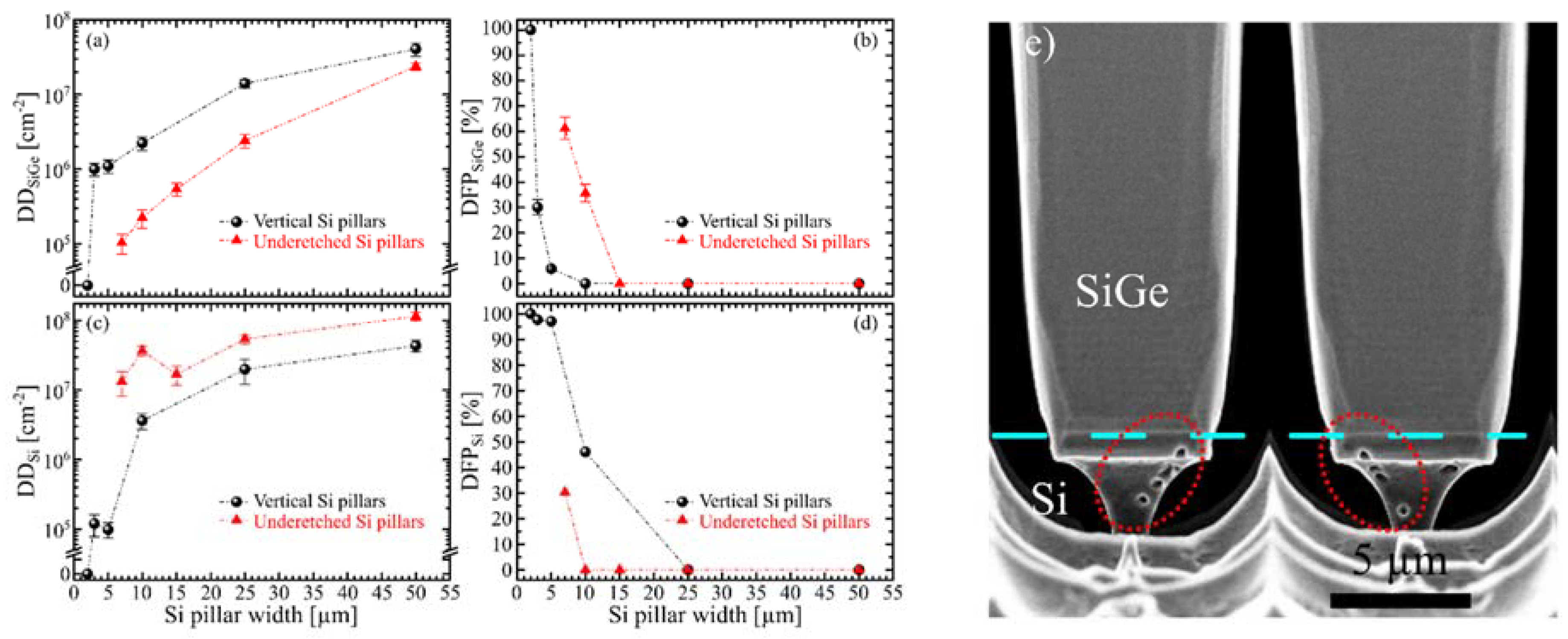
4. Deposition on Under-Etched Pillars
4.1. Graded Heterostructures on Under-Etched Pillars: Experimental Results
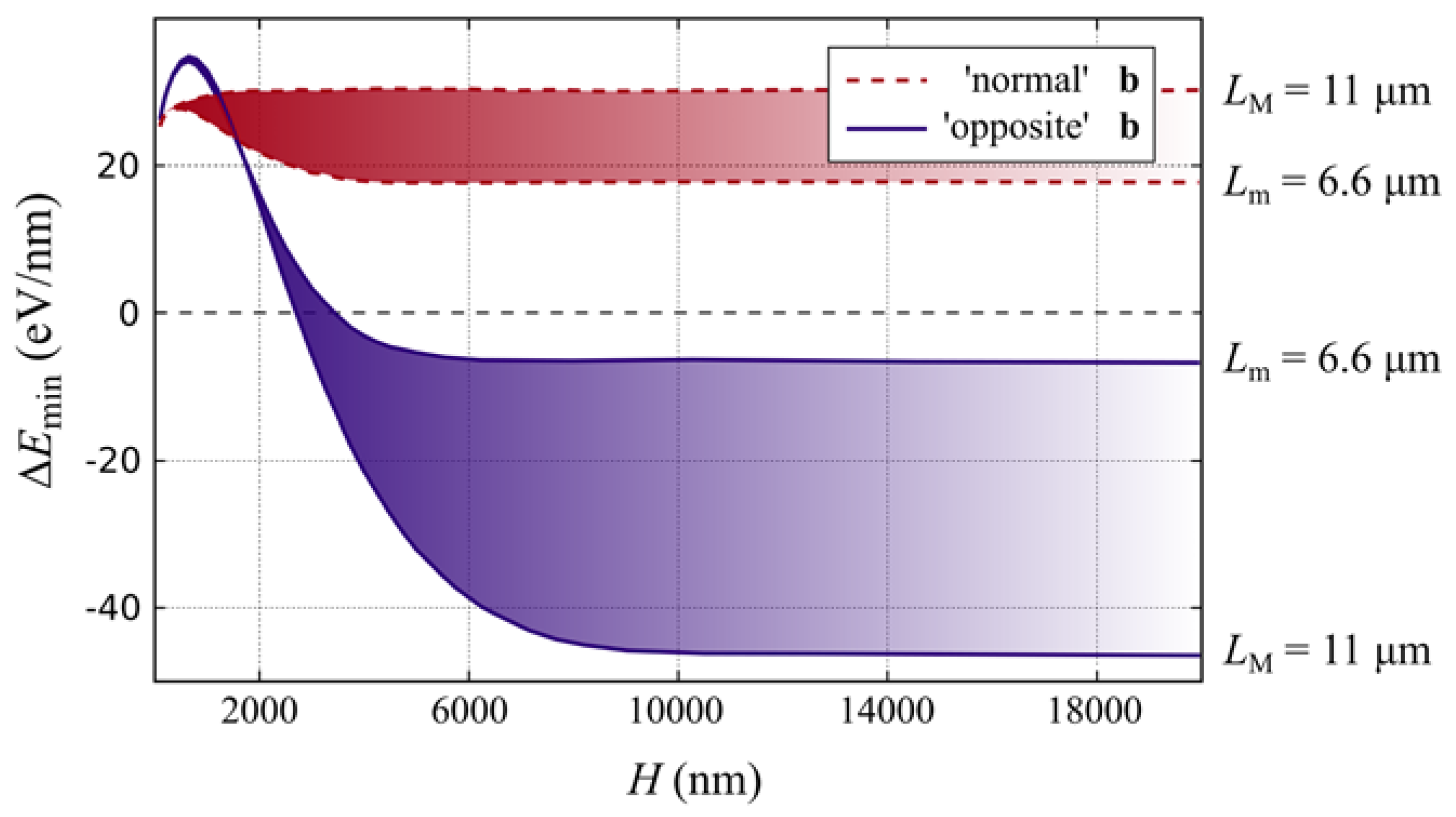
4.2. Graded Heterostructures on Under-Etched Pillars: Theoretical Interpretation
5. Conclusions and Perspectives
6. Patents
Funding
Conflicts of Interest
References
- Kazior, T.E. Beyond CMOS: Heterogeneous integration of III–V devices, RF MEMS and other dissimilar materials/devices with Si CMOS to create intelligent microsystems. Philos. Trans. R. Soc. A 2014, 372. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Loo, R.; Simoen, G.; Souriau, L.; Caymax, M.; Heyns, M.M.; Blanpain, P. A model of threading dislocation density in strain-relaxed Ge and GaAs epitaxial films on Si(100). Appl. Phys. Lett. 2009, 94, 102115. [Google Scholar] [CrossRef]
- Speck, J.S.; Brewer, M.A.; Beltz, G. Scaling laws for the reduction of threading dislocation densities in homogeneous buffer layers. J. Appl. Phys. 1996, 80, 3808. [Google Scholar] [CrossRef]
- Fitzgerald, E.A.; Xie, Y.H.; Green, M.L.; Brasen, D.; Kortan, A.R.; Michel, J.; Mii, Y.J.; Weir, B.E. Totally relaxed GexSi1−x layers with low threading dislocation densities grown on Si substrates. Appl. Phys. Lett. 1991, 59, 811. [Google Scholar] [CrossRef]
- Fitzgerald, E.A. Dislocations in strained-layer epitaxy: Theory, experiment, and applications. Mater. Sci. Rep. 1991, 7, 87–142. [Google Scholar] [CrossRef]
- Tersoff, J. Dislocations and strain relief in compositionally graded layers. Appl. Phys. Lett. 1993, 62, 693. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Kozlowski, G.; Zaumseil, P.; Tillack, B. Low threading dislocation Ge on Si by combining deposition and etching. Thin Solid Films 2012, 520, 3216–3221. [Google Scholar] [CrossRef]
- Langdo, T.A.; Leitz, C.W.; Currie, M.T.; Fitzgerald, E.A. High quality Ge on Si by epitaxial necking. Appl. Phys. Lett. 2000, 76, 3700. [Google Scholar] [CrossRef]
- Park, J.-S.; Curtin, M.; Adekore, B.; Carroll, M.; Lochtefeld, A. Defect reduction of selective Ge epitaxy in trenches on Si(001) substrates using aspect ratio trapping. Appl. Phys. Lett. 2007, 90, 052133. [Google Scholar] [CrossRef]
- Linthicum, K.; Gehrke, T.; Thomson, D.; Carlson, E.; Rajagopal, P.; Smith, T.; Batchelor, D.; Davis, R. Pendeoepitaxy of gallium nitride thin films. Appl. Phys. Lett. 1999, 75, 196. [Google Scholar] [CrossRef]
- Falub, C.V.; von Känel, H.; Isa, F.; Bergamaschini, R.; Marzegalli, A.; Chrastina, D.; Isella, G.; Müller, E.; Niedermann, P.; Miglio, L. Scaling hetero-epitaxy from layers to three-dimensional crystals. Science 2012, 335, 1330–1334. [Google Scholar] [CrossRef] [PubMed]
- Bergamaschini, R.; Isa, F.; Falub, C.V.; Niedermann, P.; Müller, E.; Isella, G.; von Känel, H.; Miglio, L. Self-aligned Ge and SiGe three-dimensional epitaxy on dense Si pillar arrays. Surf. Sci. Rep. 2013, 68, 390–417. [Google Scholar] [CrossRef]
- Laermer, F.; Schilp, A. Method of Anisotropically Etching Silicon. U.S. Patent No. 5501893, 26 March 1996. [Google Scholar]
- Rosenblad, C.; von Känel, H.; Kummer, M.; Dommann, A.; Müller, E. A plasma process for ultrafast deposition of SiGe graded buffer layers. Appl. Phys. Lett. 2000, 76, 427. [Google Scholar] [CrossRef]
- Falub, C.V.; Meduňa, M.; Chrastina, D.; Isa, F.; Marzegalli, A.; Kreiliger, T.; Taboada, A.G.; Isella, G.; Miglio, L.; Dommann, A.; et al. Perfect crystals grown from imperfect interfaces. Sci. Rep. 2013, 3, 2276. [Google Scholar] [CrossRef] [PubMed]
- Meduna, M.; Falub, C.V.; Isa, F.; Marzegalli, A.; Chrastina, D.; Isella, G.; Miglio, L.; Dommann, A.; von Känel, H. Lattice bending in three-dimensional Ge microcrystals studied by X-ray nanodiffraction and modelling. J. Appl. Cryst. 2016, 49, 976–986. [Google Scholar] [CrossRef]
- Meduna, M.; Isa, F.; Jung, A.; Marzegalli, A.; Albani, M.; Isella, G.; Zwelacker, K.; Miglio, L.; von Känel, H. Lattice tilt and strain mapped by X-ray scanning nanodiffraction in compositionally graded SiGe/Si microcrystals. J. Appl. Cryst. 2018, 51, 368–385. [Google Scholar] [CrossRef]
- Marzegalli, A.; Cortinovis, A.; Basset, F.B.; Bonera, E.; Pezzoli, F.; Scaccabarozzi, A.; Isa, F.; Isella, G.; Zaumseil, P.; Capellini, G.; et al. Exceptional thermal strain reduction by a tilting pillar architecture: Suspended Ge layers on Si(001). Mater. Des. 2017, 116, 144–151. [Google Scholar] [CrossRef]
- Marzegalli, A.; Isa, F.; Groiss, H.; Müller, E.; Falub, C.V.; Taboada, A.G.; Niedermann, P.; Isella, G.; Schaeffler, F.; Montalenti, F.; et al. Unexpected Dominance of Vertical Dislocations in High-Misfit Ge/Si(001) Films and Their Elimination by Deep Substrate Patterning. Adv. Mater. 2013, 25, 4408–4412. [Google Scholar] [CrossRef] [PubMed]
- Isa, F.; Marzegalli, A.; Taboada, A.G.; Falub, C.V.; Isella, G.; Montalenti, F.; von Känel, H.; Miglio, L. Onset of vertical threading dislocations in Si1−xGex/Si(001) at a critical Ge concentration. APL Mater. 2013, 1, 052109. [Google Scholar] [CrossRef]
- Skibitzki, O.; Capellini, G.; Yamamoto, Y.; Zaumseil, P.; Schubert, M.A.; Schroeder, T.; Ballabio, A.; Bergamaschini, R.; Salvalaglio, M.; Miglio, L.; et al. Reduced-Pressure Chemical Vapor Deposition Growth of Isolated Ge Crystals and Suspended Layers on Micrometric Si Pillars. ACS Appl. Mater. Interfaces 2016, 8, 26374–26380. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Lowengrub, J.; Ratz, A.; Voigt, A. Geometric evolution laws for thin crystalline films: Modeling and numeric. Commun. Comput. Phys. 2009, 6, 433. [Google Scholar]
- Salvalaglio, M.; Backofen, R.; Bergamaschini, R.; Montalenti, F.; Voigt, A. Faceting of Equilibrium and Metastable Nanostructures: A Phase-Field Model of Surface Diffusion Tackling Realistic Shapes. Cryst. Growth Des. 2015, 15, 2787–2794. [Google Scholar] [CrossRef]
- Von Känel, H.; Isa, F.; Falub, C.V.; Barthazy, E.J.; Müller, E.; Chrastina, D.; Isella, G.; Kreiliger, T.; Taboada, A.G.; Meduna, M.; et al. Three-dimensional Epitaxial Si1−xGex, Ge and SiC Crystals on Deeply Patterned Si Substrates. ECS Trans. 2014, 64, 631–648. [Google Scholar] [CrossRef]
- Isa, F.; Cheze, C.; Siekacz, M.; Hauswald, C.; Laehnemann, J.; Fernandez-Garrido, S.; Kreliger, T.; Ramsteiner, M.; Arroyo Rojas Da Silva, A.; Brandt, O.; Isella, G.; et al. Integration of GaN Crystals on Micropatterned Si(0 0 1) Substrates by Plasma-Assisted Molecular Beam Epitaxy. Cryst. Growth Des. 2015, 15, 4886–4892. [Google Scholar] [CrossRef]
- Bietti, S.; Scaccabarozzi, A.; Frigeri, C.; Bollani, M.; Bonera, E.; Falub, C.V.; von Känel, H.; Miglio, L.; Sanguinetti, S. Monolithic integration of optical grade GaAs on Si (001) substrates deeply patterned at a micron scale. Appl. Phys. Lett. 2013, 103, 262106. [Google Scholar] [CrossRef]
- Bergamaschini, R.; Bietti, S.; Castellano, A.; Frigeri, C.; Falub, C.V.; Scaccabarozzi, A.; Bollani, M.; von Känel, H.; Miglio, L.; Sanguinetti, S. Kinetic growth mode of epitaxial GaAs on Si(001) micro-pillars. J. Appl. Phys. 2016, 120, 245702. [Google Scholar] [CrossRef]
- Taboada, A.G.; Kreiliger, T.; Falub, C.V.; Isa, F.; Salvalaglio, M.; Wevior, L.; Fuster, D.; Richter, M.; Uccelli, E.; Niedermann, P.; et al. Strain relaxation of GaAs/Ge crystals on patterned Si substrates. Appl. Phys. Lett. 2014, 104, 022112. [Google Scholar] [CrossRef]
- Taboada, A.G.; Meduna, M.; Salvalaglio, M.; Isa, F.; Kreiliger, T.; Falub, C.V.; Barthazy Meier, E.; Müller, E.; Miglio, L.; Isella, G.; et al. GaAs/Ge crystals grown on Si substrates patterned down to the micron scale. J. Appl. Phys. 2016, 119, 055301. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Bergamaschini, R.; Isa, F.; Scaccabarozzi, A.; Isella, G.; Backofen, R.; Voigt, A.; Montalenti, F.; Capellini, G.; Schroeder, T.; et al. Engineered Coalescence by Annealing 3D Ge Microstructures into High-Quality Suspended Layers on Si. ACS Appl. Mater. Interfaces 2015, 7, 19219–19225. [Google Scholar] [CrossRef] [PubMed]
- Bergamaschini, R.; Salvalaglio, M.; Backofen, R.; Voigt, A.; Montalenti, F. Continuum modelling of semiconductor heteroepitaxy: An applied perspective. Adv. Phys. X 2016, 1, 331–367. [Google Scholar] [CrossRef]
- Mullins, W.W. Theory of Thermal Grooving. J. Appl. Phys. 1957, 28, 333. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Bergamaschini, R.; Backofen, R.; Voigt, A.; Montalenti, F.; Miglio, L. Phase-field simulations of faceted Ge/Si-crystal arrays, merging into a suspended film. Appl. Surf. Sci. 2017, 391, 33–38. [Google Scholar] [CrossRef]
- Glas, F. Critical dimensions for the plastic relaxation of strained axial heterostructures in free-standing nanowires. Phys. Rev. B 2006, 74, 121302. [Google Scholar] [CrossRef]
- Salvalaglio, M.; Montalenti, F. Fine control of plastic and elastic relaxation in Ge/Si vertical heterostructures. J. Appl. Phys. 2014, 116, 104306. [Google Scholar] [CrossRef]
- Gatti, R.; Marzegalli, A.; Zinovyev, V.A.; Montalenti, F.; Miglio, L. Modeling the plastic relaxation onset in realistic SiGe islands on Si(001). Phys. Rev. B 2008, 78, 184104. [Google Scholar] [CrossRef]
- Montalenti, F.; Salvalaglio, M.; Marzegalli, A.; Zaumseil, P.; Capellini, G.; Schülli, T.U.; Schubert, M.A.; Yamamoto, Y.; Tillack, B.; Schroeder, T. Fully coherent growth of Ge on free-standing Si(001) nanomesas. Phys. Rev. B 2014, 89, 014101. [Google Scholar] [CrossRef]
- Scarpellini, D.; Somaschini, C.; Fedorov, A.; Bietti, S.; Frigeri, C.; Grillo, V.; Esposito, L.; Salvalaglio, M.; Marzegalli, A.; Montalenti, F.; et al. InAs/GaAs Sharply Defined Axial Heterostructures in Self-Assisted Nanowires. Nano Lett. 2015, 15, 3677–3683. [Google Scholar] [CrossRef] [PubMed]
- Niu, G.; Capellini, G.; Lupina, G.; Niermann, T.; Salvalaglio, M.; Marzegalli, A.; Schubert, M.A.; Zaumseil, P.; Krause, H.-M.; Skibitzki, O.; et al. Photodetection in Hybrid Single-Layer Graphene/Fully Coherent Germanium Island Nanostructures Selectively Grown on Silicon Nanotip Patterns. ACS Appl. Mater. Interfaces 2016, 8, 2017–2026. [Google Scholar] [CrossRef] [PubMed]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; Krieger Publishing Company: Malabar, FL, USA, 1992; ISBN 0894646176. [Google Scholar]
- Matthews, J.W.; Blakeslee, A.E. Defects in epitaxial multilayers. J. Cryst. Growth 1974, 27, 118–125. [Google Scholar] [CrossRef]
- Isa, F.; Salvalaglio, M.; Arroyo Rojas Dasilva, Y.; Meduna, M.; Barget, M.; Jung, A.; Kreiliger, T.; Isella, G.; Erni, R.; Pezzoli, F.; et al. Highly Mismatched, Dislocation-Free SiGe/Si Heterostructures. Adv. Mater. 2016, 28, 884–888. [Google Scholar] [CrossRef] [PubMed]
- Isa, F.; Salvalaglio, M.; Arroyo Rojas Dasilva, Y.; Jung, A.; Isella, G.; Erni, R.; Niedermann, P.; Groening, P.; Montalenti, F.; von Känel, H. From plastic to elastic stress relaxation in highly mismatched SiGe/Si heterostructures. Acta Mater. 2016, 114, 97–105. [Google Scholar] [CrossRef]
- Isa, F.; Jung, A.; Salvalaglio, M.; Arroyo Rojas Dasilva, Y.; Marozau, I.; Meduna, M.; Barget, M.; Marzegalli, M.; Isella, G.; Erni, R.; et al. Strain Engineering in Highly Mismatched SiGe/Si Heterostructures. Mater. Sci. Semicond. Process. 2017, 70, 117–122. [Google Scholar] [CrossRef]
- Isa, F.; Salvalaglio, M.; Arroyo Rojas Dasilva, Y.; Jung, A.; Isella, G.; Erni, R.; Timotijevic, B.; Niedermann, P.; Groening, P.; Montalenti, F.; et al. Enhancing elastic stress relaxation in SiGe/Si heterostructures by Si pillar necking. Appl. Phys. Lett. 2016, 109, 182112. [Google Scholar] [CrossRef]
- Rovaris, F.; Isa, F.; Gatti, R.; Jung, A.; Isella, G.; Montalenti, F.; von Känel, H. Three-dimensional SiGe/Si heterostructures: Switching the dislocation sign by substrate under-etching. Phys. Rev. Mater. 2017, 1, 073602. [Google Scholar] [CrossRef]






| 150 nm | 0.360 | 0.23%/nm | 2 | 300 nm |
| 200 nm | 0.291 | 0.45%/nm | 3 | 600 nm |
| 300 nm | 0.210 | 73.37%/μm | 4 | 1.2 μm |
| 500 nm | 0.161 | 32.27%/μm | 6 | 3.0 μm |
| 1.0 μm | 0.116 | 11.62%/μm | 8 | 8.0 μm |
| 1.5 μm | 0.101 | 6.73%/μm | 9 | 13.5 μm |
| 2.0 μm | 0.093 | 4.66%/μm | 10 | 20.0 μm |
| 3.0 μm | 0.085 | 2.85%/μm | 11 | 33.0 μm |
| 5.0 μm | 0.079 | 1.59%/μm | 12 | 60.0 μm |
| 7.5 μm | 0.076 | 1.01%/μm | 13 | 97.5 μm |
| 10.0 μm | 0.075 | 0.75%/μm | 13 | 130.0 μm |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montalenti, F.; Rovaris, F.; Bergamaschini, R.; Miglio, L.; Salvalaglio, M.; Isella, G.; Isa, F.; Von Känel, H. Dislocation-Free SiGe/Si Heterostructures. Crystals 2018, 8, 257. https://doi.org/10.3390/cryst8060257
Montalenti F, Rovaris F, Bergamaschini R, Miglio L, Salvalaglio M, Isella G, Isa F, Von Känel H. Dislocation-Free SiGe/Si Heterostructures. Crystals. 2018; 8(6):257. https://doi.org/10.3390/cryst8060257
Chicago/Turabian StyleMontalenti, Francesco, Fabrizio Rovaris, Roberto Bergamaschini, Leo Miglio, Marco Salvalaglio, Giovanni Isella, Fabio Isa, and Hans Von Känel. 2018. "Dislocation-Free SiGe/Si Heterostructures" Crystals 8, no. 6: 257. https://doi.org/10.3390/cryst8060257
APA StyleMontalenti, F., Rovaris, F., Bergamaschini, R., Miglio, L., Salvalaglio, M., Isella, G., Isa, F., & Von Känel, H. (2018). Dislocation-Free SiGe/Si Heterostructures. Crystals, 8(6), 257. https://doi.org/10.3390/cryst8060257







