Dislocations and Plastic Deformation in MgO Crystals: A Review
Abstract
1. Introduction
- In Section 2, basic knowledge on MgO plasticity is described based on an exhaustive literature review of macro-mechanical testing. Lattice structure and slip systems are introduced as well as the main mechanical properties of MgO based on constant strain-rate and creep experiments.
- In Section 3, we focus on multi-scale modeling of MgO plasticity. This section relies on atomic scale simulations (dislocation core modeling) and their implications for large scale simulations such as dislocation dynamics and crystal plasticity.
- In Section 4, recent improvements in nano-mechanical testing, i.e., nano-indentation, micro- and nano-compression, are introduced. Special attention will be paid on elementary dislocation processes occurring in the small interrogated volumes.
- In Section 5, the role of high pressure on dislocations and MgO plasticity is detailed. Based on both modeling and experimental approaches, we describe how pressure affects basic deformation processes in MgO with implications in both materials sciences and geosciences.
2. Mechanical Properties of MgO Single Crystal: The Contribution of Macro-Mechanical Tests
2.1. Lattice, Dislocations and Slip Systems in MgO
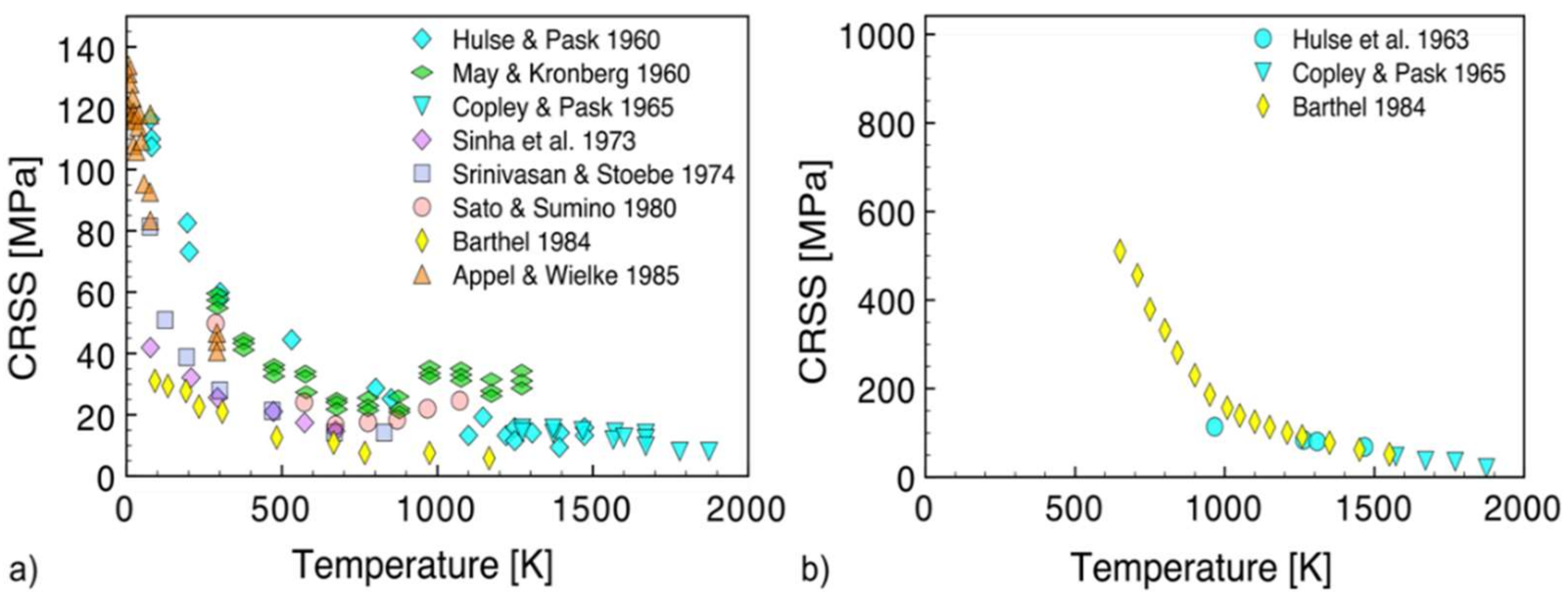
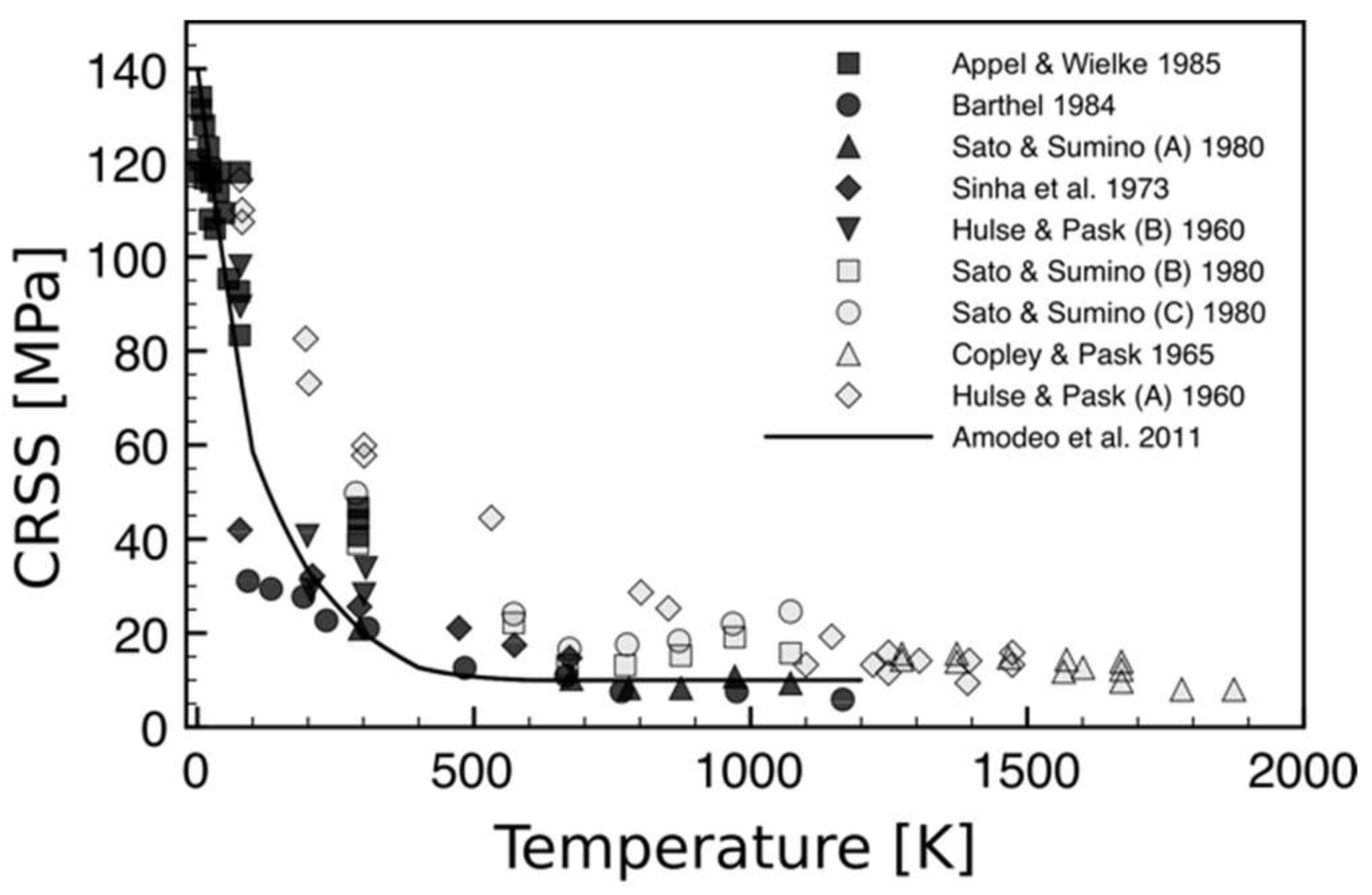
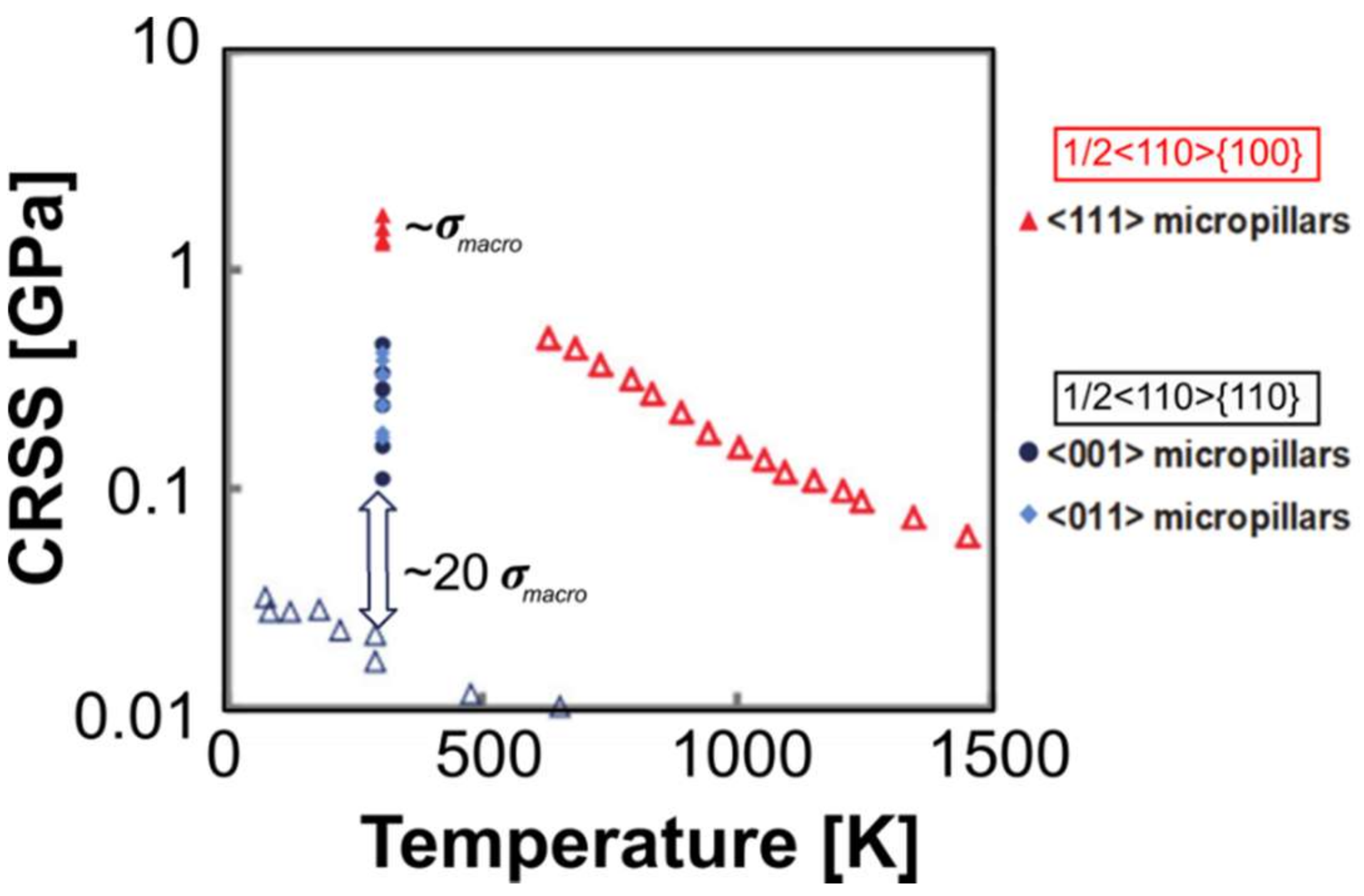
2.2. Critical Resolved Shear Stress (CRSS)
2.3. Temperature-Dependent Dislocation Microstructures
2.4. On the Role of Impurities and Heat Treatments on CRSS and Dislocation Mobility
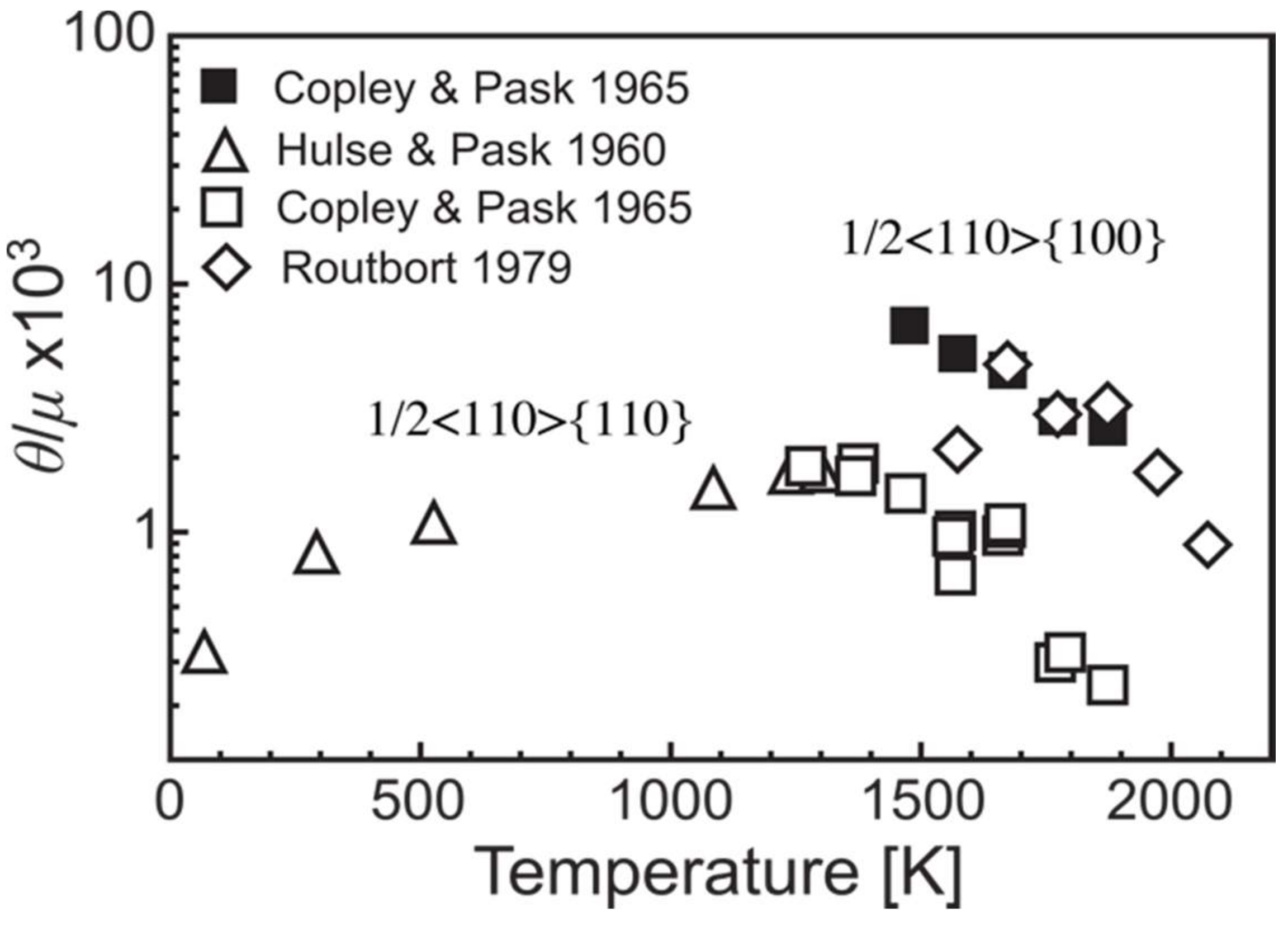
2.5. Strain Hardening in MgO Single Crystal
2.6. High-Temperature Creep of MgO
3. Multi-Scale Modeling of MgO Deformation
3.1. Dislocation Core Modeling: Methods and Results
3.1.1. Cluster-Based Embedded Models
3.1.2. Periodic Dipole Model
3.1.3. Semi-Continuum Peierls–Nabarro Model
3.2. Dislocation Mobility in MgO
3.2.1. The Kink-Pair Mechanism
3.2.2. Dislocation Glide Velocity
3.3. Grain-Scale Plasticity Modeling Using Dislocation Dynamics: On the Collective Behavior of Dislocations
3.3.1. Methods: 3D and 2.5D Dislocation Dynamics
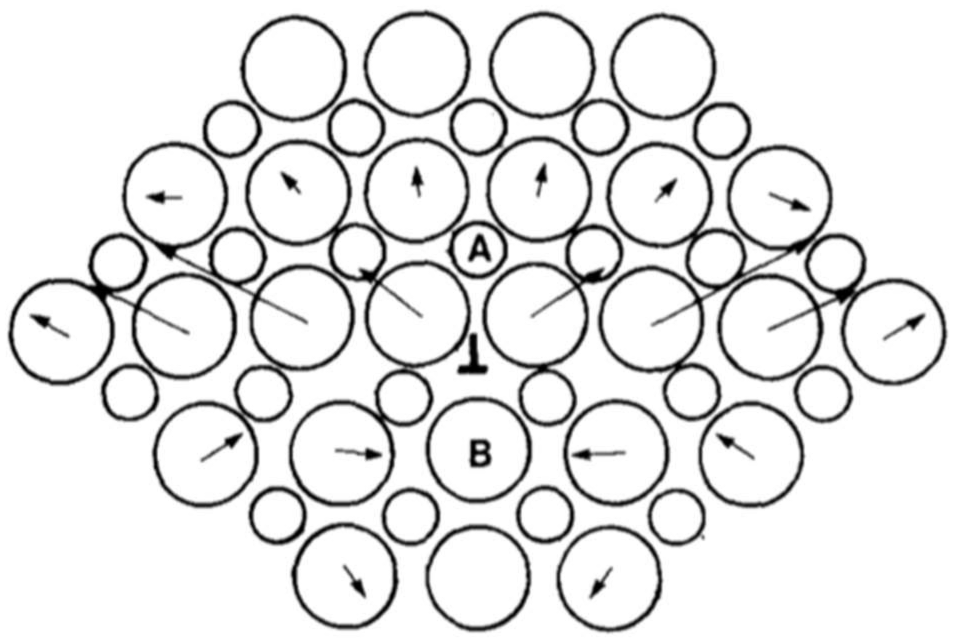
3.3.2. Dislocation Interactions Mapping
- Three maps for the {110} mode (self-interaction + {110} junction + {110} crossed/repulsive states): These reactions were investigated in Ref. [127] and show the possible formation of edge ½<110> junctions between dislocations in 60°/120° oriented slip systems. Junctions are oriented along <111> and belong to {112} slip planes. These dislocations could possibly justify {112} dislocation slip observed during nano-indentation tests (see Section 4). Ninety-degree oriented slip systems only lead to crossed or repulsive states.
- Two maps (plus self-interactions) for the {100} mode ({100} junctions + coplanar interactions): Coplanar interaction can lead to the formation of dislocation dipoles and only 90° oriented {100} slip systems can make ½<110>{110} edge junctions oriented along the <100> directions.
- Three crossed maps that involve one slip system from each {110} and {100} mode (collinear interactions + crossed junctions + crossed/repulsive states): Collinear annihilations can occur if dislocations with identical Burgers vectors interact what is the case for six combinations of slip systems. Collinear annihilation is the reaction promoting the strongest of all possible forest strengthening mechanisms [128,129]. Mixed junctions with ½<110> Burgers vectors can be made out of 60°/120° oriented slip systems.
3.3.3. Grain-Scale Deformation: On the Role of Temperature on MgO Single Crystal Flow
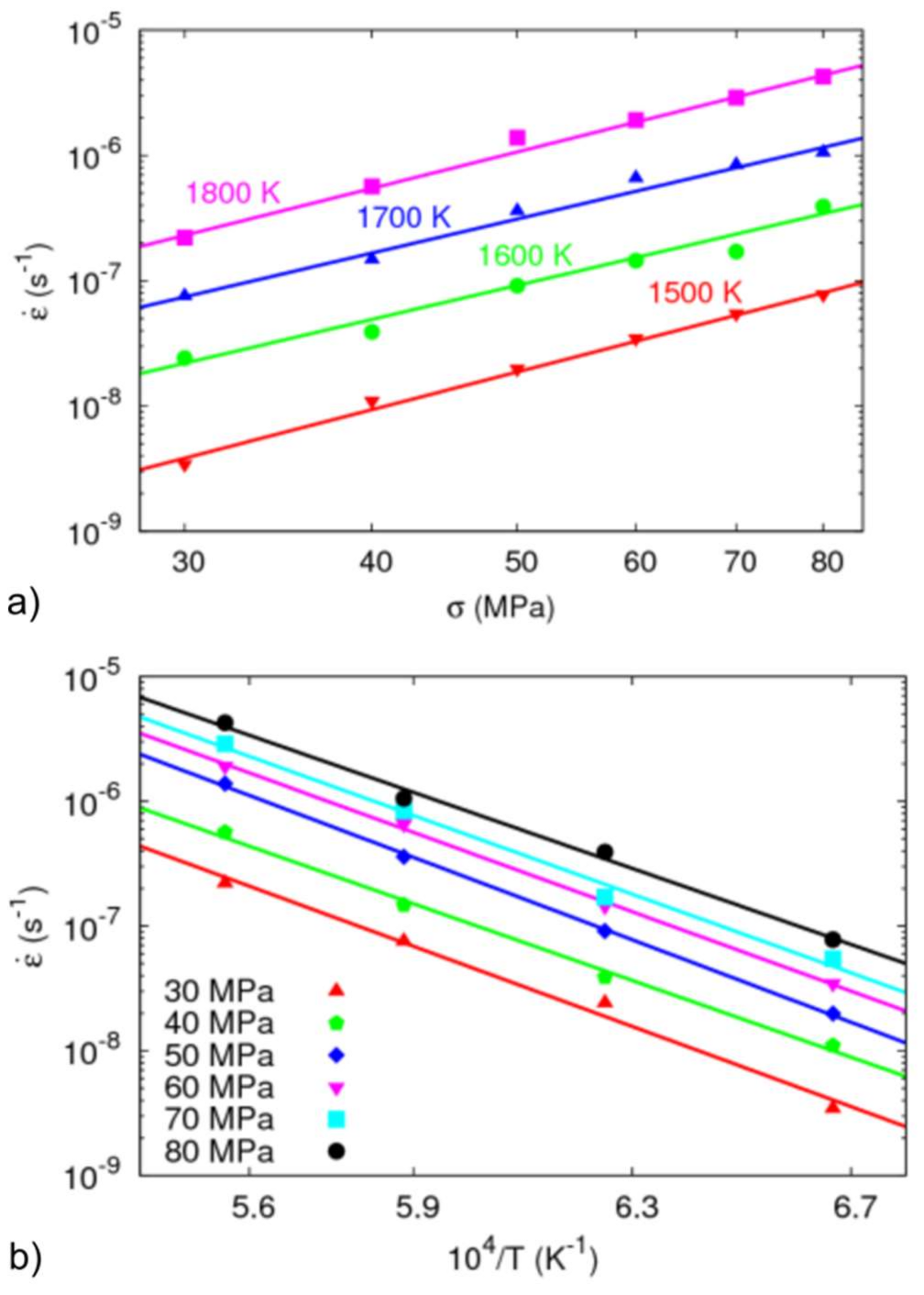
3.3.4. Creep Modeling
4. Nano-Mechanical Testing of MgO
4.1. Micro-Indentation in MgO
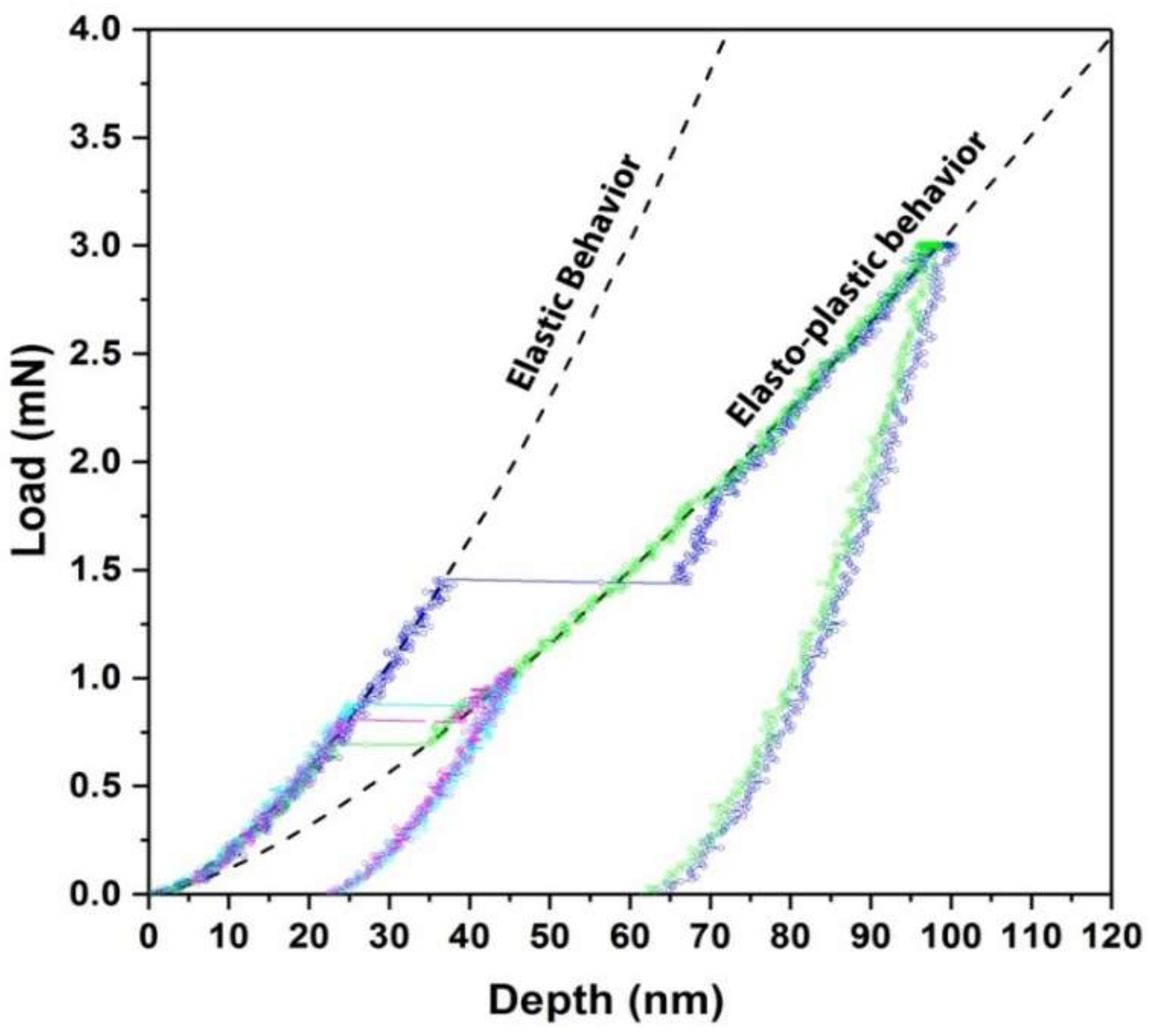
4.2. Nano-Indentation: Analysis of Elementary Deformation Mechanisms
4.3. Incipient Plasticity: Pop-In and Dislocation Nucleation
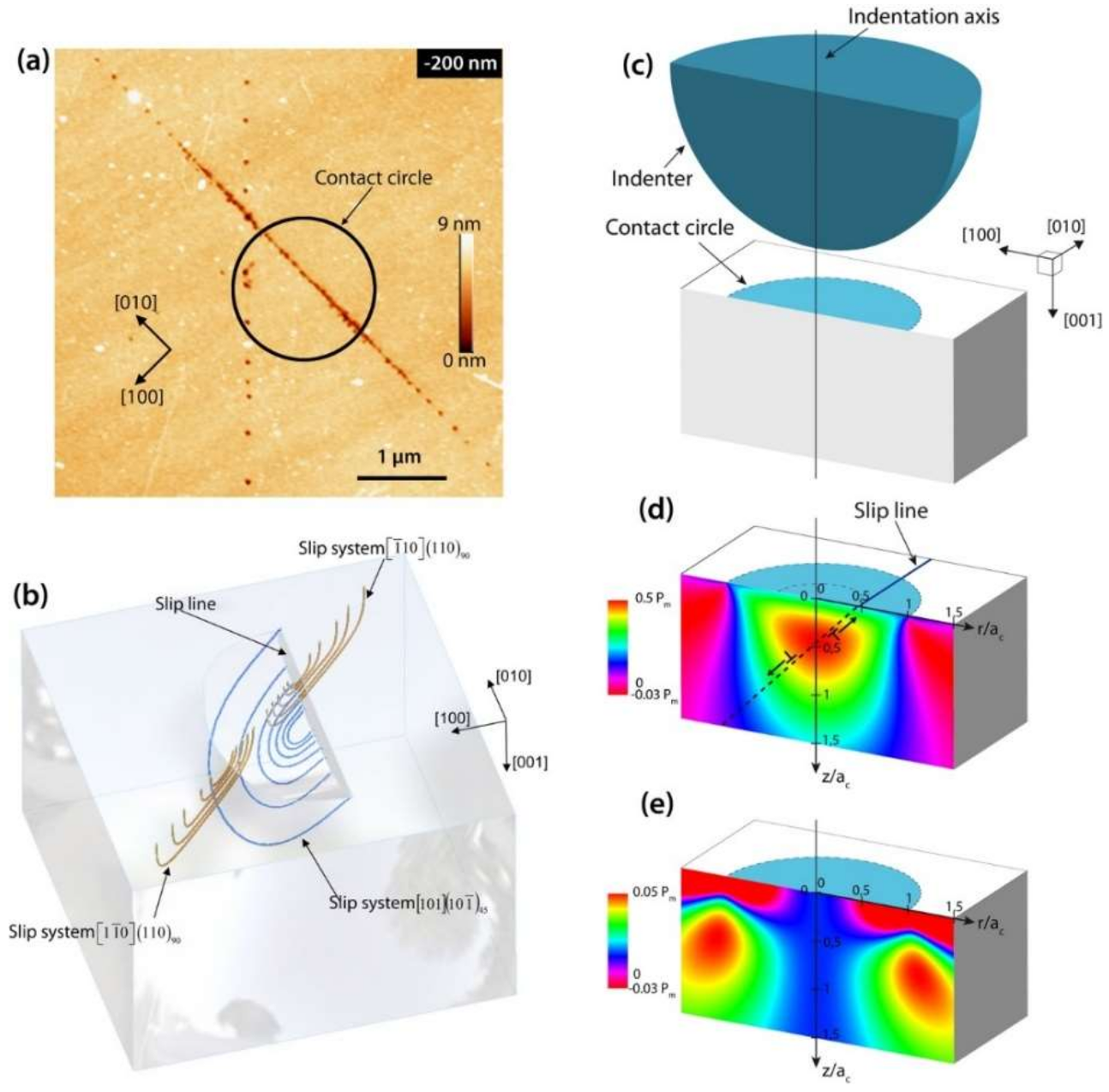
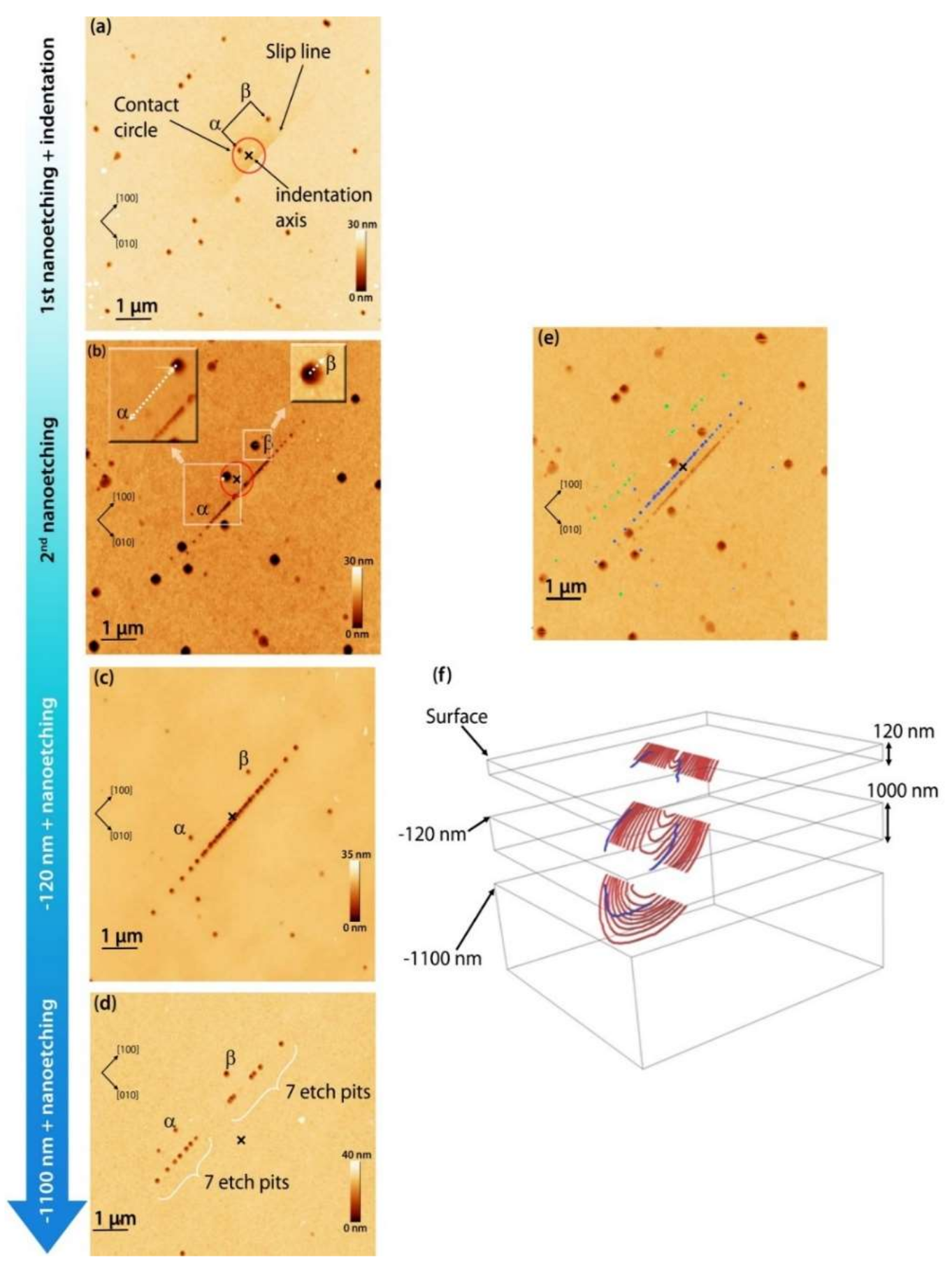
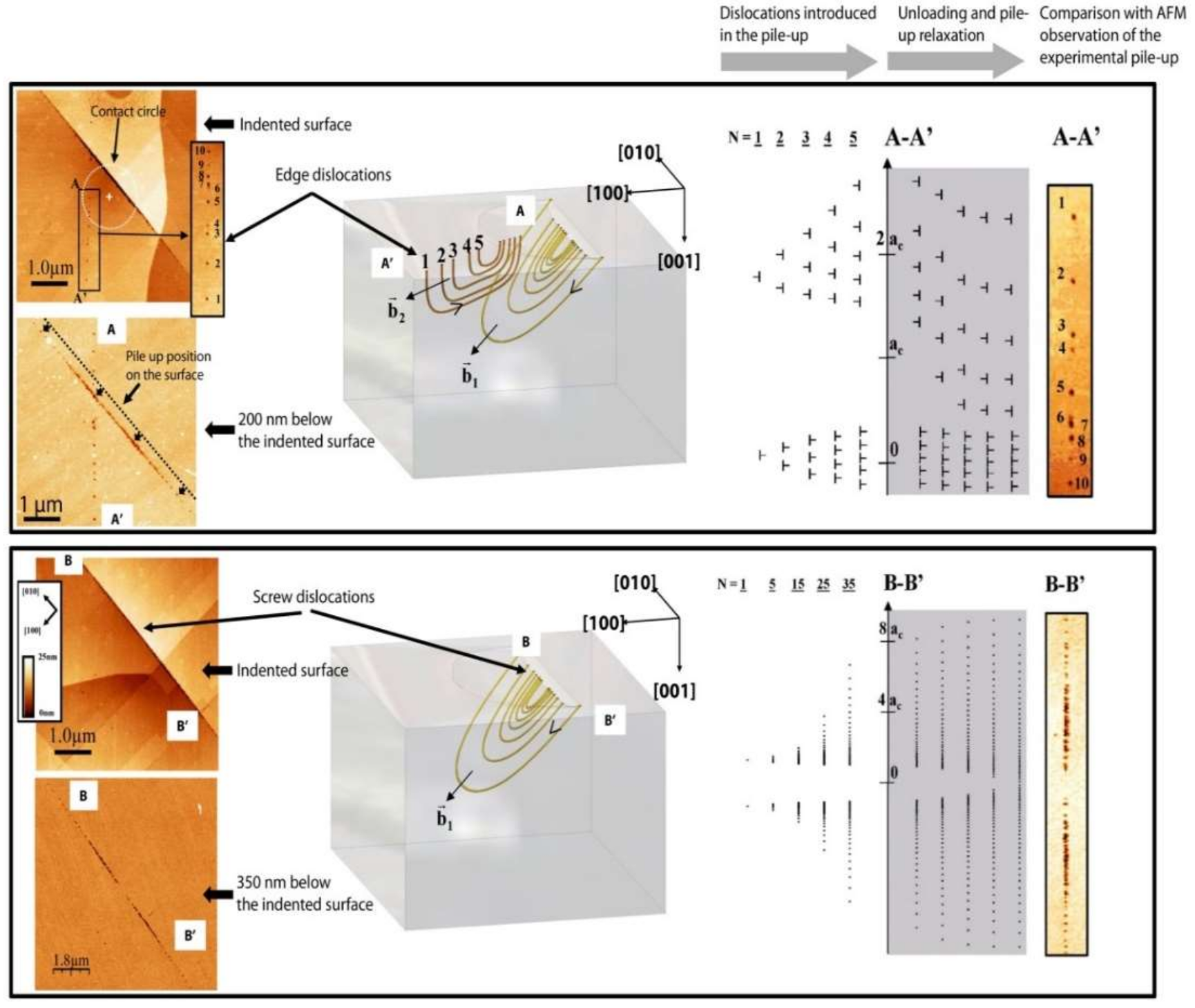
4.4. Determination of the Lattice Friction Stress through the Dislocation Structure around a Spherical Indent
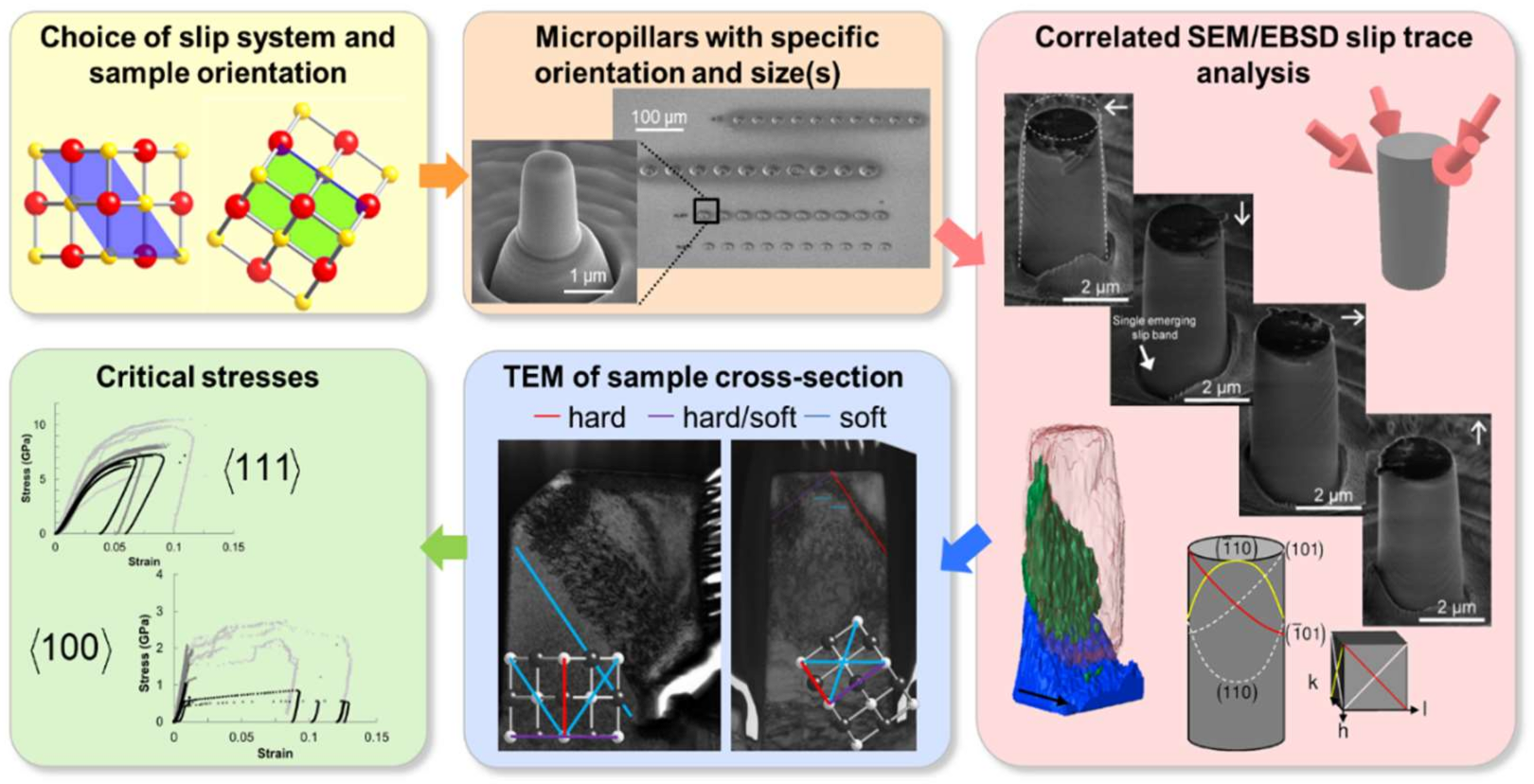
4.5. Plasticity in MgO and Other Ionic Crystals Studied by Micro-Compression
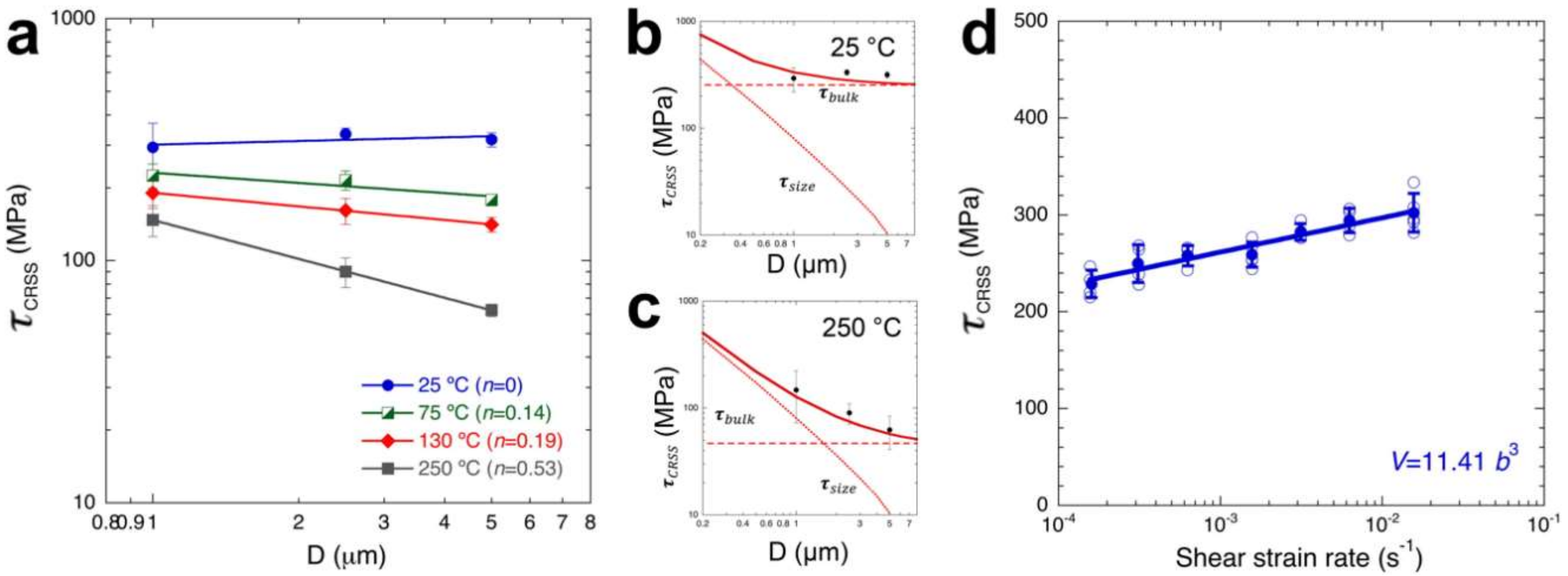
4.5.1. Measurements of CRSS in MgO and Other Rock-Salt Crystals at Room Temperature
4.5.2. Rate and Temperature Dependence in Other Ionic Rock Salt Crystals
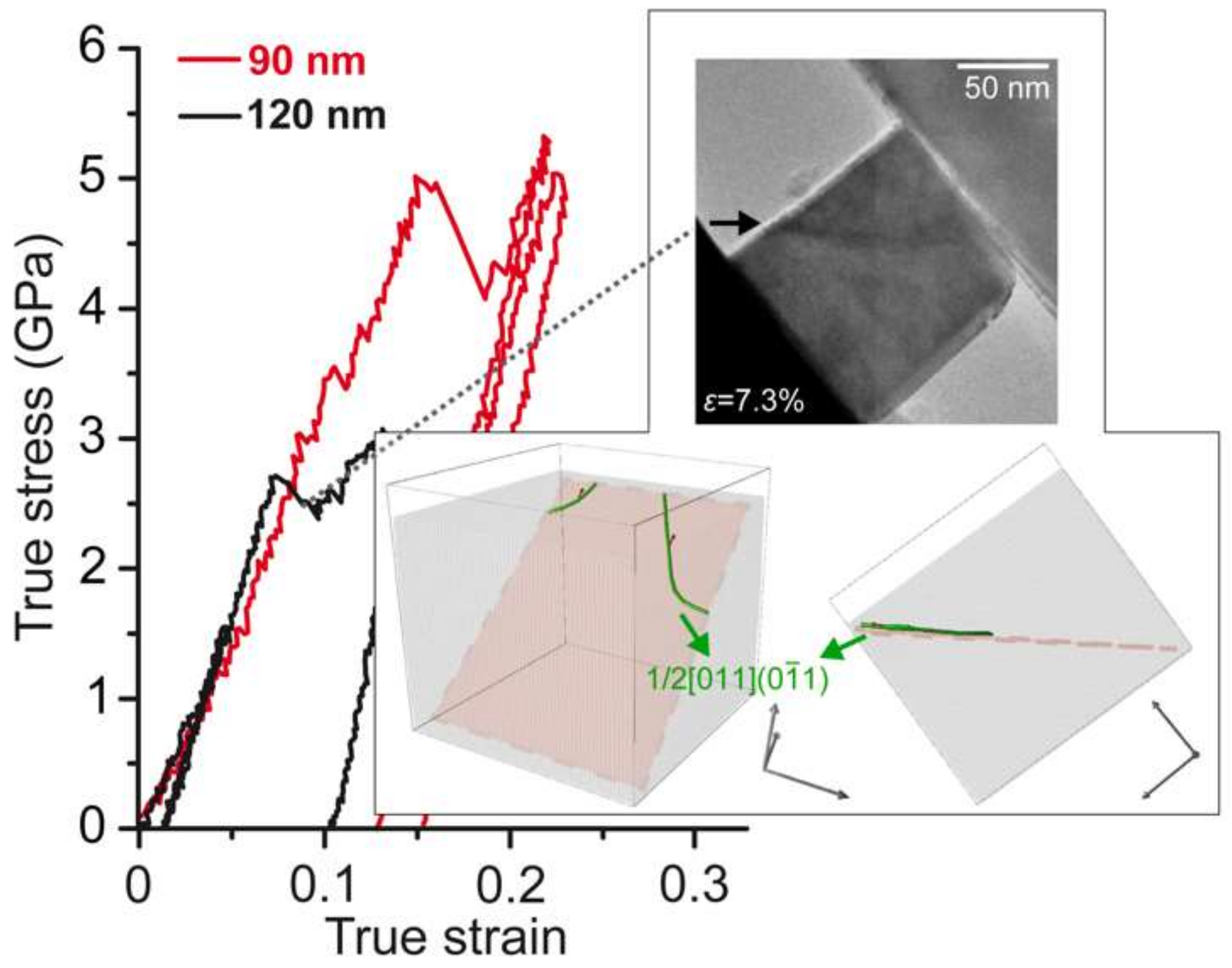
4.5.3. Dislocation Nucleation in Small MgO Volumes
5. High-Pressure Plasticity in MgO
5.1. Methods for HP Experiments and Simulations
5.1.1. Experimental Devices
5.1.2. Data Collection
5.1.3. Data Analysis and Polycrystalline Simulation Methods
5.1.4. Effect of Pressure on Rheological Laws
5.2. High-Pressure Plasticity of MgO and Iron Bearing (Mg,Fe)O
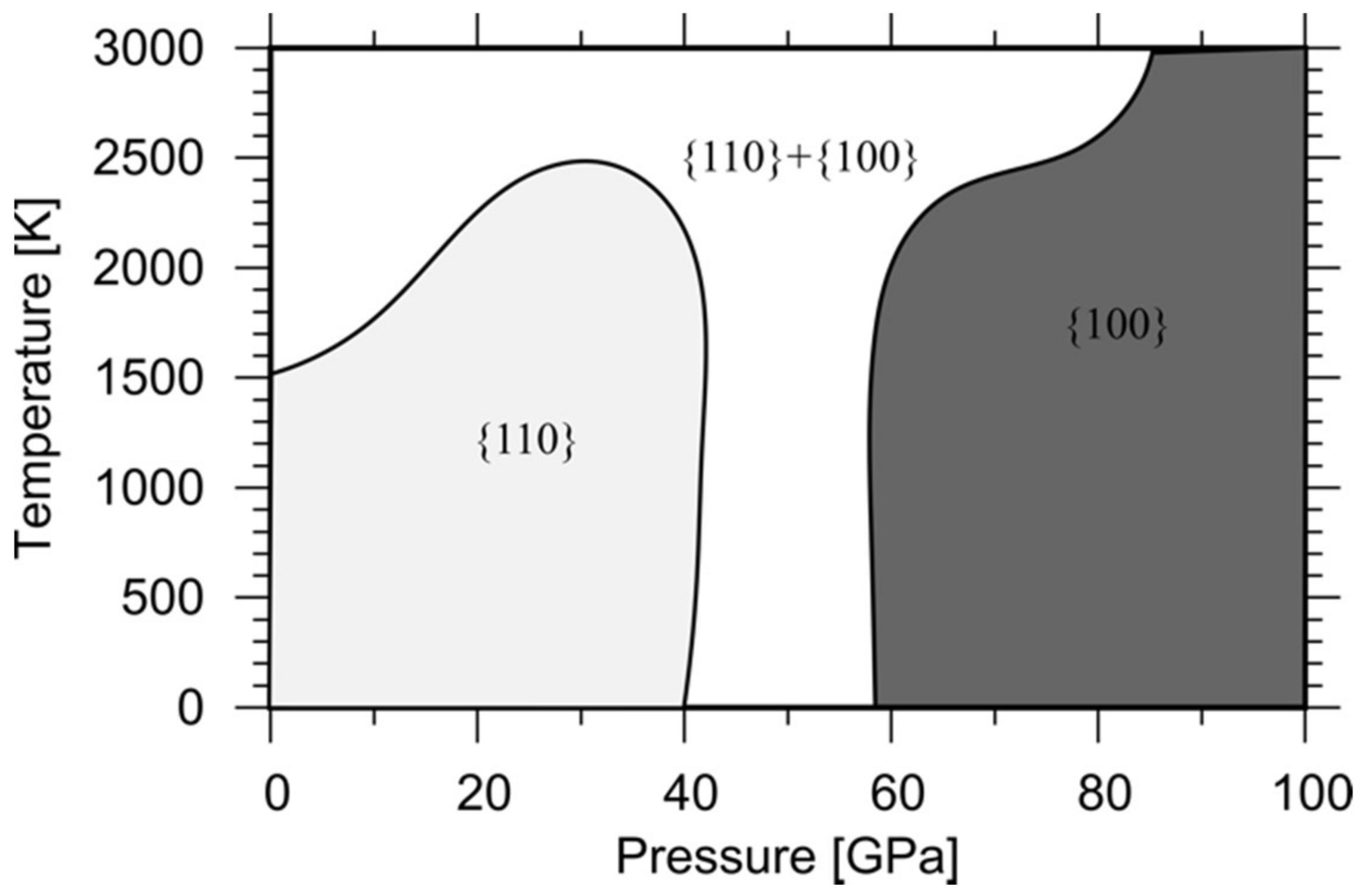
5.2.1. Effect of P and T on MgO and (Mg,Fe)O Deformation Textures
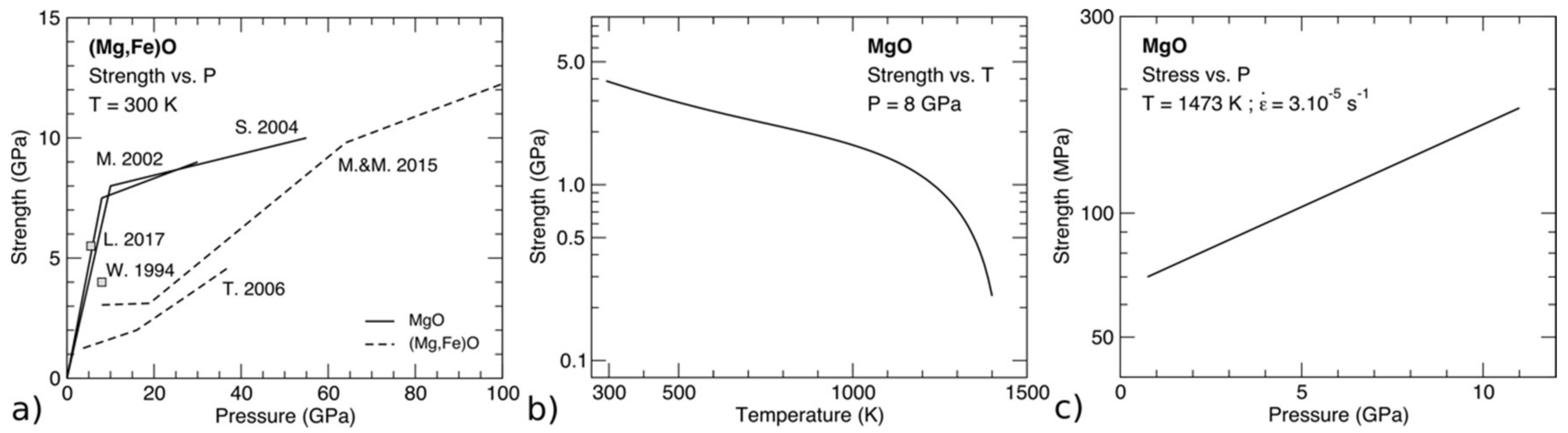
5.2.2. Effect of P, T, and Fe on the Mechanical Properties of Polycrystalline MgO and (Mgx,Fe1−x)O
5.2.3. Experimental Identification of Individual Deformation Mechanisms
6. Conclusions and Prospects
- Standard compression tests helped to describe dislocation-based plasticity processes in MgO in the 1950s. Plasticity is controlled by screw dislocations gliding in soft ½<110>{110} and hard ½<110>{100} slip systems and MgO is referred as a material with high lattice friction.
- Atomistic simulations based on dislocation core calculation confirmed the key role of screw dislocation for MgO plasticity. Multi-scale modeling approaches allow describing MgO plasticity on a wide range of temperatures and pressures, up to the polycrystal.
- The development of existing and novel experimental techniques since the 1990s, especially with the development of tests at the micro- and nano-scales, allows investigating elementary deformation processes providing a better description of dislocation mechanisms.
- Experiments and modeling show that MgO is sensitive to pressure increases. Dislocation cores and elementary deformation processes evolve under pressure inducing a softening of the ½<110>{100} mode when compared to ½<110>{110}. This change has significant consequences on macroscopic mechanical properties such as polycrystalline textures.
Author Contributions
Funding
Conflict of interest
References
- Johnston, W.G.; Gilman, J.J. Dislocation Velocities, Dislocation Densities, and Plastic Flow in Lithium Fluoride Crystals. J. Appl. Phys. 1959, 30, 1–16. [Google Scholar] [CrossRef]
- Stokes, R.J. Microstructure and Mechanical Properties of Ceramics; Accession Number: AD0407614; Defense Technical Information Center: Fort Belvoir, VA, USA, 1963.
- Haasen, P.; Barthel, C.; Suzuki, T. Choice of slip system and Peierls stresses in the NaCl structure. In Dislocations in solids; Suzuki, H., Ninomiya, T., Sumino, K., Takeuchi, S., Eds.; University of Tokyo Press: Tokyo, Japan, 1985; pp. 455–462. [Google Scholar]
- Takeuchi, S.; Koizumi, H.; Suzuki, T. Peierls stress and kink pair energy in NaCl type crystals. Mater. Sci. Eng. A 2009, 521, 90–93. [Google Scholar] [CrossRef]
- Hulse, C.; Copley, S.; Pask, J. Effect of crystal orientation on plastic deformation of magnesium oxide. J. Am. Ceram. Soc. 1963, 46, 317–323. [Google Scholar] [CrossRef]
- Groves, G.W.; Kelly, A. Independent slip systems in crystals. Philos. Mag. A 1963, 8, 877–887. [Google Scholar] [CrossRef]
- Day, R.; Stokes, R. Mechanical behavior of Magnesium Oxide at high temperatures. J. Am. Ceram. Soc. 1964, 47, 493–503. [Google Scholar] [CrossRef]
- Copley, S.; Pask, J. Plastic deformation of MgO single crystals up to 1600 C. J. Am. Ceram. Soc. 1965, 48, 139–146. [Google Scholar] [CrossRef]
- Washburn, J.; Groves, G.; Kelly, A.; Williamson, G. Electron microscope observations of deformed magnesium oxide. Philos. Mag. A 1960, 5, 991–999. [Google Scholar] [CrossRef]
- Clauer, A.; Wilcox, B. High temperature tensile creep of magnesium oxide single crystals. J. Am. Ceram. Soc. 1976, 59, 89–96. [Google Scholar] [CrossRef]
- Mariani, E.; Mecklenburgh, J.; Wheeler, J.; Prior, D.J.; Heidelbach, F. Microstructure evolution and recrystallization during creep of MgO single crystals. Acta Mater. 2009, 57, 1886–1898. [Google Scholar] [CrossRef]
- Messerschmidt, U.; Appel, F. Dislocation motion and formation of dislocation structures during in situ deformation in a high voltage electron microscope. Mater. Sci. Eng. A 1989, 113, 409–414. [Google Scholar] [CrossRef]
- Tromas, C.; Girard, J.; Woirgard, J. Study by atomic force microscopy of elementary deformation mechanisms involved in low load indentations in MgO crystals. Phil. Mag. A 2000, 80, 2325–2335. [Google Scholar] [CrossRef]
- Hulse, C.; Pask, J. Mechanical Properties of Magnesia Single Crystals Compression. J. Am. Ceram. Soc. 1960, 43, 373–378. [Google Scholar] [CrossRef]
- Appel, F.; Wielke, B. Low temperature deformation of impure MgO single crystals. Mater. Sci. Eng. 1985, 73, 97–103. [Google Scholar] [CrossRef]
- Singh, R.; Coble, R. Dynamic dislocation behavior in “pure” magnesium oxide single crystals. J. Appl. Phys. 1974, 45, 981–989. [Google Scholar] [CrossRef]
- Woo, C.H.; Puls, M.P. The Peierls mechanism in MgO. Phil. Mag. A J. Theor. Expe. Appl. Phys. 1977, 35, 1641–1652. [Google Scholar] [CrossRef]
- May, J.; Kronberg, M. Temperature Dependence of Plastic Yield Stress of Single Crystals of Magnesium Oxide. J. Am. Ceram. Soc. 1960, 43, 525–530. [Google Scholar] [CrossRef]
- Sinha, M.; Lloyd, D.; Tangri, K. Dislocation dynamics and thermally-activated deformation of MgO single crystals. Philos. Mag. A 1973, 28, 1341–1352. [Google Scholar] [CrossRef]
- Srinivasan, M.; Stoebe, T. Temperature dependence of yielding and work-hardening rates in magnesium oxide single crystals. J. Mat. Sci. 1974, 9, 121–128. [Google Scholar] [CrossRef]
- Sato, F.; Sumino, K. The yield strength and dynamic behaviour of dislocations in MgO crystals at high temperatures. J. Mat. Sci. 1980, 15, 1625–1634. [Google Scholar] [CrossRef]
- Barthel, C. Plastiche Anisotropie von Bleisulfid und Magnesiumoxid. Diploma Thesis, University of Gottingen, Göttingen, Germany, 1984. [Google Scholar]
- Amodeo, J.; Carrez, P.; Devincre, B.; Cordier, P. Multiscale modelling of MgO plasticity. Acta Mater. 2011, 59, 2291–2301. [Google Scholar] [CrossRef]
- Appel, F.; Bethge, H.; Messerschmidt, U. Dislocation motion and multiplication at the deformation of MgO single crystals in the high voltage electron microscope. Phys. Status Solidi A 1977, 42, 61–71. [Google Scholar] [CrossRef]
- Foitzik, A.; Skrotzki, W.; Haasen, P. Correlation between microstructure, dislocation dissociation and plastic anisotropy in ionic crystals. Mater. Sci. Eng. A 1989, 113, 399–407. [Google Scholar] [CrossRef]
- Messerschmidt, U. Dislocation Dynamics during Plastic Deformation; Springer Series in Materials Science: New York, NY, USA, 2010; Volume 129, pp. 1–509. [Google Scholar]
- Singh, R.; Coble, R. Dynamic dislocation behavior in iron-doped magnesium oxide crystals. J. Appl. Phys. 1974, 45, 990–995. [Google Scholar] [CrossRef]
- Dorn, J.; Rajnak, S. Nucleation of kink pairs and the Peierls mechanism of plastic deformation. Trans. Metall. Soc. AIME 1964, 230, 1052–1064. [Google Scholar]
- Guyot, P.; Dorn, J. A critical review of the Peierls mechanism. Can. J. Phys. 1967, 45, 983–1016. [Google Scholar] [CrossRef]
- Boudet, A.; Kubin, L.P. Exhaustion mechanisms in the Preyield domain of niobium single crystals at low temperatures. J. Phys. 1975, 36, 823–833. [Google Scholar] [CrossRef]
- Groves, G.; Fine, M. Solid Solution and Precipitation Hardening in Mg-Fe-O Alloys. J. Appl. Phys. 1964, 35, 3587–3593. [Google Scholar] [CrossRef]
- Srinivasan, M.; Stoebe, T. Effect of Impurities on the Mechanical Behavior of MgO Single Crystals. J. Appl. Phys. 1970, 41, 3726–3730. [Google Scholar] [CrossRef]
- Gorum, A.; Luhman, W.; Pask, J. Effect of Impurities and Heat-Treatment on Ductility of MgO. J. Am. Ceram. Soc. 1960, 43, 241–245. [Google Scholar] [CrossRef]
- Davidge, R. The distribution of iron impurity in single-crystal magnesium oxide and some effects on mechanical properties. J. Mater. Sci. 1967, 2, 339–346. [Google Scholar] [CrossRef]
- Messerschmidt, U.; Appel, F. Characterization of precipitation hardening mechanisms by investigating dislocation dynamics in the HVEM. Czechoslov. J. Phys. 1985, 35, 217–220. [Google Scholar] [CrossRef]
- Appel, F.; Messerschmidt, U. Dislocation Processes in MgO Single Crystals Observed by In-situ Deformation in the HVEM. Krist. Tech. 1979, 14, 1329. [Google Scholar] [CrossRef]
- Messerschmidt, U. Line tension model of the interaction between dislocations and extended obstacles to glide. Mater. Sci. Eng. A 1988, 100, 101–108. [Google Scholar] [CrossRef]
- Messerschmidt, U.; Appel, F.; Schmid, H. The radius of curvature of dislocation segments in MgO crystals stressed in the high-voltage electron microscope. Philos. Mag. 1985, 51, 781–796. [Google Scholar] [CrossRef]
- Kardashev, B.K.; Kustov, S.B.; Lebedev, A.B.; Berezhkova, G.V.; Perstnev, P.P.; Appel, F.; Messerschmidt, U. Acoustic and Electron Microscopy Study of the Dislocation Structure in MgO Crystals. Phys. Status Solidi A 1985, 91, 79–87. [Google Scholar] [CrossRef]
- Appel, F.; Bartsch, M.; Messerschmidt, U.; Nadgornyi, E.; Valkovskii, S. Dislocation motion and plasticity in MgO single crystals. Phys. Status Solidi A 1984, 83, 179–194. [Google Scholar] [CrossRef]
- Appel, F.; Berezhkova, G.V.; Messerschmidt, U.; Perstnev, P.P.; Rozhanskii, V.N. HVEM In-Situ Straining Experiments on MgO Specimens Predeformed at High Temperature. Cryst. Res. Technol. 1981, 16, 1309–1314. [Google Scholar] [CrossRef]
- Appel, F.; Messerschmidt, U.; Nadgornyi, E.M.; Zaitsev, S.I. The interaction between dislocations and point obstacles: A comparison of the interaction parameter distributions obtained from computer simulation and from In situ high voltage electron microscopy straining experiments. Mater. Sci. Eng. 1982, 52, 69–74. [Google Scholar] [CrossRef]
- Appel, F.; Bethge, H.; Messerschmidt, U. Distribution of point-obstacle distance during the motion of screw dislocations in MgO single crystals. Phys. Status Solidi A 1976, 38, 103–108. [Google Scholar] [CrossRef]
- Routbort, J.L. Work-Hardening and Creep of MgO. Acta Metall. 1979, 27, 649–661. [Google Scholar] [CrossRef]
- Amodeo, J.; Devincre, B.; Carrez, P.; Cordier, P. Dislocation reactions, plastic anisotropy and forest strengthening in MgO at high temperature. Mech. Mater. 2014, 71, 62–73. [Google Scholar] [CrossRef]
- Kear, B.; Taylor, A.; Pratt, P. Some dislocation interactions in simple ionic crystals. Philos. Mag. A 1959, 4, 665–680. [Google Scholar] [CrossRef]
- Ruano, O.A.; Wolfenstine, J.; Wadsworth, J.; Sherby, O.D. Harper-Dorn and power law creep in uranium dioxide. Acta Metallurgica et Materialia 1991, 39, 661–668. [Google Scholar] [CrossRef]
- Cummerow, R. High-Temperature Steady-State Creep Rate in Single-Crystal MgO. J. Appl. Phys. 1963, 34, 1724–1729. [Google Scholar] [CrossRef]
- Rothwell, W.S.; Neiman, A.S. Creep in Vacuum of MgO Single Crystals and the Electric Field Effect. J. Appl. Phys. 1965, 36, 2309–2316. [Google Scholar] [CrossRef]
- Hüther, W.; Reppich, B. Dislocation structure during creep of MgO single crystals. Philos. Mag. A 1973, 28, 363–371. [Google Scholar] [CrossRef]
- Ramesh, K.S.; Yasuda, E.; Kimura, S.; Urabe, K. High-temperature creep and dislocation structure of MgO single crystals at low stresses. J. Mater. Sci. 1986, 21, 4015–4018. [Google Scholar] [CrossRef]
- Ramesh, K.S.; Yasuda, E.; Kimura, S. Negative creep and recovery during high-temperature creep of MgO single crystals at low stresses. J. Mater. Sci. 1986, 21, 3147–3152. [Google Scholar] [CrossRef]
- Hensler, J.H.; Cullen, G.V. Stress, Temperature, and Strain Rate in Creep of Magnesium Oxide. J. Am. Ceram. Soc. 1968, 51, 557–559. [Google Scholar] [CrossRef]
- Langdon, T.G.; Pask, J.A. The mechanism of creep in polycrystalline magnesium oxide. Acta Metall. 1970, 18, 505–510. [Google Scholar] [CrossRef]
- Bilde-Sörensen, J.B. Dislocation Structures in Creep-Deformed Polycrystalline MgO. J. Am. Ceram. Soc. 1972, 55, 606–610. [Google Scholar] [CrossRef]
- Wolfenstine, J.; Kohlstedt, D.L. Creep of (Mg, Fe)O single crystals. J. Mater. Sci. 1988, 23, 3550–3557. [Google Scholar] [CrossRef]
- Stretton, I.; Heidelbach, F.; Mackwell, S.; Langenhorst, F. Dislocation creep of magnesiowüstite (Mg0.8Fe0.2). Earth Planet. Sci. Lett. 2001, 194, 229–240. [Google Scholar] [CrossRef]
- Weertman, J. Steady-state creep through dislocation climb. J. Appl. Phys. 1957, 28, 362–364. [Google Scholar] [CrossRef]
- Poirier, J.P. On the symmetrical role of cross-slip of screw dislocations and climb of edge dislocations as recovery processes controlling high-temperature creep. Revue de Physique Appliquée 1976, 11, 731–738. [Google Scholar] [CrossRef]
- Lewis, G.V.; Catlow, C.R.A. Potential models for ionic oxides. J. Phys. C Solid State Phys. 1985, 18, 1149–1161. [Google Scholar] [CrossRef]
- Sangster, M.J.L. Interionic potentials and force constant models for rocksalt structure crystals—II. J. Phys. Chem. Solids 1974, 35, 195–200. [Google Scholar] [CrossRef]
- Woodward, C. First-principles simulations of dislocation cores. Mat. Sci. Eng. A 2005, 400–401, 59–67. [Google Scholar] [CrossRef]
- Woo, C.H.; Puls, M.P. An improved method of calculating the lattice friction stress using an atomistic model. J. Phys. C Solid State Phys. 1976, 9, L27. [Google Scholar] [CrossRef]
- Puls, M.; Norgett, M. Atomistic calculation of the core structure and Peierls energy of an (a/2)[110] edge dislocation in MgO. J. Appl. Phys. 1976, 47, 466–477. [Google Scholar] [CrossRef]
- Woo, C.H.; Puls, M.P. Atomistic breathing shell model calculations of dislocation core configurations in ionic crystals. Philos. Mag. A 1977, 35, 727–756. [Google Scholar] [CrossRef]
- Watson, G.W.; Kelsey, E.T.; de Leeuw, N.H.; Harris, D.J.; Parker, S.C. Atomistic simulation of dislocations, surfaces and interfaces in MgO. Faraday Trans. 1996, 92, 433–438. [Google Scholar] [CrossRef]
- Lehto, N.; Öberg, S. Effects of Dislocation Interactions: Application to the Period-Doubled Core of the 90° Partial in Silicon. Phys. Rev. Lett. 1998, 80, 5568–5571. [Google Scholar] [CrossRef]
- Carrez, P.; Godet, J.; Cordier, P. Atomistic simulations of ½<110> screw dislocation core in magnesium oxide. Comput. Mater. Sci. 2015, 103, 250–255. [Google Scholar] [CrossRef]
- Christian, J.W.; Vítek, V. Dislocations and stacking faults. Rep. Prog. Phys. 1970, 33, 307–411. [Google Scholar] [CrossRef]
- Peierls, R. The size of a dislocation. Proc. Phys. Soc. 1940, 52, 34–37. [Google Scholar] [CrossRef]
- Nabarro, F. Dislocations in a simple cubic lattice. Proc. Phys. Soc. 1947, 59, 256–272. [Google Scholar] [CrossRef]
- Vítek, V. Intrinsic stacking faults in body-centred cubic crystals. Philos. Mag. A 1968, 18, 773–786. [Google Scholar] [CrossRef]
- Miranda, C.; Scandolo, S. Computational materials science meets geophysics: Dislocations and slip planes of MgO. Comput. Phys. Commun. 2005, 169, 24–27. [Google Scholar] [CrossRef]
- Carrez, P.; Ferré, D.; Cordier, P. Peierls-Nabarro modelling of dislocations in MgO from ambient pressure to 100 GPa. Model. Sim. Mater. Sci. Eng. 2009, 17, 035010. [Google Scholar] [CrossRef]
- Schoeck, G. The Peierls model: Progress and limitations. Mater. Sci. Eng. A 2005, 400, 7–17. [Google Scholar] [CrossRef]
- Denoual, C. Dynamic dislocation modeling by combining Peierls Nabarro and Galerkin methods. Phys. Rev. B 2004, 70, 024106. [Google Scholar] [CrossRef]
- Lu, G. The Peierls–Nabarro model of dislocations: a venerable theory and its current development. In Handbook of Materials Modeling; Springer: Dordrecht, The Netherlands, 2005; pp. 773–792. [Google Scholar]
- Joos, B.; Ren, Q.; Duesbery, M.S. Peierls-Nabarro model of dislocations in silicon with generalized stacking-fault restoring forces. Phys. Rev. B 1994, 50, 5890–5898. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; John Willey and Sons: Hoboken, NJ, USA, 1982. [Google Scholar]
- Caillard, D.; Martin, J.L. Thermally Activated Mechanisms in Crystal Plasticity; Elsevier: New York, NY, USA, 2003. [Google Scholar]
- Kamimura, Y.; Edagawa, K.; Takeuchi, S. Experimental evaluation of the Peierls stresses in a variety of crystals and their relation to the crystal structure. Acta Mater. 2013, 61, 294–309. [Google Scholar] [CrossRef]
- Vitek, V.; Yamaguchi, M. Core structure of nonscrew 1/2 (111) dislocations on (110) planes in bcc crystals. II. Peierls stress and the effect of an external shear stress on the cores. J. Phys. F Metal Phys. 1973, 3, 537. [Google Scholar] [CrossRef]
- Duesbery, M.; Vitek, V. Plastic anisotropy in bcc transition metals. Acta Mater. 1998, 46, 1481–1492. [Google Scholar] [CrossRef]
- Xu, W.; Moriarty, J.A. Accurate atomistic simulations of the Peierls barrier and kink-pair formation energy for 〈111〉 screw dislocations in bcc Mo. Comput. Mater. Sci. 1998, 9, 348–356. [Google Scholar] [CrossRef]
- Woodward, C.; Rao, S.I. Flexible Ab Initio Boundary Conditions: Simulating Isolated Dislocations in bcc Mo and Ta. Phys. Rev. Lett. 2002, 88, 216402. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Strachan, A.; Çağın, T.; Goddard, W.A. Atomistic simulations of kinks in 1/2a〈111〉screw dislocations in bcc tantalum. Phys. Rev. B Condens. Matter 2003, 68, 558. [Google Scholar] [CrossRef]
- Gröger, R.; Bailey, A.; Vitek, V. Multiscale modeling of plastic deformation of molybdenum and tungsten: I. Atomistic studies of the core structure and glide of 1/2<111> screw dislocations at 0 K. Acta Mater. 2008, 56, 5401–5411. [Google Scholar] [CrossRef]
- Rodney, D.; Proville, L. Stress-dependent Peierls potential: Influence on kink-pair activation. Phys. Rev. B 2009, 79, 1–9. [Google Scholar] [CrossRef]
- Proville, L.; Ventelon, L.; Rodney, D. Prediction of the kink-pair formation enthalpy on screw dislocations in α-iron by a line tension model parametrized on empirical potentials and first-principles calculations. Phys. Rev. B 2013, 87, 244–248. [Google Scholar] [CrossRef]
- Edagawa, K.; Koizumi, H.; Kamimura, Y.; Suzuki, T. Temperature dependence of the flow stress of III–V compounds. Philos. Mag. A 2000, 80, 2591–2608. [Google Scholar] [CrossRef]
- Pizzagalli, L.; Pedersen, A.; Arnaldsson, A.; Jonsson, H.; Beauchamp, P. Theoretical study of kinks on screw dislocation in silicon. Phys. Rev. B 2008, 77, 064106. [Google Scholar] [CrossRef]
- Pedersen, A.; Pizzagalli, L.; Jónsson, H. Finding mechanism of transitions in complex systems: Formation and migration of dislocation kinks in a silicon crystal. J. Phys. Condens. Matter 2009, 21, 084210. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, T.E.; Anderson, P.M.; Baskes, M.I.; Chen, S.P.; Hoagland, R.G.; Misra, A. Nucleation of kink pairs on partial dislocations: A new model for solution hardening and softening. Philos. Mag. A 2003, 83, 1329–1346. [Google Scholar] [CrossRef]
- Carrez, P.; Ferré, D.; Denoual, C.; Cordier, P. Modelling thermal activation of <110>{110} slip at low temperature in SrTiO3. Scr. Mater. 2010, 63, 434–437. [Google Scholar] [CrossRef]
- Castillo-Rodríguez, M.; Sigle, W. The kink-pair mechanism and low-temperature flow-stress behaviour of strontium titanate single crystals. Scr. Mater. 2011, 64, 241–244. [Google Scholar] [CrossRef]
- Celli, V.; Kabler, M.; Ninomiya, T.; Thomson, R. Theory of Dislocation Mobility in Semiconductors. Phys. Rev. 1963, 131, 58–72. [Google Scholar] [CrossRef]
- Seeger, A.; Schiller, P. Bildung und diffusion von kinken als grundprozess der versetzungsbewegung bei der messung der inneren reibung. Acta Metall. 1962, 10, 348–357. [Google Scholar] [CrossRef]
- Koizumi, H.; Kirchner, H.; Suzuki, T. Kink pair nucleation and critical shear stress. Acta Metallurgica et Materialia 1993, 41, 3483–3493. [Google Scholar] [CrossRef]
- Koizumi, H.; Kirchner, H.O.K.; Suzuki, T. Nucleation of trapezoidal kink pairs on a Peierls potential. Philos. Mag. A 1994, 69, 805–820. [Google Scholar] [CrossRef]
- Southgate, P.D.; Mendelson, K.S. Kilocycle-Range Dislocation Damping in Magnesium Oxide. J. Appl. Phys. 1966, 37, 206–215. [Google Scholar] [CrossRef]
- Joos, B.; Zhou, J. The Peierls-Nabarro model and the mobility of the dislocation line. Philos. Mag. A 2001, 81, 1329–1340. [Google Scholar] [CrossRef]
- Ventelon, L.; Willaime, F.; Leyronnas, P. Atomistic simulation of single kinks of screw dislocations in α-Fe. J. Nucl. Mater. 2009, 386–388, 26–29. [Google Scholar] [CrossRef]
- Proville, L.; Rodney, D.; Marinica, M.-C. Quantum effect on thermally activated glide of dislocations. Nat. Mater. 2012, 11, 845–849. [Google Scholar] [CrossRef] [PubMed]
- Fitzgerald, S.P. Kink pair production and dislocation motion. Sci. Rep. 2016, 6, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Nabarro, F. One-dimensional models of thermal activation under shear stress. Philos. Mag. A 2003, 83, 3047–3054. [Google Scholar] [CrossRef]
- Devincre, B.; Madec, R.; Monnet, G.; Queyreau, S.; Gatti, R.; Kubin, L. Modeling crystal plasticity with dislocation dynamics simulations: The “microMegas” code. In Mechanics of Nano-Objects; Presse des Mines: Paris, France, 2011; pp. 81–100. [Google Scholar]
- Arsenlis, A.; Cai, W.; Tang, M.; Rhee, M.; Oppelstrup, T.; Hommes, G.; Pierce, T.; Bulatov, V. Enabling strain hardening simulations with dislocation dynamics. Model. Sim. Mater. Sci. Eng. 2007, 15, 553–595. [Google Scholar] [CrossRef]
- Chang, H.-J.; Fivel, M.; Rodney, D.; Verdier, M. Multiscale modelling of indentation in FCC metals: From atomic to continuum. Comptes Rendus Physique 2010, 11, 285–292. [Google Scholar] [CrossRef]
- Queyreau, S.; Monnet, G.; Devincre, B. Orowan strengthening and forest hardening superposition examined by dislocation dynamics simulations. Acta Mater. 2010, 58, 5586–5595. [Google Scholar] [CrossRef]
- Mohles, V. Simulations of dislocation glide in overaged precipitation-hardened crystals. Philos. Mag. A 2001, 81, 971–990. [Google Scholar] [CrossRef]
- Monnet, G. Investigation of precipitation hardening by dislocation dynamics simulations. Philos. Mag. A 2006, 86, 5927–5941. [Google Scholar] [CrossRef]
- Shin, C.; Fivel, M.; Verdier, M.; Robertson, C. Dislocation dynamics simulations of fatigue of precipitation-hardened materials. Mater. Sci. Eng. A 2005, 400, 166–169. [Google Scholar] [CrossRef]
- Chang, H.-J.; Segurado, J.; Molina-Aldareguía, J.M.; Soler, R.; LLorca, J. A 3D dislocation dynamics analysis of the size effect on the strength of [1 1 1] LiF micropillars at 300K and 600K. Model. Sim. Mater. Sci. Eng. 2016, 24, 035009. [Google Scholar] [CrossRef]
- Cui, Y.; Po, G.; Ghoniem, N. Controlling Strain Bursts and Avalanches at the Nano- to Micrometer Scale. Phys. Rev. Lett. 2016, 117, 155502. [Google Scholar] [CrossRef] [PubMed]
- El-Awady, J.; Woodward, C.; Dimiduk, D.; Ghoniem, N. Effects of focused ion beam induced damage on the plasticity of micropillars. Phys. Rev. B 2009, 80, 104104. [Google Scholar] [CrossRef]
- Amodeo, R.J.; Ghoniem, N.M. Dislocation Dynamics. 1. A Proposed Methodology for Deformation Micromechanics. Phys. Rev. B Condens. Matter 1990, 41, 6958–6967. [Google Scholar] [CrossRef] [PubMed]
- Amodeo, R.J.; Ghoniem, N.M. Dislocation Dynamics. 2. Applications to the Formation of Persistent Slip Bands, Planar Arrays and Dislocation Cells. Phys. Rev. B Condens. Matter 1990, 41, 6968–6976. [Google Scholar] [CrossRef] [PubMed]
- Van der Giessen, E.; Needleman, A. Discrete dislocation plasticity: a simple planar model. Model. Sim. Mater. Sci. Eng. 1995, 3, 689–735. [Google Scholar] [CrossRef]
- Keralavarma, S.M.; Curtin, W.A. Strain hardening in 2D discrete dislocation dynamics simulations—A new “2.5D” algorithm. J. Mech. Phys. Solids 2016, 95, 132–146. [Google Scholar] [CrossRef]
- Wickham, L.; Schwarz, K.; Stölken, J. Rules for forest interactions between dislocations. Phys. Rev. Lett. 1999, 83, 4574–4577. [Google Scholar] [CrossRef]
- Madec, R.; Kubin, L.P. Dislocations interactions and symmetries in BCC crystals. In IUTAM Symposium on Mesoscopic Dynamics of Fracture Process and Materials Strength; Springer: Dordrecht, The Netherlands, 2004; pp. 69–79. [Google Scholar]
- Madec, R.; Devincre, B.; Kubin, L.P. On the nature of attractive dislocation crossed states. Comput. Mater. Sci. 2002, 23, 219–224. [Google Scholar] [CrossRef]
- Monnet, G.; Devincre, B.; Kubin, L.P. Dislocation study of prismatic slip systems and their interactions in hexagonal close packed metals: application to zirconium. Acta Mater. 2004, 52, 4317–4328. [Google Scholar] [CrossRef]
- Capolungo, L. Dislocation junction formation and strength in magnesium. Acta Mater. 2011, 59, 2909–2917. [Google Scholar] [CrossRef]
- Devincre, B. Dislocation dynamics simulations of slip systems interactions and forest strengthening in ice single crystal. Philos. Mag. A 2012, 93, 235–246. [Google Scholar] [CrossRef]
- Durinck, J.; Devincre, B.; Kubin, L.P.; Cordier, P. Modeling the plastic deformation of olivine by dislocation dynamics simulations. Am. Mineral. 2007, 92, 1346–1357. [Google Scholar] [CrossRef]
- Carrez, P.; Cordier, P.; Devincre, B.; Kubin, L.P. Dislocation reactions and junctions in MgO. Mater. Sci. Eng. A 2005, 400, 325–328. [Google Scholar] [CrossRef]
- Devincre, B.; Hoc, T.; Kubin, L.P. Collinear interactions of dislocations and slip systems. Mater. Sci. Eng. A 2005, 400, 182–185. [Google Scholar] [CrossRef]
- Madec, R.; Devincre, B.; Kubin, L.P.; Hoc, T.; Rodney, D. The role of collinear interaction in dislocation-induced hardening. Science 2003, 301, 1879–1882. [Google Scholar] [CrossRef] [PubMed]
- Cordier, P.; Amodeo, J.; Carrez, P. Modelling the rheology of MgO under Earth's mantle pressure, temperature and strain rates. Nature 2012, 481, 177–180. [Google Scholar] [CrossRef] [PubMed]
- Boioli, F.; Carrez, P.; Cordier, P.; Devincre, B.; Marquille, M. Modeling the creep properties of olivine by 2.5-dimensional dislocation dynamics simulations. Phys. Rev. B 2015, 92, 014115-1–014115-12. [Google Scholar] [CrossRef]
- Reali, R.; Boioli, F.; Gouriet, K.; Carrez, P.; Devincre, B.; Cordier, P. Modeling plasticity of MgO by 2.5D dislocation dynamics simulations. Mat. Sci. Eng. A 2017, 690, 52–61. [Google Scholar] [CrossRef]
- Soler, R.; Wheeler, J.M.; Chang, H.-J.; Segurado, J.; Michler, J.; LLorca, J.; Molina-Aldareguía, J.M. Understanding size effects on the strength of single crystals through high-temperature micropillar compression. Acta Mater. 2014, 81, 50–57. [Google Scholar] [CrossRef]
- Keralavarma, S.M.; Benzerga, A.A. High-temperature discrete dislocation plasticity. J. Mech. Phys. Solids 2015, 82, 1–22. [Google Scholar] [CrossRef]
- Yoo, H. Oxygen self-diffusion in single-crystal MgO: Secondary-ion mass spectrometric analysis with comparison of results from gas–solid and solid–solid exchange. Solid State Ion. 2002, 150, 207–221. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation; Mechanical Engineering Series; Springer: New York, NY, USA, 2004. [Google Scholar]
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Tromas, C.; Stinville, J.C.; Templier, C.; Villechaise, P. Hardness and elastic modulus gradients in plasma nitrided 316l polycrystalline stainless steel investigated by nanoindentation tomography. Acta Mater. 2012, 60, 1965–1973. [Google Scholar] [CrossRef]
- Woirgard, J.; Tromas, C.; Girard, J.C.; Audurier, V. Study of the mechanical properties of ceramic materials by the nanoindentation technique. J. Eur. Ceram. Soc. 1998, 18, 2297–2305. [Google Scholar] [CrossRef]
- Gilman, J.J.; Johnston, W.G. Dislocations in lithium fluoride crystals. Solid State Phys. 1961, 13, 147–222. [Google Scholar]
- Stokes, R.J.; Johnston, T.L.; Li, C.H. Effect of surface condition on the initiation of plastic flow in MgO. Trans. AIME 1959, 215, 437. [Google Scholar]
- Keh, A.S. Dislocations in indented magnesium oxide crystals. J. Appl. Phys. 1960, 31, 1538–1545. [Google Scholar] [CrossRef]
- Newey, C.; Davidge, R.W. Dislocations in Lithium Fluoride; Metallurgical Services: Betchworth, UK, 1965. [Google Scholar]
- Velednitskaya, M.A.; Rozhanskii, V.N.; Comolova, L.F.; Saparin, G.V.; Schreiber, J.; Brümmer, O. Investigation of the deformation mechanism of MgO crystals affected by concentrated load. Phys. Status Solidi A 1975, 32, 123–132. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Wu, C.C. Lattice Misorientation and Displaced Volume for Microhardness Indentations in MgO Crystals. J. Am. Ceram. Soc. 1978, 61, 102–106. [Google Scholar] [CrossRef]
- Chaudhri, M.M. The displacement of material and the formation of {1l0}90, cracks around spherical indentations in MgO crystals. Philos. Mag. A 1986, 53, L55–L63. [Google Scholar] [CrossRef]
- Keh, A.S. Cracks due to the piling-up of dislocations on two intersecting slip planes in MgO crystals. Acta Metall. 1959, 7, 694–696. [Google Scholar] [CrossRef]
- Hammond, B.L.; Armstrong, R.W. Recovered elastic and plastic strains at residual micro-indentations in an MgO crystal. Philos. Mag. Lett. 1988, 57, 41–47. [Google Scholar] [CrossRef]
- Gaillard, Y. Initiation de la Plasticité sous Nanoindentation dans MgO et LiF: Etude de L’organisation des Dislocations et des Contraintes Associées. PhD Thesis, Université de Poitiers, Poitiers, France, 2004. [Google Scholar]
- Tromas, C.; Girard, J.; Audurier, V.; Woirgard, J. Study of the low stress plasticity in single-crystal MgO by nanoindentation and atomic force microscopy. J. Mater. Sci. 1999, 34, 5337–5342. [Google Scholar] [CrossRef]
- Egberts, P.; Bennewitz, R. Atomic-scale nanoindentation: detection and identification of single glide events in three dimensions by force microscopy. Nanotechnology 2011, 22, 425703. [Google Scholar] [CrossRef] [PubMed]
- Filleter, T.; Maier, S.; Bennewitz, R. Atomic-scale yield and dislocation nucleation in KBr. Phys. Rev. B Condens. Matter Mater. Phys. 2006, 73, 155433. [Google Scholar] [CrossRef]
- Tromas, C.; Gaillard, Y.; Woirgard, J. Nucleation of dislocations during nanoindentation in MgO. Philos. Mag. A 2006, 86, 5595–5606. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Study of the dislocation structure involved in a nanoindentation test by atomic force microscopy and controlled chemical etching. Acta Mater. 2003, 51, 1059–1065. [Google Scholar] [CrossRef]
- Gilman, J.J.; Johnston, W.G.; Sears, G.W. Dislocation etch pit formation in lithium fluoride. J. Appl. Phys. 1958, 29, 747–754. [Google Scholar] [CrossRef]
- Shaw, M.; Brookes, C. Dislocations produced in magnesium oxide crystals due to contact pressures developed by softer cones. J. Mater. Sci. 1989, 24, 2727–2734. [Google Scholar] [CrossRef]
- Nix, W.D.; Gao, H. Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 1998, 46, 411–425. [Google Scholar] [CrossRef]
- Feng, G.; Nix, W.D. Indentation size effect in MgO. Scr. Mater. 2004, 51, 599–603. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, F.; Hwang, K.C.; Nix, W.D.; Pharr, G.M.; Feng, G. A model for size effect in nano-indentation. J. Mech. Phys. Sol. 2006, 54, 1668–1986. [Google Scholar]
- Sadrabadi, P.; Durst, K.; Göken, M. Study on the indentation size effect in CaF2: Dislocation structure and hardness. Acta Mater. 2009, 57, 1281–1289. [Google Scholar] [CrossRef]
- Ren, X.J.; Hooper, R.M.; Griffiths, C.; Henshall, J.L. Indentation-size effects in single-crystal MgO. Philos. Mag. A 2002, 82, 2113–2120. [Google Scholar] [CrossRef]
- Richter, A.; Wolf, B.; Nowicki, M.; Usov, I.O.; Valdez, J.A.; Sickafus, K. Multi-cycling nanoindentation in MgO single crystal before and after ion irradiation. J. Appl. Phys. D Appl. Phys. 2006, 39, 3342–3349. [Google Scholar] [CrossRef]
- Bahr, D.F.; Kramer, D.E.; Gerberich, W.W. Non-linear deformation mechanisms during nanoindentation. Acta Mater. 1998, 46, 3605–3617. [Google Scholar] [CrossRef]
- Chiu, Y.L.; Ngan, A.H.W. Time-dependent characteristics of incipient plasticity in nanoindentation of a Ni3Al single crystal. Acta Mater. 2002, 50, 1599–1611. [Google Scholar] [CrossRef]
- Gerberich, W.W.; Nelson, J.C.; Lilleodden, E.T.; Anderson, P.; Wyrobek, J.T. Indentation induced dislocation nucleation: The initial yield point. Acta Mater. 1996, 44, 3585–3598. [Google Scholar] [CrossRef]
- Page, T.F.; Oliver, W.C.; McHargue, C.J. Deformation behavior of ceramic crystals subjected to very low load (nano)indentations. J. Mater. Res. 1992, 7, 450–473. [Google Scholar] [CrossRef]
- Schuh, C.A.; Mason, J.K.; Lund, A.C. Quantitative insight into dislocation nucleation from high-temperature nanoindentation experiments. Nat. Mater. 2005, 4, 617–621. [Google Scholar] [CrossRef] [PubMed]
- Tymiak, N.I.; Daugela, A.; Wyrobek, T.J.; Warren, O.L. Acoustic emission monitoring of the earliest stages of contact-induced plasticity in sapphire. Acta Mater. 2004, 52, 553–563. [Google Scholar] [CrossRef]
- Kelchner, C.L.; Plimpton, S.J.; Hamilton, J.C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 1998, 58, 11085–11088. [Google Scholar] [CrossRef]
- Van Vliet, K.; Li, J.; Zhu, T.; Yip, S.; Suresh, S. Quantifying the early stages of plasticity through nanoscale experiments and simulations. Phys. Rev. B 2003, 67, 104105. [Google Scholar] [CrossRef]
- Lilleodden, E.T.; Zimmerman, J.A.; Foiles, S.M.; Nix, W.D. Atomistic simulations of elastic deformation and dislocation nucleation during nanoindentation. J. Mech. Phys. Solids 2003, 51, 901–920. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Pop-in phenomenon in MgO and LiF: Observation of dislocation structures. Philos. Mag. Lett. 2003, 83, 553–561. [Google Scholar] [CrossRef]
- Hertz, H. Über die Berührung fester elastischer Körper. J. Reine Angew. Mat. 1882, 92, 156–171. [Google Scholar]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Hanson, M.T.; Johnson, T. Elastic field for spherical Hertzian contact of isotropic bodies revisited. Some alternative expressions. J. Tribol. 1993, 115, 327–332. [Google Scholar] [CrossRef]
- Booth, A.S.; Ellis, M.; Roberts, S.G.; Hirsch, P.B. Dislocation-controlled stable crack growth in Mo and MgO. Mater. Sci. Eng. A 1993, 164, 270–274. [Google Scholar] [CrossRef]
- Burns, S.J.; Webb, W.W. Fracture surface energies and dislocation processes during dynamical cleavage of LiF. I. Theory. J. Appl. Phys. 1970, 41, 2078–2085. [Google Scholar] [CrossRef]
- Burns, S.J.; Webb, W.W. Fracture surface energies and dislocation processes during dynamical cleavage of LiF. II. Experiments. J. Appl. Phys. 1970, 41, 2086–2095. [Google Scholar] [CrossRef]
- Gilman, J.J. Nucleation of dislocation loops by cracks in crystals. J. Metall. 1957, 9, 449–454. [Google Scholar] [CrossRef]
- Gilman, J.J.; Knudsen, C.; Walsh, W.P. Cleavage cracks and dislocations in LiF crystals. J. Appl. Phys. 1958, 29, 601–607. [Google Scholar] [CrossRef]
- Robins, J.L.; Rhodin, T.N.; Gerlach, R.L. Dislocation structures in cleaved magnesium oxide. J. Appl. Phys. 1966, 37, 3893–3903. [Google Scholar] [CrossRef]
- Montagne, A.; Audurier, V.; Tromas, C. Influence of pre-existing dislocations on the pop-in phenomenon during nanoindentation in MgO. Acta Mater. 2013, 61, 4778–4786. [Google Scholar] [CrossRef]
- Gaillard, Y.; Tromas, C.; Woirgard, J. Quantitative analysis of dislocation pile-ups nucleated during nanoindentation in MgO. Acta Mater. 2006, 54, 1409–1417. [Google Scholar] [CrossRef]
- Jouiad, M.; Pettinari, F.; Coujou, A.; Clément, N. Evaluation of friction stresses in the γ phase of a nickel-base superalloy “In situ” deformation experiments. Mater. Sci. Eng. A 1997, 234–236, 1041–1044. [Google Scholar] [CrossRef]
- Bridgman, P.W.; Simon, I. Effects of Very High Pressures on Glass. J. Appl. Phys. 1953, 24, 405–413. [Google Scholar] [CrossRef]
- Paterson, M.S.; Wong, T. Experimental Rock Deformation-the Brittle Field; Springer: Berlin, Germany, 2005. [Google Scholar]
- Zambaldi, C.; Zehnder, C.; Raabe, D. Orientation dependent deformation by slip and twinning in magnesium during single crystal indentation. Acta Mater. 2015, 91, 267–288. [Google Scholar] [CrossRef]
- Lloyd, S.J.; Molina-Aldareguia, J.M.; Clegg, W.J. Deformation under nanoindents in sapphire, spinel and magnesia examined using transmission electron microscopy. Philos. Mag. A 2002, 82, 1963–1969. [Google Scholar] [CrossRef]
- McLaughlin, K.K. TEM Diffraction Analysis of the Deformation Underneath Low Load Indentations; University of Cambridge: Cambridge, UK, 2007. [Google Scholar]
- Howie, P.R.; Korte, S.; Clegg, W.J. Fracture modes in micropillar compression of brittle crystals. J. Mater. Res. 2011, 27, 141–151. [Google Scholar] [CrossRef]
- Uchic, M.D.; Dimiduk, D.M.; Florando, J.N.; Nix, W.D. Sample Dimensions Influence Strength and Crystal Plasticity. Science 2004, 305, 986–989. [Google Scholar] [CrossRef] [PubMed]
- Uchic, M.D.; Shade, P.A.; Dimiduk, D.M. Plasticity of Micrometer-Scale Single Crystals in Compression. Annu. Rev. Mater. Res. 2009, 39, 361–386. [Google Scholar] [CrossRef]
- Östlund, F.; Howie, P.R.; Ghisleni, R.; Korte, S.; Leifer, K.; Clegg, W.J.; Michler, J. Ductile–brittle transition in micropillar compression of GaAs at room temperature. Philos. Mag. A 2011, 91, 1190–1199. [Google Scholar] [CrossRef]
- Kendall, K. Impossibility of comminuting small particles by compression. Nature 1978, 272, 710–711. [Google Scholar] [CrossRef]
- Östlund, F.; Rzepiejewska-Malyska, K.; Leifer, K.; Hale, L.M.; Tang, Y.; Ballarini, R.; Gerberich, W.W.; Michler, J. Brittle-to-Ductile Transition in Uniaxial Compression of Silicon Pillars at Room Temperature. Adv. Funct. Mater. 2009, 19, 2439–2444. [Google Scholar] [CrossRef]
- Cottrell, P.A.H. Lectures. 1961. Available online: https://link.springer.com/article/10.1007%2FBF00812985 (accessed on 29 March 2018).
- Korte, S.; Barnard, J.S.; Stearn, R.J.; Clegg, W.J. Deformation of silicon–insights from microcompression testing at 25–500 C. Int. J. Plasticity 2011, 27, 1853–1866. [Google Scholar] [CrossRef]
- Korte, S.; Clegg, W.J. Micropillar compression of ceramics at elevated temperatures. Scr. Mater. 2009, 60, 807–810. [Google Scholar] [CrossRef]
- Uchic, M.; Shade, P.; Dimiduk, D. Micro-compression testing of fcc metals: A selected overview of experiments and simulations. J. Miner. Metals Mater. Soc. 2009, 61, 36–41. [Google Scholar] [CrossRef]
- Korte-Kerzel, S. Microcompression of brittle and anisotropic crystals: Recent advances and current challenges in studying plasticity in hard materials. MRS Commun. 2017, 7, 109–120. [Google Scholar] [CrossRef]
- Korte, S.; Clegg, W. Discussion of the dependence of the effect of size on the yield stress in hard materials studied by microcompression of MgO. Philos. Mag. A 2011, 91, 1150–1162. [Google Scholar] [CrossRef]
- Zou, Y. Materials selection in micro- or nano-mechanical design: Towards new Ashby plots for small-sized materials. Mat. Sci. Eng. A 2017, 680, 421–425. [Google Scholar] [CrossRef]
- Gibson, J.S.K.L.; Rezaei, S.; Rueß, H.; Hans, M.; Music, D.; Wulfinghoff, S.; Schneider, J.M.; Reese, S.; Korte-Kerzel, S. From quantum to continuum mechanics: Studying the fracture toughness of transition metal nitrides and oxynitrides. Mater. Res. Lett. 2017, 6, 142–151. [Google Scholar] [CrossRef]
- Armstrong, D.E.J.; Hardie, C.D.; Gibson, J.S.K.L.; Bushby, A.J.; Edmondson, P.D.; Roberts, S.G. Small-scale characterisation of irradiated nuclear materials: Part II nanoindentation and micro-cantilever testing of ion irradiated nuclear materials. J. Nucl. Mater. 2015, 462, 374–381. [Google Scholar] [CrossRef]
- Korte-Kerzel, S.; Schnabel, V.; Clegg, W.J.; Heggen, M. Room temperature plasticity in m-Al13Co4 studied by microcompression and high resolution scanning transmission electron microscopy. Scr. Mater. 2018, 146, 327–330. [Google Scholar] [CrossRef]
- Korte, S.; Ritter, M.; Jiao, C.; Midgley, P.; Clegg, W. Three-dimensional electron backscattered diffraction analysis of deformation in MgO micropillars. Acta Mater. 2011, 59, 7241–7254. [Google Scholar] [CrossRef]
- Zou, Y.; Spolenak, R. Size-dependent plasticity in micron- and submicron-sized ionic crystals. Philos. Mag. Lett. 2013, 93, 431–438. [Google Scholar] [CrossRef]
- Kraft, O.; Gruber, P.A.; Mönig, R. Plasticity in confined dimensions. Annu. Rev. Mater. Res. 2010, 40, 293–317. [Google Scholar] [CrossRef]
- Kiener, D.; Minor, A.M. Source Truncation and Exhaustion: Insights from Quantitative in situ TEM Tensile Testing. Nano Lett. 2011, 11, 3816–3820. [Google Scholar] [CrossRef] [PubMed]
- Kaufmann, D.; Mönig, R.; Volkert, C.A.; Kraft, O. Size dependent mechanical behaviour of tantalum. Int. J. Plasticity 2011, 27, 470–478. [Google Scholar] [CrossRef]
- Michler, J.; Wasmer, K.; Meier, S.; Östlund, F.; Leifer, K. Plastic deformation of gallium arsenide micropillars under uniaxial compression at room temperature. Appl. Phys. Lett. 2007, 90, 043123. [Google Scholar] [CrossRef]
- Parthasarathy, T.A.; Rao, S.I.; Dimiduk, D.M.; Uchic, M.D.; Trinkle, D.R. Contribution to size effect of yield strength from the stochastics of dislocation source lengths in finite samples. Scr. Mater. 2007, 56, 313–316. [Google Scholar] [CrossRef]
- Schneider, A.S.; Frick, C.P.; Arzt, E.; Clegg, W.J.; Korte, S. Influence of test temperature on the size effect in molybdenum small-scale compression pillars. Philos. Mag. Lett. 2013, 93, 331–338. [Google Scholar] [CrossRef]
- Torrents Abad, O.; Wheeler, J.M.; Michler, J.; Schneider, A.S.; Arzt, E. Temperature-dependent size effects on the strength of Ta and W micropillars. Acta Mater. 2016, 103, 483–494. [Google Scholar] [CrossRef]
- Soler, R.; Molina-Aldareguia, J.M.; Segurado, J.; LLorca, J.; Merino, R.I.; Orera, V.M. Micropillar compression of LiF [112] single crystals: Effect of size, ion irradiation and misorientation. Int. J. Plasticity 2012, 36, 50–63. [Google Scholar] [CrossRef]
- Kiener, D.; Motz, C.; Dehm, G. Micro-compression testing: A critical discussion of experimental constraints. Mater. Sci. Eng. A 2009, 505, 79–87. [Google Scholar] [CrossRef]
- Zou, Y.; Spolenak, R. Size-dependent plasticity in KCl and LiF single crystals: influence of orientation, temperature, pre-straining and doping. Philos. Mag. A 2015, 1–19. [Google Scholar] [CrossRef]
- Gibson, J.S.K.L.; Schröders, S.; Zehnder, C.; Korte-Kerzel, S. On extracting mechanical properties from nanoindentation at temperatures up to 1000°C. Extreme Mech. Lett. 2017, 17, 43–49. [Google Scholar] [CrossRef]
- Kang, W.; Merrill, M.; Wheeler, J.M. In situ thermomechanical testing methods for micro/nano-scale materials. Nano 2017, 9, 2666–2688. [Google Scholar] [CrossRef] [PubMed]
- Durst, K.; Maier, V. Dynamic nanoindentation testing for studying thermally activated processes from single to nanocrystalline metals. Curr. Opin. Solid State Mater. Sci. 2015, 19, 340–353. [Google Scholar] [CrossRef]
- Maier, V.; Durst, K.; Mueller, J.; Backes, B.; Höppel, H.W.; Göken, M. Nanoindentation strain-rate jump tests for determining the local strain-rate sensitivity in nanocrystalline Ni and ultrafine-grained Al. J. Mater. Res. 2011, 26, 1421–1430. [Google Scholar] [CrossRef]
- Moser, B.; Wasmer, K.; Barbieri, L.; Michler, J. Strength and fracture of Si micropillars: A new scanning electron microscopy-based micro-compression test. J. Mater. Res. 2007, 22, 1004–1011. [Google Scholar] [CrossRef]
- Bei, H.; Shim, S.; George, E.P.; Miller, M.K.; Herbert, E.G.; Pharr, G.M. Compressive strengths of molybdenum alloy micro-pillars prepared using a new technique. Scr. Mater. 2007, 57, 397–400. [Google Scholar] [CrossRef]
- Issa, I.; Amodeo, J.; Réthoré, J.; Joly-Pottuz, L.; Esnouf, C.; Morthomas, J.; Perez, M.; Chevalier, J.; Masenelli-Varlot, K. In situ investigation of MgO nanocube deformation at room temperature. Acta Mater. 2015, 86, 295–304. [Google Scholar] [CrossRef]
- Maaß, R.; Meza, L.; Gan, B.; Tin, S.; Greer, J.R. Ultrahigh strength of dislocation-free Ni3Al nanocubes. Small 2012, 8, 1869–1875. [Google Scholar] [CrossRef] [PubMed]
- Amodeo, J.; Lizoul, K. Mechanical properties and dislocation nucleation in nanocrystals with blunt edges. Mater. Des. 2017, 135, 223–231. [Google Scholar] [CrossRef]
- Nishiyama, N.; Katsura, T.; Funakoshi, K.-I.; Kubo, A.; Kubo, T.; Tange, Y.; Sueda, Y.-I.; Yokoshi, S. Determination of the phase boundary between the B1 and B2 phases in NaCl by in situx-ray diffraction. Phys. Rev. B Condens. Matter 2003, 68, 319. [Google Scholar] [CrossRef]
- Mao, H.K.; Wu, Y.; Hemley, R.J.; Chen, L.C.; Shu, J.F.; Finger, L.W.; Cox, D.E. High-pressure phase transition and equation of state of CsI. Phys. Rev. Lett. 1990, 64, 1749–1752. [Google Scholar] [CrossRef] [PubMed]
- Williams, Q.; Jeanloz, R. Measurements of CsI band-gap closure to 93 GPa. Phys. Rev. Lett. 1986, 56, 163–164. [Google Scholar] [CrossRef] [PubMed]
- Jeanloz, R. Physical Chemistry at Ultrahigh Pressures and Temperatures. Ann. Rev. Phys. Chem. 1989, 40, 237–259. [Google Scholar] [CrossRef]
- McWilliams, R.S.; Spaulding, D.K.; Eggert, J.H.; Celliers, P.M.; Hicks, D.G.; Smith, R.F.; Collins, G.W.; Jeanloz, R. Phase Transformations and Metallization of Magnesium Oxide at High Pressure and Temperature. Science 2012, 338, 1330–1333. [Google Scholar] [CrossRef] [PubMed]
- Coppari, F.; Smith, R.F.; Eggert, J.H.; Wang, J.; Rygg, J.R.; Lazicki, A.; Hawreliak, J.A.; Collins, G.W.; Duffy, T.S. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures. Nat. Geosci. 2013, 6, 926–929. [Google Scholar] [CrossRef]
- Karki, B.; Stixrude, L.; Clark, S.; Warren, M.; Ackland, G.; Crain, J. Structure and elasticity of MgO at high pressure. Am. Mineral. 1997, 82, 51–60. [Google Scholar] [CrossRef]
- Karato, S.-I. Some remarks on the origin of seismic anisotropy in the D” layer. Earth Planets Space 1998, 50, 1019–1028. [Google Scholar] [CrossRef]
- Wang, Y.; Durham, W.; Getting, I.; Weidner, D. The deformation-DIA: A new apparatus for high temperature triaxial deformation to pressures up to 15 GPa. Rev. Sci. Instrum. 2003, 74, 3002–3011. [Google Scholar] [CrossRef]
- Yamazaki, D.; Karato, S. High-pressure rotational deformation apparatus to 15 GPa. Rev. Sci. Instrum. 2001, 72, 4207–4211. [Google Scholar] [CrossRef]
- Hunt, S.A.; Weidner, D.J.; McCormack, R.J.; Whitaker, M.L.; Bailey, E.; Li, L.; Vaughan, M.T.; Dobson, D.P. Deformation T-Cup: A new multi-anvil apparatus for controlled strain-rate deformation experiments at pressures above 18 GPa. Rev. Sci. Instrum. 2014, 85, 085103. [Google Scholar] [CrossRef] [PubMed]
- Kawazoe, T.; Ohuchi, T.; Nishihara, Y.; Nishiyama, N.; Fujino, K.; Irifune, T. Seismic anisotropy in the mantle transition zone induced by shear deformation of wadsleyite. Phys. Earth Planet. Int. 2013, 216, 91–98. [Google Scholar] [CrossRef]
- Girard, J.; Amulele, G.; Farla, R.; Mohiuddin, A.; Karato, S.I. Shear deformation of bridgmanite and magnesiowustite aggregates at lower mantle conditions. Science 2016, 351, 144–147. [Google Scholar] [CrossRef] [PubMed]
- Raterron, P.; Merkel, S.; Holyoke, C.W. Axial temperature gradient and stress measurements in the deformation-DIA cell using alumina pistons. Rev. Sci. Instrum. 2013, 84, 043906. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Nishihara, Y.; Karato, S.-I. Development of a rotational Drickamer apparatus for large-strain deformation experiments at deep Earth conditions. In Advances in High-Pressure Technology for Geophysical Applications; Chen, J., Wang, Y., Duffy, T.S., Shen, G., Dobrzhinetskaya, L.F., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 167–182. [Google Scholar]
- Dubrovinskaia, N.; Dubrovinsky, L.; Solopova, N.A.; Abakumov, A.; Turner, S.; Hanfland, M.; Bykova, E.; Bykov, M.; Prescher, C.; Prakapenka, V.B.; et al. Terapascal static pressure generation with ultrahigh yield strength nanodiamond. Sci. Adv. 2016, 2, e1600341. [Google Scholar] [CrossRef] [PubMed]
- Tateno, S.; Hirose, K.; Ohishi, Y.; Tatsumi, Y. The Structure of Iron in Earth’s Inner Core. Science 2010, 330, 359–361. [Google Scholar] [CrossRef] [PubMed]
- Hemley, R.J.; Mao, H.K.; Shen, G.; Badro, J.; Gillet, P.; Hanfland, M.; Häusermann, D. X-ray imaging of stress and strain of diamond, iron, and tungsten at megabar pressures. Science 1997, 276, 1242–1245. [Google Scholar] [CrossRef]
- Liermann, H.P.; Merkel, S.; Miyagi, L.; Wenk, H.R.; Shen, G.; Cynn, H.; Evans, W.J. New Experimental Method for In Situ Determination of Material Textures at Simultaneous High-Pressure and Temperature by Means of Radial Diffraction in the Diamond Anvil Cell. Rev. Sci. Instrum. 2009, 80, 104501. [Google Scholar] [CrossRef] [PubMed]
- Hirose, K.; Nagaya, Y.; Merkel, S.; Ohishi, Y. Deformation of MnGeO3 post-perovskite at lower mantle pressure and temperature. Geophys. Res. Lett. 2010, 37, L20302. [Google Scholar] [CrossRef]
- Merkel, S. X-ray diffraction evaluation of stress in high pressure deformation experiments. J. Phys. Condens. Matter 2006, 18, S949–S962. [Google Scholar] [CrossRef] [PubMed]
- Meade, C.; Jeanloz, R. Yield strength of MgO to 40 GPa. J. Geophys. Res. 1988, 93, 3261–3269. [Google Scholar] [CrossRef]
- Vaughan, M.; Chen, J.; Li, L.; Weidner, D.; Li, B. Use of X-ray Imaging Techniques at High Pressure and Temperature for Strain Measurements; Manghnani, M.H., Nellis, W.J., Nicol, M.F., Eds.; Universities Press (India) Limited: Hyderabad, India, 2000; pp. 1097–1098. [Google Scholar]
- Merkel, S.; Yagi, T. X-ray transparent gasket for diamond anvil cell high pressure experiments. Rev. Sci. Instrum. 2005, 76, 046109. [Google Scholar] [CrossRef]
- Noyan, I.C.; Cohen, J.B. Residual Stress: Measurements by Diffraction and Interpretation; Springer-Verlag: New York, NY, USA, 1987. [Google Scholar]
- Merkel, S.; Wenk, H.R.; Shu, J.; Shen, G.; Gillet, P.; Mao, H.K.; Hemley, R.J. Deformation of polycrystalline MgO at pressures of the lower mantle. J. Geophys. Res. 2002, 107, 2271. [Google Scholar] [CrossRef]
- Lin, F.; Hilairet, N.; Raterron, P.; Addad, A.; Immoor, J.; Marquardt, H.; Tomé, C.N.; Miyagi, L.; Merkel, S. Elasto-viscoplastic self consistent modeling of the ambient temperature plastic behavior of periclase deformed up to 5.4 GPa. J. Appl. Phys. 2017, 122, 205902. [Google Scholar] [CrossRef]
- Singh, A.K.; Balasingh, C.; Mao, H.K.; Hemley, R.J.; Shu, J. Analysis of lattice strains measured under non-hydrostatic pressure. J. Appl. Phys. 1998, 83, 7567–7575. [Google Scholar] [CrossRef]
- Li, L. X-ray strain analysis at high pressure: Effect of plastic deformation in MgO. J. Appl. Phys. 2004, 95, 8357–8365. [Google Scholar] [CrossRef]
- Merkel, S.; Tomé, C.N.; Wenk, H.R. A modeling analysis of the influence of plasticity on high pressure deformation of hcp-Co. Phys. Rev. B 2009, 79, 064110. [Google Scholar] [CrossRef]
- Amodeo, J.; Dancette, S.; Delannay, L. Atomistically-informed crystal plasticity in MgO polycrystals under pressure. Int. J. Plasticity 2016, 82, 177–191. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.D.; Bieler, T.R.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Cordier, P. Dislocations and slip systems of mantle minerals. In Pastic Deformation of Minerals and Rocks; Karato, S., Wenk, H.R., Eds.; Reviews in Mineralogy and Geochemistry; Mineralogical Society of America: Chantilly, VA, USA, 2002; Volume 51, pp. 137–179. [Google Scholar]
- Mussi, A.; Cordier, P.; Demouchy, S.; Hue, B. Hardening mechanisms in olivine single crystal deformed at 1090 °C: an electron tomography study. Philos. Mag. 2017, 97, 3172–3185. [Google Scholar] [CrossRef]
- Amodeo, J.; Carrez, P.; Cordier, P. Modelling the effect of pressure on the critical shear stress of MgO single crystals. Philos. Mag. A 2012, 92, 1523–1541. [Google Scholar] [CrossRef]
- Girard, J.; Chen, J.; Raterron, P. Deformation of periclase single crystals at high pressure and temperature: Quantification of the effect of pressure on slip-system activities. J. Appl. Phys. 2012, 111, 112607. [Google Scholar] [CrossRef]
- Weidner, D.J.; Li, L.; Davis, M.; Chen, J. Effect of plasticity on elastic modulus measurements. Geophys. Res. Lett. 2004, 31, L06621. [Google Scholar] [CrossRef]
- Yamazaki, D.; Karato, S. Fabric development in (Mg, Fe) O during large strain, shear deformation: implications for seismic anisotropy in Earth's lower mantle. Phys. Earth Planet. Inter. 2002, 131, 251–267. [Google Scholar] [CrossRef]
- Tommaseo, C.E.; Devine, J.; Merkel, S.; Speziale, S.; Wenk, H.R. Texture development and elastic stresses in magnesiowustite at high pressure. Phys. Chem. Miner. 2006, 33, 84–97. [Google Scholar] [CrossRef]
- Badro, J.; Fiquet, G.; Guyot, F.; Rueff, J.-P.; Struzhkin, V.V.; Vankó, G.; Monaco, G. Iron partitioning in Earth's mantle: toward a deep lower mantle discontinuity. Science 2003, 300, 789–791. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.F.; Wenk, H.R.; Voltolini, M.; Speziale, S.; Shu, J.; Duffy, T.S. Deformation of lower-mantle ferropericlase (Mg,Fe)O across the electronic spin transition. Phys. Chem. Min. 2009, 36, 585–592. [Google Scholar] [CrossRef]
- Long, M.D.; Xiao, X.; Jiang, Z.; Evansa, B.; Karato, S. Lattice preferred orientation in deformed polycrystalline (Mg,Fe)O and implications for seismic anisotropy in D''. Phys. Earth Planet. Inter. 2006, 156, 75–88. [Google Scholar] [CrossRef]
- Heidelbach, F.; Stretton, I.; Langenhorst, F.; Mackwell, S. Fabric evolution during high shear strain deformation of magnesiowüstite (Mg0.8Fe0.2O). J. Geophys. Res. 2003, 108, 2154. [Google Scholar] [CrossRef]
- Immoor, J.; Marquardt, H.; Miyagi, L.; Lin, F.; Speziale, S.; Merkel, S.; Buchen, J.; Kurnosov, A.; Liermann, H.P. Evidence for {100}<011> slip in ferropericlase in Earth's lower mantle from high-pressure/high-temperature experiments. Earth. Planet. Sci. Lett. 2018, 489, 251–257. [Google Scholar] [CrossRef]
- Weaver, C.W.; Paterson, M.S. Deformation of cube-oriented MgO crystals under pressure. J. Am. Ceram. Soc. 1969, 52, 293–302. [Google Scholar] [CrossRef]
- Paterson, M.; Weaver, C. Deformation of polycrystalline MgO under pressure. J. Am. Ceram. Soc. 1970, 53, 463–471. [Google Scholar] [CrossRef]
- Mei, S.; Kohlstedt, D.L.; Durham, W.B.; Wang, L. Experimental investigation of the creep behavior of MgO at high pressures. Phys. Earth Planet. Inter. 2008, 170, 170–175. [Google Scholar] [CrossRef]
- Weidner, D.J.; Wang, Y.B.; Vaughan, M.T. Yield Strength at High-Pressure and Temperature. Geophys. Res. Lett. 1994, 21, 753–756. [Google Scholar] [CrossRef]
- Uchida, T.; Funamori, N.; Ohtani, T.; Yagi, T. Differential Stress of MgO and Mg2SiO4 under Uniaxial Stress Field: Variation with Pressure, Temperature, and Phase Transition; Trzeciatowski, W.A., Ed.; World Scientific Publishing: Singapore, 1996; pp. 183–185. [Google Scholar]
- Uchida, T.; Wang, Y.; Rivers, M.L.; Sutton, S.R. Yield strength and strain hardening of MgO up to 8 GPa measured in the deformation-DIA with monochromatic X-ray diffraction. Earth. Planet. Sci. Lett. 2004, 226, 117–126. [Google Scholar] [CrossRef]
- Weidner, D.J.; Li, L. Measurement of stress using synchrotron X-rays. J. Phys. Condens. Matter 2006, 18, S1061–S1067. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Liermann, H.P.; Saxena, S.K. Strength of magnesium oxide under high pressure: Evidence for the grain-size dependence. Solid State Commun. 2004, 132, 795–798. [Google Scholar] [CrossRef]
- Marquardt, H.; Miyagi, L. Slab stagnation in the shallow lower mantle linked to an increase in mantle viscosity. Nat. Geosci. 2015, 8, 311–314. [Google Scholar] [CrossRef]
- Kinsland, G.; Bassett, W. Strength of MgO and NaCl polycrystals to confining pressures of 250 kbar at 25 C. J. Appl. Phys. 1977, 48, 978–985. [Google Scholar] [CrossRef]
- Duffy, T.; Hemley, R.; Mao, H. Equation of state and shear strength at multimegabar pressures: Magnesium oxide to 227 GPa. Phys. Rev. Lett. 1995, 74, 1371–1374. [Google Scholar] [CrossRef] [PubMed]
- Reynard, B.; Caracas, R.; Cardon, H.; Montagnac, G.; Merkel, S. High-pressure yield strength of rocksalt structures using quartz Raman piezometry. C. R. Geosci. in press. [CrossRef]
- Li, L.; Weidner, D.J. In situ analysis of texture development from sinusoidal stress at high pressure and temperature. Rev. Sci. Instrum. 2015, 86, 125106. [Google Scholar] [CrossRef] [PubMed]
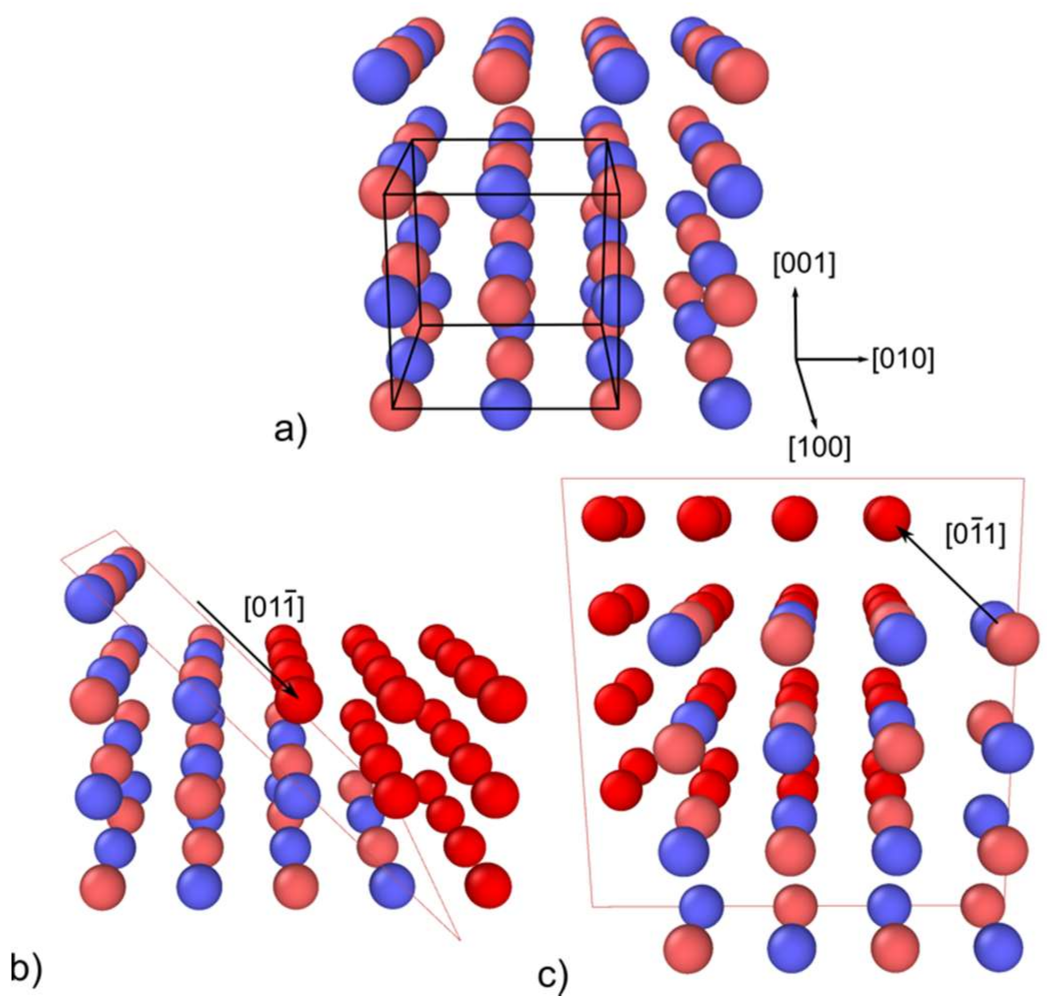

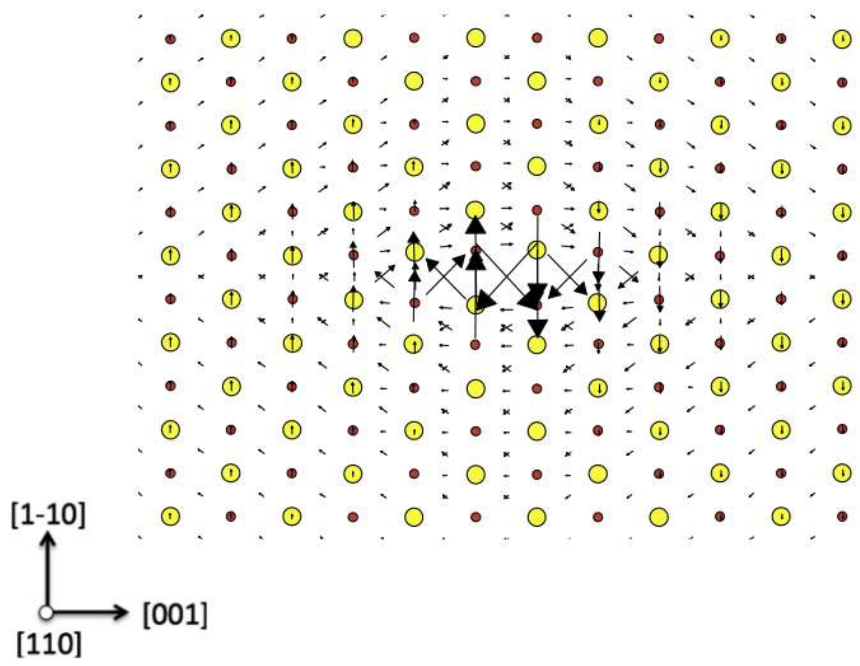
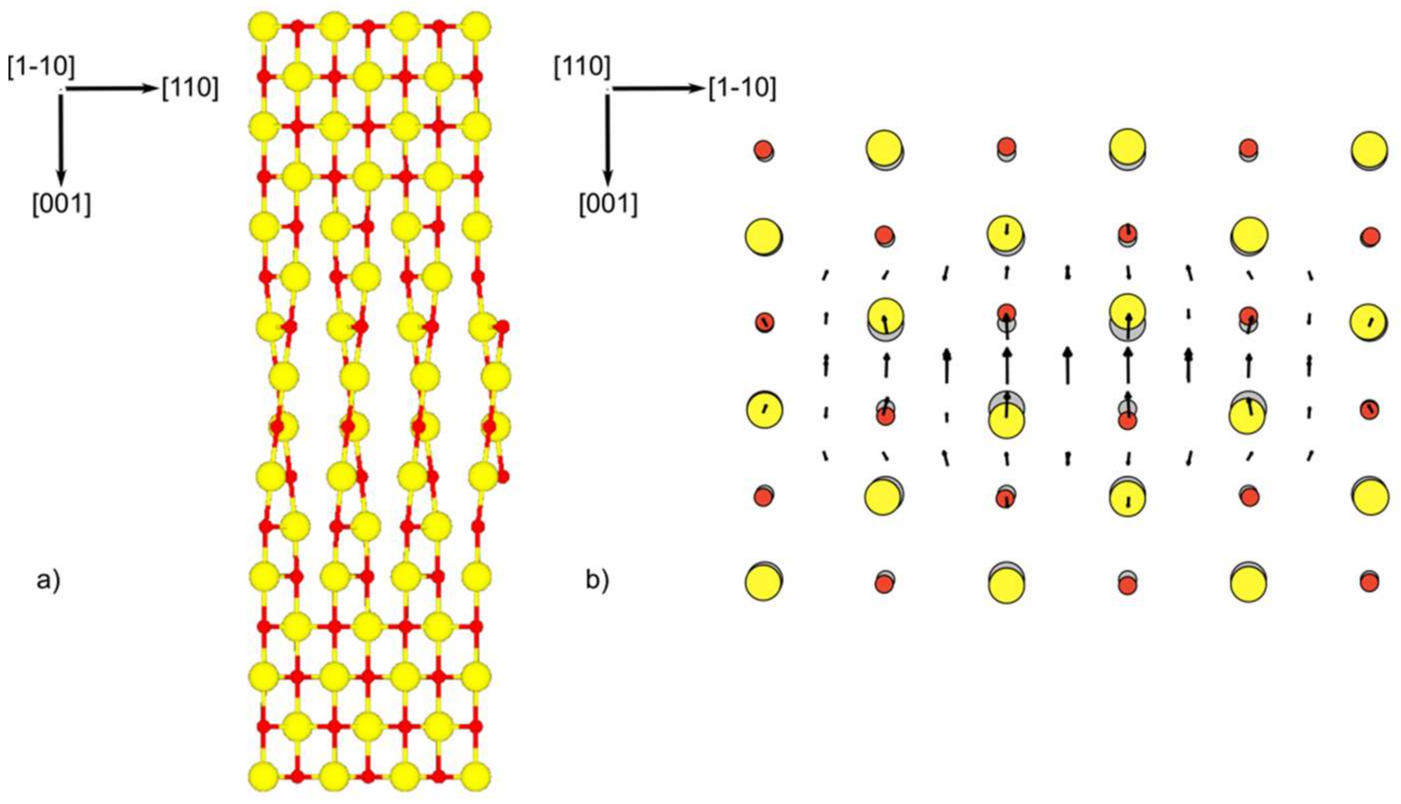
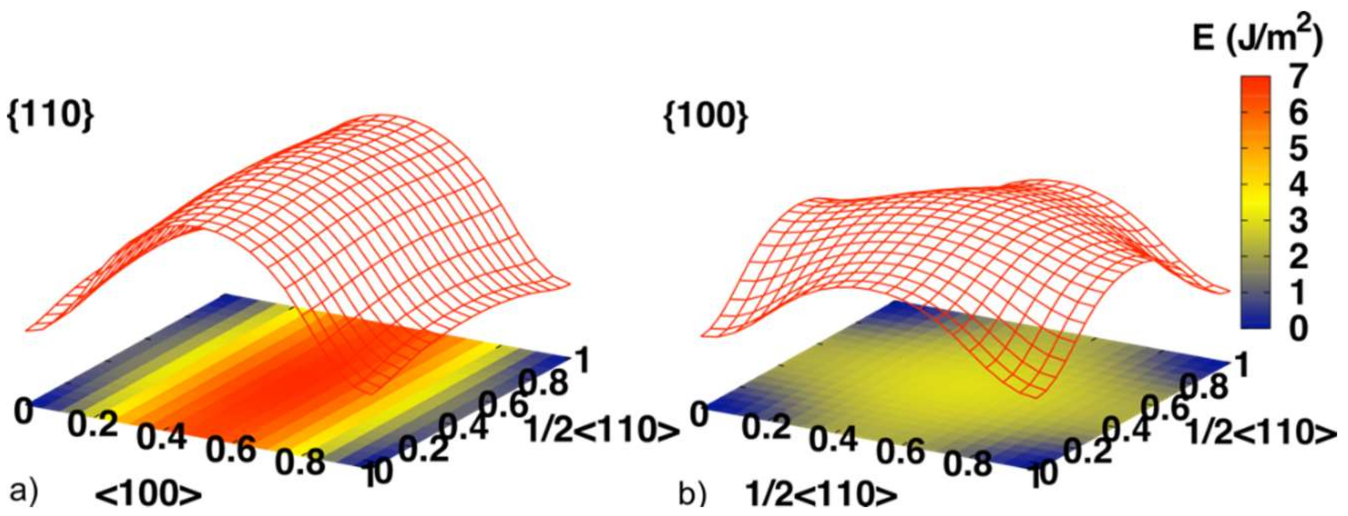
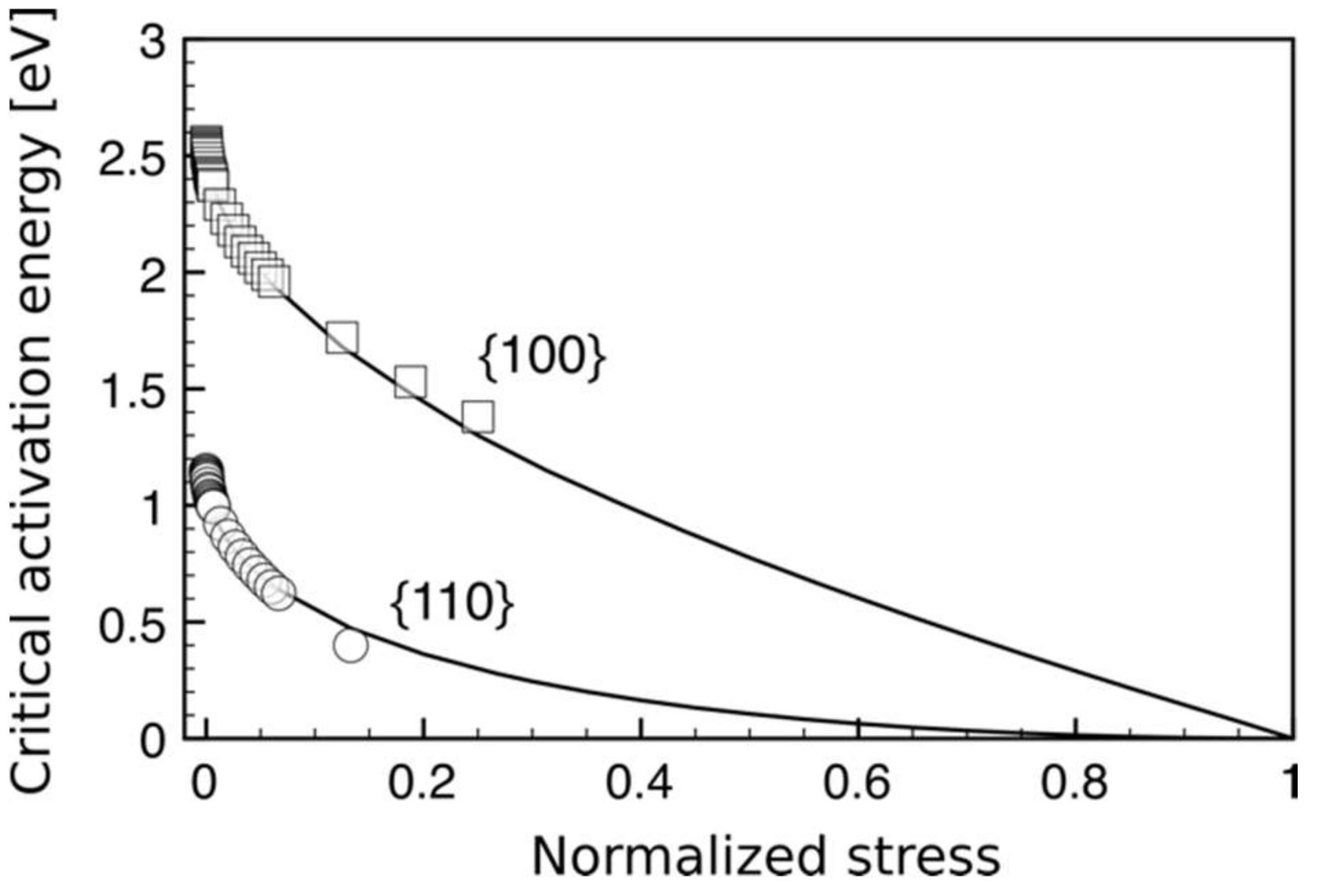
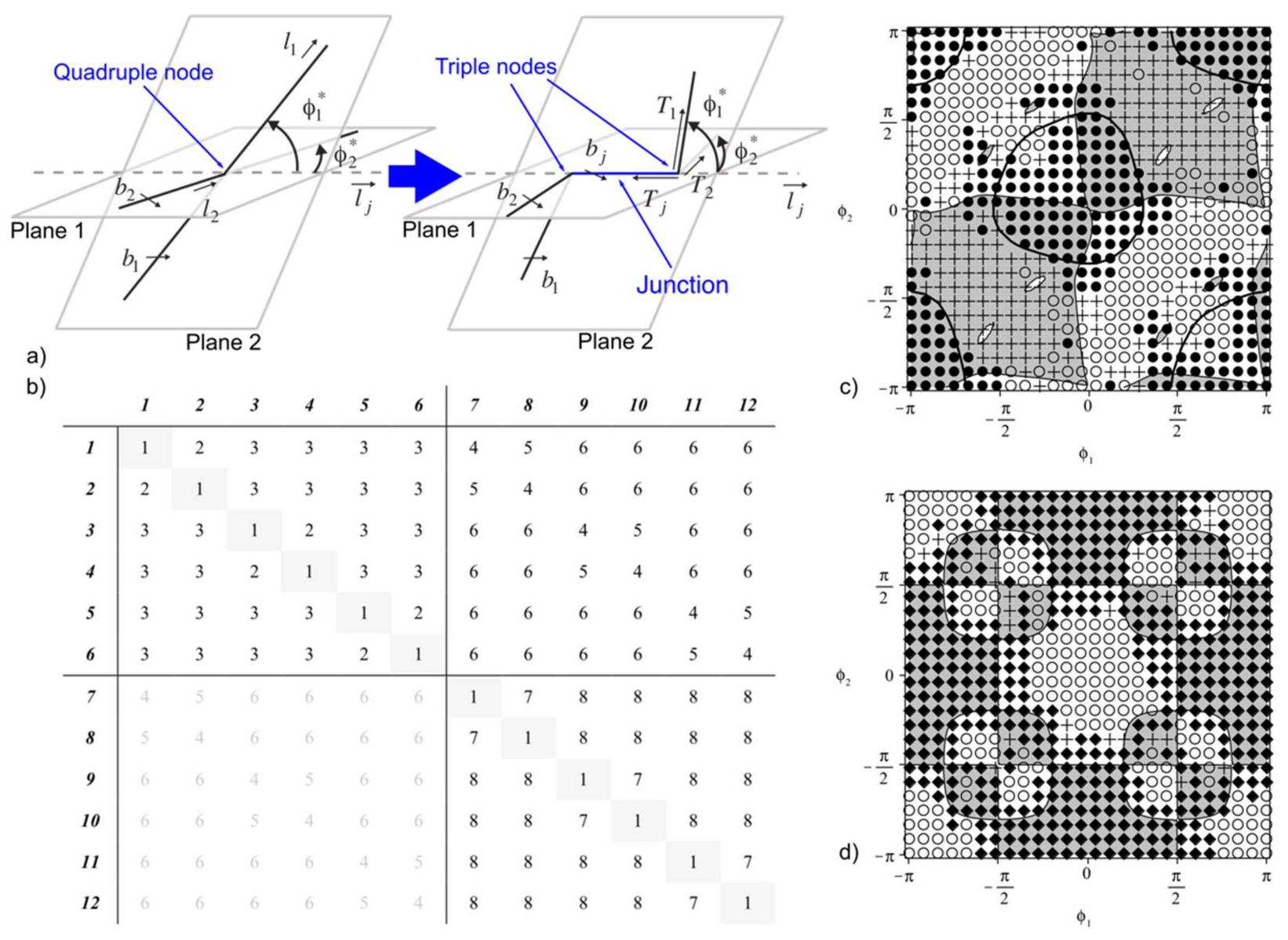
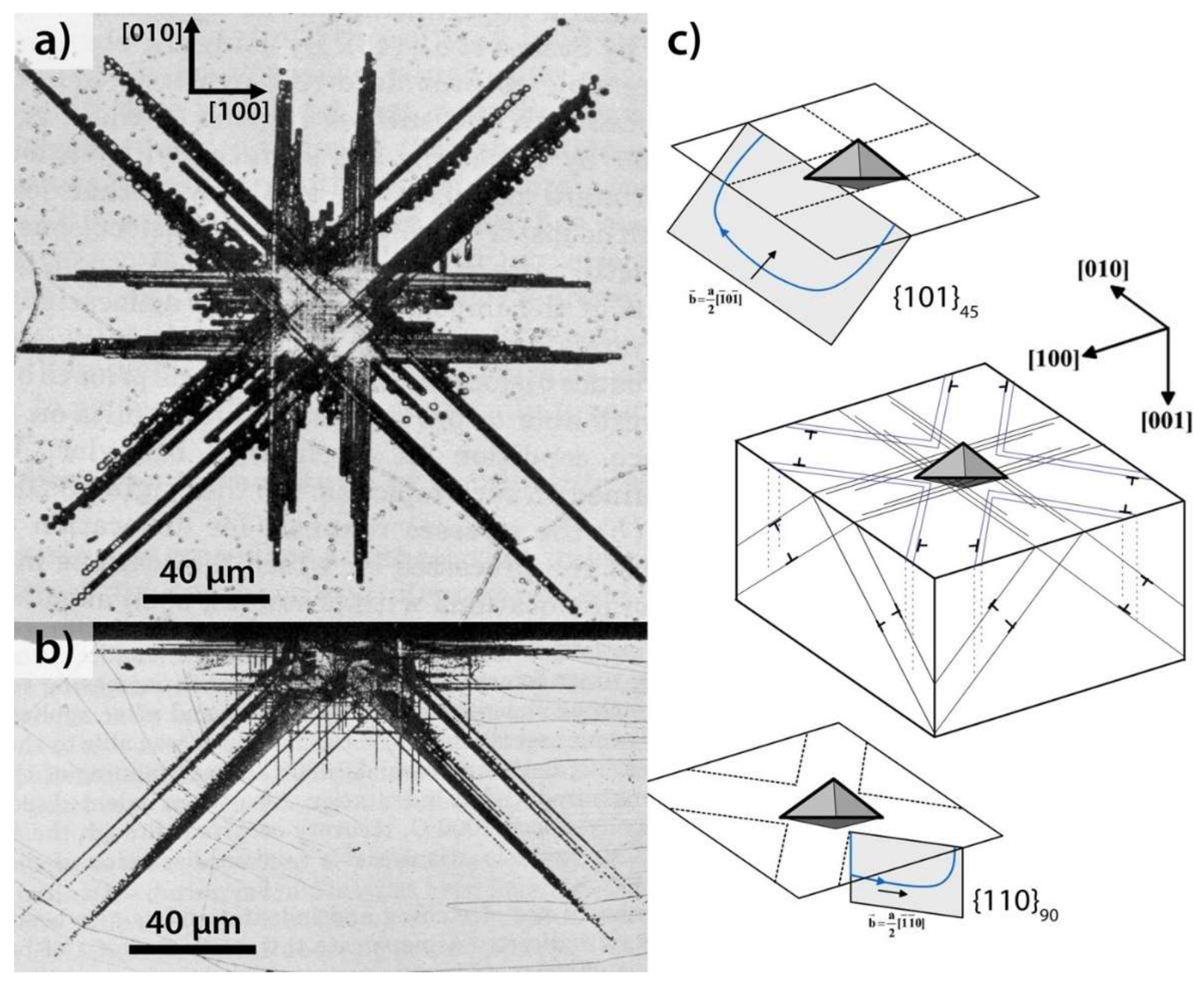
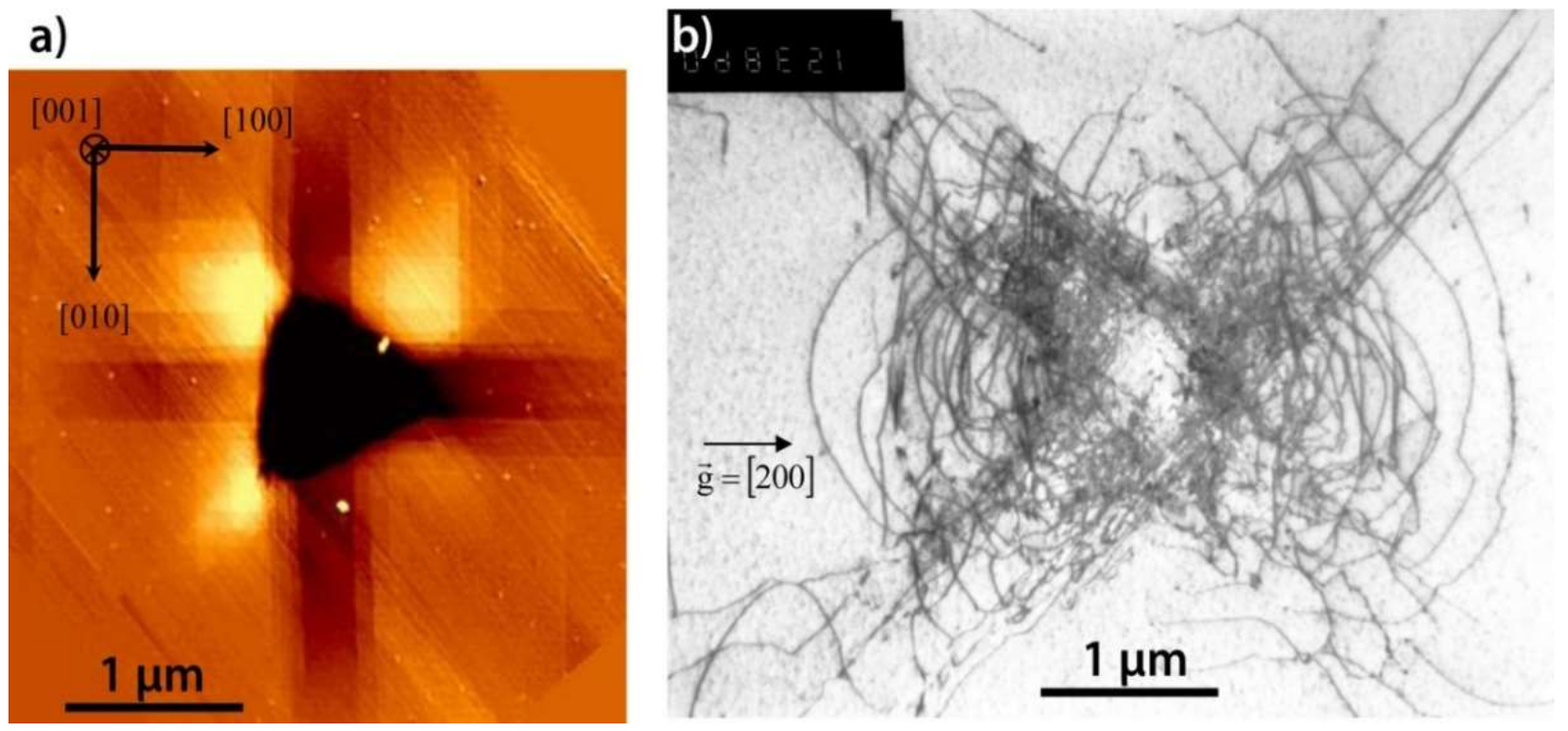
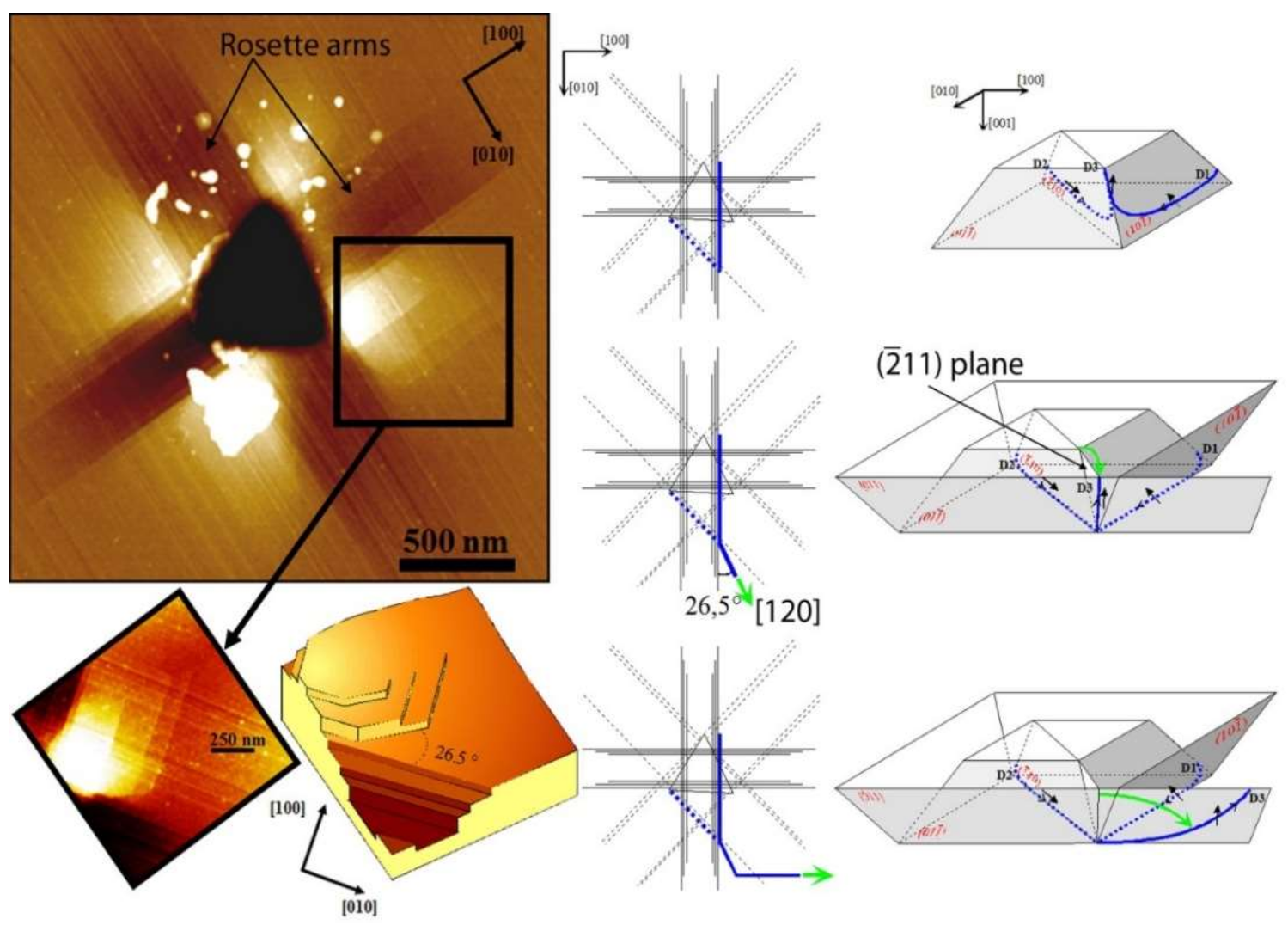
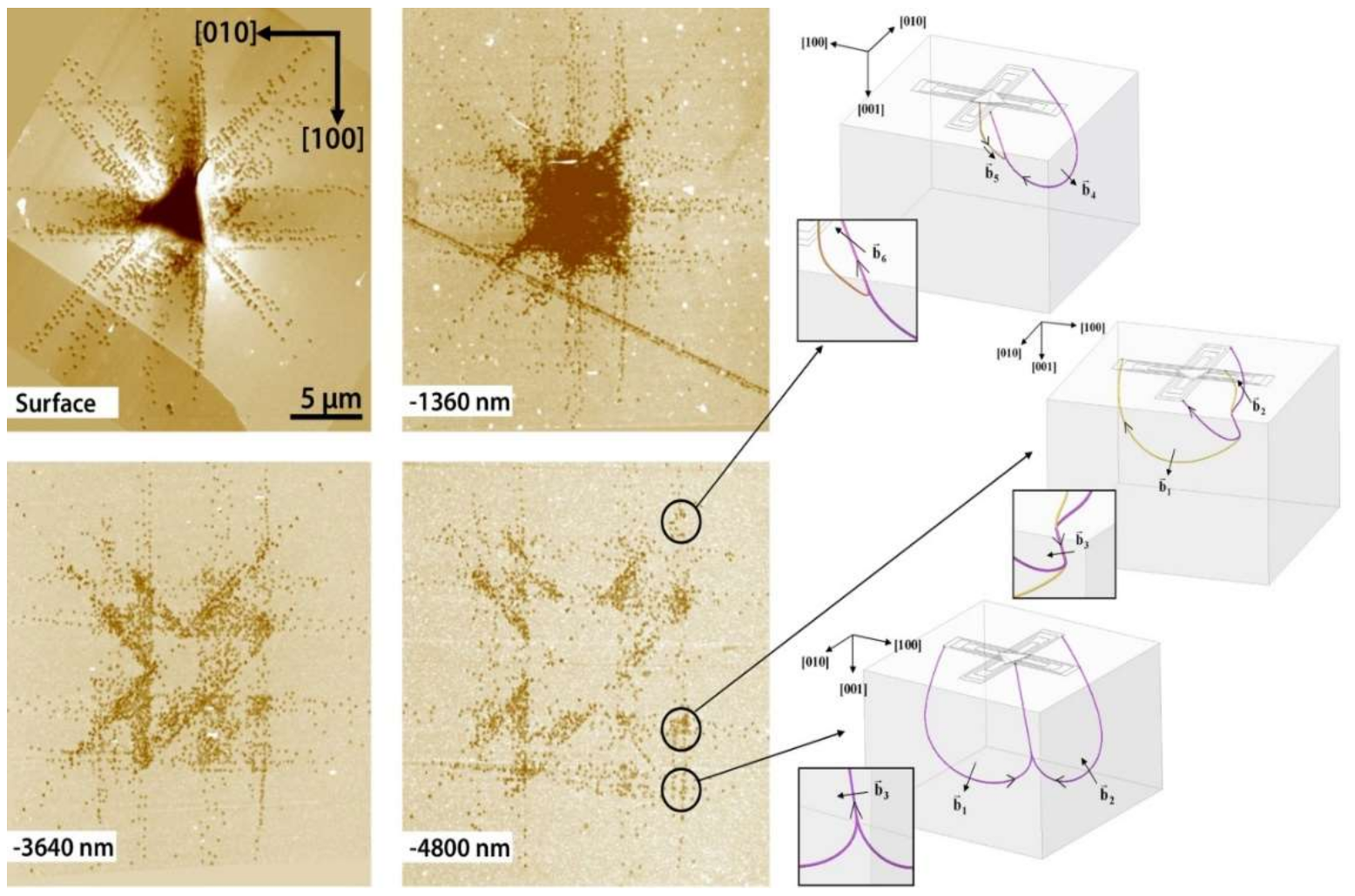


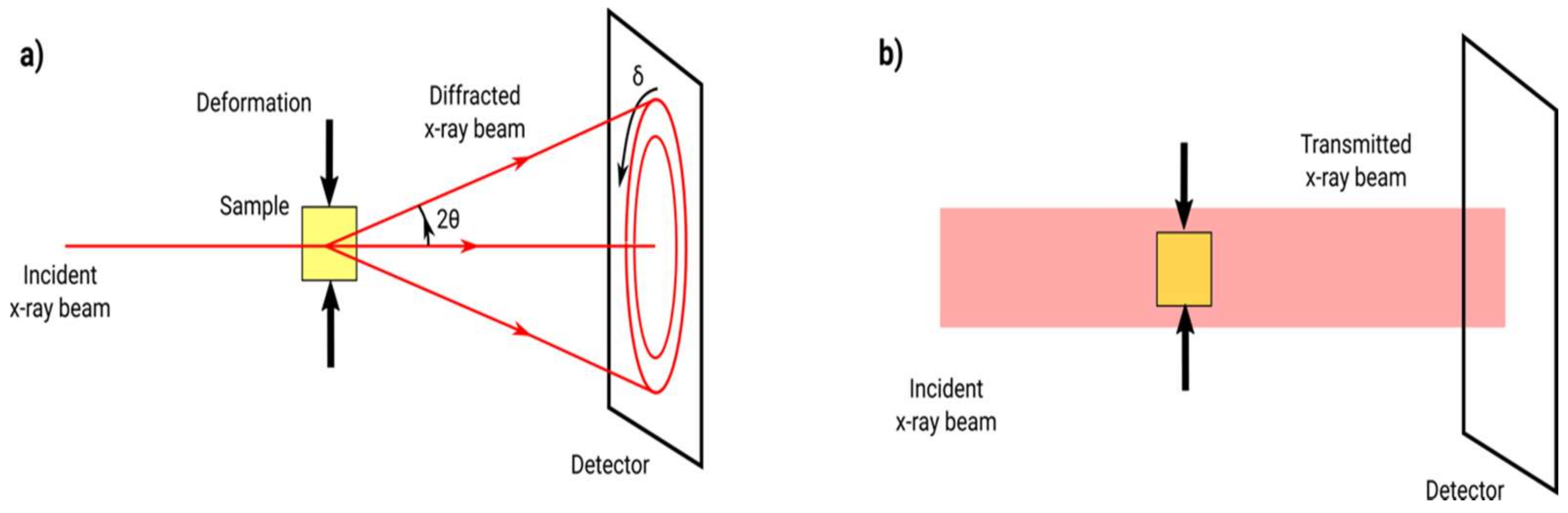

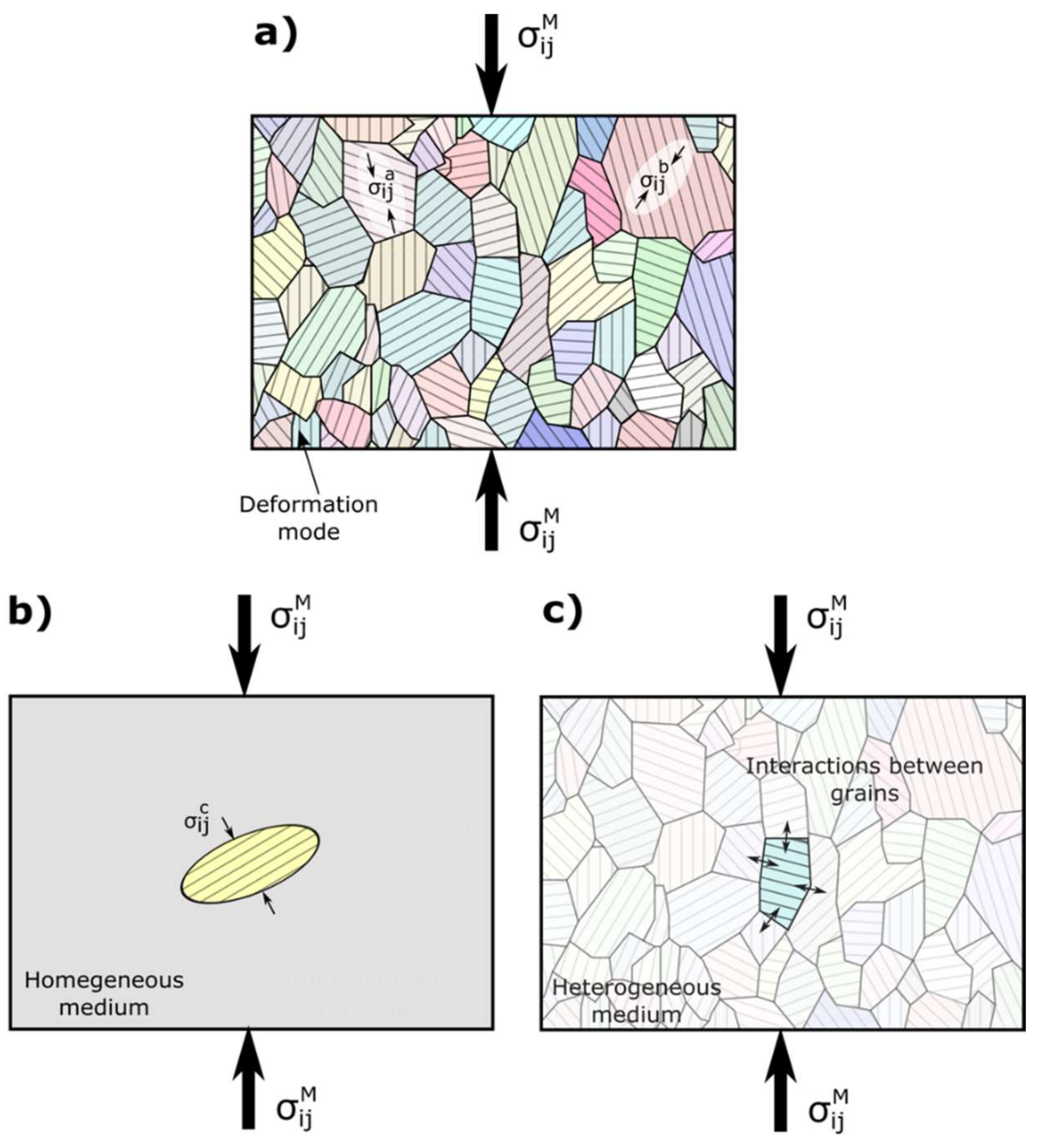
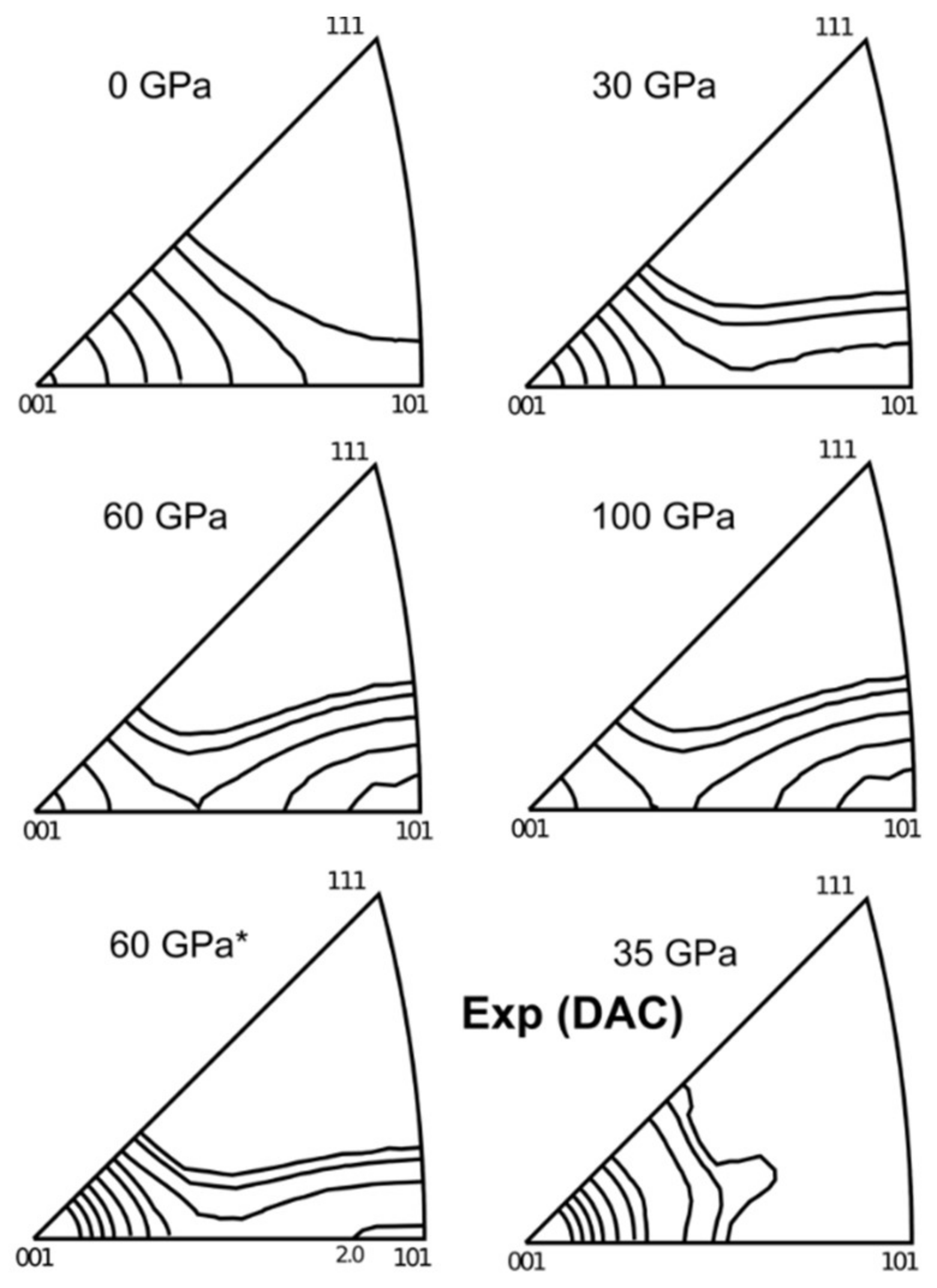
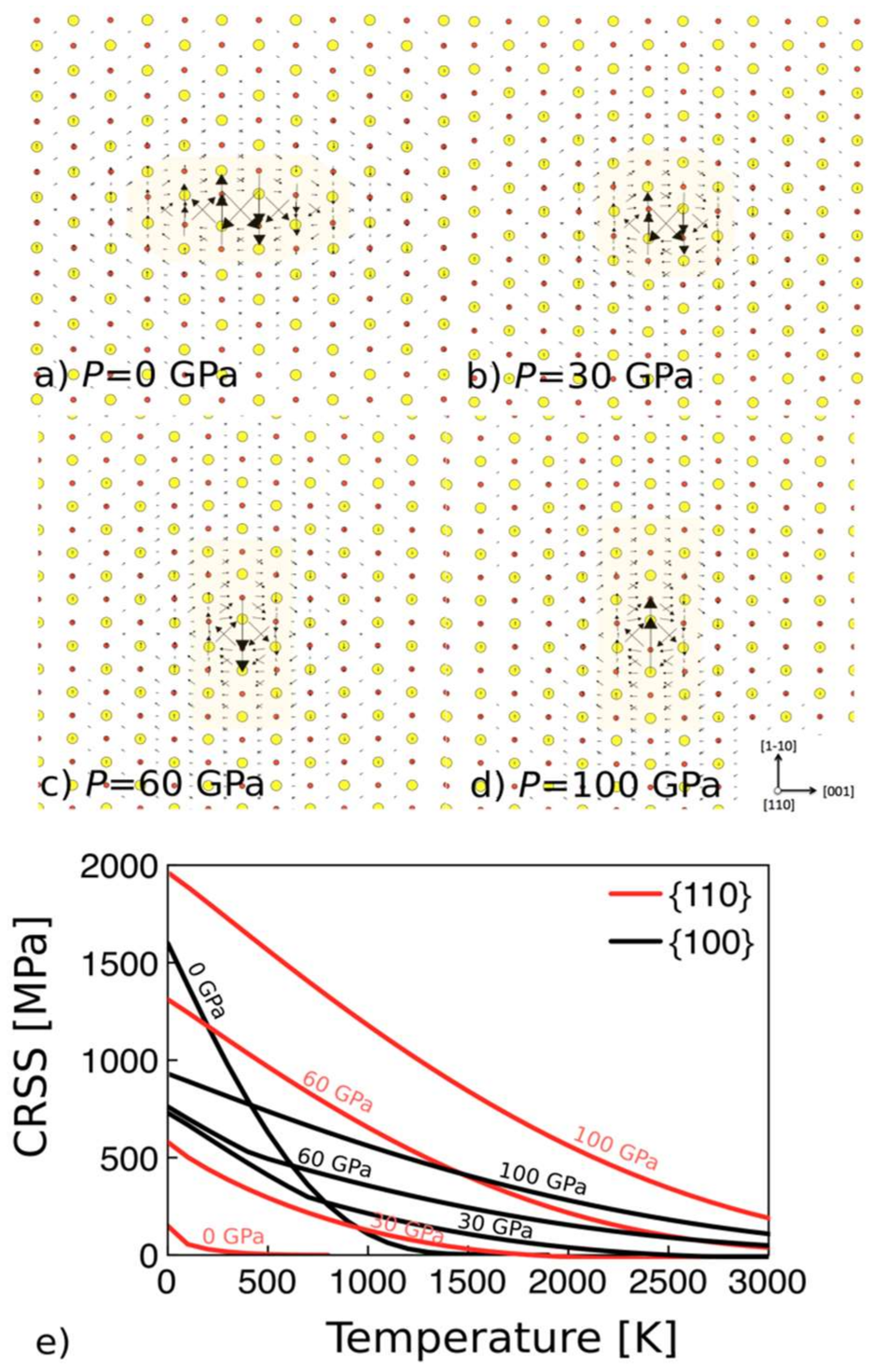
| Index | Plane | Index | Plane | ||
|---|---|---|---|---|---|
| 1 | 7 | ||||
| 2 | 8 | ||||
| 3 | 9 | ||||
| 4 | 10 | ||||
| 5 | 11 | ||||
| 6 | 12 |
| CA | ½<110>{110} | ½<110>{100} | ½<110>{111} |
|---|---|---|---|
| <100> | 0.5 for 4/6 systems | 0 for all systems | /6 (~0.41) for 8/12 systems |
| <110> | 0.25 for 4/6 systems | /4 (~0.35) for 4/6 systems | /6 (~0.41) for 4/12 systems |
| <111> | 0 for all systems | /3 (~0.47) for 3/6 systems | /9 (~0.27) for 6/12 systems |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amodeo, J.; Merkel, S.; Tromas, C.; Carrez, P.; Korte-Kerzel, S.; Cordier, P.; Chevalier, J. Dislocations and Plastic Deformation in MgO Crystals: A Review. Crystals 2018, 8, 240. https://doi.org/10.3390/cryst8060240
Amodeo J, Merkel S, Tromas C, Carrez P, Korte-Kerzel S, Cordier P, Chevalier J. Dislocations and Plastic Deformation in MgO Crystals: A Review. Crystals. 2018; 8(6):240. https://doi.org/10.3390/cryst8060240
Chicago/Turabian StyleAmodeo, Jonathan, Sébastien Merkel, Christophe Tromas, Philippe Carrez, Sandra Korte-Kerzel, Patrick Cordier, and Jérôme Chevalier. 2018. "Dislocations and Plastic Deformation in MgO Crystals: A Review" Crystals 8, no. 6: 240. https://doi.org/10.3390/cryst8060240
APA StyleAmodeo, J., Merkel, S., Tromas, C., Carrez, P., Korte-Kerzel, S., Cordier, P., & Chevalier, J. (2018). Dislocations and Plastic Deformation in MgO Crystals: A Review. Crystals, 8(6), 240. https://doi.org/10.3390/cryst8060240







