Lattice Parameters of Optical Damage Resistant In-Doped LiNbO3 Crystals
Abstract
1. Introduction
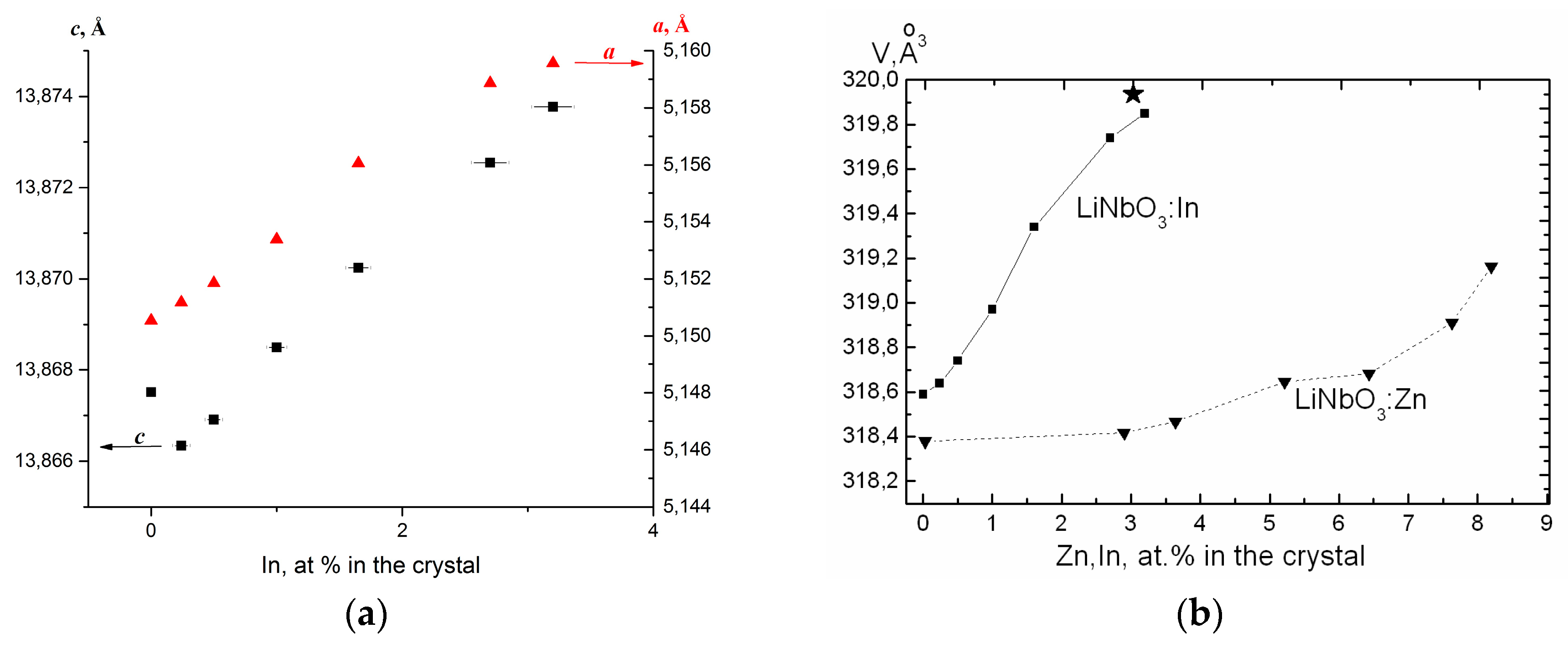
2. Results and Discussion
3. Materials and Methods
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Volk, T.; Woehlecke, M. Lithium Niobate: Defects, Photorefraction and Ferroelectric Switching; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–247. ISBN 978-540-70765-3. [Google Scholar]
- Zhong, G.G.; Jian, J.; Wu, Z.K. LiNbO3 doped with MgO. In Proceedings of the 11th IEEE International Conference on Quantum Electronics, Boston, MA, USA, 23–26 June 1980; p. 631. [Google Scholar]
- Volk, T.R.; Pryalkin, V.I.; Rubinina, N.M. Optical-damage resistant LiNbO3:Zn crystal. Opt. Lett. 1990, 15, 996–998. [Google Scholar] [CrossRef] [PubMed]
- Volk, T.R.; Rubinina, N.M. A new optical-damage resistant impurity in LiNbO3: Indium. Ferroelectr. Lett. 1992, 14, 37–43. [Google Scholar] [CrossRef]
- Yamamoto, J.K.; Kitamura, K.; Iyi, N.; Kimura, S.; Furukawa, Y.; Sato, M. Increased optical damage resistance in Sc2O3-doped LiNbO3. Appl. Phys. Lett. 1992, 61, 2156–2158. [Google Scholar] [CrossRef]
- Kokanyan, E.P.; Razzari, L.; Cristiani, I.; Degiorgio, V.; Gruber, J.B. Reduced photorefraction in hafnium-doped single-domain and periodically poled lithium niobate crystals. Appl. Phys. Lett. 2004, 84, 1880–1882. [Google Scholar] [CrossRef]
- Kong, Y.; Liu, S.; Zhao, Y.; Liu, H.; Chen, S.; Xu, J. Highly optical damage resistant crystal: Zirconium-oxide-doped lithium niobate. Appl. Phys. Lett. 2007, 91, 081908. [Google Scholar] [CrossRef]
- Wang, L.; Liu, S.; Kong, Y.; Chen, S.; Huang, Z.; Wu, L.; Rupp, R.; Xu, J. Increased optical-damage resistance in tin-doped lithium niobate. Opt. Lett. 2010, 35, 883–885. [Google Scholar] [CrossRef] [PubMed]
- Kong, Y.; Liu, S.; Xu, J.J. Recent advances in the photorefraction of doped lithium niobate crystals. Materials 2012, 5, 1954–1971. [Google Scholar] [CrossRef]
- Kovács, L.; Szaller, Z.; Lengyel, K.; Corradi, G. Hydroxyl ions in stoichiometric LiNbO3 crystals doped with optical damage resistant ions. Opt. Mater. 2014, 37, 55–58. [Google Scholar] [CrossRef]
- Kovács, L.; Szaller, Z.; Lengyel, K.; Péter, Á.; Hajdara, I.; Mandula, G.; Pálfalvi, L.; Hebling, J. Photorefractive damage resistance threshold in stoichiometric LiNbO3:Zr crystals. Opt. Lett. 2013, 38, 2861–2864. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Abrahams, S.C.; March, P. Defect structure dependence on composition in lithium niobate. Acta Crystallogr. Sect. B 1986, 42, 61–68. [Google Scholar] [CrossRef]
- Wilkinson, A.P.; Cheetham, A.K.; Jarman, R.H. The defect structure of congruently melting lithium niobate. J. Appl. Phys. 1993, 74, 3080–3083. [Google Scholar] [CrossRef]
- Zotov, N.; Boysen, H.; Frey, F.; Metzger, T.; Born, E. Cation substitution models of congruent LiNbO3 investigated by X-ray and neutron powder diffraction. J. Phys. Chem. Solids 1994, 55, 145–152. [Google Scholar] [CrossRef]
- Grabmaier, B.C.; Otto, F. Growth and investigation of MgO-doped LiNbO3. J. Cryst. Growth 1986, 79, 682–688. [Google Scholar] [CrossRef]
- Rossner, W.; Grabmaier, B.; Wersing, W. Dielectric high-temperature behaviour of undoped and MgO-doped LiNbO3 single crystals. Ferroelectrics 1989, 93, 57–65. [Google Scholar] [CrossRef]
- Grabmaier, B.C.; Wersing, W.; Koestler, W. Properties of undoped and MgO-doped LiNbO3; correlation to the defect structure. J. Cryst. Growth 1991, 110, 339–347. [Google Scholar] [CrossRef]
- Malovichko, G.; Cerclier, O.; Estienne, J.; Grachev, V.; Kokanyan, E.; Boulesteix, C. Lattice constants of K- and Mg-doped LiNbO3. Comparison with nonstoichiometric lithium niobate. J. Phys. Chem. Solids 1995, 56, 1285–1289. [Google Scholar] [CrossRef]
- Abdi, T.; Aillerie, M.; Fontana, M.; Bourson, P.; Volk, T.; Maximov, B.; Sulyanov, S.; Rubinina, N. Influence of Zn doping on electrooptical properties and structure parameters of LiNbO3. Appl. Phys. B 1999, 68, 795–799. [Google Scholar] [CrossRef]
- Volk, T.; Maximov, B.; Chernaya, T.; Rubinina, N.; Woehlecke, M.; Simonov, V. Photorefractive properties of LiNbO3:Zn crystals related to the defect structure. Appl. Phys. B 2001, 72, 647–652. [Google Scholar] [CrossRef]
- Sulyanov, S.; Maximov, B.; Volk, T.; Boysen, H.; Schneider, J.; Rubinina, N.; Hansen, T. Neutron and X-ray study of stoichiometric and doped LiNbO3:Zn0.08. Appl. Phys. A 2002, 74, S1031–S1033. [Google Scholar] [CrossRef]
- Chia, C.-T.; Lee, C.-C.; Chang, P.-J.; Hu, M.-L.; Hu, L.J. Substitution mechanism of ZnO-doped lithium niobate crystal determined by powder X-ray diffraction and coercive field. Appl. Phys. Lett. 2005, 86, 182901. [Google Scholar] [CrossRef]
- Argiolas, N.; Bazzan, M.; Ciampolillo, M.V.; Pozzobon, P.; Sada, C.; Saoner, L.; Zaltron, A.M.; Bacci, L.; Minzioni, P.; Nava, G.; et al. Structural and optical properties of zirconium doped lithium niobate crystals. J. Appl. Phys. 2010, 108, 093508. [Google Scholar] [CrossRef]
- Iyi, N.; Kitamura, K.; Izumi, F.; Yamamoto, J.K.; Hayashi, T.; Asano, H.; Kimura, S. Comparative study of defect structures in lithium niobate with different compositions. J. Solid State Chem. 1992, 101, 340–352. [Google Scholar] [CrossRef]
- Volk, T.R.; Woehlecke, M.; Rubinina, N.M.; Razumovskii, N.V.; Jermann, F.; Fischer, C.; Böwer, R. LiNbO3 with the optical-damage resistant impurity indium. Appl. Phys. A 1995, 60, 217–225. [Google Scholar] [CrossRef]
- Volk, T.; Woehlecke, M.; Rubinina, N. Optical Damage Resistance in LiNbO3 Crystals. In Photorefractive Materials and Their Applications; Guenter, P., Huignard, J.-P., Eds.; Series in Optical Sciences; Springer: Berlin, Germany, 2006; Volume II, pp. 165–203. ISBN 978-3-540-39135-7. [Google Scholar]
- Shannon, R.D.; Prewitt, C.T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B 1969, 25, 925–946. [Google Scholar] [CrossRef]
- Lerner, P.; Legras, C.; Dumas, J.P. Stoechiométrie des monocristaux de métaniobate de lithium. J. Cryst. Growth 1968, 3–4, 231–235. [Google Scholar] [CrossRef]
- Koyama, C.; Nozawa, J.; Maeda, K.; Fujiwara, K.; Uda, S. Investigation of defect structure of impurity-doped lithium niobate by combining thermodynamic constraints with lattice constant variations. J. Appl. Phys. 2015, 117, 014102. [Google Scholar] [CrossRef]
- Donnerberg, H.; Tomlinson, S.M.; Catlow, C.R.A.; Schirmer, O.F. Computer-simulation studies of extrinsic defects in LiNbO3 crystals. Phys. Rev. B 1991, 44, 4877. [Google Scholar] [CrossRef]
- Shimamura, S.; Watanabe, Y.; Sota, T.; Suzuki, K.; Iyi, N.; Kitamura, K.; Yamazaki, T.; Sugimoto, T.; Yamagishi, K. A defect structure model of LiNBO3:Sc2O3. J. Phys. Condens. Matter 1996, 8, 6825. [Google Scholar] [CrossRef]
- Kasemir, K.; Betzler, K.; Matzas, B.; Tiegel, B.; Woehlecke, M.; Gather, B.; Volk, T.; Rubinina, N. Influence of Zn/In codoping on the optical properties of lithium niobate crystals. J. Appl. Phys. 1998, 84, 5191–5193. [Google Scholar] [CrossRef]
- Boultif, A.; Louër, D. Powder pattern indexing with the dichotomy method. J. Appl. Crystallogr. 2004, 37, 724–731. [Google Scholar] [CrossRef]
| In at % in the Crystal | c, Å | a, Å | V, Å3 |
|---|---|---|---|
| 0 | 13.86753(6) | 5.15054(1) | 318.59 |
| 0.24 | 13.86634(17) | 5.15117(3) | 318.64 |
| 0.50 | 13.86691(14) | 5.15185(3) | 318.74 |
| 1.00 | 13.86850(14) | 5.15338(3) | 318.97 |
| 1.65 | 13.87024(11) | 5.15606(3) | 319.34 |
| 2.7 | 13.87255(11) | 5.15887(3) | 319.74 |
| 3.2 | 13.87377(9) | 5.15956(2) | 319.85 |
| Ion | Li+ | Nb5+ | Mg2+ | Zn2+ | Sc3+ | In3+ | Zr4+ | Hf4+ |
|---|---|---|---|---|---|---|---|---|
| ri, pm | 76 | 64 | 72 | 74 | 74.5 | 81 | 79 | 71 |
| H | K | L | DOBS | DCAL | DOBS-DCAL | 2TH.OBS | 2TH.CAL | DIF.2TH. |
| 2 | 0 | 8 | 1.36867 | 1.36865 | 0.00002 | 68.500 | 68.501 | −0.001 |
| 2 | 2 | 0 | 1.28762 | 1.28764 | −0.00002 | 73.487 | 73.486 | 0.001 |
| 3 | 1 | 2 | 1.21788 | 1.21789 | −0.00001 | 78.468 | 78.468 | 0.000 |
| 2 | 1 | 8 | 1.20857 | 1.20857 | −0.00001 | 79.191 | 79.191 | 0.000 |
| 2 | 0 | 10 | 1.17764 | 1.17766 | −0.00002 | 81.703 | 81.702 | 0.001 |
| 3 | 1 | 4 | 1.16516 | 1.16516 | 0.00000 | 82.769 | 82.769 | 0.000 |
| 2 | 2 | 6 | 1.12485 | 1.12485 | 0.00002 | 86.440 | 86.440 | 0.000 |
| 4 | 0 | 2 | 1.10097 | 1.10098 | −0.00001 | 88.798 | 88.797 | 0.001 |
| 2 | 1 | 10 | 1.07099 | 1.07099 | 0.00000 | 91.983 | 91.983 | 0.000 |
| 4 | 0 | 4 | 1.06157 | 1.06156 | 0.00001 | 93.041 | 93.042 | −0.001 |
| 1 | 1 | 12 | 1.05435 | 1.05434 | 0.00001 | 93.872 | 93.873 | −0.001 |
| 3 | 2 | 2 | 1.01236 | 1.01234 | 0.00001 | 99.086 | 99.088 | −0.002 |
| 4 | 1 | 0 | 0.97335 | 0.97336 | −0.00001 | 104.630 | 104.629 | 0.001 |
| 1 | 0 | 14 | 0.96698 | 0.96698 | 0.00000 | 105.613 | 105.613 | 0.000 |
| 4 | 0 | 8 | 0.93783 | 0.93783 | 0.00000 | 110.442 | 110.442 | 0.000 |
| 3 | 0 | 12 | 0.91243 | 0.91243 | 0.00000 | 115.178 | 115.177 | 0.001 |
| 4 | 1 | 6 | 0.89706 | 0.89706 | 0.00000 | 118.340 | 118.340 | 0.000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sulyanov, S.; Volk, T. Lattice Parameters of Optical Damage Resistant In-Doped LiNbO3 Crystals. Crystals 2018, 8, 210. https://doi.org/10.3390/cryst8050210
Sulyanov S, Volk T. Lattice Parameters of Optical Damage Resistant In-Doped LiNbO3 Crystals. Crystals. 2018; 8(5):210. https://doi.org/10.3390/cryst8050210
Chicago/Turabian StyleSulyanov, Serguei, and Tatyana Volk. 2018. "Lattice Parameters of Optical Damage Resistant In-Doped LiNbO3 Crystals" Crystals 8, no. 5: 210. https://doi.org/10.3390/cryst8050210
APA StyleSulyanov, S., & Volk, T. (2018). Lattice Parameters of Optical Damage Resistant In-Doped LiNbO3 Crystals. Crystals, 8(5), 210. https://doi.org/10.3390/cryst8050210




