Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3
Abstract
:1. Introduction
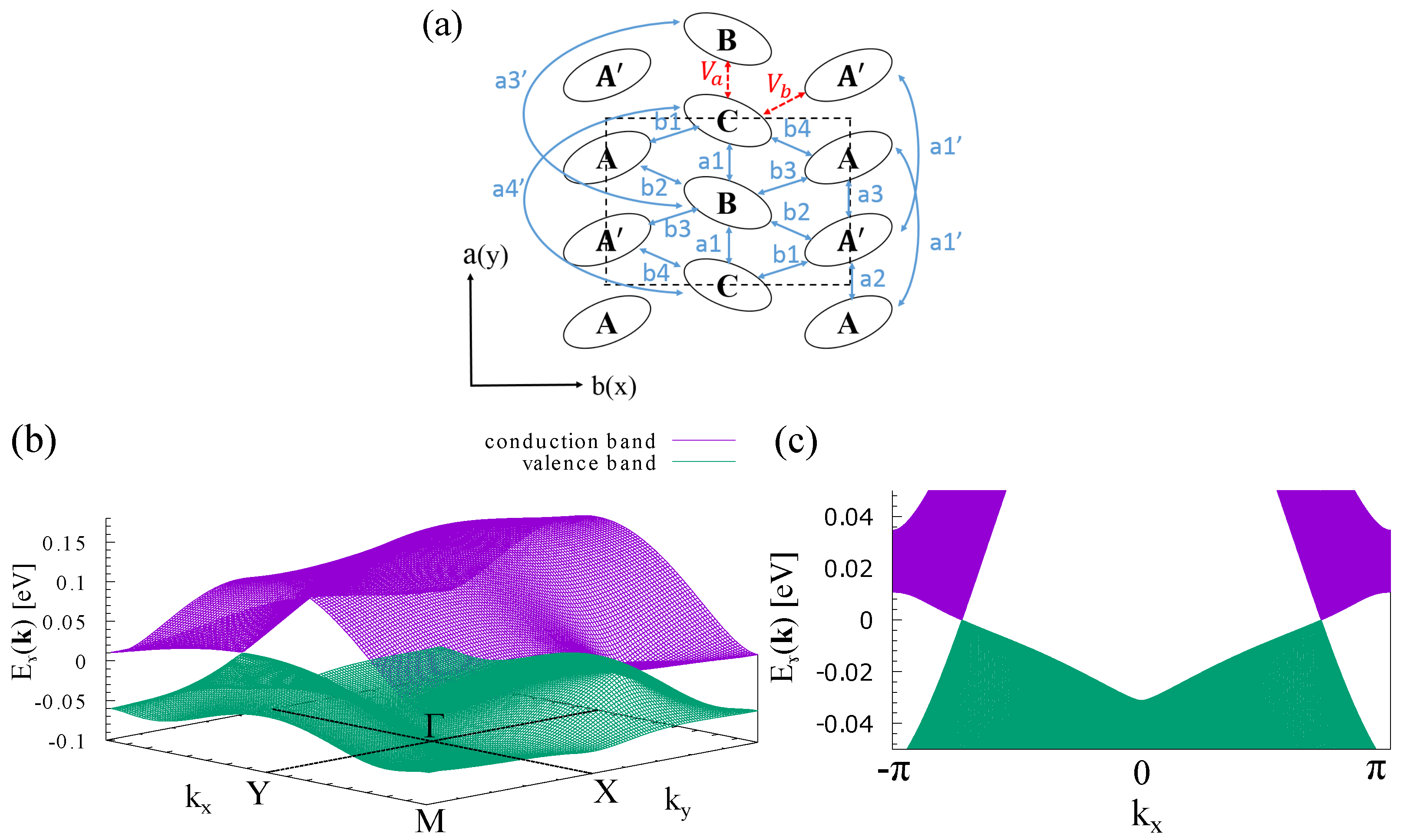
2. Formulation
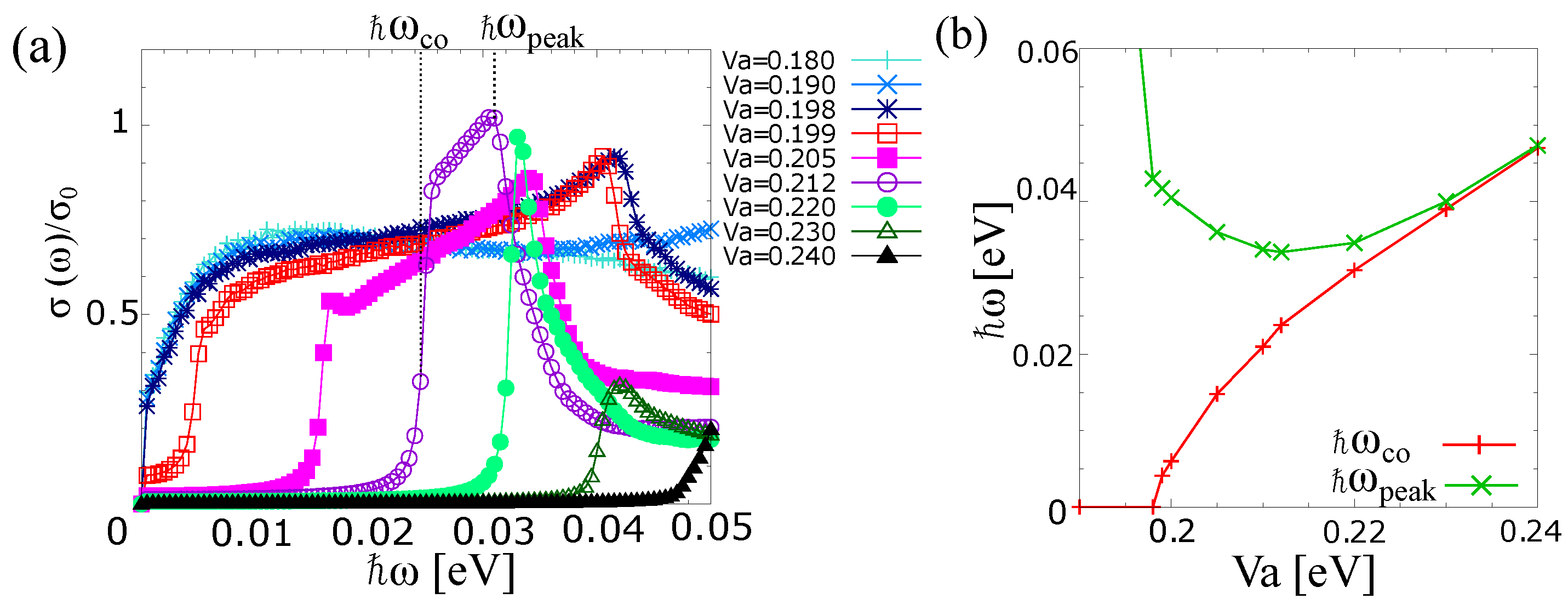
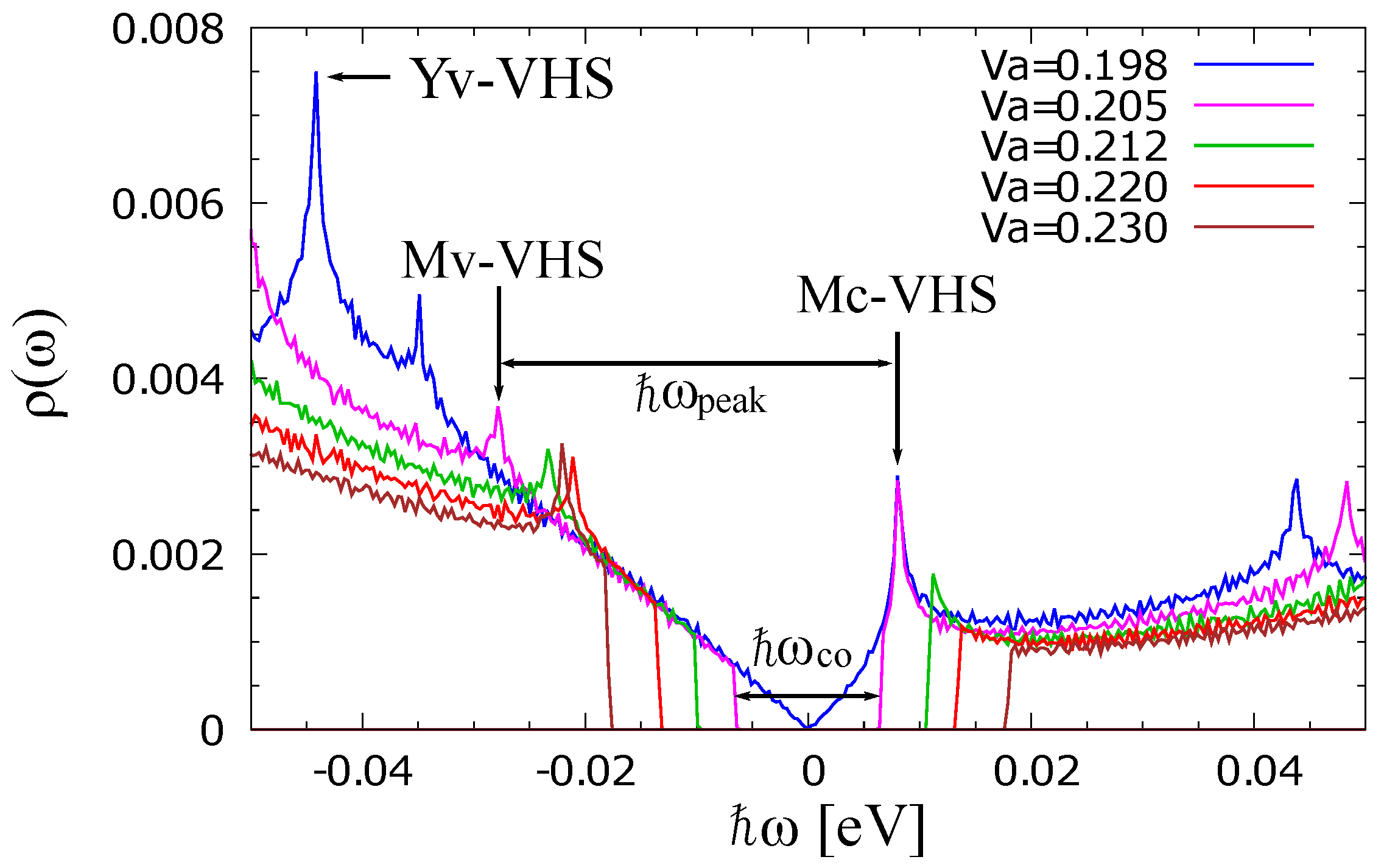
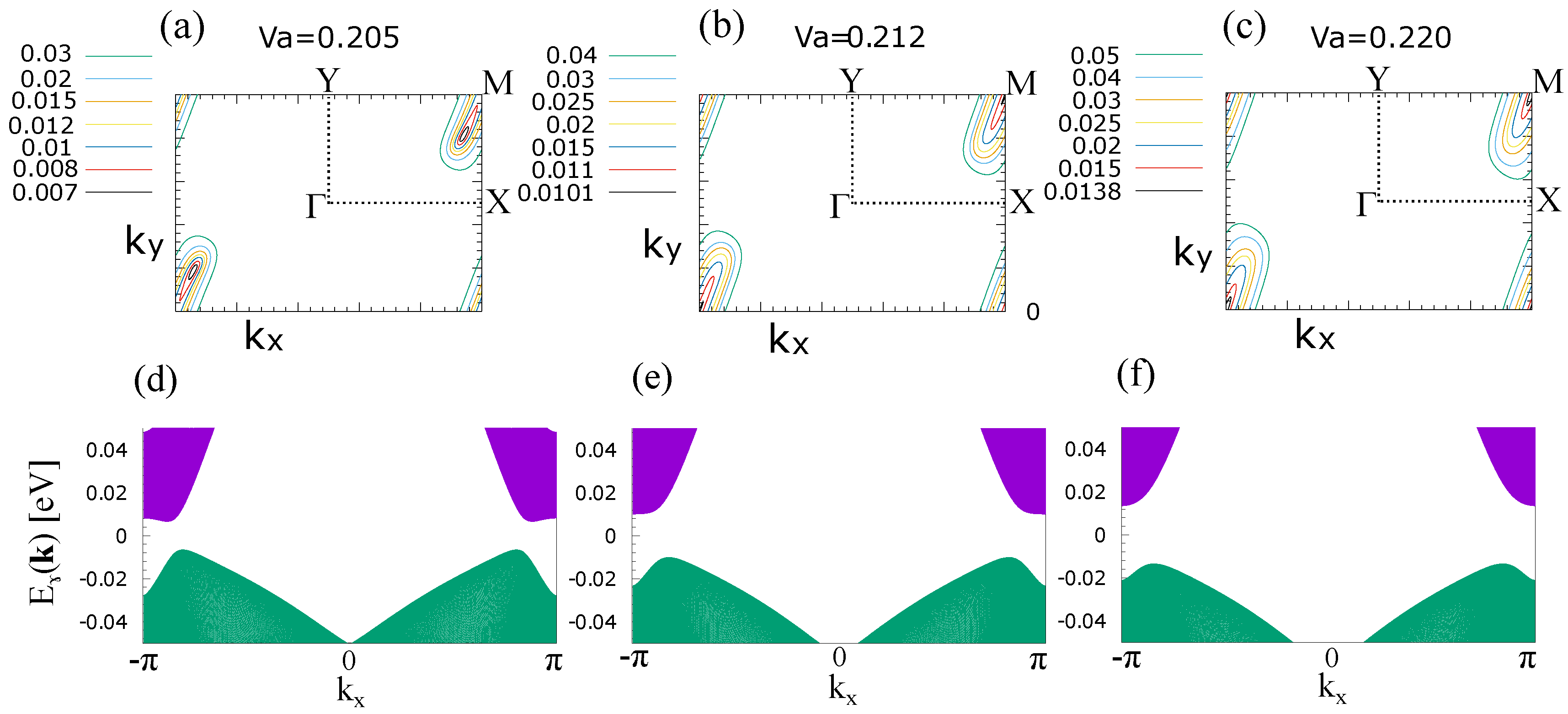
3. Results
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| DE | Dirac electron |
| CO | charge order |
| VHS | Van Hove singularity |
| DOS | density of states |
| TRIM | time reversal invariant momentum |
| Mc-VHS | Van Hove singularity at the M-point in the conduction band |
| Mv-VHS | Van Hove singularity at the M-point in the valence band |
| Yv-VHS | Van Hove singularity at the Y-point in the valence band |
References
- Kino, H.; Fukuyama, H. Interrelationship among Electronic States of α-(ET)2I3, (ET)2MHg(SCN)4 and κ-(ET)2X. J. Phys. Soc. Jpn. 1995, 64, 4523. [Google Scholar] [CrossRef]
- Seo, H. Charge Ordering in Organic ET Compounds. J. Phys. Soc. Jpn. 2000, 69, 805–820. [Google Scholar]
- Hotta, C. Classification of Quasi-Two Dimensional Organic Conductors Based on a New Minimal Model. J. Phys. Soc. Jpn. 2003, 72, 840. [Google Scholar] [CrossRef]
- Takahashi, T. 13C-NMR studies of charge ordering in organic conductors. Synth. Met. 2003, 26, 133–134. [Google Scholar] [CrossRef]
- Seo, H.; Hotta, C.; Fukuyama, T. Toward Systematic Understanding of Diversity of Electronic Properties in Low-Dimensional Molecular Solids. Chem. Rev. 2004, 104, 5005. [Google Scholar] [CrossRef] [PubMed]
- Kakiuchi, T.; Wakabayashi, Y.; Sawa, H.; Takahashi, T.; Nakamura, T. Charge Ordering in α-(BEDT-TTF)2I3 by Synchrotron X-ray Diffraction. J. Phys. Soc. Jpn. 2007, 76, 113702. [Google Scholar] [CrossRef]
- Alemany, P.; Pouget, J.-P.; Canadell, E. Essential role of anions in the charge ordering transition of α-(BEDT-TTF)2I3. Phys. Rev. B 2012, 85, 195118. [Google Scholar] [CrossRef]
- Kajita, K.; Ojiro, T.; Fujii, H.; Nishio, Y.; Kobayashi, H.; Kobayashi, A.; Kato, R. Magnetotransport Phenomena of α-Type (BEDT-TTF)2I3 under High Pressures. J. Phys. Soc. Jpn. 1992, 61, 23. [Google Scholar] [CrossRef]
- Tajima, N.; Tamura, M.; Nishio, Y.; Kajita, K.; Iye, Y. Transport Property of an Organic Conductor α-(BEDT-TTF)2I3 under High Pressure—Discovery of a Novel Type of Conductor. J. Phys. Soc. Jpn. 2000, 69, 543–551. [Google Scholar] [CrossRef]
- Ishikawa, K.; Hirata, M.; Liu, D.; Miyagawa, K.; Tamura, M.; Kanoda, K. Spin excitations in the quasi-two-dimensional charge-ordered insulator α-(BEDT-TTF)2I3 probed via 13C NMR. Phys. Rev. B 2016, 94, 085154. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Noguchi, K.; Suzumura, Y. Superconductivity in Charge Ordered Organic Conductor –α-(ET)2I3 Salt–. J. Phys. Soc. Jpn. 2004, 73, 3135. [Google Scholar] [CrossRef]
- Katayama, S.; Kobayashi, A.; Suzumura, Y. Pressure-Induced Zero-Gap Semiconducting State in Organic Conductor α-(BEDT-TTF)2I3 Salt. J. Phys. Soc. Jpn. 2006, 75, 054705. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y.; Fukuyama, H. Massless Fermions in Organic Conductor. J. Phys. Soc. Jpn. 2007, 76, 034711. [Google Scholar] [CrossRef]
- Kajita, K.; Nishio, Y.; Tajima, N.; Suzumura, Y.; Kobayashi, A. Molecular Dirac Fermion Systems—Theoretical and Experimental Approaches—. J. Phys. Soc. Jpn. 2014, 83, 072002. [Google Scholar] [CrossRef]
- Goerbig, M.O.; Fuchs, J.-N.; Montambaux, G.; Piéchon, F. Tilted anisotropic Dirac cones in quinoid-type graphene and α-(BEDT-TTF)2I3. Phys. Rev. B 2008, 78, 045415. [Google Scholar] [CrossRef]
- Tanaka, Y.; Ogata, M. Correlation Effects on Charge Order and Zero-Gap State in the Organic Conductor α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2016, 85, 104706. [Google Scholar] [CrossRef]
- Hirata, M.; Ishikawa, K.; Miyagawa, K.; Tamura, M.; Berthier, C.; Basko, D.; Kobayashi, A.; Matsuno, G.; Kanoda, K. Observation of an anisotropic Dirac cone reshaping and ferrimagnetic spin polarization in an organic conductor. Nat. Commun. 2016, 7, 12666. [Google Scholar] [CrossRef] [PubMed]
- Matsuno, G.; Kobayashi, A. Effect of Interband Fluctuation on Spin Susceptibility in Molecular Dirac Fermion System α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2017, 86, 014705. [Google Scholar] [CrossRef]
- Hirata, M.; Ishikawa, K.; Matsuno, G.; Kobayashi, A.; Miyagawa, K.; Tamura, M.; Berthier, C.; Kanoda, K. Anomalous spin correlations and excitonic instability of interacting 2D Weyl fermions. Science 2017, 358, 1403–1406. [Google Scholar] [CrossRef] [PubMed]
- Matsuno, G.; Kobayashi, A. Coexistence of velocity renormalization and ferrimagnetic fuctuation in an organic Dirac electron system α-(BEDT-TTF)2I3. accepted to J. Phys. Soc. Jpn. 2018, 87. [Google Scholar]
- Beyer, R.; Dengl, A.; Peterseim, T.; Wackerow, S.; Ivek, T.; Pronin, A.V.; Schweitzer, D.; Dressel, M. Pressure- dependent optical investigations of α-(BEDT-TTF)2I3: Tuning charge order and narrow gap towards a Dirac semimetal. Phys. Rev. B 2016, 93, 195116. [Google Scholar] [CrossRef]
- Ivek, T.; Korin-Hamzić, B.; Milat, O.; Tomić, S.; Clauss, C.; Drichko, N.; Schweitzer, D.; Dressel, M. Electrodynamic response of the charge ordering phase: Dielectric and optical studies of α-(BEDT-TTF)2I3. Phys. Rev. B 2011, 83, 165128. [Google Scholar] [CrossRef]
- Liu, D.; Ishikawa, K.; Takehara, R.; Miyagawa, K.; Tamura, M.; Kanoda, K. Insulating nature of strongly correlated massless Dirac fermions in an organic crystal. Phys. Rev. Lett. 2016, 116, 226401. [Google Scholar] [CrossRef] [PubMed]
- Hasegawa, Y.; Kishigi, K. Edge States in the Three-Quarter Filled System, α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2011, 80, 054707. [Google Scholar] [CrossRef]
- Omori, Y.; Matsuno, G.; Kobayashi, A. Edge States in Molecular Solid α-(BEDT-TTF)2I3: Effects of Electron Correlations. JPS Conf. Proc. 2014, 1, 012119. [Google Scholar] [CrossRef]
- Matsuno, G.; Omori, Y.; Eguchi, T.; Kobayashi, A. Topological Domain Wall and Valley Hall Effect in Charge Ordered Phase of Molecular Dirac Fermion System α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2016, 85, 094710. [Google Scholar] [CrossRef]
- Omori, Y.; Matsuno, G.; Kobayashi, A. Longitudinal Conductivity on Edge and Domain Wall Molecular Dirac Electron System α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2017, 86, 074708. [Google Scholar] [CrossRef]
- Montambaux, G.; Piéchon, F.; Fuchs, J.-N.; Goerbig, M.O. Merging of Dirac points in a two-dimensional crystal. Phys. Rev. B 2009, 80, 153412. [Google Scholar] [CrossRef]
- Montambaux, G.; Piéchon, F.; Fuchs, J.-N.; Goerbig, M.O. A universal Hamiltonian for the motion and the merging of Dirac cones in a two-dimensional crystal. Eur. Phys. J. B 2009, 72, 509. [Google Scholar] [CrossRef]
- Mori, T.; Kobayashi, A.; Sasaki, Y.; Kobayashi, H.; Saito, G.; Inokuchi, H. BAND STRUCTURES OF TWO TYPES OF (BEDT-TTF)2I3. Chem. Lett. 1984, 13, 957–960. [Google Scholar] [CrossRef]
- Mori, T.; Mori, H.; Tanaka, S. Structural Genealogy of BEDT-TTF-Based Organic Conductors II. Inclined Molecules: θ, α, and κ Phases. Bull. Chem. Soc. Jpn. 1999, 72, 179. [Google Scholar] [CrossRef]
- Kondo, R.; Kagoshima, S.; Harada, J. Crystal structure analysis under uniaxial strain at low temperature using a unique design of four-axis x-ray diffractometer with a fixed sample. Rev. Sci. Instrum. 2005, 76, 093902. [Google Scholar] [CrossRef]
- Kino, H.; Miyazaki, T. First-Principles Study of Electronic Structure in α-(BEDT-TTF)2I3 at Ambient Pressure and with Uniaxial Strain. J. Phys. Soc. Jpn. 2006, 75, 034704. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tamura, T.; Kohyama, M.; Terakura, K. Ab Initio Electronic-Structure Calculations for α-(BEDT-TTF)2I3. J. Phys. Soc. Jpn. 2006, 75, 015005. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y. Superconductivity in Charge Ordered Metal for Quasi-Two- Dimensional Organic Conductor. J. Phys. Soc. Jpn. 2005, 74, 2897. [Google Scholar] [CrossRef]
- Kobayashi, A.; Katayama, S.; Suzumura, Y. Theoretical study of the zero-gap organic conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024309. [Google Scholar] [CrossRef] [PubMed]
- Tajima, N.; Kajita, K. Experimental study of organic zero-gap conductor α-(BEDT-TTF)2I3. Sci. Technol. Adv. Mater. 2009, 10, 024308. [Google Scholar] [CrossRef] [PubMed]
- Stauber, T.; Peres, N.M.R.; Geim, A.K. Optical conductivity of graphene in the visible region of the spectrum. Phys. Rev. B 2008, 78, 085432. [Google Scholar] [CrossRef]
- Gusynin, V.P.; Sharapov, S.G.; Carbotte, J.P. Unusual Microwave Response of Dirac Quasiparticles in Graphene. Phys. Rev. Lett. 2006, 96, 256802. [Google Scholar] [CrossRef] [PubMed]
- Suzumura, Y.; Proskurin, I.; Ogata, M. Dynamical Conductivity of Dirac Electrons in Organic Conductors. J. Phys. Soc. Jpn. 2014, 83, 094705. [Google Scholar] [CrossRef]
- Suzumura, Y.; Proskurin, I.; Ogata, M. Reflectance of Dirac electrons in organic conductor. J. Phys. Conf. Ser. 2015, 603, 012011. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohki, D.; Matsuno, G.; Omori, Y.; Kobayashi, A. Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals 2018, 8, 137. https://doi.org/10.3390/cryst8030137
Ohki D, Matsuno G, Omori Y, Kobayashi A. Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals. 2018; 8(3):137. https://doi.org/10.3390/cryst8030137
Chicago/Turabian StyleOhki, Daigo, Genki Matsuno, Yukiko Omori, and Akito Kobayashi. 2018. "Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3" Crystals 8, no. 3: 137. https://doi.org/10.3390/cryst8030137
APA StyleOhki, D., Matsuno, G., Omori, Y., & Kobayashi, A. (2018). Optical Conductivity in a Two-Dimensional Extended Hubbard Model for an Organic Dirac Electron System α-(BEDT-TTF)2I3. Crystals, 8(3), 137. https://doi.org/10.3390/cryst8030137



