A Study of Extended Defects in Surface Damaged Crystals
Abstract
:1. Introduction
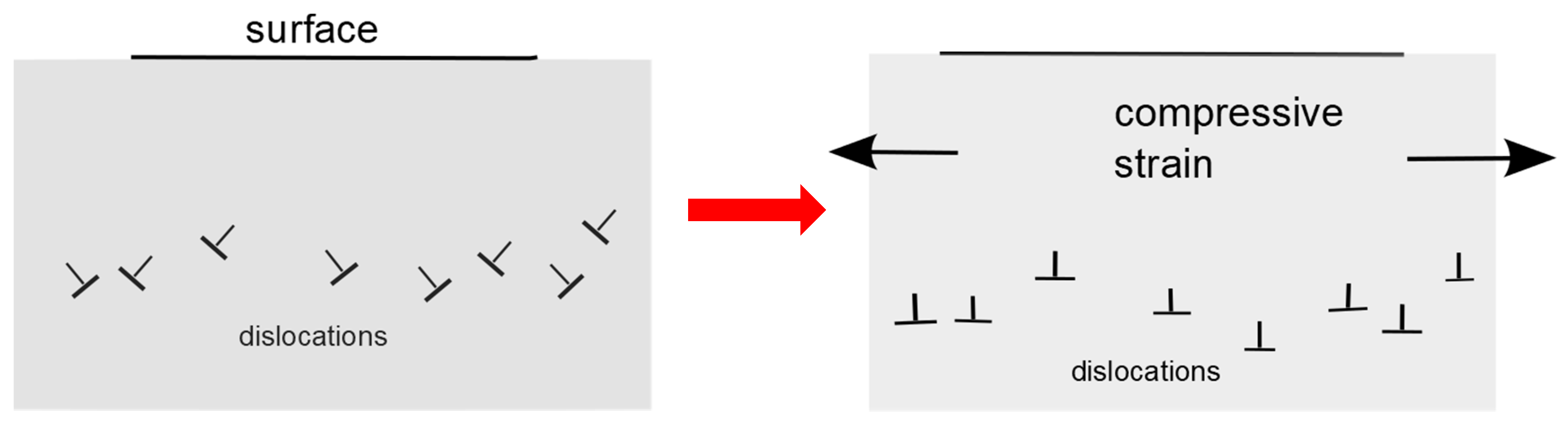
- The curvature obtained is always convex, as seen from the damaged side of the crystal, and the same treatment induces curvatures depending on the orientation of the crystal surface and on the polarity of the crystal: a spherical curvature in (001)-oriented Si or Ge crystals and an elliptical curvature in (001)-oriented GaAs or InP crystals.
- The curvature 1/R is inversely proportional to the square of the sample thickness.
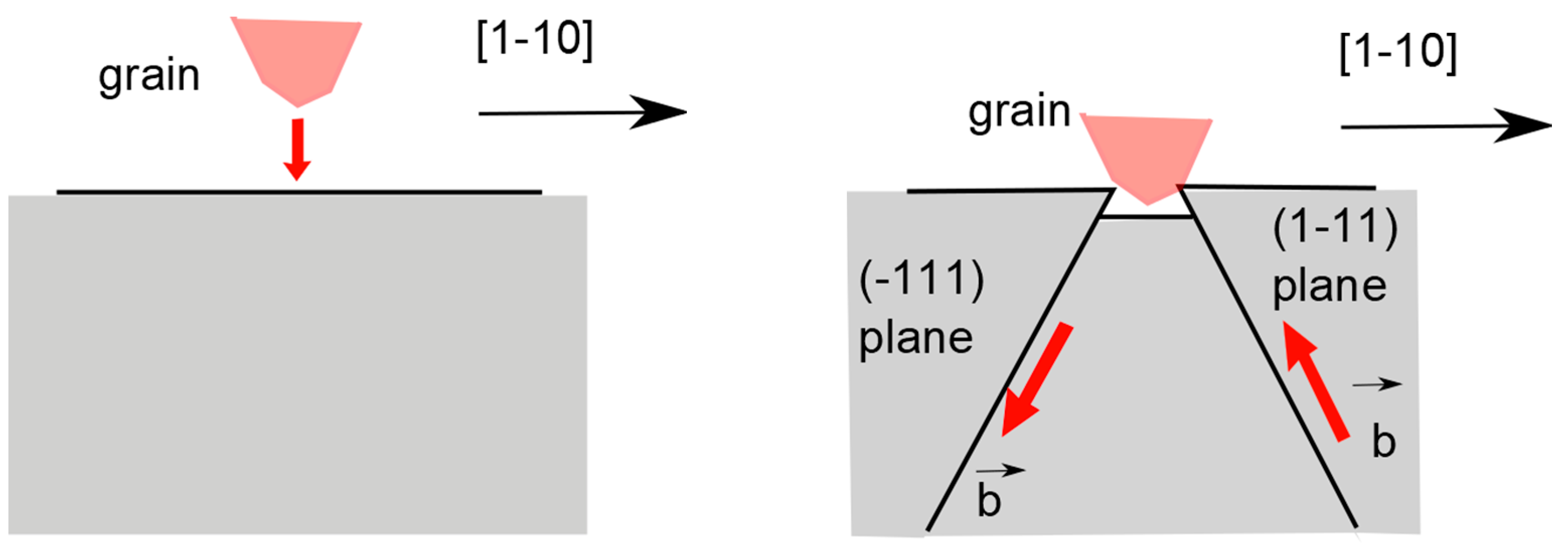
- the formation of an amorphous layer near the surface of the crystal generated by the relevant forces acting of the tips of the grains [11];
2. Experimental and Observation
2.1. Preparation of Crystals
2.2. TEM Analysis
- -
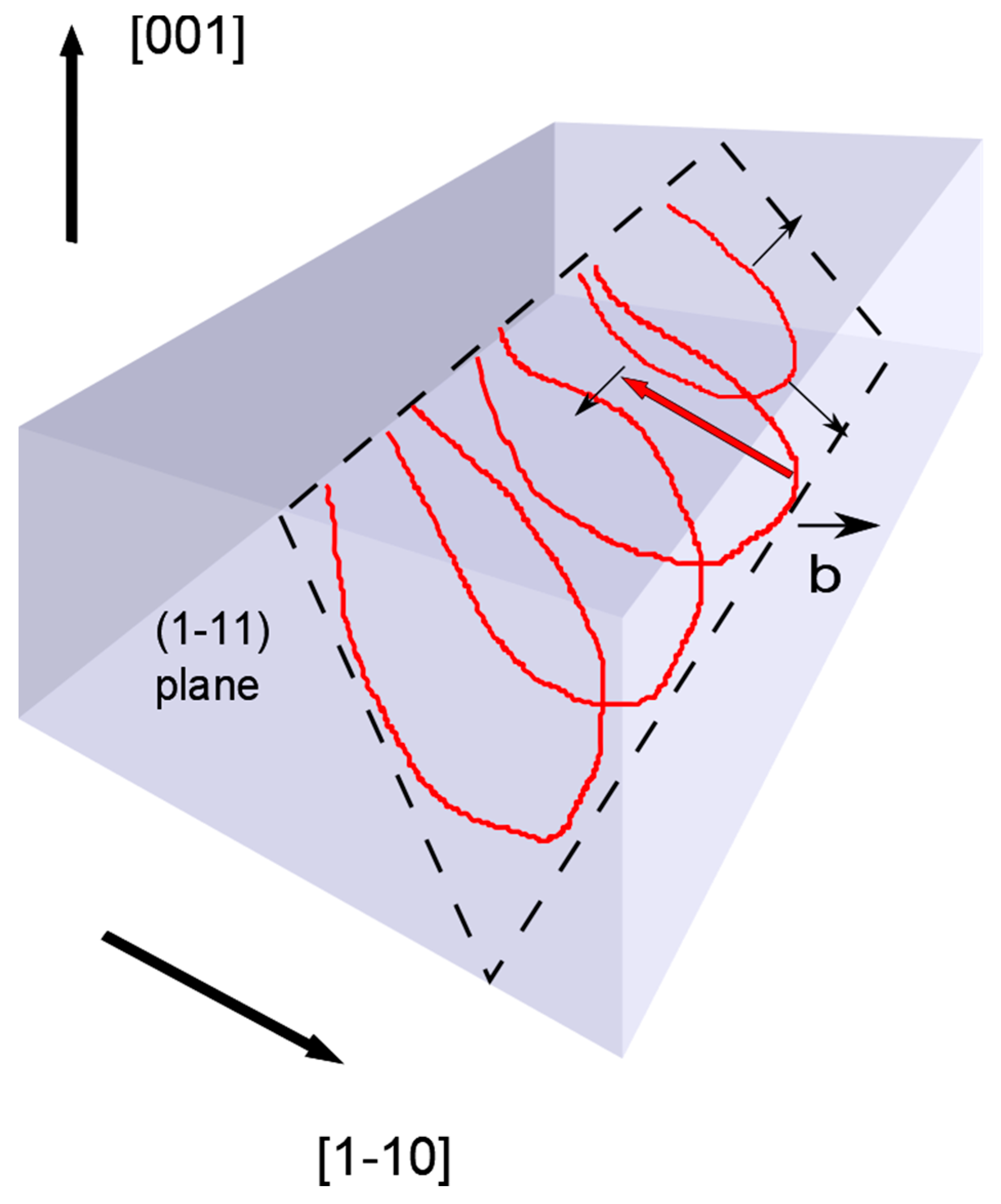
- these dislocations have the lowest elastic energy among perfect dislocations in the face-centered-cubic (fcc) crystals;
- -
- non-perfect dislocations are always associated to stacking faults increasing the elastic energy and limiting their mobility;
- -
- these dislocations are typically observed in indented fcc crystals.
3. Model
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ferrari, C.; Buffagni, E.; Bonnini, E.; Zappettini, A. X-ray diffraction efficiency of bent GaAs mosaic crystals for the LAUE project. Proc. SPIE 2013, 88610D. [Google Scholar] [CrossRef]
- Roa, D.E.; Smither, R.K.; Zhang, X.; Nie, K.; Shie, Y.Y.; Ramsinghani, N.S.; Milone, N.; Kuo, J.V.; Redpath, J.L.; Al-Ghazi, M.S.A.L.; et al. Crystal diffraction lens for medical imaging. Exp. Astron. 2005, 20, 229. [Google Scholar] [CrossRef]
- Courtois, P.; Bigault, T.; Andersen, K.H.; Baudin-Cavallo, J.; Ben Saıdane, K.; Berneron, M.; El-Aazzouzzi, A.; Gorny, D.; Graf, W.; Guiblain, T.; et al. Status and recent developments in diffractive neutron optics at the ILL. Phys. B Condens. Matter 2006, 385, 1271–1273. [Google Scholar] [CrossRef]
- Borbély, A.; Kaysser-Pyzalla, A.R. X-ray diffraction microscopy: Emerging imaging techniques for nondestructive analysis of crystalline materials from the millimetre down to the nanometre scale. J. Appl. Cryst. 2013, 46, 295–296. [Google Scholar] [CrossRef]
- Zachariasen, W.H. Theory of X-ray Diffraction in Crystals; Dover Pub. Inc.: New York, NY, USA, 1945. [Google Scholar]
- Malgrange, C. X-ray Propagation in Distorted Crystals: From Dynamical to Kinematical Theory. Cryst. Res. Technol. 2002, 37, 654–662. [Google Scholar] [CrossRef]
- Ferrari, C.; Buffagni, E.; Bonnini, E.; Korytar, D. High diffraction efficiency in crystals curved by surface damage. J. Appl. Cryst. 2013, 46, 1576–1581. [Google Scholar] [CrossRef]
- Virgilli, E.; Frontera, F.; Rosati, P.; Bonnini, E.; Buffagni, E.; Ferrari, C.; Stephen, J.B.; Caroli, E.; Auricchio, N.; Basili, A.; et al. Focusing effect of bent GaAs crystals for γ-ray Laue lenses: Monte Carlo and experimental results. Exp. Astron. 2016, 41, 307–326. [Google Scholar] [CrossRef]
- Liccardo, V.; Virgilli, E.; Frontera, F.; Valsan, V.; Buffagni, E.; Ferrari, C.; Bonnini, E.; Zappettini, A.; Guidi, V.; Bellucci, V.; et al. Study and characterization of bent crystals for Laue lenses. Exp. Astron. 2014, 38, 401–416. [Google Scholar] [CrossRef]
- Buffagni, E.; Ferrari, C.; Rossi, F.; Marchini, L.; Zappettini, A. X-ray diffraction efficiency of bent GaAs mosaic crystals for the Laue project. Opt. Eng. 2014, 53, 047104. [Google Scholar]
- Yan, J.; Asami, T.; Harada, H.; Kuriyagawa, T. Fundamental investigation of subsurface damage in single crystalline silicon caused by diamond machining. Precis. Eng. 2009, 33, 378–386. [Google Scholar] [CrossRef]
- Davim, J.P.; Jackson, M.J. (Eds.) Nano and Micromachining; ISTE Ltd.: London, UK; John Wiley & Sons: Hoboken, NJ, USA, 2009; ISBN 978-1-84821-103-2. [Google Scholar]
- Haapalinna, A.; Nevas, S.; Pähler, D. Rotational grinding of silicon wafers—Sub-surface damage inspection. Mater. Sci. Eng. B 2004, 107, 321–331. [Google Scholar] [CrossRef]
- Holmström, E.; Kotakoski, J.; Lechner, L.; Kaiser, U.; Nordlund, K. Atomic-scale effects behind structural instabilities in Si lamellae during ion beam thinning. AIP Adv. 2012, 2. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Guénolé, J.; Salvati, E.; Sui, T.; Mousavi, M.; Prakash, A.; Bitzek, E. Quantifying eigenstrain distributions induced by focused ion beam damage in silicon. Mater. Lett. 2016, 185, 47–49. [Google Scholar] [CrossRef]
- White, J.E. X-ray Diffraction by Elastically Deformed Crystals. J. Appl. Phys. 1950, 21, 855. [Google Scholar] [CrossRef]
- Bradby, J.E.; Williams, J.S.; Wong-Leung, J.; Swain, M.V.; Munroe, P. Mechanical deformation of InP and GaAs by spherical indentation. Appl. Phys. Lett. 2001, 78, 3235. [Google Scholar] [CrossRef]
- Stoney, G.G. The Tension of Metallic Films Deposited by Electrolysis. Proc. R. Soc. 1909, 82, 172–175. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferrari, C.; Ghica, C.; Rotunno, E. A Study of Extended Defects in Surface Damaged Crystals. Crystals 2018, 8, 67. https://doi.org/10.3390/cryst8020067
Ferrari C, Ghica C, Rotunno E. A Study of Extended Defects in Surface Damaged Crystals. Crystals. 2018; 8(2):67. https://doi.org/10.3390/cryst8020067
Chicago/Turabian StyleFerrari, Claudio, Corneliu Ghica, and Enzo Rotunno. 2018. "A Study of Extended Defects in Surface Damaged Crystals" Crystals 8, no. 2: 67. https://doi.org/10.3390/cryst8020067
APA StyleFerrari, C., Ghica, C., & Rotunno, E. (2018). A Study of Extended Defects in Surface Damaged Crystals. Crystals, 8(2), 67. https://doi.org/10.3390/cryst8020067





