Superradiant MeV γ Scattered by a Room-Temperature Spinor Quantum Fluid
Abstract
:1. Introduction
2. Results
2.1. Suppression of Atomic Channels
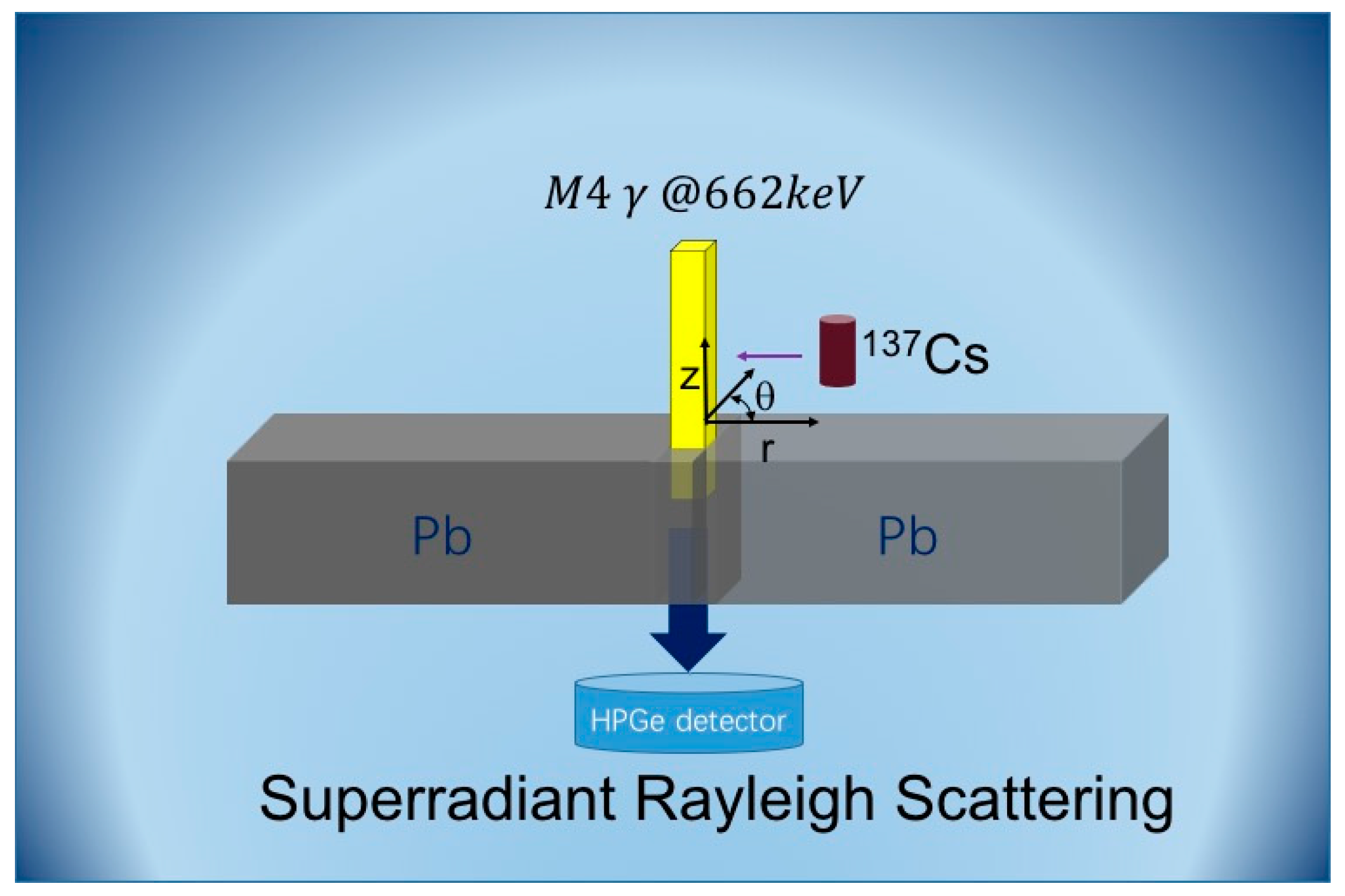
2.2. Superradiant Rayleigh Scattering and Its Near-Field Diffraction
2.3. Room-Temperature BEC as Proven by End-Fire Superradiance
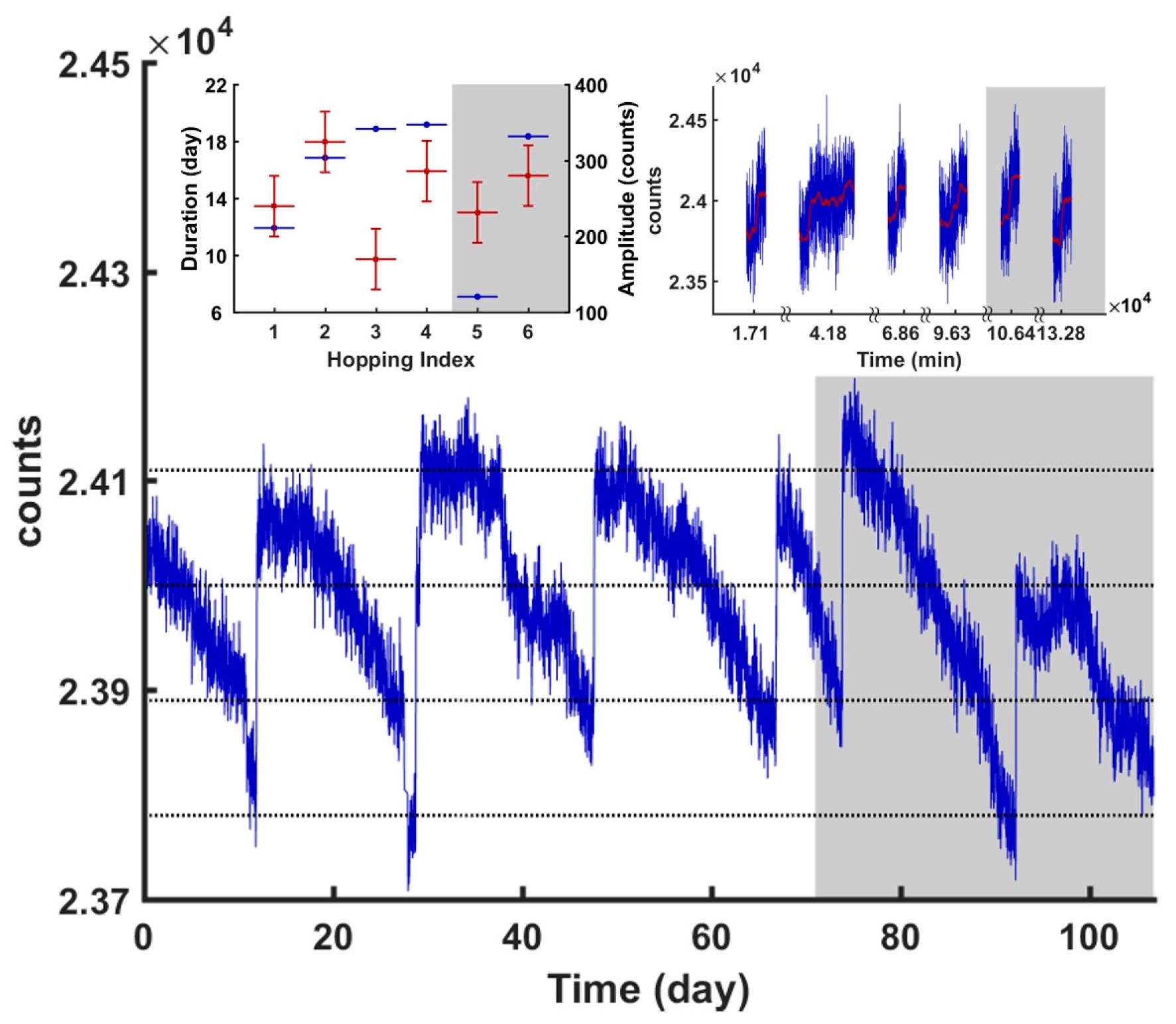
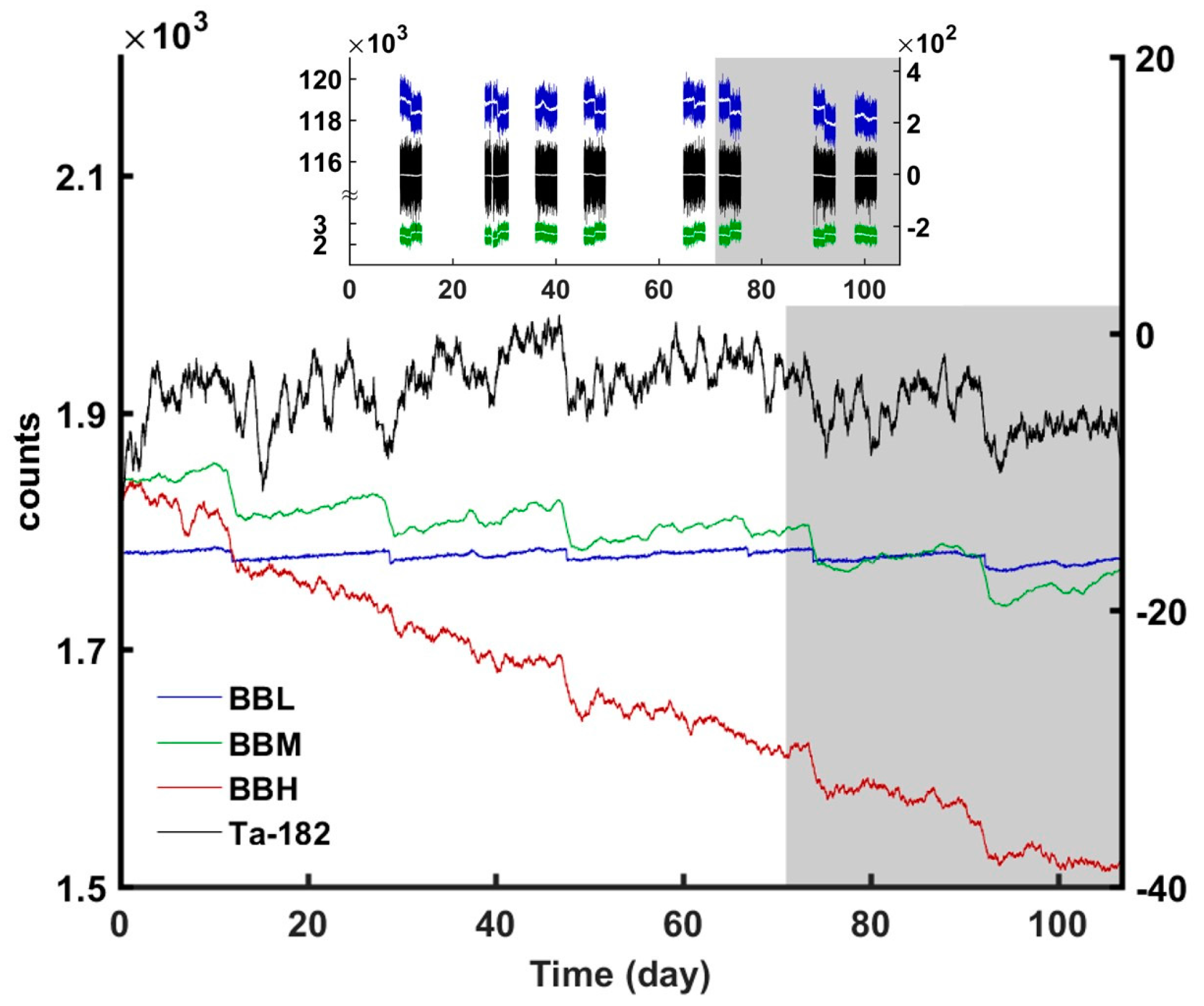
2.4. Mode Hopping of the Matter-Wave Grating
2.5. Surficial Superradiance
3. Discussion
- (1)
- The 182Ta γs gave a fast negative response to the mode hopping of the M4 γ. The matter-wave grating at 662 keV enabled the rejection of the coexisting superradiant 182Ta γs.
- (2)
- The M4 superradiance contracted into a shallow region beneath the sample surface depending on the γ intensity. However, the spatial shrinkage of the M4 superradiance gave more room for the 182Ta superradiance.
- (3)
- It is clear that a Raman pumps 182Ta to the allowed β transitions, which accelerates the decay. For example, a hyper-Raman pumped 94Nb to a virtual state of Jπ = 6+, β transitions from which to two 94Mo excitations of Jπ = 6+ were allowed (see Figure S3C in the Supplementary Information). In contrast, the slowdown 182Ta decay is subtle. It is well known that a suppression effect incorporates a destructive interference between two paths, as demonstrated by the Borrmann effect [13]. Observations of the 182Ta lifetimes depending on the M4 intensity has shed some light on the problem. The remaining questions are to construct a model of the β decay encountering multiple branching, splittings of which are opened by the highly-concentrated mixing of M4 and E2 fields.
- (4)
- The impinging M4 γ activated the 93mNb excitation, as shown by Figure S3A in the Supplementary Information. Increasing NSDW density provides a stronger matter-wave grating to promote the collective forward scattering of 182Ta γs.
- (5)
- Superradiance of both the impinging γs and the internal 182Ta γs showed systematic oscillations, which were most likely driven by external sources.
4. Materials and Methods
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BEC | Bose-Einstein Condensation |
| ODLRO | off-diagonal long-ranged order |
| ME | magnetoelectric effect |
| NSDW | nuclear spin-density wave |
| SAC | suppression of atomic channels |
| BBL | broad-band x-rays in low-energy range |
| BBM | broad-band x-rays in middle-energy range |
| BBH | broad-band x-rays in high-energy range |
| HPGe | high-purity germanium |
| Cps | counts per second |
References
- Anderson, M.H.; Ensher, J.R.; Matthews, M.R.; Wieman, C.E.; Cornell, E.A. Observation of Bose-Einstein condensation in a dilute atomic Vapor. Science 1995, 269, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Davis, K.B.; Mewes, M.-O.; Andrews, M.R.; van Druten, N.J.; Durfee, D.S.; Kurn, D.M.; Ketterle, W. Bose–Einstein condensation in a gas of sodium atoms. Phys. Rev. Lett. 1995, 75, 3969–3973. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.N. Concept of off-diagonal long-range order and the quantum phases of liquid He and of superconductors. Rev. Mod. Phys. 1964, 34, 694–703. [Google Scholar] [CrossRef]
- Ueda, M. Fundamentals of Bose-Einstein Condensation. In Fundamentals and New Frontiers of Bose-Einstein Condensation; Ryan, B., Ed.; World Scientific Co., Pte. Ltd.: Singapore, 2010; pp. 1–32. [Google Scholar]
- Deng, H.; Haung, H.; Yamamoto, Y. Exciton-polariton Bose-Einstein condensation. Rev. Mod. Phys. 2010, 82, 1489–1537. [Google Scholar] [CrossRef]
- Carusotto, I.; Ciuti, C. Quantum fluid of light. Rev. Mod. Phys. 2013, 85, 299–366. [Google Scholar] [CrossRef]
- Cheng, Y.; Guo, Z.-Y.; Liu, Y.-L.; Lee, C.-H.; Young, B.-L. Magnetoelectric effect induced by the delocalised 93mNb state. Radiat. Eff. Defects Solids 2015, 170, 43–54. [Google Scholar] [CrossRef]
- Liu, Y.-Y.; Cheng, Y. Impurity channels of the long-lived Mossbauer effect. Sci. Rep. 2015, 5, 15741. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Yang, S.-H.; Lan, M.; Lee, C.-H. Observations on the long-lived Mossbauer effects of 93mNb. Sci. Rep. 2016, 6, 36144. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Xia, B.; Chen, C.P. Cooling effect in emissions of 103mRh excited by bremsstrahlung. Phys. Scr. 2009, 79, 055703. [Google Scholar] [CrossRef]
- Cheng, Y. A possible scheme for measuring gravitational waves using a spinful quantum fluid. In Proceedings of the ISEG5–Fifth International Symposium on Experimental Gravitation (EPJ Web of Conferences 2014), Nanjing, China, 8–13 July 2013; p. 02001. [Google Scholar]
- Maggiore, M. Spontaneous symmetry breaking. In A Modern Introduction to Quantum Field Theory; Oxford University Press: New York, NY, USA, 2007; pp. 253–265. [Google Scholar]
- Hannon, J.P.; Trammell, G.T. Coherent γ-ray optics. Hyperfine Interact. 1999, 123, 127–274. [Google Scholar] [CrossRef]
- Fox, M. Resonant light-atom interactions. In Quantum Optics; Oxford University Press: New York, NY, USA, 2006; pp. 167–193. [Google Scholar]
- Greiner, M.; Mandel, O.; Hansch, T.W.; Bloch, I. Collapse and revival of the matter wave field of a Bose–Einstein condensate. Nature 2002, 419, 51–54. [Google Scholar] [CrossRef] [PubMed]
- Khaymovich, I.M.; Silaev, M.A. Magnetic resonance within vortex cores in the B phase of superfluid 3He. Phys. Rev. B 2010, 82, 094507. [Google Scholar] [CrossRef]
- Mizushima, T.; Tsutsumi, Y.; Kawakami, T.; Sato, M.; Ichioka, M.; Machida, K. Symmetry-Protected Topological Superfluids and Superconductors—From the Basics to 3He—. J. Phys. Soc. Jpn. 2016, 85, 022001. [Google Scholar] [CrossRef]
- Qi, X.-L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057–1101. [Google Scholar] [CrossRef]
- Inouye, S.; Chikkatur, A.P.; Stamper-Kurn, D.M.; Stenger, J.; Pritchard, D.E.; Ketterle, W. Superradiant Rayleigh scattering from a Bose-Einstein condensate. Science 1999, 285, 571–574. [Google Scholar] [CrossRef] [PubMed]
- Yoshikawa, Y.; Torii, Y.; Kuga, T. Superradiant light scattering from thermal atomic vapors. Phys. Rev. Lett. 2005, 94, 83602–83605. [Google Scholar] [CrossRef] [PubMed]
- Ritsch, H.; Domokos, P.; Brennecke, F.; Esslinger, T. Cold atoms in cavity-generated dynamical optical potentials. Rev. Mod. Phys. 2013, 85, 553–601. [Google Scholar] [CrossRef]
- Hecht, E. Optics, 4th ed.; Addison Wesley: San Francisco, CA, USA, 2002. [Google Scholar]
- Krause, M.O.; Oliver, J.H. Natural widths of atomic K and L levels, Kα X-ray lines and several KLL Auger lines. J. Phys. Chem. Ref. Data 1979, 8, 329–338. [Google Scholar] [CrossRef]
- Belger, M.; Schimming, R.; Wunsch, V. A survey on Huygens’ principle. Z. Anal. Anwend. 1997, 16, 9–36. [Google Scholar] [CrossRef]
- Baumann, K.; Guerlin, C.; Brennecke, F.; Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optic cavity. Nature 2010, 464, 1301–1306. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Moore, K.L.; Murch, K.W.; Stamper-Kurn, D.M. Cavity Nonlinear Optics at Low Photon Numbers from Collective Atomic Motion. Phys. Rev. Lett. 2007, 99, 213601. [Google Scholar] [CrossRef] [PubMed]
- Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 1987, 58, 1799–1802. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.L.; Park, H.C.; Ihm, J.; Son, Y.-W. Manifestation of axion electrodynamics through magnetic ordering on edges of a topological insulator. Proc. Natl. Acad. Sci. USA 2015, 112, 11514–11518. [Google Scholar] [CrossRef] [PubMed]
- Braginsky, V.B.; Vyatchanin, S.P. Low quantum noise tranquilizer for Fabry–Perot interferometer. Phys. Lett. A 2002, 293, 228–234. [Google Scholar] [CrossRef]
| γ in keV | γ Type | Half-Life | Calibration | Pristine | Active | DAS |
|---|---|---|---|---|---|---|
| 40 | E1 | 0.01 fs | 15.6 ± 0.1 | 0 | 0 | -- |
| 45 | E1 | 0.01 fs | 18.1 ± 0.1 | 0 | 0 | -- |
| 296 | E1 | 27 fs | 5.78 ± 0.05 | 5.16 ± 0.02 | 5.16 ± 0.01 | 0.5 ± 0.4 |
| 368 | E1 | 0.2 ps * | 8.95 ± 0.05 | 7.35 ± 0.02 | 7.39 ± 0.01 | 1.0 ± 0.3 |
| 444 | E1 | 27 fs | 24.23 ± 0.05 | 22.29 ± 0.02 | 22.31 ± 0.02 | 0.5 ± 0.1 |
| 779 | E1 | 0.2 ps * | 60.86 ± 0.07 | 56.81 ± 0.02 | 56.73 ± 0.02 | 0.22 ± 0.05 |
| 1408 | E1 | 27 fs | 61.48 ± 0.06 | 59.05 ± 0.02 | 58.84 ± 0.02 | 0.0 |
| 122 | E2 | 1.4 ns | 652.7 ± 0.2 | 376.18 ± 0.05 | 385.71 ± 0.05 | 2.90 ± 0.017 |
| 245 | E2 | 58 ps | 108.2 ± 0.1 | 94.02 ± 0.03 | 94.27 ± 0.03 | 0.62 ± 0.04 |
| 344 | E2 | 32 ps | 282.8 ± 0.1 | 252.04 ± 0.04 | 252.25 ± 0.04 | 0.44 ± 0.02 |
| 964 | E2 + M1 | 0.87 ps | 59.25 ± 0.07 | 56.46 ± 0.02 | 56.29 ± 0.02 | 0.05 ± 0.05 |
| 1121 | E2 + M1 | 114.13 d | 133.54 ± 0.09 | 134.57 ± 0.03 | 134.39 ± 0.03 | 0.22 ± 0.03 |
| DT | -- | -- | 16.21% | 15.28% | 15.30% | -- |
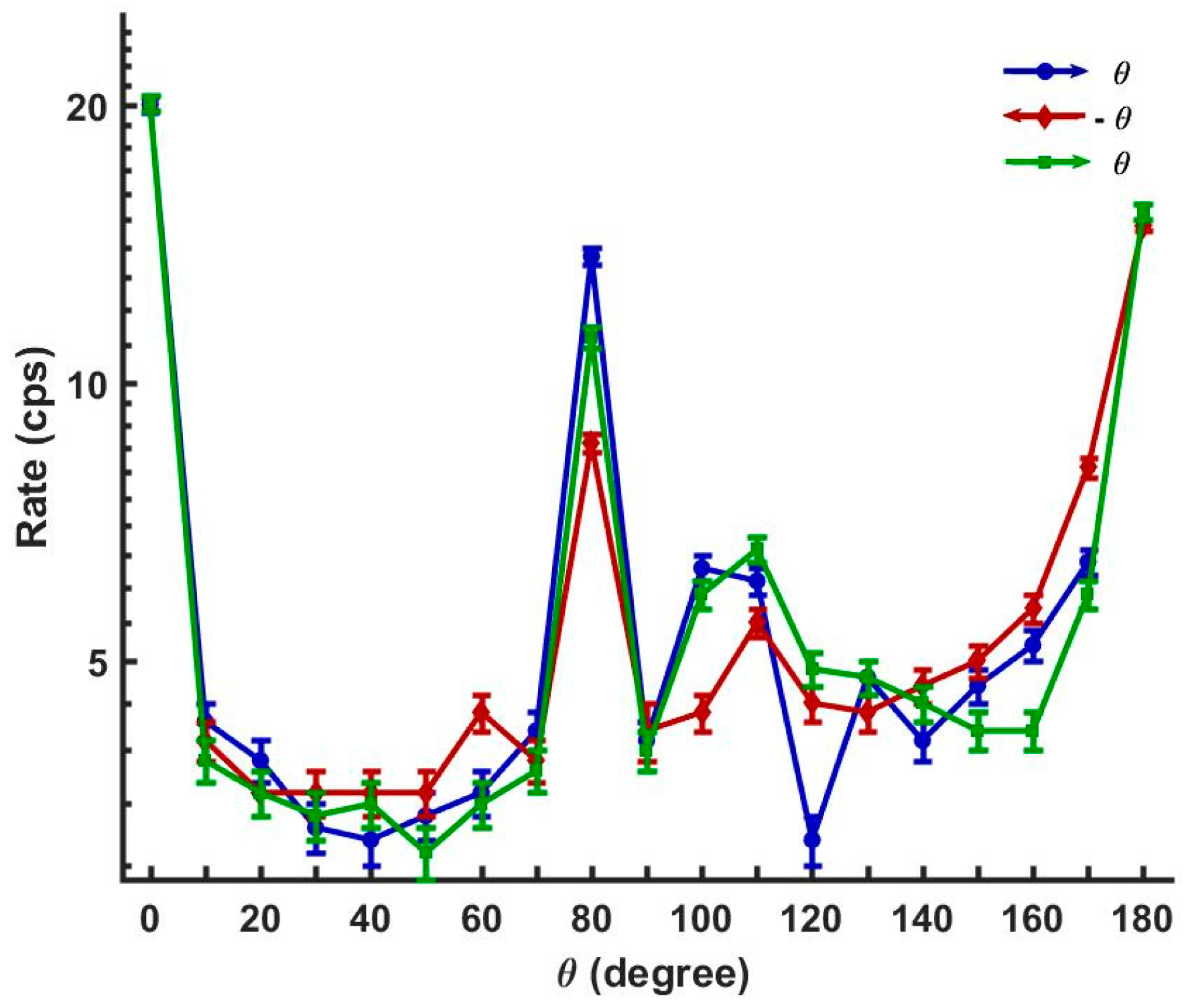
| θ in Degree | θ | −θ | θ |
|---|---|---|---|
| 0 | 20.0 ± 0.4 | -- | 20.1 ± 0.4 |
| 10 | 4.3 ± 0.2 | 4.1 ± 0.2 | 3.9 ± 0.2 |
| 20 | 3.9 ± 0.2 | 3.6 ± 0.2 | 3.6 ± 0.2 |
| 30 | 3.3 ± 0.2 | 3.6 ± 0.2 | 3.4 ± 0.2 |
| 40 | 3.2 ± 0.2 | 3.6 ± 0.2 | 3.5 ± 0.2 |
| 50 | 3.4 ± 0.2 | 3.6 ± 0.2 | 3.1 ± 0.2 |
| 60 | 3.6 ± 0.2 | 4.4 ± 0.2 | 3.5 ± 0.2 |
| 70 | 4.2 ± 0.2 | 3.9 ± 0.2 | 3.8 ± 0.2 |
| 80 | 13.7 ± 0.3 | 8.6 ± 0.3 | 11.2 ± 0.3 |
| 90 | 4.1 ± 0.2 | 4.2 ± 0.2 | 4.0 ± 0.2 |
| 100 | 6.3 ± 0.2 | 4.4 ± 0.2 | 5.9 ± 0.2 |
| 110 | 6.1 ± 0.2 | 5.5 ± 0.2 | 6.6 ± 0.2 |
| 120 | 3.2 ± 0.2 | 4.5 ± 0.2 | 4.9 ± 0.2 |
| 130 | 4.8 ± 0.2 | 4.4 ± 0.2 | 4.8 ± 0.2 |
| 140 | 4.1 ± 0.2 | 4.7 ± 0.2 | 4.5 ± 0.2 |
| 150 | 4.7 ± 0.2 | 5.0 ± 0.2 | 4.2 ± 0.2 |
| 160 | 5.2 ± 0.2 | 5.7 ± 0.2 | 4.2 ± 0.2 |
| 170 | 6.4 ± 0.2 | 8.1 ± 0.2 | 5.9 ± 0.2 |
| 180 | -- | 14.8 ± 0.3 | 15.3 ± 0.3 |
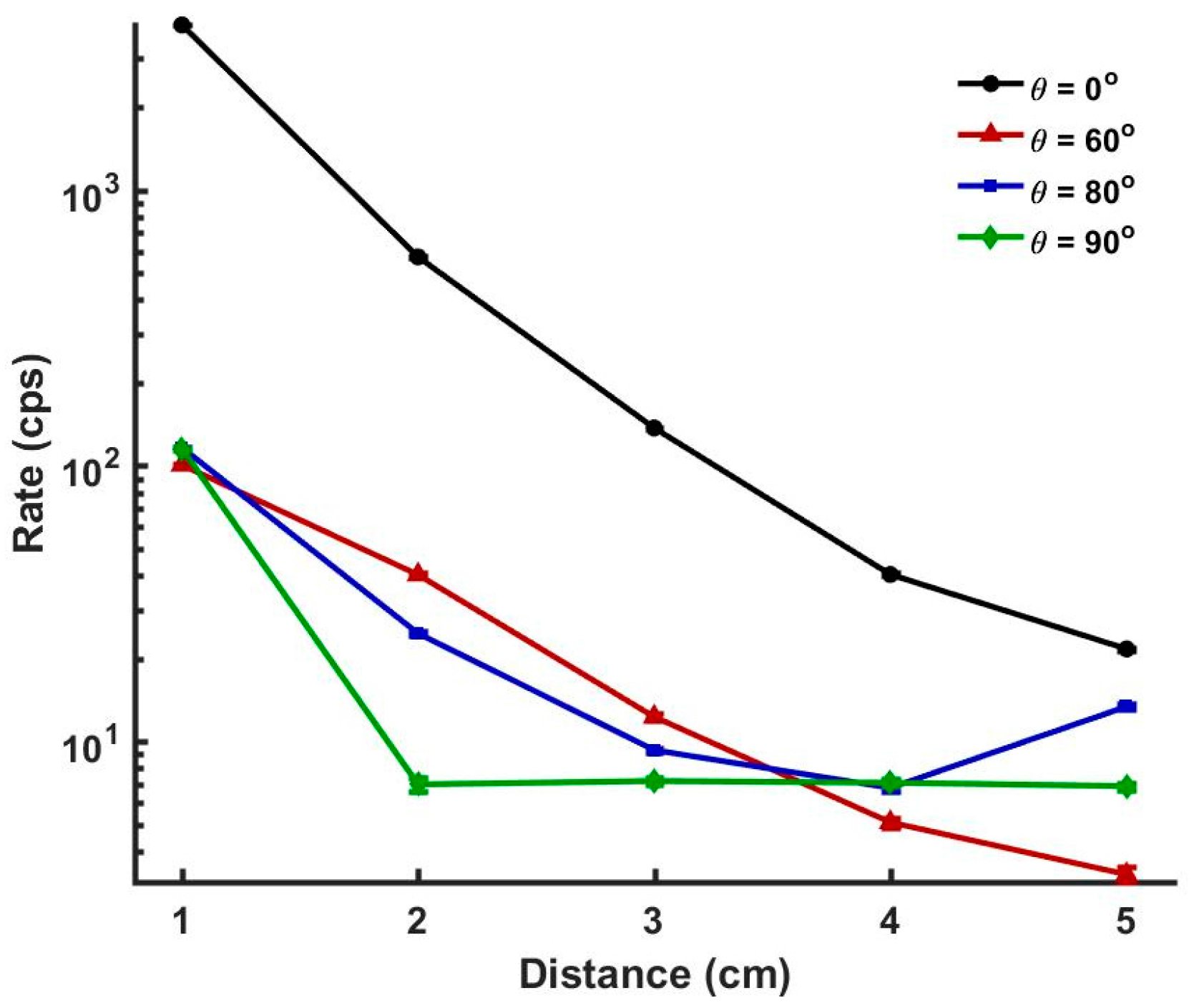
| θ/r | 1 cm | 2 cm | 3 cm | 4 cm | 5 cm |
|---|---|---|---|---|---|
| 0° 662 keV | 3973 ± 5 | 572.8 ± 1.7 | 137.3 ± 0.6 | 40.4 ± 0.4 | 21.7 ± 0.3 |
| 0° 1121 keV | 5.9 ± 0.4 | 6.9 ± 0.2 | 6.5 ± 0.2 | 7.1 ± 0.2 | 6.9 ± 0.2 |
| 60° 662 keV | 100.8 ± 0.7 | 40.3 ± 0.5 | 12.3 ± 0.3 | 5.1 ± 0.2 | 3.3 ± 0.2 |
| 60° 1121keV | 6.8 ± 0.2 | 7.0 ± 0.2 | 7.2 ± 0.2 | 7.1 ± 0.2 | 7.2 ± 0.2 |
| 80° 662 keV | 116.5 ± 0.8 | 24.7 ± 0.4 | 9.3 ± 0.2 | 6.8 ± 0.2 | 13.4 ± 0.3 |
| 80° 1121 keV | 6.8 ± 0.2 | 6.7 ± 0.2 | 7.0 ± 0.2 | 6.9 ± 0.2 | 7.1 ± 0.2 |
| 90° 662 keV | 115.5 ± 0.7 | 22.3 ± 0.4 | 8.6 ± 0.2 | 5.3 ± 0.2 | 3.9 ± 0.2 |
| 90° 1121 keV | 7.0 ± 0.2 | 7.0 ± 0.2 | 7.2 ± 0.2 | 7.1 ± 0.2 | 6.9 ± 0.2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Lin, T.-H.; Lee, C.-H.; Wu, S.-C. Superradiant MeV γ Scattered by a Room-Temperature Spinor Quantum Fluid. Crystals 2017, 7, 196. https://doi.org/10.3390/cryst7070196
Cheng Y, Lin T-H, Lee C-H, Wu S-C. Superradiant MeV γ Scattered by a Room-Temperature Spinor Quantum Fluid. Crystals. 2017; 7(7):196. https://doi.org/10.3390/cryst7070196
Chicago/Turabian StyleCheng, Yao, Ting-Han Lin, Chih-Hao Lee, and Shun-Chi Wu. 2017. "Superradiant MeV γ Scattered by a Room-Temperature Spinor Quantum Fluid" Crystals 7, no. 7: 196. https://doi.org/10.3390/cryst7070196
APA StyleCheng, Y., Lin, T.-H., Lee, C.-H., & Wu, S.-C. (2017). Superradiant MeV γ Scattered by a Room-Temperature Spinor Quantum Fluid. Crystals, 7(7), 196. https://doi.org/10.3390/cryst7070196






