First Principles Study on Structure Stability and Mechanical Properties of YNi₂B₂C and LuNi₂B₂C under Pressure

Abstract

The pressure effects on the lattice parameters and elastic constants of the tetragonal RNi${}_2$B${}_2$C (R=Y, Lu) are investigated by means of the first principles. The predicted lattice constants and elastic constants of YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C at 0 GPa agree well with the available data. By the elastic stability criteria under isotropic pressure, it is predicted that YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C with tetragonal structure are not mechanically stable above 93 GPa and 50 GPa, respectively. Pugh’s modulus ratio, Poisson’s ratio, Vickers hardness, elastic anisotropy and Debye temperature of YNi${}_2$B${}_2$C in the pressure range of 0–100 GPa and LuNi${}_2$B${}_2$C in the pressure range of 0-60 GPa are further investigated. It is shown that the ductility and Debye temperature of tetragonal RNi${}_2$B${}_2$C (R=Y, Lu) increase with increasing pressure, and LuNi${}_2$B${}_2$C is more ductile and lower Debye temperature than YNi${}_2$B${}_2$C under different pressures.

1. Introduction

Since the pioneering and seminal discovery of the superconducting alloy system Y-Ni-B-C [1,2] by Nagarajan et al., much attention has been paid to synthesizing single phase samples of quaternary boro-carbides. Cava et al. [3] have synthesized the quaternary nickel borocarbides RNi${}_2$B${}_2$C (R=Y and rare earths), and found that Lu and Y compounds exhibit the highest superconducting transition temperatures ($T_c=$ 16.6 and 15.6 K, respectively), while compounds with magetic rare earths exhibit lower $T_c$: T${}_{\mathrm{m}}$ ($T_c=11$ K), E${}_{\mathrm{r}}$ ($T_c=10.5$ K), H${}_{\mathrm{o}}$ ($T_c=8$ K). The body-centered-tetragonal RNi${}_2$B${}_2$C (R=Y, Lu) have $I4/mmm$ space group and their crystal structure is shown in Figure 1, which also can be seen as a layered structure consisting of the NaCl-type Y-C layers separated by the Ni${}_2$-B${}_2$ layers with 1:1 approaching each other alternately stacked [4]. Because RNi${}_2$B${}_2$C (R=Y, Lu) have high-$T_c$ superconductivity, considerable theoretical as well as experimental attention has been focused on these borocarbide system. From experimental measurements, inelastic-neutron-scattering curve techniques [5] were employed to measure the low-lying phonon-dispersion curves of LuNi${}_2$B${}_2$C along the [100] and [001] symmetry directions, while results of Raman measurements on RNi${}_2$B${}_2$C (R=Lu, Ho, and Y) single crystals were reported by Park et al. [6]. Meenakshi et al. [7] investigated the high pressure behaviour of YNi${}_2$B${}_2$C at room temperature by electrical resistivity, thermopower and X-ray diffraction incorporating imaging plate. Recently, Weber et al. [8] reported an inelastic neutron scattering investigation of phonons with energies up to 159 meV in YNi${}_2$B${}_2$C. From theoretical research, Mattheiss [9] calculated band structures of LuNi${}_2$B${}_2$C and YNi${}_2$B${}_2$C via the linearized augmented-plane-wave (LAPW) method. Lee et al. [10] systematically researched the electronic structures of Ni-based superconducting quaternary compounds YNi${}_2$B${}_2$X (X=B, C, N, and O) by employing the linearized muffin-tin orbital band method. The effect of pressure on the compressibilities of LuNi${}_2$B${}_2$C and YNi${}_2$B${}_2$C has been investigated within the local-density approximation (LDA) to density-functional theory (DFT) [11,12]. Recently, Wang et al. [13] calculated the elastic and electronic structure properties of YNi${}_2$B${}_2$C under pressure by performing the generalized gradient approximation (GGA) and LDA correction scheme in the frame of DFT. More recently, Tütüncü et al. [14] systematically investigated the structural, electronic, vibrational, and superconducting properties of borocarbide superconductors RM${}_2$B${}_2$C (R=Lu, La, Y; M=Ni, Pd, Pt) by employing the ab initio pseudopotential calculations. All these researches are very important to further scientific and technical investigations. However, so far, the influence of pressure on the structural, elastic and mechanical properties of tetragonal RNi${}_2$B${}_2$C (R=Y, Lu) has received little attention.

Figure 1. Crystal structure of YNi${}_2$B${}_2$C.

Elastic properties of a solid are very important because they are closely associated with some physical properties such as bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, the velocity of sound of longitudinal wave and shear wave. f And the pressure dependence of the elastic constants of a material is important for predicting and understanding the mechanical strength, stability, and phase transitions of a material. Motivated by the interest in the elastic and mechanical properties of RNi${}_2$B${}_2$C (R=Y, Lu), in this paper we will take the first-principles calculations to further investigate the structural, elastic and mechanical properties of RNi${}_2$B${}_2$C (R=Y, Lu) under pressure. The rest of the paper is organized as follows. The theory and computational details are given in Section 2. Results and discussions are presented in Section 3. Finally, the summary of our main results are drawn in Section 4.

2. Theory and Computational Details

Our first-principles calculations are performed using the VASP code, which is based on the DFT [15,16,17]. The ion-electron interaction is described by the projector augmented wave (PAW) method [18,19], and the exchange-correlation function is described within the GGA according to the Perdew-Burke-Ernzerhof (PBE) functional [20]. In this work, the 4s, 4p, 4d and 5s electrons for Y, the 5d and 6s electrons for Lu, the 2s and 2p electrons for C, the 2s and 2p electrons for B, and the 3d and 4s electrons for Ni are treated as valence and the remaining electrons are kept frozen. Reciprocal space is represented by Monkhorst-Pack special k-point scheme [21] with 15 × 15 × 5 grid meshes. The plane wave cutoff energy is chosen to be 600 eV and the energy convergence criterion is set to 10${}^{-6}$ eV for all calculations.

In this paper, the finite-strain continuum elastic theory is employed to calculate the elastic constants [22,23,24,25]. The deformation tensor

$$\begin{array}{c}\hfill J_{ij}=\frac{\partial x_i^{\prime }}{\partial x_j}\end{array}$$

(1)

where $x_i$ and $x_i^{\prime }$ are the initial and strained configurations at the equilibrium, respectively, with i and j (= 1, 2, 3) represent Cartesian coordinates. The relation between the elastic constants and the strain energy density can be expressed as [22,23]

$$\begin{array}{c}\hfill \frac{\Delta E}{V}=\frac{1}{2!}\sum _{ijkl}{C}_{ijkl}{\eta }_{ij}{\eta }_{kl}+\cdots \end{array}$$

(2)

where ${\eta }_{ij}$ is the Lagrangian strain tensor, which is defined as [24]

$$\begin{array}{c}\hfill {\eta }_{ij}=\frac{1}{2}\sum _k(J_{ik}{J}_{jk}-{\delta }_{ij})\end{array}$$

(3)

For RNi${}_2$B${}_2$C (R=Y, Lu) with tetragonal structure, there are six independent elastic constants $C_{11}$, $C_{12}$, $C_{13}$, $C_{33}$, $C_{44}$ and $C_{66}$. To calculate the complete elastic constants, we introduce six Lagrangian strain tensors in terms of a single strain parameter $\xi$, and the strain energy density $\frac{\Delta E}{V}$ can be Taylor expanded in powers of the strain parameter $\xi$ as

$$\begin{array}{c}\hfill \frac{\Delta E}{V}=\frac{1}{2}\Lambda {\xi }^2+O\left({\xi }^3\right)\end{array}$$

(4)

where V is the volume at the given pressure and $\Lambda$ is the combination of the elastic constants. We consider six sets of deformations:

$$\begin{array}{ccc}{A}_1=\left(\begin{array}{ccc}\xi & 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),& A_2=\left(\begin{array}{ccc}\xi & 0& 0\\ 0& \xi & 0\\ 0& 0& 0\end{array}\right),& A_3=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& \xi \end{array}\right),\\ A_4=\left(\begin{array}{ccc}\xi & 0& 0\\ 0& 0& 0\\ 0& 0& \xi \end{array}\right),& A_5=\left(\begin{array}{ccc}\xi & 0& 0\\ 0& 0& \xi \\ 0& \xi & 0\end{array}\right),& A_6=\left(\begin{array}{ccc}\xi & \xi & 0\\ \xi & 0& 0\\ 0& 0& 0\end{array}\right).\end{array}$$

(5)

The corresponding strain energy density on deformation parameter $\xi$ for each considered strain mode $A_{\alpha }(\alpha =1,2,\cdots ,6)$ can be expressed as

$$\begin{array}{c}\hfill \begin{array}{c}\Delta E\left(A_1\right)/V=\frac{1}{2}{C}_{11}{\xi }^2\\ \Delta E\left(A_2\right)/V=(C_{11}+C_{12}){\xi }^2\\ \Delta E\left(A_3\right)/V=\frac{1}{2}{C}_{33}{\xi }^2\\ \Delta E\left(A_4\right)/V=(\frac{1}{2}{C}_{11}+C_{13}+\frac{1}{2}{C}_{33}){\xi }^2\\ \Delta E\left(A_5\right)/V=(\frac{1}{2}{C}_{11}+2C_{44}){\xi }^2\\ \Delta E\left(A_6\right)/V=(\frac{1}{2}{C}_{11}+2C_{66}){\xi }^2\end{array}\end{array}$$

(6)

$\xi$ varies between −0.012 and 0.012 with step 0.003 for each strain mode $A_{\alpha }(\alpha$ = 1,2, …, 6). Taking YNi${}_2$B${}_2$C at 0 GPa as an example, Figure 2 shows the strain energy density as a function of deformation parameter $\xi$ for the considered six strain modes. The discrete points indicate the values from the first principles calculations and the solid curves represent the results obtained from the second-order polynomial fitting.

Figure 2. The strain-energy density relations of YNi${}_2$B${}_2$C at 0 GPa. The discrete points indicate the values from the first principles calculations and the solid curves represent the results obtained from the second-order polynomial fitting.

Based on the calculated elastic constants, the bulk modulus B and shear modulus G can be evaluated in terms of the Voigt-Reuss-Hill (VRH) scheme [26]. The Voigt modulus [27] are

$$\begin{array}{c}\hfill \begin{array}{c}{B}_V=\frac{1}{9}[2(C_{11}+C_{12})+C_{33}+4C_{13}]\\ G_V=\frac{1}{30}(M+3C_{11}-3C_{12}+12C_{44}+6C_{66})\\ M=C_{11}+C_{12}+2C_{33}-4C_{13}\end{array}\end{array}$$

(7)

and the Reuss modulus [28] are

$$\begin{array}{c}\hfill \begin{array}{c}{B}_R=C^2/M\\ G_R=15/(\left(18B_V\right)/C^2+6/(C_{11}-C_{12})+6/C_{44}+3/C_{66})\\ C^2=(C_{11}+C_{12})C_{33}-2C_{13}^2\end{array}\end{array}$$

(8)

Hill [26] proposed that the effective bulk and shear moduli should be the arithmetic mean values of the Voigt and Reuss moduli and thus obtained by

$$\begin{array}{c}\hfill \begin{array}{c}B=(B_V+B_R)/2G=(G_V+G_R)/2\end{array}\end{array}$$

(9)

3. Results and Discussion

For RNi${}_2$B${}_2$C (R=Y, Lu) with tetragonal structure, the initial structural model is built according to the previous available lattice parameters. There are six atoms per unit cell, with Y(Lu) located at (0, 0, 0), the two Ni atoms at (0, 0.5, 0.25) and (0, 0.5, 0.75), the two B atoms at positions (0, 0, z) and (1, 1, 1−z), and the C atom at (0, 0, 0.5), where z is the so-called internal parameter. Therefore, this structure is defined by two lattice parameters (a and c) and one internal parameter (z). These lattice parameters under different pressures are calculated by optimizing crystal structure at the given pressure. When optimizing the structural parameters of RNi${}_2$B${}_2$C (R=Y, Lu), the full relaxations with respect to the volume, shape and all internal atomic positions for the unit cell are carried out until the change in the total energy is smaller than 10${}^{-5}$ eV between two ionic steps relaxation. The calculated equilibrium lattice constants (a and c) and the internal parameter (z) at 0 GPa are presented and compared with available experimental [29,30,31,32,33,34,35,36,37,38] and theoretical results [11,13,14,39] in Table 1. The maximum deviations of the calculated equilibrium lattice constants a and c for RNi${}_2$B${}_2$C (R=Y, Lu) correspond to 1.22% and 1.37% as compared with the respective experimental values, while the internal parameters z are almost equal to their experimental values. This level of disagreement in the lattice constants is quite common for theories based on the GGA. Besides, the pressure dependent parameters $a/a_0$, $c/c_0$ and the ratio $c/a$ are illustrated in Figure 3, where $a_0$ and $c_0$ are the equilibrium structure parameters at $p=0$ GPa. In both systems the ratio $c/c_0$ decreases more quickly than $a/a_0$ with increasing pressure, indicating that the compression along c-axis is larger.

Table 1. Comparison of the calculated lattice parameters (Å) for RNi${}_2$B${}_2$C (R=Y, Lu) at $p=0$ GPa with the previous theoretical results and experimental data.

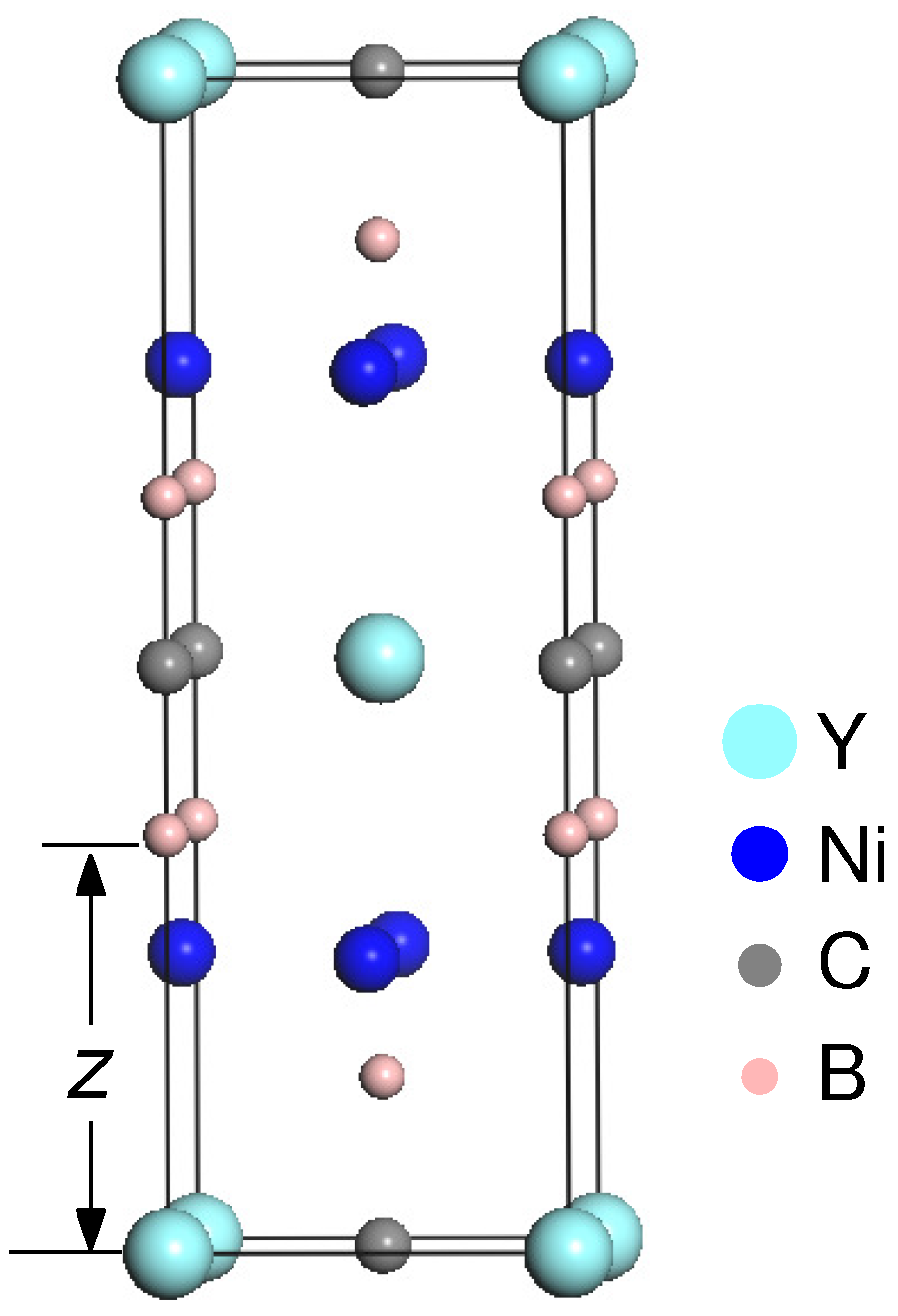
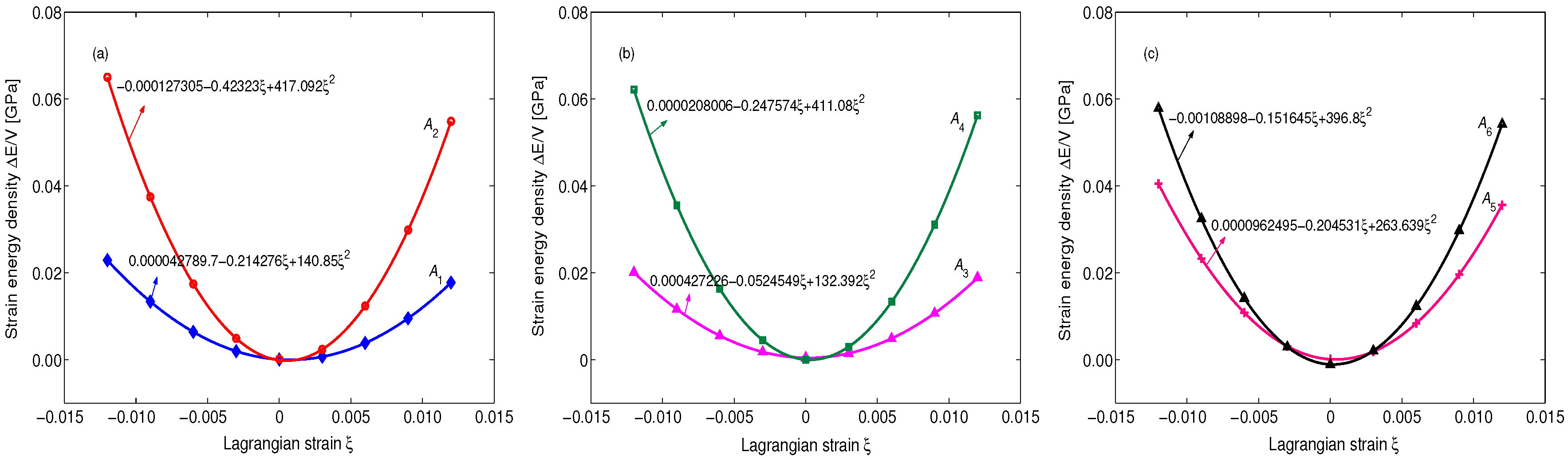
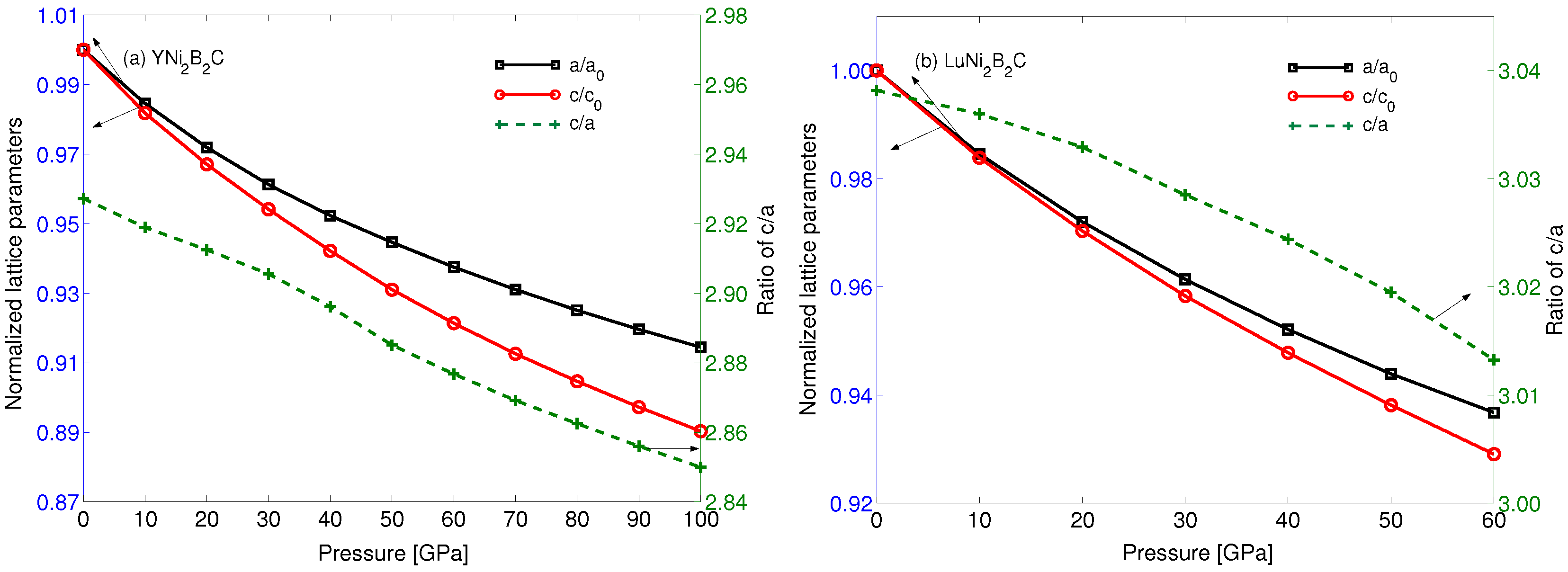
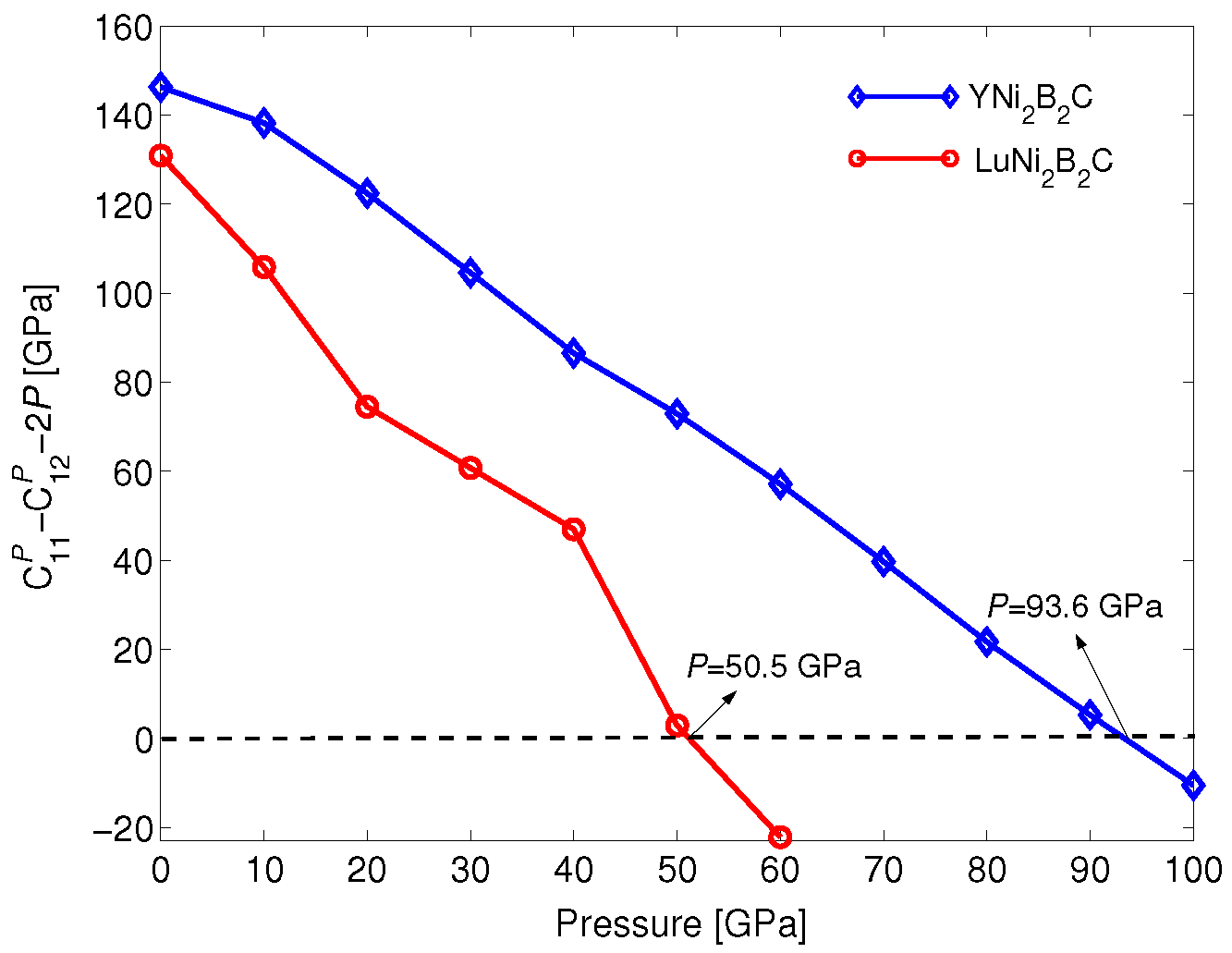
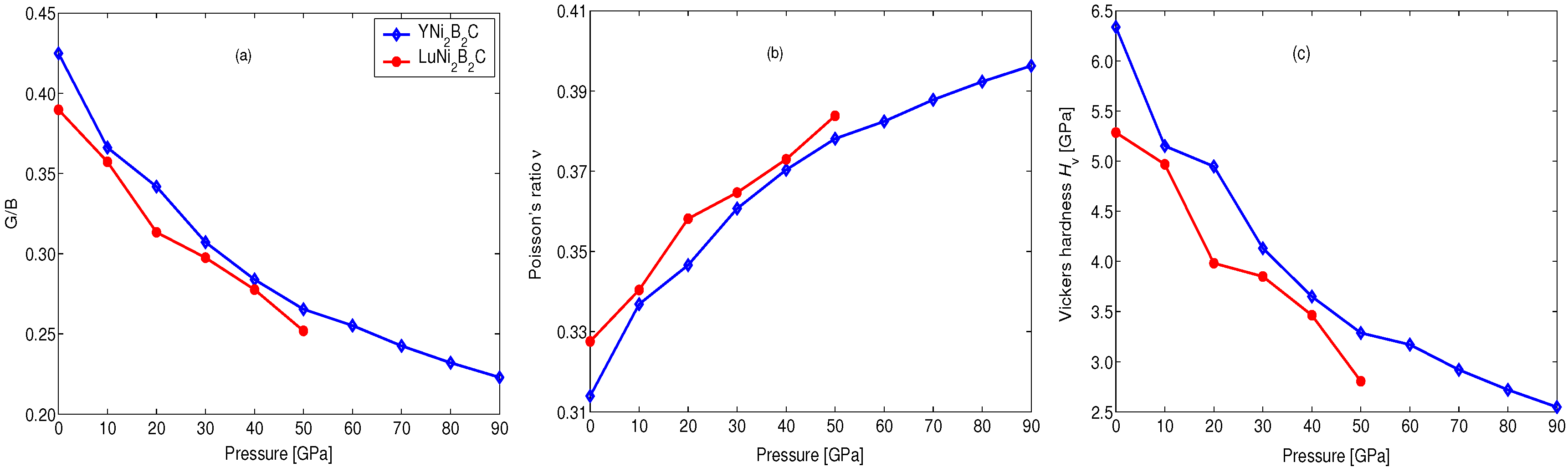
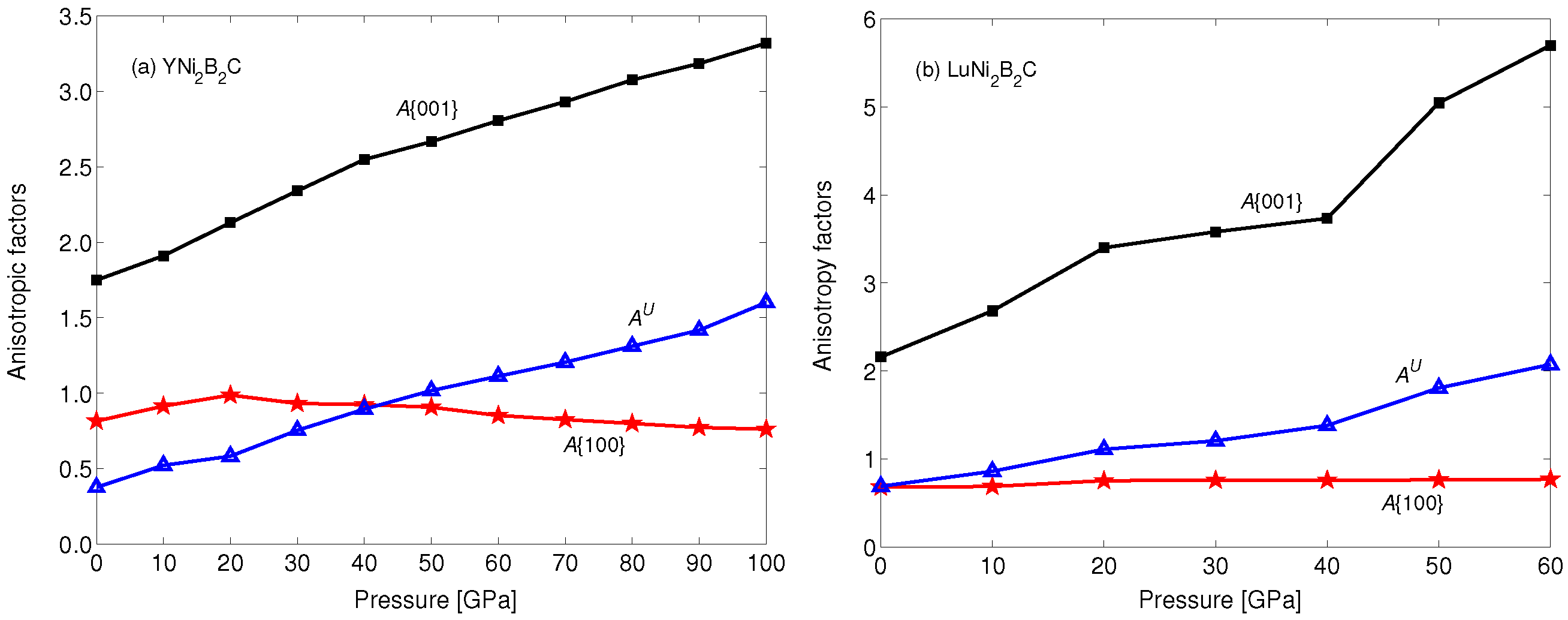
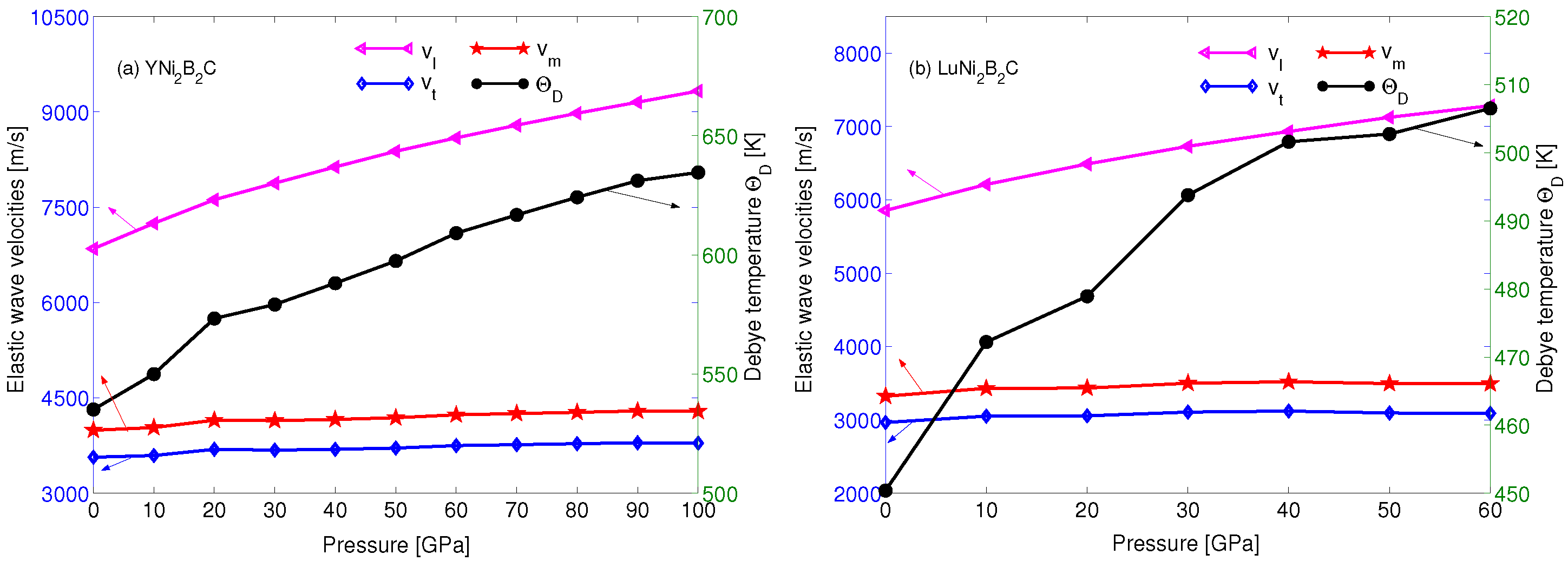
Material	Method	a/Å	c/Å	c/a	z
YNi${}_2$B${}_2$C	Present GGA	3.553	10.400	2.927	0.356
	GGA [13]	3.541	10.482	2.960	0.358
	LMTO [39]	3.507	10.485	2.937	0.353
	Experimental [29]	3.526	10.543	2.990	0.358
	Experimental [30]	3.524	10.545	2.992	0.375
	Experimental [31]	3.5258	10.5425	2.990
	Experimental [32]	3.51	10.53	3.0
LuNi${}_2$B${}_2$C	Present GGA	3.473	10.552	3.038	0.359
	GGA [14]	3.508	10.597	3.021	0.360
	LDA [11]	3.457	9.989	2.889
	Experimental [33]	3.464	10.631	3.069	0.362
	Experimental [34]	3.467	10.633	3.067
	Experimental [35]	3.464	10.623	3.067
	Experimental [36]	3.464	10.635	3.070
	Experimental [37]	3.464	10.623	3.067
	Experimental [38]	3.464	10.631	3.069

Figure 3. Normalized parameters $a/a_0$, $c/c_0$, $c/a$ of (a) YNi${}_2$B${}_2$C and (b) LuNi${}_2$B${}_2$C as a function of pressure.

Knowledge of the values of elastic constants is crucial for understanding the structural stability. The calculated elastic constants of RNi${}_2$B${}_2$C (R=Y, Lu) under different pressures are tabulated in Table 2, together with the experimental data [40] and other theoretical results [13]. It is found that our calculated elastic constants of YNi${}_2$B${}_2$C agree well with the previous results. From Table 2, whatever YNi${}_2$B${}_2$C or LuNi${}_2$B${}_2$C, it is clearly found that $C_{11}$, $C_{12}$, $C_{13}$, $C_{33}$, $C_{66}$ increase and the change of $C_{44}$ remains almost invariant with increasing pressure. The change of the elastic constants of YNi${}_2$B${}_2$C is similar to the Ref. [13] reported by Wang et al. It is also noted that $C_{11}>C_{33}$ for YNi${}_2$B${}_2$C, which indicates that atomic bonding strength along the $\left\{100\right\}$ plane between the nearest neighbors is stronger than that along the $\left\{001\right\}$ plane in the whole range of pressure, but LuNi${}_2$B${}_2$C has the opposite change trend. Besides, the relation $C_{44}<C_{66}$ for RNi${}_2$B${}_2$C (R=Y, Lu) predicts that the [100](001) shear is expected to be relatively easy in comparison with the [100](010) shear in the whole range of pressure. Moreover, the elastic stability criterion for a tetragonal crystal under isotropic pressure is as follows [25,41,42]:

$$\begin{array}{c}\hfill {\tilde{C}}_{11}^P-{\tilde{C}}_{12}^P>0,{\tilde{C}}_{11}^P+{\tilde{C}}_{33}^P-2{\tilde{C}}_{13}^P>0\\ \hfill {\tilde{C}}_{\alpha \alpha }^P>0(\alpha =1,3,4,6),2{\tilde{C}}_{11}^P+{\tilde{C}}_{33}^P+2{\tilde{C}}_{12}^P+4{\tilde{C}}_{13}^P>0\end{array}$$

(10)

where ${\tilde{C}}_{\alpha \alpha }^P=C_{\alpha \alpha }^P-P$ ($\alpha =1,3,4,6$), ${\tilde{C}}_{12}^P=C_{12}^P+P$, ${\tilde{C}}_{13}^P=C_{13}^P+P$. With increasing pressure ${\tilde{C}}_{11}^P-{\tilde{C}}_{12}^P>0$ can not be firstly satisfied among all the mechanical stability conditions for RNi${}_2$B${}_2$C (R=Y, Lu). Figure 4 shows $C_{11}^P-C_{12}^P-2P$ versus pressure for RNi${}_2$B${}_2$C (R=Y, Lu). It is observed that the $C_{11}^P-C_{12}^P-2P$ values of YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C are equal to zero at pressures about 93.6 GPa and 50.5 GPa, respectively, which indicates that the tetragonal structure is not mechanically stable above pressures about 93.6 GPa and 50.5 GPa for YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C, respectively. Wang et al. [13] suggested that the structure phase transition of YNi${}_2$B${}_2$C may happen when $p>80$ GPa.

Table 2. Calculated elastic constants $C_{ij}$ (GPa) of RNi${}_2$B${}_2$C (R=Y, Lu) under different pressures and compared with available data.

Material	Pressure	${\mathit{C}}_{11}$	${\mathit{C}}_{12}$	${\mathit{C}}_{13}$	${\mathit{C}}_{33}$	${\mathit{C}}_{44}$	${\mathit{C}}_{66}$
YNi${}_2$B${}_2$C	0	281.7	135.4	130.3	279.9	61.4	127.9
		292.7 ${}^a$, 294.6 ${}^b$	133.6 ${}^a$, 157.7 ${}^b$	138.6 ${}^a$	282.4 ${}^a$	68.6 ${}^a$, 64.4 ${}^b$	129.8 ${}^a$, 142.1 ${}^b$
		284.7 ${}^c$, 292 ${}^d$	145.7 ${}^c$, 149.8 ${}^d$	125.6 ${}^b$	261.5 ${}^b$	67.1 ${}^c$, 67.4 ${}^d$	143.3 ${}^c$, 132 ${}^d$
	10	332.6	174.4	175.9	308.3	66.0	151.1
	20	378.2, 381.3 ${}^a$	215.8, 211.3 ${}^a$	212.2, 211.2 ${}^a$	348.8, 362.6 ${}^a$	74.7, 72.8 ${}^a$	172.9, 174.9 ${}^a$
	30	420.5	255.9	247.7	388.4	73.0	192.6
	40	461.2, 462.2 ${}^a$	294.7, 298.9 ${}^a$	283.4, 281.5 ${}^a$	427.1, 427.0 ${}^a$	74.3, 75.9 ${}^a$	212.2, 211.8 ${}^a$
	50	503.9	331.1	319.7	467.1	75.2	230.5
	60	544.8, 534.6 ${}^a$	367.7, 373.3 ${}^a$	347.1, 338.7 ${}^a$	507.1, 519.5 ${}^a$	76.3, 80.3 ${}^a$	248.4, 245.8 ${}^a$
	70	584.4	404.6	378.8	546.3	76.9	263.4
	80	622.6, 617.8 ${}^a$	440.9, 449.4 ${}^a$	409.7, 404.0 ${}^a$	584.8, 609.3 ${}^a$	77.6, 84.8 ${}^a$	279.4, 279.4 ${}^a$
	90	661.3	475.9	440.2	622.1	77.9	295.0
	100	699.7, 690.0 ${}^a$	510.3, 529.6 ${}^a$	477.5, 470.0 ${}^a$	658.2, 683.1 ${}^a$	76.7, 87.1 ${}^a$	314.4, 311.7 ${}^a$
LuNi${}_2$B${}_2$C	0	287.9	157.1	134.9	297.8	53.8	141.4
	10	330.3	204.5	167.7	356.6	60.5	168.9
	20	367.9	253.4	210.8	394.2	64.2	194.7
	30	411.2	290.5	242.0	432.8	68.4	216.3
	40	455.7	328.7	273.3	466.0	67.9	237.0
	50	484.1	381.2	310.4	511.2	71.4	259.6
	60	519.7	421.9	341.9	542.3	72.8	278.9

${}^a$ Ref. [13] obtained from first-principles calculations; ${}^b$ Exp. (RUS, 300 K) from Ref. [40]; ${}^c$ Exp. (time-of-flight, 300 K) from Ref. [40]; ${}^d$ Exp. (time-of-flight, 2 K) from Ref. [40].

Figure 4. $C_{11}^P-C_{12}^P-2P$ versus pressure for RNi${}_2$B${}_2$C (R=Y, Lu).

In order to predict the plastic properties of solids, Pugh [43] introduced a simple relationship that linked empirically the brittle or ductile behavior of materials with their elastic moduli by $G/B$. A ductile manner of material with lower $G/B$ and brittle materials with higher $G/B$, the critical value which separates ductile and brittle materials is about 0.57. Figure 5a shows the $G/B$ value as a function of pressure for RNi${}_2$B${}_2$C (R=Y, Lu). It is clear that the $G/B$ ratio decreases with increasing pressure and the calculated $G/B$ values are all lower than 0.57 regardless of YNi${}_2$B${}_2$C or LuNi${}_2$B${}_2$C, which indicates that they display ductile nature and pressure can improve their ductilities. Furthermore, it is observed from Figure 5a that the $G/B$ value of LuNi${}_2$B${}_2$C is always smaller than that of YNi${}_2$B${}_2$C, illustrating that LuNi${}_2$B${}_2$C is more ductility than YNi${}_2$B${}_2$C under different pressures. In addition, Poisson’s ratio with $\nu =\frac{3B-2G}{2(3B+G)}$ can also reflect the ductile properties, which usually ranges from −1 to 0.5, the smaller the Poisson’s ratio leading to more brittle behavior of a material. Figure 5b presents the pressure dependent Poisson’s ratio $\nu$ for RNi${}_2$B${}_2$C (R=Y, Lu). The values of $\nu$ increase accordingly along with pressure increasing regardless of YNi${}_2$B${}_2$C or LuNi${}_2$B${}_2$C, and the $\nu$ value of LuNi${}_2$B${}_2$C is always larger than that of YNi${}_2$B${}_2$C under different pressures. That is, we can obtain the same conclusion from both the $G/B$ and $\nu$. Moreover, hardness is another important parameter to describe the mechanical properties of a material, which is employed to characterize the ability of a material resistance to elastic and permanent plastic deformation or brittle failure [44]. Both the $G/B$ and $\nu$ have close relationship with the hardness of materials. Recently, based on the Teter’s famous empirical correlation [45], a simplified formula of Vickers hardness proposed by Chen et al. [46,47] can be expressed as $H_v=2{\left(k^{2}G\right)}^{0.585}-3$, where $k=G/B$. The calculated values of Vickers hardness for RNi${}_2$B${}_2$C (R=Y, Lu) under different pressures are plotted in Figure 5c. Obviously, the hardness of RNi${}_2$B${}_2$C (R=Y, Lu) decreases with increasing pressure and LuNi${}_2$B${}_2$C has smaller Vickers hardness value than YNi${}_2$B${}_2$C under different pressures, suggesting that the metallic bonding of LuNi${}_2$B${}_2$C is stronger than that of YNi${}_2$B${}_2$C under different pressures. In other words, high pressure results in increase of ductility for both YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C, and LuNi${}_2$B${}_2$C is more ductility than YNi${}_2$B${}_2$C under different pressures.

Figure 5. (a) Quotient of shear to bulk modulus $G/B$; (b) Poisson’s ratio $\nu$ and (c) Vickers hardness $H_v$ as a function of pressure for RNi${}_2$B${}_2$C (R=Y, Lu).

The elastic anisotropy of crystal is one of the most important parameters for engineering science and estimating mechanical properties of compounds. For a tetragonal crystal the elastic anisotropy can be described by the two shear factors $A_1$ and $A_2$. In the case of an isotropic crystal, $A_1$ or $A_2$ equals to one, while any value smaller or larger than one is anisotropy. For RNi${}_2$B${}_2$C (R=Y, Lu), $A_1$ and $A_2$ can be expressed as [48]:

$$\begin{array}{c}\hfill \begin{array}{c}{A}_1=A_{\left\{100\right\}}=\frac{4C_{44}}{C_{11}+C_{33}-2C_{13}}\\ A_2=A_{\left\{001\right\}}=\frac{2C_{66}}{C_{11}-C_{33}}\end{array}\end{array}$$

(11)

The anisotropy factors $A_1$ along $\left\{100\right\}$ shear plane and $A_2$ along $\left\{001\right\}$ shear plane for RNi${}_2$B${}_2$C (R=Y, Lu) are plotted in Figure 6. It is a pity that there are still no experimental data for comparison. For YNi${}_2$B${}_2$C the shear anisotropic factor along $\left\{001\right\}$ shear plane $A_{\left\{001\right\}}$ increases sharply from 1.75 to 3.32, and for LuNi${}_2$B${}_2$C it increases sharply from 2.16 to 5.69. However, the change of $A_{\left\{100\right\}}$ remains almost invariant with increasing pressure regardless of YNi${}_2$B${}_2$C or LuNi${}_2$B${}_2$C. In addition, Ranganathan and Ostoja-Starzewski [49] summarized the existing anisotropy theories and developed a universal elastic anisotropy index $A^U$, which is defined as

$$\begin{array}{c}\hfill A^U=5\frac{G_V}{G_R}+\frac{B_V}{B_R}-6\end{array}$$

(12)

Figure 6. The pressure dependence of the shear anisotropy factors ($A_{\left\{001\right\}}$, $A_{\left\{100\right\}}$) and universal anisotropy factor ($A^U$) for (a) YNi${}_2$B${}_2$C and (b) LuNi${}_2$B${}_2$C, respectively.

$A^U=0$ represents an isotropic material and a nonzero value of $A^U$ is a measure of the anisotropy. Figure 6 also shows the pressure dependence of the $A^U$ for RNi${}_2$B${}_2$C (R=Y, Lu). It is clear that both YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C are anisotropic materials and their anisotropy can be enhanced with increasing pressure. Besides, LuNi${}_2$B${}_2$C has more anisotropy than YNi${}_2$B${}_2$C under different pressures.

The Debye temperature (${\Theta }_D$) is also an important fundamental parameter since it is closely related to the specific heat, thermal conductivity, melting temperature, etc. The ${\Theta }_D$ can be obtained from elastic constants by the following equations [50,51]:

$${\Theta }_D=\frac{h}{k}{\left[\frac{3n}{4\pi }\left(\frac{N_A\rho }{M}\right)\right]}^{1/3}{v}_m$$

(13)

$$v_m=\left[\frac{1}{3}\left(\frac{2}{v_t^3}+\frac{1}{v_l^3}\right)\right]$$

(14)

$$v_t=\sqrt{G/\rho }$$

(15)

$$v_l=\sqrt{\left(B+\frac{4}{3}G\right)/\rho }$$

(16)

where h is the Plank’s constant, k is the Boltzmann’s constant, n is the number of atoms per unit cell, $N_A$ is the Avogadro’s number, $\rho$ is the density, M is the molecular weight, respectively. $v_m$, $v_t$ and $v_l$ are the average, shear and longitudinal sound velocities, respectively.

Table 3 displays the pressure dependence of $\rho$, $v_l$, $v_t$, $v_m$ and ${\Theta }_D$ for RNi${}_2$B${}_2$C (R=Y, Lu). Meanwhile, various elastic wave velocities and Debye temperature with pressure are also showed in Figure 7 in order to clearly see their change with pressure. It can be found that, as the pressure increases, the densities $\rho$ and the longitudinal sound velocities $v_l$ increase monotonously, for YNi${}_2$B${}_2$C the shear sound velocity $v_t$ firstly increases from 3566.17 m/s and then starts to decrease from 3793.77 m/s to 3788.02 m/s after 90 GPa, and for LuNi${}_2$B${}_2$C it firstly increases from 2965.24 m/s and then starts to decrease from 3120.50 m/s to 3088.95 m/s after 40 GPa. Because of the pressure effect on the shear and longitudinal sound velocities, for YNi${}_2$B${}_2$C the average sound velocity $v_m$ firstly increases from 3990.44 m/s and then starts to decrease from 4294.42 m/s to 4288.85 m/s after 90 GPa, and for LuNi${}_2$B${}_2$C it firstly increases from 3323.92 m/s and then starts to decrease from 3519.38 m/s to 3492.15 m/s after 40 GPa. The Debye temperature of YNi${}_2$B${}_2$C at 0 GPa is 535.15 K, which is close to the available experimental value ${\Theta }_D=537$ K obtained through low temperature specific heat by Hong et al. [52] and the theoretical result ${\Theta }_D=549.70$ obtained by Wang et al. [13] from the first principles. However, the Debye temperature of LuNi${}_2$B${}_2$C at 0 GPa is 450.39 K, which has larger discrepancy with the experimental value 345 K [53]. Whatever YNi${}_2$B${}_2$C or LuNi${}_2$B${}_2$C, the Debye temperature increases with pressure increasing, and the Debye temperature of YNi${}_2$B${}_2$C is always larger than that of LuNi${}_2$B${}_2$C under different pressures. However, there are no experimental data of the Debye temperature of RNi${}_2$B${}_2$C (R=Y, Lu) under high pressure for comparison. Therefore, the present results could be served as a prediction for future experiment.

Table 3. The density ($\rho$ in g/cm${}^3$), longitudinal ($v_l$), shear ($v_t$) and average ($v_m$) elastic wave velocities (in m/s) and Debye temperature (${\Theta }_D$ in K) of RNi${}_2$B${}_2$C (R=Y, Lu) under different pressures.

Material	Pressure	$\mathit{\rho }$	${\mathit{v}}_{\mathit{l}}$	${\mathit{v}}_{\mathit{t}}$	${\mathit{v}}_{\mathit{m}}$	${\mathsf{\Theta }}_{\mathit{D}}$
YNi${}_2$B${}_2$C	0	6.069	6847.77	3566.17	3990.44	535.15
	10	6.377	7246.30	3594.23	4033.93	549.98
	20	6.643	7617.45	3691.12	4148.07	573.32
	30	6.883	7878.95	3678.01	4141.22	579.19
	40	7.102	8134.20	3691.23	4161.57	588.14
	50	7.305	8381.16	3710.74	4188.02	597.45
	60	7.494	8591.38	3749.03	4233.73	609.13
	70	7.671	8791.34	3763.58	4253.32	616.75
	80	7.839	8977.65	3779.16	4273.58	624.16
	90	7.998	9152.06	3793.77	4294.42	631.14
	100	8.151	9327.74	3788.02	4288.85	634.60
LuNi${}_2$B${}_2$C	0	8.505	5855.49	2965.24	3323.92	450.39
	10	8.917	6210.38	3050.63	3430.36	472.20
	20	9.277	6489.19	3055.01	3433.64	478.92
	30	9.602	6730.18	3106.51	3499.64	493.77
	40	9.898	6932.53	3120.50	3519.38	501.61
	50	10.175	7125.55	3094.35	3495.08	502.75
	60	10.432	7285.06	3088.95	3492.15	506.51

Figure 7. The pressure dependence of the longitudinal ($v_l$), shear ($v_t$) and average ($v_m$) elastic wave velocities and Debye temperature ${\Theta }_D$ for (a) YNi${}_2$B${}_2$C and (b) LuNi${}_2$B${}_2$C, respectively.

4. Conclusions

In summary, we have investigated the structure stability and mechanical properties of RNi${}_2$B${}_2$C (R=Y, Lu) under different pressures by means of the first principles. The pressure dependent normalized lattice parameters ($a/a_0$, $c/c_0$ and $c/a$) and elastic constants of RNi${}_2$B${}_2$C (R=Y, Lu) are also presented. It is found that their lattice parameters and elastic constants agree well with the previous theoretical results and experimental data. By the elastic stability criteria under isotropic pressure, it is predicted that YNi${}_2$B${}_2$C and LuNi${}_2$B${}_2$C with tetragonal structure are not mechanically stable above 93.6 GPa and 50.5 GPa, respectively. On the basis of the pressure dependent elastic constants, the Pugh’s modulus ratio, Poisson’s ratio, Vickers hardness, elastic anisotropy and Debye temperature of YNi${}_2$B${}_2$C in the pressure range of 0–100 GPa and LuNi${}_2$B${}_2$C in the pressure range of 0–60 GPa are further investigated. It is shown that the ductility and Debye temperature of the tetragonal RNi${}_2$B${}_2$C (R=Y, Lu) increase with increasing pressure, and LuNi${}_2$B${}_2$C is more ductility and lower Debye temperature than YNi${}_2$B${}_2$C under different pressures. It is a pity that there are no available experimental values under pressure for comparison, the present results could be served as a prediction for future experiment.