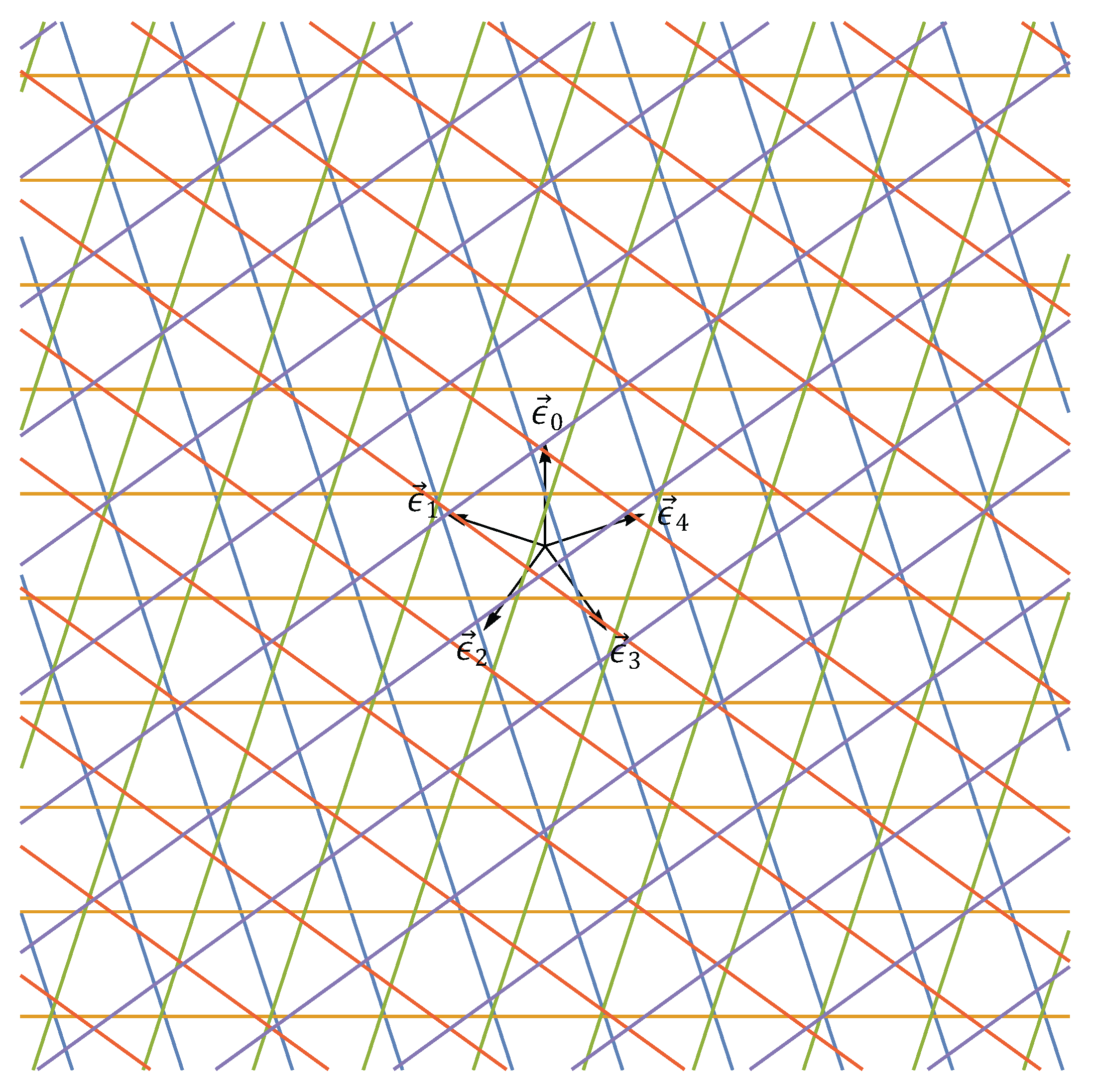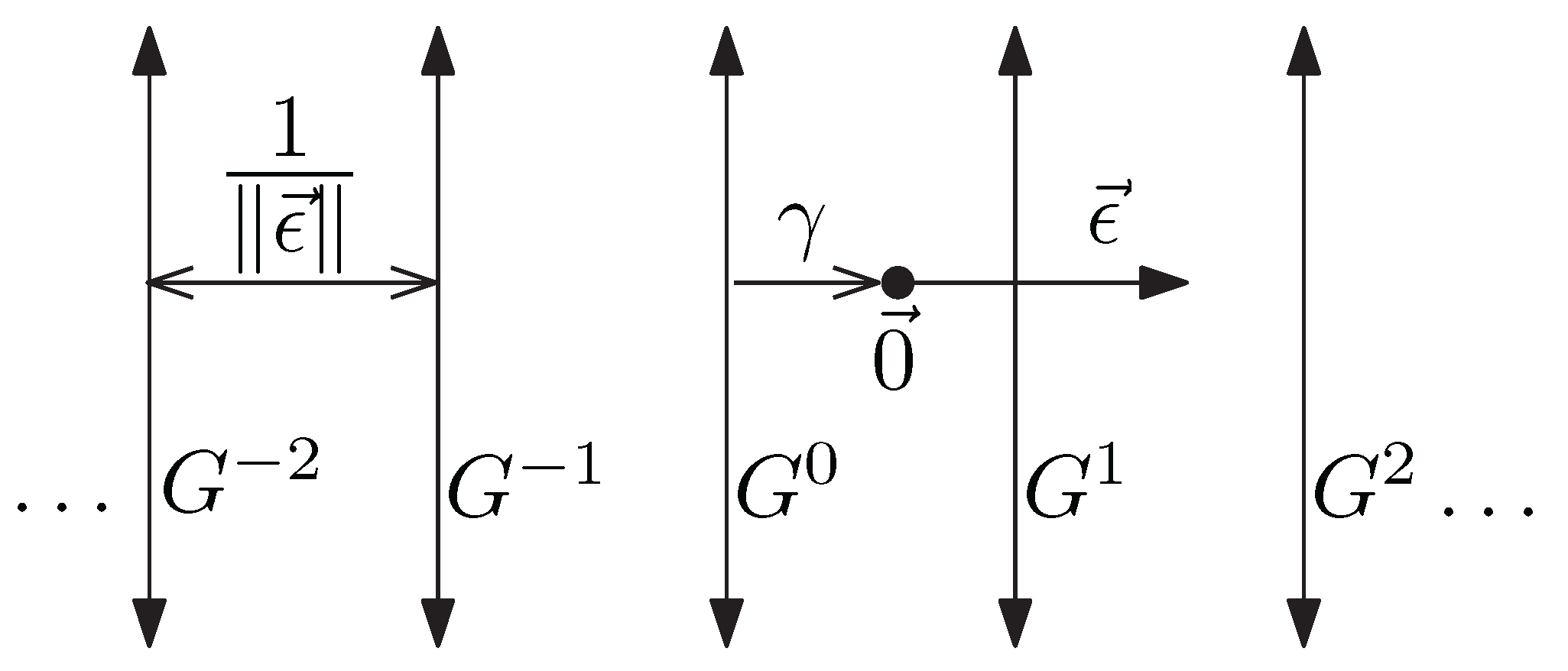2. The Fibonacci-Grid Method
The empire problem, the problem of finding out which tiles are forced given an initial set of tiles, was first explored by analyzing Ammann bars, a decoration for Penrose tiles realized as a network of five sets of parallel lines. This method was extended by Minnick [
8]. Due to the fact that it uses the empire of the Ammann bars, which is in fact a Fibonacci pentagrid [
9] of the Penrose tiling, we name the method used in this case the Fibonacci-grid method.
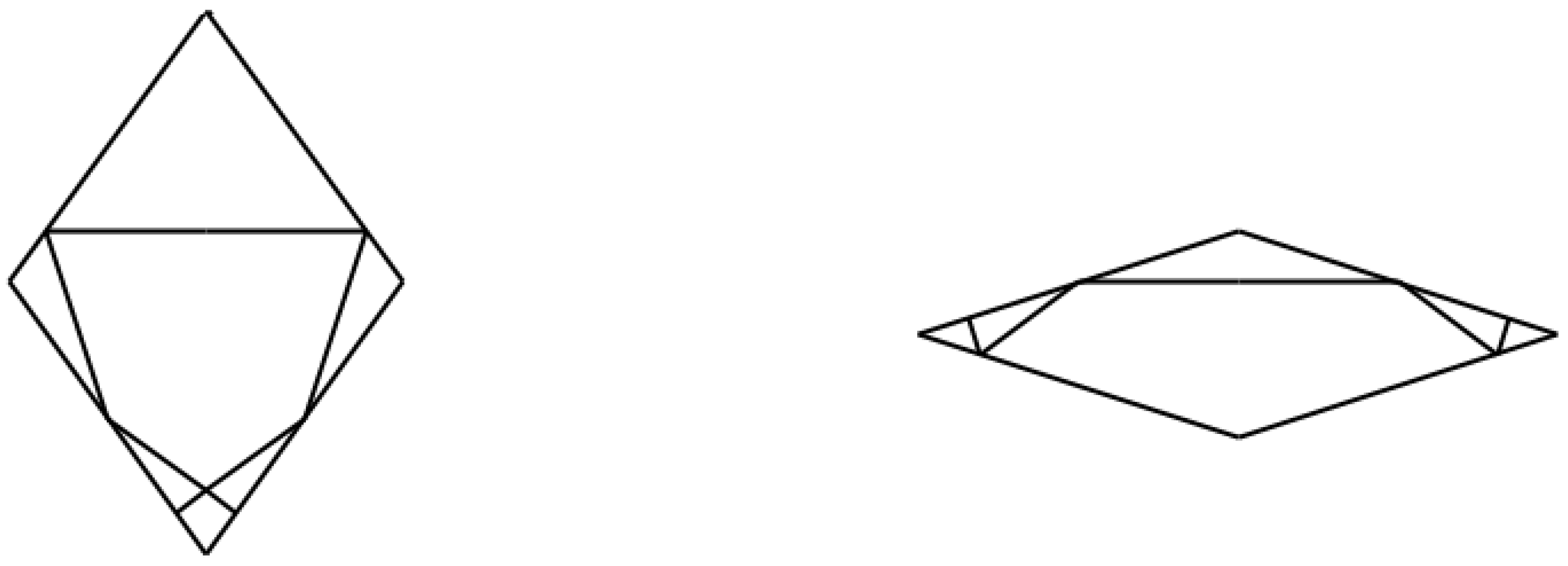
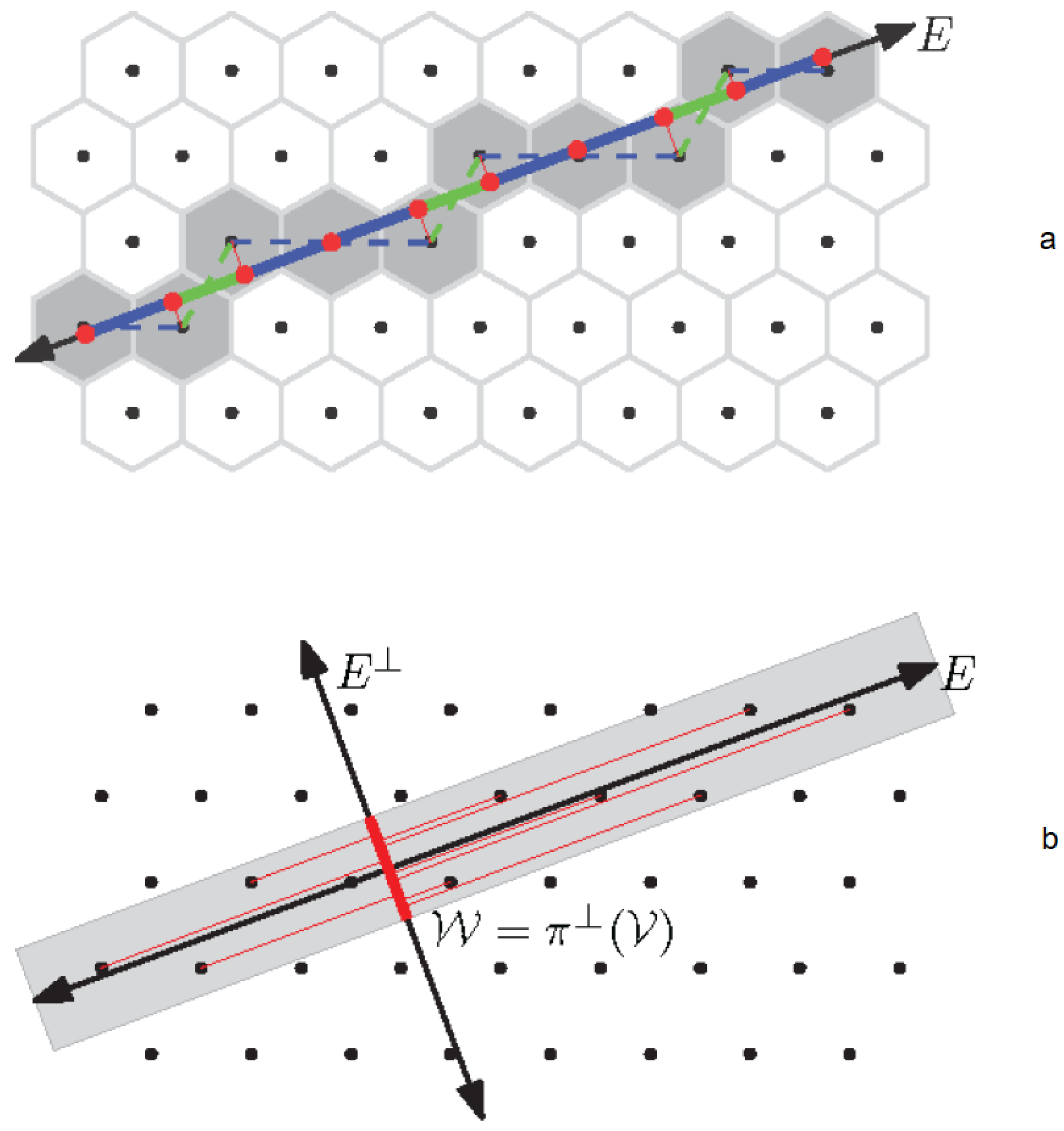
The prolate and oblate rhombuses in Penrose tiling can be decorated using line segments as shown in
Figure 1. When two tiles meet along an edge, the line segments from one tile meet the segments from the other at straight angles, forming extended lines which are called the Ammann bars [
2]. These matching rules using the Ammann bars are equivalent to the single- and double-arrow matching rules for Penrose tiling.
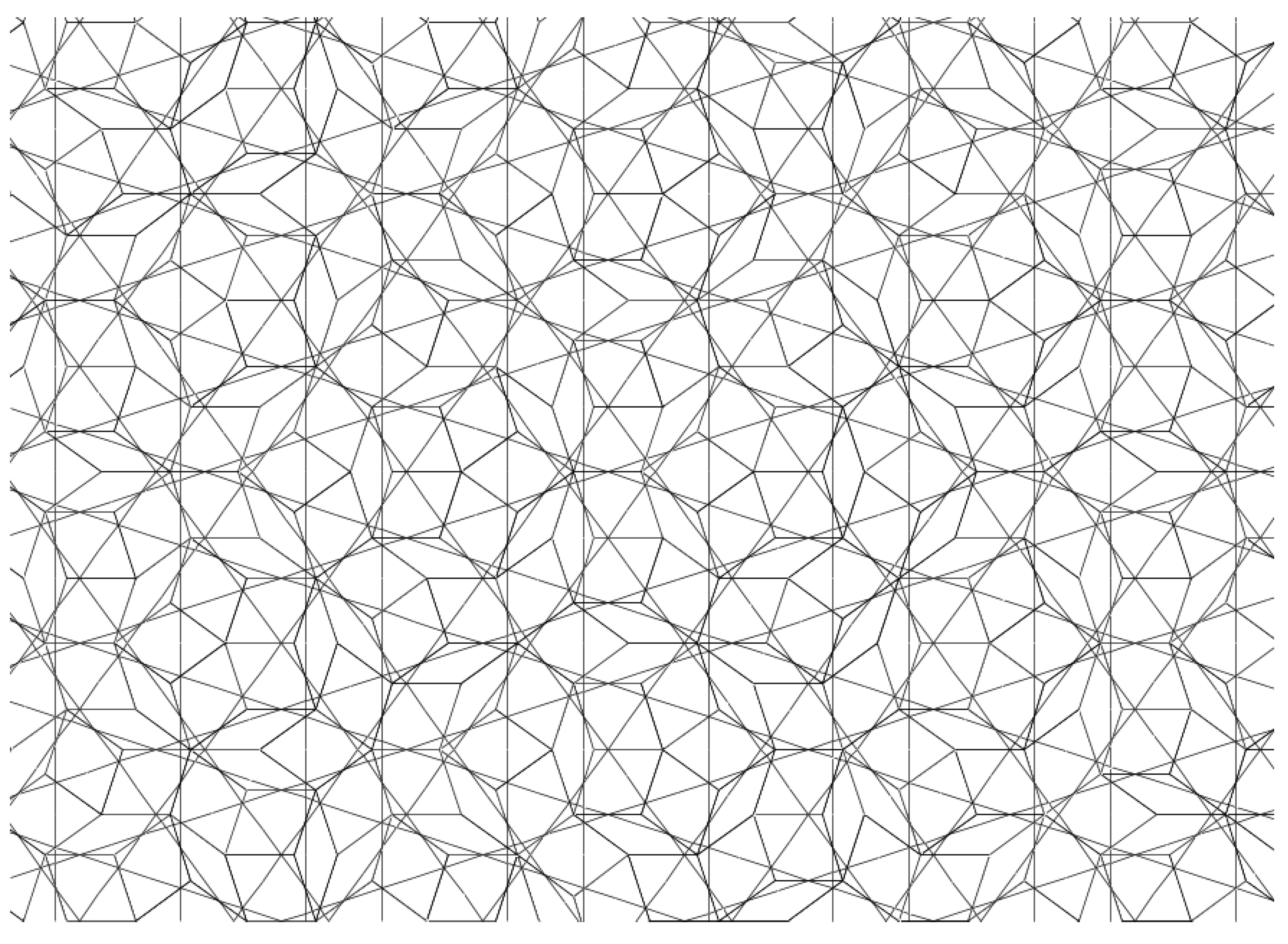
When looking at a large enough Penrose tiling, the Ammann bars extend to form lines which crisscross the plane in a very structured way, as shown in
Figure 2. These lines can be grouped together to form five distinct families of parallel lines called
, where each grid consists of lines normal to one of the following five vectors
, where
. The gaps between neighboring parallel lines are represented by two values, a “long” gap
L and a “short” gap
S, where the ratio between these two distances is the golden ratio
. The gaps for a particular grid from a sequence of long and short gaps, denoted by a sequence of
L’s and
S’s.
These sequences turn out to be Fibonacci chains, or Fibonacci words, which represent the simplest one dimensional quasicrystals and which can be generated by the following iterative process. Let us start with the two words
and
and let
be the concatenation of the previous two words. The infinite Fibonacci word is defined to be the limit
. Alternatively, one can start with
and apply the following substitution rules to iterate one word
to the next
.
The rules for creating the infinite Fibonacci word prohibit the formation of certain sub-words. For instance, there cannot be three consecutive L’s appearing in nor can there be two S’s next to each other. So and are not valid Fibonacci chains, and if one has then the next letter must be S. Likewise an S must always be followed by an L.
Since the Penrose tiling is indeed a network of these Fibonacci words, calculating the empires in the Fibonacci words will directly lead us to the empires of the Penrose tiling.
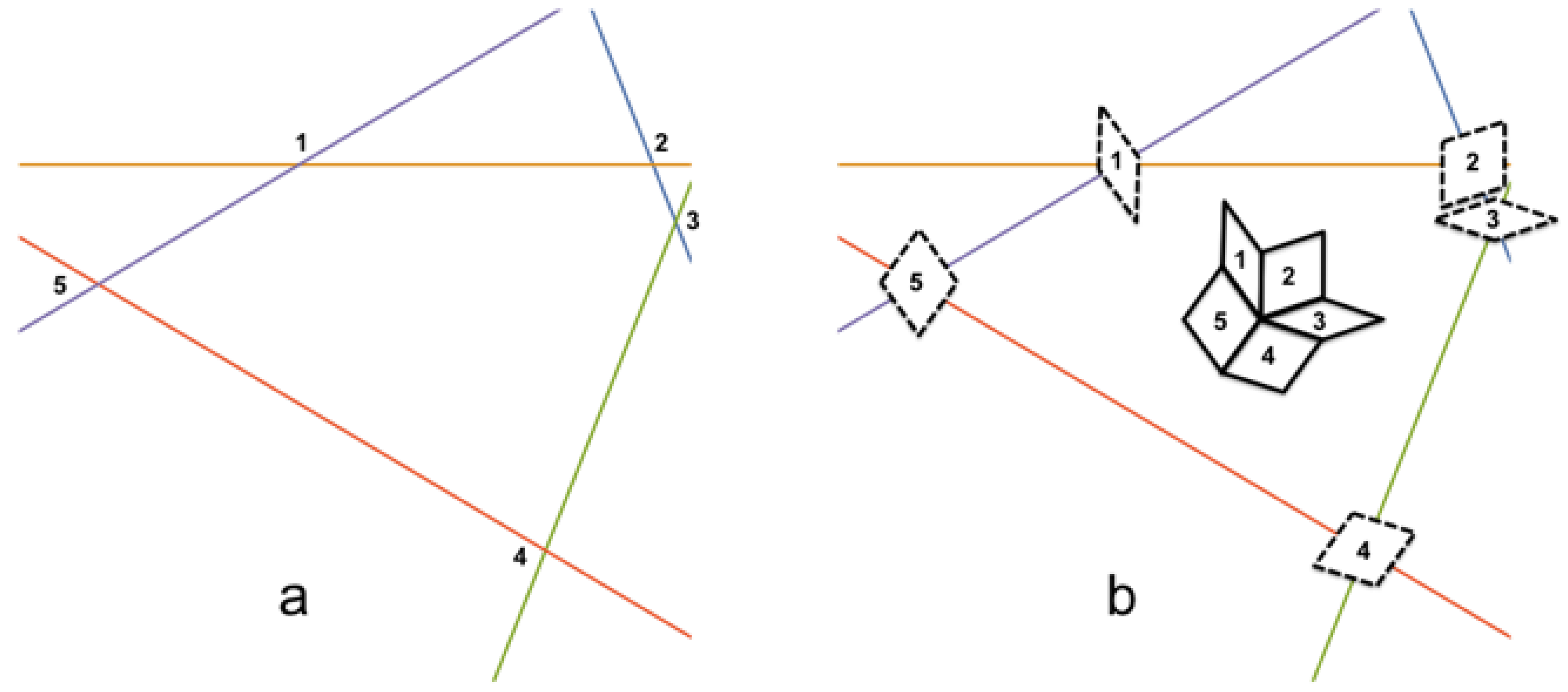
Given an initial sub-word,
W, one can identify its empires, which consists of all the letters that are forced by the presence of
W. For example, the word
(shown in red) has the following empire (shown in blue):
While there is some freedom in choosing letters for the gaps in the empires, there is no freedom in choosing letters at positions shown in blue. Whenever an is present in a Fibonacci chain, the 13th letter following the is forced to be an and the 19th letter is forced to be an . The empires extend to include an infinite number of letters.
We can apply this method to the Ammann bars, with the purpose of finding the empires in Penrose tiling. For a given patch of tiles , where n is the number of tiles in T, there will be some Ammann bars (from the same or from different parallel line sets) running through P. Within each parallel line set i, the bars are separated with long and/or short gaps between them forming the given initial word , where . The empires associated with each can be thus calculated and as a result, all other forced Ammann bars within the same grid can be found.
An example is shown in
Figure 3, where the given patch at the center is colored red, the associated bars are colored green and the empire or forced bars are colored blue. A tile or a small cluster of tiles is forced where the Ammann lines intersect in a certain configuration. Detailed rules are discussed in [
8]. As a result, the first set of the forced tiles are determined (colored blue in
Figure 3). As the first set of forced tiles are decided, more Ammann bars (colored red in
Figure 3) can be forced by these tiles, which in turn will force other tiles, as a result of the intersection of the red bars with other red or blue bars, as shown in
Figure 3. For solving the empire problem, this approach is workable but tedious, therefore impractical in modeling the growth or dynamics of quasicrystals.
3. The Multigrid Method
The
multigrid method offers a robust algorithm for generating quasicrystalline tilings or quasicrystals of Euclidean space
as well as the empires of the quasicrystals. A multigrid
is the superposition of distinct grids. A grid
is a family of parallel hyperplanes. A grid with an equal spacing between hyperplanes can be expressed as a countable union of hyperplanes which are all normal to a non-zero grid vector
:
where each hyperplane
is indexed by an integer
and the quantity
provides a shift of the grid away from the origin. The distance between neighboring hyperplanes is equal to
.
A tiling
of
can be constructed by taking the dual of the multigrid, meaning a point where
m hyperplanes intersect in the multigrid space will correspond to a
-sided polytope in the tiling space, with opposite sides being parallel [
10].
For constructing a Penrose tiling in , the pentagrid, a multigrid consisting of five grids is used.
We define a pentagrid as a set of five grids in the plane (
Figure 4)
for
, where each grid
has an associated unit-length grid vector
and shift
(
Figure 5), but rather than indexing the grids using the integers, we use the half-integers instead
.
The quantities
form a 5-tuple called the shift vector
. They satisfy condition
to obtain the true Penrose tiling, which obeys the Penrose matching rules. Let the multigrid
denote the superposition of all grids
for a given shift vector
and let
be the tiling of
which is dual to
. It is important to choose
so that the pentagrid is nonsingular and no more than two grid lines intersect at a given point [
6]. This can be achieved by choosing only the rational and non-complimentary distinct values for
. This restriction ensures that
consists only of rhombuses. The dualizing procedure is shown in
Figure 6.
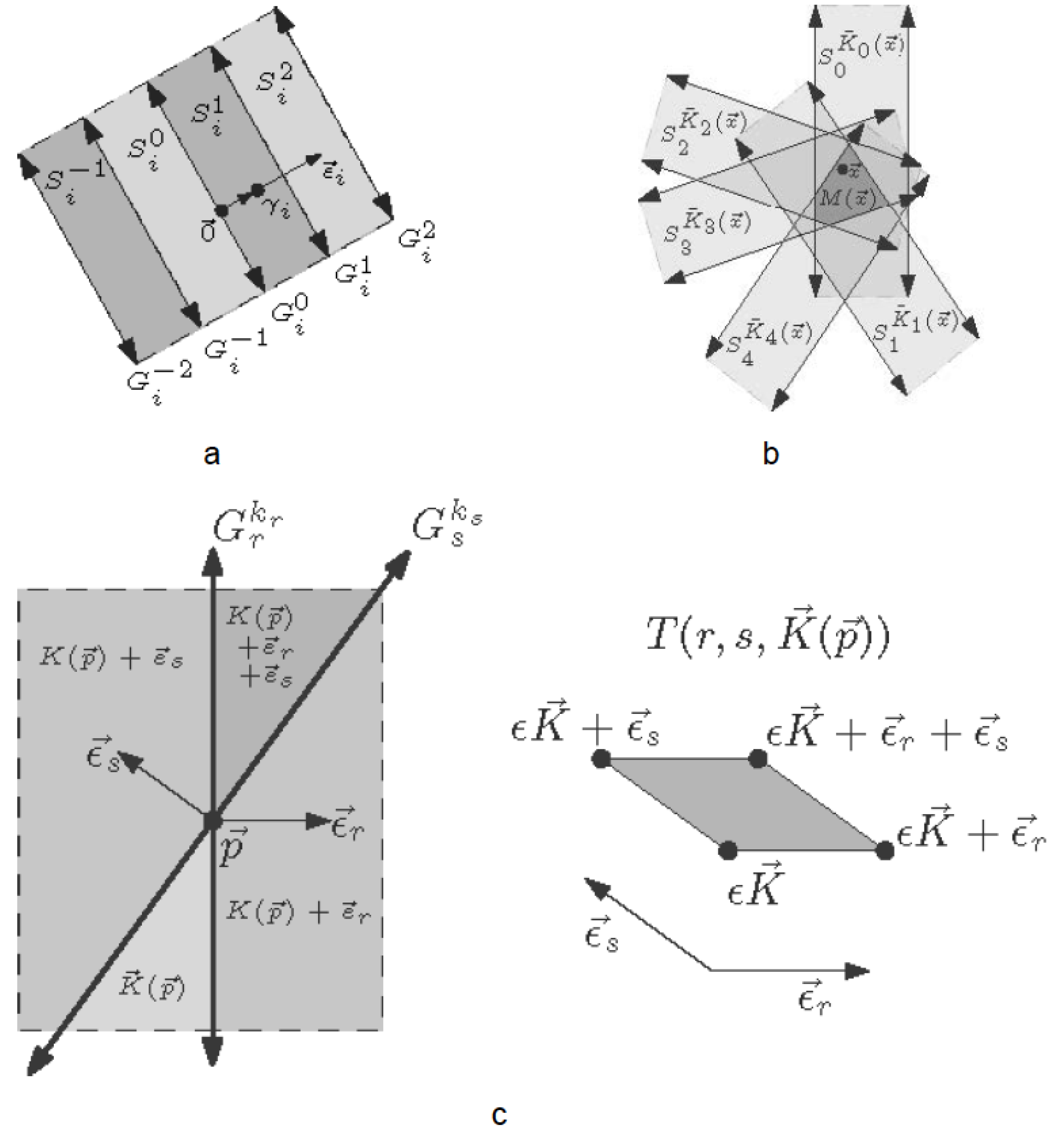
Each grid
divides the plane into open strips,
, which lay between neighboring grid lines (
Figure 7a).
Each region
is constant with respect to the function
, where the right-hand term denotes the rounding function returning the nearest integer. Each strip
can be rewritten as (the open interior of) the preimage of
k under
.
The open regions of the plane
between the grid lines are called meshes, which correspond to vertices in the dual. For a point
, which is not located on any of the grid lines, the mesh region
(
Figure 7b) that contains
can be expressed as the intersection of the five strips, which contain
, namely
(where
). If
represents the 5-tuple
, then the mesh
can be written as the interior of the preimage
.
In this way, each mesh M can be identified with the point , where is equal to for arbitrary choice of .
To associate a point on the plane with each mesh, we use the linear transformation
, defined by taking the linear combination of grid vectors
with coefficients
. This can be written in matrix form as
, where
is the matrix with column vectors
.
Given two grid lines
and
, let
denote their intersection point, as shown in
Figure 7c.
The point
represents a rhombus in the dual tiling
. The four vertices of this rhombus correspond to the mesh regions adjacent to
which are indexed by four 5-tuples
(
Figure 7c), where
and
are the standard basis vectors for
. After applying the transformation
, the vertices of tile
T can be written as points in the plane:
.
We can write
to indicate the tile which is dual to the point
at the intersection of the two grid lines
and
. When the shift vector
is perturbed to a new value,
, the grid lines change position and the location of the intersection
changes accordingly. A tile
remains included in the dual tiling associated to the new shift vector
as long as
has the same value, as long as
remains within the same three strips
for
. The three conditions
for
provide the constraints necessary to keep
included in the dual tiling
. The constraints
are equivalent to the linear inequalities:
where
and
are given by the simultaneous solution to the equations:
These equations can be rewritten in matrix notation. Let
be the matrix with column vectors
and
. For
the vectors
and
are non-collinear and the matrix
is non-degenerate, with the inverse
. The intersection
can be written in terms of
and
. Again, for convenience we use
.
The dot product
can be expressed as:
The inequalities
can be expressed in terms of
and
:
To simplify the algebra, we define the linear functions [
4]
for
and
:
The functions
can be expressed in terms of the indices
and
.
The inequality
can be rewritten as:
For a given tile , these inequalities define a region of suitable shift vectors so that for any , the tile is included in the tiling .
For Penrose tiling, another restriction on
is imposed by the sum condition,
, which N. G. de Bruijn [
11] has shown to be a necessary condition that ensures that the tiling
obeys the matching rules. Consequently, we add the following as a further restriction which defines
[
11].
For a collection of tiles
let
denote the mutual intersection of all the regions
.
We define the empire to be the set of tiles T for which contains . Indeed, for any it is true that , and if for some tile T, then it is also true that , implying that .
In order to compute , a linear program can be employed. Each tile gives three inequalities for . We collect all the linear inequalities given by all tiles and add to this list the sum condition as a linear equality. This list provides the linear constraints that define , which are to be used in the linear program.
We use each function as an objective function in the linear program in order to find the minimum and maximum values that achieves on . Let and be the values obtained from the linear program.
A tile
is included in the empire
if and only if:
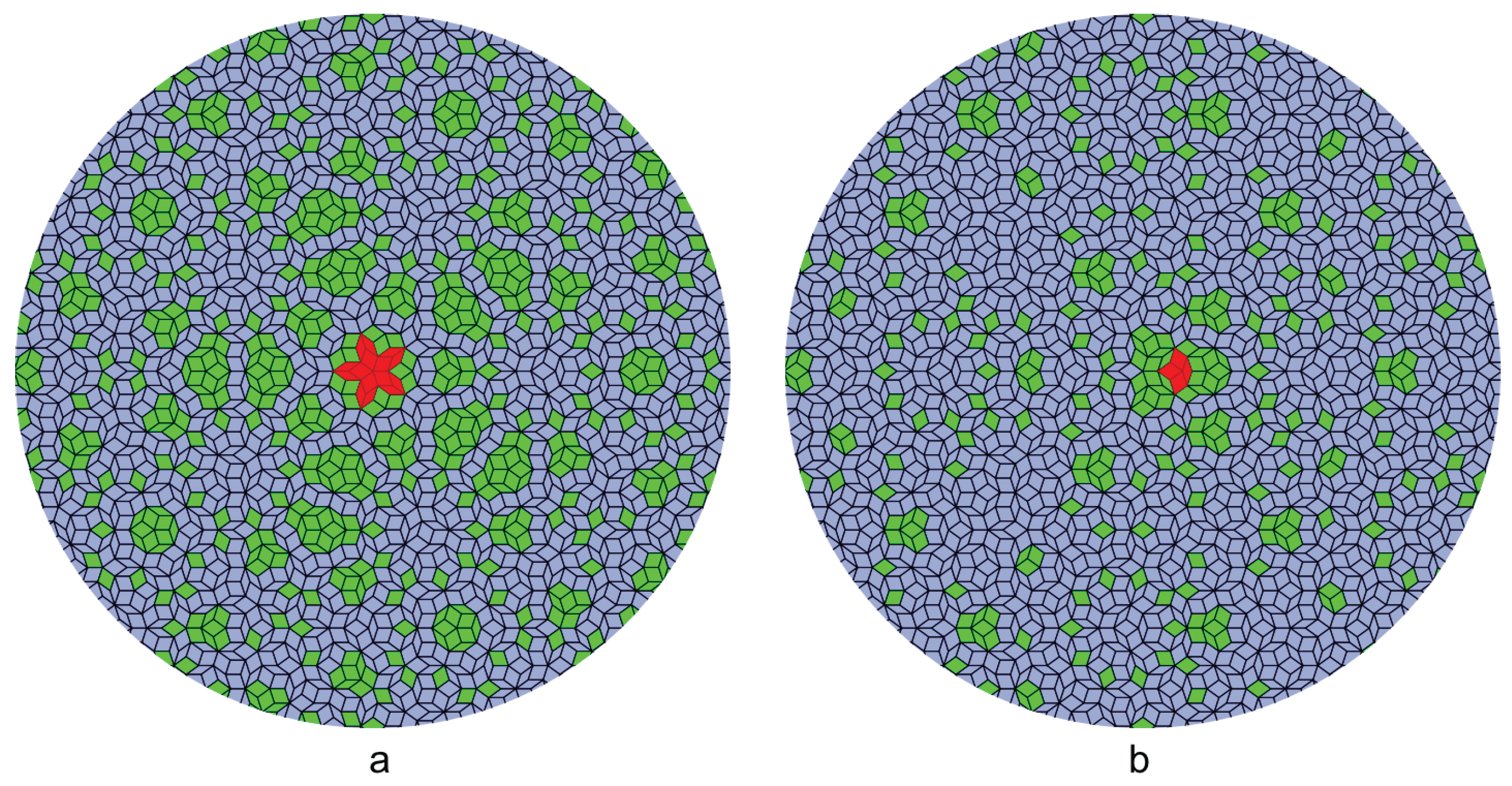
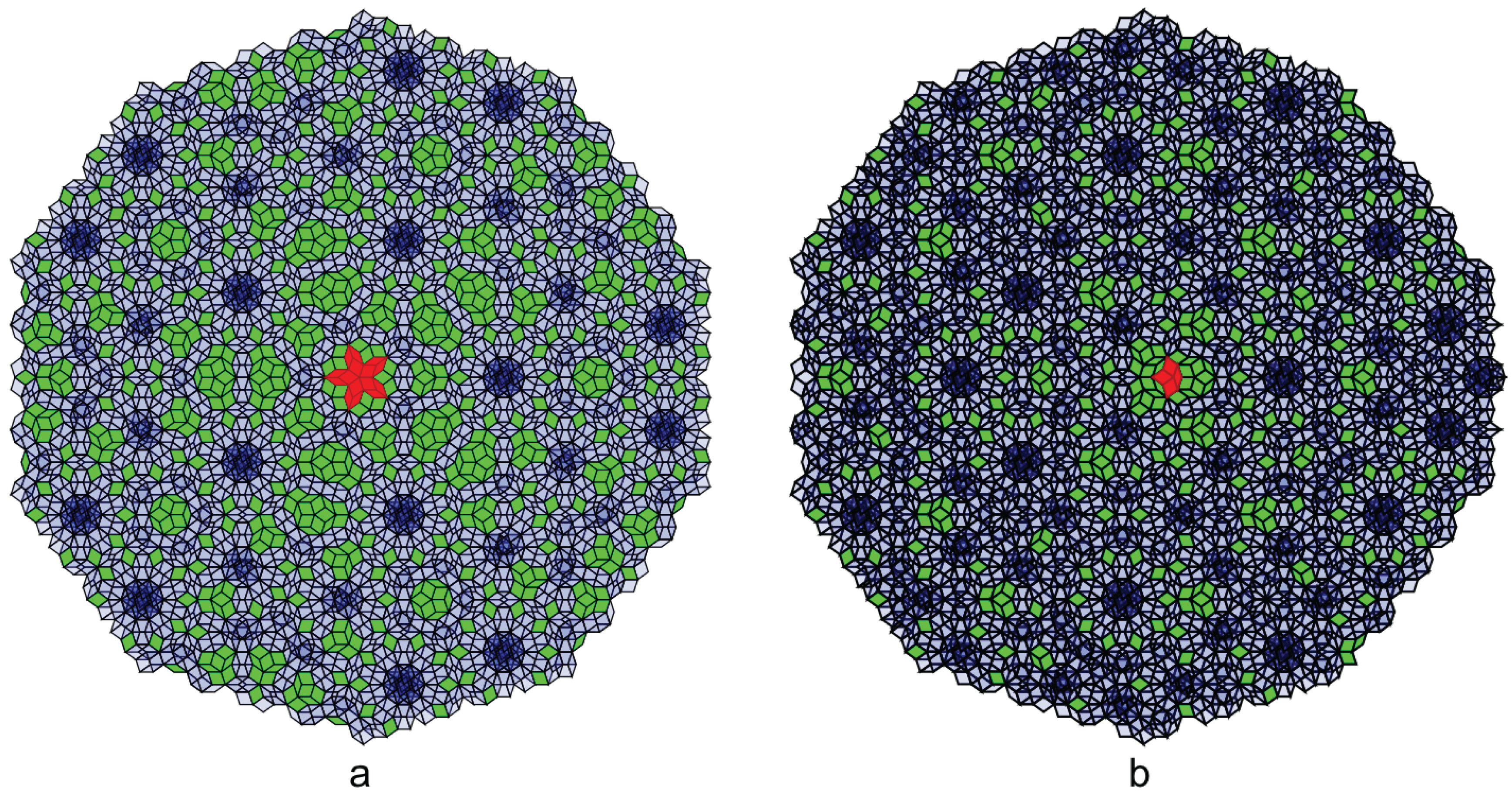
Figure 8 shows a sample result of the empire calculation for two different local vertex types in Penrose tiling, one with 5-fold symmetry and one without. The green tiles are the forced tiles that belong to the empire of the local vertex configuration (red), while the blue tiles are not forced.
Figure 9 shows the empire of the rest of local vertex types in Penrose tiling. Notice that the density of the empires differs for different vertex types and one of the empires is completely empty. Mathematically, the density of the empire is determined by the volume of the empire-window. For example, the empire-window of the vertex type shown in
Figure 8a is too narrow to capture any other tiles in it, therefore the empire is empty. The density of the empires is also related to the frequency of the vertex types [
12] so that more frequent vertex types have lower empire densities.
The multigrid method is relatively simpler and faster when compared with the Fibonacci-grid method, but might not be practical in cases where there is not an obvious simple dual grid for the quasicrystal. Also, when there is a defect in the quasicrystal, this method will no longer work because the dual of the quasicrystal in this case will no longer be a perfect multigrid. However, we discovered a new method, named the cut-and-project method, that solves these issues. Details about this method will be discussed in the following section.
4. The Cut-and-Project Method
The cut-and-project technique for generating quasiperiodic tilings from a higher dimensional lattice is well developed [
7]. For a regular lattice
and lattice point
, let
denote the Voronoi cell centered at
.
For a regular lattice, the Voronoi cells for each lattice point are identical up to translation, so let denote the generic Voronoi cell for the origin and let denote the translation , where .
Let
E be a totally irrational [
7]
m-dimensional affine subspace,
for
, where
is a linear subspace and
E is the translation of
V by the shift vector
and let
be the orthogonal projection onto
E. A quasicrystalline tiling of
E can be generated by taking the projected points
for all lattice points
with Voronoi cells intersecting
E non-trivially,
, as shown in
Figure 10a. This higher dimensional lattice is called the mother lattice of the quasicrystalline tiling in the lower dimension.
If two points are neighboring vertices in the lattice (sharing a common lattice edge), then the projected points and are to be connected by an edge as well.
The Voronoi cell centered at , , intersects E if and only if the translation of the Voronoi cell, centered at includes the lattice point (this follows from the definition of the Voronoi cell and the fact that is the point of E that is closest to ). Let be the orthogonal complement of E and let be the projection onto . If , then . Conversely, if , then there is some translation , where such that contains , in which case contains and so does intersect E.
The orthogonal projection of
onto
is called the cut-window,
(
Figure 11). A lattice point
is included in the tiling if and only if
, as shown in
Figure 10b.
To construct a Penrose tiling, let
be the lattice
,
be the plane with the basis
and
be the translation of
V away from the origin.
For the orthogonal space
, we choose the basis
as follows:
The projection is given by the matrix and the linear map into the orthogonal space is given by the matrix .
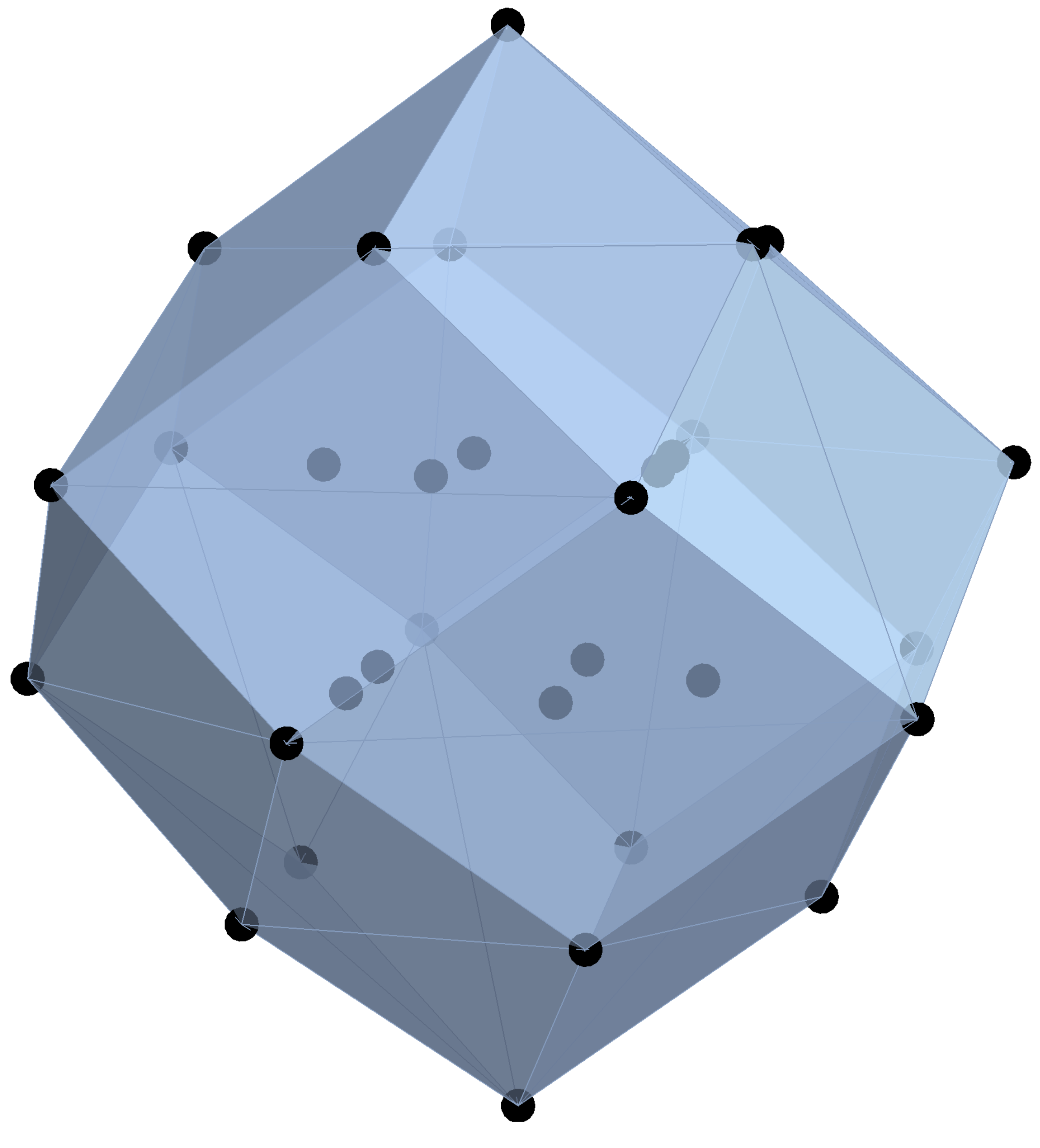
The Voronoi cell at the origin is a unit 5-cube with 32 vertices . The 5-dimensional volume contained within projects to a 3-dimensional volume in , which is computed as the convex hull of the point set . This describes the cut-window and it has the form of a rhombic-icosidodecahedron with 32 vertices and 20 rhombic faces.
The 3-dimensional volume contained within
is defined in terms of the 20 vectors
, which are normal to the rhombic facets and the projected points
. These normal vectors are computed as the normalized cross products of the projected images of pairs of the standard basis vectors
.
The volume
can now be expressed in terms of
and
W as the intersection of 20 half spaces:
A lattice point
is to be included in the tiling
as long as the projected point
falls inside of the 3-dimensional volume
.
Unit squares in the lattice project to rhombic tiles in E as long as all four of its vertices fall within the cut-window when projected into .
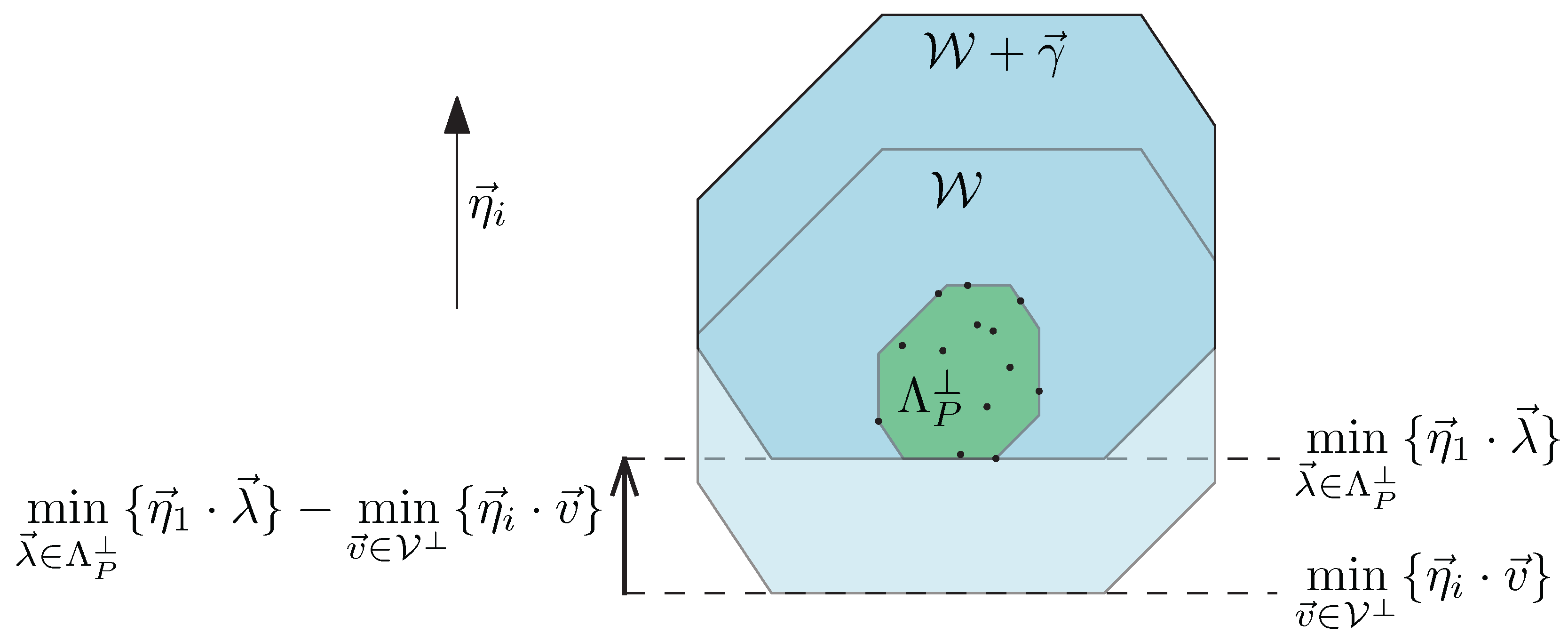
Now that the quasicrystalline tiling is generated by the cut-and-project method, the next step is to calculate the empires or forced tiles by a local patch of the tiling, using this method. The concept is simple: given a local patch, all the tiles in this patch can be reversed to the mother lattice, hence giving the restriction for the cut-window. In other words, the projection of the given patch to the orthogonal space must fall inside the cut-window. The union of all cut-windows that satisfies this restriction is called a possibility-space-window, for that all the tiles inside this window can potentially legally coexist with the given patch. The intersection of all these possible cut-windows is called the empire-window for that all tiles inside this window must coexist with the given patch.
The empire for a patch of tiles can be computed using a linear solver. We start with the set of tiles in the local patch and reverse them to a set of unit squares in the mother lattice. Then we project all the vertices of these squares, , to the orthogonal space, where the convex-hull of the projected forms the local-patch-window. To compute the empire , the next step is to find all the shift vectors so that the corresponding shifted cut-window covers the local-patch-window. The intersection of all the valid cut-windows is in fact the empire-window for the local patch P, which works as the cut-window for the forced tiles.
The
-window for the true Penrose tiling,
, is defined implicitly by linear constraints imposed on
, firstly satisfying the sum condition:
and keeping
constant. The other linear constraints are defined in terms of the norm vectors of the cut-window
. For each
(Equation (
27)), the movement of the cut-window
in the positive direction
is limited so as to keep the points
inside the translated cut-window
. The maximum amount that
can translate in the positive direction
before the “bottom” face of the cut-window
moves past the “bottom” point of
is given by
, as shown in
Figure 12.
This tells us just how far in the positive direction , the vector may extend so as to keep the projected points of the selected patch within the moving cut-window .
The twenty linear constraints for
can now be expressed as:
which is used to define the possibility-space-window:
The window, which determines the empire for the patch
P is also the intersection of half-spaces defined using the normal vectors
. For each
, we use a linear solver with
as the objective function to find the minimum value of
subject to the constraints for
listed above. Adding
will give the maximum bound for
in the direction of
.
The empire-window is a subset of and a tile is in the empire for the patch P as long as the projections of all four of its vertices fall within .
Figure 13a shows all the tiles whose projection in the orthogonal space falls in the possibility-space-window of the given patch (colored red) - the star vertex configuration of the Penrose tiling. These tiles are called the
possibility space for the given patch. Notice that in this possibility space, the green tiles are the only possible tiles for that location, while the blue ones superimpose with each other. This implies that the green tiles are forced by the given local patch and therefore belong to the empire of the patch, while the blue tiles are not forced. Also, from the discussion in previous paragraphs, the projection of all the forced green tiles in the orthogonal space falls inside of the empire-window. One can also see that the part of the tiling outside the empire consists completely of the projection of full cubes from the mother lattice and forms a network of strings of these rows of projected cubes.
Figure 13b shows the results for a local patch that does not have 5-fold symmetry. One can see that its empire has similar symmetry patterns as the given patch itself.
The key process of the cut-and-project method for calculating empires is to reverse the given patch to its mother lattice and apply the restrictions there. This enables us to calculate the empires for very complicated quasicrystals whose mother lattice is a complex decoration of the simple lattices and even a defected quasicrystal, which is a cut-and-project from a defected mother lattice by a defected cut-window [
13].
Figure 14 shows the cut-and-project results for the rest of local vertex types in Penrose tiling. Notice that the empire calculated by the cut-and-project method perfectly matches the result by the multigrid method. Indeed these two methods are mathematically equivalent, although the cut-and-project method has more advantages that will be discussed in the following section.
5. Comparison between the Multigrid Method and the Cut-and-Project Method
In this section, we first prove the mathematical equivalence of the multigrid method and the cut-and-project method in generating the empires in Penrose tiling. Then, in the second part, we give a one dimensional example of the advantage of the cut-and-project method that allows us to calculate the empires in a defected quasicrystal.
5.1. The Parallel between the Multigrid Method and the Cut-and-Project Method
To see the correspondence between the pentagrid and cut-and-project methods for generating Penrose tiling, we begin with
, where
are the norm vectors of the grids, as used in the pentagrid method. The transpose of
is
The matrix represents a linear map where . This is the same transformation used in the pentagrid method to map each mesh to its corresponding dual point .
Notice from Equation (
25) that
and
are the row-vectors of
, which are orthogonal in
as their dot product is zero. We take
to be the normalized vectors
and
the subspace spanned by the orthonormal basis
, with
, the orthogonal projection onto
E.
The standard basis vectors
of
project orthogonally down onto
E symmetrically, creating a pentagonal star of vectors inscribed on
E. All the projected vectors
have equal length
and in fact, when expressed in terms of the basis
, are a direct scaling of the pentagonal star of unit-length vectors
, as used in the pentagrid method.
Let
denote the grid in
, which lies perpendicular to the coordinate vector
and which is shifted away from the origin by
.
We consider the translation of the plane
E by a shift vector
,
. Each grid
intersects
in a series of evenly spaced parallel lines, which are perpendicular to the projected vector
. Let
be the grid inscribed in
defined as the intersection
. The spacing between grid lines is
and each grid line
can be expressed in the basis
as
. The factor
provides the dilation necessary to relate the copy of
from
Section 3 (which contains a pentagrid with unit-length grid vectors
and unit-spacing between grid lines), with the copy of
parametrized by the basis
(which contains a pentagrid with grid vectors
with a uniform grid spacing of
).
In other words, if we choose to parametrize
with the basis
where
, then the grid line
can be written relative to
as
. This is precisely the equation used to define the pentagrid in
Section 3.
In , the mesh regions located between the grid hyperplanes have the form . This describes the interior of a unit 5-cubes, which is centered around a certain coordinate integer lattice point . This coincides with the Voronoi cells for the lattice . In other words, each mesh is exactly the interior of a certain Voronoi cell centered at a lattice point .
Consider now a mesh , intersecting non-trivially, so that . The boundary of intersects with to form the grid lines inscribed in , which define the boundary of the planar mesh region . The region is expressed as , in terms of the basis for E.
In the multigrid method, a vertex of the form is included in the dual tiling as long as the mesh region corresponding to , , is non-empty, in which case the strips have a non-trivial intersection in the plane . When a planar strip is mapped onto using the basis , the image is equal to the intersection of with the corresponding strip in defined by . If the planar strips intersect in a non-empty planar mesh region , then maps onto as the non-empty mutual intersection of the strips with the plane . In other words, there is a Voronoi cell such that . In this way, the multigrid method and the cut-and-project method produce the same set of lattice points that are to be mapped to to be included as vertices in the dual.
In the multigrid method, the transformation is used to map lattice points to the dual vertices. With the cut-and-project method, the points are mapped onto by orthogonal projection . This projected point is expressed in the basis as . So the mapping is identical (up to a scaling by ) to the mapping .
This shows that the two methods are equivalent mathematically. However, from
Figure 13 and
Figure 14, we can see the the cut-and-project method is conceptually clearer and easier to understand using the possibility space. Also, due to the fact that in the cut-and-project method there is a one-to-one correspondence between the quasicrystal tiles and the facets in the multidimensional lattice, the cut-and-project method has its unique advantages, that is, it can calculate the empires in a defected quasicrystal. The common defects in the quasicrystal can be translated into defects in the cut-window in the mother lattice, which will not affect the calculation of the empires for the local patches. These kind of defects can be used to guide the quasicrystal growth and the phason dynamics in the quasicrystals. A one dimensional example of calculating the empires in a defected quasicrystal is shown below.
5.2. Empires in a Defected Quasicrystal
The empires for the Fibonacci word addressed in
Section 2 can also be obtained using the cut-and-project method applied to the lattice
projecting onto a line
of slope
.
A lattice point
whose orthogonal projection
onto
falls within the cut-window,
, is selected to have its projection
onto
E included in a tiling of
E, as shown in
Figure 15a. In
Figure 15a, the black points are the
lattice points, which are rotated by
, so that the horizontal axis is aligned with the quasicrystal space
E. In this case,
E is 1-dimensional so the tiling will consist of points and the edges connecting the neighboring points. If two lattice points
are neighbors in
, then the unit-length edge connecting them projects onto
E as the edge connecting the projected points
and
. There are two parallel edge classes in these selected edges, one class projects to
E to a longer length
(colored red in
Figure 15a) and the other projects to
E to a shorter length
(colored blue in
Figure 15a), where
. The pattern of
L’s and
S’s along
E is the infinite Fibonacci word
.
Selecting a sub-word
W corresponds to selecting the appropriate edges in
, the edges connecting the red points in
Figure 15b. The corresponding lattice points (colored red) project onto
and their convex hull in
gives a new interval
as the local-patch-window defined earlier. The intersection of all the valid cut-window,
, that cover this
, defines the empire-window (colored red in
Figure 15b).
The lattice edges whose projection onto
falls within the empire-window
project onto
E as the empire of the selected word
W, as the red horizontal segments shown in
Figure 15b. Also in the Ammann bar case mentioned in
Section 2, all points, not only the segments that have two end points, belong to the empire. That is because we are concerned with all bars (corresponding to points in the quasicrystal), instead of adjacent-bar pairs. In
Figure 15b, these extra stand-alone points are from the projection marked by the red dashed lines. These points, each corresponding to a bar, are considered part of the empire in the Ammann bar case.
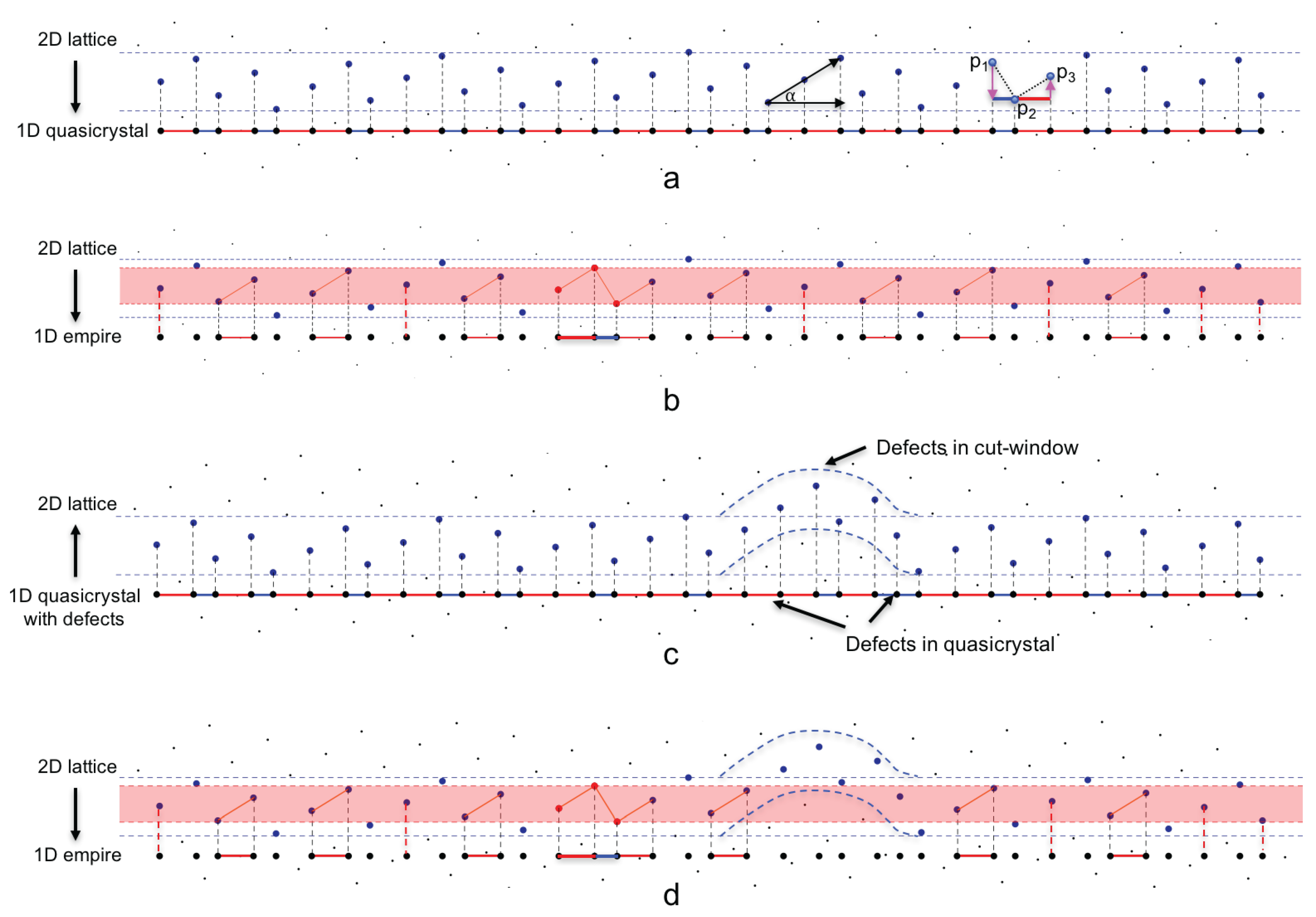
What if the Fibonacci word is not perfect, or in other words, it has defects in it? Here we introduce a reversing algorithm to bring the one dimensional quasicrystal to its two dimensional mother lattice, with a one-to-one mapping between both the points and the edges. In this case the defect in the one dimensional quasicrystal corresponds to a “defected” cut-window in the lattice. By forcing the cut-window to be perfect, without “defect”, we can still calculate the empire of local patches.
To reverse the Fibonacci words to two dimensions, first we reverse the points in the one dimensional quasicrystal to its corresponding points in
, which implies that we keep the one dimensional coordinates of the points to be the
x coordinate and add a
y coordinate or “height” to the points. The relative height between two adjacent points depends on whether there is an
L or
S between the points. The pink arrows in
Figure 15a show that an
S corresponds to a drop of height of
, and an
L corresponds to a rise of height of
. Therefore, knowing the height of one point, the heights of all other points can be determined using this algorithm. Since the height of the points are relative, we can always pick one point and set its height to be zero and from there, the height or
y coordinates of all other points can be calculated.
Figure 15c shows this reversing procedure. We start with the same Fibonacci word used in
Figure 15a, but with some defects added in. First, we reverse all points in this one dimensional quasicrystal to points in two dimensions, using the aforementioned method. After reversing to two dimensions, some of the points at the defected place are off the cut-window used in
Figure 15a. It is as though the defects in the one dimensional quasicrystal are translated to the defects in the cut-window in two dimension.
The next step is to calculate the empire of a local patch in this defected quasicrystal by applying the empire-window of the same local patch to these reversed points, based on the fact that the empire of a local patch should only include the valid tiles from the quasicrystal. Comparing
Figure 15a,d, we see that the empire-window, colored red, misses three points and one edge, therefore, the empire filters out the defects in the quasicrystal. Thus, this property of the empire can be used for error-corrections in quasicrystal dynamics and growth.
6. Summary and Outlook
A quasicrystal carries non-local information since it is a projection from a higher dimensional crystal. This leads to interesting properties in its growth and dynamics. For example, the quasicrystalline relaxation of a dynamic system and the self-correction in quasicrystal growth. The non-local feature of a quasicrystal is best represented in the empires of this quasicrystal, which can serve as an important guiding principle for crystal growth and dynamics.
In this paper we first reviewed two existing methods, the Fibonacci grid method and the multigrid method, for computing the empires for a local patch in quasicrystals using Penrose tiling as an example and we introduced a new and more efficient method, the cut-and-project method.
The Fibonacci grid method using Ammann bars provides some interesting insights but ultimately is inconvenient in practice. Moreover, it is known that the method sometimes does not capture all the forced Ammann bars and so it may fail to identify all the forced tiles in a given empire. The multigrid method provides a robust algorithm not only for generating Penrose tiling but for computing empires as well. There is a disconnect, however, between the tiling and the pentagrid which was used to create it. Namely, given a set with defected tiles, it is difficult to find an appropriate arrangement of grid lines which provides those tiles somewhere in their dual.
The existing methods for generating the empires in a quasicrystal are not very efficient in simulating a dynamics system, while the new method we discovered, a method that uses the cut-and-project technique, is very efficient computationally and also, it provides an explanation of the relaxation and self-correction of quasicrystals. Our new method, the cut-and-project method, provides the same amount of computational robustness as the pentagrid method, but has the added benefit of providing a direct link between the tiles of the quasicrystal and the corresponding facets of the mother lattice. Also, the fact that it can calculate the empires for defected quasicrystals makes it an important tool for the error-correction in quasicrystal growth and dynamics.
Defects occur during the dynamics or growth of quasicrystals and the empires can self correct them by help perfecting the cut-window. We conjecture that a perfect cut-window, reinforced by the sum of the empires of all the stabilized local patches, corresponds to a relaxed ground energy state. And fluctuation in the energy will cause modulation/defects in the cut-window, therefore resulting in defects in the projected quasicrystal. Relaxing the system indicates perfecting the cut-window which leads to the self-correction in quasicrystal dynamics, especially in quasicrystal growth, where at the center, the quasicrystal is relaxed, therefore with no or fewer defects, while at the edge, the quasicrystal is unstable, therefore with more defects. But as soon as this part is relaxed and stabilized, the defects will be corrected. This conjecture is consistent with the results of [
1]. Our group has been working on a Hamiltonian model based on the empires of one dimensional and two dimensional quasicrystals. The work has successfully simulated the relaxation of a one dimensional system and will soon finish simulating a two dimensional system [
13].