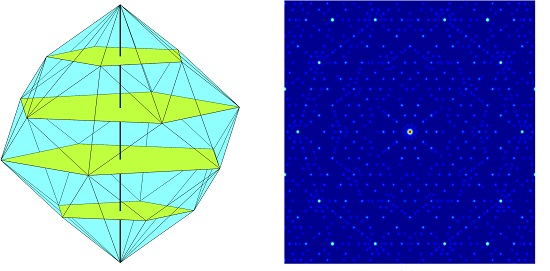
An Exact Method to Determine the Photonic Resonances of Quasicrystals Based on Discrete Fourier Harmonics of Higher-Dimensional Atomic Surfaces
Abstract
:1. Introduction
- (1)
- The approach attempts to capture the properties of an infinite structure with a finite lattice. Thus, the truncated lattice must be large enough to display the long-range order characteristics of the QC.
- (2)
- The reciprocal space of QCs is densely filled [19]; thus, the sampling of the FT must be performed with a very fine resolution to capture all of the diffraction spots.
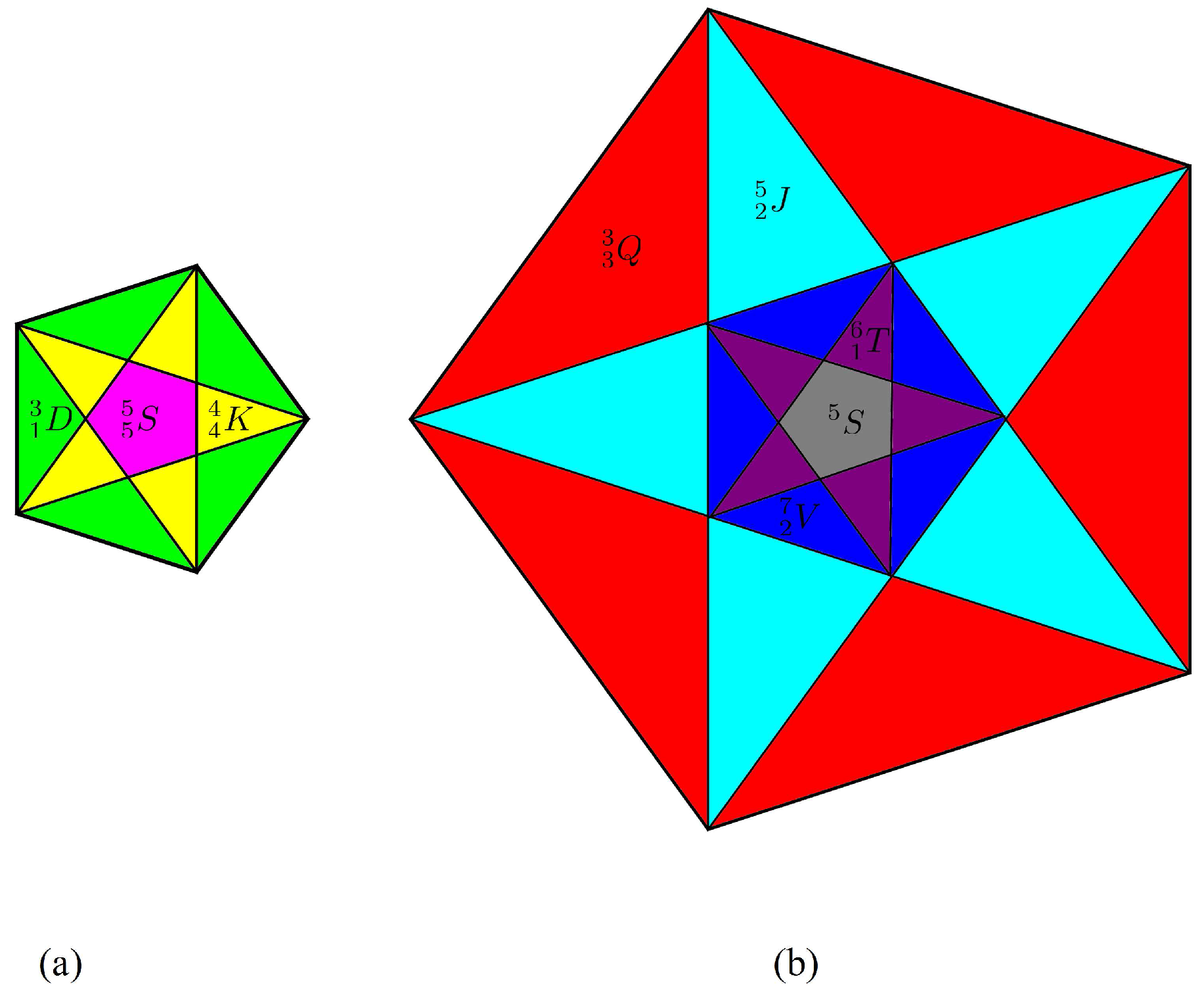
2. Quasicrystals
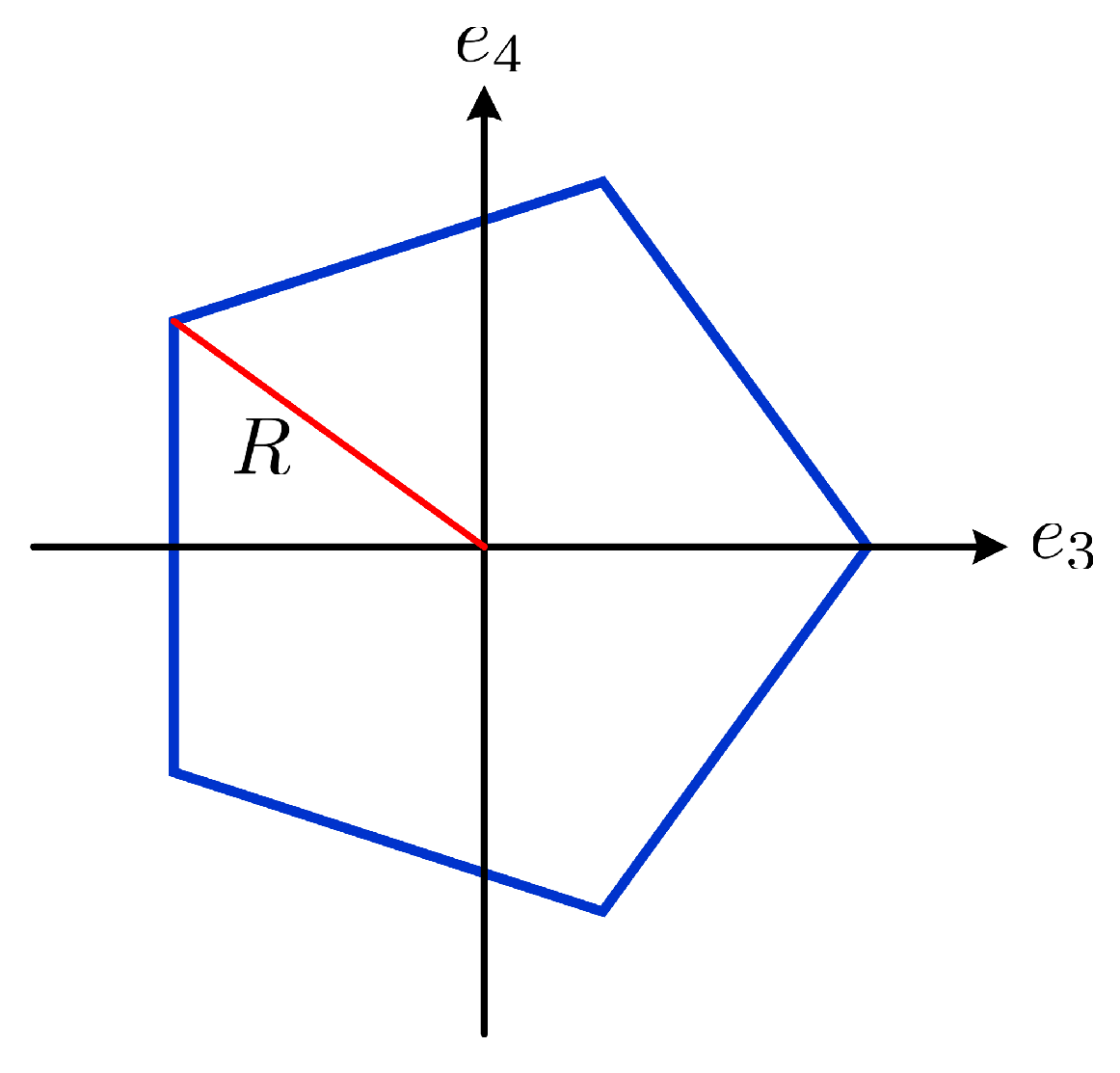
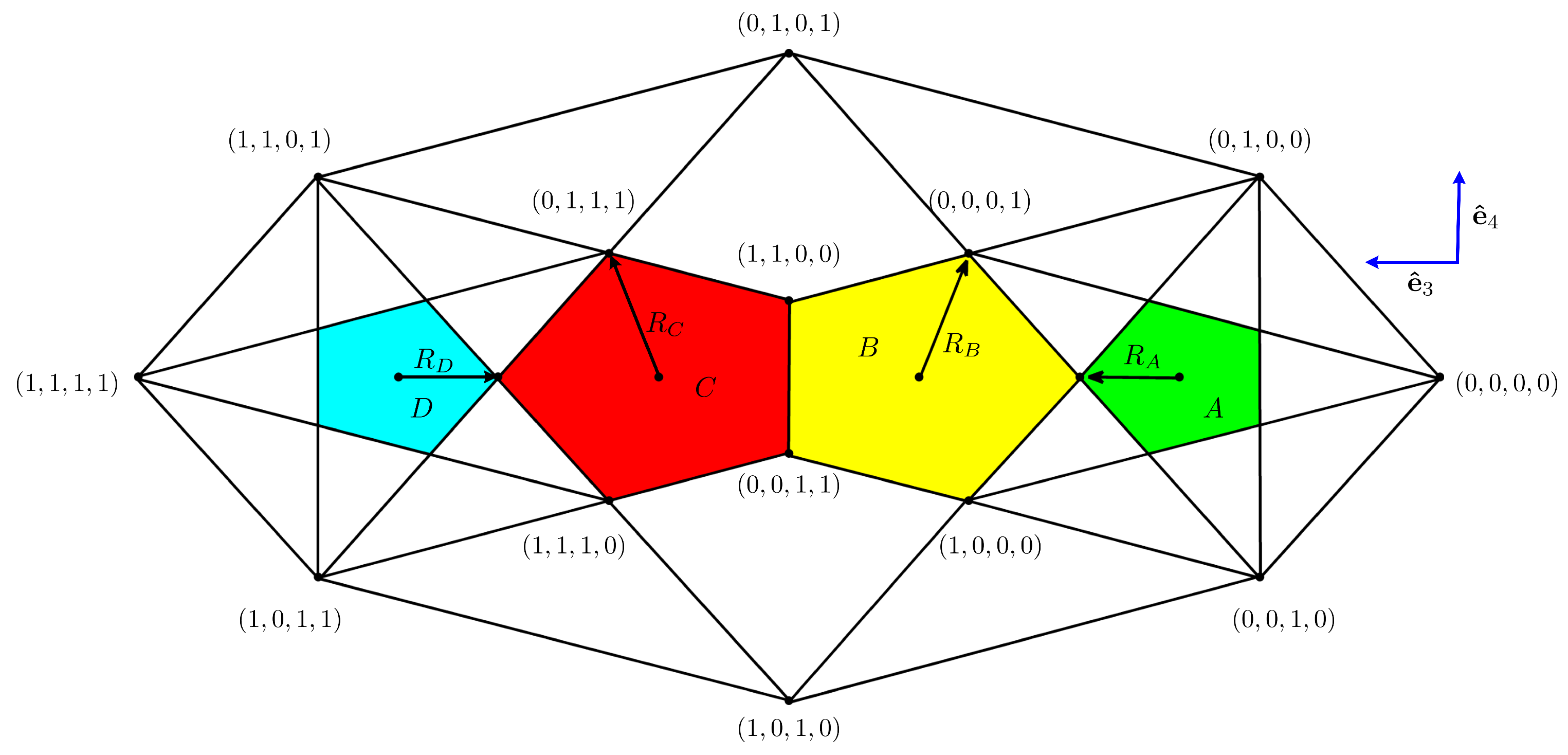
3. Higher Dimensional Approach
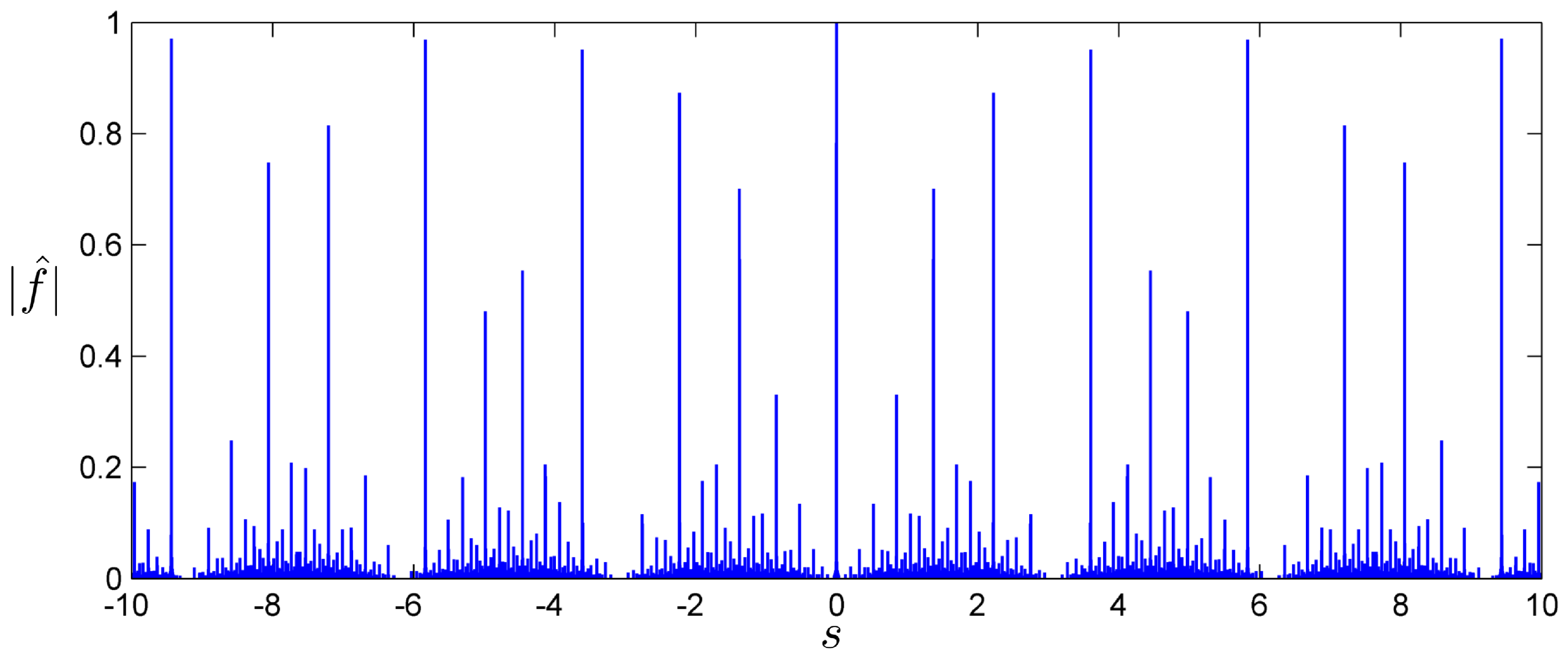
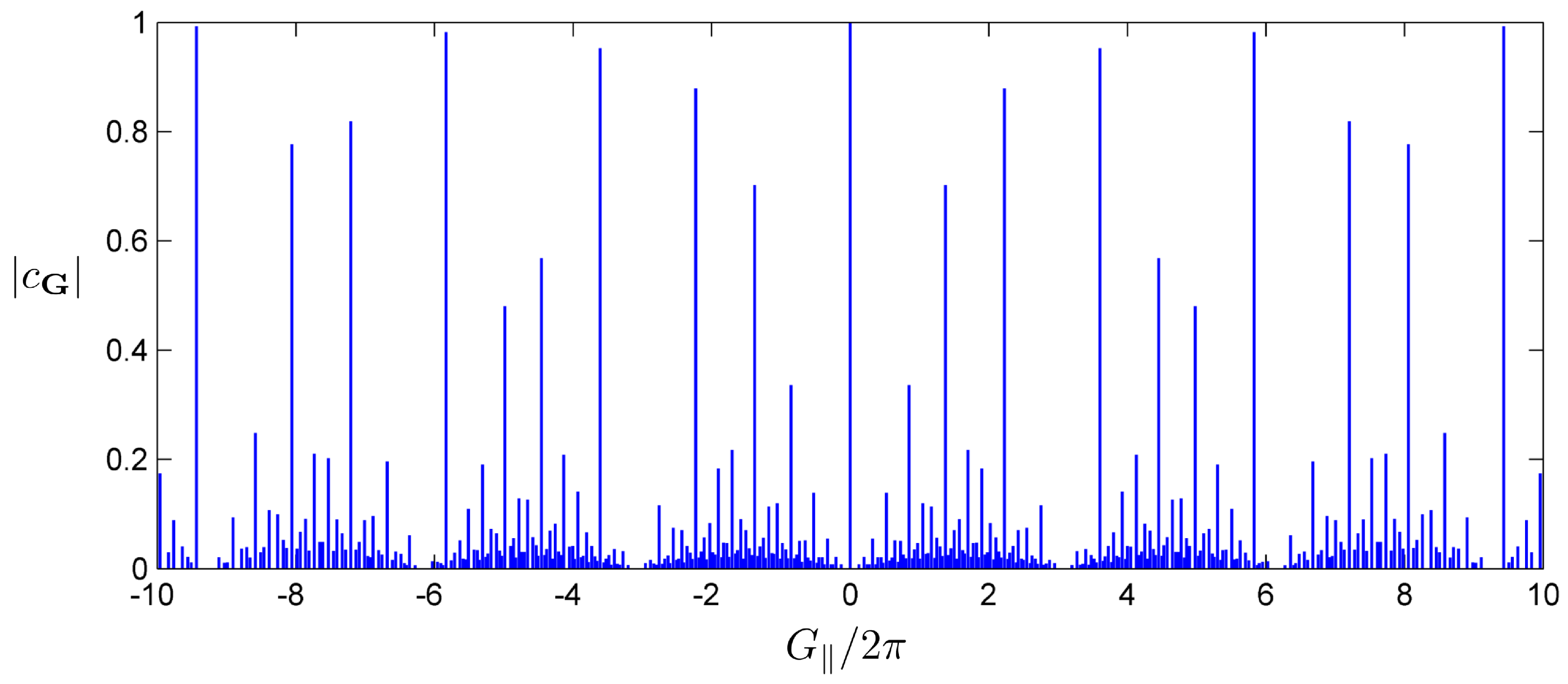
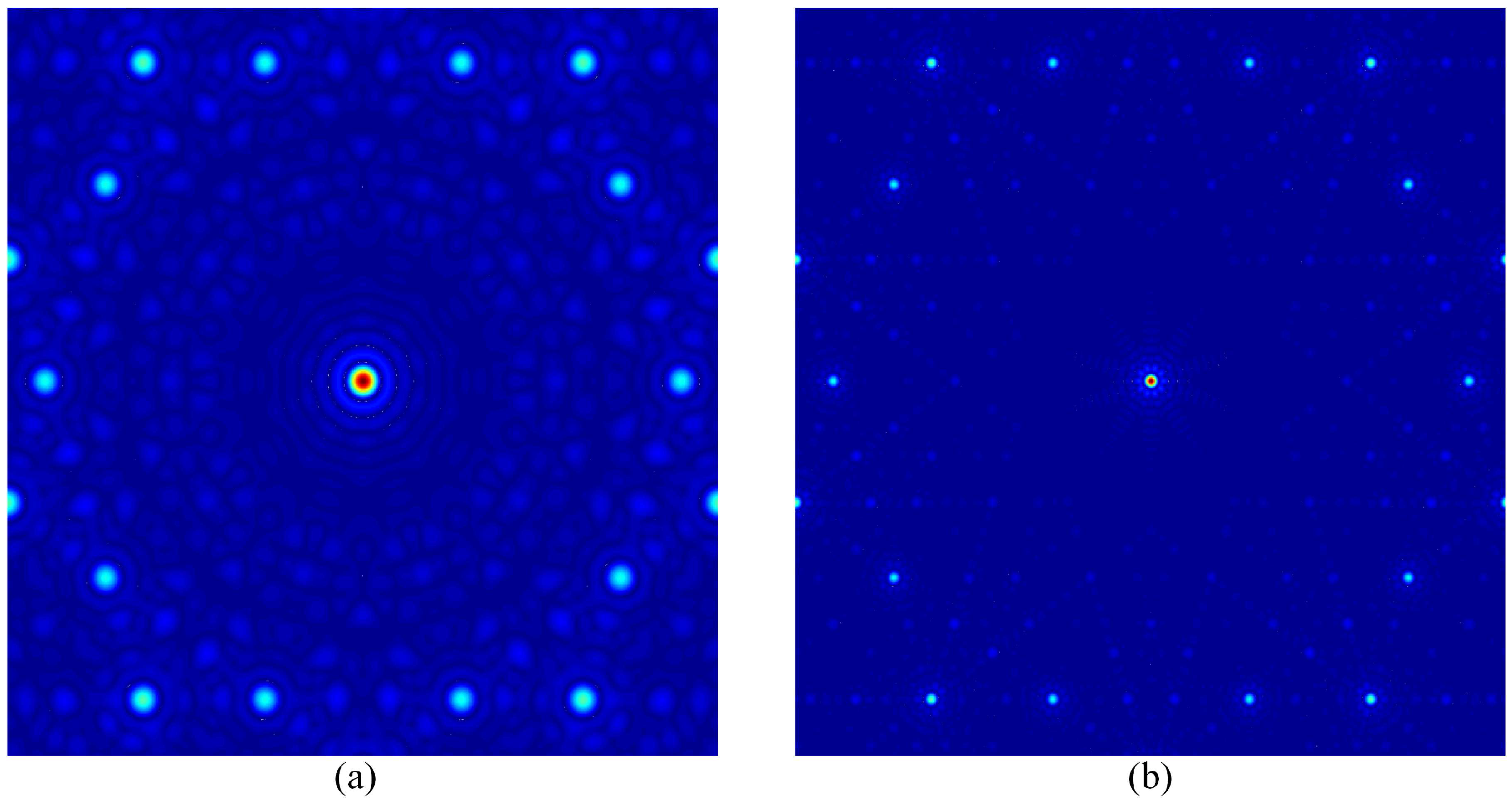
4. Diffraction Patterns Based on Fourier Series Expansion of Higher Dimensional Atomic Surfaces
4.1. Fibonacci QC
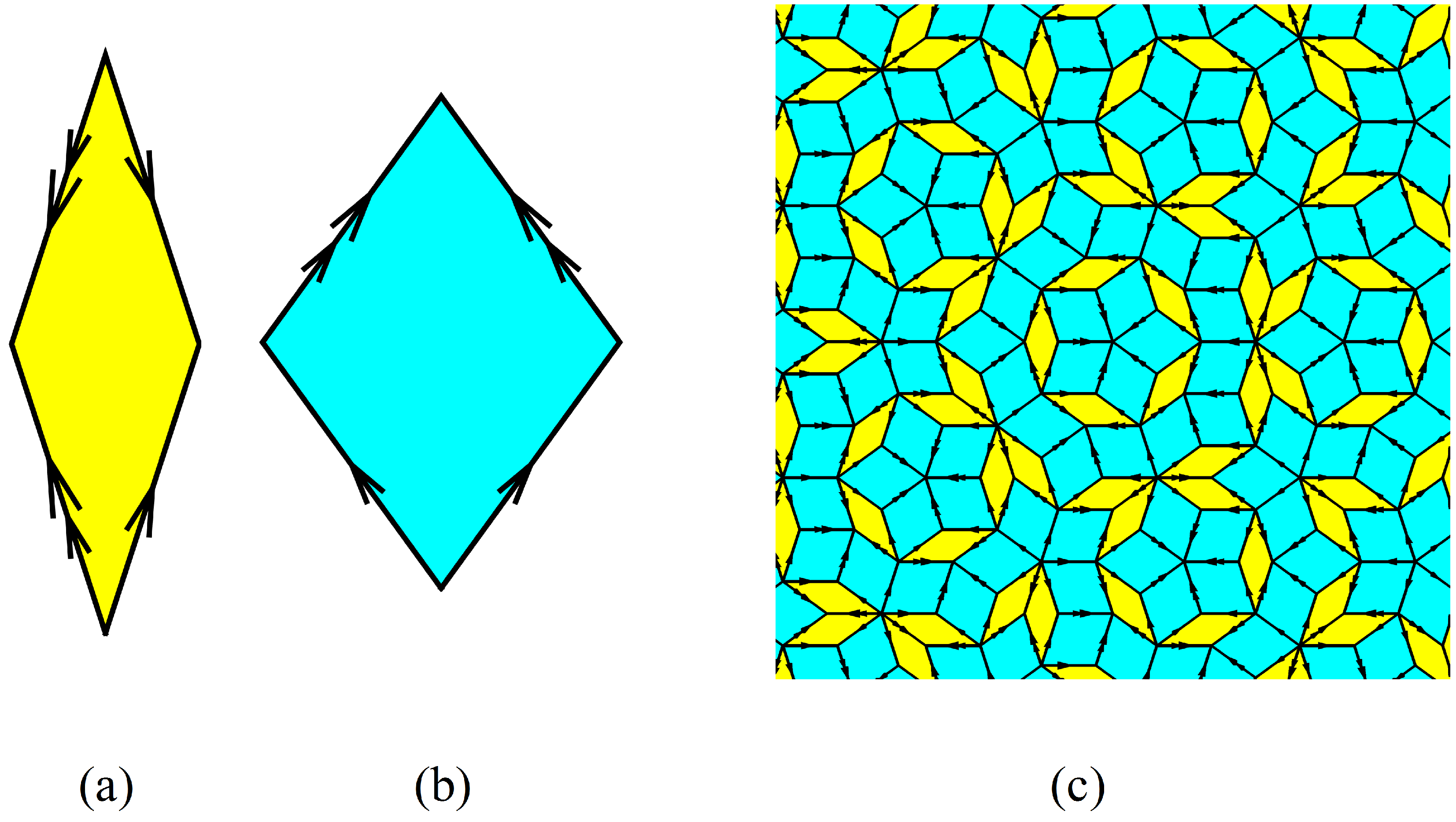
4.2. Penrose QC
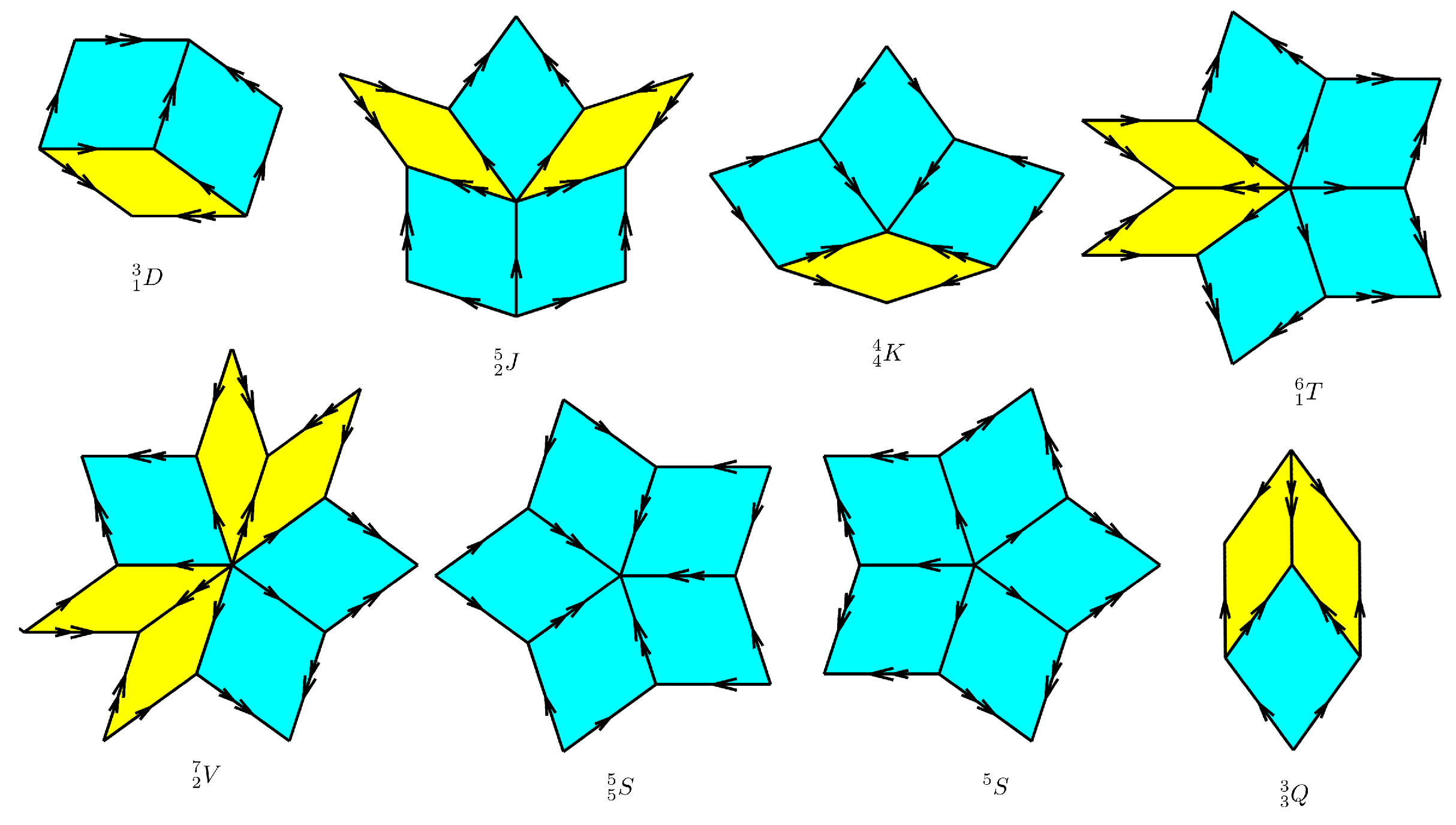
5. From the Vertex Model to Natural QCs
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix: Fourier Series Expansion of a Pentagonal Atomic Surface in the A4 Root Lattice
References
- Senechal, M. Quasicrystals and Geometry; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 2013, 53, 1951–1953. [Google Scholar] [CrossRef]
- Gopinath, A.; Boriskina, S.V.; Reinhard, B.M.; Negro, L.D. Deterministic aperiodic arrays of metal nanoparticles for surface-enhanced Raman scattering (SERS). Opt. Express 2009, 17, 3741–3753. [Google Scholar] [CrossRef] [PubMed]
- Villa, A.D.; Galdi, V.; Capolino, F.; Pierro, V.; Enoch, S.; Tayeb, G. A comparative study of representative categories of EBG dielectric quasi-crystals. IEEE Antennas Wirelss Propagat. Lett. 2006, 5, 331–334. [Google Scholar] [CrossRef]
- Wang, X.; Werner, D.; Turpin, J. Investigation of scattering properties of large-scale aperiodic tilings using a combination of the characteristic basis function and adaptive integral methods. IEEE Trans. Antenn. Propag. 2013, 61, 3149–3160. [Google Scholar] [CrossRef]
- Mittra, R. (Ed.) Computational Electromagnetics: Recent Advances and Engineering Applications; Springer: New York, NY, USA, 2014; Chapter 12.
- Spence, T.G.; Werner, D.H. Design of broadband planar arrays based on the optimization of aperiodic tilings. IEEE Trans. Antenn. Propag. 2008, 56, 76–86. [Google Scholar] [CrossRef]
- Namin, F.; Petko, J.S.; Werner, D.H. Analysis and design optimization of robust aperiodic micro-UAV swarm-based antenna arrays. IEEE Trans. Antenn. Propag. 2012, 60, 2295–2308. [Google Scholar] [CrossRef]
- Gross, F.B. (Ed.) Frontiers in Antennas: Next Generation Design & Engineering; McGraw-Hill: New York, NY, USA, 2011; Chapter 1.
- Gopinath, A.; Boriskina, S.V.; Feng, N.; Reinhard, B.M.; Negro, L.D. Photonic-plasmonic scattering resonances in deterministic aperiodic structures. Nano Lett. 2008, 8, 2423–2431. [Google Scholar] [CrossRef] [PubMed]
- Namin, F.; Wang, X.; Werner, D.H. Reflection and transmission coefficients for finite-sized aperiodic aggregates of spheres. J. Opt. Soc. Am. B 2013, 30, 1008–1016. [Google Scholar] [CrossRef]
- Namin, F.A.; Yuwen, Y.A.; Liu, L.; Panaretos, A.H.; Werner, D.H.; Mayer, T.S. Efficient design , accurate fabrication and effective characterization of plasmonic quasi-crystalline arrays of nano- spherical particles 2016. Sci. Rep. 2016, 6, 22009. [Google Scholar] [CrossRef] [PubMed]
- Pala, R.A.; White, J.; Barnard, E.; Liu, J.; Brongersma, M.L. Design of plasmonic thin-film solar cells with broadband absorption enhancements. Adv. Mat. 2009, 21, 3504–3509. [Google Scholar] [CrossRef]
- Bauer, C.; Kobiela, G.; Giessen, H. 2D quasiperiodic plasmonic crystals. Sci. Rep. 2012, 2, 681. [Google Scholar] [CrossRef] [PubMed]
- Kaliteevski, M.A.; Brand, S.; Abram, R.A.; Krauss, T.F.; Millar, P.; Rue, R.M.D.L. Diffraction and transmission of light in low-refractive index Penrose-tiled photonic quasicrystals. J. Phys. Condens. Matter 2001, 13, 10459–10470. [Google Scholar] [CrossRef]
- Matsui, T.; Agrawal, A.; Nahata, A.; Vardeny, Z.V. Transmission resonances through aperiodic arrays of subwavelength apertures. Nature 2007, 446, 517–521. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, A.; Matsui, T.; Vardeny, Z.V.; Nahata, A. Terahertz transmission properties of quasiperiodic and aperiodic aperture arrays. J. Opt. Soc. Am. B 2007, 24, 2545–2555. [Google Scholar] [CrossRef]
- Steurer, W.; Deloudi, S. Crystallography of Quasicrystals: Concepts, Methods and Structures; Springer: Berlin, Germany, 2009. [Google Scholar]
- Achanta, V.G. Plasmonic quasicrystals. Prog. Quant. Electron. 2015, 39, 1–23. [Google Scholar] [CrossRef]
- Janssen, T.; Chapuis, G.; de Boissieu, M. Aperiodic Crystals: From Modulated Phases to Quasicrystals; Oxford University Press: Oxford, UK, 2007. [Google Scholar]
- Baake, M.; Kramer, P.; Schlottmann, M.; Zeidler, D. Planar patterns with fivefold symmetry as sections of periodic structures in 4-space. Int. J. Mod. Phys. B 1990, 04, 2217–2268. [Google Scholar] [CrossRef]
- Penrose, R. The role of aesthetics in pure and applied mathematical research. Inst. Math. Appl. Bull. 1974, 10, 266–271. [Google Scholar]
- Yamamoto, A.; Hiraga, K. Structure of an icosahedral Al-Mn quasicrystal. Phys. Rev. B 1988, 37, 6207. [Google Scholar] [CrossRef]
- Ishihara, K.N.; Yamamoto, A. Penrose patterns and related structures. I. Superstructure and generalized Penrose patterns. Acta Crystallogr. Sect. A 1988, 44, 508–516. [Google Scholar] [CrossRef]
- Rodriguez, A.W.; McCauley, A.P.; Avniel, Y.; Johnson, S.G. Computation and visualization of photonic quasicrystal spectra via Bloch’s theorem. Phys. Rev. B 2008, 77, 104201. [Google Scholar] [CrossRef]
- Namin, F.A.; Werner, D.H. Rigorous analysis of diffraction from quasicrystalline gratings via Floquet’s theorem in higher-dimensional space. ACS Photonics 2014, 1, 212–220. [Google Scholar] [CrossRef]
- Dubois, J. Useful Quasicrystals; World Scientific: Hackensack, NJ, USA, 2005. [Google Scholar]
- Pavlovitch, A.; Kléman, M. Generalised 2D Penrose tilings: structural properties. J. Phys. A 1987, 20, 687. [Google Scholar] [CrossRef]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Namin, F.A.; Werner, D.H. An Exact Method to Determine the Photonic Resonances of Quasicrystals Based on Discrete Fourier Harmonics of Higher-Dimensional Atomic Surfaces. Crystals 2016, 6, 93. https://doi.org/10.3390/cryst6080093
Namin FA, Werner DH. An Exact Method to Determine the Photonic Resonances of Quasicrystals Based on Discrete Fourier Harmonics of Higher-Dimensional Atomic Surfaces. Crystals. 2016; 6(8):93. https://doi.org/10.3390/cryst6080093
Chicago/Turabian StyleNamin, Farhad A., and Douglas H. Werner. 2016. "An Exact Method to Determine the Photonic Resonances of Quasicrystals Based on Discrete Fourier Harmonics of Higher-Dimensional Atomic Surfaces" Crystals 6, no. 8: 93. https://doi.org/10.3390/cryst6080093
APA StyleNamin, F. A., & Werner, D. H. (2016). An Exact Method to Determine the Photonic Resonances of Quasicrystals Based on Discrete Fourier Harmonics of Higher-Dimensional Atomic Surfaces. Crystals, 6(8), 93. https://doi.org/10.3390/cryst6080093