Soda Cans Metamaterial: A Subwavelength-Scaled Phononic Crystal

Abstract

Photonic or phononic crystals and metamaterials, due to their very different typical spatial scales—wavelength and deep subwavelength—and underlying physical mechanisms—Bragg interferences or local resonances—, are often considered to be very different composite media. As such, while the former are commonly used to manipulate and control waves at the scale of the unit cell, i.e., wavelength, the latter are usually considered for their effective properties. Yet we have shown in the last few years that under some approximations, metamaterials can be used as photonic or phononic crystals, with the great advantage that they are much more compact. In this review, we will concentrate on metamaterials made out of soda cans, that is, Helmholtz resonators of deep subwavelength dimensions. We will first show that their properties can be understood, likewise phononic crystals, as resulting from interferences only, through multiple scattering effects and Fano interferences. Then, we will demonstrate that below the resonance frequency of its unit cell, a soda can metamaterial supports a band of subwavelength varying modes, which can be excited coherently using time reversal, in order to beat the diffraction limit from the far field. Above this frequency, the metamaterial supports a band gap, which we will use to demonstrate cavities and waveguides, very similar to those obtained in phononic crystals, albeit of deep subwavelength dimensions. We will finally show that multiple scattering can be taken advantage of in these metamaterials, by correctly structuring them. This allows to turn a metamaterial with a single negative effective property into a negative index metamaterial, which refracts waves negatively, hence acting as a superlens.

1. Introduction

It is well known in solid states physics that the periodicity of atoms composing crystals is responsible for the existence of both conducting bands and band gaps for electrons. This property is a direct consequence of the Bloch theorem [1,2] applied to the wavefunction of electrons. Similarly, optical waves propagating in periodically stratified media are subject to the same theorem giving rise to the existence of ranges of frequencies for which no propagation is allowed, so-called optical band gaps. At an interface with free space, such a medium acts as a mirror for incoming waves, termed a Bragg mirror [3]. Physically, this can be quite easily understood since at each interface between two layers of different indices of refraction, part of the waves is transmitted and part of them is reflected. The total wave field travelling forward is thus the summation of many multiply scattered waves, that all interfere. Those interferences can be destructive when the optical path difference between two multiply scattered waves correspond to a multiple of half a cycle. In these periodic media, this Bragg condition typically occurs when the period of the medium scales with the optical wavelength. As a consequence, Bragg mirrors are typically structured with a period corresponding to half the operating wavelength.

Analogously to crystals for electrons, this property is not limited to one dimensional periodic problems and, in the late 80s of the past century, similar frequency bands prohibiting the propagation of optical waves have been observed in 3D periodic media [4,5]: the name of photonic crystals was born. As acoustic waves are subject to the same Helmholtz equation as optical ones, similar results were demonstrated later on in this domain, in one dimension [6] and in higher dimensions [7]. Again, and by analogy, these periodic composite media were named phononic crystals. Similarly to the applications found in optics with the Bragg mirror, those photonic/phononic crystals are mostly used for their ability to inhibit the propagation of waves at specific frequencies. Since they are governed only by interferences, they have been proved to be ideal candidates for controlling the propagation of waves at the scale of their unit cell. Indeed, local modifications of these media can be realized without altering the properties of the whole medium, notably its ability to support band gaps, resulting in the creation of cavities or waveguides [8]. Yet the lowest frequency exhibiting this property is typically the frequency for which the wavelength corresponds to twice the medium periodicity. Therefore, any application of those composite materials suffers from the fact that the medium typical period has to scale with the operating wavelength, which can become very impractical when dealing with lower frequency waves.

To circumvent this issue, in 2000 Pr. Ping Sheng proposed a new class of acoustic composite media: a locally resonant sonic crystal [9]. This proposal echoes to preliminary works in the field of electromagnetic waves [10,11] where the medium, even if periodic, exhibits a band gap at low frequencies, meaning for operating wavelengths much bigger than the typical scale of the medium. Those composite media owe their fascinating properties to their unit cell which resonantly interacts with the incident wave field. This resonant effect is very specific to the object composing the medium and is no longer linked to the typical distance between adjacent cells. Many efforts have been made to diminish the size of those resonant inclusions in order to build media that are now described with effective parameters. Indeed, because the spacing between resonators is small compared to the wavelength, they all supposedly see the same incident field and their responses can henceforth be averaged. The field of metamaterials was born and with it its typical terminology and viewpoint. Notably, metamaterials are usually not studied using dispersion relations and band structures, but rather using concepts of effective properties which can be negative, near-zero or very high [12]. For example, the initial proposal of Ping Sheng [9], which is now considered as the first example of an acoustic metamaterial, can be described in terms of a negative mass density. For this reason, metamaterials are usually studied using homogenization procedures. A relatively large variety of acoustic metamaterials have been proposed within the last 15 years [9,13,14,15,16,17,18,19,20,21,22,23].

In this article, we review recent results that we have obtained in the field of locally resonant metamaterials. The latter are defined as composite media made out of unit cells that resonantly interact with waves. In airborne acoustics, there is a typical object that fulfills the resonant condition on which these metamaterials are based: the Helmholtz resonator [24]. Incidentally, many objects of the everyday life are Helmholtz resonators, for instance bottles or glasses, and we have used in all our experiments very well calibrated and widely available Helmholtz resonators: soda cans [25]. In the first section of this article, we show that arranging several soda cans on a subwavelength scale builds a propagating medium that typically behaves as a locally resonant metamaterial. Notably, the propagation in this medium can be described by effective parameters, one of them being typical of a resonant behavior. We show that it can equivalently be described by a polariton-like dispersion relation that results from the coupling of a continuum of propagating waves and a local resonance. We stress that the mechanism underlying the physics of this type of metamaterial is solely governed by interferences, analogous to phononic crystals, and we make the analogy between the negative effective property of the metamaterial and the so-called hybridization band gap in acoustics. In the next two sections, we exploit this specific dispersion relation for applications in different frequency ranges. Below the intrinsic resonance of one resonator, the wave propagation exhibits an effective wavelength that is of the order of the spacing between two cans, meaning deeply subwavelength compared to the free space wavelength. We show that one can exploit this property in order to beat the diffraction limit in air from the far field using time reversal. At higher frequency, the medium can be described with a negative compressibility which overall results in an inhibited propagation of waves, a phenomenon which we refer to as the hybridization band gap. The latter resulting from interferences only, we show how one can exploit it in order to trap and guide sound waves on scales that are much smaller than the wavelength in air, by introducing small defects in the structure. We underline that these defects cannot be caught by the usual homogenization approaches which average the response of the unit cells of a metamaterial over a wavelength. This last observation eventually leads us to the last section of this article where we study the physics of a novel type of metamaterial, that is, a metamaterial consisting of a single resonant unit cell, that has been slightly modified to impact directly the metamaterial structure. This proves that it is possible to build a double negative metamaterial just with one type of resonator that should expectedly only bring one negative effective property, using a clever structuration of the metamaterial. This last result opens the era of metamaterial crystals, thereby highlighting clearly the fact that metamaterials are similar to phononic crystals, even if the typical spatial scales of the former are much smaller than those of the latter, and although they are ruled by different physical mechanisms.

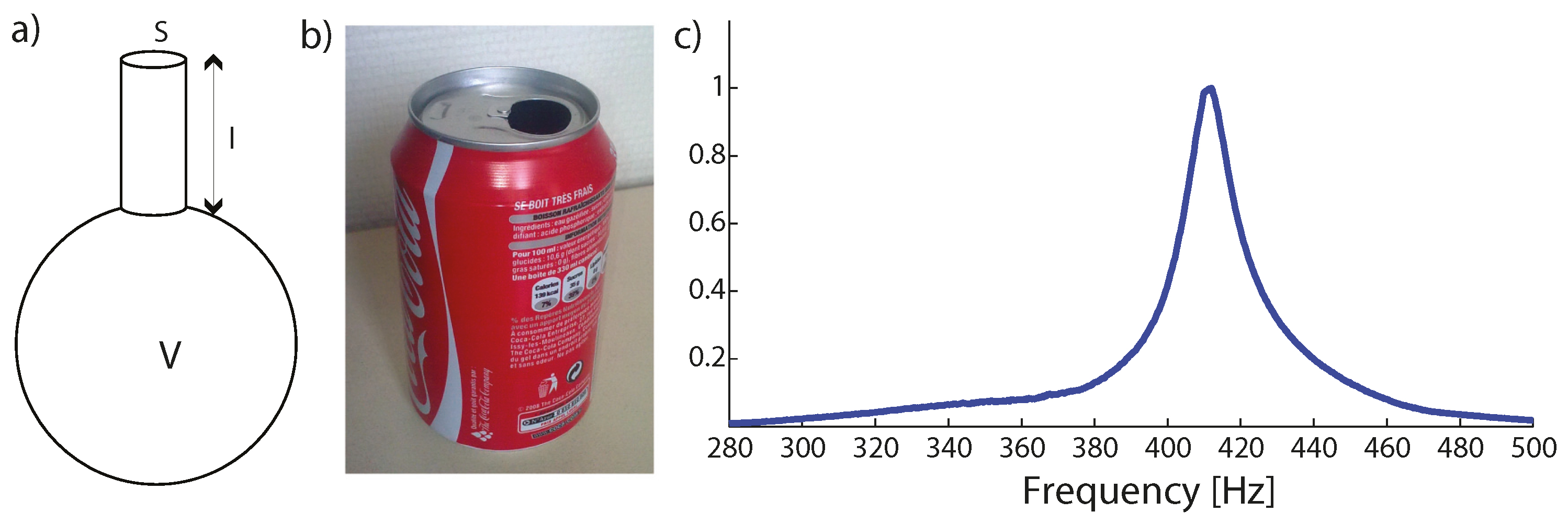
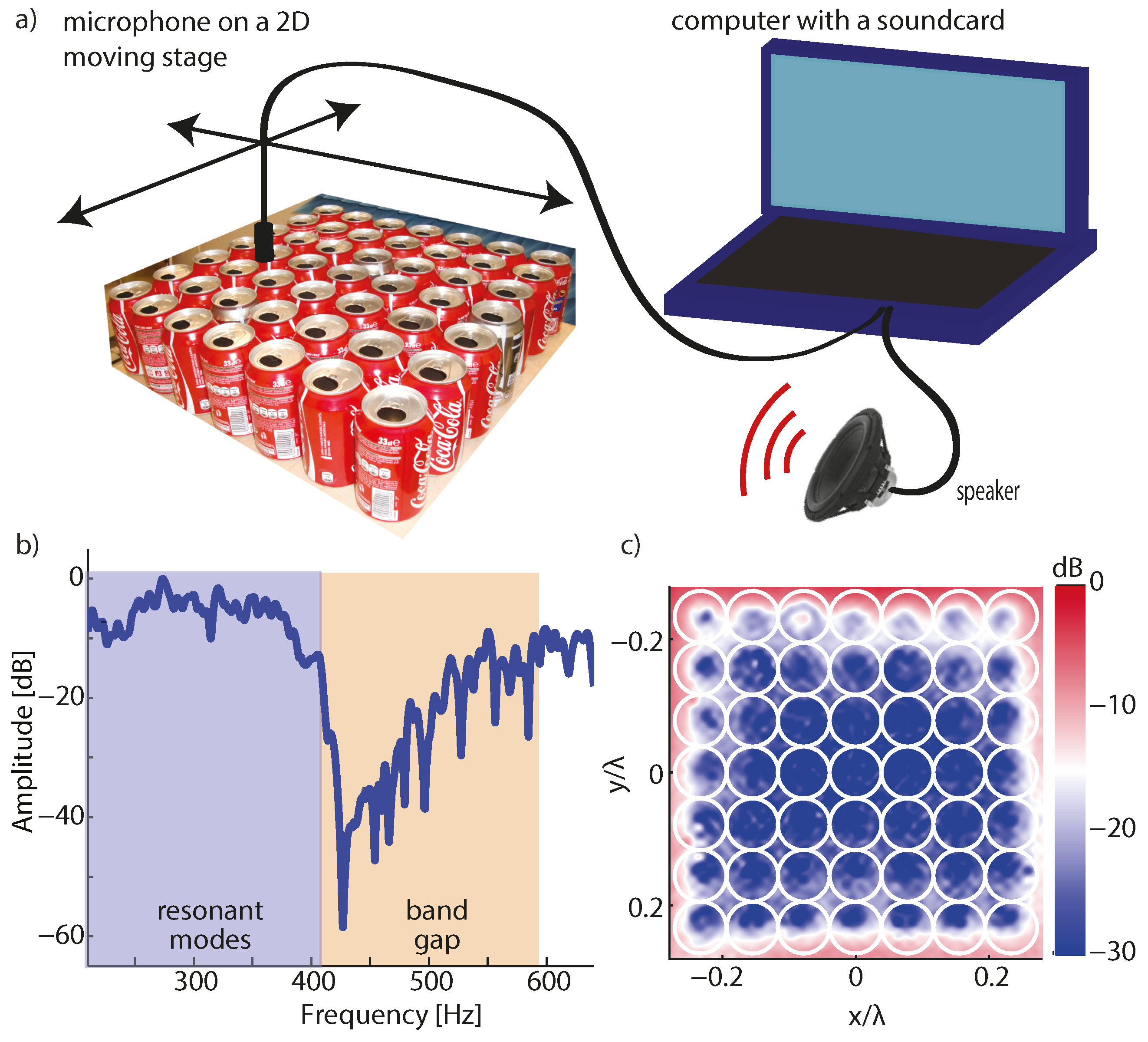
2. The Soda Can: A Resonant Building Block

2.1. Why the Soda Can?

Our research started in electromagnetics in the microwave range where we studied a wire medium [26,27,28]. The latter consists of a subwavelength arrangement of identical conducting wires. It is well known that each of these wires exhibits a resonance resulting from the stationary current in the wire when the length of the wire is a multiple of half the freespace wavelength. Therefore, such a wire can be seen from the top as a physically tiny object compared to the wavelength. Packing such resonant wires on a small scale we end up on a composite medium that falls within the class of locally resonant metamaterials.

To transpose this electromagnetic example to acoustic, the first idea was therefore to reproduce the behavior of the half-wavelength-long conducting wire by using an open-ended half-wavelength-long pipe [29,30]. Indeed, there is always a propagating mode in a rigid-walled pipe whatever its cross section. Especially, at low frequency when the wavelength becomes large compared to the typical scale of the cross section, the pipe behaves as a single mode waveguide. This propagating mode presents a uniform profile of pressure along the cross section and propagates at the speed of sound. When cutting the pipe with two open-ended terminations, the impedance mismatch at both extremities builds a stationary resonant mode inside the pipe. The resonance frequency occurs when the frequency $f=n\frac{c}{2L}$ (where L is the pipe’s length and n an integer). Such a pipe is therefore the acoustic equivalent of the conducting wire in our microwave experiment. We built the acoustic equivalent of the wire medium and we unfortunately did not manage to reproduce the physics of the wire medium. This comes from a strong difference between the two types of resonators: while the electromagnetic resonator can be considered as almost lossless because copper is a good conductor, the acoustic resonance suffers from severe damping. Indeed, the attenuation in the pipe originates from the viscous damping along the walls by the sliding layer near the interface. The ratio between the damping volume, which is located on a skin layer along the pipes walls, and the overall volume in the pipe increases while reducing the cross-section of the pipe. As a consequence, a pipe with a small cross-section (remember that we want to have a subwavelength resonator) is described by an attenuation length that can be much smaller than the attenuation length in air [31].

After this first try, we had to look for another acoustic resonator that fulfills the requirements of being small compared to the wavelength while presenting relatively low losses due to viscous damping. This drove us to consider the case of the well known acoustic resonator introduced by Herman von Helmholtz [24] more than one century ago. The latter consists of a rigid container embedding a volume V, terminated by an open-ended neck of length l and cross section S (Figure 1a). The resonant behavior of such an object is due to the oscillation of the mass of the gaz column located in the neck, while the cavity behaves as the restoring force of the harmonic oscillator. The resonant frequency of the Helmholtz resonator therefore simply writes:

$$f=\frac{c}{2\pi }\sqrt{\frac{S}{Vl}}$$

(1)

The resonance frequency can occur in the low frequency range where the operating wavelength is much larger than the resonator dimension. In our case, we want a subwavelength unit cell so we prefer to choose a relatively high volume V. We also know from the pipe’s experiment that most of the damping effects occur in the small cross-section, so short neck’s length l is preferred. As a consequence, keeping the resonance in the low frequency range imposes to decrease S. Then started a real experimental strategy during which we tested dozens of mass-produced objects: glass bottles, glasses of different geometries, Christmas baubles or even chemical flasks... We ended up on the use of a 33 cL soda can as a Helmholtz resonator (Figure 1b) for which the neck’s length is indeed short hence minimizing the viscous damping. Experimentally, we measure a resonance frequency of 420 Hz (Figure 1c) meaning that the lateral dimension of the can (i.e., 6.6 cm) is roughly $\lambda /12$ at resonance.

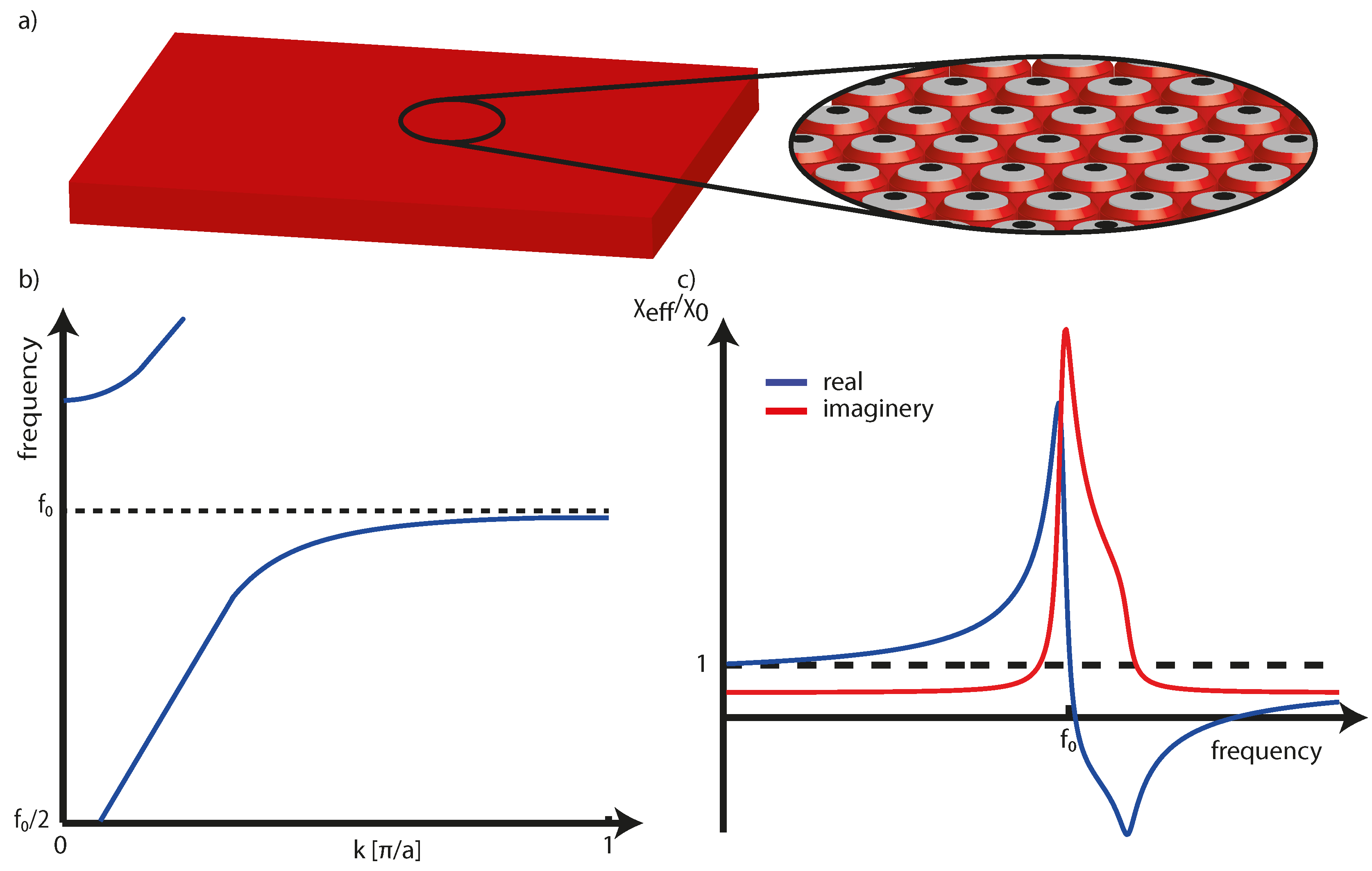
2.2. Band Structure of the Soda Can Medium

Now that we have our unit cell, we want to study the propagation of waves in a locally resonant metamaterial based on it by moving from the single soda can to a medium made of several ones. And since the resonance occurs in the low frequency range, namely in the large wavelength regime, this medium in first approximation can be seen as a homogenous medium as sketched in Figure 2a. This homogenization procedure which is the scope of most of the metamaterials research is the exact analogue of dielectrics for light. Indeed, in this case the resonant unit cells are the atoms, which are deep subwavelength resonators. They are excited by the incoming optical waves and their relaxation participate to the total transmitted optical field. This gives rise to variations of the optical index of refraction, which can present values larger or lower than that of vacuum. Stated otherwise, the interaction of light with microscopic resonant scatterers creates at the macroscopic scale an effective index of refraction. Our locally resonant metamaterial behaves just the same way: the interaction of acoustic waves with the soda cans gives birth, at the macroscopic scale, to effective properties that are linked to the resonant behavior of each of them. There is, however, a big difference between atoms in dielectrics and the soda cans. While the former present an albedo that is close to zero, meaning that their scattering cross-section is much smaller than their absorption cross-section, the latter present an albedo close to unity [32]. In other words, while most of the incoming light on dielectrics is absorbed by atoms through inelastic scattering, the soda can is able to re-radiates most of the stored energy at resonance because we typically looked for the least lossy acoustic resonator.

Nevertheless, the physics of dielectrics is very similar to that of locally resonant metamaterials. We make the approximation that the metamaterial unit cells are not strongly coupled by any near field interaction. This approximation is not valid for any unit cell, but in the present case it means that the soda can’s walls are rigid enough to guarantee that the pressure field inside a given one does not directly influence the pressure field on its nearest neighbors. Under this approximation, the interaction of acoustic waves with the subwavelength resonators creates a polariton, just as light interacts with atoms in a dielectric. Namely, there is an avoided crossing between the local resonance of the soda can and the plane wave dispersion line, which gives rise to a binding branch of subwavelength modes below the resonant frequency $f_0$ of a single can, a band gap above it, and above this band gap an anti-binding branch of supra-wavelength modes. We have recently interpreted this behavior in terms of Fano interferences [33] between the continuum of plane waves propagating in the matrix and the local resonance [34]. In the case of the soda cans medium, the dispersion relation is therefore obtained by measuring the transmission coefficient in the far field through a single can. The latter necessarily takes into account the resonant nature of the unit cell by exhibiting the Fano-like profile, and the multiple scattering is taken into account by applying the Bloch theorem with respect to the periodicity of the medium. The result of COMSOL multiphysics simulations applied to the lossless problem is presented in Figure 2b.

A more common way of describing the physics of locally resonant metamaterials consists in using the idea of effective properties. In acoustics, a given unit cell acts on macroscopic properties which are typically the effective mass density ${\rho }_{\mathrm{eff}}$ and the effective compressibility ${\chi }_{\mathrm{eff}}$ depending on which type of excitation it is sensitive to [35]. For the soda can medium, the volume V behaves as an extra compressive volume for the incident wave encountering it and it therefore locally affects the effective compressibility seen by the incident pressure field. Applying the parameters retrieving procedure from [36] to a simulation including losses of a can, the complex effective compressibility is obtained (Figure 2c). The soda can creates below its resonance frequency a band of very high effective compressibility—equivalent to the branch of subwavelength modes in the polariton description—, then a band of negative effective properties—the band gap—, and finally a band of low effective property—the supra-wavelength modes branch.

3. Exploiting the First Propagating Band with High Bloch Wavenumbers for Subwavelength Focusing from the Far Field

3.1. Subwavelength Focusing in the Context of Metamaterials

In the community of metamaterials, much attention has been paid in the past 10 years to using the negative effective property band for wave focusing below the diffraction limit. Indeed, if one can realize a metamaterial presenting two almost co-localized subwavelength unit cells which are resonant at the same frequency and which act on both properties of the medium, one can obtain a metamaterial that has both its effective properties negative. This results, as was pointed out more than 40 years ago by Veselago [37], in a medium whose effective index is negative. John Pendry proposed in a seminal paper in 2000 [38] that a slab of such a medium should behave as a perfect lens for imaging and focusing purposes since it amplifies infinitely the evanescent waves coming from a source or object, making them measurable in the far field with conventional optical components. This approach has been shown to be largely hampered by losses of materials, especially for applications in optics where materials are relatively dissipative.

Subwavelength control of acoustic waves has not been studied as much as in electromagnetic, but there have been few proposals in order to realize super-resolution imaging based on canalization [39] or hyperlens [40]. Concerning focusing under the diffraction limit, there have been propositions based on the analogue of the optical “Bull’s eye” [41], or based on the use of negative index material [16]. Nevertheless, none of those proposals clearly demonstrated subwavelength control of the acoustic waves below the wavelength scale. The only experimental proofs that clearly showed super-focusing come from the use of an acoustic sink [42] which requires an active source at the focal point, or a proposal which uses a phononic crystal where both the source and the image stand in the near field of it [43].

While most groups were focused on the negative index metamaterial, we realized that the high effective property band offered by the locally resonant metamaterial could be used for such a purpose. Indeed, this band is inherently composed of evanescent waves since at a fixed frequency the wavenumber is higher than the freespace one. In the following, we explain, based on the soda can metamaterial example, how and under which conditions they can indeed be used. The reader has to keep in mind that the soda can medium is a very good airborne acoustic example for this study which has been published in [25], but similar results have been obtained in underwater acoustics in the ultrasonic range with a bubble as a unit cell [44], with Lamb waves in a thin plate [45], in electromagnetics in the microwave regime [27,46], and in the optical range [47,48], making this approach very robust and general.

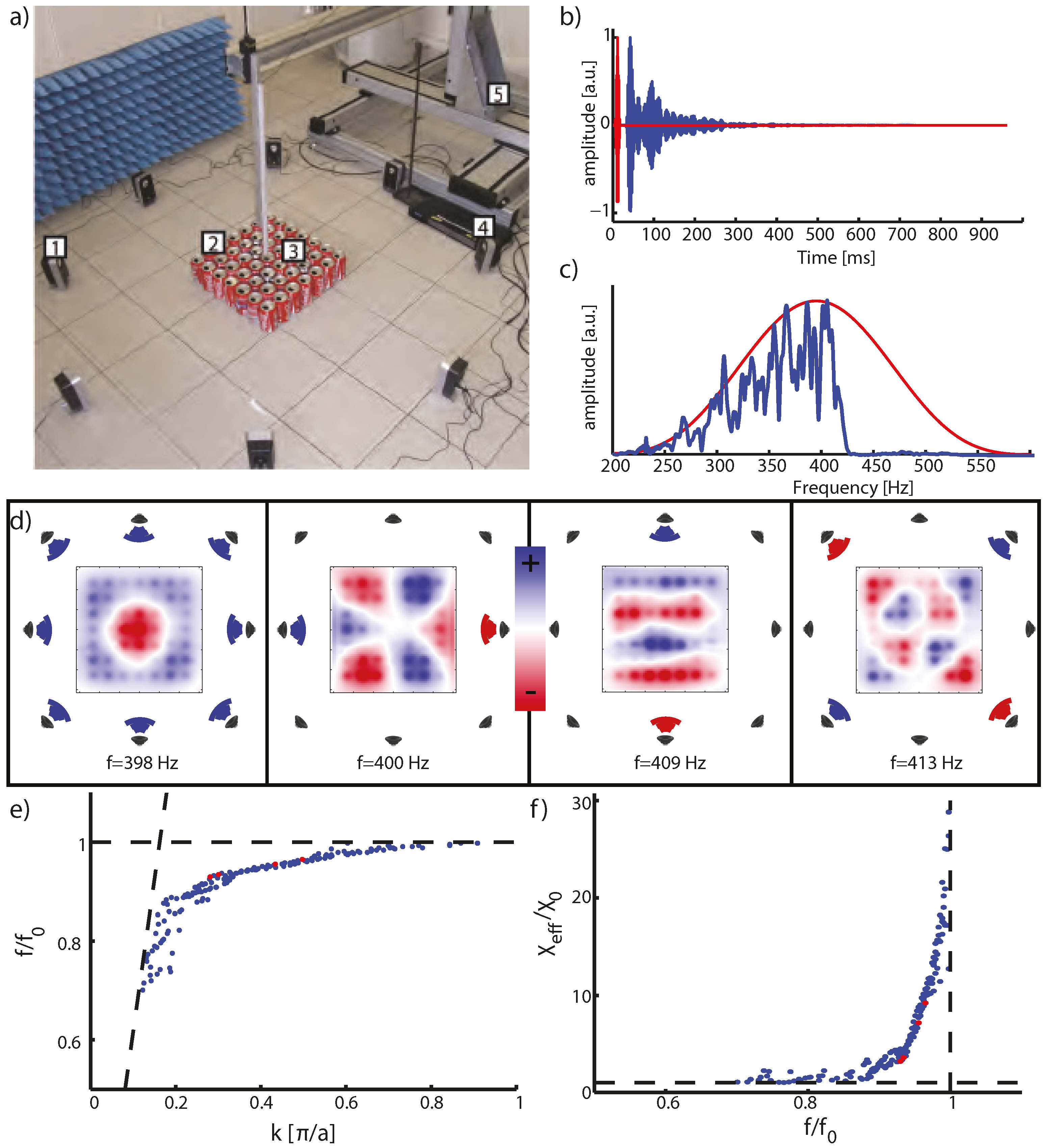
3.2. Eigenmodes of a Finite-Sized Array of Soda Cans

The infinite medium described in the previous section is not experimentally realizable and we will see in this section that the finite dimension of a real medium plays a crucial role for the subwavelength focusing application. So, let us first start by the experimental measurements that we have been able to perform. We conducted experiments on a two-dimensional array of $7\times 7$ closed-packed square lattice of soda cans as shown in Figure 3a. The medium is surrounded by a set of 8 computer-controlled speakers, and a motorized microphone is placed on top of the array of Helmholtz resonators. We first emit a short pulse (actually we used chirped emission and apply matched filtering to recover a short pulse) from one speaker and record the temporal signal received by the microphone placed 1 cm on top of the aperture of one can. The typical temporal signal obtained is shown in Figure 3b. It extends over hundreds of milliseconds, compared to the initial pulse duration of 20 ms, which is a clear signature of the resonant effect. The spectrum of this signal (Figure 3c) reveals the existence of many resonant peaks ranging from 250 Hz up to the resonant frequency of a single resonator, that is $f_0=420$ Hz.

We then repeat the same experiment when each speaker emits a short pulse while moving the microphone on top of the array. Knowing the entire set of temporal Green’s functions relating the pressure field at a given position in the medium to the emission from one of the speakers, we can then mimic different monochromatic experiments. We show in Figure 3d the monochromatic field maps at various frequencies and with different emission patterns (a monopolar, a dipolar along the x-direction, a dipolar along the y-direction and a quadrupolar). All of those maps clearly show the subwavelength nature of the modes supported by the medium. For example the first mode shows two nodes of the field while the entire dimension of the medium is roughly $\lambda /2$. We have not yet discussed the importance of the different radiation patterns but we will come back on this aspect later on.

The measured bank of data does not limit to those 4 modes and we therefore performed an automatic treatment of all the measurements in order to draw a dispersion relation. For each frequency and for each radiation pattern the wave field is spatially Fourier transformed in order to extract an effective wavenumber of the mode. The result of such a treatment is summarized in Figure 3e. The measured dispersion relation exhibits the expected polariton behavior that has been introduced in the first section. One can note that some wave fields oscillate on a scale as small as the medium’s lattice. From this dispersion curve, the effective compressibility can be extracted (Figure 3f): the high effective compressibility below the resonance frequency $f_0$ is revealed. Above, the absence of modes has two origins: in the band gap regime there is no propagating wave so no mode is measured, higher the modes correspond to leaky modes that radiate acoustic waves out of plane.

Interestingly, and quite surprisingly, the homogenization procedure that applies for an infinite medium can be probed on a physical two-dimensional metamaterial which typical dimension is only half a free space wavelength. Notably, the finiteness of the sample as well as the boundaries shape do not influence on the measured dispersion relation. Because of the finiteness of the medium however, other phenomena have to be discussed. Indeed, as the typical spectrum shows in Figure 3c the finite size medium only supports a discrete set of resonant eigenmodes. This has several consequences that are the key features for the next paragraph where we demonstrate subwavelength focusing. First, because of the finiteness, the supported eigenmodes are stationary modes trapped inside the medium and therefore they experience a resonance phenomenon. Second, such collective eigenmodes can leak some energy through radiative damping to the far field area, and this is the reason why we have been able to probe them when doing the reciprocal operation, namely exciting from the far field and probing in the near-field of the medium. As a consequence, the high effective compressibility which results in the existence of subwavelength (with respect to the freespace wavelength) modes cannot be used as it in order to build a focal point: if one excites the medium with a single monochromatic source placed in the far field one only excites the combination of eigenmodes that can radiate energy in the direction of the source, and for our small medium (i.e., $\lambda /2\times \lambda /2$) it reduces to four modes (monopolar, dipolar and quadrupolar radiation patterns). Furthermore, one has no control over the relative phases between the 4 trapped monochromatic eigenmodes by using only one source. Increasing the number of sources allows the manipulation of the relative phases between the different types of radiation patterns but actually it is not sufficient enough to focus waves everywhere on the sample. This strategy has been adopted in [49] where the authors demonstrated the ability to build a focal hot spot in the middle of the sample that is thinner than the free space wavelength. If we want to be able focus everywhere in the sample we need to have access to all the different spatial scales which is only realizable by taking advantage of the dispersion of the medium: at one frequency the spatial variation of the field is given by the dispersion relation. Consequently, we proposed to use a polychromatic approach, namely time reversal [50], in order to treat coherently the spatio-temporal degrees of freedom of the metamaterial [51,52,53].

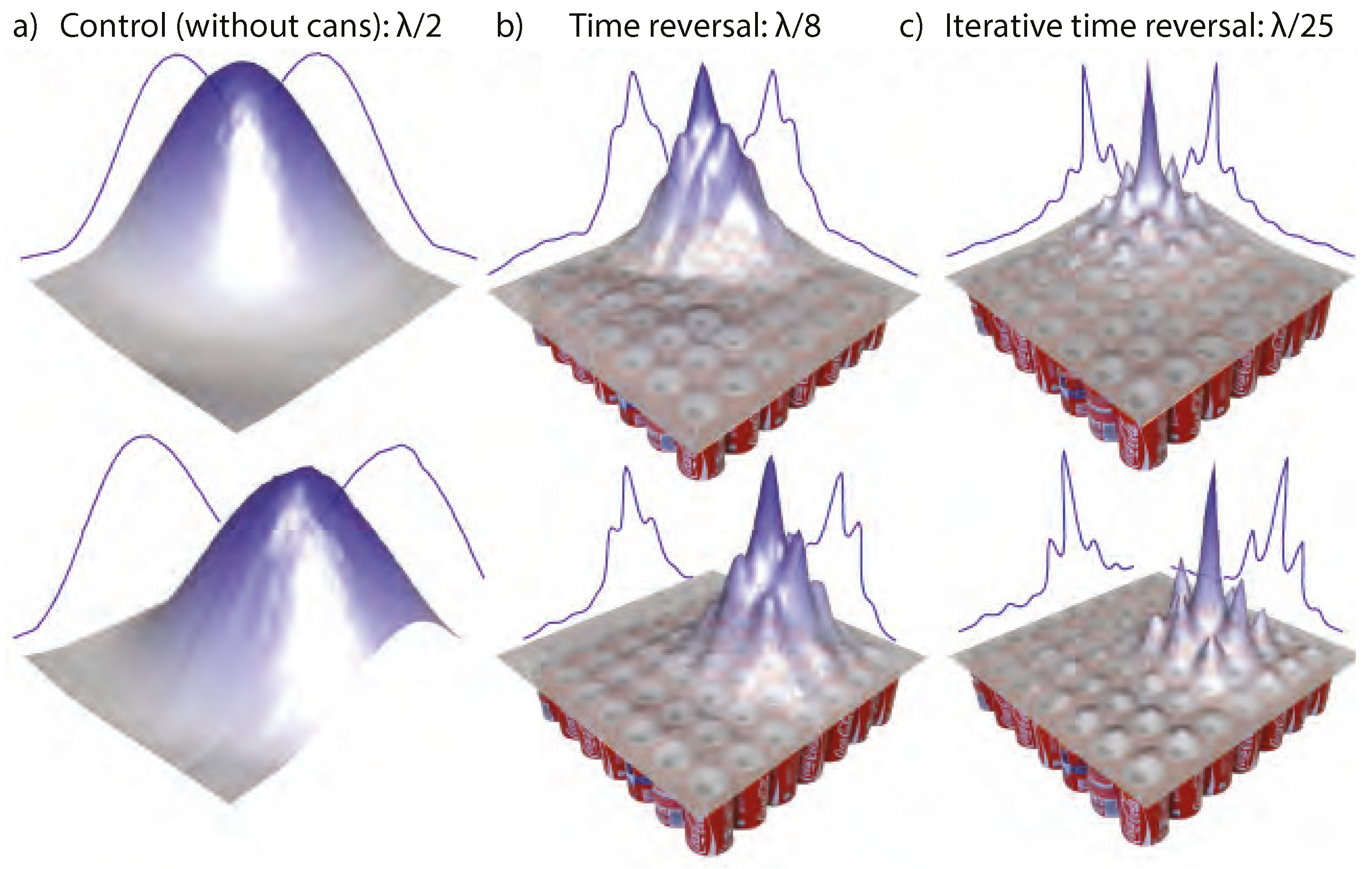
3.3. Subwavelength Focusing from the Far Field

Before entering the case of the soda can medium, let us start by a control experiment while removing the Helmholtz resonators’ array: the microphone, placed at a given position, records the set of 8 Green’s functions when each of the speakers emits a short pulse. Each of those signals is time reversed, and they are simultaneously reemitted by their corresponding speaker, meaning that each speaker emits first what arrives later in time and reciprocally. Note that in this experiment, we also take advantage of the spatial reciprocity of the wave equation since we did not place a source at the position where we want to focus, but we learn the Green’s functions from the speakers to the microphone. We then map the wave field generated around the initial microphone’s position by moving it (and repeating the simultaneous emission each time the microphone has moved). As a result of such a procedure, we plot the square of the maximum in time of each received signal. This is equivalent to show the maximum power received on each position. The result of such an operation is displayed in Figure 4a. The obtained field maps show that 8-channel time reversal in a typical laboratory room permits to focus waves on isotropic focal spots whose dimension is half-wavelength, only limited by the diffraction limit [54].

The same procedure in the presence of the cans is then performed. This time, the set of emitting signals span a longer time range as a signature of the modes resonances and the time reversal permits to synchronize at the desired location and at the desired time all of the eigenmodes that are non-zero. This results in a spatio-temporal focusing of the acoustic waves. The measure of the focal width is as thin as $\lambda /8$ (Figure 4b), far beyond the diffraction limit. This is a consequence of the subwavelength nature of the modes inside the metamaterial. This experiment clearly shows that thanks to the resonant nature of the eigenmodes trapped inside the metamaterial, the conversion from free space wavelength to subwavelength varying fields is guaranteed. This permits to beat the diffraction limit from the far field and to focus waves on a thinner scale compared to the free space wavelength.

But, we have not yet reached the limit of the device since we initially probed eigenmodes that oscillate on scales as thin as the distance between two cans. This limitation comes from the fact that time reversal does not compensate for losses during the propagation. It only recombines the different frequency components by coherently adding them—they all add in phase at the focus—but does not play any role on their relative amplitudes. And, we know that the modes that suffer most from the losses are the highest Q ones, or equivalently the ones with the smallest group velocity, which exactly corresponds to the most subwavelength ones. Compensating for the losses is performed by increasing the relative weight of these modes at the emission. To do so, signals, that are the equivalent of an inverse filter [55], are built. This procedure first requires the knowledge of the set of all impulse responses between the 8 speakers and each desired focal position on top of the resonators, which we limited to 49 as the number of cans. Then we numerically compute a bank of 8 × 49 signals based on an iterative scheme of time reversal [56] that supposedly focus on each position with the lowest possible level of spatio-temporal side lobes. 8 of those signals are simultaneously emitted with the speakers. Eventually, we map the wavefield on top of the cans while emitting those signals and we end up on the result shown in Figure 4c with focal spots as thin as $\lambda /25$. Of course, because we cannot focus waves in between cans, the focusing resolution is actually limited by the period of the medium. Overall, we prove that we can beat the diffraction limit by a factor of 12.5 with a positioning accuracy of $\lambda /12$. We only present two maps but this focusing can indeed be performed at any position on top of a can. We stress here that the $\lambda /25$ hot spot is due to extra evanescent feature of the Bloch wave near the can aperture. Therefore, measuring the acoustic field slightly upper of the cans decreases this effect.

Apart from its evident fundamental interest, this experiment opens up many avenues in terms of applications for sound and ultrasound. We believe that our approach is very promising for the design of arrays of actuators, micro-mechanical actuators in general and, by reciprocity, of sensors. Indeed, using subwavelength coupled resonators offers three tremendous advantages. First, it introduces the possibility to engineer matrix of actuators or sensors that are arranged on a subwavelength scale. Second, because our approach takes advantage of dispersion, it allows to address independently many sensors using their temporal signature. Finally, as we initially proved [25], it also enhances the intensity deposited onto one location, because of the subwavelength dimensions of the focal spots. This entails that our approach can be utilized for subwavelength-sized actuators and micro-electromechanical systems as proved recently by Lani et al. [57].

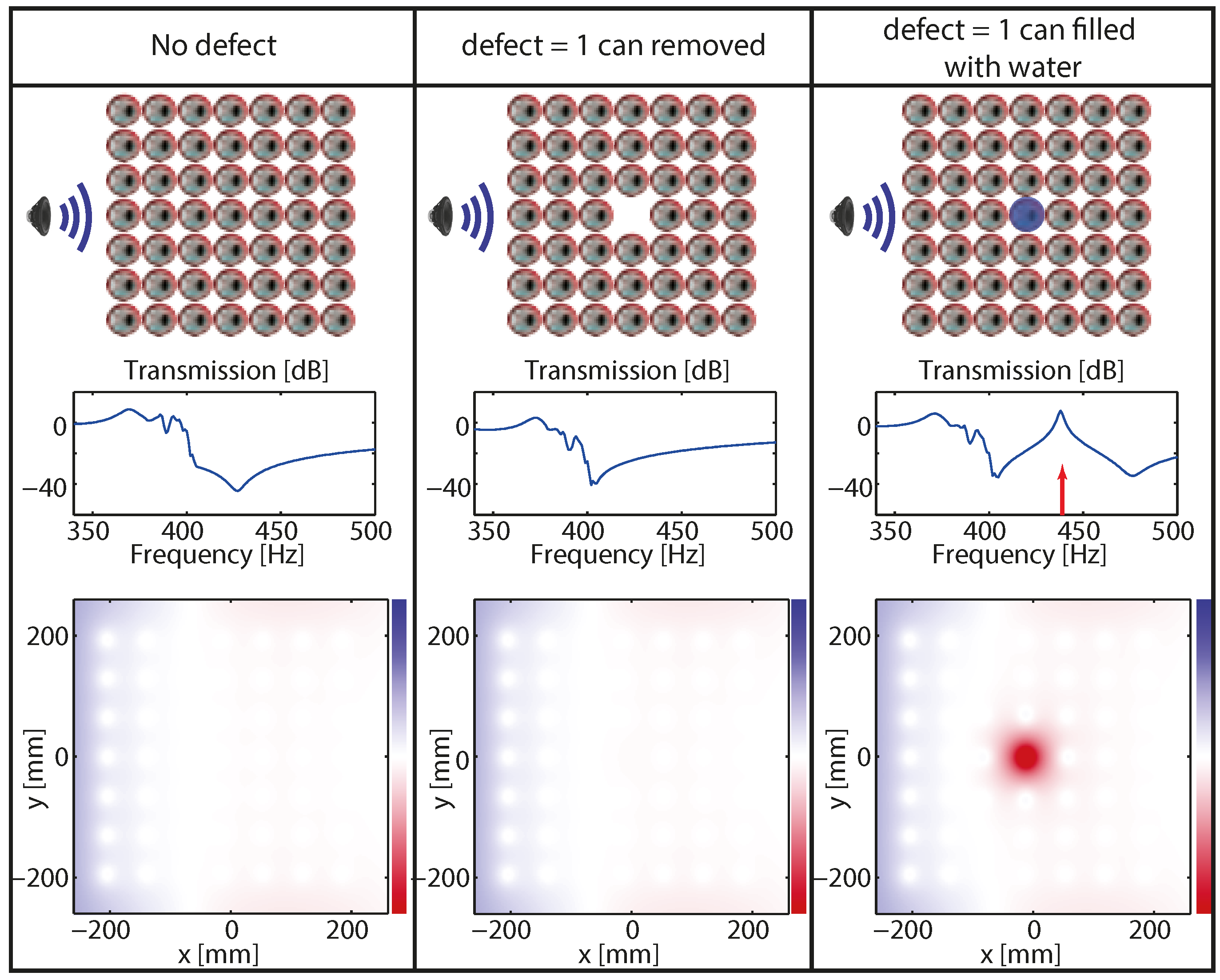
4. Subwavelength Trapping and Waveguiding by Exploiting the Low Frequency Band Gap

4.1. Existence of a So-Called Hybridization Band Gap

Now, we move to a slightly higher frequency range, just above the resonance frequency of a single soda can. In the previous experiment, we were not able to measure any wavenumber because of the absence of resonant eigenmodes, and therefore we were not able to extract the effective compressibility this way. In order to show what happens in this spectral domain, we represent in Figure 5a the sketch of the new experiment that is conducted. A speaker placed in the far field emits a short pulse that spans frequencies ranging from 200 Hz to 600 Hz and a microphone measures the signal received on top of one can. The spectrum represented in a logarithmic scale (Figure 5b) clearly shows two distinct regimes. Below the resonance frequency of one can (blue shaded area), the transmission is high and evidences the existence of the resonant peaks discussed in the previous section; Above the resonance, the transmission drops down to −60 dB and almost no energy is transmitted from the speaker to the microphone. This frequency region is therefore associated to a so-called band gap (red shaded area). One has to keep in mind that the overall dimension of the soda can remains smaller than the free space wavelength, meaning that the attenuation length is really short. In order to investigate deeper this attenuation effect, we mapped the field at a frequency within the band gap (450 Hz) while we emit from the loudspeaker. We represent in Figure 5c the absolute value of the measured monochromatic field in decibel scale again. This map highlights that the field cannot penetrate inside the soda can metamaterial at this frequency and that the attenuation length is really short since after only one layer of cans the transmission is already reduced by a factor ten. Again, we stress that in the specific case of our two dimensional medium, the destructive interferences responsible for the absence of propagating solutions occur in the near field of the cans. As a consequence if one moves the microphone up the attenuation effect decreases.

This band gap was actually introduced initially when we mentioned the polariton dispersion relation. In terms of effective parameters, the existence of the band gap is associated to the negativeness of the effective compressibility which results in an imaginary propagating velocity, or equivalently evanescent waves. We have to mention here that in the acoustic community this type of band gap has been observed before the emergence of metamaterials and in the early 1990s researchers referred to them as “hybridization band gap” [58,59,60,61,62,63,64]. Hybridization is a very generic term originating from solid state physics that refers to the coupling between two states resulting on the existence of two hybrid states [65]. In the context of wave propagation it mostly refers to the avoided crossing between two modes that share a common geometry. Yet the term “hybridization band gap” clearly refers to the avoided crossing between the free space dispersion relation and the localized resonator, as depicted in the polariton picture at the beginning of this article. We have therefore reinterpreted this band gap in terms of Fano interferences [33,66] since it is clearly the interaction between a continuum of modes (the free space waves) and a resonator [34]. Note that there are several works in the acoustic community that have tried to mix in the same frequency range the “hybridization band gap” and the Bragg gap that is due to the periodicity of the medium and mostly occurs when the lattice constant is half a wavelength [62,67,68,69].

4.2. Creating a Defect within the Hybridization Band Gap

This kind of band gap that occurs in the low frequency regime, i.e., when the wavelength is large compared to the typical distance between resonators, presents an important difference compared to the well documented ones in the context of phononic crystals [6,58,70,71,72,73,74]. In the phononic crystals, the forbidden band is due to Bragg interferences which are inherently the consequence of the periodic nature of the medium: the destructive interferences occur thanks to the periodic patterning of the medium. As a consequence, the proposed applications exploiting the forbidden propagation consists in locally breaking the translational symmetry of the medium. Indeed, when doing so, solely evanescent waves can penetrate from this location on small distances inside the crystal. For example, a point defect can be created in a phononic crystal by locally removing a scatterer. This results in a small cavity because a resonant mode is created by the defect within the band gap. Following this concept, many components have been demonstrated based on periodic media such as waveguides using line defects [75,76,77,78] and the envisioned applications span a large amount of domains from optronics [79] to light matter interactions [80]. However, because of their wavelength scale period, phononic crystals result in relatively large devices. This seriously restrains the range of applications, especially in the low frequency regimes where the wavelength is large. Contrary to Bragg interferences based band gap, the hybridization one, which originates from the destructive interferences between the resonant response and the incident wave, is robust to a spatial disorder: breaking the translational periodicity of the medium does not close the band gap [60,63,81]. As a consequence we cannot use the trick of breaking the periodicity of the medium as performed in phononic crystals in order to create a defect state.

To illustrate the strong difference between those Bragg band gaps and the hybridization one observed in the soda cans medium, we run a set of simulations where we created a defect by removing one can inside the array. We show in Figure 6 (middle) the spectrum of the transmission between an incident plane wave and the location where we removed the soda can. It has to be compared to the one in Figure 6 (left) where no defect within the array has been created. We do not notice any difference between the two spectra in the band gap, and this is confirmed by the typical maps obtained at 440 Hz where no significant changes are observed. This makes a big difference compared to a Bragg based band gap: the defect that we created this way is actually too small to support a resonant mode, while in a phononic crystal removing one scatterer allows the existence of a stationary defect mode since the typical scale of such a defect is the wavelength. In order to tackle this issue, we have to physically introduce a resonant defect inside the soda can medium, which is simply performed by detuning one resonator compared to the rest of the medium. In the case of the soda can medium, this is fairly easy to build this defect resonator: the Helmholtz resonance of a single can is parametrized by the volume of the air cavity. So, we create a detuned resonator just by changing this volume which is realized by filling it with a few centiliters of water. It results in a resonance frequency that is upward shifted, thus falling within the forbidden band. Again, we stress that since the medium is governed by interferences only, akin to phononic crystals, introducing such a defect should not destroy the bulk properties of the metamaterial. The simulation corresponding to a water volume of 6 cL clearly shows that this trick permits to create a defect: the spectrum of the transmission exhibits a resonant peak near 440 Hz and the corresponding field map confirms the existence of confinement at the defect position (Figure 6 (right)).

The existence of this defect mode deserves few comments. First, given the very small spatial scale of the soda can medium, one would expect very strong near field interactions between the resonators. Yet the polariton origin of the band gap, that is the coupling of a freespace plane wave and a local resonance, actually proves that the dispersion in this deep subwavelength scaled medium is solely due to interference effects, therefore guaranteeing the existence of this defect mode. Second, because the unit cell is very small compared to the freespace wavelength, the modal volume of the confined mode in this medium is deeply subwavelength. Third, while the quality factor of a single can is around 10 the quality factor of the defect mode reaches 80 solely limited by the viscous losses. This comes from the fact that the can filled with 6 cL of waters cannot radiate waves toward far field thus canceling any radiative damping of its intrinsic resonance. Those two effects, namely a high quality factor and a low mode volume, are typical quantities that opticians are researching to enhance the emission rate of an emitter and it is known under the name of Purcell factor [82]. Here, we have shown with an acoustic example that high Purcell factors are attainable in metamaterial defect cavities. We have obtained similar results for microwaves [34,81] that allows us to be confident on the fact that the optical community can certainly reach this goal.

4.3. Molding Experimentally the Flow of Acoustic Waves at a Subwavelength Scale

We now come back to the experimental setup described in Figure 5a and we use it to experimentally prove that it is possible to control the waves at the subwavelength scale, by introducing defects similarly as we numerically performed. Obviously, the first experiment consists in reproducing the point defect. So, we locally introduce a defect state by introducing 6 cL of water in the central can. While emitting sound with the loudspeaker, the microphone mounted on the 2D moving stage maps the field on top of the array. The real part of the monochromatic map of the field is given in Figure 7a as well as the absolute value profile along the dashed line. Clearly, we observe that the pressure field is localized within one can of the array, meaning that waves have tunneled through the metamaterial, and filled the cavity. The effective cavity size of λ/15 is much smaller than in any realized phononic crystal. And again, experimentally the measured quality factor for the cavity is around 80, in very good agreement with the numerical results.

We now concentrate on a second type of defect that probably can lead to more applications in acoustics: a line defect. To that aim, using a 5 × 12 cans array, a subwavelength line defect is obtained by filling the soda cans of the central line with 6 cL of water. Now, instead of having a resonant cavity we actually create a subwavelength waveguide in the soda can array. Again, we measure the acoustic field distributions on top of this array. The map of the measured acoustic field for a frequency of 447 Hz is presented in Figure 7b, as well as a transverse profile of the waveguide mode. This demonstrates a λ/14 wide waveguide and we measure an attenuation transversely of 25 dB after the first row of cans. This kind of waveguide is therefore extremely confined on the defect line at the operating frequency. We cannot present all of the results here but similar propagating behavior has been obtained for frequencies around the presented one, except that the effective wavelength within the waveguide is changing while changing the frequency. The bandwidth is centered on the defect’s resonance frequency, which is typical of a tight binding coupling. Indeed, the filled cans creating the waveguide are embedded in a medium that does not support any propagating waves, therefore the only channel for the coupling is tunneling from can to can. Note that we stated initially that the physics of the soda can medium can be described by neglecting any near field coupling because the picture of the polariton catches all of the physics. The tunneling channel that we discuss here is created by the hybridization band gap of the entire array so this is not in contradiction with the previous statement.

Using the same experimental protocol, we now move to more complex components to manipulate waves. We designed a corner waveguide and a splitter by inserting those partly filled Helmholtz resonators in a $7\times 7$ array of empty cans. Maps of the spatial distributions of the fields in those samples are presented in Figure 7c and d alongside the profiles of their modulus in the directions of interest. From those new experiments, we make a series of conclusions. First, one can force the guided waves in any given direction, with no specific engineering of the material structure, owing to the resonant nature of the unit cell. In our case, we bend the waves 90${}^{\circ }$ with unity efficiency and within a λ/14 long unit cell. Actually, because a soda can has an isotropic radiation pattern, there is no difference between the 90${}^{\circ }$ bend and the linear waveguide. This is in great contrast with designs based on designer’s plasmons for instance [83], where scattering impairs seriously the ability of those structures to bend waves within small propagation distances. Here, since the waveguide lies in a band gap material, no scattering occurs. Second, we can use this approach to split waves into two arms, which ensures the possibility to realize deep subwavelength interconnections and routing of acoustic energy.

As a conclusion, the approach presented in this section gives unprecedented solutions to manipulate acoustic waves, especially those for which the wavelength is large compared to the envisioned applications. It paves the way to the design of ultra compact components. We insist here that this article is dedicated to the soda can medium but this approach is very general and applies to any locally resonant medium with no near field coupling. Similarly, this guiding property was observed in underwater acoustics in a bubbly liquid. Indeed, air bubbles in water present a very low frequency resonance known as the Minnaert resonance for which the bubble size is very small compared to the free space wavelength, thus creating a hybridization band gap [84]. By modifying a row of a bubble crystal, the existence of guided modes exhibiting a tight-binding dispersion curve was demonstrated [85], but it was not clear that the modification of the row led to the creation of upper-shifted resonators within the hybridization band gap, nor was it explained in this way. Also, in our initial paper [34], we demonstrated very similar results in the context of electromagnetic waves with a unit cell consisting of a half-wavelength-long metallic wire. We also performed experiments in microwaves where the subwavelength resonators were placed in a disordered way: locally introducing a detuned resonator in such a medium still creates a very confined cavity [81]. Being robust to disorder is a great advantage compared to phononic crystals, in which most of the experimental realizations suffer from fabrication imperfections. Eventually, parametric experiments again performed in the microwave range demonstrate very interesting applications for this kind of waveguides: thanks to the S-shaped dispersion relation the waves can travel very slowly with unprecedented bandwidth-group index product [86]. In the latter experiment a perfect matching to co-axial lines is performed, demonstrating the ability to connect this component to other types of networks.

In the same time, those results raise interesting questions regarding the physics of metamaterials. Indeed, with the conventional homogenization approach one cannot predict what happens inside metamaterials containing one or several defects because this procedure averages the response of all the resonators. For example, a straight waveguide or a 90${}^{\circ }$ bending one present the same number of defects but give completely different results. Our microscopic approach nevertheless permits to understand that the interferences phenomena occurring at the deep subwavelength scale of the metamaterial are actually very similar to the ones occuring at the wavelength scale in phononic crystals.

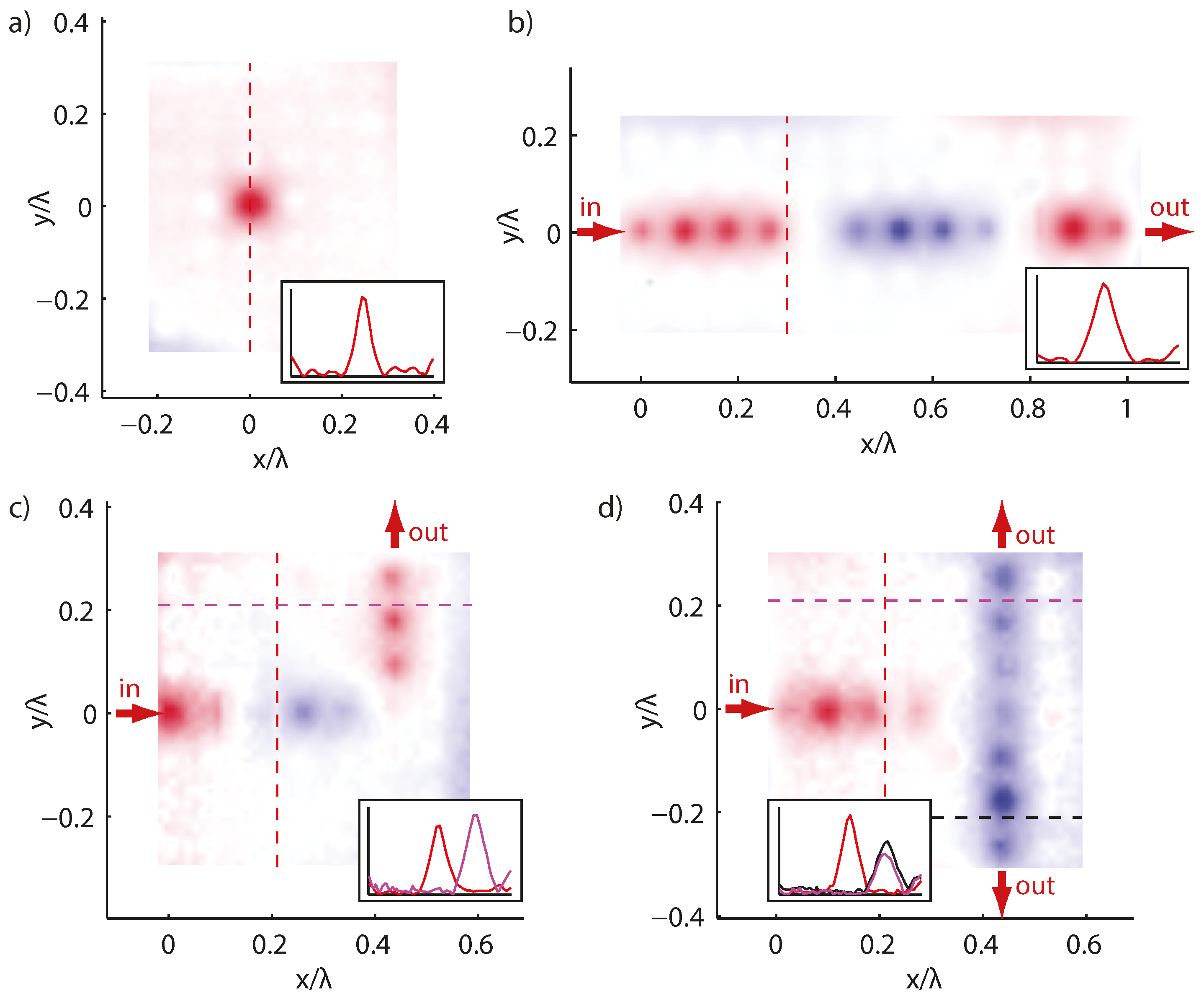
5. Spatial Structuration and Multiple Scattering Lead to Negative Refraction

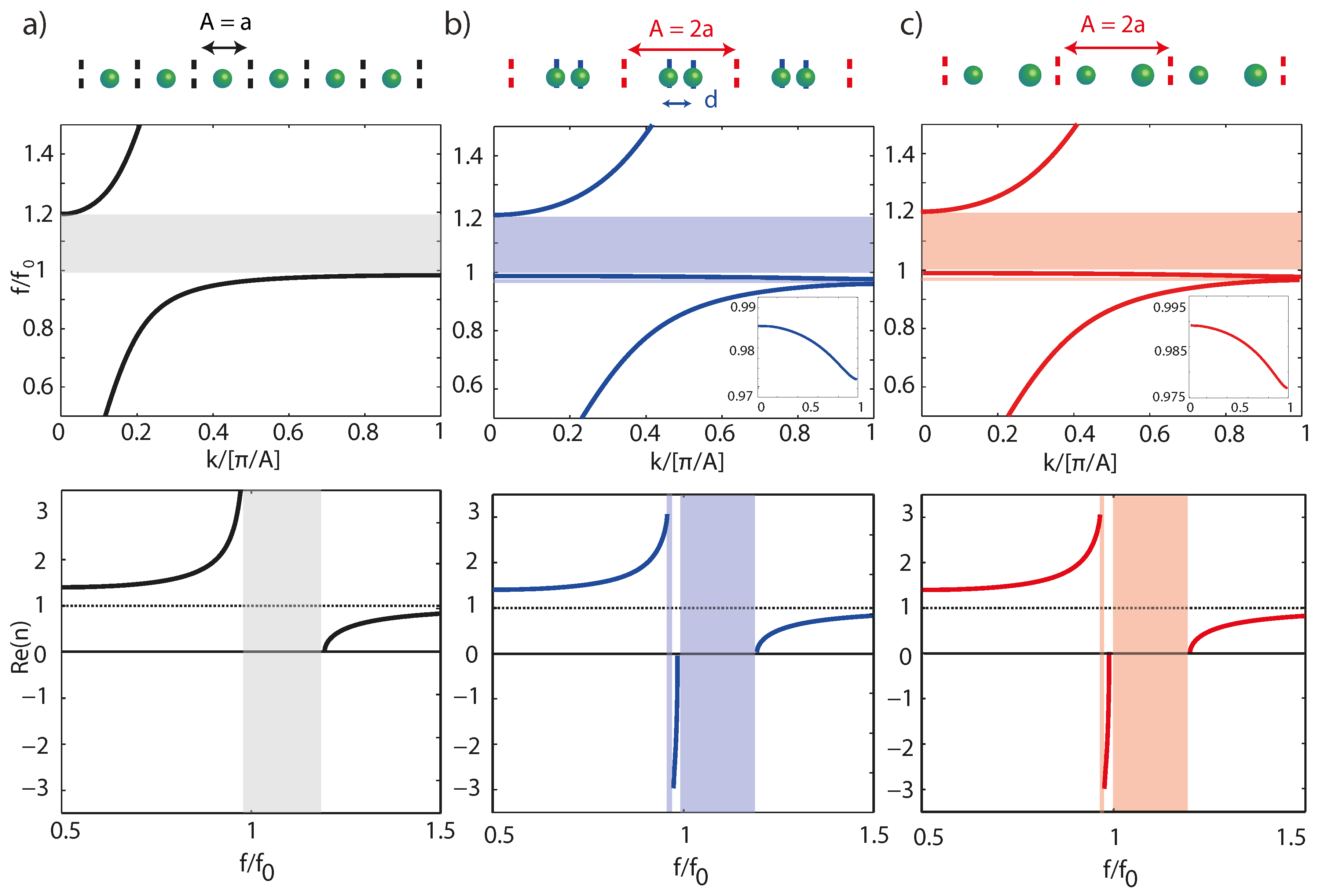
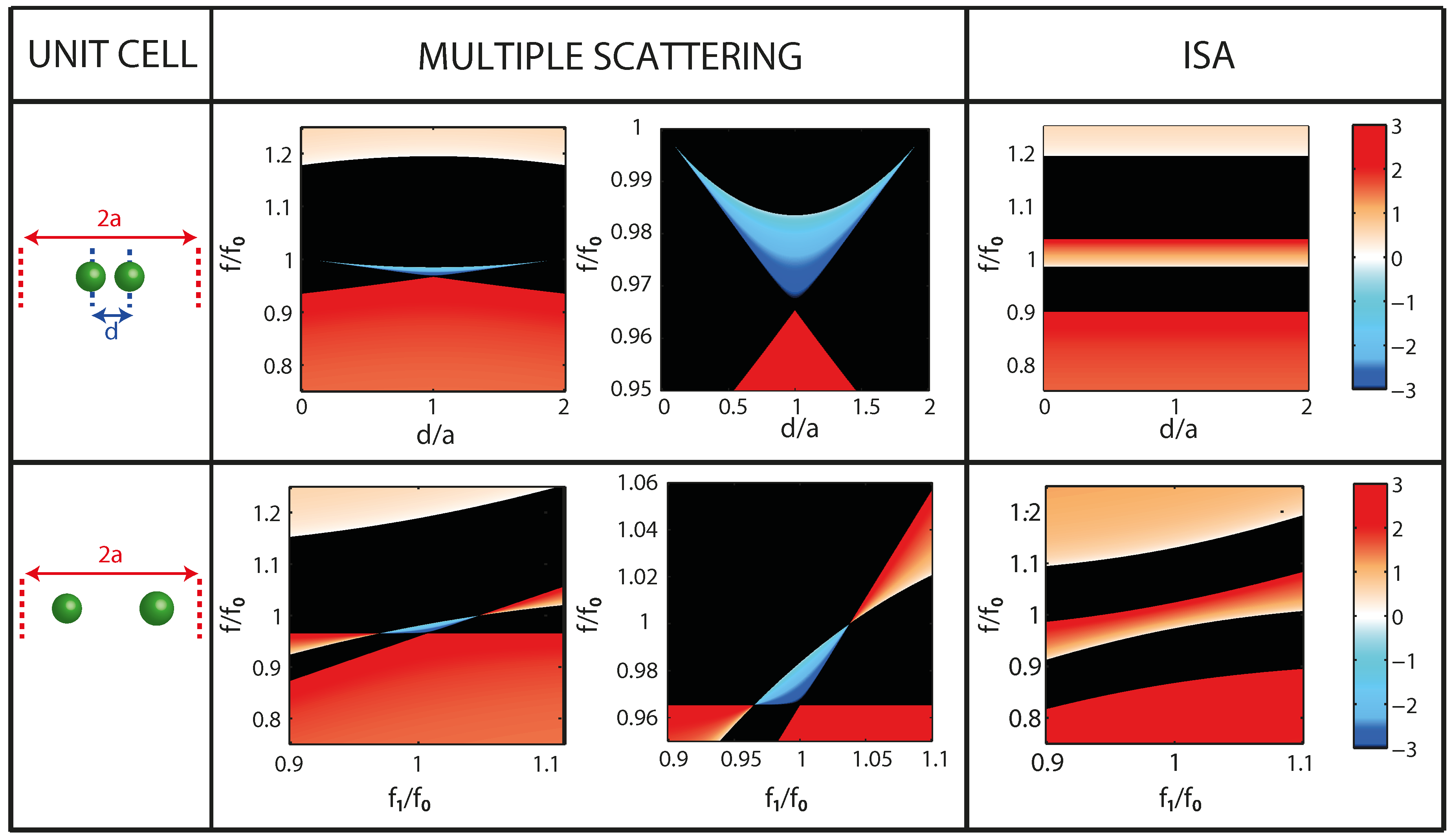
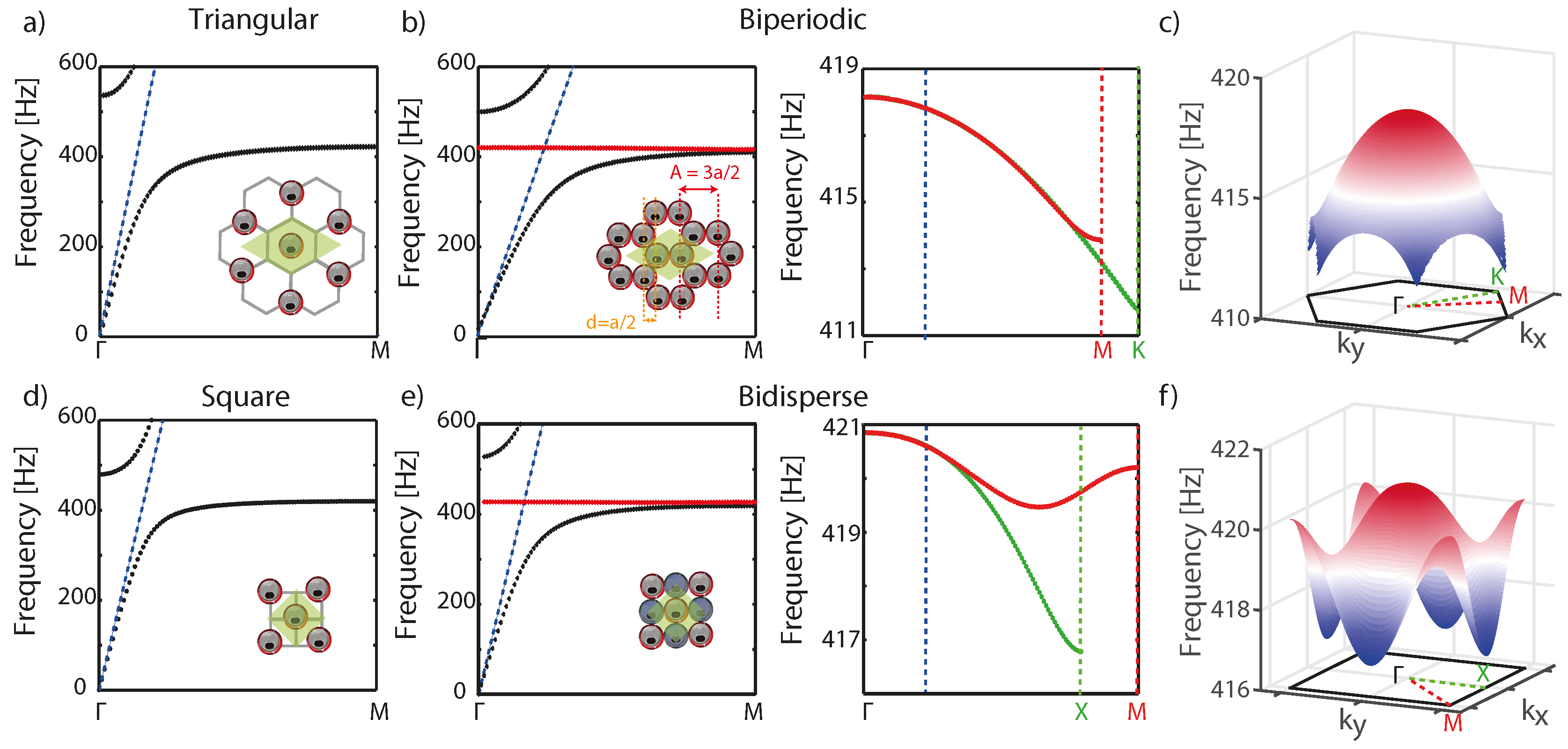
5.1. Toward More Complex Metamaterial Crystals by Complexifying the Unit Cell

In this section, instead of introducing very localized defects we decide to engineer the material with local defects that respect a given translational symmetry of the metamaterial. The previous experiment has highlighted the fact that local modifications of the metamaterial gives rise to interferences effect at the scale of the material no matter what is the free space wavelength. Therefore here we slightly change the periodicity of the initial metamaterial either by changing the resonance frequency of one resonator out of two, or by slightly off-centering one resonator out of two. Consequently, the unit cell of the medium becomes a dimer, made of two resonant unit cells. This type of new cells because of its dimeric nature should support a dipolar resonance overlapping with the monopolar one that gives the metamaterial its effective macroscopic property.

For the sake of simplicity, we start with the simplest example of locally resonant metamaterial which consists in a one dimensional chain of point scatterers organized periodically on a deep subwavelength scale. The dispersion relation of such a chain of resonant unit cells, with $a={\lambda }_0/12$, is calculated analytically using a combination of a Green’s function formalism and a transfer matrix approach [87,88]. As seen before, the obtained dispersion is typical of the soda can array already studied and exhibits the polaritonic behavior (Figure 8a). Or again, equivalently, the medium can be described by a set of two effective parameters with only one of them being negative, the medium acting as a single negative metamaterial in the band gap region.

From this single negative medium, two new configurations are created just by breaking the symmetry in two different ways: either a bi-periodic chain is built by off-centering one resonator out of two, or a bi-disperse one is generated by slightly shifting the resonance frequency of half of the resonators. In both cases, we again analytically calculate the dispersion relation and extract the corresponding effective refractive index (Figure 8b,c). Both of the new symmetry broken metamaterials now exhibit, in the band gap of the single negative medium, a new propagating band that is characterized by a negative phase velocity.

5.2. Physical Origin of the Negative Index Branch

To understand the origin of the negativeness of the band, we parametrically study those two symmetry-broken formal metamaterials. In the case of the bi-periodic chain, the parameter is the shift in position, while for the bi-disperse one the frequency detuning between the resonators is varied. For each parameter, we analytically calculate the new dispersion relation with the same approach that takes into account multiple scattering and extract an effective index from it. The results are shown in color-coded maps (Figure 9). For the bi-periodic chain, a negative index exists whatever the shift in position. In the bi-disperse case, however, this negative band only appears on a narrow frequency detuning range. This suggests that multiple scattering may be involved since it seems that the resonances due to each resonator have to overlap. To confirm this intuition, we extract for the same set of parameters, the effective index only by considering the independent scattering approximation at the scale of the new unit cell made of two resonators. Namely, we do not consider the Fabry-Perot resonator that is built on a deep subwavelength scale between the two resonators. This approximation does not permit to retrieve the existence of a negative index, and only positive index bands typical of a double polariton appear. This clearly shows that the negative index arises from multiple scattering between the resonators of the unit cell, even if the distance is far below the wavelength. This, in turn, explains why, for the bi-disperse chain, the existence of the negative index depends strongly on the chosen detuning: for too large a resonance frequency mismatch, the two resonators cannot couple any longer owing to multiple scattering.

To grasp the physics of the approach, we carefully studied the fields created by a dimer (the new unit cell of the symmetry-broken media) and made the following observation: multiple scattering creates a dipolar resonance (the two resonators are out-of-phase) overlapping with a monopolar resonance of the dimer. This dipolar resonance is responsible for the opening of a narrow transparency window within the large out-of-phase response of the monopolar resonance of the dimer. This is analogous to electromagnetic induced transparency in quantum physics [89], or more precisely to its metamaterial equivalents [90]. This dipolar resonance results from multiple scattering occurring between the two adjacent resonators. Moving from the unit cell to the infinite medium, this dipolar mode gives rise to a band of propagating waves within the band gap of the single negative medium, the latter being a consequence of the monopolar resonance of the unit cell. This band has a negative slope, or equivalently, the metamaterial now presents a negative index and this originates physically from the fact that owing to the symmetry breaking, the lower polaritonic band folds in the first Brillouin zone, analogous to optical branches in diatomic crystals or band folding in phononic crystals. Here, though, the band folding, owing to the change of sign of the Bloch mode between the two edges of the unit cell has a different origin. Indeed, while in phononic crystals, it arises from the fact that the host medium wavelength becomes smaller than twice the lattice constant, in the former the change of sign results from the dipolar nature of the resonant mode within the unit cell. This implies that, contrary to negative refraction in crystals, this new phenomenon exists even if the scale of the metamaterial is deeply subwavelength, and happens at the same frequency as the resonance of the original building block, which we can qualify as the low frequency regime. Furthermore, since the original single negative effective property does not rely on spatial order [81], this negative index band should be robust even in a metamaterial constituted of randomly placed dimers: both the monopolar and the multiple-scattering-induced dipolar resonances should remain, hence leading to a negative index medium [91].

5.3. From 1D to 2D Media

This idea of breaking symmetry is rather simple in one dimension and we need to move on the two dimensional world before performing a soda cans experiment. Finding a lattice that paves the space and presents a bi-periodicity in all directions is far more complicated that in one dimension. In order to stay as isotropic as possible, we choose the Bravais lattice that presents the first Brillouin zone that is the closest to the circle which is the hexagonal lattice. Then, as we mentioned in the one dimensional case the unit cell needs two resonant objects in order to have the dipolar resonance creating the transparency window within the band gap created by the monopolar one. Therefore, we ended up on the well-known honeycomb lattice. Carefully looking at the positions of the Bragg planes one can see that it exhibits this double periodicity in any of the ΓM directions. This crystal is made of a diamond-like unit cell consisting of two resonators, and is compared to the triangular lattice which has the same unit cell but with only one resonator. Numerical simulations using Comsol Multiphysics give the dispersion of both the regular and the symmetry-broken lattices (Figure 10a,b). The triangular lattice medium presents a polaritonic dispersion relation, while the honeycomb lattice (which actually consists of the superposition of two identical triangular lattice crystals) displays a negative band. The dispersion depends slightly on the propagation direction but remains rather isotropic as shown in the surface plot (Figure 10c) and can thus be described with an isotropic negative effective index of refraction for almost all frequencies.

For the bi-disperse two-dimensional lattice, we have not found ideal solution to deal with the isotropy issue so we decided to mix two square lattices of slightly detuned Helmholtz resonators in order to build a new square lattice whose unit cell contains two resonators (Figure 10d,e). Again, the detuning is really easy to build since it is experimentally realized by pouring some water in the can in order to reduce its volume. This bi-disperse resonant crystal exhibits a negative branch although it is simply the superposition of two almost identical single negative media. In this case, the propagation is less isotropic, since the geometry of a square unit cell tends to deform the isofrequency contours near the corners of the first Brillouin zone as shown from the surface plot describing the dispersion relation of the negative band within the entire first Brillouin zone (Figure 10f). There is, however, no doubt that one can find a more isotropic medium.

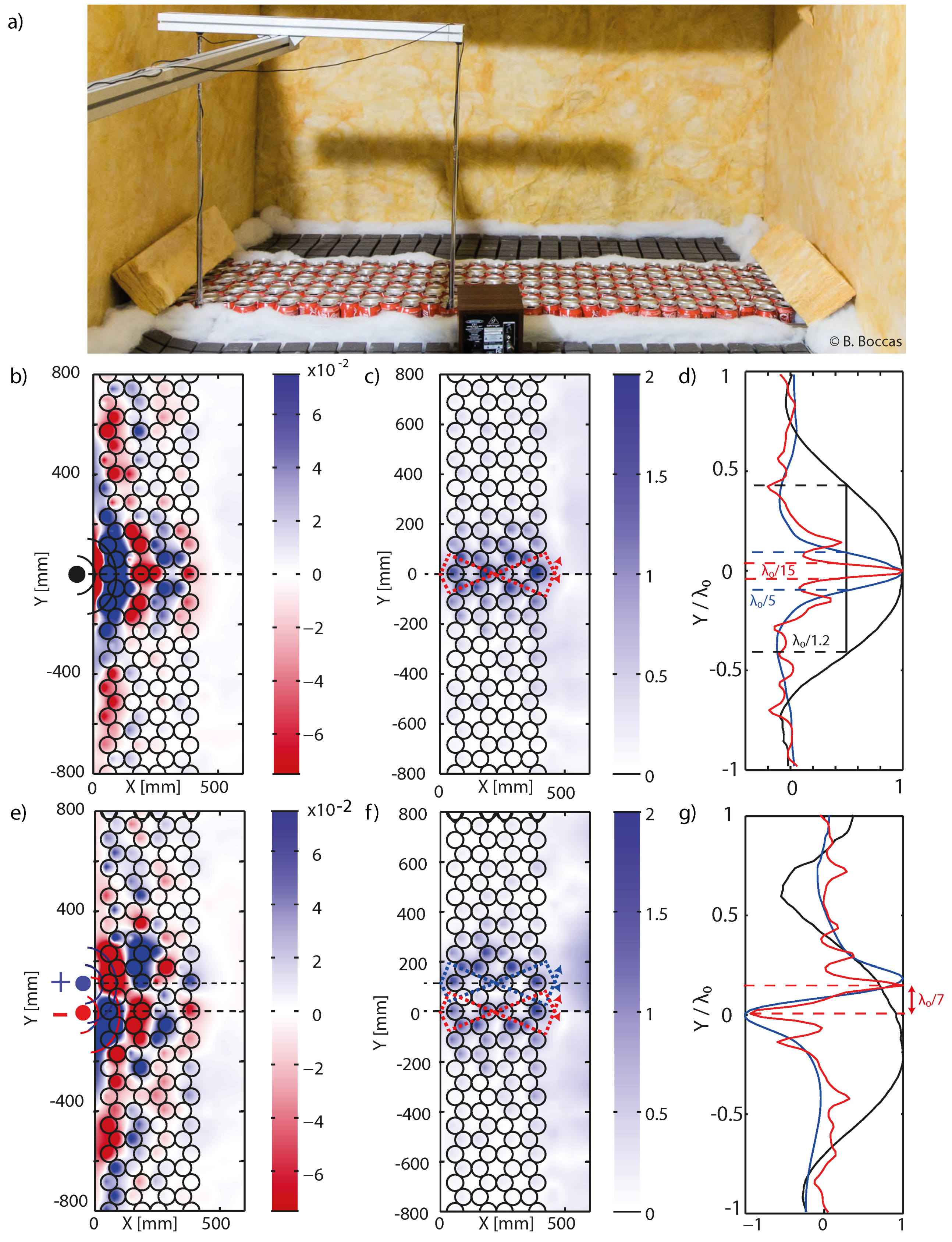
5.4. Experimental Demonstration: Acoustic Superlensing

In order to prove the existence of the negative refraction, we build an experiment which consists on a point source illuminating a slab that should behave as a flat lens. We focus on the bi-periodic medium, i.e., the honeycomb arrangement of soda cans. We build a slab with 124 cans, surrounded by acoustic absorbers to avoid reflections of sound off the boundaries of the room as shown in the photography of the experiment (Figure 11a). An 8-cm-wide loudspeaker located approximately 5 cm away from the input interface of the medium is used as the source of sound while 2 microphones mounted on a two-dimensional translational stage measure the acoustic field above the medium. The loudspeaker emits a long chirp ranging from 100 Hz to 800 Hz and the data are treated by Fourier transform in order to have the field maps at the desired frequency. Here, we work at the frequency of 417.5 Hz, which corresponds to the frequency at the lower edge of the negative band, that is, where the effective negative index norm is the highest.

The real part of the field at this frequency is shown Figure 11b and is hard to interpret. We thus show the intensity within the slab by numerically compensating for the losses that occur during the propagation in the lens (Figure 11c) and we can clearly distinguish the path for sound refraction, with a focal spot inside the lens, in very good agreement with the Snell law for a metamaterial with an effective index of −3, consistent with the numerical results. On the other side of the slab, in the vicinity of the surface, we record the image of the source with a ${\lambda }_0/15$ full-width at half-maximum (Figure 11d). This is much smaller than the diffraction limited focus obtained without the lens (black curve), and even smaller than the width of the source, ${\lambda }_0/5$, owing to a hotspot created by the aperture of a single soda can: not only this demonstrates the negative refraction property of the medium but it also proves a superlensing effect. This effect owes to the high norm of the effective index of refraction that allows the propagation of waves within the slab that are evanescent in air.

Super-resolution can also be demonstrated by being able to discriminate two sources separated by less than half a wavelength. Two loudspeakers, emitting out-of-phase, are placed near the input interface, separated by 13 cm (${\lambda }_0/7$). The measured pressure field, as well as the loss-compensated intensity maps (Figure 11e,f) show that the slab produces two distinguishable foci inside the superlens. In the focal plane, the two images are efficiently separated (Figure 11g), thereby demonstrating a ${\lambda }_0/7$ imaging resolution, far beyond the diffraction limit, contrary to the control experiment realized without the superlens (black curve). We have further verified that the two sources can be distinguished whatever the phase shift between them [87].

As a conclusion of this part, we have demonstrated that it is fairly easy to build double negative media starting from a single negative one. Breaking the symmetry of the unit cell of a single negative medium (either by changing the spacing or by adding a frequency detuning), multiple scattering of waves guarantees the existence of an overlap between a dipolar resonance and a monopolar one. This ends on a negative effective index of refraction when considering the infinite medium. This approach is very general and brings a new paradigm to the physics of metamaterials since multiple scattering is often neglected owing to the subwavelength spatial scale of those media. We emphasize that such a negative effective index of refraction should be insensitive to the random positioning of dimers, and that it should be easily transposable to three-dimensional metamaterials.

6. Conclusions

In this article we have exemplified through the acoustic example of the soda cans medium that the physics of many locally resonant metamaterials is very similar to the physics of phononic crystals albeit the small scale with respect to the freespace wavelength. Indeed, the soda can interacts resonantly with the continuum of freespace plane waves which results in Fano interferences. The π-shift occurring at the resonance frequency is equivalent to the π-shift accumulated during propagation in usual phononic crystals. And, because this phase shift is only obtained at the resonator position we can pack the medium to reach deeply subwavelength scales as opposed to phononic crystals that are inherently at the wavelength scale. Therefore, we can envision all of the applications of phononic crystals but at a scale that is completely independent of the freespace wavelength. And, while phononic crystals are mostly use for their ability to block the propagation of waves in some frequency ranges, the propagating bands of the locally resonant metamaterials are also very interesting.

For instance, the low frequency band, below the resonance frequency, presents a dispersion relation that is far below the cone shape of the freespace dispersion relation. This is a consequence of the subwavelength nature of the soda cans packing. In other words, because the spacial scale is very subwavelength the field can oscillate on scales that are now related to the physical one and reach extremely large wavenumbers. By using the modes of a finite-sized medium in this frequency range, we have demonstrated that one can focus acoustic waves far below the freespace diffraction limit. By smartly exciting simultaneously those modes, we build interference patterns that are constructive only at a desired position thus resulting on focal spots with dimensions much smaller than the freespace wavelength.

By exploiting the low frequency band gap, one can mold the flow of acoustic waves at a scale that is again completely independent of the wavelength. This is performed by introducing a resonant defect, that is a new subwavelength unit cell which has a resonant frequency falling into the band gap created by the others. In the context of the soda can medium it is really easy to realize since diminishing the volume of the can by adding few centiliters of water at the bottom increases its resonant frequency. We therefore demonstrated trapping, waveguiding, bending and splitting abilities at the subwavelength scale without any engineering methods.

Eventually, we showed that moving to more complex unit cells of the crystal leads to the creation of propagating bands with interesting properties. Indeed, we demonstrated that introducing some local correlations by adding a local order like in the biperiodic medium, or by adding some spectral correlations by introducing a small frequency detuning by pairs, we build media exhibiting negative refraction. But, more interestingly, again because of the subwavelength nature of the medium, all of the diffraction orders are evanescent at the exit of such a medium and it macroscopically behaves like a homogeneous medium described with a negative effective index of refraction. This, in turns, creates many opportunities in the context of metamaterials because we can now take advantage of the spatial ordering in order to create new macroscopic properties: this paves the way to a new class of media that are the “metamaterial crystals”.

There is no doubt that we are far from having exploited all of the properties offered from such a locally resonant medium. We have exploited separately the subwavelength modes , the band gap or the local correlations, but there is no doubt that by combining two of those properties one can easily find new applications. For example, by adding resonators creating a band gap between the adjacent cans in the honey-comb crystal we turn the coupling between them from a polariton-like to a tight binding one, and we therefore build a macroscopic analogue of graphene for the propagation of electrons. By adding some disorder in the structure but by keeping the pair-correlations in positions we should also keep the negative effective property. All of this will be the scope of future works and the soda can medium is a fairly good platform to demonstrate experimentally all of these fascinating physics.