Influence of Defects in Boron Nitride Nanotubes in the Adsorption of Molecules. Insights from B3LYP-D2* Periodic Simulations
Abstract
:1. Introduction
2. Results and Discussion
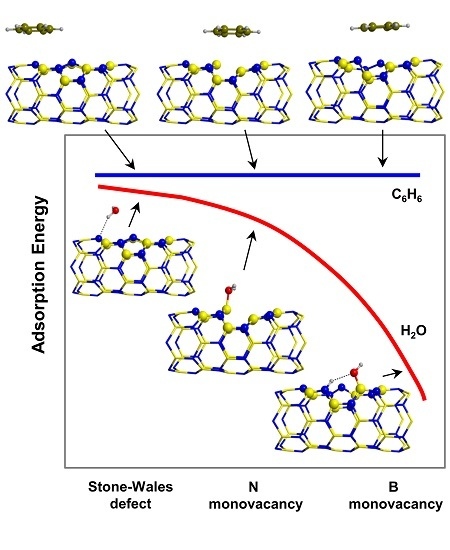
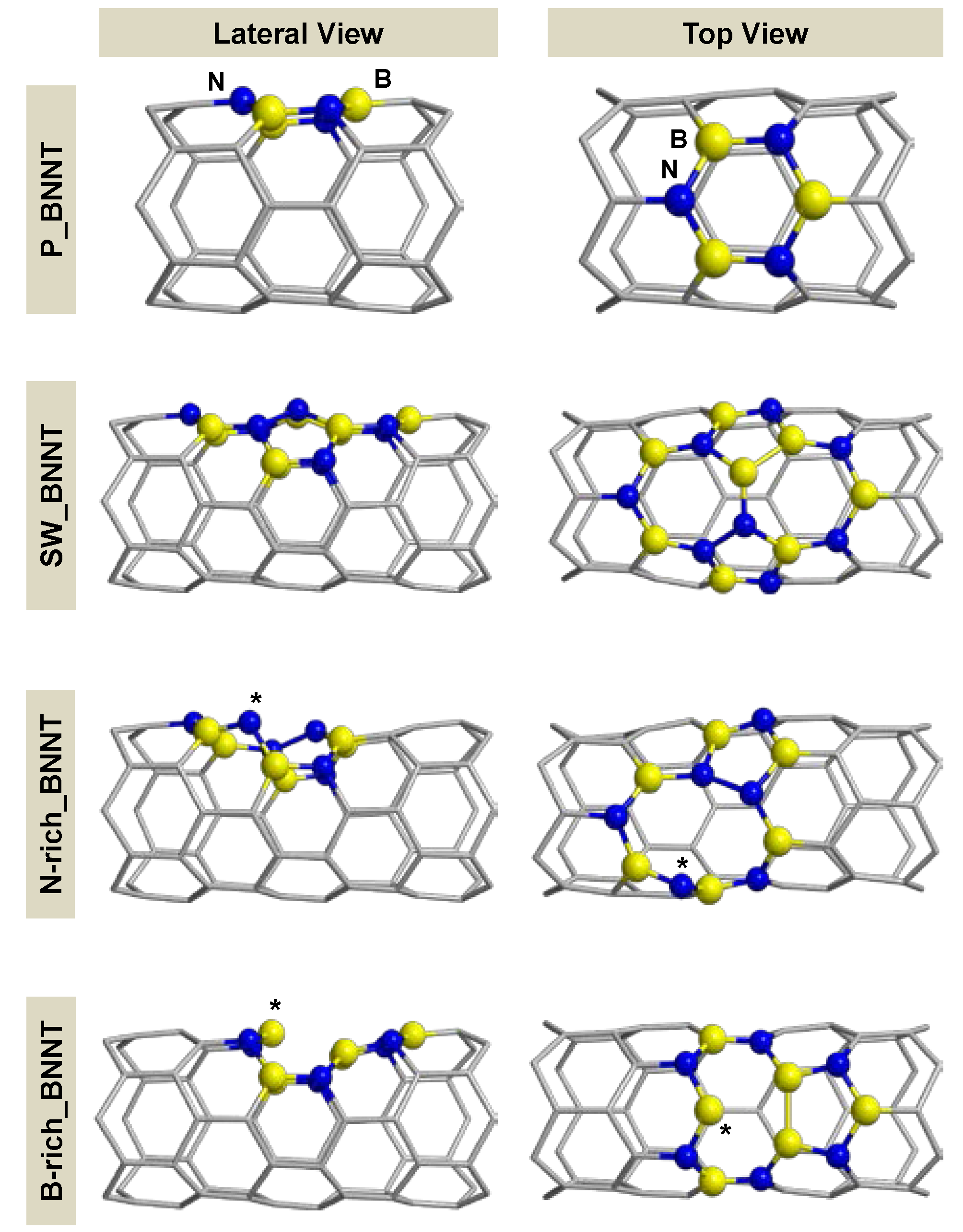
2.1. Models for Perfect and Defective BNNTs
2.2. Features on the Adsorption of Probe Molecules
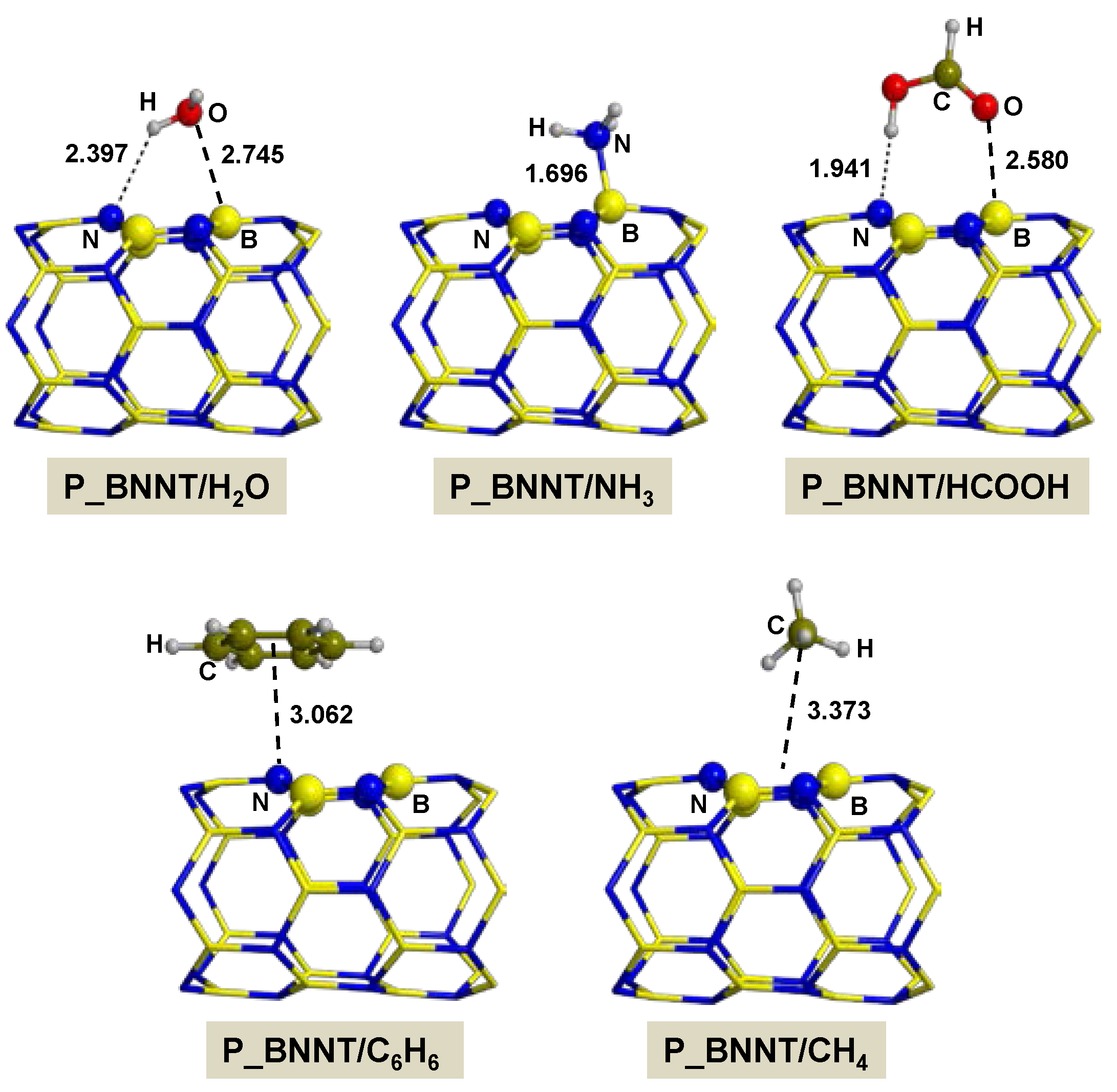
2.2.1. On P_BNNT
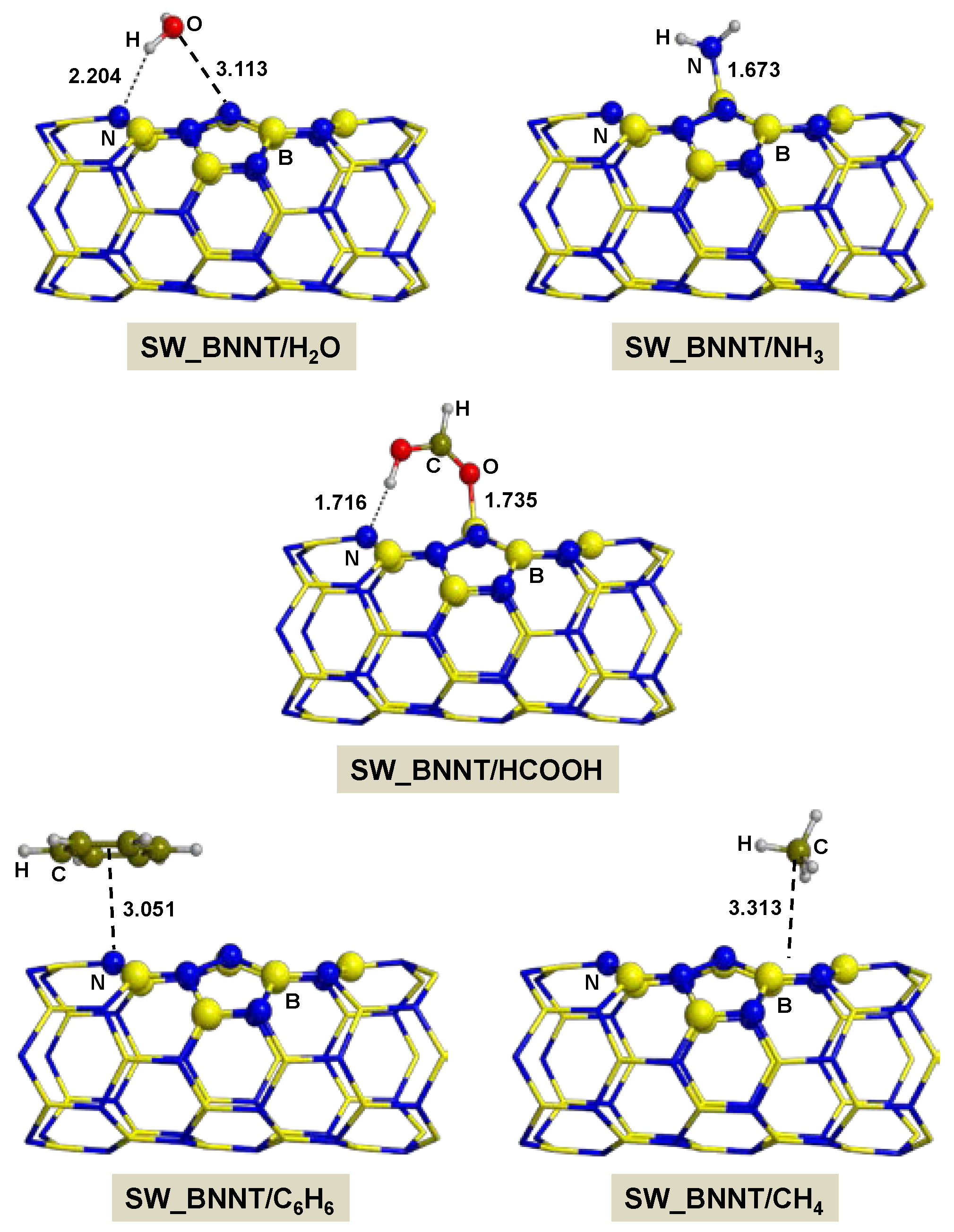
2.2.2. On SW_BNNT
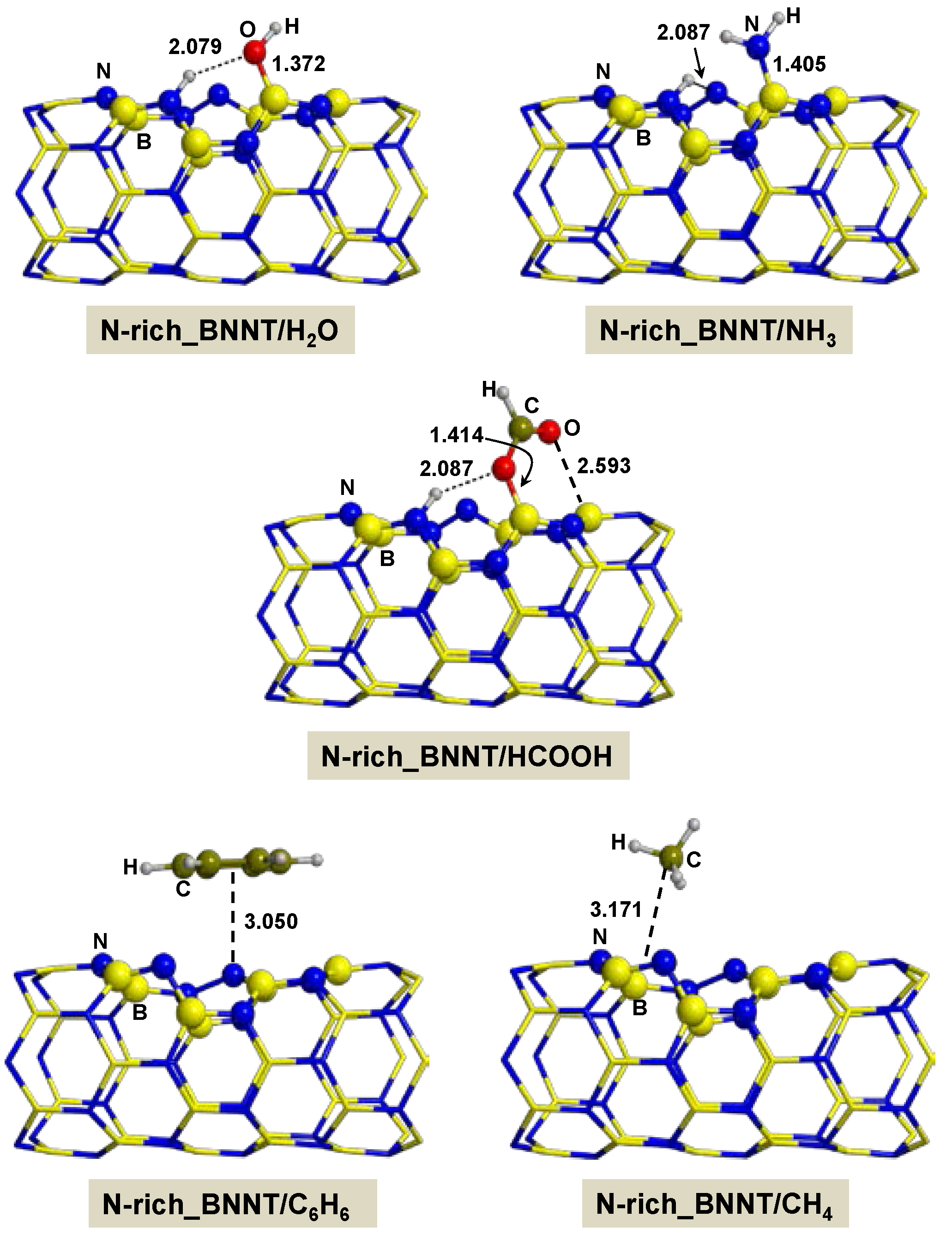
2.2.3. On N-rich_BNNT
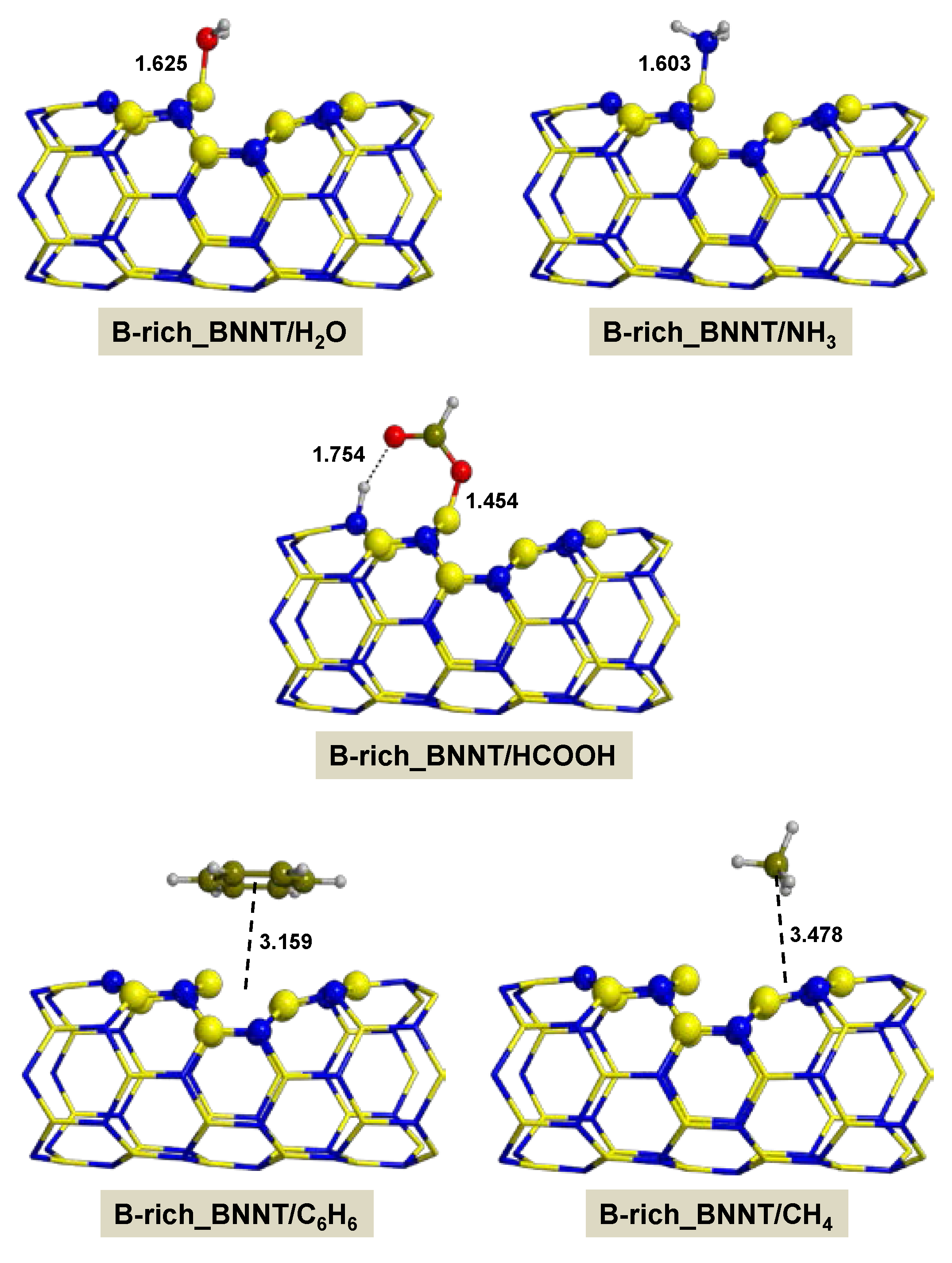
2.2.4. On B-rich_BNNT
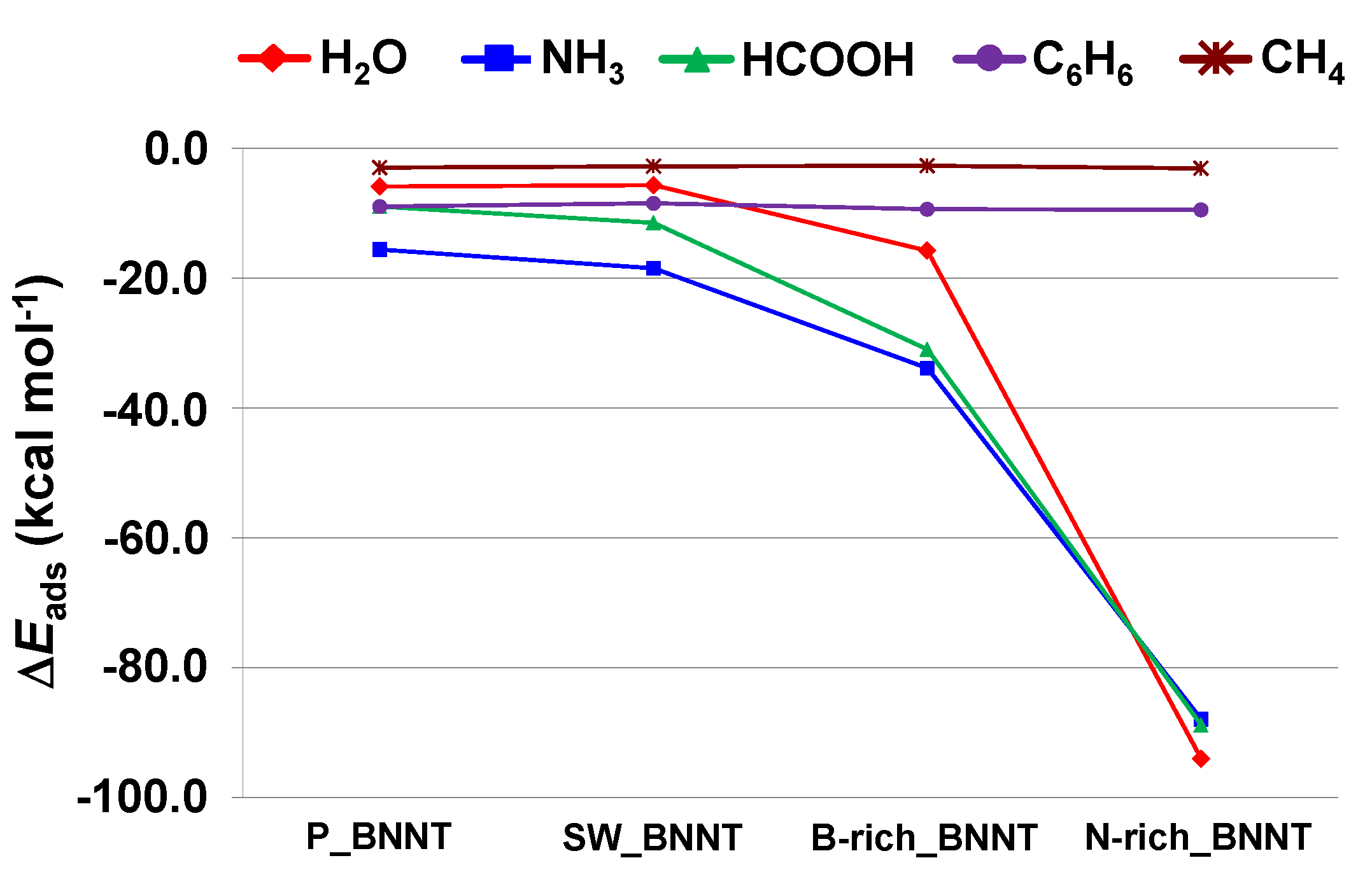
2.3. Trends of the Adsorption Energies
3. Computational Details
4. Conclusions
- (i)
- Adsorption of polar molecules (with lone pair electrons) on the defective BNNTs is in general dictated by dative interactions established between the electron donor atoms of the molecules and the B atoms of the BNNTs, which produce large charge transfers from the molecules to the BNNT. Such transfers increase the acidity of the polar molecules and the basicity of the N atoms of the BNNTs in such a way that significant H-bond interactions are also established. On the N-rich_BNNT, which presents an N atom fully exposed to the surfaces as a consequence of the B monovacancy, the increase of acidity promotes proton transfers to this N atom, thus forming ion pair adducts. This deprotonation also occurs for the adsorption of HCOOH on the B-rich_BNNT.
- (ii)
- For the polar molecules, the strength of their chemisorption strongly depends on the type of the nanotube and the class of the molecule. General trends on the calculated adsorption energies (from more to less favorable) are, as a function of the type of BNNT: N-rich_BNNT > B-rich_BNNT > SW_BNNT > P_BNNT; and as a function of the class of the polar molecule: NH3 > HCOOH > H2O. However, the most stable adduct found in this work is that for H2O interacting with N-rich_BNNT due to the very stable B···OH− chemical bond.
- (iii)
- C6H6 and CH4 are physisorbed on the different BNNTs, mainly governed by π-stacking (C6H6) and CH-π (CH4) dispersion interactions. For each molecule, the magnitude of the adsorption energies does not depend on the type of BNNT and accordingly they are almost constant, C6H6 being more favorable than for CH4 (about −9 kcal mol−1 and −3 kcal mol−1, respectively).
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rubio, A.; Corkill, J.L.; Cohen, M.L. Theory of graphitic boron nitride nanotubes. Phys. Rev. B 1994, 49, 5081–5084. [Google Scholar] [CrossRef]
- Blase, X.; Rubio, A.; Louie, S.G.; Cohen, M.L. Stability and Band Gap Constancy of Boron Nitride Nanotubes. Europhys. Lett. 1994, 28, 335–340. [Google Scholar] [CrossRef]
- Chopra, N.G.; Luyken, R.J.; Cherrey, K.; Crespi, V.H.; Cohen, M.L.; Louie, S.G.; Zettl, A. Boron Nitride Nanotubes. Science 1995, 269, 966–967. [Google Scholar] [CrossRef] [PubMed]
- Zhi, C.; Bando, Y.; Tang, C.; Honda, S.; Kuwahara, H.; Golberg, D. Boron nitride nanotubes/polystyrene composites. J. Mater. Res. 2006, 21, 2794–2800. [Google Scholar] [CrossRef]
- Zhi, C.; Bando, Y.; Terao, T.; Tang, C.; Kuwahara, H.; Golberg, D. Towards Thermoconductive, Electrically Insulating Polymeric Composites with Boron Nitride Nanotubes as Fillers. Adv. Funct. Mater. 2009, 19, 1857–1862. [Google Scholar] [CrossRef]
- Sun, Q.; Li, Z.; Searles, D.J.; Chen, Y.; Lu, G.; Du, A. Charge-Controlled Switchable CO2 Capture on Boron Nitride Nanomaterials. J. Am. Chem. Soc. 2013, 135, 8246–8253. [Google Scholar] [CrossRef] [PubMed]
- Reddy, A.L.M.; Tanur, A.E.; Walker, G.C. Synthesis and hydrogen storage properties of different types of boron nitride nanostructures. Int. J. Hydrog. Energy 2010, 35, 4138–4143. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Tang, C.C.; Zhi, C.Y. Boron Nitride Nanotubes. Adv. Mater. 2007, 19, 2413–2432. [Google Scholar] [CrossRef]
- Golberg, D.; Bando, Y.; Huang, Y.; Terao, T.; Mitome, M.; Tang, C.; Zhi, C. Boron Nitride Nanotubes and Nanosheets. ACS Nano 2010, 4, 2979–2993. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Connell, J.W. Advances in 2D boron nitride nanostructures: Nanosheets, nanoribbons, nanomeshes, and hybrids with graphene. Nanoscale 2012, 4, 6908–6939. [Google Scholar] [CrossRef] [PubMed]
- Stone, A.J.; Wales, D.J. Theoretical studies of icosahedral C60 and some related species. Chem. Phys. Lett. 1986, 128, 501–503. [Google Scholar] [CrossRef]
- Zobelli, A.; Ewels, C.P.; Gloter, A.; Seifert, G.; Stephan, O.; Csillag, S.; Colliex, C. Defective Structure of BN Nanotubes: From Single Vacancies to Dislocation Lines. Nano Lett. 2006, 6, 1955–1960. [Google Scholar] [CrossRef] [PubMed]
- Miyamoto, Y.; Rubio, A.; Berber, S.; Yoon, M.; Tománek, D. Spectroscopic characterization of Stone-Wales defects in nanotubes. Phys. Rev. B 2004, 69, 121413. [Google Scholar] [CrossRef]
- Schmidt, T.M.; Baierle, R.J.; Piquini, P.; Fazzio, A. Theoretical study of native defects in BN nanotubes. Phys. Rev. B 2003, 67, 113407. [Google Scholar] [CrossRef]
- Shevlin, S.A.; Guo, Z.X. Hydrogen sorption in defective hexagonal BN sheets and BN nanotubes. Phys. Rev. B 2007, 76, 024104. [Google Scholar] [CrossRef]
- Kang, H.S. Theoretical Study of Boron Nitride Nanotubes with Defects in Nitrogen-Rich Synthesis. J. Phys. Chem. B 2006, 110, 4621–4628. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Zhou, Z.; Golberg, D.; Bando, Y.; Schleyer, P.v.R.; Chen, Z. Stone−Wales Defects in Single-Walled Boron Nitride Nanotubes: Formation Energies, Electronic Structures, and Reactivity. J. Phys. Chem. C 2008, 112, 1365–1370. [Google Scholar] [CrossRef]
- An, W.; Wu, X.; Yang, J.L.; Zeng, X.C. Adsorption and Surface Reactivity on Single-Walled Boron Nitride Nanotubes Containing Stone−Wales Defects. J. Phys. Chem. C 2007, 111, 14105–14112. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Yu, G.; Zhou, Z.; Chen, Z. Electronic Structure and Reactivity of Boron Nitride Nanoribbons with Stone-Wales Defects. J. Chem. Theory Comput. 2009, 5, 3088–3095. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.X.; Ding, Y.H. Theoretical investigation of the divacancies in boron nitride nanotubes: Properties and surface reactivity toward various adsorbates. J. Chem. Phys. 2009, 131, 014706. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hu, C.L.; Li, J.Q.; Jia, G.X.; Zhang, Y.F. Theoretical study of O2 adsorption and reactivity on single-walled boron nitride nanotubes. Chem. Phys. Lett. 2007, 449, 149–154. [Google Scholar] [CrossRef]
- Piquini, P.; Baierle, R.J.; Schmidt, T.M.; Fazzio, A. Formation energy of native defects in BN nanotubes: An ab initio study. Nanotechnology 2005, 16, 827. [Google Scholar] [CrossRef]
- Bettinger, H.F.; Dumitrică, T.; Scuseria, G.E.; Yakobson, B.I. Mechanically induced defects and strength of BN nanotubes. Phys. Rev. B 2002, 65, 041406. [Google Scholar] [CrossRef]
- Rimola, A.; Sodupe, M. Physisorption vs. chemisorption of probe molecules on boron nitride nanomaterials: The effect of surface curvature. Phys. Chem. Chem. Phys. 2013, 15, 13190–13198. [Google Scholar] [CrossRef] [PubMed]
- Rimola, A.; Sodupe, M. Gas-Phase and Microsolvated Glycine Interacting with Boron Nitride Nanotubes. A B3LYP-D2* Periodic Study. Inorganics 2014, 2, 334–350. [Google Scholar] [CrossRef]
- Rimola, A. Intrinsic Ladders of Affinity for Amino-Acid-Analogues on Boron Nitride Nanomaterials: A B3LYP-D2* Periodic Study. J. Phys. Chem. C 2015, 119, 17707–17717. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL09 User’s Manual; University of Torino: Torino, Italy, 2009. [Google Scholar]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Civalleri, B.; Zicovich-Wilson, C.M.; Valenzano, L.; Ugliengo, P. B3LYP augmented with an empirical dispersion term (B3LYP-D*) as applied to molecular crystals. CrystEngComm 2008, 10, 405–410. [Google Scholar] [CrossRef]
- Rimola, A.; Civalleri, B.; Ugliengo, P. Physisorption of aromatic organic contaminants at the surface of hydrophobic/hydrophilic silica geosorbents: A B3LYP-D modeling study. Phys. Chem. Chem. Phys. 2010, 12, 6357–6366. [Google Scholar] [CrossRef] [PubMed]
- Civalleri, B.; Maschio, L.; Ugliengo, P.; Zicovich-Wilson, C.M. Role of dispersive interactions in the CO adsorption on MgO (001): Periodic B3LYP calculations augmented with an empirical dispersion term. Phys. Chem. Chem. Phys. 2010, 12, 6382–6386. [Google Scholar] [CrossRef] [PubMed]
- Schafer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Doll, K. Implementation of analytical Hartree–Fock gradients for periodic systems. Comput. Phys. Commun. 2001, 137, 74–88. [Google Scholar] [CrossRef]
- Doll, K.; Dovesi, R.; Orlando, R. Analytical Hartree–Fock gradients with respect to the cell parameter for systems periodic in three dimensions. Theor. Chem. Acc. 2004, 112, 394–402. [Google Scholar] [CrossRef]
- Doll, K.; Saunders, V.R.; Harrison, N.M. Analytical Hartree–Fock gradients for periodic systems. Int. J. Quantum Chem. 2001, 82, 1–13. [Google Scholar] [CrossRef]
- Civalleri, B.; D’Arco, P.; Orlando, R.; Saunders, V.R.; Dovesi, R. Hartree-Fock geometry optimisation of periodic systems with the CRYSTAL code. Chem. Phys. Lett. 2001, 348, 131–138. [Google Scholar] [CrossRef]
| Complex | ΔU | ΔED | ΔEads | Q (e) | Eg (eV)2 |
|---|---|---|---|---|---|
| P_BNNT/H2O | −2.3 | −3.6 | −5.9 | 0.03 | 4.41 |
| P_BNNT/NH3 | −10.5 | −5.1 | −15.6 | 0.29 | 4.45 |
| P_BNNT/HCOOH | −3.5 | −5.5 | −9.0 | −0.03 | 4.42 |
| P_BNNT/C6H6 | +3.8 | −12.8 | −9.0 | −0.02 | 4.40 |
| P_BNNT/CH4 | +1.0 | −4.0 | −3.0 | −0.02 | 4.42 |
| SW_BNNT/H2O | −2.4 | −3.3 | −5.7 | −0.01 | 4.36 |
| SW_BNNT/NH3 | −14.1 | −4.4 | −18.5 | 0.33 | 4.02 |
| SW_BNNT/HCOOH | −5.8 | −5.7 | −8.5 | 0.17 | 4.08 |
| SW_BNNT/C6H6 | +3.6 | −12.1 | −8.5 | −0.02 | 4.36 |
| SW_BNNT/CH4 | +1.3 | −4.1 | −2.8 | −0.02 | 4.37 |
| N-rich_BNNT/H2O | −93.7 | −0.4 | −94.1 | −0.131 | conductor |
| N-rich _BNNT/NH3 | −86.7 | −1.3 | −88.0 | −0.051 | conductor |
| N-rich _BNNT/HCOOH | −84.9 | −4.0 | −88.9 | −0.231 | conductor |
| N-rich _BNNT/C6H6 | +3.6 | −13.1 | −9.5 | 0.03 | conductor |
| N-rich _BNNT/CH4 | +0.9 | −4.0 | −3.1 | −0.03 | conductor |
| B-rich_BNNT/H2O | −12.0 | −3.8 | −15.8 | 0.31 | conductor |
| B-rich _BNNT/NH3 | −28.7 | −5.2 | −33.9 | 0.41 | conductor |
| B-rich _BNNT/HCOOH | −23.5 | −7.5 | −31.0 | −0.22 1 | conductor |
| B-rich _BNNT/C6H6 | +3.2 | −12.6 | −9.4 | 0.03 | conductor |
| B-rich _BNNT/CH4 | +1.0 | −3.7 | −2.7 | −0.01 | conductor |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matarín, O.; Rimola, A. Influence of Defects in Boron Nitride Nanotubes in the Adsorption of Molecules. Insights from B3LYP-D2* Periodic Simulations. Crystals 2016, 6, 63. https://doi.org/10.3390/cryst6050063
Matarín O, Rimola A. Influence of Defects in Boron Nitride Nanotubes in the Adsorption of Molecules. Insights from B3LYP-D2* Periodic Simulations. Crystals. 2016; 6(5):63. https://doi.org/10.3390/cryst6050063
Chicago/Turabian StyleMatarín, Oriol, and Albert Rimola. 2016. "Influence of Defects in Boron Nitride Nanotubes in the Adsorption of Molecules. Insights from B3LYP-D2* Periodic Simulations" Crystals 6, no. 5: 63. https://doi.org/10.3390/cryst6050063
APA StyleMatarín, O., & Rimola, A. (2016). Influence of Defects in Boron Nitride Nanotubes in the Adsorption of Molecules. Insights from B3LYP-D2* Periodic Simulations. Crystals, 6(5), 63. https://doi.org/10.3390/cryst6050063