Comparisons between Crystallography Data and Theoretical Parameters and the Formation of Intramolecular Hydrogen Bonds: Benznidazole
Abstract
:1. Introduction
2. Computational Procedure
3. Results and Discussion
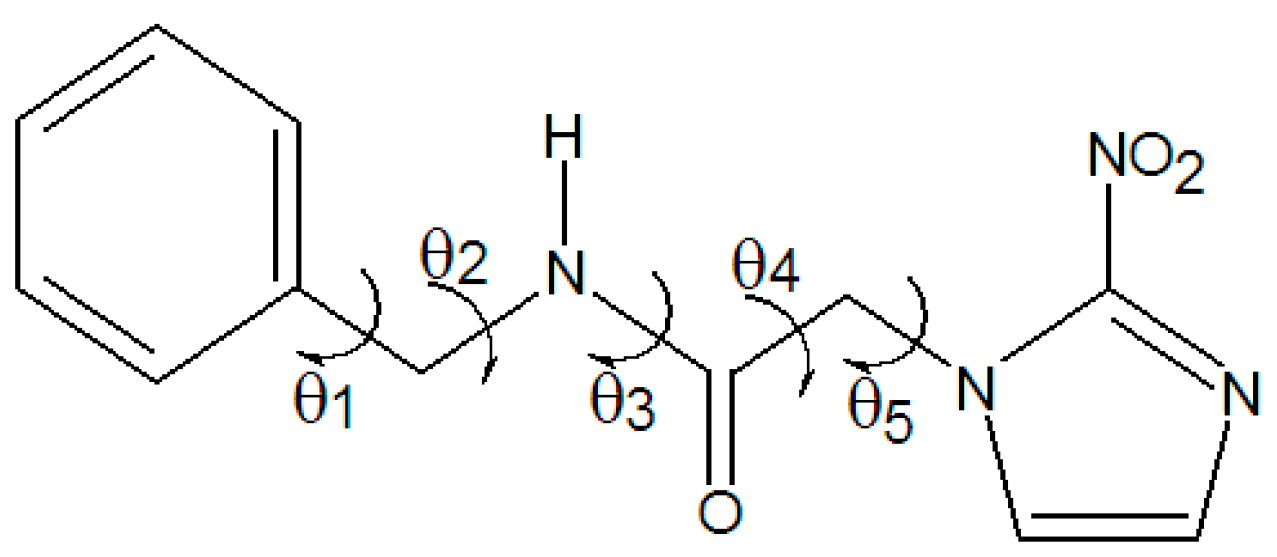
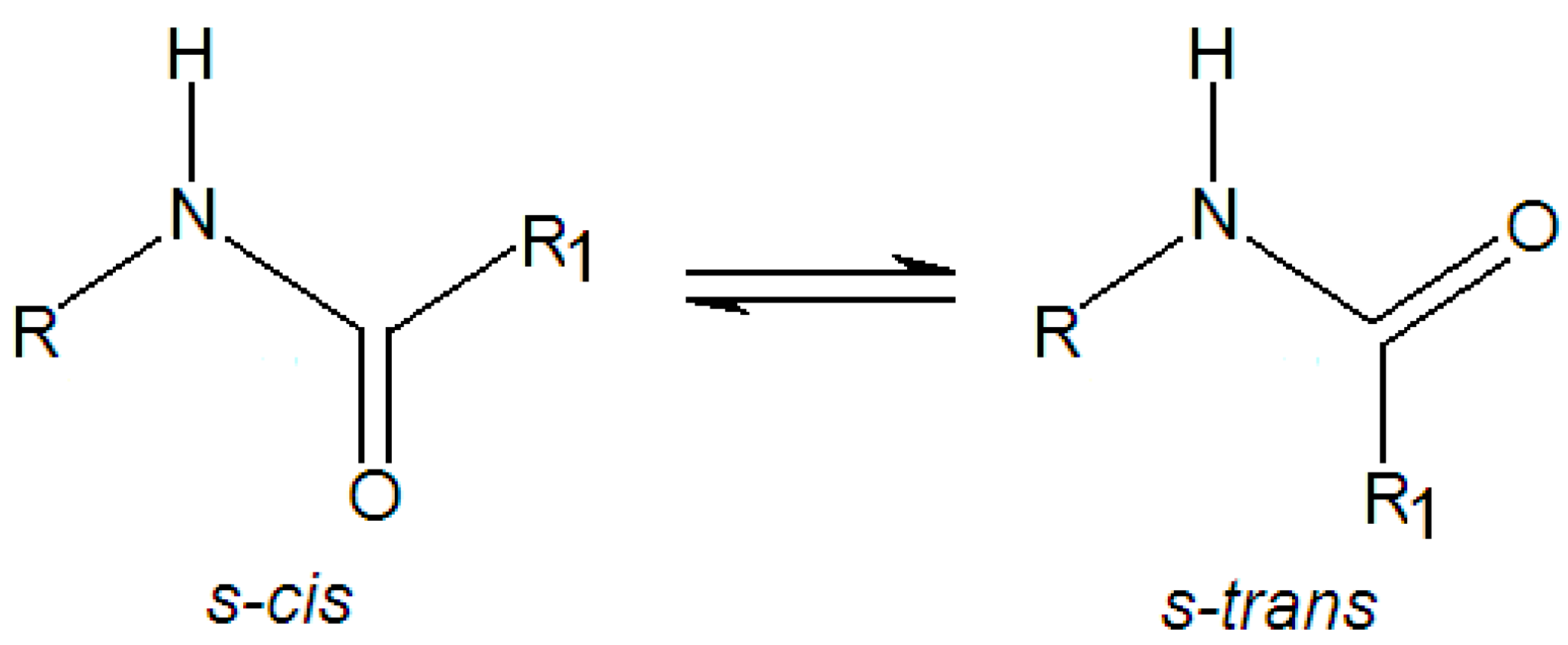
3.1. Minimum Structure, Bond Lenghts and Vibration Modes
3.2. PCM Calculations
3.3. QTAIM Parameters and Intramolecular Hydrogen Bonds
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Thomas, G. Medicinal Chemistry: An Introduction; John Wiley and Sons: Chichester, UK, 2000. [Google Scholar]
- Pitta, M.G.R.; Silva, A.C.A.; Neves, J.K.A.L.; Silva, P.G.; Irmão, J.I.; Malagueño, E.; Santana, J.V.; Lima, M.C.A.; Galdino, S.L.; Pitta, I.R.; et al. New imidazolidinic bioisosters: Potencial candidates for antischistosomal drugs. Mem. Inst. Oswaldo Cruz 2006, 101, 313–316. [Google Scholar] [CrossRef] [PubMed]
- Goodell, J.R.; Ougolkov, A.V.; Hiasa, H.; Kaur, H.; Remmel, R.; Billadeau, D.D.; Ferguson, D.M. Acridine-based agents with Topoisomerase II activity inhibit pancreatic cancer cell proliferation and induce apoptosis. J. Med. Chem. 2008, 51, 179–182. [Google Scholar] [CrossRef] [PubMed]
- World Health Organization. Available online: http://www.who.int/whr/2004/en/ (accessed on 14 September 2009).
- Tarleton, R.L.; Reithinger, R.; Urbina, J.A.; Kitron, U.; Gurtler, R.E. The challenges of Chagas disease—Grim outlook or glimmer of hope? PLoS Med. 2007, 4, 1852–1957. [Google Scholar] [CrossRef] [PubMed]
- Tonin, L.T.D.; Barbosa, V.A.; Bocca, C.C.; Ramos, E.R.F.; Nakamura, C.V.; Costa, W.F.; Basso, E.A.; Nakamura, T.U.; Sarragiotto, M.H. Comparative study of the trypanocidal activity of the methyl 1-nitrophenyl-1,2,3,4-9H-tetrahydro-β-carboline-3-carboxylate derivatives and benznidazole using theoretical calculations and cyclic voltammetry. Eur. J. Med. Chem. 2008, 44, 1745–1750. [Google Scholar] [CrossRef] [PubMed]
- Soares-Sobrinho, J.L.; Cunha-Filho, M.S.S.; Rolim-Neto, P.J.; Torres-Labandeira, J.J.; Dacunha-Marinho, B. Benznidazole. Acta Crystallogr. E 2008, 64, o634. [Google Scholar] [CrossRef] [PubMed]
- Höltje, H.-H.; Sippl, W.; Rognan, D.; Folkers, G. Molecular Modeling: Basic Principles and Applications; Wiley-VHC: Weinhelm, Germany, 2003. [Google Scholar]
- Filho, E.B.A.; Ventura, E.; do Monte, A.S.; Oliveira, B.G.; Junior, C.G.L.; Rocha, G.B.; Vasconcellos, M.L.A.A. Synthesis and conformational study of a new class of highly bioactive compounds. Chem. Phys. Lett. 2007, 449, 336–340. [Google Scholar] [CrossRef]
- Santos Filho, J.M.; Leite, A.C.L.; Oliveira, B.G.; Moreira, D.R.M.; Lima, M.S.; Soares, M.B.P.; Leite, L.F.C.C. Design, synthesis and cruzain docking of 3-(4-substituted-aryl)-1,2,4-oxadiazole-N-acylhydrazones as anti-Trypanosoma cruzi agents. Bioorg. Med. Chem. 2009, 17, 6682–6691. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araujo, R.C.M.U.; Carvalho, A.B.; Ramos, M.N. DFT calculations on the cyclic ethers hydrogen-bonded complexes: Molecular parameters and the non-linearity of the hydrogen bond. Spectrochim. Acta A 2007, 68, 626–631. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Leite, L.F.C.C. A quantum chemical study of red-shift and blue-shift hydrogen bonds in bimolecular and trimolecular methylhydrazine-hydrate complexes. J. Mol. Struct. THEOCHEM 2009, 915, 38–42. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Araujo, R.C.M.U.; Carvalho, A.B.; Ramos, M.N. A chemometrical study of intermolecular properties of hydrogen-bonded complexes formed by C2H4O∙∙∙HX and C2H5N∙∙∙HX with X = F, CN, NC, and CCH. J. Mol. Model. 2009, 15, 421–432. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araujo, R.C.M.U. Theoretical aspects of binary and ternary complexes of aziridine⋯ammonia ruled by hydrogen bond strength. J. Mol. Model. 2012, 18, 2845–2854. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araújo, R.C.M.U.; Ramos, M.N. Evidence for blue-shifting and red-shifting effects in the C2H4⋯HCF3, C2H3(CH3)⋯HCF3 and C2H2(CH3)2∙∙∙HCF3 complexes: π and improper-π hydrogen bonds. J. Mol. Struct. THEOCHEM 2010, 944, 168–172. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Zabardasti, A.; Goudarziafshar, H.; Salehnassaj, M. The electronic mechanism ruling the dihydrogen bonds and halogen bonds in weakly bound systems of H3SiH∙∙∙HOX and H3SiH∙∙∙XOH (X = F, Cl, and Br). J. Mol. Model. 2015, 21, 77–87. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Cortés-Guzmán, F.; Bader, R.F.W. Complementarity of QTAIM and MO theory in the study of bonding in donor-acceptor complexes. Coord. Chem. Rev. 2005, 249, 633–662. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Šafář, P.; Žúžiová, J.; Marchalín, Š.; Prónayová, N.; Švorc, Ľ.; Vrábel, V.; Šesták, S.; Rendić, D.; Tognetti, V.; Joubert, L.; et al. Combined chemical, biological and theoretical DFT-QTAIM study of potent glycosidase inhibitors based on quaternary indolizinium salts. Eur. J. Org. Chem. 2012, 2012, 5498–5514. [Google Scholar] [CrossRef]
- LaPointe, S.M.; Farrag, S.; Bohrquez, H.J.; Boyd, R.J. QTAIM study of an alpha-helix hydrogen bond network. J. Phys. Chem. B 2009, 113, 10957–10964. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Lima, M.C.A.; Pitta, I.R.; Galdino, S.L.; Hernandes, M.Z. A theoretical study of red-shifting and blue-shifting hydrogen bonds occurring between imidazolidine derivatives and PEG/PVP polymers. J. Mol. Model. 2010, 16, 119–127. [Google Scholar] [CrossRef] [PubMed]
- Rozas, I.; Alkorta, I.; Elguero, J. Intramolecular hydrogen bonds in ortho-substituted hydroxybenzenes and in 8-susbtituted 1-hydroxynaphthalenes: Can a methyl group be an acceptor of hydrogen bonds? J. Phys. Chem. A 2001, 105, 10462–10467. [Google Scholar] [CrossRef]
- Zevallos, J.; Toro-Labbé, A.; Mó, O.; Yáñez, M. The role of intramolecular hydrogen bonds versus other weak interactions on the conformation of hyponitrous acid and its mono- and dithio-derivatives. Struct. Chem. 2005, 16, 295–303. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Małecka, M. Intramolecular H-Bonds: DFT and QTAIM studies on 3-(aaminomethylene)pyran-2,4-dione and its derivatives. J. Phys. Chem. A 2006, 110, 11847–11854. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.M.; Gadre, S.R.; Bartolotti, L.J. Estimation of intramolecular hydrogen bond energy via molecular tailoring approach. J. Phys. Chem. A 2006, 110, 12519–12523. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.M.; Suresh, C.H.; Gadre, S.R. Intramolecular hydrogen bond energy in polyhydroxy systems: A critical comparison of molecular tailoring and isodesmic approaches. J. Phys. Chem. A 2007, 111, 6472–6480. [Google Scholar] [CrossRef] [PubMed]
- Sørensen, J.; Clausen, H.F.; Poulsen, R.D.; Overgaard, J.; Schiøtt, B. Short strong hydrogen bonds in 2-acetyl-1,8-dihydroxy-3,6-dimethylnaphthalene: An outlier to current hydrogen bonding theory? J. Phys. Chem. A 2007, 111, 345–351. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.M.; Gadre, S.R. Estimation of N−H∙··O=C intramolecular hydrogen bond energy in polypeptides. J. Phys. Chem. A 2009, 113, 7927–7932. [Google Scholar] [CrossRef] [PubMed]
- Fuster, F.; Grabowski, S.J. Intramolecular hydrogen bonds: The QTAIM and ELF characteristics. J. Phys. Chem. A 2011, 115, 10078–10086. [Google Scholar] [CrossRef] [PubMed]
- Deshmukh, M.M.; Bartolotti, L.J.; Gadre, S.R. Intramolecular hydrogen bond energy and cooperative interactions in α-, β-, and γ-cyclodextrin conformers. J. Comput. Chem. 2011, 32, 2996–3004. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G. Structure, energy, vibrational spectrum, and Bader’s analysis of π∙∙∙H hydrogen bonds and H−δ∙∙∙H+δ dihydrogen bonds. Phys. Chem. Chem. Phys. 2013, 15, 37–79. [Google Scholar] [CrossRef] [PubMed]
- Reichardt, C. Solvents and Solvent Effects in Organic Chemistry; Wiley-VCH: Weinheim, Germany, 1988. [Google Scholar]
- Tomasi, J.; Persico, M. Molecular interactions in solution: An overview of methods based on continuous distributions of the solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Yasuda, T.; Ikawa, S.-I. On the dielectric continuum solvent model for theoretical estimates of the conformational equilibrium of molecules with an intramolecular hydrogen bond. Chem. Phys. 1998, 238, 173–178. [Google Scholar] [CrossRef]
- Abkowicz-Bieńko, A.; Biczysko, M.; Latajka, Z. Solvent effect on hydrogen bonded ammonia-hydrogen halide complexes: Continuum medium versus cluster models. Comput. Chem. 2000, 24, 303–309. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Araújo, R.C.M.U.; Carvalho, A.B.; Ramos, M.N.; Hernandes, M.Z.; Cavalcante, K.R. A theoretical study of the solvent effects in ethylene oxide: Hydrofluoric acid complex using continuum and new discrete models. J. Mol. Struct. THEOCHEM 2007, 802, 91–97. [Google Scholar] [CrossRef]
- López-Vallejo, F.; Medina-Franco, J.L.; Hernández-Campos, A.; Rodríguez-Morales, S.; Yépez, L.; Cedillo, R.; Castillo, R. Molecular modeling of some 1H-benzimidazole derivatives with biological activity against Entamoeba histolytica: A comparative molecular field analysis study. Bioorg. Med. Chem. 2007, 15, 1117–1126. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1933, 98, 1372–1377. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03 Revision D.02; Gaussian Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Biegler-König, F. AIM 2000 1.0; University of Applied Sciences: Bielefeld, Germany, 2000. [Google Scholar]
- Wang, W.; Pu, X.; Zheng, W.; Wong, N.-B.; Tian, A. Hyperconjugation versus intramolecular hydrogen bond: Origin of the conformational preference of gaseous glycine. Chem. Phys. Lett. 2003, 370, 147–153. [Google Scholar] [CrossRef]
- Shagidullin, R.R.; Chernova, A.V.; Shagidullin, R.R. Intramolecular hydrogen bonds and conformations of the 1,4-butanediol molecule. Rus. Chem. Bull. 1993, 42, 1505–1510. [Google Scholar] [CrossRef]
- Lee, H.-J.; Jung, H.-J.; Kim, J.K.; Park, H.-M.; Lee, K.-B. Conformational preference of azaglycine-containing dipeptides studied by PCM and IPCM methods. Chem. Phys. 2003, 294, 201–210. [Google Scholar] [CrossRef]
- Hopkins, W.S.; Hasan, M.; Burt, M.; Marta, R.A.; Fillion, E.; McMahon, T.B. Persistent intramolecular C–H···X (X = O or S) hydrogen-bonding in benzyl meldrum’s acid derivatives. J. Phys. Chem. A 2014, 118, 3795–3803. [Google Scholar] [CrossRef] [PubMed]
- Alcântara, A.F.C.; Teixeira, A.F.; Silva, I.F.; Almeida, W.B.; Piló-Veloso, D. NMR Investigation and theoretical calculations of the effect of solvent on the conformational analysis of 4’,7-di-hydroxy-8-prenylflavan. Quim. Nova 2004, 27, 371–377. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Tanabe, K. The magnitude of the CH/π interaction between benzene and some model hydrocarbons. J. Am. Chem. Soc. 2000, 122, 3746–3753. [Google Scholar] [CrossRef]
- Takahashi, O.; Kohno, Y.; Gondoh, Y.; Saito, K.; Nishio, M. General preference for alkyl/phenyl folded conformations. Relevance of the CH/pi and CH/O interactions to stereochemistry as evidenced by ab Initio MO calculations. Bull. Chem. Soc. Jpn. 2003, 76, 369–374. [Google Scholar] [CrossRef]
- Lithoxoidou, A.T.; Bakalbassis, E.G. PCM study of the solvent and substituent effects on the conformers, intramolecular hydrogen bonds and bond dissociation enthalpies of 2-substituted phenols. J. Phys. Chem. A 2005, 109, 366–377. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araújo, R.C.M.U. Bonding topology, hydrogen bond strength, and vibrational chemical shifts on hetero-ring hydrogen-bonded complexes—Theoretical insights revisited. Can. J. Chem. 2012, 90, 368–375. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Araújo, R.C.M.U.; Carvalho, A.B.; Ramos, M.N. The molecular properties of heterocyclic and homocyclic hydrogen-bonded complexes evaluated by DFT calculations and AIM densities. J. Mol. Model. 2009, 15, 123–131. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araújo, R.C.M.U.; Chagas, F.F.; Carvalho, A.B.; Ramos, M.N. The electronic structure of the C2H4O∙∙∙2HF tri-molecular heterocyclic hydrogen-bonded complex: A theoretical study. J. Mol. Model. 2008, 14, 949–955. [Google Scholar] [CrossRef] [PubMed]
- Gilli, P.; Bertolasi, V.; Ferretti, V.; Gilli, G. Evidence for resonance-assisted hydrogen bonding. 4. Covalent nature of the strong homonuclear hydrogen bond. Study of the O–H--O system by crystal structure correlation methods. J. Am. Chem. Soc. 1994, 116, 909–915. [Google Scholar] [CrossRef]
- Małecka, M. Intramolecular N–H∙∙∙O resonance-assisted hydrogen bonds in crystal structures of oxaphosphinanes and chromones—DFT calculations and AIM analysis. J. Mol. Struct. 2007, 831, 135–143. [Google Scholar] [CrossRef]
- Sanz, P.; Mó, O.; Yáñez, M.; Elguero, J. Bonding in tropolone, 2-aminotropone, and aminotroponimine: No evidence of resonance-assisted hydrogen-bond effects. Chemistry 2008, 14, 4225–4232. [Google Scholar] [CrossRef] [PubMed]
- Trujillo, C.; Sánchez-Sanz, G.; Alkorta, I.; Elguero, J.; Mó, O.; Yáñez, M. Resonance assisted hydrogen bonds in open-chain and cyclic structures of malonaldehyde enol: A theoretical study. J. Mol. Struct. 2013, 1048, 138–151. [Google Scholar] [CrossRef]
- Grabowski, S.J. What is the covalency of hydrogen bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, B.G.; Araújo, R.C.M.U.; Silva, J.J.; Ramos, M.N. A theoretical study of three and four proton donors on linear HX∙∙∙BeH2∙∙∙HX and bifurcate BeH2∙∙∙2HX trimolecular dihydrogen-bonded complexes with X = CN and NC. Struct. Chem. 2010, 21, 221–228. [Google Scholar] [CrossRef]
- Oliveira, B.G.; Vasconcellos, M.L.A.A.A. B3LYP and QTAIM study of a new proton donor for dihydrogen bonds: The case of the C2H5+∙∙∙nBeH2 complexes (n = 1 or 2). Struct. Chem. 2010, 20, 897–902. [Google Scholar] [CrossRef]
- Oliveira, B.G. Interplay between dihydrogen and alkali–halogen bonds: Is there some covalency upon complexation of ternary systems? Comput. Theor. Chem. 2012, 998, 173–182. [Google Scholar] [CrossRef]
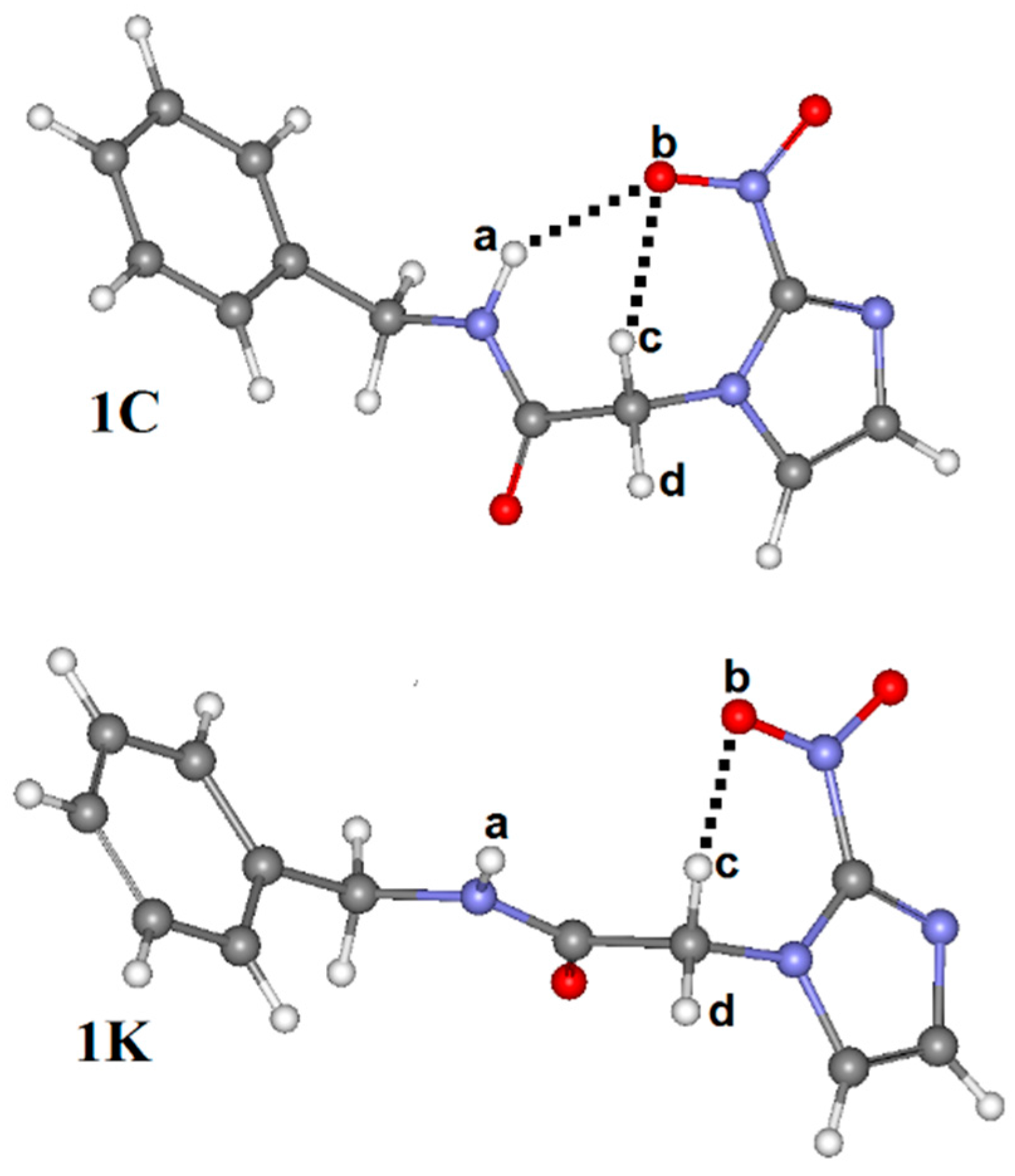
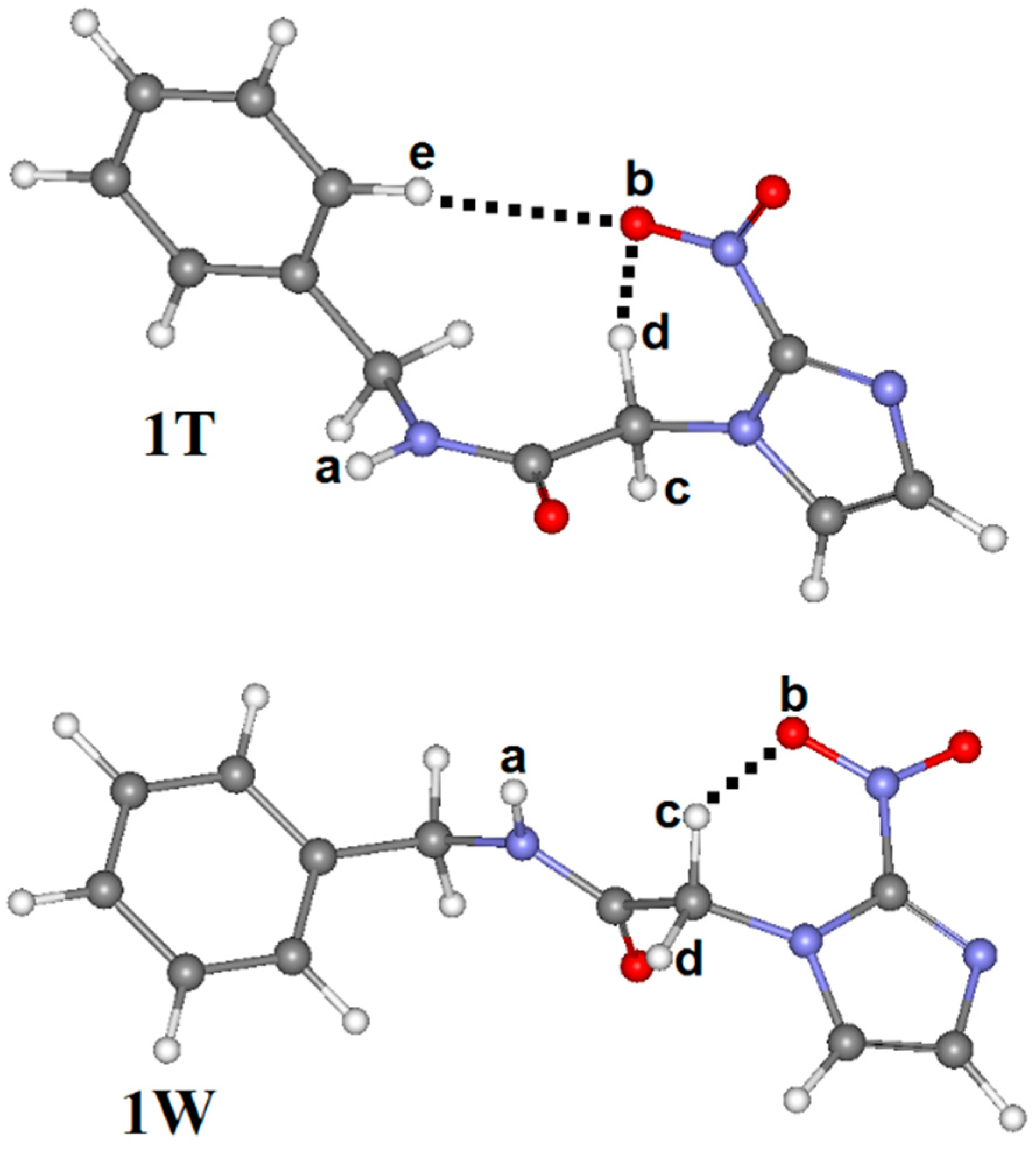
| HBonds and Bonds * | Conformations | |||
|---|---|---|---|---|
| 1C | 1T | 1K | 1W | |
| RN–Ha∙∙∙Ob=N | 2.125 | - | - | - |
| RC–Hc∙∙∙Ob=N | 2.287 | - | 2.340 | 2.468 |
| RC–Hd∙∙∙Ob=N | - | 2.347 | - | - |
| RC–He∙∙∙Ob=N | - | 2.562 | - | - |
| rN–Ha | 1.012 | - | 1.013 | - |
| rC–Hc | 1.085 | - | 1.086 | 1.085 |
| rC–He | - | 1.084 | - | - |
| rC–Hd | - | 1.085 | - | - |
| rOb=N | 1.243 | 1.239 | 1.243 | 1.242 |
| υN–Ha | 3570.1 | - | 3562.7 | - |
| IN–Ha | 97.3 | - | 107.6 | - |
| υC–Hc | 3172.3 | - | 3172.4 | 3172.3 |
| IC–Hc | 0.70 | - | 0.20 | 0.40 |
| υC–He | - | 3183.0 | - | - |
| IC–He | - | 8.0 | - | - |
| υC–Hd | - | 3160.0 | - | - |
| IC–Hd | - | 2.4 | - | - |
| Conformations | Parameters | ||
|---|---|---|---|
| (ε0 + ZPE) | (ε0 + Gcorr) | ΔG | |
| 1C | −909.100529 | −909.149975 | - |
| 1T | −909.093925 | −909.142360 | 4.78 |
| 1W | −909.138240 | −909.186911 | −23.17 |
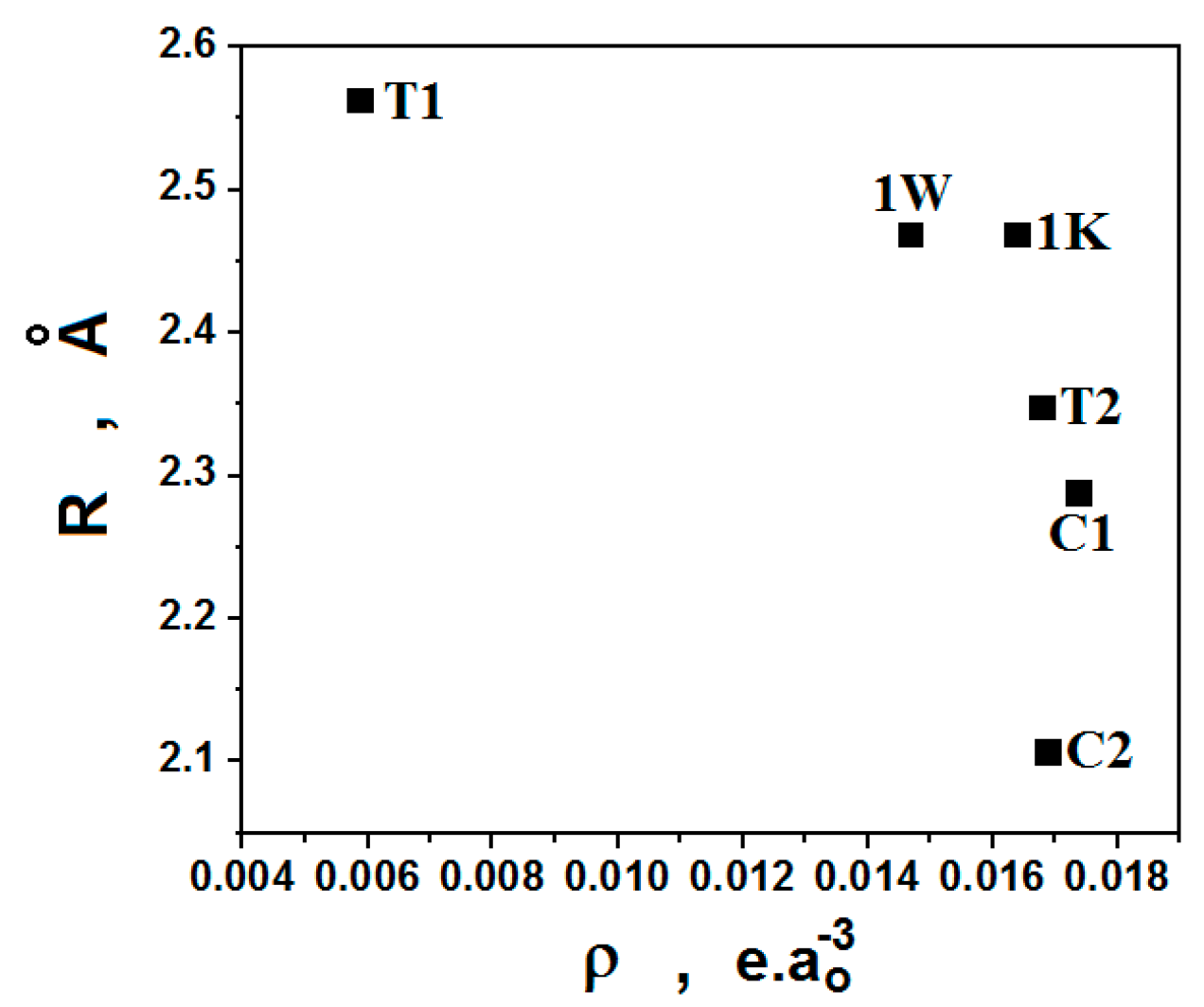
| QTAIM Parameters * | Conformations | |||
|---|---|---|---|---|
| 1C | 1T | 1K | 1W | |
| N–Ha∙∙∙Ob=N | ||||
| ρ (∇2ρ) | 0.0169 (0.0634) | - | - | - |
| U (G) | −0.0114 (0.0136) | - | - | - |
| −G/U | 1.192 | - | - | - |
| C–Hc∙∙∙Ob=N | ||||
| ρ (∇2ρ) | - | - | 0.0164 (0.0645) | 0.0147 (0.0561) |
| U (G) | - | - | −0.0191 (0.0140) | −0.0168 (0.0124) |
| −G/U | - | - | 0.733 | 0.738 |
| C–He∙∙∙Ob=N | ||||
| ρ (∇2ρ) | - | 0.0059 (0.0213) | - | - |
| U (G) | - | −0.0036 (0.0044) | - | - |
| −G/U | - | 1.222 | - | - |
| C–Hd∙∙∙Ob=N | ||||
| ρ (∇2ρ) | - | 0.0168 (0.0648) | - | - |
| U (G) | - | −0.0121 (0.0141) | - | - |
| −G/U | - | 1.165 | - | - |
| C–Hd∙∙∙Hf–C | ||||
| ρ (∇2ρ) | - | 0.0130 (0.0570) | - | - |
| U (G) | - | −0.0074 (0.0096) | - | - |
| −G/U | - | 1.297 | - | - |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oliveira, B.G.; Filho, E.B.A.; Vasconcellos, M.L.A.A. Comparisons between Crystallography Data and Theoretical Parameters and the Formation of Intramolecular Hydrogen Bonds: Benznidazole. Crystals 2016, 6, 56. https://doi.org/10.3390/cryst6050056
Oliveira BG, Filho EBA, Vasconcellos MLAA. Comparisons between Crystallography Data and Theoretical Parameters and the Formation of Intramolecular Hydrogen Bonds: Benznidazole. Crystals. 2016; 6(5):56. https://doi.org/10.3390/cryst6050056
Chicago/Turabian StyleOliveira, Boaz G., Edilson B. Alencar Filho, and Mário L. A. A. Vasconcellos. 2016. "Comparisons between Crystallography Data and Theoretical Parameters and the Formation of Intramolecular Hydrogen Bonds: Benznidazole" Crystals 6, no. 5: 56. https://doi.org/10.3390/cryst6050056
APA StyleOliveira, B. G., Filho, E. B. A., & Vasconcellos, M. L. A. A. (2016). Comparisons between Crystallography Data and Theoretical Parameters and the Formation of Intramolecular Hydrogen Bonds: Benznidazole. Crystals, 6(5), 56. https://doi.org/10.3390/cryst6050056