Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed With the Empty Lattice Model
Abstract
:1. Introduction
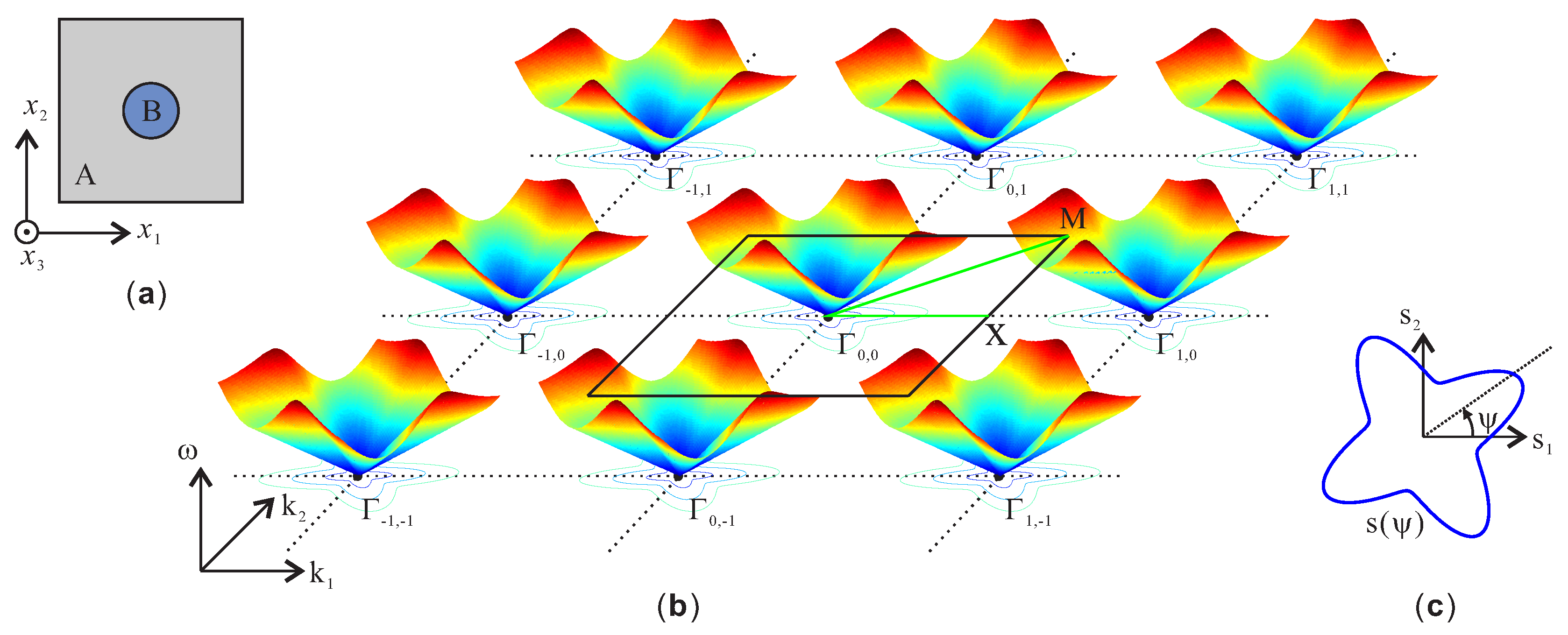
2. Empty Lattice Model
2.1. Analytical Model
2.2. Empty Lattice Model for Scalar Waves in an Isotropic Medium
2.3. Empty Lattice Model for Vector Waves in an Isotropic Solid
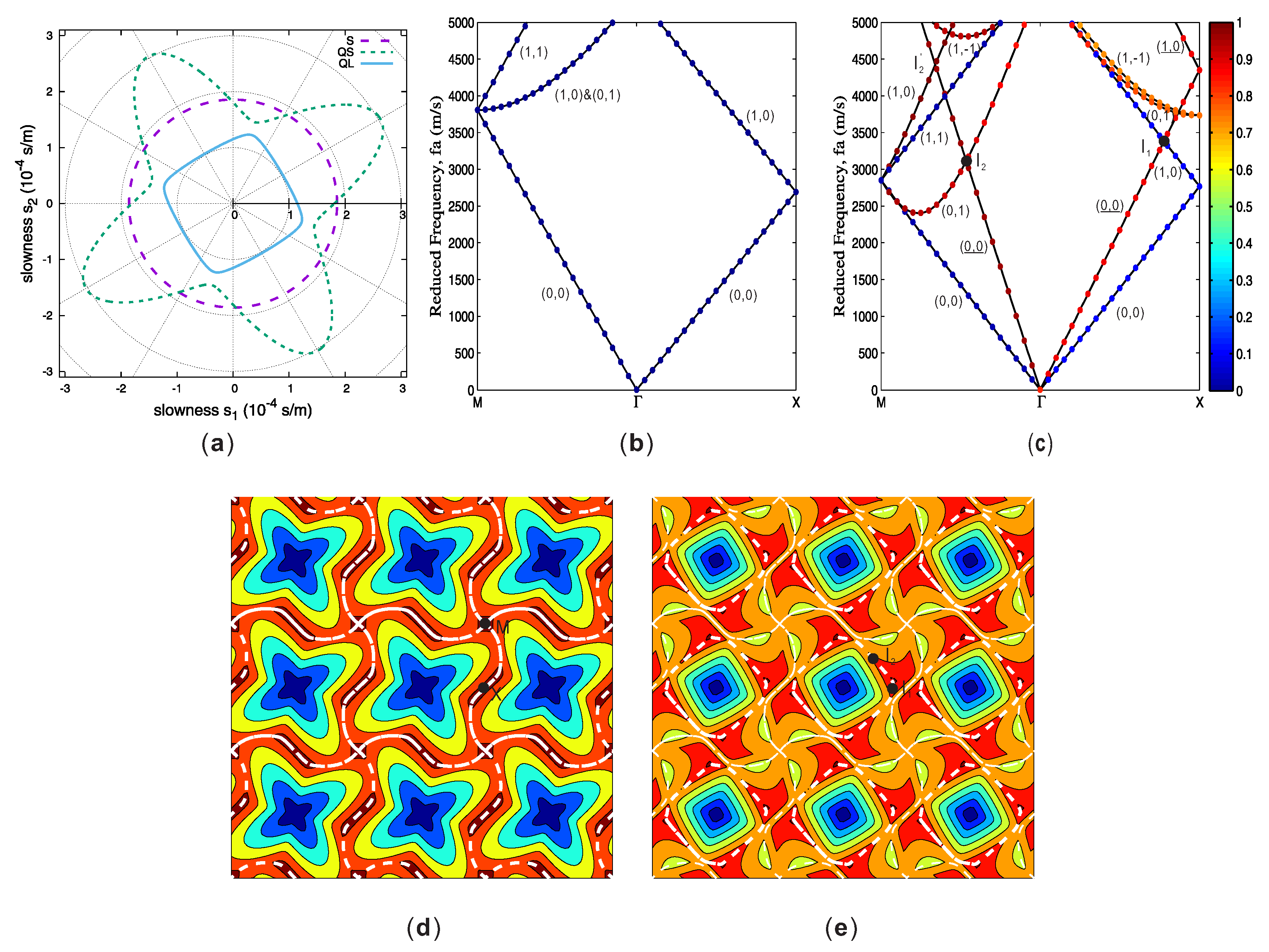
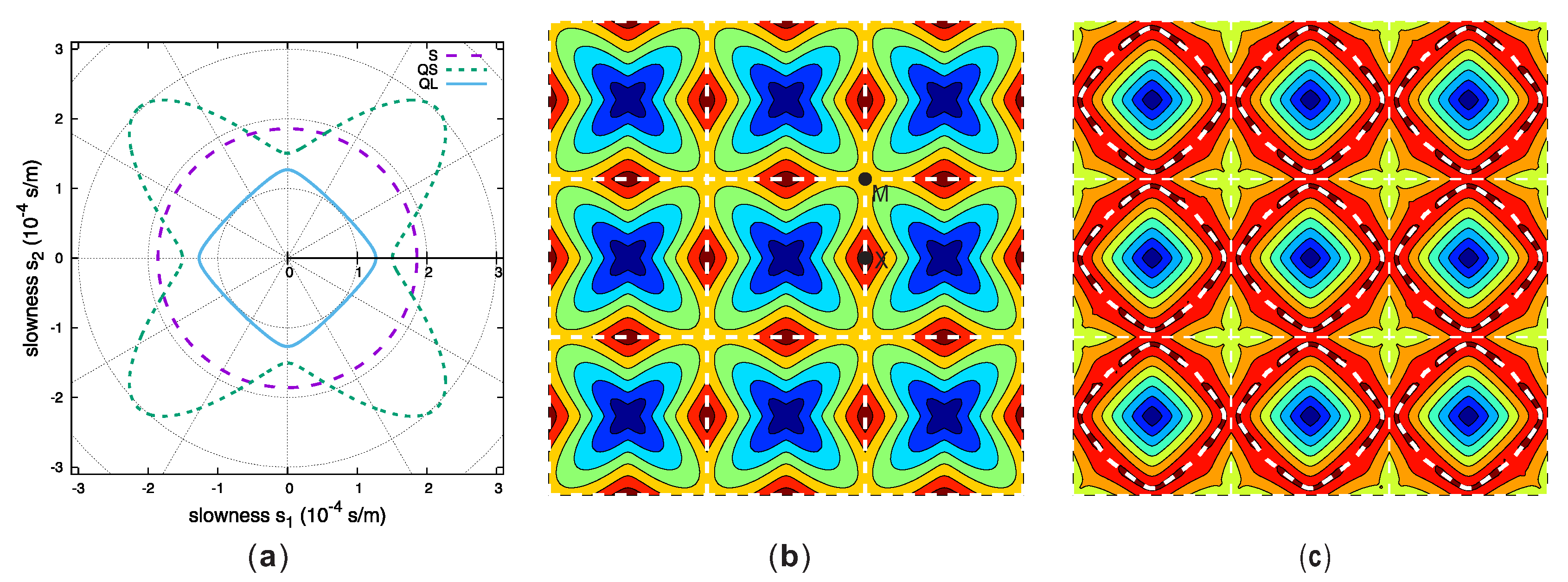
2.4. Empty Lattice Model for Vector Waves in an Anisotropic Solid
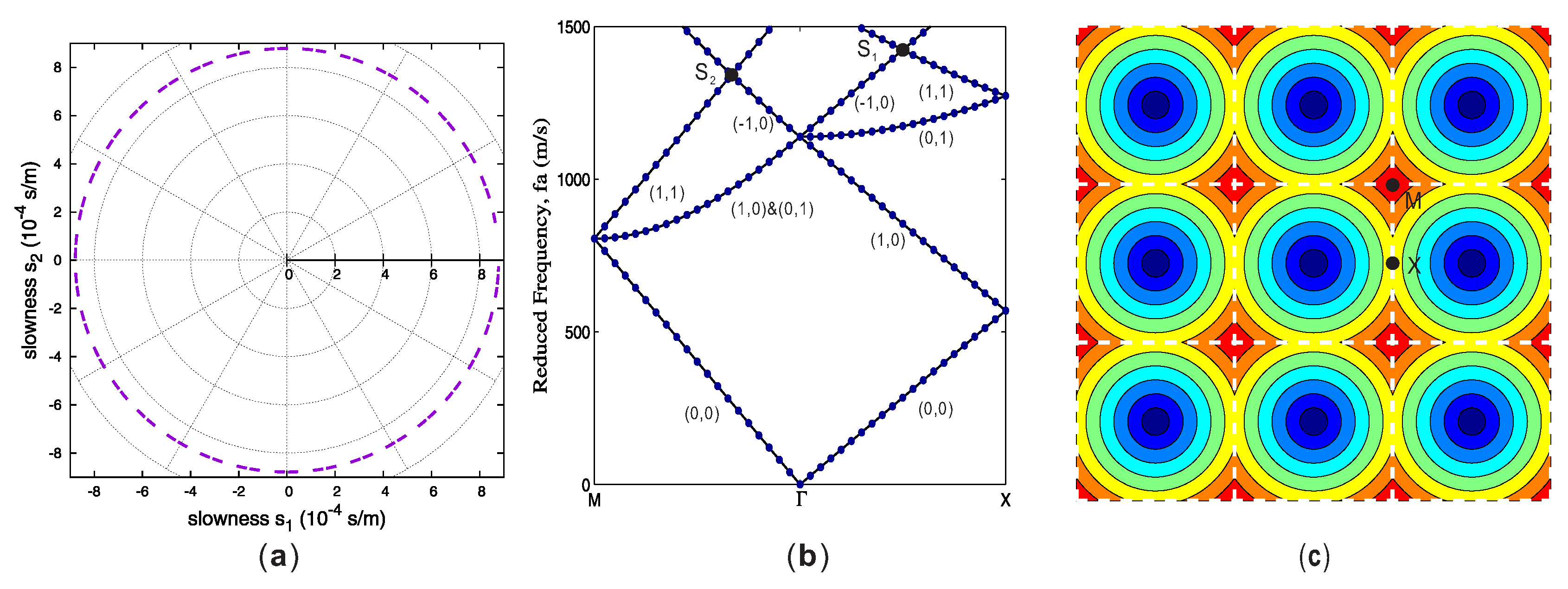
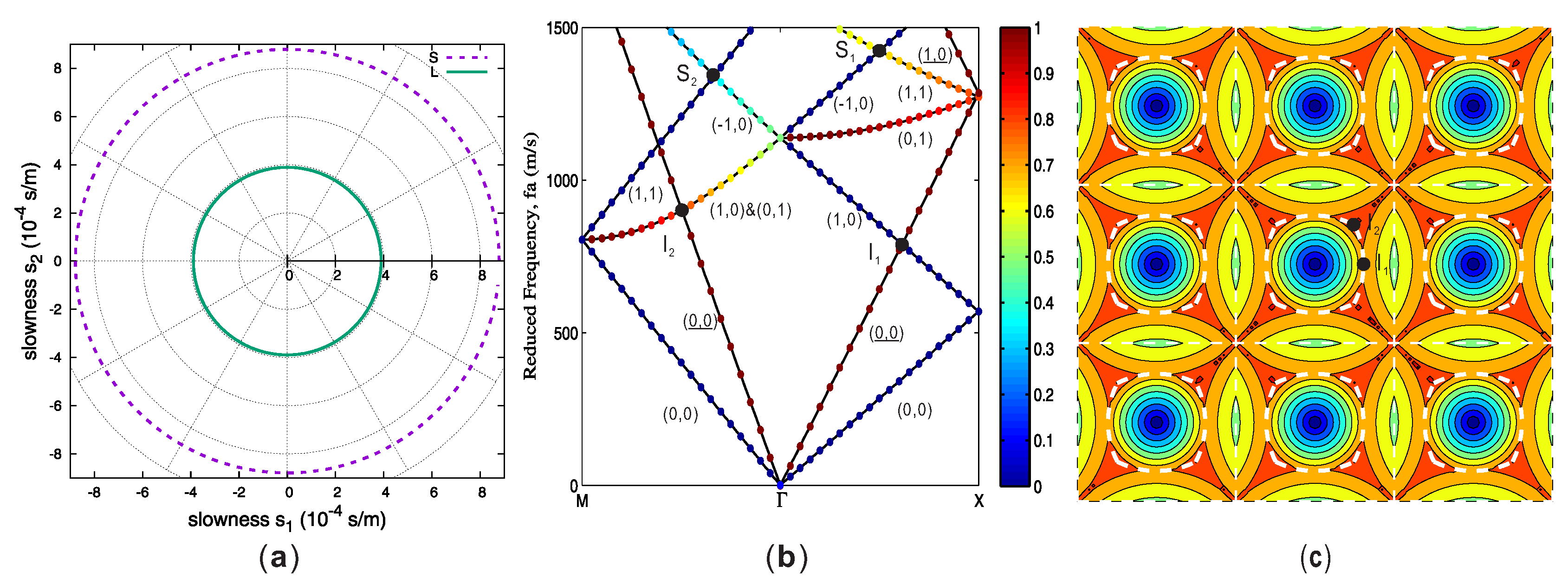
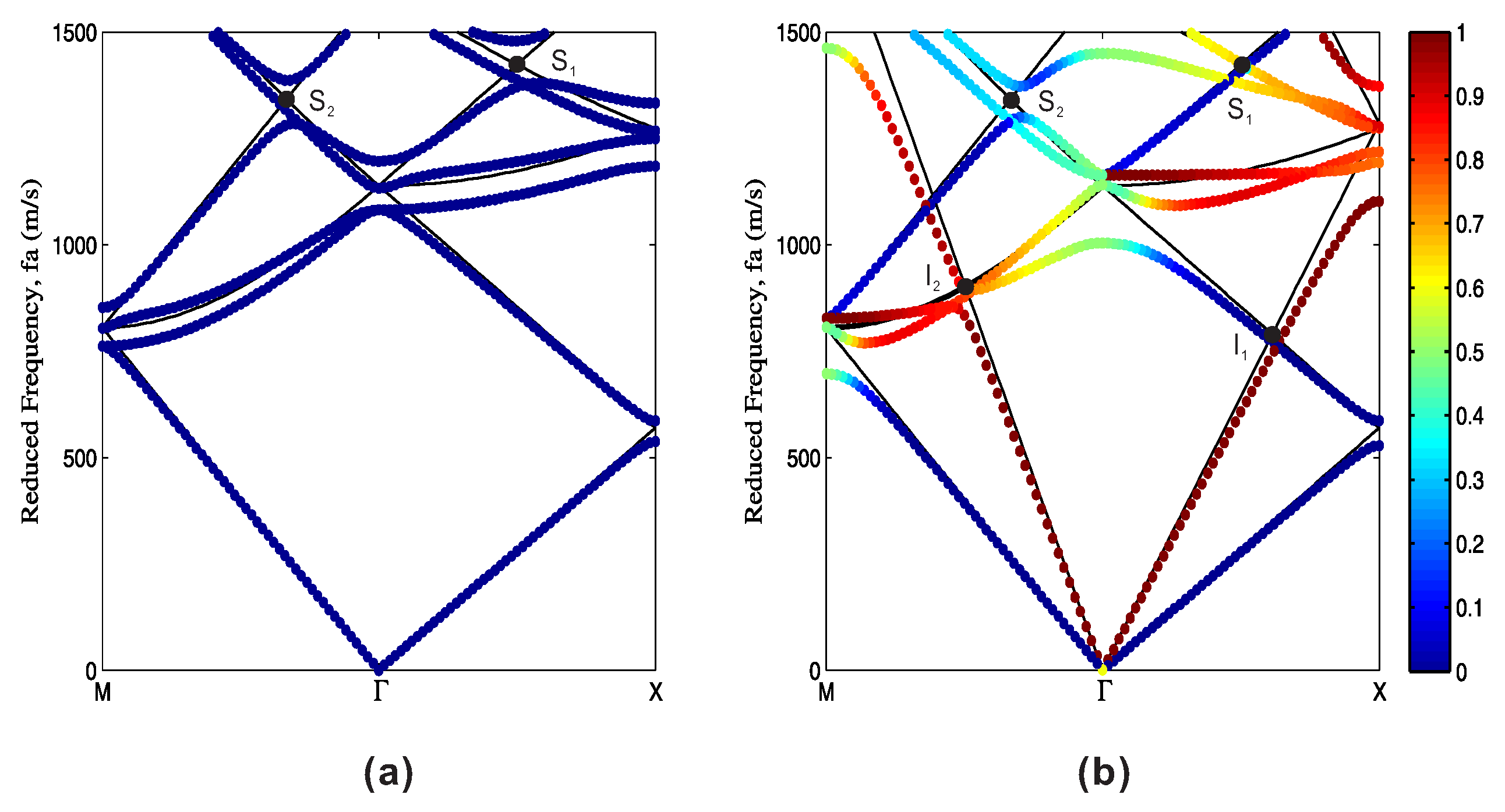
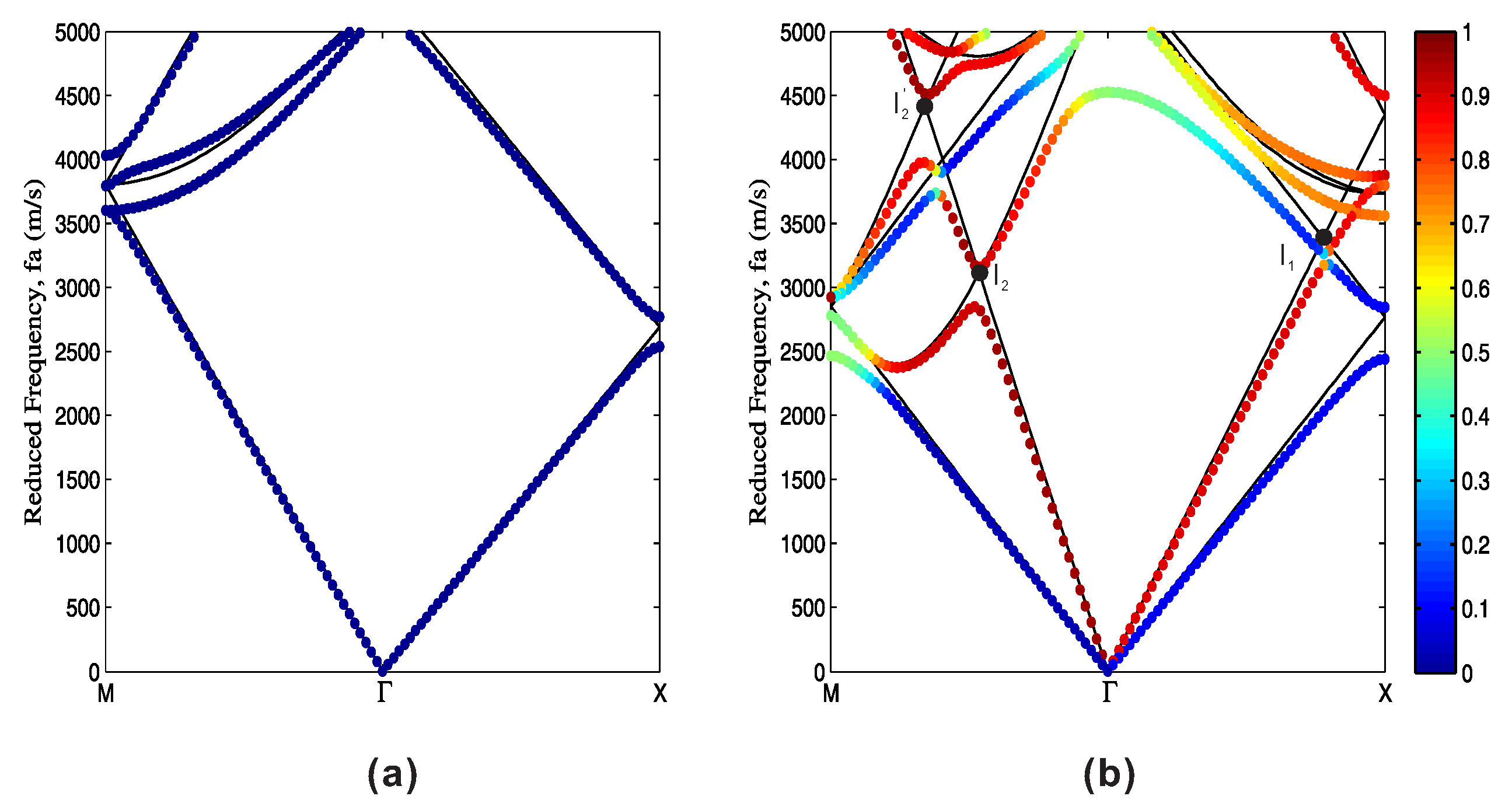
3. Formation of Bragg Band Gaps in Phononic Crystals
4. Conclusions
5. Materials and Methods
5.1. Materials
5.2. Methods
Acknowledgments
Author Contributions
Conflicts of Interest
References and Notes
- Laude, V. Phononic Crystals: Artificial Crystals for Sonic, Acoustic, and Elastic Waves; Walter de Gruyter: Berlin, Germany, 2015. [Google Scholar]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Kafesaki, M.; Economou, E.N. Multiple-scattering theory for three-dimensional periodic acoustic composites. Phys. Rev. B 1999, 60, 11993. [Google Scholar] [CrossRef]
- Liu, Z.; Chan, C.; Sheng, P.; Goertzen, A.; Page, J. Elastic wave scattering by periodic structures of spherical objects: Theory and experiment. Phys. Rev. B 2000, 62, 2446. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022. [Google Scholar] [CrossRef] [PubMed]
- Sigalas, M.; Economou, E. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Moiseyenko, R.P.; Laude, V. Material loss influence on the complex band structure and group velocity in phononic crystals. Phys. Rev. B 2011, 83, 064301. [Google Scholar] [CrossRef]
- Wang, Y.F.; Wang, Y.S.; Su, X.X. Large bandgaps of two-dimensional phononic crystals with cross-like holes. J. Appl. Phys. 2011, 110, 113520. [Google Scholar] [CrossRef]
- Laude, V.; Moiseyenko, R.P.; Benchabane, S.; Declercq, N.F. Bloch wave deafness and modal conversion at a phononic crystal boundary. AIP Adv. 2011, 1, 041402. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.F.; Wang, Y.S.; Laude, V. Wave propagation in two-dimensional viscoelastic metamaterials. Phys. Rev. B 2015, 92, 104110. [Google Scholar] [CrossRef]
- Martinezsala, R.; Sancho, J.; Sánchez, J.; Gómez, V.; Llinares, J.; Meseguer, F. Sound-attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Suzuki, T.; Paul, K. Complex elastic wave band structures in three-dimensional periodic elastic media. J. Mech. Phys. Solids 1998, 46, 115–138. [Google Scholar] [CrossRef]
- Dowling, J.P. Sonic band structure in fluids with periodic density variations. J. Acoust. Soc. Am. 1992, 91, 2539–2543. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices; Dover Publications: New York, NY, USA, 1946. [Google Scholar]
- Ashcroft, J.; Mermin, N. Solid State Physics; Harcourt Inc.: San Diego, CA, USA, 1976. [Google Scholar]
- Tamura, S.; Hurley, D.; Wolfe, J. Acoustic-phonon propagation in superlattices. Phys. Rev. B 1988, 38, 1427–1449. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G. Level repulsions of bulk acoustic waves in composite materials. Phys. Rev. B 2004, 70, 214304. [Google Scholar] [CrossRef]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Laude, V. Polarization state and level repulsion in two-dimensional phononic crystals and waveguides in the presence of material anisotropy. J. Phys. D: Appl. Phys. 2010, 43, 185401. [Google Scholar] [CrossRef]
- Sivarajah, P.; Maznev, A.; Ofori-Okai, B.; Nelson, K. What is the Brillouin zone of an anisotropic photonic crystal? Phys. Rev. B 2016, 93, 054204. [Google Scholar] [CrossRef]
- Wang, Y.Z.; Li, F.M.; Huang, W.H.; Jiang, X.; Wang, Y.S.; Kishimoto, K. Wave band gaps in two-dimensional piezoelectric/piezomagnetic phononic crystals. Int. J. Solids Struct. 2008, 45, 4203–4210. [Google Scholar] [CrossRef]
- Lin, S.C.S.; Huang, T.J. Tunable phononic crystals with anisotropic inclusions. Phys. Rev. B 2011, 83, 174303. [Google Scholar] [CrossRef]
- Auld, B.A. Acoustic Fields and Waves in Solids; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Inoue, K.; Ohtaka, K. Photonic Crystals: Physics, Fabrication and Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- At the minimum of these branches, the group velocity vanishes in the Γ-M direction. However, the orthogonal group velocity component is non-zero since the equifrequency contour centered on Γ0,1 or Γ1,−1 is tangent to the propagation direction at these points. Energy propagation is then orthogonal to the Bloch wavevector.
- Lai, Y.; Wu, Y.; Sheng, P.; Zhang, Z.Q. Hybrid elastic solids. Nat. Mater. 2011, 10, 620–624. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Liu, X.; Hu, G.; Sun, C.; Huang, G. Negative refraction of elastic waves at the deep-subwavelength scale in a single-phase metamaterial. Nat. Commun. 2014, 5, 5510. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.F.; Wang, Y.S.; Zhang, C. Two-dimensional locally resonant elastic metamaterials with chiral comb-like interlayers: Bandgap and simultaneously double negative properties. J. Acoust. Soc. Am. 2016. accepted for publication. [Google Scholar]
- Gorishnyy, T.; Jang, J.H.; Koh, C.; Thomas, E.L. Direct observation of a hypersonic band gap in two-dimensional single crystalline phononic structures. Appl. Phys. Lett. 2007, 91, 121915. [Google Scholar] [CrossRef]
- Still, T.; Cheng, W.; Retsch, M.; Sainidou, R.; Wang, J.; Jonas, U.; Stefanou, N.; Fytas, G. Simultaneous occurrence of structure-directed and particle-resonance-induced phononic gaps in colloidal films. Phys. Rev. Lett. 2008, 100, 194301. [Google Scholar] [CrossRef] [PubMed]
- Sato, A.; Pennec, Y.; Yanagishita, T.; Masuda, H.; Knoll, W.; Djafari-Rouhani, B.; Fytas, G. Cavity-type hypersonic phononic crystals. New J. Phys. 2012, 14, 113032. [Google Scholar] [CrossRef]
- Zhu, G.; Swinteck, N.Z.; Wu, S.; Zhang, J.S.; Pan, H.; Bass, J.D.; Deymier, P.A.; Banerjee, D.; Yano, K. Direct observation of the phonon dispersion of a three-dimensional solid/solid hypersonic colloidal crystal. Phys. Rev. B 2013, 88, 144307. [Google Scholar] [CrossRef]
- Schneider, D.; Liaqat, F.; El Abouti, O.; Tremel, W.; Butt, H.J.; Djafari-Rouhani, B.; Fytas, G.; El Boudouti, E.H. Defect-controlled hypersound propagation in hybrid superlattices. Phys. Rev. Lett. 2013, 111, 164301. [Google Scholar] [CrossRef] [PubMed]
- Beltramo, P.J.; Schneider, D.; Fytas, G.; Furst, E.M. Anisotropic hypersonic phonon propagation in films of aligned ellipsoids. Phys. Rev. Lett. 2014, 113, 205503. [Google Scholar] [CrossRef] [PubMed]
- Alonso-Redondo, E.; Schmitt, M.; Urbach, Z.; Hui, C.; Sainidou, R.; Rembert, P.; Matyjaszewski, K.; Bockstaller, M.; Fytas, G. A new class of tunable hypersonic phononic crystals based on polymer-tethered colloids. Nat. Commun. 2015, 6, 8309. [Google Scholar] [CrossRef] [PubMed]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- FreeFEM++ Codes. Available online: http://members.femto-st.fr/vincent-laude/freefem-scripts-numerical-simulation-phononic-crystals (accessed on 5 May 2016).
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.-F.; Maznev, A.A.; Laude, V. Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed With the Empty Lattice Model. Crystals 2016, 6, 52. https://doi.org/10.3390/cryst6050052
Wang Y-F, Maznev AA, Laude V. Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed With the Empty Lattice Model. Crystals. 2016; 6(5):52. https://doi.org/10.3390/cryst6050052
Chicago/Turabian StyleWang, Yan-Feng, Alexei A. Maznev, and Vincent Laude. 2016. "Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed With the Empty Lattice Model" Crystals 6, no. 5: 52. https://doi.org/10.3390/cryst6050052
APA StyleWang, Y.-F., Maznev, A. A., & Laude, V. (2016). Formation of Bragg Band Gaps in Anisotropic Phononic Crystals Analyzed With the Empty Lattice Model. Crystals, 6(5), 52. https://doi.org/10.3390/cryst6050052