Development of a CA-FVM Model with Weakened Mesh Anisotropy and Application to Fe–C Alloy
Abstract
:1. Introduction
2. Model Description
2.1. Nucleation Model
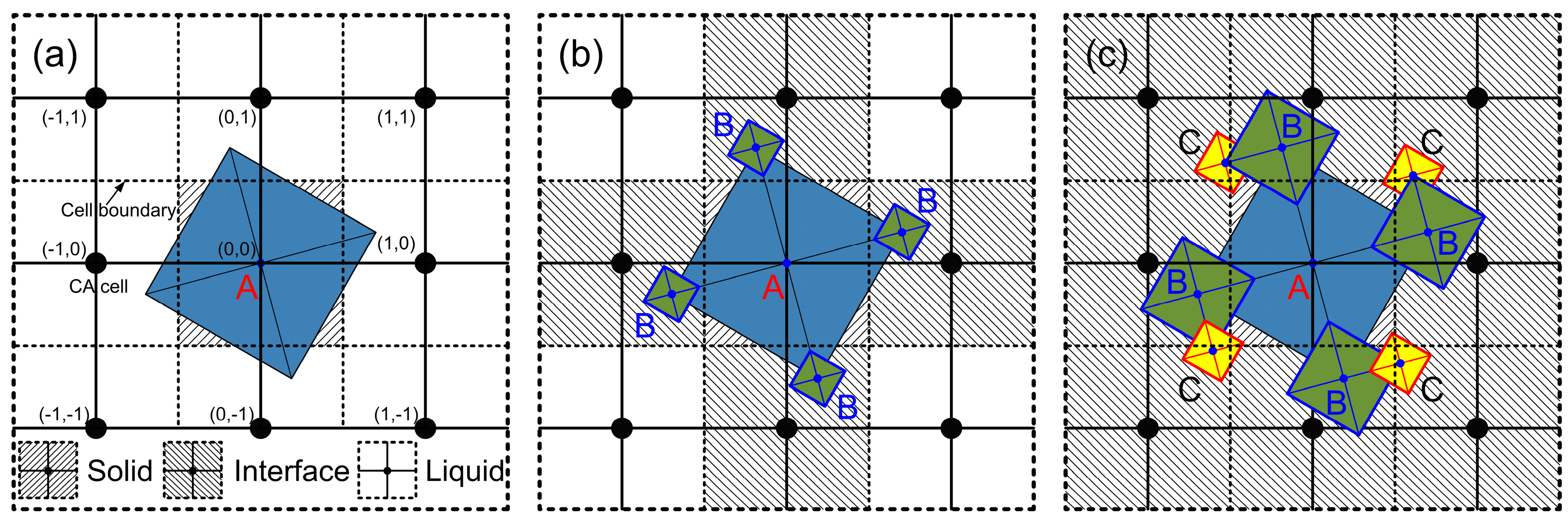
2.2. CA Model
2.3. Transport Models
3. Model Evaluation and Application
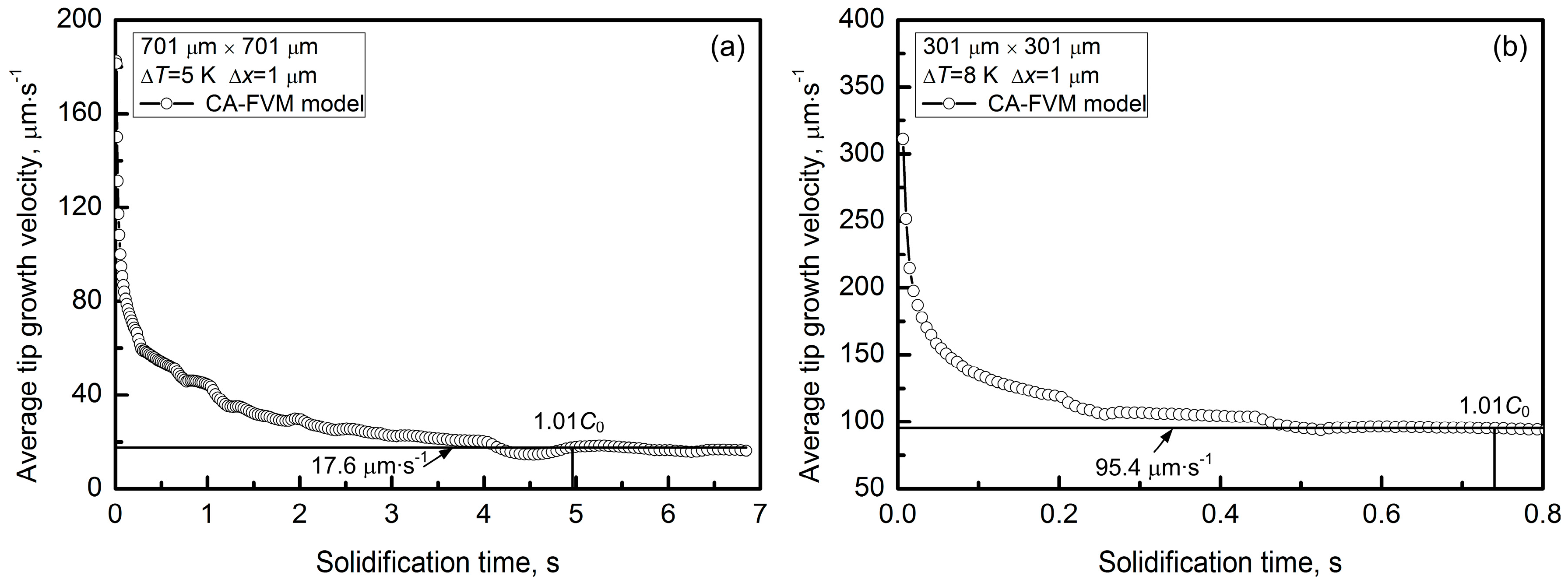
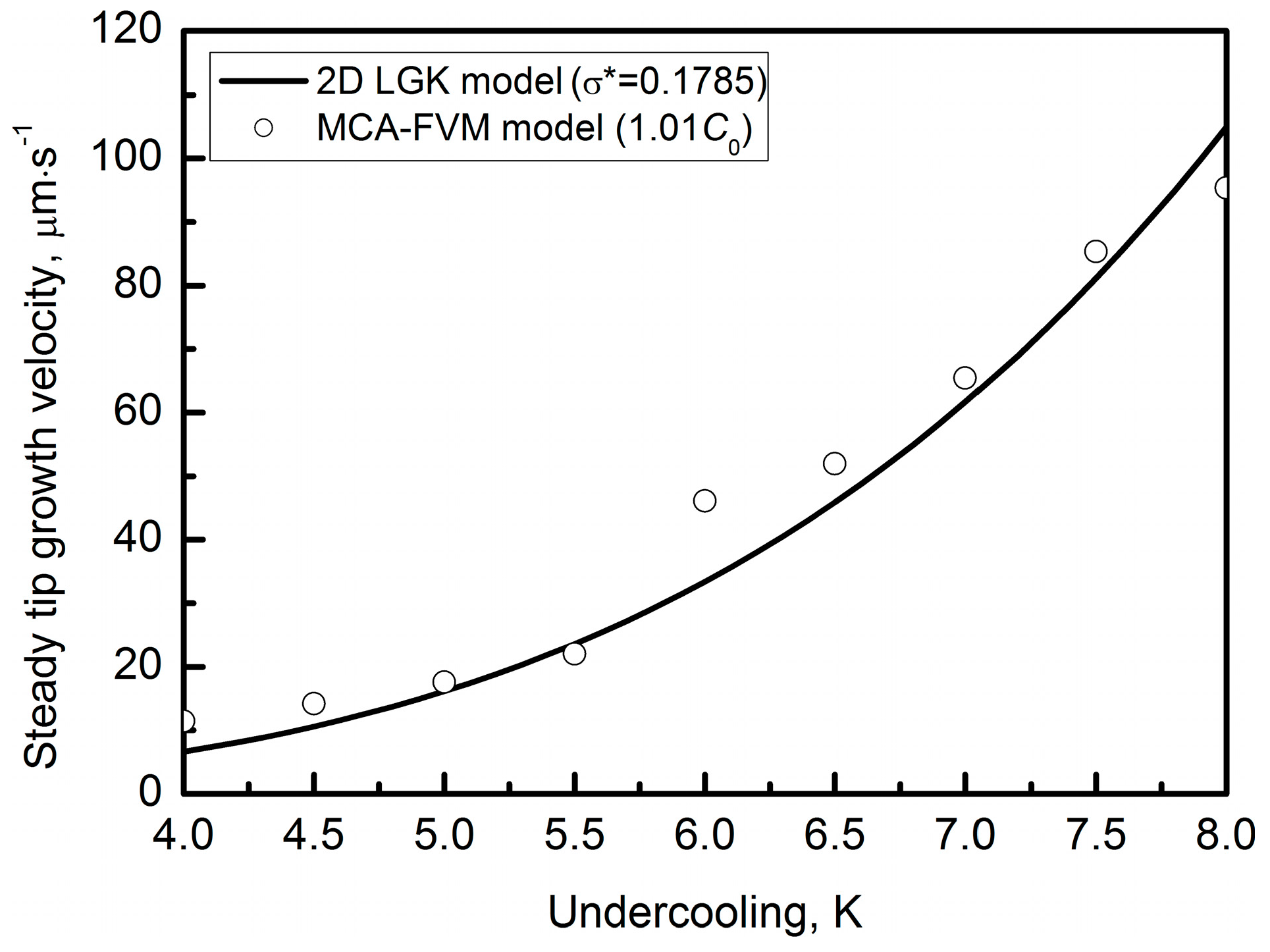
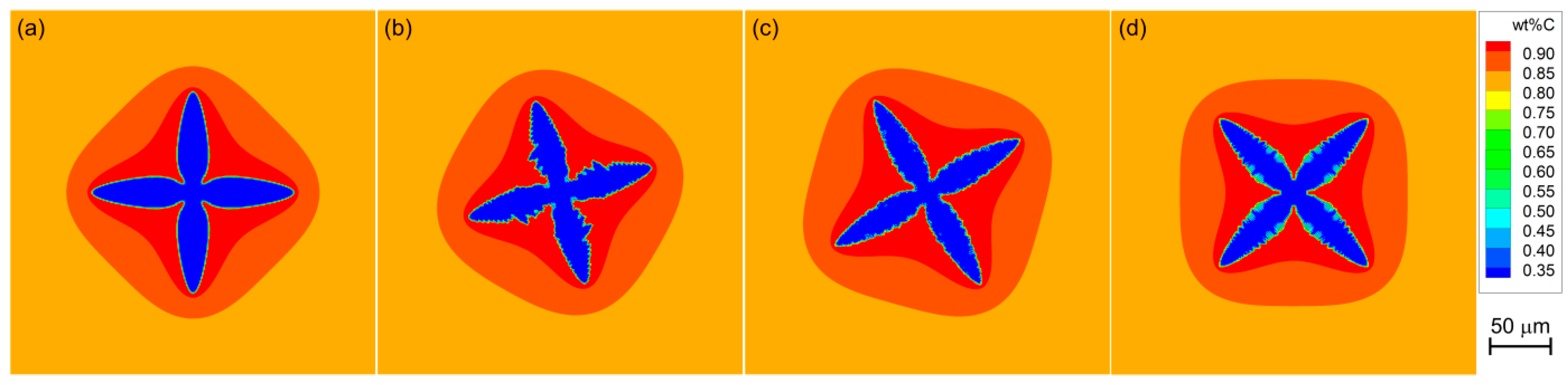
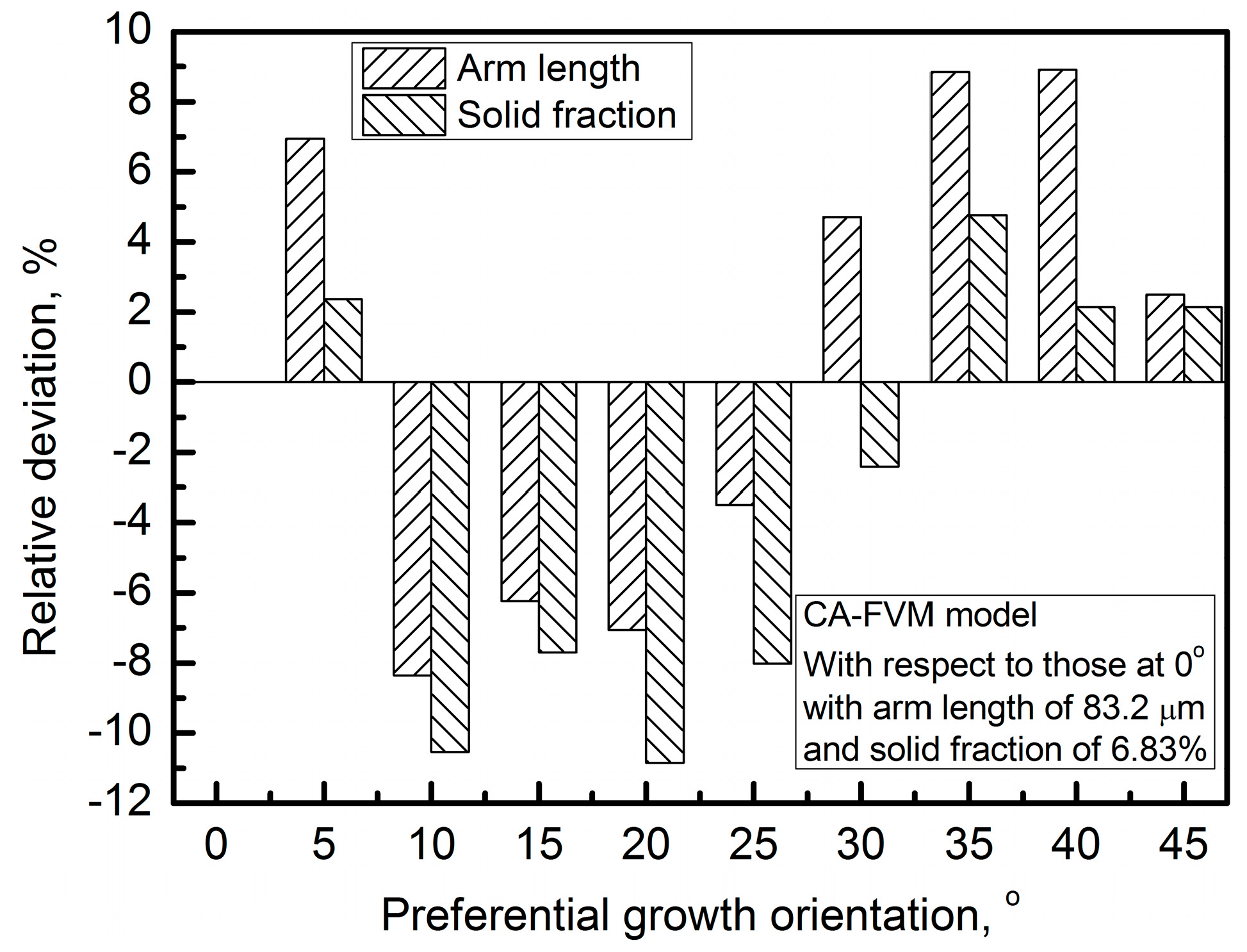
3.1. Free Growth of Equiaxed Dendrite
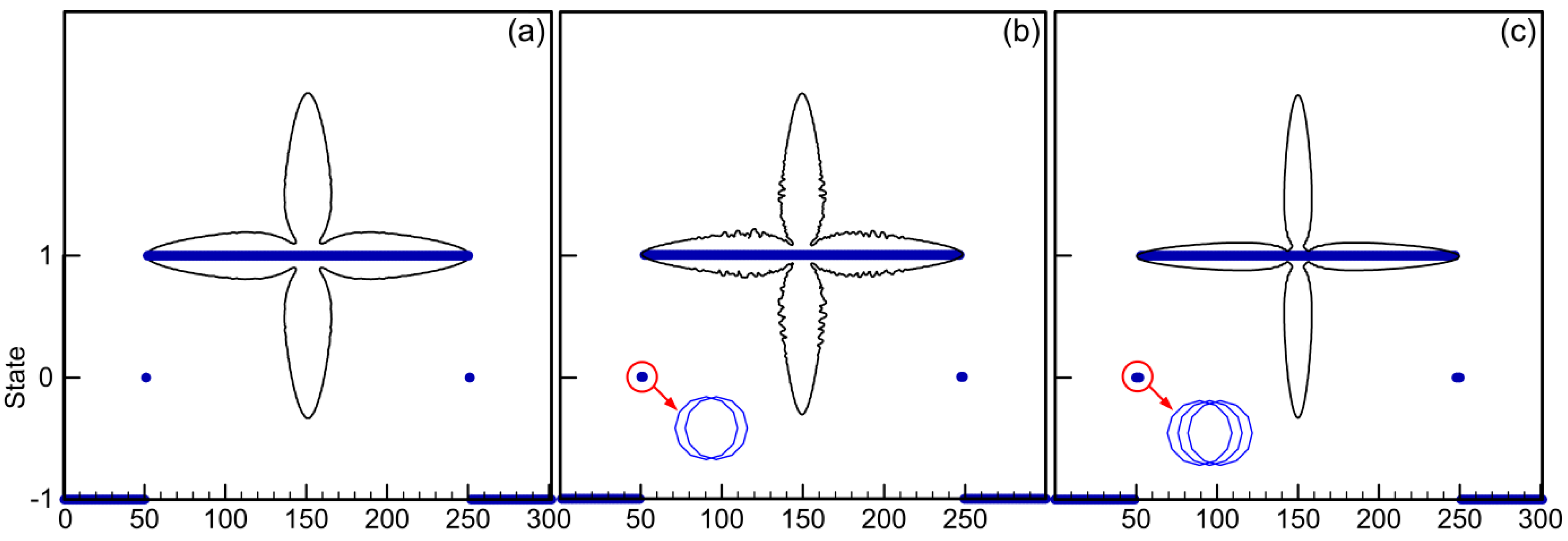
3.2. Interface Type and Growth Consistence
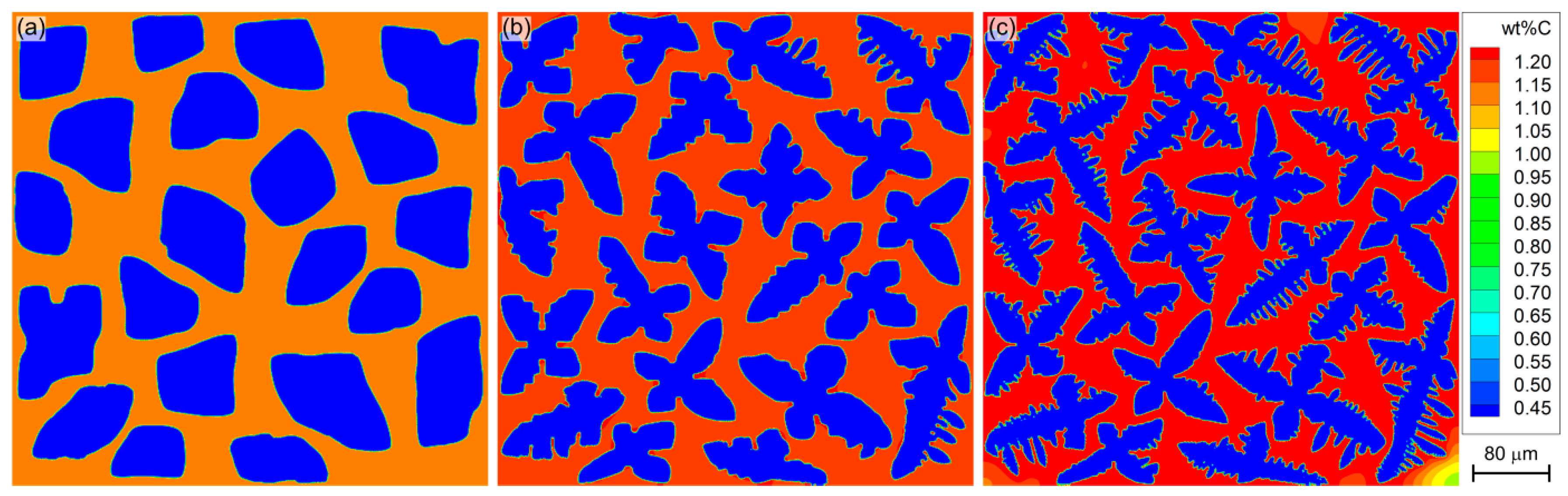
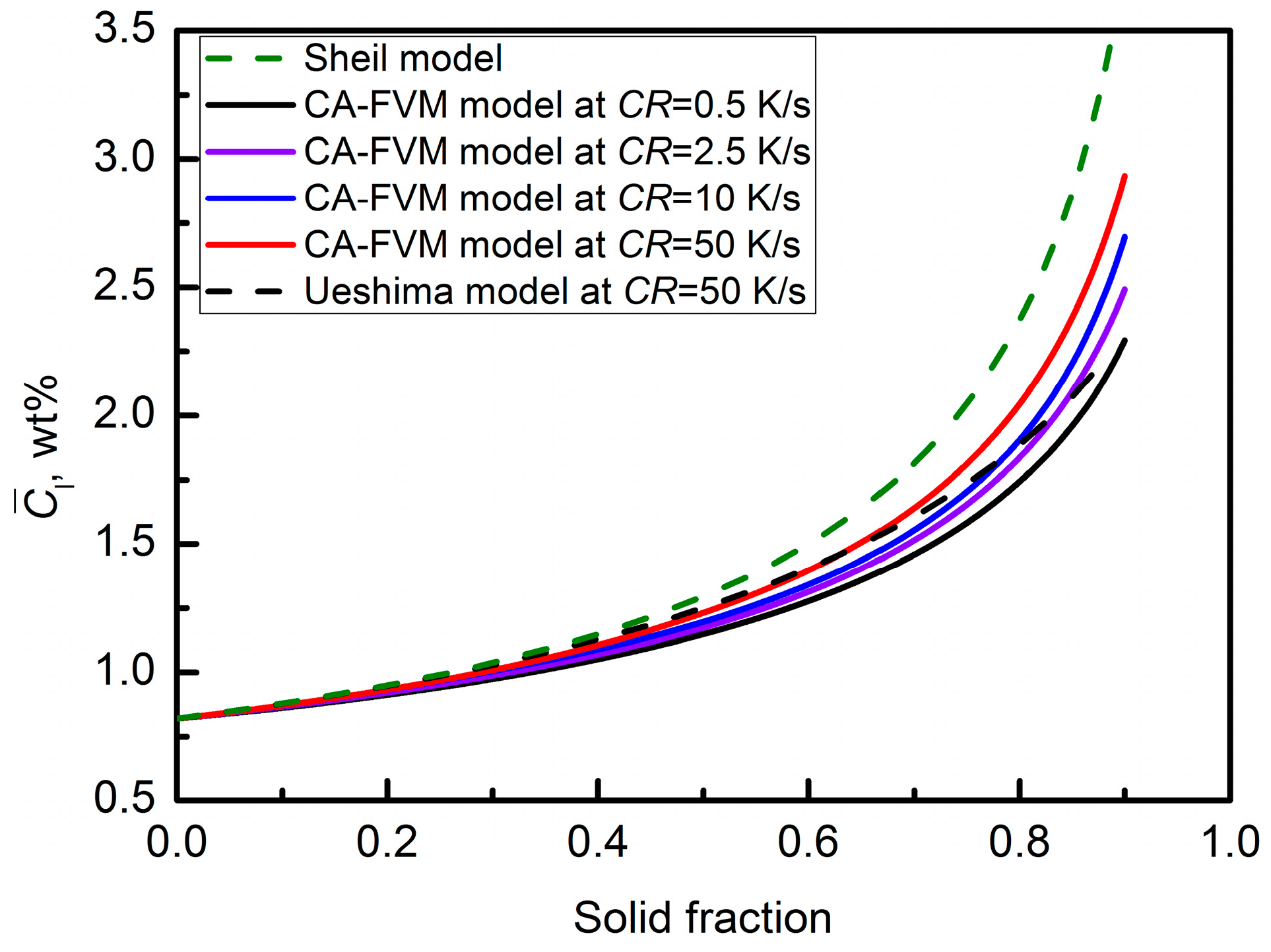
3.3. Segregation among Equiaxed Dendrites
3.4. Constrained Growth of Columnar Dendrite
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Presoly, P.; Pierer, R.; Bernhard, C. Identification of defect prone peritectic steel grades by analyzing high-temperature phase transformations. Metall. Mater. Trans. A 2013, 44, 5377–5388. [Google Scholar] [CrossRef]
- Ogibayashi, S. Mechanism of centerline segregation in continuous casting and current status of the mathematical model and future subject. Sanyo Tech. Rep. 2012, 19, 2–14. [Google Scholar]
- Stefanescu, D.M. Science and Engineering of Casting Solidification, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2015; pp. 1–5. [Google Scholar]
- Ji, C.; Luo, S.; Zhu, M.Y. Analysis and application of soft reduction amount for bloom continuous casting process. ISIJ Int. 2014, 54, 504–510. [Google Scholar] [CrossRef]
- Zhu, M.F.; Stefanescu, D.M. Virtual front tracking model for the quantitative modeling of dendritic growth in solidification of alloys. Acta Mater. 2007, 55, 1741–1755. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification—A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Beltran-Sanchez, L.; Stefanescu, D.M. A quantitative dendrite growth model and analysis of stability concepts. Metall. Mater. Trans. A 2004, 35, 2471–2485. [Google Scholar] [CrossRef]
- Shin, Y.H.; Hong, C.P. Modeling of dendritic growth with convection using a modified cellular automaton model with a diffuse interface. ISIJ Int. 2002, 42, 359–367. [Google Scholar] [CrossRef]
- Zhu, M.F.; Chen, J.; Sun, G.X.; Hong, C.P. Numerical modeling of dendritic growth. Acta Metall. Sin. 2005, 41, 583–587. [Google Scholar]
- Zhang, X.F.; Zhao, J.Z. Effect of forced flow on three dimensional dendritic growth of Al-Cu alloys. Acta Metall. Sin. 2012, 48, 615–620. [Google Scholar] [CrossRef]
- Yu, J.; Xu, Q.Y.; Cu, K.; Liu, B.C. Numerical simulation of microstructure evolution based on a modified CA method. Acta Metall. Sin. 2007, 43, 731–738. [Google Scholar]
- Zhan, X.H.; Wei, Y.H.; Dong, Z.B. Cellular automaton simulation of grain growth with different orientation angles during solidification process. J. Mater. Process. Technol. 2008, 208, 1–8. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W.D. A cellular automaton model for the solidification of a pure substance. Appl. Phys. A 2010, 103, 123–133. [Google Scholar] [CrossRef]
- Wei, L.; Lin, X.; Wang, M.; Huang, W.D. Cellular automaton simulation of the molten pool of laser solid forming process. Acta Phys. Sin. 2015, 64, 018103. [Google Scholar]
- Krane, M.J.M.; Johnson, D.R.; Raghavan, S. The development of a cellular automaton-finite volume model for dendritic growth. Appl. Math. Model. 2009, 33, 2234–2247. [Google Scholar] [CrossRef]
- Rappaz, M.; Gandin, C.A. Probabilistic modelling of microstructure formation in solidification processes. Acta Metall. Mater. 1993, 41, 345–360. [Google Scholar] [CrossRef]
- Gandin, C.A.; Rappaz, M. A 3D cellular automaton algorithm for the prediction of dendritic grain growth. Acta Mater. 1997, 45, 2187–2195. [Google Scholar] [CrossRef]
- Rappaz, M. Modeling and characterization of grain structures and defects in solidification. Curr. Opin. Solid State Mat. Sci. 2016, 20, 37–45. [Google Scholar] [CrossRef]
- Wang, W.; Lee, P.D.; Mclean, M. A model of solidification microstructures in nickel-based superalloys: Predicting primary dendrite spacing selection. Acta Mater. 2003, 51, 2971–2987. [Google Scholar] [CrossRef]
- Dong, H.B.; Lee, P.D. Simulation of the columnar-to-equiaxed transition in directionally solidified Al-Cu alloys. Acta Mater. 2005, 53, 659–668. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P.D.; Djambazov, G.; Pericleous, K. Numerical simulation of the effect of fluid flow on solute distribution and dendritic morphology. Int. J. Cast. Met. Res. 2009, 22, 204–207. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P.D. Dendritic solidification under natural and forced convection in binary alloys: 2D versus 3D simulation. Model. Simul. Mater. Sci. Eng. 2010, 18, 055008. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P.D. A new mechanism for freckle initiation based on microstructural level simulation. Acta Mater. 2012, 60, 4917–4926. [Google Scholar] [CrossRef]
- Nakagawa, M.; Natsume, Y.; Ohsasa, K. Dendrite growth model using front tracking technique with new growth algorithm. ISIJ Int. 2006, 46, 909–913. [Google Scholar] [CrossRef]
- Yamazaki, M.; Satoh, J.; Ohsasa, K.; Matsuura, K. Numerical model of solidification structure formation in Fe-C alloy with peritectic transformation. ISIJ Int. 2008, 48, 362–367. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, D.F.; Long, M.J.; Arif, T.T.; Qin, R.S. A three-dimensional cellular automata model for dendrite growth with various crystallographic orientations during solidification. Metall. Mater. Trans. B 2014, 45, 719–725. [Google Scholar] [CrossRef]
- Yin, H.; Felicelli, S.D. Dendrite growth simulation during solidification in the LENS process. Acta Mater. 2010, 58, 1455–1465. [Google Scholar] [CrossRef]
- Yin, H.; Felicelli, S.D.; Wang, L. Simulation of a dendritic microstructure with the lattice Boltzmann and cellular automaton methods. Acta Mater. 2011, 59, 3124–3136. [Google Scholar] [CrossRef]
- Yin, H.B.; Felicelli, S.D. A cellular automaton model for dendrite growth in magnesium alloy AZ91. Model. Simul. Mater. Sci. Eng. 2009, 17, 075011. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.Y.; Liu, B.C. A modified cellular automaton model for the quantitative prediction of equiaxed and columnar dendritic growth. J. Mater. Sci. Technol. 2014, 30, 1311–1320. [Google Scholar] [CrossRef]
- Chen, R.; Xu, Q.Y.; Liu, B.C. Cellular automaton simulation of three-dimensional dendrite growth in Al–7Si–Mg ternary aluminum alloys. Comput. Mater. Sci. 2015, 105, 90–100. [Google Scholar] [CrossRef]
- Han, R.H.; Dong, W.C.; Lu, S.P.; Li, D.Z.; Li, Y.Y. Modeling of morphological evolution of columnar dendritic grains in the molten pool of gas tungsten arc welding. Comput. Mater. Sci. 2014, 95, 351–361. [Google Scholar] [CrossRef]
- Han, R.H.; Lu, S.P.; Dong, W.C.; Li, D.Z.; Li, Y.Y. The morphological evolution of the axial structure and the curved columnar grain in the weld. J. Cryst. Growth 2015, 431, 49–59. [Google Scholar] [CrossRef]
- Luo, S.; Zhu, M.Y. A two-dimensional model for the quantitative simulation of the dendritic growth with cellular automaton method. Comput. Mater. Sci. 2013, 71, 10–18. [Google Scholar] [CrossRef]
- Tan, W.D.; Bailey, N.S.; Shin, Y.C. A novel integrated model combining cellular automata and phase field methods for microstructure evolution during solidification of multi-component and multi-phase alloys. Comput. Mater. Sci. 2011, 50, 2573–2585. [Google Scholar] [CrossRef]
- Tan, W.D.; Wen, S.Y.; Bailey, N.; Shin, Y.C. Multiscale modeling of transport phenomena and dendritic growth in laser cladding processes. Metall. Mater. Trans. B 2011, 42, 1306–1318. [Google Scholar] [CrossRef]
- Wang, W.L.; Luo, S.; Zhu, M.Y. Numerical simulation of dendritic growth of continuously cast high carbon steel. Metall. Mater. Trans. A 2015, 46, 396–406. [Google Scholar] [CrossRef]
- Wang, W.L.; Luo, S.; Zhu, M.Y. Dendritic growth of high carbon iron-based alloy under constrained melt flow. Comput. Mater. Sci. 2014, 95, 136–148. [Google Scholar] [CrossRef]
- Thévoz, P.; Desbiolles, J.L.; Rappaz, M. Modeling of equiaxed microstructure formation in casting. Metall. Trans. A 1989, 20, 311–322. [Google Scholar] [CrossRef]
- Lipton, J.; Glicksman, M.E.; Kurz, W. Dendritic growth into undercooled alloy metals. Mater. Sci. Eng. 1984, 65, 57–63. [Google Scholar] [CrossRef]
- Luo, S.; Wang, W.L.; Zhu, M.Y. Validation and simulation of cellular automaton model for dendritic growth during the solidification of Fe-C binary alloy with fluid flow. ISIJ Int. 2016, 56, 564–573. [Google Scholar] [CrossRef]
- Nastac, L. Analytical modeling of solute redistribution during the initial unsteady unidirectional solidification of binary dilute alloys. J. Cryst. Growth 1998, 193, 271–284. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Simulating dendritic solidification using an anisotropy-free meshless front-tracking method. J. Comput. Phys. 2014, 279, 63–66. [Google Scholar] [CrossRef]
- Wang, W.L.; Zhu, M.Y.; Cai, Z.Z.; Luo, S.; Ji, C. Micro-segregation behavior of solute elements in the mushy zone of continuous casting wide-thick slab. Steel Res. Int. 2012, 83, 1152–1162. [Google Scholar] [CrossRef]

| Physical Property | Symbol | Unit | Value |
|---|---|---|---|
| Melt temperature of pure iron | Tm | K | 1809.15 |
| Liquidus line slope of Fe–C alloy | ml | K·wt%−1 | −78.0 |
| Thermal conductivity | λ | W·m−1·K−1 | 33.0 |
| Density of solid phase | ρs | kg·m−3 | 7400 |
| Density of liquid phase | ρl | kg·m−3 | 7020 |
| Specific heat capacity of solid phase | cp,s | J·kg−1·K−1 | 648 |
| Specific heat capacity of liquid phase | cp,l | J·kg−1·K−1 | 824 |
| Specific heat capacity at mushy state | cp,m | J·kg−1·K−1 | 770 |
| Solidification latent heat | L | J·kg−1 | 27,200 |
| Diffusion coefficient in solid phase | Ds | cm2·s−1 | 0.0761exp(−16,185.2/T) |
| Diffusion coefficient in liquid phase | Dl | cm2·s−1 | 0.0767exp(−12,749.6/T) |
| Partition coefficient | k0 | -- | 0.34 |
| Anisotropy parameter | ε | -- | 0.04 |
| Gibbs–Thomson coefficient | Γ | K·m | 1.9 × 10−7 |
| Maximum nucleus density | nmax | m−1 | 16,736 |
| Standard deviation of nucleation undercooling | ΔTσ | K | 0.1 |
| Average nucleation undercooling | ΔTn | K | 1.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Luo, S.; Zhu, M. Development of a CA-FVM Model with Weakened Mesh Anisotropy and Application to Fe–C Alloy. Crystals 2016, 6, 147. https://doi.org/10.3390/cryst6110147
Wang W, Luo S, Zhu M. Development of a CA-FVM Model with Weakened Mesh Anisotropy and Application to Fe–C Alloy. Crystals. 2016; 6(11):147. https://doi.org/10.3390/cryst6110147
Chicago/Turabian StyleWang, Weiling, Sen Luo, and Miaoyong Zhu. 2016. "Development of a CA-FVM Model with Weakened Mesh Anisotropy and Application to Fe–C Alloy" Crystals 6, no. 11: 147. https://doi.org/10.3390/cryst6110147
APA StyleWang, W., Luo, S., & Zhu, M. (2016). Development of a CA-FVM Model with Weakened Mesh Anisotropy and Application to Fe–C Alloy. Crystals, 6(11), 147. https://doi.org/10.3390/cryst6110147





