Determination of the Projected Atomic Potential by Deconvolution of the Auto-Correlation Function of TEM Electron Nano-Diffraction Patterns
Abstract
:1. Introduction
2. Results and Discussion
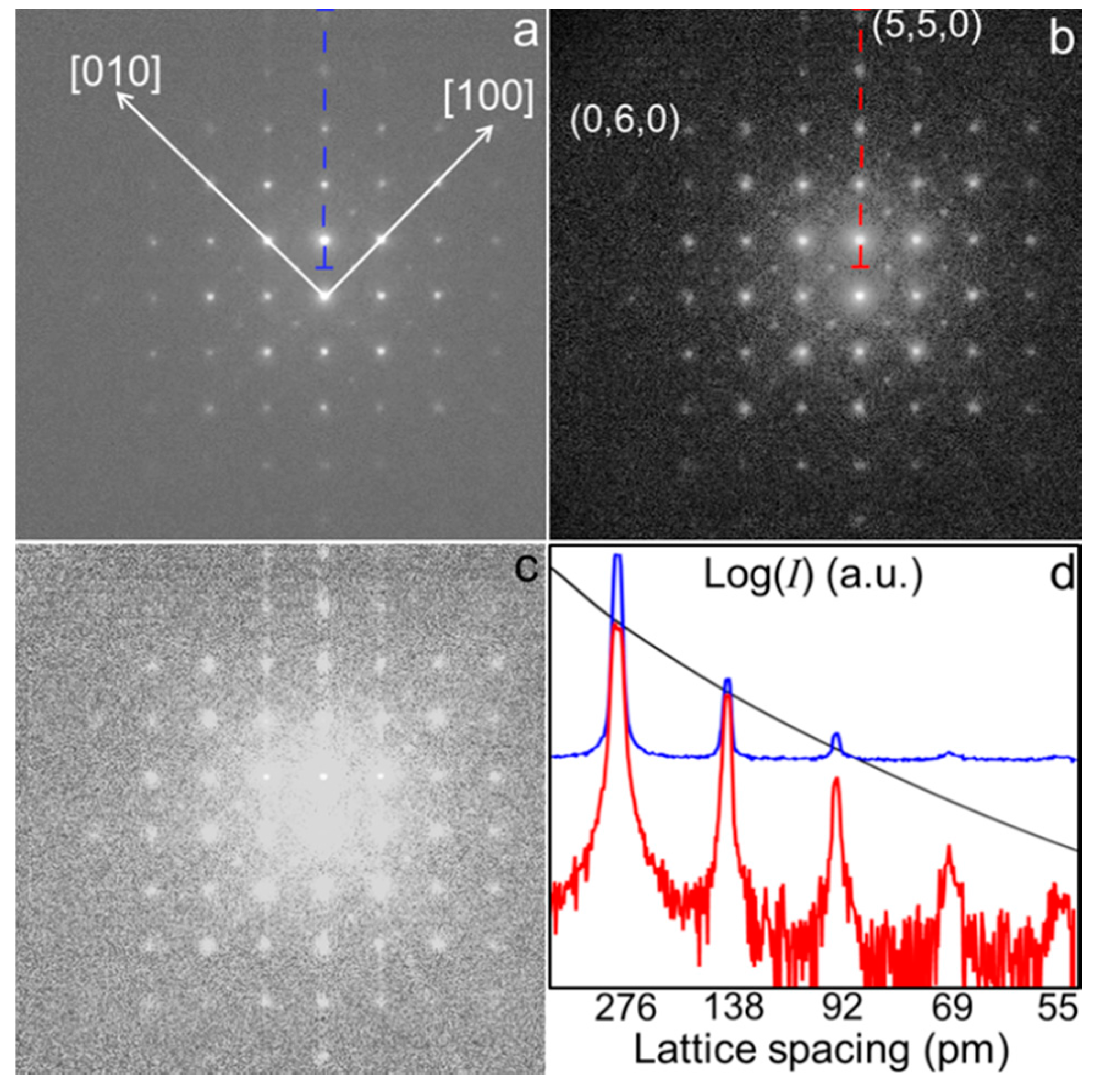
2.1. Electron Diffraction Experiments with Nano-Sized Coherent Illumination
2.2. Intensity Rescaling of the Nano-Diffraction Pattern
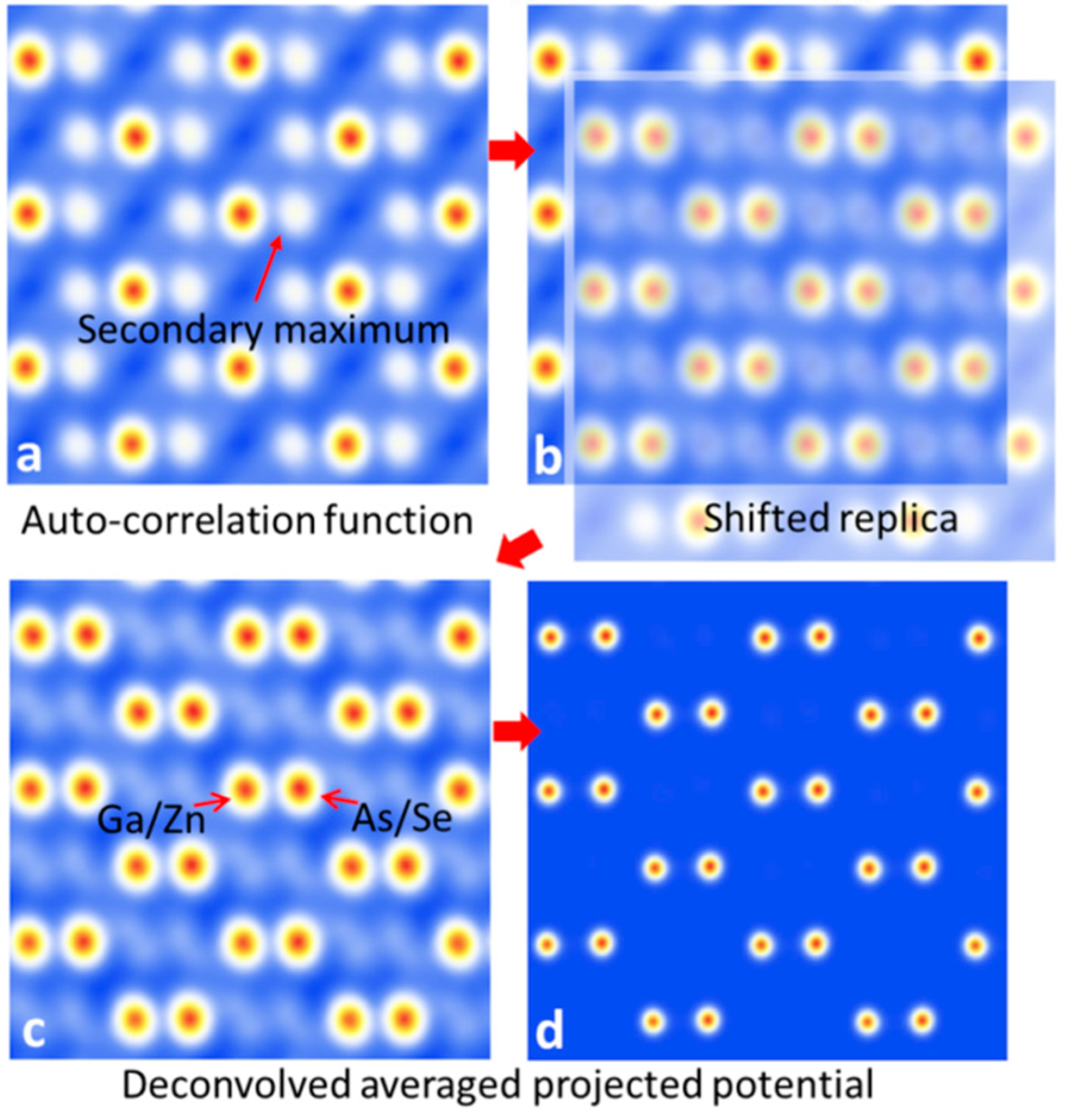
2.3. Auto-Correlation Function
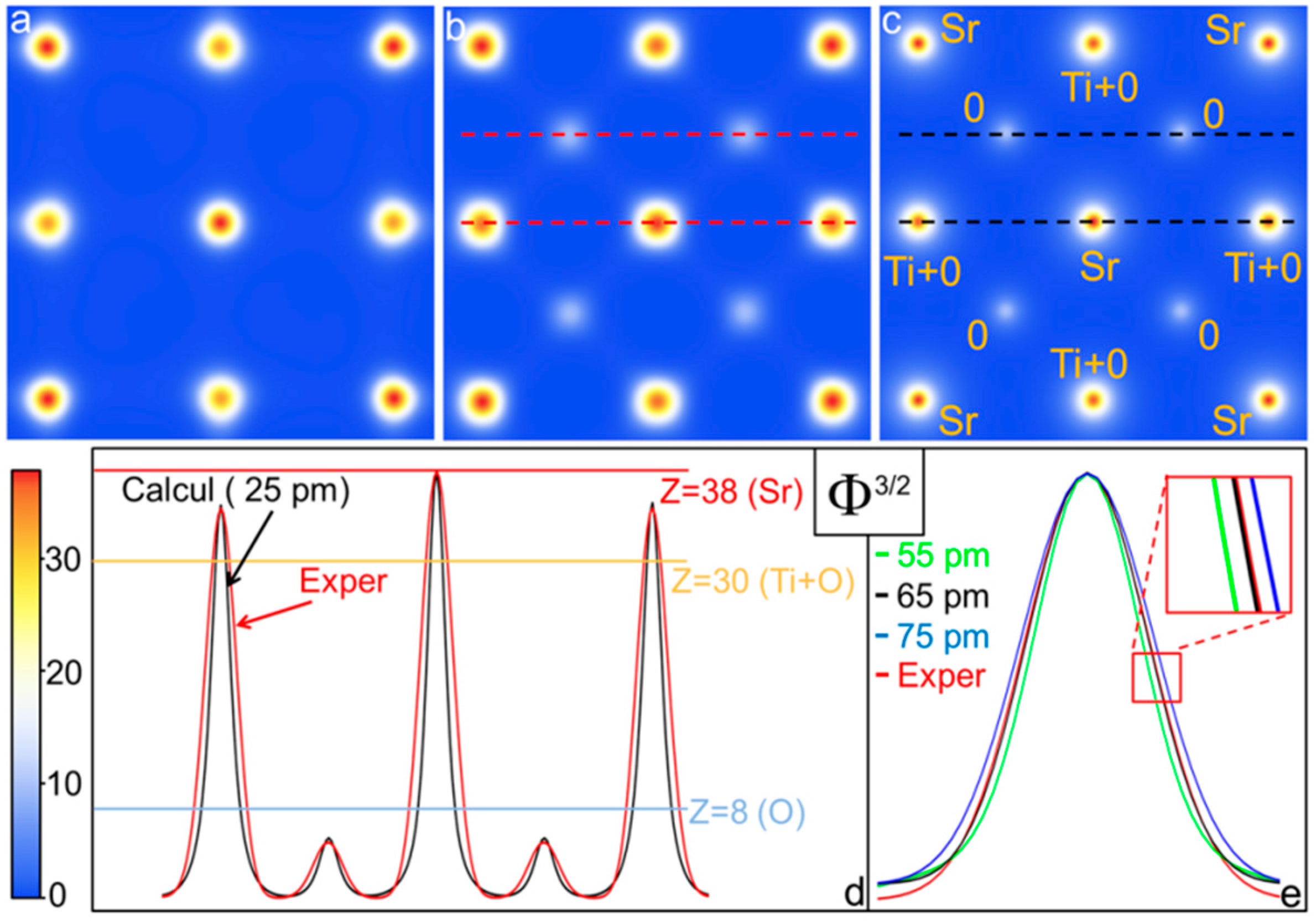
2.4. Deconvolution of C(R): Centrosymmetric Case
2.5. Deconvolution of C(R): Non-Centrosymmetric Case
3. Methods
Deconvolution of the Autocorrelation Function
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A: Theory
Appendix A1. Electron Wave Function for a Nano-Sized Illumination Beam
Appendix A2. Transverse Coherence Length
Appendix A3. Compensation of Non-Linear Phase Shifts
Appendix A4. Dynamical Effects on the Non-Centrosymmetry of the Diffraction Pattern
Appendix A5. Weak Phase Approximation
Appendix A6. Second-Order Dynamical Perturbation to the Weak Phase-Approximation
Appendix A7. General Equations
Appendix A8. Incoherent Source Approximation
Appendix A9. Further Insight for the Kinematical Approximation
References
- Reimer, L. Transmission Electron Microscopy: Physics of Image Formation and Microanalysis; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Cowley, J.M. Electron Nanodiffraction. Microsc. Res. Tech. 1999, 46, 75–97. [Google Scholar] [CrossRef]
- Haider, M.; Rose, H.; Uhlemann, S.; Kabius, B.; Urban, K. Towards 0.1 nm resolution with the first spherically corrected transmission electron microscope. J. Electron. Microsc. 1998, 47, 395–405. [Google Scholar]
- Hawkes, P.W. Aberration correction past and present. Phil. Trans. R. Soc. A 2009, 367, 3637–3664. [Google Scholar] [CrossRef] [PubMed]
- Zuo, J.M.; Vartanyants, I.; Gao, M.; Zhang, M.R.; Nagahara, L.A. Atomic resolution imaging of a carbon nanotube from diffraction intensities. Science 2003, 300, 1419–1421. [Google Scholar] [CrossRef] [PubMed]
- Huang, W.J.; Zuo, J.M.; Jiang, B.; Kwon, K.W.; Shim, M. Sub-ångström-resolution diffractive imaging of single nanocrystals. Nat. Phys. 2009, 5, 129–133. [Google Scholar] [CrossRef]
- De Caro, L.; Carlino, E.; Caputo, G.; Cozzoli, P.D.; Giannini, C. Electron diffractive imaging of oxygen atoms in nanocrystals at sub-ångström resolution. Nat. Nanotech. 2010, 5, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Zuo, J.M. Electron detection characteristics of a slow-scan CCD camera, imaging plates and film, and electron image restoration. Microscopy Res. Tech. 2000, 49, 245–268. [Google Scholar] [CrossRef]
- De Caro, L.; Carlino, E.; Siliqi, D.; Giannini, C. Coherent Diffractive Imaging: From Nanometric Down to Picometric Resolution. In Handbook of Coherent-Domain Optical Methods; Springer: Berlin, Germany, 2012. [Google Scholar]
- Sayre, D. Some implications of a theorem due to Shannon. Acta Cryst. 1952, 5, 843. [Google Scholar] [CrossRef]
- Miao, J.; Charalambous, P.; Kirz, J.; Sayre, D. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens. Nature 1999, 400, 342–344. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the presence of noise. Proc. Inst. Radio Eng. 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Nyquist, H. Certain Topics in Telegraph Transmission Theory. Trans. AIEE 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Zuo, J.M.; Zhang, J.; Huang, W.; Ran, K.; Jiang, B. Combining Real and Reciprocal Space Information for Aberration Free Coherent Electron Diffractive Imaging. Ultramicroscopy 2011, 111, 817–823. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.; Hovmoeller, S.; Oleynikov, P. Electron Crystallography: Electron Microscopy and Electron Diffraction, 2nd ed.; International Union of Crystallography, Oxford Science Publications-Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- De Caro, L.; Carlino, E.; Vittoria, A.F.; Siliqi, D.; Giannini, C. Keyhole electron diffractive imaging (KEDI). Acta Cryst. A 2012, 68, 687–702. [Google Scholar] [CrossRef] [PubMed]
- Doyle, P.A.; Turner, P.S. Relativistic Hartree-Fock X-ray and electron scattering factors. Acta Crys. A 1968, 24, 390–397. [Google Scholar] [CrossRef]
- Caliandro, R.; Carrozzini, B.; Cascarano, G.L.; De Caro, L.; Giacovazzo, C.; Siliqi, D. Advances in ab initio protein phasing by Patterson deconvolution techniques. J. Appl. Crys. 2007, 40, 883–890. [Google Scholar] [CrossRef]
- Liu, A.Y.; Lumpkin, G.R.; Petersen, T.C.; Etheridge, J.; Bourgeois, L. Interpretation of angular symmetries in electron nanodiffraction patterns from thin amorphous specimens. Acta Cryst. A 2015, 71, 473–482. [Google Scholar] [CrossRef] [PubMed]
- Radi, G. Complex lattice potentials in electron diffraction calculated for a number of crystals. Acta Cryst. A 1970, 26, 41–56. [Google Scholar] [CrossRef]
- Humphreys, C.J.; Hirsh, P.B. Absorption parameters in electron diffraction. Philos. Mag. 1968, 18, 115. [Google Scholar] [CrossRef]
- Wang, A.; Chen, F.R.; Van Aert, S.; Van Dyck, D. Direct structure inversion from exit waves: Part I: Theory and simulations. Ultramicroscopy 2010, 110, 527–534. [Google Scholar] [CrossRef]
- Vainshtein, B.K. Structure Analysis by Electron Diffraction; Pergamon Press Ltd.: London, UK, 1964; p. 208. [Google Scholar]
- J E M S-S A A S. Version 4.3931U2016. Available online: http://www.jems-saas.ch/ (accessed on 16 September 2016).
- Kirkland, E.J. Advanced Computing in Electron Microscopy; Plenum Press: New York, NY, USA, 1998. [Google Scholar]
- Colli, A.; Carlino, E.; Pelucchi, E.; Grillo, V.; Franciosi, A. Local interface composition and native stacking fault density in ZnSe /GaAs(001) heterostructures. J. Appl. Phys. 2004, 96, 2592–2602. [Google Scholar] [CrossRef]
- De Caro, L.; Altamura, D.; Vittoria, F.A.; Carbone, G.; Qiao, F.; Manna, L.; Giannini, C. A superbright X-ray laboratory micro-source empowered by a novel restoration algorithm. J. Appl. Cryst. 2012, 45, 1228–1235. [Google Scholar] [CrossRef]
- Peng, L.M. Quasi-dynamical electron diffraction-a kinematic type of expression for the dynamical diffracted-beam amplitudes. Acta Cryst. A 2000, 56, 511–518. [Google Scholar] [CrossRef]
- Abbey, B.; Nugent, K.A.; Williams, G.J.; Clark, J.N.; Peele, A.G.; Pfeifer, M.A.; de Jonge, M.; McNulty, I. Keyhole coherent diffractive imaging. Nat. Phys. 2008, 4, 394–398. [Google Scholar] [CrossRef]
- Rodenburg, J.M.; Faulkner, H.M.L. A phase retrieval algorithm for shifting illumination. Appl. Phys. Lett. 2004, 85, 4795–4797. [Google Scholar] [CrossRef]
- Rodenburg, J.M.; Hurst, A.C.; Cullis, A.G.; Dobson, B.R.; Pfeiffer, F.; Bunk, O.; David, C.; Jefimovs, K.; Johnson, I. Hard-X-Ray Lensless Imaging of Extended Objects. Phys. Rev. Lett. 2007, 98, 034801. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics, VI edition; Pergamon Press plc: Oxford, UK, 1991; p. 510. [Google Scholar]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Caro, L.; Scattarella, F.; Carlino, E. Determination of the Projected Atomic Potential by Deconvolution of the Auto-Correlation Function of TEM Electron Nano-Diffraction Patterns. Crystals 2016, 6, 141. https://doi.org/10.3390/cryst6110141
De Caro L, Scattarella F, Carlino E. Determination of the Projected Atomic Potential by Deconvolution of the Auto-Correlation Function of TEM Electron Nano-Diffraction Patterns. Crystals. 2016; 6(11):141. https://doi.org/10.3390/cryst6110141
Chicago/Turabian StyleDe Caro, Liberato, Francesco Scattarella, and Elvio Carlino. 2016. "Determination of the Projected Atomic Potential by Deconvolution of the Auto-Correlation Function of TEM Electron Nano-Diffraction Patterns" Crystals 6, no. 11: 141. https://doi.org/10.3390/cryst6110141
APA StyleDe Caro, L., Scattarella, F., & Carlino, E. (2016). Determination of the Projected Atomic Potential by Deconvolution of the Auto-Correlation Function of TEM Electron Nano-Diffraction Patterns. Crystals, 6(11), 141. https://doi.org/10.3390/cryst6110141





