Next Article in Journal
Synthesis and Reactivity of Novel Boranes Derived from Bulky Salicylaldimines: The Molecular Structure of a Maltolato Compound
Previous Article in Journal
Band Structure of Photonic Crystals Fabricated by Two-Photon Polymerization
Previous Article in Special Issue
High-Yield Synthesis of Helical Carbon Nanofibers Using Iron Oxide Fine Powder as a Catalyst
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 5
Issue 1
10.3390/cryst5010074
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Dispersability of Carbon Nanotubes in Biopolymer-Based Fluids

by
Franco Tardani
and
Camillo La Mesa
*
Department of Chemistry, La Sapienza University, Cannizzaro Building, P.le A. Moro 5, I-00185 Rome, Italy
*
Author to whom correspondence should be addressed.
Crystals 2015, 5(1), 74-90; https://doi.org/10.3390/cryst5010074
Submission received: 30 September 2014 / Accepted: 19 December 2014 / Published: 16 January 2015
(This article belongs to the Special Issue Carbon Nanostructures)
Browse Figures
Versions Notes

Abstract

:
In this review the dispersability of carbon nanotubes in aqueous solutions containing proteins, or nucleic acids, is discussed. Data reported previously are complemented by unpublished ones. In the mentioned nanotube-based systems several different phases are observed, depending on the type and concentration of biopolymer, as well as the amount of dispersed nanotubes. The phase behavior depends on how much biopolymers are adsorbing, and, naturally, on the molecular details of the adsorbents. Proper modulation of nanotube/biopolymer interactions helps switching between repulsive and attractive regimes. Dispersion or phase separation take place, respectively, and the formation of liquid crystalline phases or gels may prevail with respect to dispersions. We report on systems containing ss-DNA- and lysozyme-stabilized nanotubes, representative of different organization modes. In the former case, ss-DNA rolls around CNTs and ensures complete coverage. Conversely, proteins randomly and non-cooperatively adsorb onto nanotubes. The two functionalization mechanisms are significantly different. A fine-tuning of temperature, added polymer, pH, and/or ionic strength conditions induces the formation of a given supra-molecular organization mode. The biopolymer physico-chemical properties are relevant to induce the formation of different phases made of carbon nanotubes.

Graphical Abstract

1. Introduction

The combination of their outstanding mechanical, optical, thermal, and electrical conductive properties [1,2] makes nanoparticles useful in the preparation of advanced composites. This holds, in particular, for carbon nanotubes, CNTs [3]. The peculiar features of such materials allow them to be used to build devices, sensors [4], actuators, drug delivery systems [5], and scaffolds for tissue engineering [6,7]. Despite the many possibilities reported to date, the poor dispersability of CNTs in aqueous media drastically limits the preparation of bio-compatible materials. This is because the presence of π–π orbitals on their outer surface gives rise to an extended aromatic character [8], and does not allow energetically favored interactions with water. Therefore, stabilization methods are required. Some require the chemical modification of nanotubes, via oxidation and covalent functionalization [9]. That procedure largely increases CNTs’ solubility, at the expense of significant modifications in size. It also decreases the inherent physical performances.
Functionalization favors the formation of specific groups on CNTs and offers the possibility to anchor binding sites on their surface. Such new sites are potentially reactive towards many chemicals. This holds, provided the binding energy associated to the mentioned sites is high and the binding of a given reactant is selective. Sometimes, site selectivity in binding on functionalized CNTs fulfills key-lock mechanisms, and is particularly relevant in bio-oriented applications [10].
If the original properties of CNTs must be retained, non-covalent functionalization procedures had better suit. These involve the adsorption of surfactants [11], polymers [12], and combinations thereof. Polymers must have the due conformation for effective stabilization. What is more, they maintain, or improve, the peculiarities of nanotube-based composites. For effective bio-intended applications, adsorbing polymers must be fully compatible with the tissues in which the composites find location. Currently used synthetic polymers do not fulfill the above requirements. This is why biopolymers are progressively used. Accordingly, proteins [13], polypeptides [14], polysaccharides [15,16], and nucleic acids [17] are considered. The interactions between CNTs and amino acids or nucleotides functionalize their surface, through anchorage of a given functional group [18]. The latter composites, obviously, do not enter into the category of biopolymer-based stabilization. Despite their recognized utility as sensors [19], such technically-oriented items are outside the scope of this study.
The “philosophical” foundations underlying the deep interest towards organic/inorganic hybrid systems, including the present ones, are manifold. An appealing aspect is the possibility to get composites with a hybrid soft/hard character [20]. Generally, the core is hard and serves as an anchoring site for biopolymers. Biological macromolecules effectively adsorb and fruitfully interact with inorganic matrices, forming locally ordered domains. The wonderful structures observed in sea urchins and shellfish, for instance, are examples of systems bearing at the same time inorganic and biological moieties which self-help and self-complement.
A detailed knowledge of the processes occurring at the interfaces between inorganic materials, or CNTs, and biological macromolecules is, thus, of fundamental and practical relevance. Understanding the details governing the interactions between nanoparticles and biopolymers is required to design materials for drug delivery, implants, and devices. Surface functionalization of orthopedic implants is an example [21]. However, the interactions effectively taking place at biological/inorganic interfaces are not fully understood. The more reliable forecasts on nanoparticle/biopolymer composites rely on previous studies and on an efficient modeling of the given surface at the nanometer scale level [22].
The effectiveness of CNT surfaces in adsorbing chemicals and biopolymers cannot be forecast a priori. This occurs when unrealistic models of their surface state are accounted for. CNTs and inorganic surfaces, in fact, are different in composition and structure from the corresponding bulk materials, and are characterized by peculiar topographies at the nanometer scale level [23]. Therefore, the presence of kinks, defects, disclinations, heterogeneity at a local level, and the presence of specific binding sites play a substantial role in adsorption [24]. It must be kept in mind that the acidity and hydrophobicity of inorganic surfaces play a substantial role in the interaction with biopolymers. What is more, the local topology induced by manufacturing nanoparticles, such as chemical functionalization [25], thermal cycling [26], or milling [27], are more relevant in favoring adsorption than chemical composition.
The characterization of nanoparticles is analyzed by approaches that do not have much to do with real systems. For instance, models based on biopolymer binding onto uniformly smooth cylindrical surfaces of CNTs are commonly used, but their predicting power is poor. If the effective surface properties are not properly considered, the analysis of the interactions taking place between CNTs and bio-macromolecules may give questionable results [28]. This is because adsorption preferentially takes place onto surface defects, kinks, or at the particles’ edges [29].
Interpretative problems may occur when the intrinsic properties of biopolymers are not accounted for. As it is known, bio-macromolecules are endowed with complex and deformable architectures, with many functional groups available to binding. Only certain conformations permit globular proteins an extensive and homogeneous adsorption onto nanoparticles [30]. Sometimes, the biopolymers are properly modified for interactions with CNTs to be significant, to ensure effective stabilization. For instance, DNA is transformed in its single-strand form, ss-DNA, to get significant interaction modes with CNTs [31]. Its location onto the given surfaces, therefore, is the sum of several different contributions to the binding energy. Optimizing the performances leading to an effective biopolymer-based CNT stabilization requires determining the optimal working conditions, well-focused experimental analysis, realistic theoretical models, and data elaboration.
The formation of stable CNT/biopolymer adducts is described below. We present and discuss results relative to the adsorption of selected proteins and/or DNA onto CNTs and report on aspects not fully elucidated in previous work. In the forthcoming sections, we report on:
Some physico-chemical properties of dispersed CNTs;
The technicalities required for an efficient surface coverage; and
The structure and the organization modes met in the mentioned systems.
Well-founded previous knowledge and a cogent analysis of experimental approaches to the field may give rise to new perspectives, allowing us to clarify the properties of these systems on solid grounds [32]. In what follows, we report on different aspects and available information on CNT-biopolymer systems. Hopefully, our efforts may shed light on points still under debate and forecast which research lines are substantial and deserve more experimental/theoretical investigation. The following parts mention CNT properties and focus on selected aspects of the phase behavior met when they interact with biopolymers. Data reported by us or other researchers, indicated in the following, are complemented by unpublished work.

2. Physico-Chemical Properties of CNT Dispersions

Since Iijima [33] discovered carbon nanotubes, efforts were devoted to optimizing the synthetic procedures giving such materials. Focus is essentially on their physical properties, such as structural, electronic conductivity, elasticity, thermal/mechanical stability, dispersability, etc. [34,35]. Nowadays, it is possible to get CNTs in many forms and degrees of purity, depending on the synthetic conditions. We shall not consider the ubiquitous presence of iron, or metallic residues deriving from the catalysts used in the preparation. In fact, metallic clusters are almost always embedded into CNTs [36,37], and operate as junctions between different carbon-based sub-units. Very presumably, these are the places where oxidation preferentially occurs.
Currently available nanotubes are single-, SWCNTs, or multi-walled, MWCNTs. The mentioned categories have different reactivity, solubility, electrical and/or thermal conductivity, and elasticity. MWCNTs have relatively large diameters, D. Distinguishing them from carbon-based fibers can be cumbersome when D values are high. SWCNTs, conversely, are long, thin, and characterized by high aspect ratios, L/D. There L is the average nanotube length, and the meaning of D is as above. Given the large dispersity in both quantities, Figure 1B and Figure 2, estimates of aspect ratios are subject to large uncertainties, and must be considered with due caution. In any case, the ability to distinguish between the two classes is substantial.
It is hardly possible to detect reliable (L/D) ratios from dynamic light scattering, DLS, since data elaboration in terms of non-spherical objects is cumbersome. Fits based on a rigid cylindrical symmetry of the scattering entities require evaluating two different diffusive components [38]. The DLS correlation decay, in fact, is related to both the rotational (dr) and the translational (dt) diffusion coefficients. It is possible to determine the average length and diameter of particles if L and D are measured independently. In polarized mode, the scattered intensity is dominated by translational diffusion and the light intensity decay is approximated by an exp{−[(q2dt)t]α} term. There q is the scattering vector, t is the measuring time, and α is a stretching exponent, accounting for size dispersity. The rotational diffusion coefficient, dr, conversely, is obtained by depolarized DLS.
Crystals 05 00074 g001 1024
Figure 1. (A) Schematic picture of SWCNTs; (B) major axis length, L, and diameter, D, from which axial ratios are determined. In (C) is reported a scheme indicating the case when kinks are present.
Figure 1. (A) Schematic picture of SWCNTs; (B) major axis length, L, and diameter, D, from which axial ratios are determined. In (C) is reported a scheme indicating the case when kinks are present.
Crystals 05 00074 g001
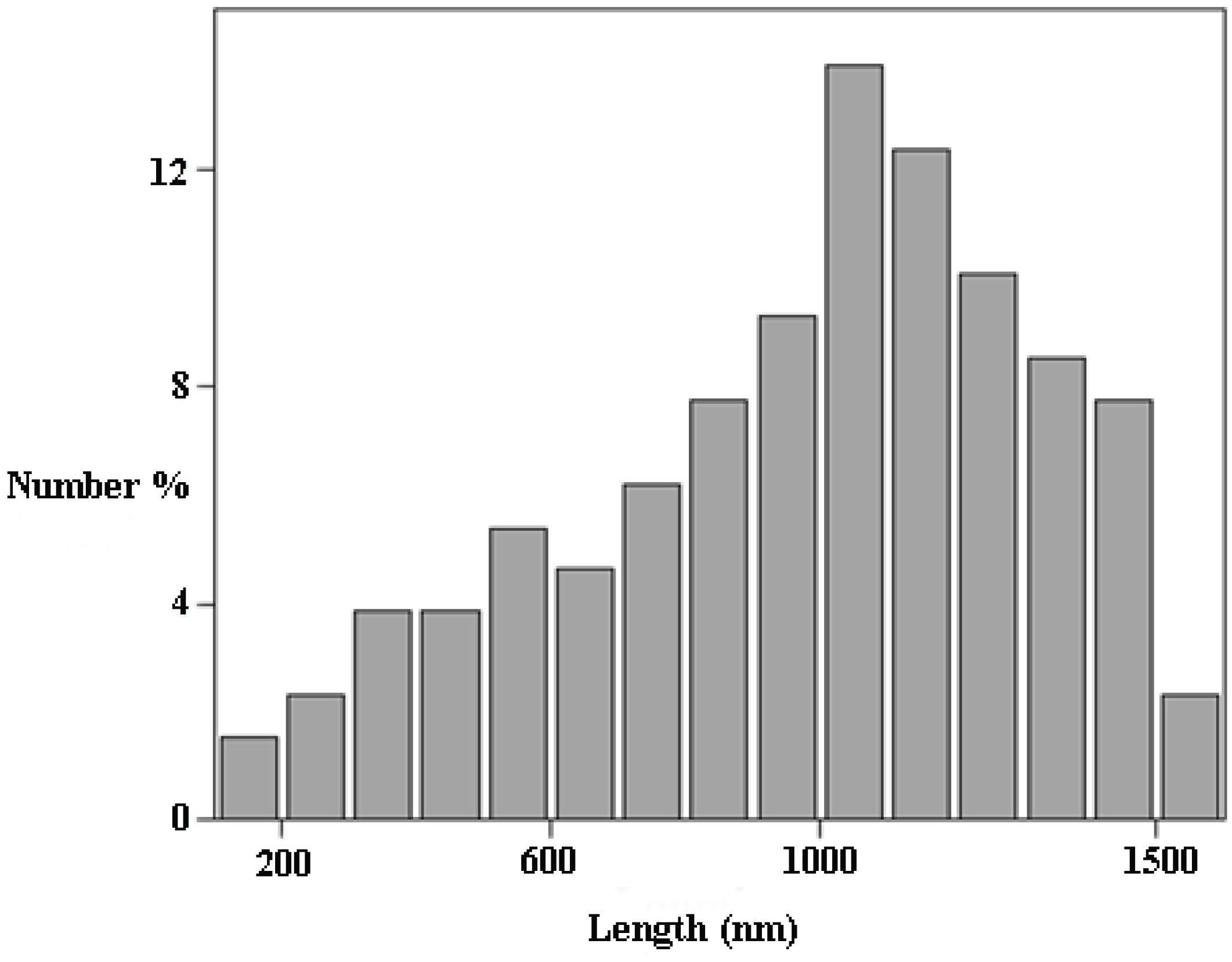
Crystals 05 00074 g002 1024
Figure 2. SWCNT size distribution function based on TEM for a SDS/stabilized dispersion (0.1 wt% in 1.00 wt% SDS). Mesh size is 100 nm; lengths > 1600 nm are not reported. The RMS length is 1235 nm and the standard deviation 570: the nominal one is 1000 nm. The distribution is based on ~500 counts.
Figure 2. SWCNT size distribution function based on TEM for a SDS/stabilized dispersion (0.1 wt% in 1.00 wt% SDS). Mesh size is 100 nm; lengths > 1600 nm are not reported. The RMS length is 1235 nm and the standard deviation 570: the nominal one is 1000 nm. The distribution is based on ~500 counts.
Crystals 05 00074 g002
In single-walled CNTs, D << L; therefore, depolarized light intensity contributions are small, and the related statistics poor. Because of such drawbacks, DLS bi-exponential fits are not applicable, unless extra constraints are imposed. A rationale approach to the problem implies determining dr and dt separately by independent methods, such as DLS and transmission electron microscopy, TEM [39]. When the average diameter of CNTs is determined by TEM, it is possible to deduce L from polarized light scattering, and estimates of (L/D) ratios are at hand. An evaluation of such values allows us to forecast some properties of CNTs. In particular:
(a)
Surface area per unit volume;
(b)
Different solubility in a given medium;
(c)
Possible bundling or clustering, and;
(d)
Elasticity, which is in direct proportion to L/D.
Knowledge of aspect ratios allows us to predict the possibility of CNTs forming dispersions, gels, or nematic fluids. In Onsager’s theory for the phase separation of anisometric entities, the isotropic-nematic phase boundary shifts downward in proportion to L/D values [40]. The above hypothesis, originally proposed for polymers [41,42], holds since CNTs are straight, rigid rods. Their conformation is a random distribution of rigid sub-units, held together by covalent forces (Figure 1C). Each unit terminates in a kink, which is a junction between the mentioned sub-units. Therefore, the effective CNT aspect ratios are different from what is expected, and decrease in proportion to the number of kinks. Consequences of the above behavior are observed when the experimental phase boundaries are compared to predicted ones.
The phase sequence for dispersions of rigid rods fulfills the scheme:
Homogeneous dispersion * → two-phase → nematic fluid
(N.B. * the relation holds when density gradients with respect to the solvent are immaterial.)
The phase boundaries are predicted by the semi-empirical relations [43]:
X i , 2 φ = [ 0.3588 1 − 0.3648 + 0.0091 h ]
X 2 φ , n = [ 0.3588 0.3648 + 0.0091 h − ( 0.3648 + 0.0091 h ) ]
where Xi,2φ is the dispersion/two-phase boundary, in number of moles, and X2φ,n the two-phase/nematic one. The h term in Equations (1) and (2) is a twisting parameter, related to the preferred orientation of one rod with respect to another [44]. Usually, a shift to higher concentrations is found by comparing values predicted from Equations (1) and (2) with experimental ones. This is because kinks in CNTs considerably reduce the fully extended length in favor of D. Thus, effective aspect ratios are lower than expected and the phase boundaries shift to higher values.
Another relevant effect in building the phase diagrams of CNT-based systems is depletion [45,46]. It always occurs in colloid systems, when non-covalent surface stabilization is effective. The rationale is that the partition of the stabilizer between bulk and surface phases is controlled by its affinity for such media. In equilibrium conditions, the chemical potential of a surface-adsorbed species is equal to that in the bulk. Even though the adsorbent is preferentially located on the particles’ surfaces, some is still present in the bulk. The latter gives rise to an unbalanced osmotic effect, when its volume fraction in such a medium reaches a critical value [47]. Polymers and/or micelles are responsible for unbalanced osmotic effects, which become relevant at concentrations close to the critical threshold. To our knowledge, no experimental studies have reported on depletion in CNT/polymer mixtures. However, evidence arising from surfactant/SWCNT systems gave convincing evidence in favor of depletion [47]. Threshold shifts to lower concentrations are in inverse proportion to the particle hydrodynamic volume, and sensitive to ionic strength. For these reasons, dispersability of CNTs in surfactant systems is moderate and limited. It is useless adding surfactant in excess with respect to the quantity required for stabilization. Similar conclusions apply for nanotubes dispersed in solutions of polymers. Vincent reported convincing evidence on the depletion of silica particles covalently covered by PEO-like polymers in presence of the same in the bulk [48]. In the case of proteins, depletion depends on biopolymer content, pH, and ionic strength [49].

3. Dispersions of CNTS in Protein Solutions

3.1. Generalities

Proteins used as CNT dispersants are lysozyme, LYSO, and bovine serum albumin, BSA. It is possible to use other proteins [50] and/or synthetic polypeptides [51]. Under normal conditions, LYSO and BSA are globular in shape. Their compact structure does not allow fruitful interactions with CNTs, unless they are denatured or properly functionalized [52]. Interactions take place because of hydrophobic interactions [53]. Protein conformation depends on its secondary structure. As a rule, all β-sheet proteins are less prone to denaturation than α or α/β ones. This is due to the large number of contacts in α-helical proteins, allowing helices to remain intact even after the tertiary structure is lost and helical segments start to unfold. In globular proteins, adsorption reduces the amount of α-helix in favor of the β-sheet conformation [54]. The former is regained when dissolution of the complexes takes place. The tertiary structure of proteins in complexes with CNTs is, very presumably, lost and never recovered. Such evidence suggests the occurrence of a molten globule conformation for biopolymers [49]. The protein conformational state is responsible for adsorption studies. For instance, they refer to pH-driven lysozyme binding in dilute dispersions of oxidized SWCNTs [52]. It is difficult, in such cases, to separate pH-induced conformational changes from the ionization of carboxylate groups.

3.2. Dispersions in Protein-Based Gels

The combination of the dispersing and gelling ability of globular proteins with the properties inherent to carbon nanotubes is relevant for future applications. Thus, understanding the optimal working conditions is fundamental in designing gel composites with tunable properties. The possibility to disperse CNTs therein is substantial because of the presumed biocompatibility of such materials.
Proteins may form gels at low pH, in semi-dilute regimes, and at mild temperature conditions. Gelation implies complex pathways, whose main steps are: (i) partial exposure of their hydrophobic residues; (ii) clustering in seeds; (iii) and coalescence. Finally, a three-dimensional network is achieved. Its formation requires that the protein volume fraction is higher than a critical threshold, ΦC,P, and the temperature higher than the thermal gelation threshold, Tg [55]. The latter is controlled by protein volume fraction, pH, and, to a much lower extent, ionic strength. In lysozymes, for instance, gel strength depends on pH and optimal conditions are in the range 2.0–3.0. Too much acidity favors the formation of a glassy solid, useless for practical purposes [56].
For protein-based gels embed CNTs, the properties of such composites depend on the nanotube/protein weight ratios. Usually, nanotubes are dispersed in protein solutions in conditions suitable for gelation. In particular, the maximum concentration of SWCNT effectively dispersed in protein-based gels is <1.0 wt% [56]. The dispersions equilibrate for a sufficient lapse of time, some minutes, until gelation. Added CNTs modify the gelation pathways and their kinetics, and shift Tg upward or downward. This fact helps when forming hydrogels with over 90 wt% water, and significantly improves the performances of the final composites. The behavior of composite gels is different from that pertinent to the former ones, as inferred by optical microscopy, SEM, rheology, and DLS.
To shed light on the processes, the gelation temperature and the kinetic of the processes were determined. When T ≥ Tg, the gelation kinetics scales with the amount of nanotubes, Figure 3. Tiny amounts of carbon nanotubes do not disturb the gel properties, and Tg does not change upon their addition. When φV,CNT > 0.3 wt%, gels become continuous in both protein and nanotubes, and percolating networks do form. As mentioned above, support for the above statements comes from rheology [56].
Crystals 05 00074 g003 1024
Figure 3. Zero shear viscosity vs. measuring time, s, for a 6.30 wt% LYSO dispersion at pH 2.5, (white symbols), and to the same dispersion with 0.03 wt% SWCNTs. Data are taken at Tg. Gelation times are the salient points of the curves.
Figure 3. Zero shear viscosity vs. measuring time, s, for a 6.30 wt% LYSO dispersion at pH 2.5, (white symbols), and to the same dispersion with 0.03 wt% SWCNTs. Data are taken at Tg. Gelation times are the salient points of the curves.
Crystals 05 00074 g003

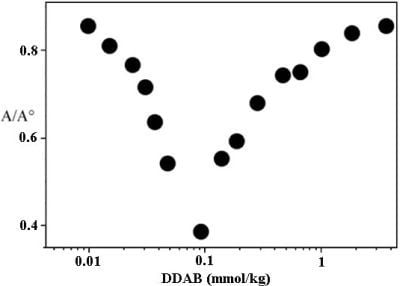
3.3. Dispersions of CNTs in DNA and RNA

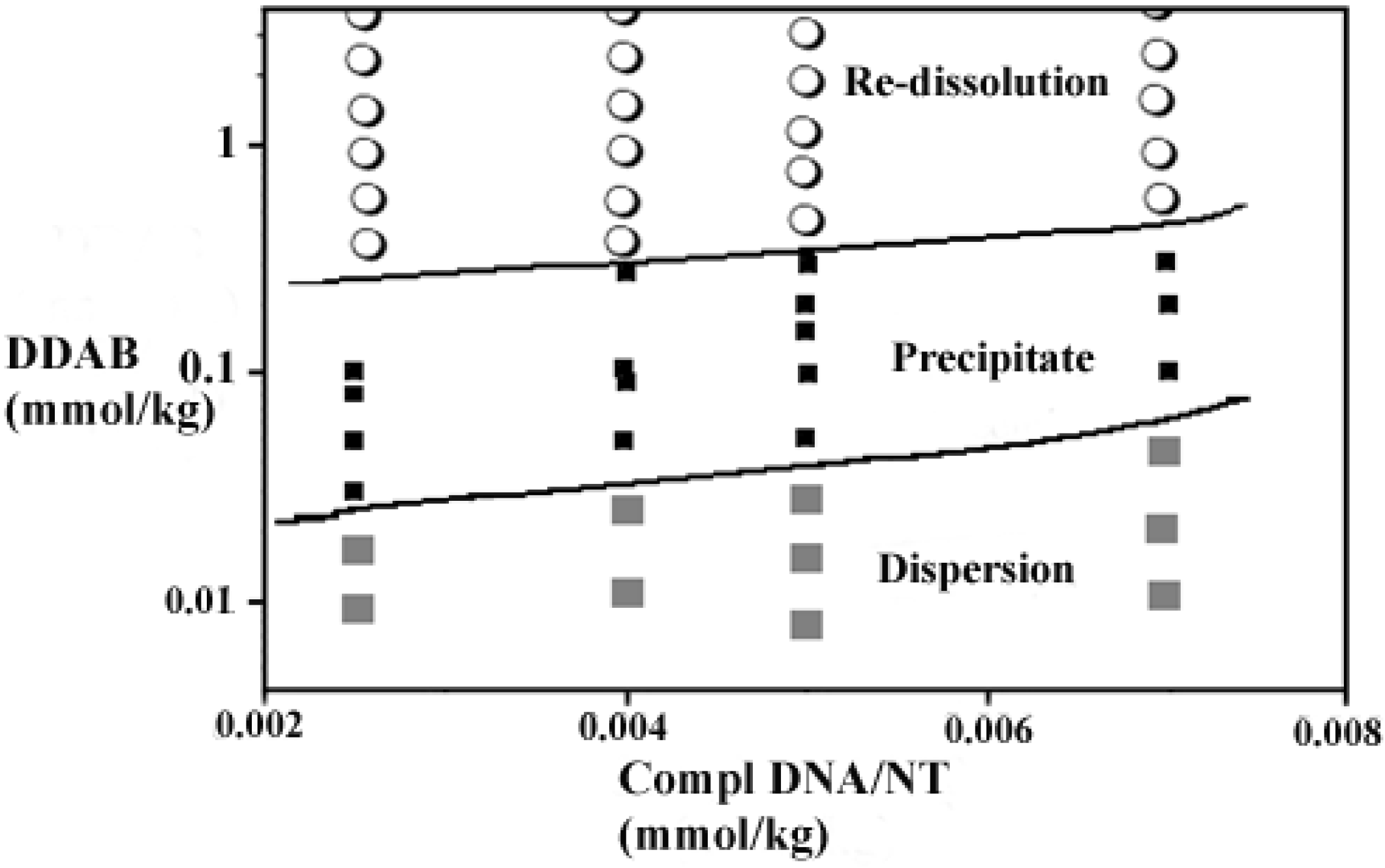
3.3.1. Phase Behavior

Double-stranded DNA shares structural features in common with ss-DNA/SWCNT ones. In particular, its cross section, DH, is close to the diameter of covered single-walled nanotubes. ds-DNA mixes with CNTs in all proportions. The final mixtures form mixed nematic fluids when the volume fraction reaches a critical threshold, φcr (= φcr,DNA + φcr,CNT, and φcr,DNA > φcr,CNT) [57]. In such cases, CNTs are embedded in a polar matrix and do not disturb significantly the state of the mixtures. It was observed that the rheological properties, G’ and G”, increase with the volume fraction of the dispersed phase. Presumably, CNTs disturb the shear flow when their amount in the mixtures is high.
The case is different when DNA is in its single strand form, ss-DNA. In cases like this, the single filaments are much more prone to interact significantly with CNTs [31]. ss-DNA filaments have both polar and non-polar moieties, and are more plastic and deformable than ds-DNA. They roll around CNTs, with PO4− groups, uniformly covering them; that is why the solubility of complexes is significant. It is orders of magnitude higher than that pertinent to bare nanotubes and can be as high as 6.0 wt% [58].
The resulting ss-DNA/CNT complexes are extremely stable, and it is inconceivable to get back the components by dilution. This is because the number of links between CNTs and the a-polar residues of DNA base pairs can be thousand units high (the Gibbs energy contribution is some kJ·mol−1 per link). In addition to the easy preparation procedures, this implies a significant advantage for preparing stable adducts. Presumably, messenger RNA behaves accordingly, although no evidence exists on this regard. It is presumed that ss-DNA/CNT and, eventually, RNA/CNT complexes will find applications in biomedicine.
Concerning their reactivity, it was observed that such complexes undergo charge neutralization when mixed with oppositely charged surfactants (Figure 4) [59]. Titration experiments were performed with single- and double-chained species. Both have a multi-task ability, neutralize the charges on ss-DNA/CNT complexes, and favor re-dissolution of the precipitates. Bound surfactants are also nucleation centers for aggregation. Very presumably, micelles or vesicles do form thereon, depending on the concentration and number of alkyl chains in the surfactant. Turbidity experiments (Figure 4) support the above hypotheses. There are no significant differences with the behavior observed in surfactant/polyelectrolyte mixtures [60]; indeed, a low number of conformational degrees of freedom is allowed. The phase diagrams of such mixtures resemble those observed in systems made of polyelectrolytes and oppositely charged surfactants (Figure 5).
Crystals 05 00074 g004 1024
Figure 4. Absorbance, at 660 nm, of 0.01 wt% ss-DNA/SWCNT dispersions of 1/1 complex vs. DDAB concentration, at 25 °C. The minimum is the charge neutralization.
Figure 4. Absorbance, at 660 nm, of 0.01 wt% ss-DNA/SWCNT dispersions of 1/1 complex vs. DDAB concentration, at 25 °C. The minimum is the charge neutralization.
Crystals 05 00074 g004
Crystals 05 00074 g005 1024
Figure 5. Plot of DDAB vs. 1/1 ss-DNA/CNT concentration, at 25.0 °C. Precipitation occurs between the two lines.
Figure 5. Plot of DDAB vs. 1/1 ss-DNA/CNT concentration, at 25.0 °C. Precipitation occurs between the two lines.
Crystals 05 00074 g005

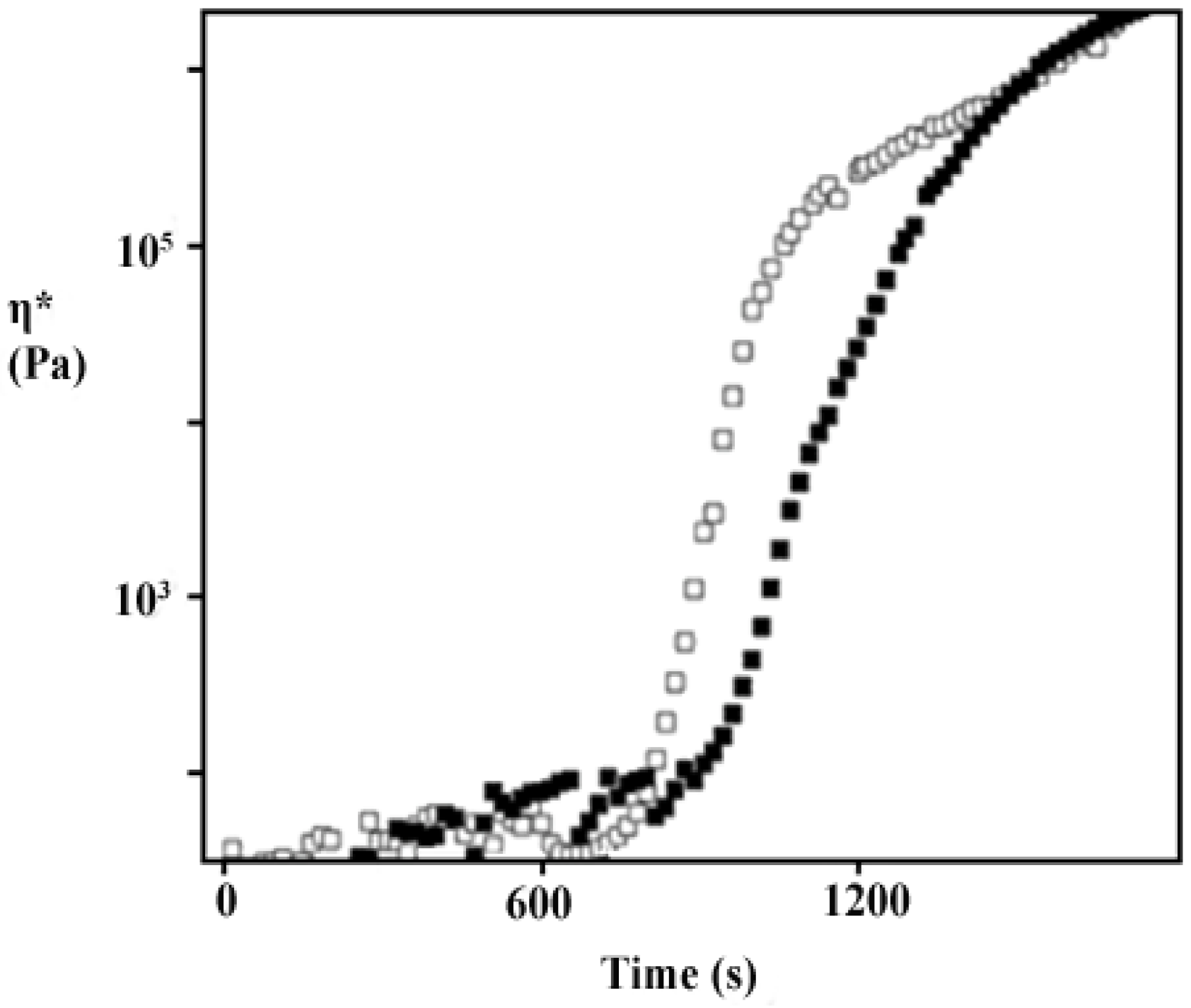
3.3.2. Formation of Nematic Liquid Crystalline Phases

ds-DNA forms phases characterized by nematic liquid crystalline order [61]. The relatively rigid rods of that biopolymer align parallel to each other in a hexagonally ordered assembly. The same holds for the filamentous form of ss-DNA rolling around CNTs. The transitions taking place in ss-DNA/CNT complexes depend on ionic strength, addition of polymer, and/or a combination thereof. The two-phase area between the dispersion and the liquid crystalline region is usually wide. Definition of the phase boundaries is hardly attained, unless a solid polyelectrolyte bearing a negative charge is added to ss-DNA/CNT dispersions [58]. Addition results in the onset of a “segregative” phase separation mechanism [62]. As a result, one of the fluid layers is rich in the polyelectrolyte and almost completely depleted of the complex; the reverse holds in the other. This fact gives the opportunity to concentrate the dispersion containing ss-DNA/CNT complexes. Therefore, the formation of a pure nematic phase is at hand.
It is possible to observe the phase boundaries and the two-phase area by rheological methods (Figure 6) [63,64,65]. The former are clearly defined by the intersection of different zero shear viscosity, η, regimes. For each of them, a different power-law behavior occurs [63,64]. In the two-phase region, the increase in viscosity is less steep than in the homogeneous dispersion. The onset of nematic order, with occurrence of hexagonal domains, is concomitant with a decrease in η compared to the two-phase one. In other words, rigid and charged rods are less likely to disturb the reciprocal motions when ordered; this is a consequence of fewer available possibilities for entanglement. Flow occurs among parallel planes containing equally spaced complexes. At high volume fractions, the viscosity increases again.
Crystals 05 00074 g006 1024
Figure 6. Normalized zero shear viscosity, ηrel, vs. the volume fraction of the complex, Φcompl, in percent units. Data refer to 1/1 mixtures of ss-DNA/CNT complexes, at 25.0 °C. Vertical lines indicate the phase boundaries.
Figure 6. Normalized zero shear viscosity, ηrel, vs. the volume fraction of the complex, Φcompl, in percent units. Data refer to 1/1 mixtures of ss-DNA/CNT complexes, at 25.0 °C. Vertical lines indicate the phase boundaries.
Crystals 05 00074 g006
The pure nematic phase is orientationally ordered, as inferred by polarizing microscopy, 2H NMR, and SAXS (data not reported) [66]. The fan-like textures observed by microscopy are a powerful tool to infer the reciprocal orientation of anisotropic domains. As a rule, applied shear modifies the optical textures (Figure 7). The NMR spectral shapes indicate macroscopic order. SAXS indicates the effective arrangement of the complexes in the sample, and the distance between rods.
Crystals 05 00074 g007 1024
Figure 7. Optical polarizing microscopy of a nematic phase obtained by concentrating 2.05 wt% ss-DNA/CNT complexes, at 25.0 °C, upon adding 1.54 wt% dextran sulfate and separating the two phases. Bar size is 200 μm.
Figure 7. Optical polarizing microscopy of a nematic phase obtained by concentrating 2.05 wt% ss-DNA/CNT complexes, at 25.0 °C, upon adding 1.54 wt% dextran sulfate and separating the two phases. Bar size is 200 μm.
Crystals 05 00074 g007
When observed by polarizing microscopy, the phase orients in pseudo-homeotropic textures, with axis directors normal with respect to the shear plane. Ordering may give rise to homogeneous domains some 100 μm large. This fact gives the opportunity to get domains in which carbon nanotubes face along the same direction.
At the same time, the homogeneous polar covers of ss-DNA avoid the CNT collapse into bundles. These facts give the opportunity to get a preferred orientation to electronic conductivity. No such studies reported on the above items, which are potentially useful in the preparation of anisotropic materials having directional character.
In these materials, directional order is retained for long times. Evidence was inferred by dispersing droplets of the nematic ss-DNA/CNT phase in solutions containing oppositely charged species, i.e., a cationic surfactant or a protein [65,66,67]. Diffusion gradients set up at the interface between the droplet and the solution; as a result, a peel forms on the interface and confinement of nematic droplets is attained. The confined domains remain as such for an indefinitely long time. This gives the chance to prepare nano-, meso-, and macroscopic ordered entities, and a good opportunity for preparing anisotropic advanced materials with controlled sizes, layered, and possible multifunctional entities. The possibility of effectively creating hybrid materials with diverse morphologies and functionalities is a key strategy for future research. The strong similarity between such possibilities and those observed in naturally occurring composites also deserves due attention from scientists involved in the field.

4. Conclusions

In the present review, we focused on the possibilities offered by mixing carbon nanotubes and biopolymers. There are substantial possibilities for CNTs’ functionalization by proteins and/or nucleic acids. Non-covalent functionalization is reversible or not, depending on the substances involved in the processes. The resulting mixtures give homogeneous dispersions [68], gels, and/or liquid crystalline materials [69,70,71,72,73]. The physical forces operating in such media compel the systems towards one possible state with respect to another. This is the result of a delicate balance between attractive/repulsive forces active among the composites formed by CNTs and biopolymers. Uniform CNT coverage ensures the onset of dispersions and, eventually, liquid crystalline order. Formation of gels occurs in stabilized CNT dispersions, in the presence of proteins; their surface covering ability is moderate with respect to, say, ss-DNA.
A detailed explanation of the forces acting in such systems is beyond current knowledge [74,75], but preliminary information is at hand. Binding efficiency is a prerequisite for uniform coverage and formation of long-range order. This condition holds in ss-DNA/CNT complexes, which behave as long, rigid rods and undergo isotropic-nematic phase transitions. Conversely, mild and heterogeneous coverage ensures dispersion. These preliminary results offer the opportunity for more substantial studies, and allow us to pinpoint the molecular/functional details responsible for one organization mode with respect to others.

Acknowledgments

Thanks are due to la Sapienza for partly financing the present research line, through a university project.

Appendix

A.1. Materials

The materials preparation procedures are given throughout the manuscript. More detailed information is given in the original papers, to which the reader is referred. See, in particular [13,31,47,56,58,59,65,66].

A.2. Methods

Optical Microscopy. A Ceti Laborlux unit, working in white and/or polarized light, checked the state of the dispersions. The samples were located on accurately cleaned glass slides; Teflon spacers located between slides and cover-slides controlled the sample thickness. Epoxy resins sealed the individual samples. Shear was applied parallel to the major axis of the slides. Measurements were run at 25 °C.
Dynamic Light Scattering, DLS. Measurements were run by a Malvern Zeta Nanosizer (Malvern, Malvern, UK), working at 632.8 nm in back scattering mode (at 173°), at 25 °C. A digital correlator analyzed the scattered light intensity fluctuations, I(q, t). Intensity distributions are obtained by analyzing the autocorrelation functions through CONTIN [22,23]. Cumulants provide information on the particle(s)’s self-diffusion, D, on their average hydrodynamic radii, and on the poly-dispersity index, PdI.
ζ-Potential. Measurements were run by a Laser-Doppler facility available in the DLS unit. The apparatus operates with cells equipped with gold-coated electrodes, at 25 °C. ζ-potential is obtained from electrophoretic mobility values [24]. Smoluckowski’s approximation holds, since the electrical double layer thickness around particles, δ, is much lower than the hydrodynamic radius [25].
Atomic Force Microscopy, AFM. It was run with a Dimension Icon (Bruker AXS, Karlsruhe, Germany) unit. Images were acquired in air, at room temperature, and ambient conditions, in tapping mode. We used a high-resolution RTESP (Rotated Tapping Etched Silicon) probe, VEECO Probes USA. (Veeco Instruments Inc., Plainview, NY, USA). A sharp tip with radius of curvature R < 8 nm is connected to a rectangular cantilever. The latter, 125 μm long, has a nominal resonant frequency of 300 KHz and a spring constant of 40 N·m−1. Samples are deposited on freshly cleaved mica, incubated for 10 min, rinsed with Milli-Q water, flushed with nitrogen, and analyzed after 30 min. Images are analyzed by Gwiddion facilities (Gwiddion, Department of Nanometrology, Czech Metrology Institute, Brno, Czech Republic) and reported as such, except in flattening mode.
Optical Absorbance. Measurements were run with a Jenway 6400 spectrophotometer (Keyson Intern. Ltd., Chelmsford, Essex, UK). The samples were centrifuged for 1 h at 2600 g. Centrifugation induces the precipitation of complexes and bundles and promotes the aggregation of poorly stabilized entities. The supernatant was collected and examined. Absorbance was measured at 660 nm, to avoid interference due to DNA. Each run is in triplicate, on three different samples. Values were normalized for the absorbance of the formerly centrifuged mother dispersion. The ratio A/A° is proportional to the number of stabilized complexes r in the medium.
Ionic Conductivity. A Wayne Kerr unit, model 6425, equipped with a small-volume conductivity cell, measured the electrical conductance, κ. The cell is thermostated at 25.000 ± 0.002 °C. Stirring during the titration avoids the onset of concentration gradients. A weight burette added known aliquots of surfactant.
For more details, see the references mentioned above.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Feynmn, R. There’s plenty of room at the bottom. Caltech Eng. Sci. 1960, 23, 22–36. [Google Scholar]
  2. French, R.H.; Parsegian, V.A.; Podgornik, R.; Rajter, R.F.; Jagota, A.; Luo, J.; Asthagiri, D.; Chandury, M.K.; Chiang, Y.-M.; Granick, S.; et al. Long range interactions in nanoscale science. Rev. Mod. Phys. 2010, 82, 1887–1944. [Google Scholar] [CrossRef]
  3. Saito, R.; Dresselhaus, G.; Dresselhaus, M.S. Physical Properties of Carbon Nanotubes; Imperial College Press: London, UK, 1998. [Google Scholar]
  4. Baugham, R.H.; Zakhidov, A.A.; de Heer, W.A. Carbon nanotubes: The route towards applications. Science 2002, 297, 787–792. [Google Scholar] [CrossRef] [PubMed]
  5. Zhou, O.; Shimoda, H.; Gao, B.; Oh, S.; Fleming, L.; Yue, G.Z. Materials science of carbon nanotubes: Fabrication, integration, and properties of macroscopic structures of carbon nanotubes. Acc. Chem. Res. 2002, 35, 1045–1053. [Google Scholar] [CrossRef] [PubMed]
  6. Byrne, M.T.; Gun’ko, Y.K. Recent advances in research on carbon nanotube-polymer composites. Adv. Mater. 2010, 22, 1672–1688. [Google Scholar] [CrossRef] [PubMed]
  7. Ivanov, E.; Nesheva, D.; Krusteva, E.; Dobreva, T.; Kotsilkova, R. Rheological and electrical properties of epoxy nanocomposites filled with multiwalled carbon nanotubes. Nanosci. Nanotechnol. 2009, 9, 40–43. [Google Scholar]
  8. Talyzin, A.V.; Anoshkin, I.V.; Krasheninnikov, A.V.; Nieminen, R.M.; Nasibulin, A.G.; Jiang, H.; Kauppinen, E.I. Synthesis of Graphene Nanoribbons Encapsulated in Single-Walled Carbon Nanotubes. Nano Lett. 2011, 11, 4352–4356. [Google Scholar] [CrossRef] [PubMed]
  9. Sun, J.P.; Fu, K.; Lin, Y.; Huang, W. Functionalized carbon nanotubes: Properties and applications. Acc. Chem. Res. 2002, 35, 1096–1104. [Google Scholar] [CrossRef] [PubMed]
  10. Colombo, M.; Mazzucchelli, S.; Montenegro, J.M.; Galbiati, E.; Corsi, F.; Parak, W.J.; Prosperi, D. Protein Oriented Ligation on Nanoparticles Exploiting O6-Alkylguanine-DNA Transferase (SNAP) Genetically Encoded Fusion. Small 2012, 8, 1492–1497. [Google Scholar] [CrossRef] [PubMed]
  11. Moore, V.C.; Strano, M.S.; Haroz, E.H.; Hauge, R.H.; Smalley, R.E.; Schmidt, J.; Talmon, Y. Individually suspended single-walled carbon nanotubes in various surfactants. Nano Lett. 2003, 3, 1379–1382. [Google Scholar] [CrossRef]
  12. O’Connell, M.J.; Boul, P.; Ericson, L.M.; Huffman, C.; Wang, Y.; Haroz, E.; Kuper, C.; Tour, J.; Ausman, K.D.; Smalley, R.E. Reversible water-solubilization of single-walled carbon nanotubes by polymer wrapping. Chem. Phys. Lett. 2001, 342, 265–271. [Google Scholar] [CrossRef]
  13. Bomboi, F.; Bonincontro, A.; la Mesa, C.; Tardani, F. Interactions between single-walled carbon nanotubes and lysozyme. J. Colloid Interface Sci. 2011, 355, 342–347. [Google Scholar] [CrossRef] [PubMed]
  14. Dieckmann, G.R.; Dalton, A.B.; Johnson, P.A.; Razal, J.; Chen, J.; Giordano, G.M.; Munoz, E.; Musselman, J.H.; Baugham, R.H.; Draper, R.K. Controlled assembly of carbon nanotubes by designed amphiphilic peptide helices. J. Am. Chem. Soc. 2003, 125, 1770–1777. [Google Scholar] [CrossRef] [PubMed]
  15. Huang, W.; Yang, X.; Zhao, S.; Zhang, M.; Hu, X.; Wang, J.; Zhao, H. Fast and selective recognizes polysaccharide by surface molecularly imprinted film coated onto aldehyde-modified magnetic nanoparticles. Analyst 2013, 138, 6653–6661. [Google Scholar] [CrossRef] [PubMed]
  16. Devi, K.S.P.; Sahoo, B.; Behera, B.; Maiti, T.K. Nanoparticle and polysaccharide conjugate: A potential candidate vaccine to improve immunological stimuli. Intern. J. Biol. Macromol. 2015, 72, 1254–1264. [Google Scholar] [CrossRef]
  17. Cathcart, H.; Quinn, S.; Nicolosi, V.; Kelly, J.M.; Blau, W.J.; Coleman, J.N. Spontaneous debuldling of single-walled carbon nanotubes in DNA-based dispersions. J. Phys. Chem. C 2007, 111, 66–74. [Google Scholar] [CrossRef]
  18. Boxus, T.; Touillaux, R.; Dive, G.; Marchand-Brynaert, J. Synthesis and evaluation of RGD peptidomimetics aimed at surface bioderivatization of polymer substrates. Bioorg. Med. Chem. 1998, 6, 1577–1595. [Google Scholar] [CrossRef] [PubMed]
  19. Rivas, G.A.; Rubianes, M.D.; Pedano, M.L.; Ferreyra, N.F.; Luque, G.; Miscoria, S.A. Carbon Nanotubes: A New Alternative for Electrochemical Sensors; Nunez, M., Ed.; Nova Science Publishers, Inc.: Hauppauge, NY, USA, 2006; pp. 1–46. [Google Scholar]
  20. Shin, S.; Yoon, S.; Kim, Y.; Lee, C. Effect of particle parameters on the deposition characteristics of a hard/soft-particles composite in kinetic spraying. Surface Coat. Technol. 2006, 201, 3457–3461. [Google Scholar] [CrossRef]
  21. Samuel, R.E.; Shukla, A.; Paik, D.H.; Wang, M.X.; Fang, J.C.; Schmidt, D.J.; Hammond, P.T. Osteoconductive protamine-based polyelectrolyte multilayer functionalized surfaces. Biomaterials 2011, 32, 7491–7502. [Google Scholar] [CrossRef] [PubMed]
  22. Roach, P.; Farrar, D.; Perry, C.C. Surface Tailoring for Controlled Protein Adsorption: Effect of Topography at the Nanometer Scale and Chemistry. J. Am. Chem. Soc. 2006, 128, 3939–3945. [Google Scholar] [CrossRef] [PubMed]
  23. Ojamaee, L.; Aulin, C.; Pedersen, H.; Kaell, P.-O. IR and quantum-chemical studies of carboxylic acid and glycine adsorption on rutile TiO2 nanoparticles. J. Colloid Interface Sci. 2006, 296, 71–78. [Google Scholar] [CrossRef] [PubMed]
  24. Verboekend, D.; Milina, M.; Perez-Ramirez, J. Hierarchical Silicoaluminophosphates by Postsynthetic Modification: Influence of Topology, Composition, and Silicon Distribution. Chem. Mater. 2014, 26, 4552–4562. [Google Scholar] [CrossRef]
  25. Liu, J.; Cui, L.; Wang, L.; Ni, X.; Zhang, S.; Jin, Y. Alkaline-acid treated mordenite and beta zeolites featuring mesoporous dimensional uniformity. Mater. Lett. 2014, 132, 78–81. [Google Scholar] [CrossRef]
  26. Creti, A.; Epifani, M.; Taurino, A.; Catalano, M.; Casino, F.; Lomascolo, M.; Milanese, M.; de Risi, A. Optical absorption measurements at high temperature (500 °C) of oxide nanoparticles for application as gas-based nanofluid in solar thermal collector systems. Adv. Mater. Res. 2013, 773, 80–86. [Google Scholar] [CrossRef]
  27. Di Crescenzo, A.; Demurtas, D.; Renzetti, A.; Siani, G.; de Maria, P.; Meneghetti, M.; Prato, M.; Fontana, A. Disaggregation of single-walled carbon nanotubes (SWNTs) promoted by the ionic liquid-based surfactant 1-hexadecyl-3-vinyl-imidazolium bromide in aqueous solution. Soft Matter 2009, 5, 62–66. [Google Scholar] [CrossRef]
  28. Van Blaaderen, A. Materials science: Colloids get complex. Nature 2006, 439, 545–546. [Google Scholar] [CrossRef] [PubMed]
  29. Xu, S.-F.; Yuan, G.; Li, C.; Liu, W.-H.; Mimura, H. Modulation of the Work Function of Capped Single-Walled Carbon Nanotube by Alkali-Metal Adsorption: A Theoretical Study. J. Phys. Chem. C 2011, 115, 8928–8933. [Google Scholar] [CrossRef]
  30. Lystvet, S.M.; Volden, S.; Halskau, O.; Glomm, W.R. Immobilization onto gold nanoparticles alters alpha-lactalbumin interaction with pure and mixed phospholipid monolayers. Soft Matter 2011, 7, 11501–11509. [Google Scholar] [CrossRef]
  31. Badaire, S.; Zakri, C.; Maugey, M.; Derré, A.; Barisci, J.N.; Wallace, G.; Poulin, P. Liquid crystals of DNA-stabilized carbon nanotubes. Adv. Mater. 2005, 17, 1673–1676. [Google Scholar] [CrossRef]
  32. Karachevtsev, M.V.; Gladchenko, G.O.; Plokhotnichenko, A.M.; Leontiev, V.S.; Karachevtsev, V.A. Adsorption of Biopolymers on SWCNT: Ordered Poly(rC) and Disordered Poly(rI). J. Phys. Chem. B 2013, 117, 2636–2644. [Google Scholar] [CrossRef] [PubMed]
  33. Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
  34. Battigelli, A.; Menard-Moyon, C.; Bianco, A. Carbon nanomaterials as new tools for immunotherapeutic applications. J. Mater. Chem. B Mater. Biol. Med. 2014, 2, 6144–6156. [Google Scholar] [CrossRef]
  35. Lee, H.S. Classification of Mass-Produced Carbon Nanotubes and Their Physico-Chemical Properties. In Syntheses and Applications of Carbon Nanotubes and Their Composites; Suzuki, S., Ed.; InTech: Rijeka, Croatia, 2013; pp. 39–53. [Google Scholar]
  36. Weidenkaff, A.; Ebbinghaus, S.G.; Mauron, Ph.; Reller, A.; Zhang, Y.; Zuttel, A. Metal nanoparticles for the production of carbon nanotube composite materials by decomposition of different carbon sources. Mater. Sci. Eng. C 2002, 19, 119–123. [Google Scholar] [CrossRef]
  37. Charlier, J.C. Defects in carbon nanotubes. Acc. Chem. Res. 2002, 35, 1063–1069. [Google Scholar] [CrossRef] [PubMed]
  38. Berne, B.J.; Pecora, R. Dynamic Light Scattering: With Applications to Chemistry, Biology and Physics; Courier Dover Publications: New York, NY, USA, 2013. [Google Scholar]
  39. Tardani, F.; la Mesa, C. Elasticity of dispersions based on carbon nanotubes dissolved in a lyotropic nematic solvent. J. Phys. Chem. C 2011, 115, 9424–9431. [Google Scholar] [CrossRef]
  40. Onsager, L. The effects of shapes on the interaction of colloidal particles. Ann. N.Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
  41. Matsuyama, A. Theory of binary mixtures of a rodlike polymer and a liquid crystal. J. Chem. Phys. 2010, 132, 214902:1–214902:10. [Google Scholar]
  42. Binder, K.; Mognetti, B.; Paul, W.; Virnau, P.; Yelash, L. Computer simulations and coarse-grained molecular models predicting the equation of state of polymer solutions. Adv. Polym. Sci. 2011, 238, 329–387. [Google Scholar]
  43. Van den Pol, E.; Thies-Weesie, D.M.E.; Petukhov, A.V.; Vroege, G.J.; Kvashnina, K. Influence of polydispersity on the phase behavior of colloidal goethite. J. Chem. Phys. 2008, 129, 164715:1–164715:8. [Google Scholar] [CrossRef]
  44. Stroobants, A.; Lekkerkerker, H.N.W.; Odiik, T. Effect of electrostatic interaction on the liquid crystal phase transition in solutions of rodlike polyelectrolytes. Macromolecules 1986, 19, 2232–2238. [Google Scholar] [CrossRef]
  45. Feigin, R.I.; Napper, D.H. Depletion stabilization and depletion flocculation. J. Colloid Interface Sci. 1980, 75, 525–541. [Google Scholar] [CrossRef]
  46. De Gennes, P.G. Polymer solutions near an interface. Adsorption and depletion layers. Macromolecules 1981, 14, 1637–1644. [Google Scholar] [CrossRef]
  47. Tardani, F.; la Mesa, C. Attempts to control depletion in the surfactant-assisted stabilization of single-walled carbon nanotubes. Colloids Surf. A 2014, 443, 123–128. [Google Scholar] [CrossRef]
  48. Li-In-On, F.K.R.; Vincent, B.; Waite, F.A. Stability of sterically stabilized dispersions at high polymer concentrations. ACS Symp. Ser. 1975, 9, 165–172. [Google Scholar]
  49. Brash, J.L.; Horbett, T.A. Proteins at Interfaces: An Overview. ACS Symp. Ser. 1995, 602, 1–23. [Google Scholar]
  50. Karchemsky, F.; Drug, E.; Mashiach-Farkash, E.; Fadeev, L.; Wolfson, H.J.; Gozin, M.; Regev, O. Diameter-selective dispersion of carbon nanotubes by beta-lactoglobulin whey protein. Colloids Surf. B 2013, 112, 16–22. [Google Scholar] [CrossRef]
  51. Hirano, A.; Tanaka, T.; Kataura, H.; Kameda, T. Arginine Side Chains as a Dispersant for Individual Single-Wall Carbon Nanotubes. Chem. Eur. J. 2014, 20, 4922–4930. [Google Scholar] [CrossRef] [PubMed]
  52. Bomboi, F.; Tardani, F.; Gazzoli, D.; Bonincontro, A.; La Mesa, C. Lysozyme binds onto functionalized carbon nanotubes. Colloids Surf. B 2013, 108, 16–22. [Google Scholar] [CrossRef]
  53. Moridi, Z.; Mottaghitalab, V. Recent Advances of Carbon Nanotube/Biopolymers Nanocomposites: A Technical Review. In Modern Trends in Chemistry and Chemical Engineering; Apple Academic Press: Waretown, NJ, USA, 2011; pp. 104–119. [Google Scholar]
  54. Van der Sman, R.G.M. Thermodynamics of meat proteins. Food Hydrocoll. 2012, 27, 529–535. [Google Scholar] [CrossRef]
  55. Chodankar, S.; Aswal, V.K.; Kohlbrecher, J.; Vavrin, R.; Wagh, A.G. Small-angle neutron scattering study of structure and kinetics of temperature-induced protein gelation. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef]
  56. Tardani, F.; la Mesa, C. Effects of single-walled carbon nanotubes on lysozyme gelation. Colloids Surf. B 2014, 121, 165–170. [Google Scholar] [CrossRef]
  57. Tardani, F.; Strobbia, P.; Scipioni, A.; la Mesa, C. Encapsulating carbon nanotubes in aqueous ds-DNA anisotropic phases: Shear orientation and rheological properties. RSC Adv. 2013, 3, 25917–25923. [Google Scholar] [CrossRef]
  58. Tardani, F.; la Mesa, C.; Poulin, P.; Maugey, M. Phase Behavior of DNA-Based Dispersions containing Carbon Nanotubes: Effects of Added Polymers and Ionic Strength on Excluded Volume. J. Phys. Chem. C 2012, 116, 9888–9894. [Google Scholar] [CrossRef]
  59. Tardani, F.; Sennato, S. Phase behavior of DNA-stabilized carbon nanotubes dispersions: Association with oppositely-charged additives. J. Phys. Chem. C 2014, 118, 9268–9274. [Google Scholar] [CrossRef]
  60. Goddard, E.D. Polymer-Surfactant Interactions; Part II. Polymers and Surfactants of Opposite Charge. In Interactions of Surfactants with Polymers and Proteins; Goddard, E.D., Ananthapadmanabhan, K.P., Eds.; CRC Press: Boca Raton, FL, USA, 1993; Chapter IV; pp. 171–201. [Google Scholar]
  61. Rill, R.L.; Strzelecka, T.E.; Davidson, M.W.; van Winkle, D.H. Ordered phases in concentrated DNA solutions. Phys. A Stat. Mech. Appl. 1991, 176, 87–116. [Google Scholar] [CrossRef]
  62. Bergfeldt, K.; Piculell, L. Segregation and Association in Mixed Polymer Solutions from Flory-Huggins Model Calculations. J. Phys. Chem. 1996, 100, 3680–3687. [Google Scholar] [CrossRef]
  63. Marrucci, G. Rheology of liquid crystalline polymers. Pure Appl. Chem. 1985, 57, 1545–1552. [Google Scholar] [CrossRef]
  64. Marrucci, G. Rheology of Nematic Polymers. In Liquid Crystallinity in Polymers; Ciferri, A., Ed.; Wiley-VCH: New York, NY, USA, 1991; pp. 395–422. [Google Scholar]
  65. Tardani, F.; Pucci, C.; la Mesa, C. Confining ss-DNA/carbon nanotube complexes in ordered droplets. Soft Matter 2014, 10, 1024–1031. [Google Scholar] [CrossRef] [PubMed]
  66. Tardani, F.; la Mesa, C. Titration of ss-DNA/CNT complexes. Unpublished work. 2015. [Google Scholar]
  67. Svensek, D.; Veble, G.; Podgornik, R. Confined nematic polymers: Order and packing in a nematic drop. Phys. Rev. E 2010, 82, 011708:1–011708:14. [Google Scholar] [CrossRef]
  68. Davis, V.A.; Parra-Vasquez, A.N.G.; Green, M.J.; Raj, P.K.; Behabtu, N.; Prieto, V.; Booker, R.D.; Schmidt, J.; Kesselman, E.; Zhou, W.; et al. True Solutions of Single-Walled Carbon Nanotubes for Assembly into Macroscopic Materials. Nat. Nanotechnol. 2009, 4, 830–834. [Google Scholar] [CrossRef] [PubMed]
  69. Scalia, G.; von Buhler, C.; Hagele, C.; Roth, S.; Giesselmann, F.; Lagerwall, J.P.F. Spontaneous Macroscopic Carbon nanotube Alignment via Colloidal Suspension in Hexagonal Columnar Lyotropic Liquid Crystals. Soft Matter 2008, 4, 570–576. [Google Scholar] [CrossRef]
  70. Lagerwall, J.P.F.; Scalia, G.; Haluska, M.; Dettlaff-Weglikowska, U.; Roth, S.; Giesselmann, F. Nanotube Alignment Using Lyotropic Liquid Crystals. Adv. Mater. 2007, 19, 359–364. [Google Scholar] [CrossRef]
  71. Ao, G.; Nepal, D.; Aono, M.; Davis, V.A. Cholesteric and Nematic Liquid Crystalline Phase Behavior of Double Stranded DNA Stabilized Single-Walled Carbon Nanotube Dispersions. ACS Nano 2011, 5, 1450–1458. [Google Scholar] [CrossRef] [PubMed]
  72. Bravo-Sanchez, M.; Simmons, T.J.; Vidal, M.A. Liquid Crystal Behavior of Single Wall Carbon Nanotubes. Carbon 2010, 48, 3531–3542. [Google Scholar] [CrossRef]
  73. Puech, N.; Blanc, C.; Grelet, E.; Zamora-Ledezma, C.; Maugey, M.; Zakri, C.; Anglaret, E.; Poulin, P. Highly Ordered Carbon Nanotube Nematic Liquid Crystals. J. Phys. Chem. C 2011, 115, 3272–3278. [Google Scholar] [CrossRef]
  74. Whitesides, G.M.; Boncheva, M. Beyond molecules: Self-assembly of meso-scopic and macroscopic components. Proc. Nat. Acad. Sci. USA 2002, 99, 4769–4774. [Google Scholar] [CrossRef] [PubMed]
  75. Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef] [PubMed]

Share and Cite

MDPI and ACS Style

Tardani, F.; Mesa, C.L. Dispersability of Carbon Nanotubes in Biopolymer-Based Fluids. Crystals 2015, 5, 74-90. https://doi.org/10.3390/cryst5010074

AMA Style

Tardani F, Mesa CL. Dispersability of Carbon Nanotubes in Biopolymer-Based Fluids. Crystals. 2015; 5(1):74-90. https://doi.org/10.3390/cryst5010074

Chicago/Turabian Style

Tardani, Franco, and Camillo La Mesa. 2015. "Dispersability of Carbon Nanotubes in Biopolymer-Based Fluids" Crystals 5, no. 1: 74-90. https://doi.org/10.3390/cryst5010074

Article Metrics

Back to TopTop