Next Article in Journal / Special Issue
Preparation and Characterization of Lead-Free (K0.5Na0.5)NbO3-LiNbO3 and (K0.5Na0.5)NbO3-LiTaO3 Ferroelectric Single Crystals
Previous Article in Journal / Special Issue
Temperature-Dependent Phase Transition in Orthorhombic [011]c Pb(Mg1/3Nb2/3) O3-0.35PbTiO3 Single Crystal
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 4
Issue 3
10.3390/cryst4030273
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3–BaTiO3 Single Crystals under Electric Fields

by
Motohiro Ogino
1,
Yuji Noguchi
1,*,
Yuuki Kitanaka
1,
Masaru Miyayama
1,
Chikako Moriyoshi
2 and
Yoshihiro Kuroiwa
2
1
Research Center for Advanced Science and Technology, The University of Tokyo, 4-6-1 Komaba, Meguro, Tokyo 153-8904, Japan
2
Graduate School of Science, Hiroshima University, 1-3-1 Kagamiyama, Higashihiroshima, Hiroshima 739-8526, Japan
*
Author to whom correspondence should be addressed.
Crystals 2014, 4(3), 273-295; https://doi.org/10.3390/cryst4030273
Submission received: 1 May 2014 / Revised: 26 June 2014 / Accepted: 27 June 2014 / Published: 16 July 2014
(This article belongs to the Special Issue Piezoelectric Crystals)
Browse Figures
Versions Notes

Abstract

:
The features of the crystal structures and spontaneous polarization (Ps) under an electric field (E) have been reviewed for (1 − x)(Bi0.5Na0.5)TiO3–xBaTiO3 (BNT–BT). In-situ measurements of high-resolution synchrotron radiation X-ray diffraction (SR-XRD) under electric fields show that single crystals with x = 0 (BNT) and 5% have a monoclinic distortion in space group Cc at 25 °C. The SR-XRD study combined with density functional theory (DFT) calculations demonstrates that BNT–5%BT exhibits a rotation of Ps in the monoclinic a–c plane by 2° under an E of 70 kV/cm along the <001> pseudo-cubic direction, which is much larger than BNT.

Graphical Abstract

1. Introduction

Lead-based ferroelectric oxides of Pb(Zr,Ti)O3 (PZT) and related materials have been widely used for piezoelectric devices such as sensors, actuators, and nonvolatile memories. Enhanced piezoelectric performance of relaxor-based ferroelectrics of Pb(Zn1/3Nb2/3)O3–PbTiO3 (PZN–PT) and Pb(Mg1/3Nb2/3)O3–PbTiO3 (PMN–PT) has attracted much attention from scientific and technological points of view. Single crystals of PZN–PT and PMN–PT exhibit an ultrahigh piezoelectric response (a strain constant d over 2500 pC/N) near morphotropic phase boundary (MPB) compositions between rhombohedral (R) and tetragonal (T) structures [1,2]. Various mechanisms have been proposed to explain the origin of the high piezoelectric response. Fu and Cohen [3] have reported the polarization rotation mechanism in which spontaneous polarization (Ps) rotates by the application of an electric field (E) from the <111>pc (pseudo-cubic notation) direction in the R phase to the <001> direction in the T phase via an intermediate monoclinic (M) phase. The M phase provides a bridging pathway between the R and T phases and then the Ps vector easily rotates under a weak E [3]. It is stated that the polarization rotation is a consequence of the flat energy profile in which a small E can lead to a large change in polarization angle [3]. Lately, Damjanovic [4] has pointed out that the polarization rotation is an old concept to explain the enhanced piezoelectric properties of PZT near the MPB region and that not only the polarization rotation but also a polarization extension plays an important role in some cases in the piezoresponse of ferroelectric materials.
A growing concern regarding the toxicity in lead-containing devices and their environmental impact has, however, triggered extensive research on lead-free piezoelectric materials [5,6,7,8,9]. Bismuth sodium titanate (Bi0.5Na0.5)TiO3 (BNT) has been recognized as one of the most promising candidates for the lead-free piezoelectric material [5,10,11,12,13]. To clarify the origin of its ferroelectricity, the crystal structure has been intensively analyzed in detail [14,15,16,17,18,19,20,21,22]. The averaged structure of BNT has been reported to be a rhombohedral structure in space group R3c. A high resolution synchrotron radiation X-ray diffraction (SR-XRD) study reveals that BNT has a slight monoclinic distortion in the monoclinic Cc space group. The monoclinic Cc structure has been recently observed in BNT single crystals by optical birefringence microscopy [22].
Since Takenaka et al. [5,23,24,25] first reported the piezoelectric properties of (1 − x)(Bi0.5Na0.5)TiO3–xBaTiO3 (BNT–BT), polycrystalline ceramics and films of BNT–BT have been extensively studied to improve the piezoelectric performance, to investigate the phase diagram [24,26,27,28], the domain structure [29,30], and the relaxor behavior [31,32,33,34,35], and to elucidate the effect of the application of E [27,28] etc. Single crystals of BNT–BT have been grown and the influence on dc-bias E on the phase stability [36] and the diffuse X-ray scattering [37] have been investigated. Recently, a bifurcated polarization rotation model in BNT has been postulated by a neutron pair distribution analysis [38] and the piezoelectric response is suggested to originate from a polarization rotation.
Although there have been detailed studies on the crystal structures of BNT and BNT–BT [39,40,41,42,43], their underlying mechanism of ferroelectricity and piezoelectricity is not well understood, e.g., how the local structures near Bi and Na are developed, how the constituent ions are displaced, and how the vector of spontaneous polarization (Ps) responds to the application of E. The study on the responses of the unit-cell parameters and atomistic polarization with respect to E are essential to clarifying the origin of the ferroelectric polarization and piezoelectric properties in the BNT system.
In this review, the intrinsic responses of unit-cell parameters, local atomic polarization and Ps to E are summarized for BNT and BNT–5%BT. The investigation of in-situ measurements of high-energy synchrotron radiation X-ray diffraction (SR-XRD) under an E is conducted to analyze the structural deformation by the application of E. In addition, density functional theory (DFT) calculations are used to derive the positions in the unit cell, Born effective charges, dipole moments of the constituent atoms and therefore the Ps with respect to E is finally determined.
High-quality single crystals of BNT and BNT–5%BT grown by a high-Po2 (oxygen pressure) top-seeded solution growth (TSSG) method were used for the structural analyses as well as for the measurements of polarization and E-field-induced strain properties. It is emphasized that all SR-XRD data were collected under an application of E, i.e., that the in-situ measurements of the SR-XRD under an E were conducted. To definitely distinguish the state in which an E is applied to the crystals during the measurements from the one after an electric poling, the E applied during the in-situ SR-XRD measurements is defined as “Ein-situ”. It is demonstrated that a rotation of the Ps vector is induced by applying an Ein-situ for the BNT–5%BT crystals.

2. Experiments

Single crystals of BNT [44,45] and BNT–BT were grown at a high oxygen pressure (Po2) of 0.9 MPa using a TSSG method [46,47,48,49]. The crystals were annealed at 950 °C for 50 h, cut into plates with a thickness of 0.2 mm. Au electrodes were sputtered onto the cut surfaces. X-ray fluorescence analysis showed that the BNT–BT crystals obtained had a composition of 0.95BNT–0.05BT (BNT–5%BT). Properties of polarization (P) and electric-induced-strain (S) were investigated along the <001>pc direction at 25 °C using the ferroelectric test system (Toyo Corporation, Tokyo, Japan, Model 6252 Rev. B). The pseudo-cubic (pc) notation is used for denoting the crystallographic axes of the pc cell.
For the SR-XRD measurements, the crystals were cut into plates with a thickness of 0.2 mm, and then gold electrodes with a thickness of 20 nm were sputtered onto the cut surfaces. The details of the SR-XRD experiments are described in the references [50,51]. The direction of E, i.e., the axis normal to the crystal plates was set to be along the <001>pc direction. SR-XRD data were collected with a transmission geometry using a large cylindrical two-dimensional imaging plate (IP) camera with a 1/4χ three-axis goniometer at BL02B1 in the SPring-8 synchrotron radiation facility [50,51,52,53]. A high SR energy of 35 keV [wavelength: 0.035313(2) nm for BNT and 0.035345(2) nm for BNT–5%BT] was adopted so that X-rays with a high transmission ratio could penetrate through the crystals and that a high-angle diffraction pattern could be observed. The X-ray beam incident to the crystals was 150 μm in diameter. The diffraction patterns were measured in a wide ω range of 30°–67°. The diffraction patterns were exposed on the IP camera in the following ∆ω of 30°–40°, 39°–49°, 48°–58°, and 57°–67°. A ∆ω of 1° was set to be overlapped to superimpose each of the 4 diffraction patterns.
The SR-XRD measurement temperature was kept at 25 °C, at which BNT has the monoclinic space group Cc [19,22] (see Figure 1a), where Ps is approximately aligned along the <111>pc direction. Prior to the diffraction measurements, an E of 30–50 kV/cm, which was higher than the coercive field (Ec) [54], was applied to the crystals along <001>pc as a poling treatment. To investigate the intrinsic response of the unit cell to an Ein-situ, SR-XRD measurements were performed at Ein-situ = 0, 30, 50, 70, and 100 kV/cm. During the measurements, Ein-situ was applied in the same <001>pc direction of the E in the poling treatment.
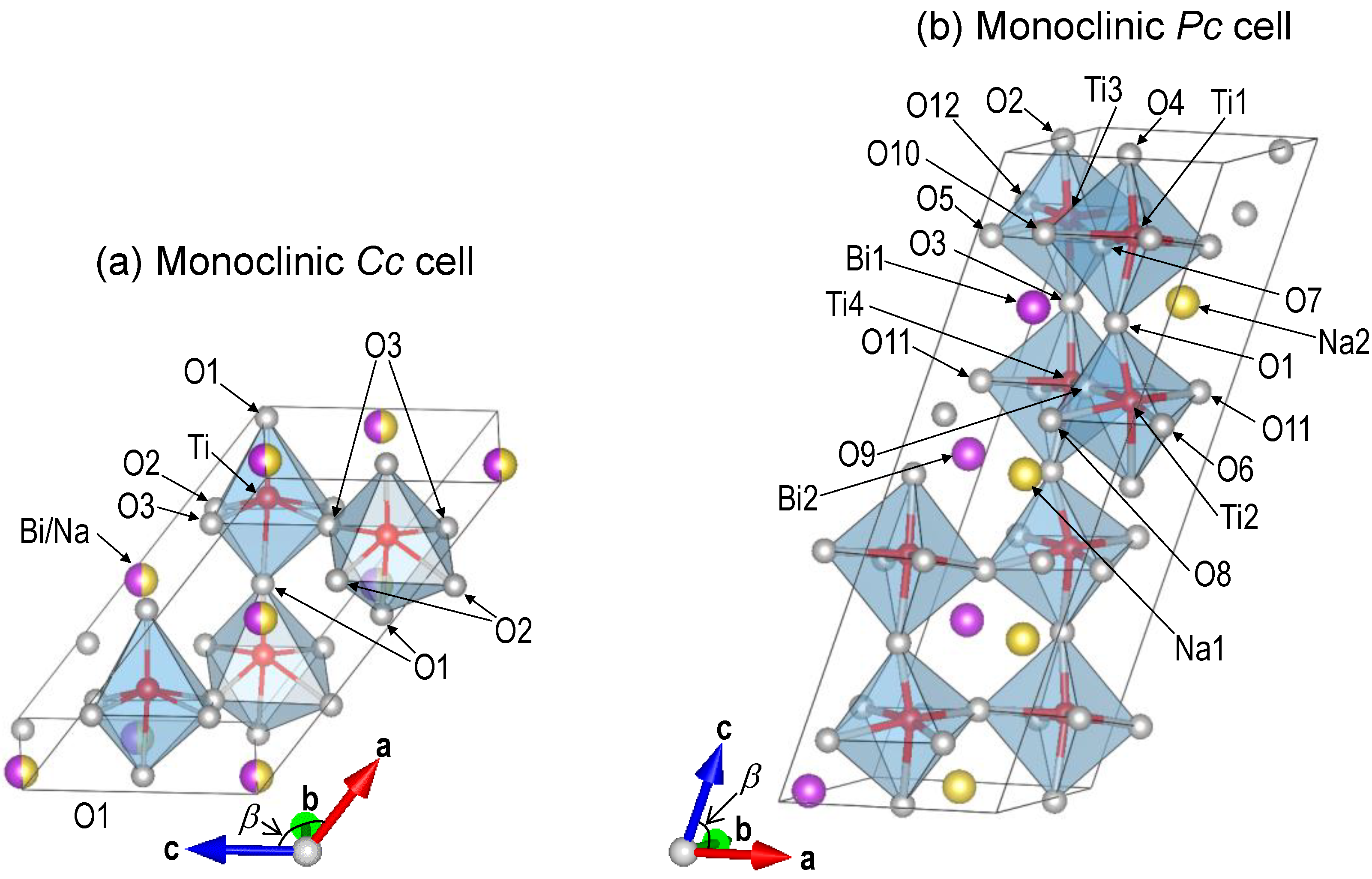
Crystals 04 00273 g001 1024
Figure 1. Crystal structures of BNT in the monoclinic space group (a) Cc and (b) Pc cells. The Cc structure in (a) is drawn from the structural parameters reported by Aksel et al. [19]. In this Cc cell, Bi and Na are randomly distributed on the A site. The monoclinic supercell in space group Pc [BiNaTi2O6, Z = 4, see (b)], in which the structural feature in the Cc cell can be taken into account. In the Pc cell, the nearest-neighbor (NN) A-site bonds consist of five Bi–Na and one Bi–Bi or Na–Na.
Figure 1. Crystal structures of BNT in the monoclinic space group (a) Cc and (b) Pc cells. The Cc structure in (a) is drawn from the structural parameters reported by Aksel et al. [19]. In this Cc cell, Bi and Na are randomly distributed on the A site. The monoclinic supercell in space group Pc [BiNaTi2O6, Z = 4, see (b)], in which the structural feature in the Cc cell can be taken into account. In the Pc cell, the nearest-neighbor (NN) A-site bonds consist of five Bi–Na and one Bi–Bi or Na–Na.
Crystals 04 00273 g001
Figure 2a exhibits a diffraction pattern observed for BNT with Ein-situ = 0 kV/cm. In the 30°–67° ω range, ca. 880 reflections were observed in a resolution limit of the lattice spacing (d) larger than 0.04 nm for the BNT crystals. To improve the accuracy of determining the lattice parameters ca. 500 reflections in the d range of 0.055–0.04 nm were selected in the structure analysis. For the BNT–5%BT crystals, 660 reflections in the d range of 0.058–0.038 nm were used for the analysis. The structure analysis under an application of Ein-situ was also conducted in a similar manner. In the SR-XRD analysis, the C base centered cell with the Laue class 2/m was selected to determine the lattice parameters.
It is evident that the BNT crystals with an Ein-situ along the <001>pc direction has a multidomain structure (the details are described in [51]). The intensity data recorded were therefore obtained as the summation of diffraction spots from each domain. The multidomain structure makes the structure analysis of the atomic positions difficult. Here, we focus our attention on the monoclinic lattice parameters as a function of Ein-situ applied along the <001>pc direction. In the structural analysis, the diffraction spot with a higher intensity was selected in the same hkl reflections to calculate the lattice parameters. In the data in the small d range, the diffraction spots resulting from each domain were clearly separated (see Figure 4 in [51]).
Crystals 04 00273 g002 1024
Figure 2. Synchrotron radiation X-ray diffraction (SR-XRD) patterns at Ein-situ = 0 kV/cm observed for the single crystals of (a–c) BNT and (d) BNT–5%BT. (b) and (c) indicate the expansions of the square parts in (a). The superlattice 1/2 (o o o) reflections (o: odd) in addition to the fundamental hkl reflections from the ABO3 primitive unit cell were detected for both crystals.
Figure 2. Synchrotron radiation X-ray diffraction (SR-XRD) patterns at Ein-situ = 0 kV/cm observed for the single crystals of (a–c) BNT and (d) BNT–5%BT. (b) and (c) indicate the expansions of the square parts in (a). The superlattice 1/2 (o o o) reflections (o: odd) in addition to the fundamental hkl reflections from the ABO3 primitive unit cell were detected for both crystals.
Crystals 04 00273 g002
The relation between the monoclinic and pc cells is depicted in Figure 3a, in which the axes of the monoclinic and pc cells are denoted by the subscript as “m” and “pc”, respectively. The monoclinic cell size used for our structure analysis is different from those of the monoclinic Cc and Pc cells. The C base centered cell with 2/m symmetry can describe the crystal structures of Cc and Pc and the structural parameters can be transformed to each other.
Crystals 04 00273 g003 1024
Figure 3. Unit cells of pseudo-cubic (pc) and monoclinic (m) structures: (a) the relation between the pc cell and the monoclinic cell (the C base centered one with 2/m symmetry) adapted for the SR-XRD analysis. In rhombohedral R3c symmetry, the Ps vector is aligned along <111>pc and forms an angle of αpc with the apc-bpc plane. (b) depicts the schematic image of the Ps rotation by applying an E. In this monoclinic cell, αpc is defined as the angle of the Ps vector with the am–bm plane.
Figure 3. Unit cells of pseudo-cubic (pc) and monoclinic (m) structures: (a) the relation between the pc cell and the monoclinic cell (the C base centered one with 2/m symmetry) adapted for the SR-XRD analysis. In rhombohedral R3c symmetry, the Ps vector is aligned along <111>pc and forms an angle of αpc with the apc-bpc plane. (b) depicts the schematic image of the Ps rotation by applying an E. In this monoclinic cell, αpc is defined as the angle of the Ps vector with the am–bm plane.
Crystals 04 00273 g003

3. Method of DFT Calculations

DFT calculations were performed to investigate the behavior of the local structure, atomic and macroscopic polarization, and their dependence on Ein-situ in the crystals of BNT and BNT–5%BT. The random distribution of Bi and Na on the A site leads to the averaged crystal structure in space group Cc [19] while the structure of BNT for the DFT calculations should have a lower symmetry due to an arrangement of Bi and Na [55]. We selected the monoclinic supercell in space group Pc (BiNaTi2O6, Z = 4, see Figure 1b), in which the structural feature in the Cc cell can be taken into account. As for the A site atoms in the Pc cell, the nearest-neighbor (NN) A-site bonds consist of 5 Bi–Na and one Bi–Bi or Na–Na. Since the bonding of Bi–O in addition to that of Ti–O plays an important role in the ferroelectricity and piezoelectricity in the BNT system, the Pc cell in which many Bi–O–Na bonds are constructed without sacrificing the monoclinic Cc symmetry.
To determine the fractional coordinates of the constituent atoms by the DFT calculations, the lattice parameters determined by the SR-XRD analysis were employed. As described in detail below, the lattice parameters were dependent on Ein-situ and determined by the SR-XRD analysis with a high accuracy. The use of the lattice parameters obtained by the SR-XRD analysis in the DFT calculations enables us to investigate the influence of Ein-situ on the polarization (patom) of the atoms and the resultant Ps with respect to Ein-situ in the crystals of BNT and BNT–5%BT in an indirect manner. In addition, similar DFT calculations were performed using the unit-cell parameters of BNT reported by Aksel et al. [19] for comparison.
The DFT calculations were performed with the generalized gradient approximation [56] using a plane wave basis set as implemented in the Vienna ab-initio simulation package (VASP). We used the projector-augmented wave potentials [57] with the valence-electron configurations of 5d106s26p3 for Bi, 2p63s1 for Na, 3p63d24s2 for Ti, and 2s22p4 for O. The Perdew-Burke-Ernzerhof functional modified for solids (PBEsol) [58] was employed for the exchange-correlation potential. A plane-wave cut-off energy of 520 eV was adopted, and electronic energy was converged to less than 10−6 eV in all calculations. The Monkhorst-Pack k-mesh of 7 × 7 × 3 was adopted for geometrical optimization calculations (atomic positions were relaxed with the fixed lattice parameters determined by the SR-XRD analysis). Born effective charge (Z*) tensors were evaluated by using a density-functional perturbation theory (DFPT) [59] for BNT with Ein-situ = 0 kV/cm. Throughout our manuscript, Ps and patom denotes the vectors of spontaneous polarization and atomic polarization, respectively, and the absolute values of these vectors are defined as follows: Ps = ǀPsǀ and patom = ǀpatomǀ.

4. Results and Discussion

Figure 2a shows the SR-XRD pattern at Ein-situ = 0 kV/cm observed for the single crystals of BNT. Figure 2b,c depict the expansions of the square parts in Figure 2a. In addition to the fundamental hkl reflections from the ABO3 primitive unit cell, the superlattice 1/2 (o o o) reflections (o: odd) such as 1/2 3/2 3/2 and 1/2 5/2 5/2 are clearly observed. These 1/2 (o o o) reflections originate from the tilting of TiO6 octahedra with a−a−a− (Glazer notation [60]), which is described in the space group of rhombohedral R3c [17] or monoclinic Cc [61]. As clearly seen in Figure 2d for the BNT–5%BT crystals, apparent 1/2 (o o o) reflections were observed. If the tetragonal phase in space group P4bm reported in the MPB region (x = 0.05–0.11) [28] is present, superlattice 1/2 (o o e) reflections (o: odd, e: even) should be observed, but our BNT and BNT–5%BT crystals did not exhibit any 1/2 (o o e) reflection in the Ein-situ range of 0–100 kV/cm.
Figure 4a represents the polarization-electric field [P(E)] hysteresis loop measured for the BNT–5%BT crystals along <001>pc at 25 °C. The crystals exhibited a remanent polarization (Pr) of 36 μC/cm2 and a coercive field (Ec) of 24 kV/cm. This Pr is comparable to the value (34 μC/cm2) observed for the BNT crystals along <001>pc [47].
Our crystals had a relatively large Pr and a small Ec compared with the reported values for other BNT–BT crystals [54,62,63]. It has been reported that the high-Po2 TSSG method provides high-quality crystals with low concentrations of the vacancies of Bi and O due to a suppression of the defect-formation reaction at high temperatures during the crystal-growth process [46,47,48,49]. Figure 4b shows the bipolar strain-electric field [S(E)] curve measured for the BNT–5%BT crystals along <001>pc at 25 °C.
Crystals 04 00273 g004 1024
Figure 4. (a) Polarization-electric field [P(E)] hysteresis loop and (b) bipolar strain-electric field [S(E)] curve measured for the BNT–5%BT crystals along <001>pc at 25 °C.
Figure 4. (a) Polarization-electric field [P(E)] hysteresis loop and (b) bipolar strain-electric field [S(E)] curve measured for the BNT–5%BT crystals along <001>pc at 25 °C.
Crystals 04 00273 g004
A typical butterfly curve, mainly due to a domain switching and the converse piezoelectric effect, was observed. The E at which the S had the minimum value was ca. 30 kV/cm, which is slightly higher than the Ec determined by the P(E) measurements. The crystals had a maximum strain (Smax) up to 0.9% at an E of 100 kV/cm, which is much larger than those observed for the single crystals of BNT [64] and BNT–12%BT [46].
Figure 5a shows the unipolar strain curve (Sbulk) observed for the BNT–5%BT crystals along <001>pc. The unit-cell strain (Sunit-cell) calculated from the lattice parameter cpc with respect to Ein-situ in the SR-XRD analysis is also plotted. The piezoelectric strain constant d33* estimated from the Sbulk data in the low-E region (0–5 kV/cm) was 138 pm/V, which is comparable to the strain constant d33(unit-cell) of 175(28) pm/V determined from the Sunit-cell data. The d33(unit-cell) originates from the unit-cell deformation by applying an Ein-situ mainly due to the intrinsic contribution, i.e., the converse piezoelectric effect. In the low-Ein-situ region below 20 kV/cm, Sbulk and Sunit-cell are in reasonable agreement with each other. In contrast, the Smax/Emax value determined by the Sbulk was 408 pm/V, which is much larger than the d33* and d33(unit-cell) values. The hysteresis observed in the unipolar Sbulk curve and our SR-XRD analysis suggest that the large Smax/Emax is attributed to an extrinsic contribution by non-180° ferroelastic domains.
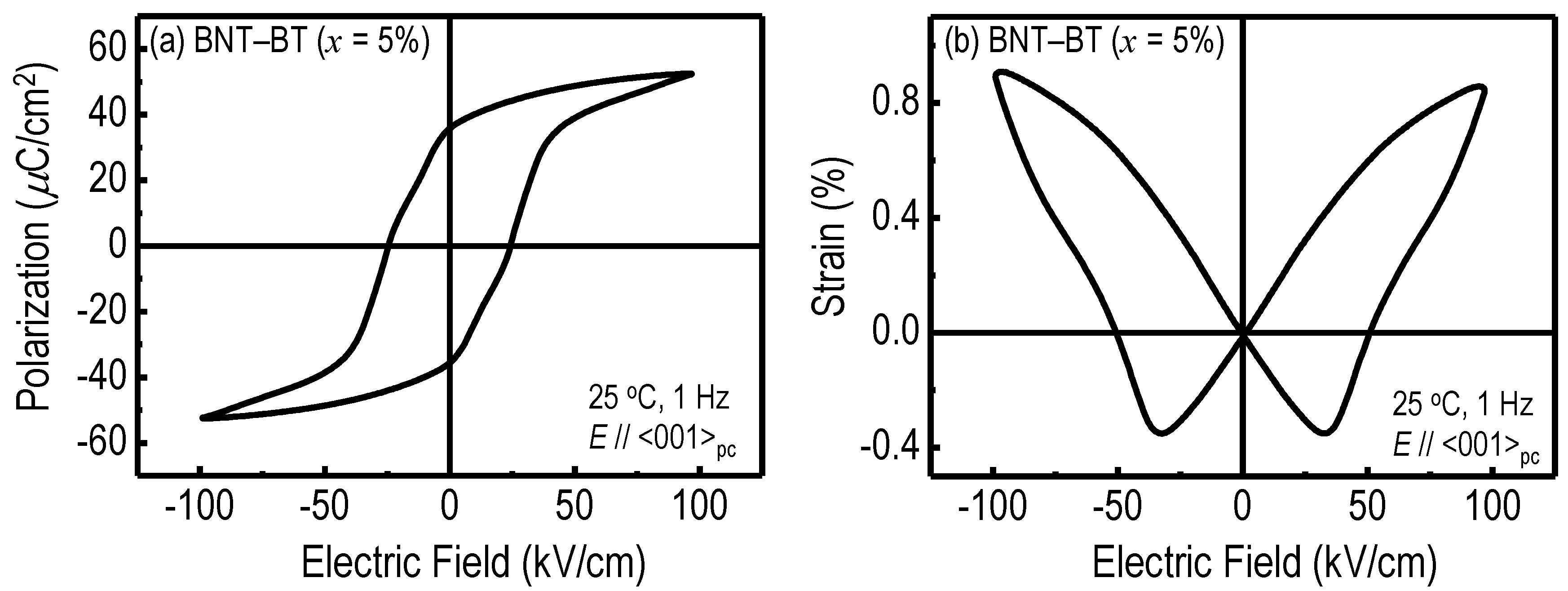
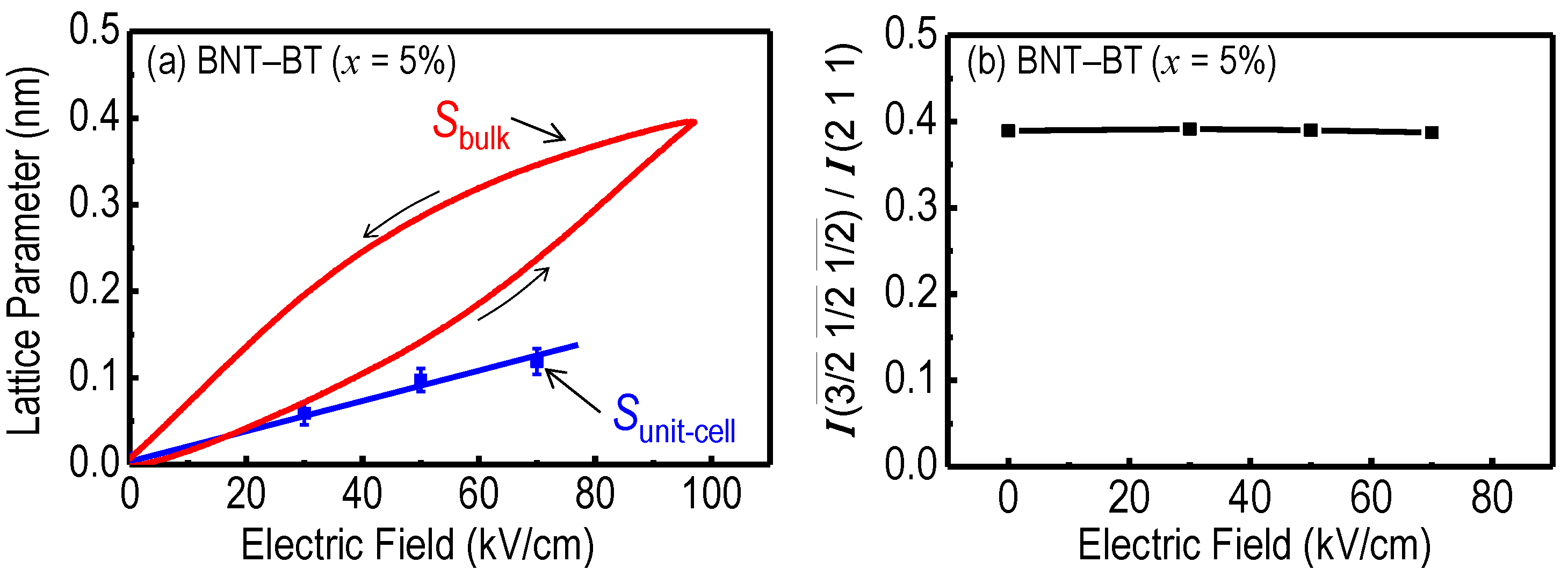
Crystals 04 00273 g005 1024
Figure 5. (a) Unipolar strain curve (Sbulk) observed for the BNT–5%BT crystals along <001>pc at 25 °C. The unit-cell strain (Sunit-cell) calculated from the lattice parameter cpc with respect to Ein-situ determined in the SR-XRD analysis is also plotted. Figure (b) represents the intensity (I) ratio of superlattice 3/2 1/2 1/2 reflection to fundamental 2 1 1 one as a function of Ein-situ applied along <001>pc for the BNT–5%BT crystals.
Figure 5. (a) Unipolar strain curve (Sbulk) observed for the BNT–5%BT crystals along <001>pc at 25 °C. The unit-cell strain (Sunit-cell) calculated from the lattice parameter cpc with respect to Ein-situ determined in the SR-XRD analysis is also plotted. Figure (b) represents the intensity (I) ratio of superlattice 3/2 1/2 1/2 reflection to fundamental 2 1 1 one as a function of Ein-situ applied along <001>pc for the BNT–5%BT crystals.
Crystals 04 00273 g005
When an Ein-situ is applied along <001>pc to R(or M) crystals with Ps mainly along <111>pc, an E-induced phase transition from the R(or M) to a T phase is expected, as observed for PZN–PT and PMN–PT crystals [3]. Such an E-induced phase transition should change the intensity of the 1/2 (o o o) reflections with respect to the fundamental hkl ones. Figure 5b represents the intensity of the 3/2 1/2 1/2 superlattice spot as a function of Ein-situ observed for the BNT–5%BT crystals. The intensity of 3/2 1/2 1/2 normalized by the fundamental spot of 2 1 1 exhibits no change by applying an Ein-situ up to 70 kV/cm. These results clearly show that the BNT–5%BT crystals do not undergo any E-induced phase transition and that they remain as the monoclinic Cc (described in detail below).
Figure 6 shows the pc unit cell parameters as a function of Ein-situ along <001>pc. The rhombohedral R3c cell has the relations of apc = bpc = cpc and αpc = βpc = γpc, but both the crystals of BNT and BNT–5%BT exhibit a structural deviation from the R3c cell. These results are direct evidence that the BNT and BNT–5%BT crystals have monoclinic Cc symmetry.
With increasing Ein-situ, apc was compressed while cpc was elongated mainly due to the converse piezoelectric effect. For the BNT crystals, αpc and γpc remained constant around 89.63° and 89.69°, respectively, regardless of Ein-situ. It is worth noting that the BNT–5%BT crystals presented increasing trends of αpc and γpc with Ein-situ. In particular, γpc markedly increased by 0.04° by Ein-situ, which is much larger than the detection limit of 0.005°–0.007°.
Ma et al. [27] have reported that BNT ceramics exhibited an E-induced phase transition from the Cc to R3c phase at a poling E of ca. 50 kV/cm. It is interesting to note that the transition is found to be irreversible, i.e., that the R3c phase is shown to be maintained in the ceramics without the application of E. This is quite different from the E-induced phase transitions reported for BaTiO3-based [65,66,67] and PbTiO3-based [2,68,69,70,71] single crystals. Considering the fact that the BNT single crystals did not exhibit any change in crystal symmetry, the Cc-R3c phase transition induced by the poling is considered peculiar only for the ceramic forms in the BNT system.
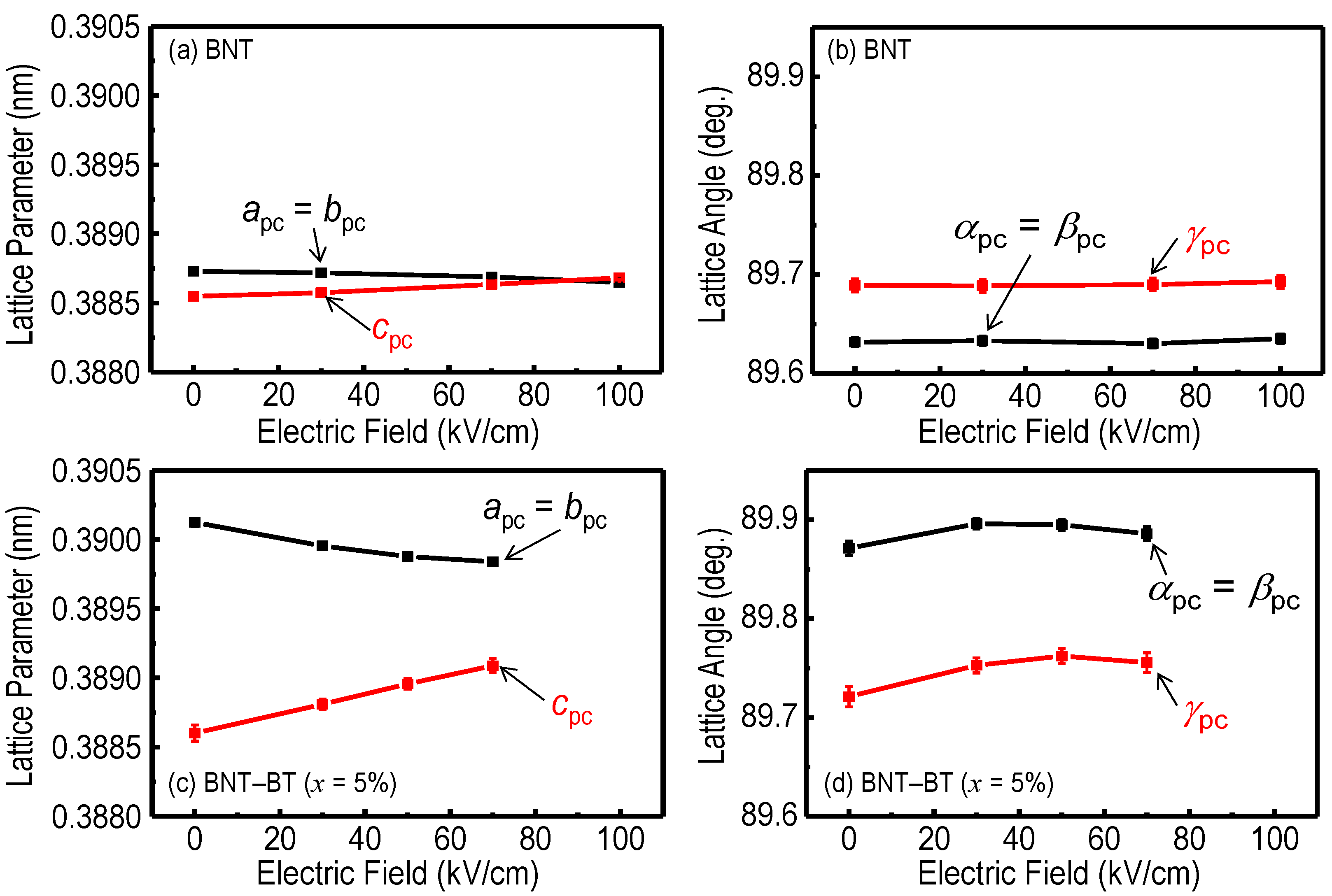
Crystals 04 00273 g006 1024
Figure 6. Pseudo-cubic (pc) unit-cell parameters as a function of Ein-situ along <001>pc : (a) lattice parameters and (b) lattice angel observed for the BNT crystals, (c) lattice parameters and (d) lattice angel observed for the BNT–5%BT crystals.
Figure 6. Pseudo-cubic (pc) unit-cell parameters as a function of Ein-situ along <001>pc : (a) lattice parameters and (b) lattice angel observed for the BNT crystals, (c) lattice parameters and (d) lattice angel observed for the BNT–5%BT crystals.
Crystals 04 00273 g006
The bond lengths obtained by the DFT calculations by employing the lattice parameters at Ein-situ = 0 kV/cm are listed in Table 1, Table 2 and Table 3. The absolute values of the bond length are quite similar for BNT(Aksel et al. [19]), BNT, and BNT–5%BT and their differences are as small as 0.8% at most. With respect to the cages composed of O atoms, Ti and Bi display an averaged displacement along <111>pc, which results in short and long bonding characteristics. For the Ti–O bonding, the three short bonds with 0.181–0.195 nm are seen, which leads to three long bonds with 0.20–0.22 nm. The bond valence sum (BVS) [72] of Ti is calculated to be 3.95–4.05, which accords well with the nominal ionic valence of Ti4+. It is interesting to note that Bi exhibits an enhanced off-centering with respect to the cage of twelve O atoms approximately along the c axis in the Pc cell (Figure 1b). These large displacements of Bi cause a considerable difference between the short and long Bi–O bonds. The short Bi–O bonds are in the range of 0.22–0.25 nm while the long Bi–O bonds are found in 0.30–0.33 nm. The averaged short and long bonds of Bi–O are quantitatively in good agreement with 0.22 nm and 0.32 nm determined by the neutron pair distribution analysis [38] The short bond of Bi–O also accords with 0.22 nm estimated by the extended X-ray absorption fine structure studies [73]. The BVS of Bi is estimated to be 3.14–3.16, which is slightly larger than the nominal ionic valence of Bi3+. For the Na–O bonding, the short and long bonds are formed, whereas the off-centering of Na is not significant compared with that of Bi due to the ionic nature of Na atoms. Actually, the BVS of Na is ca. 1.1, which is almost the same as that of the nominal formal valence of Na+.
Table
Table 1. Bond lengths of Ti–O obtained by the density functional theory (DFT) calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Table 1. Bond lengths of Ti–O obtained by the density functional theory (DFT) calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Bond length (nm)BNT bBNT (Ein-situ = 0 kV/cm)BNT–5%BT (Ein-situ = 0 kV/cm)
Ti1–O120.18120.18130.1812
Ti1–O50.18610.18640.1863
Ti1–O40.18940.18930.1900
Ti1–O10.20690.20850.2080
Ti1–O100.21200.21160.2133
Ti1–O70.21790.21780.2193
BVS a4.023.993.95
Ti2–O110.18690.18760.1874
Ti2–O60.18750.18800.1882
Ti2–O10.19050.19040.1915
Ti2–O20.20480.20690.2064
Ti2–O80.20750.20720.2083
Ti2–O90.20760.20710.2082
BVS a4.023.983.93
Ti3–O20.18590.18560.1859
Ti3–O70.19060.19080.1909
Ti3–O100.19450.19530.1954
Ti3–O50.20060.20050.2014
Ti3–O120.20200.20220.2030
Ti3–O30.20690.20890.2087
BVS a4.054.013.97
Ti4–O30.18480.18450.1847
Ti4–O80.18510.18540.1851
Ti4–O90.18690.18710.1870
Ti4–O60.21020.21040.2118
Ti4–O40.21170.21360.2133
Ti4–O110.21280.21250.2145
BVS a4.023.993.96
a Bond valence sum (BVS) (see text); b The lattice parameters in the monoclinic Cc structure reported by Aksel et al. [19] are employed.
Table 4 lists the Z* tensors of the constituent atoms obtained for the Pc cell calculated using the unit-cell parameters of BNT (Ein-situ = 0 kV/cm). The Z* tensors reflects the relations expected from symmetry, as reported for monoclinic ZrO2 [74]. In the Pc cell, as all of the constituent atoms are on the 2a site, an atom at (x, y, z) and its partner atom at (x, −y, z + 1/2) are structurally equivalent. For the atoms on the same 2a site, the absolute values of the matrix elements are the same. The off-diagonal matrix elements of xy, yx, yz and zy change sign between the partners while those of xz and zx and the diagonal matrix elements of xx, yy and zz have the same sign.
Table
Table 2. Bond lengths of Bi–O obtained by the DFT calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Table 2. Bond lengths of Bi–O obtained by the DFT calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Bond length (nm)BNT bBNT (Ein-situ = 0 kV/cm)BNT–5%BT (Ein-situ = 0 kV/cm)
Bi1–O70.22710.22740.2270
Bi1–O10.22980.23020.2293
Bi1–O100.23580.23490.2352
Bi1–O90.24030.24220.2426
Bi1–O30.24570.24610.2473
Bi1–O50.24720.24730.2495
Bi1–O80.30740.30950.3100
Bi1–O30.30820.30960.3107
Bi1–O120.31200.31200.3135
Bi1–O110.31990.32080.3207
Bi1–O60.32450.32520.3252
Bi1–O10.32980.32770.3302
BVS a3.163.133.10
Bi2–O40.22770.22770.2270
Bi2–O60.23320.23290.2327
Bi2–O110.23550.23500.2354
Bi2–O20.24190.24310.2444
Bi2–O100.24330.24510.2452
Bi2–O80.24640.24700.2490
Bi2–O70.30640.30840.3078
Bi2–O90.30890.31020.3123
Bi2–O20.31090.31180.3128
Bi2–O50.31340.31390.3138
Bi2–O120.31520.31580.3160
Bi2–O40.33160.32980.3321
BVS a3.143.103.07
a Bond valence sum (BVS) (see text); b The lattice parameters in the monoclinic Cc structure reported by Aksel et al. [19] are employed.
In Pc space group, Ps lies in the a–c plane and contains x and z components, which emphasizes the importance of the xx and zz elements of the Z* tensors. It is worth noting that the xx and zz elements are quite different from the nominal ionic charges of Bi3+, Ti4+, and O2− whereas only Na exhibits the similar value expected from that of Na+. The large Z* is considered as a result of a strong dynamic charge transfer between Bi–O and Ti–O. The Z* much larger than the nominal ionic charge reflects the delocalized structure of the electronic charge distributions, which is quite common in other ferroelectric perovskite oxides [74,75].
Considering the relations between the Z* tensors and the bond lengths, we find the characteristic feature of the large effective charge elements caused by the dynamic charge transfer. The zz elements in the Z* tensors of O1–O4 are extraordinarily large compared with other elements whereas other O atoms except for O10 exhibit the zz elements close to the nominal ionic valence (−2). The quite large zz elements of O1–O4 are a result of the dynamic charge transfer due to the formation of the short bonds of Ti1–O4, Ti2–O1, Ti3–O2, and Ti4–O3, which are approximately normal to the a–b plane in the Pc cell. As for the Z* tensors of O5–O12, the xx and yy elements are relatively large compared with their zz elements, which is attributed to the formation of the short bonds between Ti and O parallel to the a–b plane. These short Ti–O bonds form an angle of ca. 45° with the a and b axes, which enlarges both the xx and zz elements. The relatively large zz element of O10 results from the formation of the short bonds with Bi1 and Bi2 that are aligned averagely along the c axis.
Table
Table 3. Bond lengths of Na–O obtained by the DFT calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Table 3. Bond lengths of Na–O obtained by the DFT calculations for BNT and BNT–5%BT with Ein-situ = 0 kV/cm in the Pc cell.
Bond length (nm)BNT bBNT (Ein-situ = 0 kV/cm)BNT–5%BT (Ein-situ = 0 kV/cm)
Na1–O40.24230.24390.2454
Na1–O120.24300.24510.2463
Na1–O60.24470.24560.2479
Na1–O80.25080.25160.2519
Na1–O90.25100.25150.2518
Na1–O20.25820.25890.2590
Na1–O20.29970.29740.2990
Na1–O110.30650.30610.3072
Na1–O50.30710.30930.3095
Na1–O40.31080.31090.3116
Na1–O100.31240.31290.3128
Na1–O70.31780.31780.3177
BVS a1.141.111.09
Na2–O10.24320.24460.2461
Na2–O70.24340.24420.2465
Na2–O110.24340.24540.2465
Na2–O50.25300.25390.2542
Na2–O120.25540.25590.2560
Na2–O30.25650.25680.2577
Na2–O30.30230.30030.3011
Na2–O90.30260.30220.3016
Na2–O80.30580.30520.3046
Na2–O60.30810.30880.3089
Na2–O10.30840.30870.3096
Na2–O100.30960.31080.3123
BUS a1.141.111.08
a Bond valence sum (BVS) (see text); b The lattice parameters in the monoclinic Cc structure reported by Aksel et al. [19] are employed.
Table
Table 4. Born effective charge (Z*) tensors of the constituent atoms obtained for the Pc cell calculated using the unit-cell parameters of BNT (Ein-situ = 0 kV/cm). The elements in the Z* tensors are listed below.
Table 4. Born effective charge (Z*) tensors of the constituent atoms obtained for the Pc cell calculated using the unit-cell parameters of BNT (Ein-situ = 0 kV/cm). The elements in the Z* tensors are listed below.
Atomxxyyzzxyxzyxyzzxzy
Bi14.185.055.030.29−0.64 −0.350.31−0.41−0.33
Bi24.415.085.090.28−0.44 −0.240.33−0.66−0.37
Na11.171.181.11−0.030.02 0.02−0.04−0.030.03
Na21.191.201.14−0.02−0.03 0.03−0.020.040.04
Ti16.585.295.770.33−0.78 −0.100.67−0.44−0.38
Ti25.427.216.48−0.36−0.98 0.34−0.51−1.380.54
Ti35.078.136.62−0.07−0.37 0.520.08−0.490.10
Ti46.036.055.97−0.02−0.08 0.000.080.070.06
O1−2.77−1.32−5.020.020.46 −0.16−0.170.59−0.24
O2−1.15−2.90−5.440.23−0.06 0.100.300.040.56
O3−1.27−2.88−5.220.110.36 0.090.360.170.51
O4−3.02−1.25−4.690.080.87 −0.09−0.220.60−0.24
O6−3.31−3.91−2.08−1.46−0.10 −1.490.96−0.140.73
O7−2.96−3.70−2.14−1.220.06 −1.270.810.160.76
O9−2.89−4.08−2.19−1.490.32 −1.59−0.660.59−0.55
O10−2.76−3.98−2.971.260.09 1.10−0.010.070.09
O11−2.99−4.06−2.171.54−0.29 1.44−0.55−0.34−0.73
O12−3.37−3.96−1.42−2.05−0.05−2.15−0.070.050.17
The charge transfer feature can be evaluated by electronic density of states (DOS). If Ti atoms have the nominal ionic valence of +4, the electronic configuration of Ti4+ is expressed as [Ar]3d0 and should not possess partial DOS (PDOS) in the valence band (VB). Similarly, Bi3+ with 6s26p0 does not have PDOS in the VB if Bi atoms behave as an ion with the nominal valence of +3. Figure 7 exhibits the (a) total DOS and (b)–(g) PDOS of the representative constituent atoms of BNT (Ein-situ = 0 kV/cm). In these plot, the valence band maximum (VBM) is set to be the Fermi level, i.e., 0 eV. As reported for BaTiO3 and PbTiO3 [76,77], the PDOS of the Ti–3d states are found in the valence band (VB, −5 to 0 eV) due to the dynamic charge transfer, i.e., the orbital hybridization between the 3d states of Ti and the 2p states of the neighboring O forming the short bonds with Ti. It is interesting to note that Bi has some PDOS of 6p in the VB resulting from the Bi–6p–O–2p hybridization, which is similar to the Pb–6p–O–2p one reported for PbTiO3 [78]. In contrast, Na has almost no PDOS in the VB, showing that Na has an ionic nature in BNT. This result is consistent with the calculation of the Z* tensor of Na. The orbital hybridizations of Bi and Ti with O lower the energy levels with occupied electrons, leading to the characteristic short bonds, as listed in Table 1, Table 2 and Table 3.
Table 5 lists the structural parameters obtained by the DFT calculations for BNT (Ein-situ = 0 kV/cm). The displacements of atoms along the a (∆x) and c (∆z) axes in the Pc cell are estimated from the center of the polyhedral cages. For example, the center of a TiO6 octahedron is determined to be the position at which the sum of the displacements of the six O atoms becomes zero both along the a and c axes. Using these displacements and the Z* tensors, the x (pa) and z (pc) components of patom are obtained as a dipole moment per the unit-cell volume. The angle of patom with the a–b plane is defined as αpatom, which is obtained by the pa, pc, and the monoclinic angle β. The direction of αpatom is expressed by [uuv], as listed in Table 5, where [uuv] is calculated to be [11v] in the pc cell. As the sum values of pa and pc are denoted as Pa and Pc, respectively, Pa = 35.8 μC/cm2 and Pc = 41.9 μC/cm2 are obtained. To estimate the contributions of Bi, Na, Ti, and O to the macroscopic polarization, the polarization vectors of Bi, Na, Ti, and O are calculated and the results are as follows: pBi = 28.2 μC/cm2 (αm = 35.6°), pNa = 5.3 μC/cm2 (αm = 36.8°), pTi = 34.5 μC/cm2 (αm = 36.8°), and pO = −4.8 C/cm2 (αm = −11.0°). The summation of these p vectors leads to a Ps of 63.7 μC/cm2 with its angle (αm) of 38.2° with the a–b plane. Table 6 lists the structural parameters obtained by the DFT calculations for BNT–5%BT (Ein-situ = 0 kV/cm) in the same manner, and Pa = 38.6 μC/cm2 and Pc = 40.4 μC/cm2 are obtained.
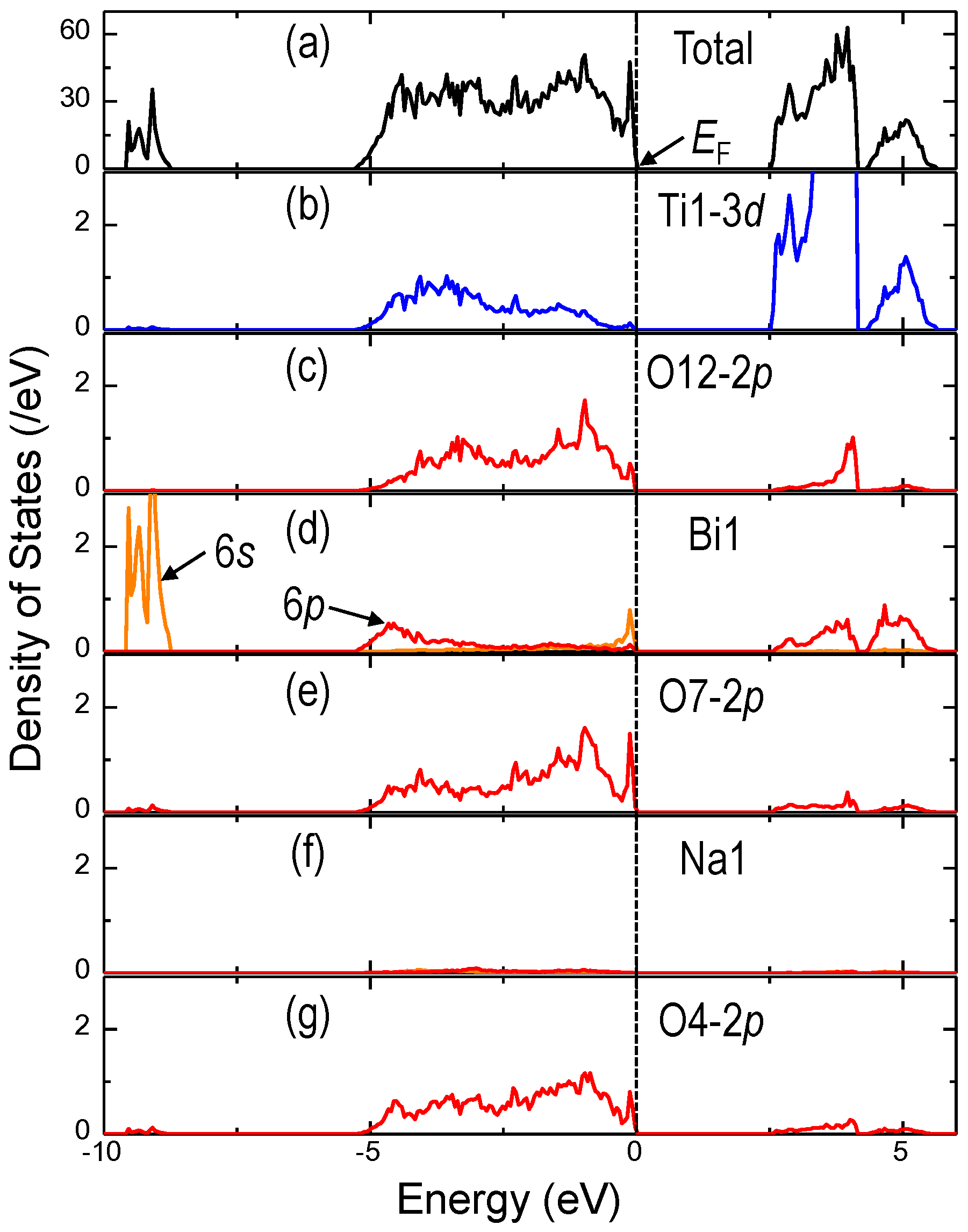
Crystals 04 00273 g007 1024
Figure 7. (a) Total and (b–g) partial density of states (DOS) of the representative constituent atoms of BNT (Ein-situ = 0 kV/cm) obtained by the DFT calculations in which the Pc cell with its fixed lattice parameters determined by the SR-XRD analysis is adapted The valence band maximum (VBM) is set to be the Fermi level, i.e., 0 eV.
Figure 7. (a) Total and (b–g) partial density of states (DOS) of the representative constituent atoms of BNT (Ein-situ = 0 kV/cm) obtained by the DFT calculations in which the Pc cell with its fixed lattice parameters determined by the SR-XRD analysis is adapted The valence band maximum (VBM) is set to be the Fermi level, i.e., 0 eV.
Crystals 04 00273 g007
The Ps of BNT is found to be 63.7 μC/cm2, which leads to a <001>pc component of 39.4 μC/cm2. This agrees well with the Pr (34 μC/cm2) observed for the BNT crystals along <001>pc [47]. The angle (αm) of Ps with the am–bm plane (Figure 3b) is estimated to be 38.2°, which is slightly higher than the <111>pc angle (αpc) of 35.3° (Figure 3a). This result shows that the crystal structure of BNT is well described by the rhombohedral R3c symmetry [38]. The Ps of BNT–5%BT is obtained to be 64.6 μC/cm2, which results in a <001>pc component of 38.0 μC/cm2. This Ps component accords qualitatively with the Pr of 36 μC/cm2 observed for the BNT–5%BT crystals along <001>pc.
Figure 8 exhibits the αm of Ps and patom as a function of Ein-situ. The DFT calculations in the Pc cell were conducted using the lattice parameters determined by the SR-XRD analysis (see Figure 6) to incorporate the influence of Ein-situ on Ps and patom. The values of Ps and patom did not depend on Ein-situ and the difference in patom caused by the application of Ein-situ was less than 0.1 μC/cm2 for both BNT and BNT–5%BT. It is interesting to note that αm displays a characteristic trend with Ein-situ. BNT is found to show an almost constant αm of around 38.2° and the rotation angle (∆αm) of Ps by Ein-situ was as small as 0.2°, which is due to the constant lattice parameters of BNT regardless of Ein-situ. Note that the αm of BNT–5%BT varies significantly from 36.0° (Ein-situ = 0 kV/cm) to 37.3° (Ein-situ = 70 kV/cm) and that its ∆αm reaches 1.3°. These results clearly show that BNT–5%BT features an electrically soft with respect to the rotation of Ps by Ein-situ.
One of the possible origins of the Ps rotation observed for the BNT–5%BT crystals is that this composition is present near the MPB between monoclinic Cc and tetragonal P4bm. Transmission electron microscopy observations by Ma et al. [28] have revealed that (1 − x)BNT–xBT ceramics without an application of E exhibit P4bm symmetry in the x range of 6%–10%. Neutron powder diffraction study conducted by Kitanaka et al. [79] have reported direct evidence of tetragonal P4bm for BNT–7%BT powder. The P4bm phase has a Ps of 4 μC/cm2 [79] along <001>pc, as depicted in Figure 3b. It is suggested that the MPB between monoclinic Cc and tetragonal P4bm lies around x of 6%. This implies that the Cc and P4bm phases are energetically competitive but that an energy barrier for the E-induced phase transition from the Cc to P4bm phase is not overcome in the BNT–5%BT crystals under an Ein-situ along <001>pc up to 70 kV/cm. Although the application of Ein-situ does not lead to a phase transition, the Ps rotation observed is considered as a sign of the E-induced phase transition. A materials design for enhancing piezoelectric response of Bi-based ferroelectric oxides based on the Ps rotation is expected to be developed by the studies of the structural analyses under Ein-situ combined with DFT calculations.
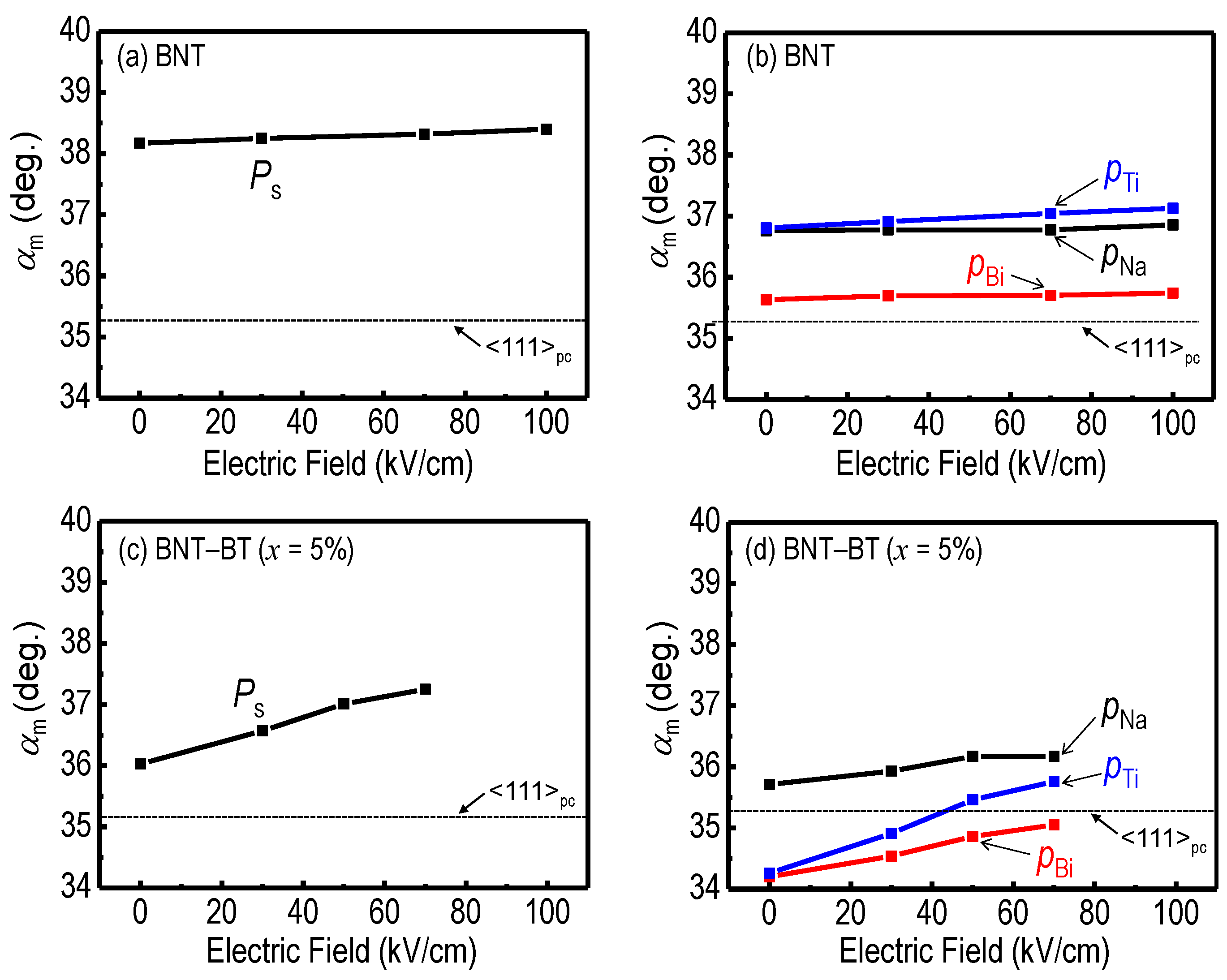
Crystals 04 00273 g008 1024
Figure 8. Angles (αm) of the (a,c) Ps and (b,d) patom vectors as a function of Ein-situ along <001>pc. The αm is defined as the angle of Ps or patom with the am–bm plane. Ps and patom denotes Ps = ǀPsǀ and patom = ǀpatomǀ. Ps and patom are estimated from the off-center displacements and the Born effective charge (Z*) tensors obtained by the DFT calculations.
Figure 8. Angles (αm) of the (a,c) Ps and (b,d) patom vectors as a function of Ein-situ along <001>pc. The αm is defined as the angle of Ps or patom with the am–bm plane. Ps and patom denotes Ps = ǀPsǀ and patom = ǀpatomǀ. Ps and patom are estimated from the off-center displacements and the Born effective charge (Z*) tensors obtained by the DFT calculations.
Crystals 04 00273 g008
Table
Table 5. Structural parameters obtained by the DFT calculations for BNT (Ein-situ = 0 kV/cm) in the Pc cell. The following lattice parameters were used: a = 0.55124 nm, b = 0.54825 nm, c = 1.65376 nm, α = γ = 90.0000°, and β = 70.0105°. The Ps of 63.7 μC/cm2 with its angle (αm) of 38.2° is estimated.
Table 5. Structural parameters obtained by the DFT calculations for BNT (Ein-situ = 0 kV/cm) in the Pc cell. The following lattice parameters were used: a = 0.55124 nm, b = 0.54825 nm, c = 1.65376 nm, α = γ = 90.0000°, and β = 70.0105°. The Ps of 63.7 μC/cm2 with its angle (αm) of 38.2° is estimated.
Atomx (−)y (−)z (−)∆x (nm) a∆z (nm) apa b (μC/cm2)pc b (μC/cm2)αpatom c (deg)[uuv] d
Bi10.2726 0.7478 0.2566 0.032960.027728.248.6435.96111.03
Bi20.0203 0.2544 0.0077 0.031720.029448.718.8535.32111.00
Na10.4986 0.7498 0.0034 0.019760.022311.631.6635.36111.00
Na20.7470 0.2538 0.2529 0.018850.021621.481.7438.19111.11
Ti10.6218 0.7584 0.3732 0.018760.013817.734.9026.08110.69
Ti20.8627 0.7524 0.1224 0.013710.012374.274.2034.69110.98
Ti30.0977 0.2557 0.3733 0.005440.013941.546.1557.76112.24
Ti40.3670 0.2498 0.1247 0.016090.016286.566.7435.56111.01
O10.6980 0.8128 0.2421 −0.008140.003621.66−1.58−52.9011−1.87
O20.9758 0.6910 −0.0088 0.007190.00222−0.58−0.8141.79111.26
O30.2194 0.1891 0.2410 0.003620.00190−0.27−0.6451.02111.75
O40.4440 0.3116 −0.0093 −0.010370.001442.24−0.89−23.4011−0.61
O50.8876 0.5307 0.3518 0.02746−0.02158−8.303.77−26.8011−0.71
O60.1304 −0.0168 0.0979 0.02352−0.02803−5.153.78−42.6311−1.30
O70.3762 0.4831 0.3456 0.02119−0.03195−4.434.93−59.3211−2.38
O80.6378 0.0294 0.1000 0.02754−0.02457−8.595.22−35.7711−1.02
O90.5488 0.5333 0.1308 −0.021470.026314.84−4.83−54.9211−2.01
O100.2898 0.9599 0.3780 −0.026450.021705.13−4.54−49.9911−1.69
O110.0448 0.4676 0.1279 −0.023670.021584.43−2.66−35.3911−1.00
O120.8008 0.0293 0.3814 −0.020410.027344.63−2.73−34.7811−0.98
a Displacements of atoms along the a (∆x) and c (∆z) axes; b x (pa) and z (pc) components of patom; c Angle of patom with the a–b plane; d The direction of α patom.
Table
Table 6. Structural parameters obtained by the DFT calculations for BNT–5%BT (Ein-situ = 0 kV/cm) in the Pc cell. The following lattice parameters were used: a = 0.55306 nm, b = 0.55037 nm, c = 1.65152 nm, α = γ = 90.0000°, and β = 70.2530°. The Ps of 64.6 μC/cm2 with its angle (αm) of 36.0° is estimated.
Table 6. Structural parameters obtained by the DFT calculations for BNT–5%BT (Ein-situ = 0 kV/cm) in the Pc cell. The following lattice parameters were used: a = 0.55306 nm, b = 0.55037 nm, c = 1.65152 nm, α = γ = 90.0000°, and β = 70.2530°. The Ps of 64.6 μC/cm2 with its angle (αm) of 36.0° is estimated.
Atomx (−)y (−)z (−)∆x (nm) a∆z (nm) apa b (μC/cm2)pc b (μC/cm2)αpatom c (deg)[uuv] d
Bi10.2739 0.7477 0.2565 0.034200.027298.618.4634.76110.98
Bi20.0222 0.2542 0.0074 0.033280.028809.208.5633.65110.94
Na10.4994 0.7495 0.0032 0.020660.021881.701.6234.18110.96
Na20.7472 0.2539 0.2528 0.019400.021121.531.7037.28111.08
Ti10.6232 0.7589 0.3731 0.019980.013348.314.6723.98110.63
Ti20.8635 0.7520 0.1220 0.014640.011654.663.7930.98110.85
Ti30.0979 0.2557 0.3731 0.006010.013441.765.9055.97112.09
Ti40.3688 0.2496 0.1246 0.017570.015957.186.6233.49110.94
O10.6960 0.8121 0.2422 −0.008870.003731.80−1.64−51.0811−1.75
O20.9750 0.6913 −0.0088 0.007160.00207−0.57−0.7640.68111.22
O30.2194 0.1894 0.2410 0.004060.00166−0.31−0.5546.05111.47
O40.4429 0.3104 −0.0092 −0.010580.001402.28−0.88−22.8111−0.59
O50.8864 0.5309 0.3521 0.02726−0.02123−8.233.72−26.6411−0.71
O60.1289 −0.0165 0.0982 0.02313−0.02769−5.063.73−42.7411−1.31
O70.3741 0.4837 0.3459 0.02048−0.03148−4.284.85−59.9211−2.44
O80.6373 0.0297 0.1001 0.02781−0.02452−8.665.23−35.5511−1.01
O90.5488 0.5326 0.1310 −0.021140.026374.77−4.82−55.3011−2.04
O100.2893 0.9609 0.3781 −0.026400.021635.12−4.52−49.8411−1.68
O110.0452 0.4690 0.1279 −0.023140.021264.32−2.62−35.7011−1.02
O120.8013 0.0287 0.3812 −0.019760.026804.48−2.67−35.1611−1.00
a Displacements of atoms along the a (∆x) and c (∆z) axes; b x (pa) and z (pc) components of patom; c Angle of patom with the a–b plane; d The direction of α patom.

5. Conclusions

The intrinsic responses of unit-cell parameters and local atomic polarization to Ein-situ were investigated by high-energy SR-XRD analyses combined with density functional theory (DFT) calculations for the single crystals of BNT and BNT–5%BT. High-quality single crystals of BNT and BNT–5%BT grown by a high-Po2 TSSG method exhibited a Pr of 34–36 μC/cm2 along <001>pc, which quantitatively is in good agreement with the components of <001>pc of the Ps vectors estimated by the DFT calculations. The structural analyses provide direct evidence that the BNT and BNT–5%BT crystals have monoclinic Cc symmetry under an Ein-situ up to 70 kV/cm along <001>pc. The BNT–5%BT crystals are found to exhibit a Ps rotation by ca. 2° by an Ein-situ of 70 kV/cm along <001>pc whereas the Ps vector remains unchanged in the BNT crystals.

Acknowledgments

The synchrotron radiation experiments were carried out with the approval of the Japan Synchrotron Radiation Research Institute (JASRI; Proposal Nos. 2011B1386, 2012A1359, and 2012B1243). This study was partly supported by a Grant-in-Aid for Research Fellows of the Japan Society for the Promotion of Science (No. 11J06837).

Author Contributions

Masaru Miyayama and Yuji Noguchi initiated and supervised the project. Motohiro Ogino and Yuuki Kitanaka contributed to the crystal growth and analyzed the structural data. Yoshihiro Kuroiwa and Chikako Moriyoshi initiated work on in-situ SR-XRD measurements under electric fields. Motohiro Ogino and Yuji Noguchi suggested the principle idea and wrote the manuscript. Yuji Noguchi performed DFT calculations.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Shrout, T.R. Characteristics of relaxor-based piezoelectric single crystals for ultrasonic transducers. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1997, 44, 1140–1147. [Google Scholar] [CrossRef]
  2. Noheda, B.; Zhong, Z.; Cox, D.; Shirane, G.; Park, S.-E.; Rehrig, P. Electric-field-induced phase transitions in rhombohedral Pb(Zn1/3Nb2/3)1−xTixO3. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
  3. Fu, H.; Cohen, R. Polarization rotation mechanism for ultrahigh electromechanical response in single-crystal piezoelectrics. Nature 2000, 403, 281–283. [Google Scholar] [CrossRef]
  4. Damjanovic, D. Comments on origins of enhanced piezoelectric properties in ferroelectrics. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 1574–1585. [Google Scholar] [CrossRef]
  5. Takenaka, T.; Maruyama, K.; Sakata, K. (Bi1/2Na1/2)TiO3-BaTiO3 system for lead-free piezoelectric ceramics. Jpn. J. Appl. Phys. 1991, 30, 2236–2239. [Google Scholar] [CrossRef]
  6. Guo, Y.; Kakimoto, K.; Ohsato, H. (Na0.5K0.5)NbO3–LiTaO3 lead-free piezoelectric ceramics. Mater. Lett. 2005, 59, 241–244. [Google Scholar] [CrossRef]
  7. Maeder, M.D.; Damjanovic, D.; Setter, N. Lead free piezoelectric materials. J. Electroceram. 2004, 13, 385–392. [Google Scholar] [CrossRef]
  8. Nagata, H.; Yoshida, M.; Makiuchi, Y.; Takenaka, T. Large piezoelectric constant and high curie temperature of lead-free piezoelectric ceramic ternary system based on bismuth sodium titanate-bismuth potassium titanate-barium titanate near the morphotropic phase boundary. Jpn. J. Appl. Phys. 2003, 42, 7401–7403. [Google Scholar] [CrossRef]
  9. Shrout, T.R.; Zhang, S.J. Lead-free piezoelectric ceramics: Alternatives for PZT? J. Electroceram. 2007, 19, 113–126. [Google Scholar] [CrossRef]
  10. Vakhrushev, S.B.; Isupov, V.A.; Kvyatkovsky, B.E.; Okuneva, N.M.; Pronin, I.P.; Smolensky, G.A.; Syrnikov, P.P. Phase transitions and soft modes in sodium bismuth titanate. Ferroelectrics 1985, 63, 153–160. [Google Scholar] [CrossRef]
  11. Takenaka, T.; Sakata, K. Dielectric, piezoelectric and pyroelectric properties of (BiNa)1/2TiO3-based ceramics. Ferroelectrics 1989, 95, 153–156. [Google Scholar] [CrossRef]
  12. Sasaki, A.; Chiba, T.; Mamiya, Y.; Otsuki, E. Dielectric and piezoelectric properties of (Bi0.5Na0.5)TiO3–(Bi0.5K0.5)TiO3 systems. Jpn. J. Appl. Phys. 1999, 38, 5564–5567. [Google Scholar] [CrossRef]
  13. Roleder, K.; Franke, I.; Glazer, A.M.; Thomas, P.A.; Miga, S.; Suchanicz, J. The piezoelectric effect in Na0.5Bi0.5TiO3 ceramics. J. Phys. Condens. Matter 2002, 14, 5399–5406. [Google Scholar] [CrossRef]
  14. Jones, G.O.; Thomas, P.A. The tetragonal phase of Na0.5Bi0.5TiO3—A new variant of the perovskite structure. Acta Crystallogr. Sect. B Struct. Sci. 2000, 56, 426–430. [Google Scholar] [CrossRef]
  15. Elkechai, O.; Manier, M.; Mercurio, J.P. Na0.5Bi0.5TiO3–K0.5Bi0.5TiO3 (NBT-KBT) system: A structural and electrical study. Phys. Status Solidi 1996, 157, 499–506. [Google Scholar] [CrossRef]
  16. Kreisel, J.; Glazer, A.M.; Jones, G.; Thomas, P.A.; Abello, L.; Lucazeau, G. An X-ray diffraction and Raman spectroscopy investigation of A-site substituted perovskite compounds: The (Na1−xKx)0.5Bi0.5TiO3 (0 ≤ x ≤ 1) solid solution. J. Phys. Condens. Matter 2000, 12, 3267–3280. [Google Scholar]
  17. Jones, G.O.; Kreisel, J.; Jennings, V.; Geday, M.A.; Thomas, P.A.; Glazer, A.M. Investigation of a peculiar relaxor ferroelectric: Na0.5Bi0.5TiO3. Ferroelectrics 2002, 270, 191–196. [Google Scholar] [CrossRef]
  18. Aleksandrova, I.P.; Sukhovsky, A.A.; Ivanov, Y.N.; Yablonskaya, Y.E.; Vakhrushev, S.B. Local and average structure of relaxor Na1/2Bi1/2TiO3 from the point of view of NMR. Ferroelectrics 2009, 378, 16–22. [Google Scholar] [CrossRef]
  19. Aksel, E.; Forrester, J.S.; Jones, J.L.; Thomas, P.A.; Page, K.; Suchomel, M.R. Monoclinic crystal structure of polycrystalline Na0.5Bi0.5TiO3. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
  20. Picht, G.; Töpfer, J.; Hennig, E. Structural properties of (Bi0.5Na0.5)1−xBaxTiO3 lead-free piezoelectric ceramics. J. Eur. Ceram. Soc. 30, 2010, 3445–3453. [Google Scholar]
  21. Jones, G.O.; Thomas, P.A. Investigation of the structure and phase transitions in the novel A-site substituted distorted perovskite compound Na0.5Bi0.5TiO3. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 168–178. [Google Scholar] [CrossRef]
  22. Gorfman, S.; Glazer, A.M.; Noguchi, Y.; Miyayama, M.; Luo, H.; Thomas, P.A. Observation of a low-symmetry phase in Na0.5Bi0.5TiO3 crystals by optical birefringence microscopy. J. Appl. Crystallogr. 2012, 45, 444–452. [Google Scholar] [CrossRef]
  23. Chiang, Y.-M.; Farrey, G.W.; Soukhojak, A.N. Lead-free high-strain single-crystal piezoelectrics in the alkaline–bismuth–titanate perovskite family. Appl. Phys. Lett. 1998, 73, 10–1063. [Google Scholar]
  24. Jo, W.; Daniels, J.E.; Jones, J.L.; Tan, X.; Thomas, P.A.; Damjanovic, D.; Rödel, J. Evolving morphotropic phase boundary in lead-free (Bi1/2Na1/2)TiO3–BaTiO3 piezoceramics. J. Appl. Phys. 2011, 109. [Google Scholar] [CrossRef]
  25. Cernea, M.; Trupina, L.; Dragoi, C.; Vasile, B.S.; Trusca, R. Structural and piezoelectric characteristics of BNT–BT0.05 thin films processed by sol-gel technique. J. Alloys Compd. 2012, 515, 166–170. [Google Scholar] [CrossRef]
  26. Cordero, F.; Craciun, F.; Trequattrini, F.; Mercadelli, E.; Galassi, C. Phase transitions and phase diagram of the ferroelectric perovskite (Na0.5Bi0.5)1−xBaxTiO3 by anelastic and dielectric measurements. Phys. Rev. B 2010, 81. [Google Scholar] [CrossRef]
  27. Ma, C.; Guo, H.; Tan, X. A New Phase Boundary in (Bi1/2Na1/2)TiO3−BaTiO3 Revealed via a Novel Method of Electron Diffraction Analysis. Adv. Funct. Mater. 2013, 23, 5261–5266. [Google Scholar] [CrossRef]
  28. Ma, C.; Guo, H.; Beckman, S.P.; Tan, X. Creation and destruction of morphotropic phase boundaries through electrical poling: A case study of lead-free (Bi1/2Na1/2)TiO3–BaTiO3 piezoelectrics. Phys. Rev. Lett. 2012, 109. [Google Scholar] [CrossRef]
  29. Yao, J.; Yan, L.; Ge, W.; Luo, L.; Li, J.; Viehland, D.; Zhang, Q.; Luo, H. Evolution of domain structures in Na1/2Bi1/2TiO3 single crystals with BaTiO3. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
  30. Kling, J.; Tan, X.; Jo, W.; Kleebe, H.-J.; Fuess, H.; Rödel, J. In situ transmission electron microscopy of electric field-triggered reversible domain formation in bi-based lead-free piezoceramics. J. Am. Ceram. Soc. 2010, 93, 2452–2455. [Google Scholar] [CrossRef]
  31. Kreisel, J.; Glazer, A.M. Estimation of the compressibility of Na0.5Bi0.5TiO3 and related perovskite-type titanates. J. Phys. Condens. Matter 2000, 12, 9689–9698. [Google Scholar] [CrossRef]
  32. Kreisel, J.; Glazer, A.; Bouvier, P.; Lucazeau, G. High-pressure raman study of a relaxor ferroelectric: The Na0.5Bi0.5TiO3 perovskite. Phys. Rev. B 2001, 63. [Google Scholar] [CrossRef]
  33. Kreisel, J.; Bouvier, P.; Dkhil, B.; Thomas, P.; Glazer, A.; Welberry, T.; Chaabane, B.; Mezouar, M. High-pressure X-ray scattering of oxides with a nanoscale local structure: Application to Na1/2Bi1/2TiO3. Phys. Rev. B 2003, 68. [Google Scholar] [CrossRef]
  34. Kreisel, J.; Bouvier, P.; Dkhil, B.; Chaabane, B.; Glazer, A.M.; Thomas, P.A.; Welberry, T.R. Effect of high pressure on the relaxor ferroelectrics Na1/2Bi1/2TiO3 (NBT) and PbMg1/3Nb2/3O3 (PMN). Ferroelectrics 2004, 302, 293–298. [Google Scholar] [CrossRef]
  35. Thomas, P.A.; Trujillo, S.; Boudard, M.; Gorfman, S.; Kreisel, J. Diffuse X-ray scattering in the lead-free piezoelectric crystals Na1/2Bi1/2TiO3 and Ba-doped Na1/2Bi1/2TiO3. Solid State Sci. 2010, 12, 311–317. [Google Scholar] [CrossRef]
  36. Ge, W.; Cao, H.; Li, J.; Viehland, D.; Zhang, Q.; Luo, H. Influence of dc-bias on phase stability in Mn-doped Na0.5Bi0.5TiO3–5.6 at.%BaTiO3 single crystals. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
  37. Daniels, J.E.; Jo, W.; Rödel, J.; Rytz, D.; Donner, W. Structural origins of relaxor behavior in a 0.96(Bi1/2Na1/2)TiO3–0.04BaTiO3 single crystal under electric field. Appl. Phys. Lett. 2011, 98. [Google Scholar] [CrossRef]
  38. Keeble, D.S.; Barney, E.R.; Keen, D.A.; Tucker, M.G.; Kreisel, J.; Thomas, P.A. Bifurcated polarization rotation in bismuth-based piezoelectrics. Adv. Funct. Mater. 2013, 23, 185–190. [Google Scholar] [CrossRef]
  39. Oh, T.; Kim, M.-H. Phase relation and dielectric properties in (Bi1/2Na1/2)1−xBaxTiO3 lead-free ceramics. Mater. Sci. Eng. B Solid State Mater. Adv. Technol. 2006, 132, 239–246. [Google Scholar] [CrossRef]
  40. Xu, C.; Lin, D.; Kwok, K.W. Structure, electrical properties and depolarization temperature of (Bi0.5Na0.5)TiΟ–BaTiΟ3 lead-free piezoelectric ceramics. Solid State Sci. 2008, 10, 934–940. [Google Scholar] [CrossRef]
  41. Maurya, D.; Pramanick, A.; An, K.; Priya, S. Enhanced piezoelectricity and nature of electric-field induced structural phase transformation in textured lead-free piezoelectric Na0.5Bi0.5TiO3–BaTiO3 ceramics. Appl. Phys. Lett. 2012, 100. [Google Scholar] [CrossRef]
  42. Rödel, J.; Jo, W.; Seifert, K.T.P.; Anton, E.-M.; Granzow, T.; Damjanovic, D. Perspective on the Development of Lead-free Piezoceramics. J. Am. Ceram. Soc. 2009, 92, 1153–1177. [Google Scholar] [CrossRef]
  43. Chen, M.; Xu, Q.; Kim, B.H.; Ahn, B.K.; Ko, J.H.; Kang, W.J.; Nam, O.J. Structure and electrical properties of (Na0.5Bi0.5)1−xBaxTiO3 piezoelectric ceramics. J. Eur. Ceram. Soc. 2008, 28, 843–849. [Google Scholar] [CrossRef]
  44. Roleder, K.; Suchanicz, J.; Kania, A. Time dependence of electric permittivity in Na0.5Bi0.5TiO3 single crystals. Ferroelectrics 1989, 89, 1–5. [Google Scholar] [CrossRef]
  45. Suchanicz, J.; Roleder, K.; Kania, A.; Hańaderek, J. Electrostrictive strain and pyroeffect in the region of phase coexistence in Na0.5Bi0.5TiO3. Ferroelectrics 1988, 77, 107–110. [Google Scholar] [CrossRef]
  46. Onozuka, H.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M. Crystal Growth and characterization of (Bi0.5Na0.5)TiO3–BaTiO3 single crystals obtained by a top-seeded solution growth method under high-pressure oxygen atmosphere. Jpn. J. Appl. Phys. 2011, 50. [Google Scholar] [CrossRef]
  47. Kitanaka, Y.; Onozuka, H.; Noguchi, Y.; Miyayama, M. High-performance ferroelectric Bi0.5Na0.5TiO3 Single crystals grown by top-seeded solution growth method under high-pressure oxygen atmosphere. Ferroelectrics 2011, 414, 24–29. [Google Scholar] [CrossRef]
  48. Kitanaka, Y.; Noguchi, Y.; Miyayama, M. High-Performance ferroelectric Bi4Ti3O12 single crystals grown by top-seeded solution growth method under high-pressure oxygen atmosphere. Jpn. J. Appl. Phys. 2010, 49. [Google Scholar] [CrossRef]
  49. Hirano, K.; Onozuka, H.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M. Leakage current and polarization properties of (Bi0.5Na0.5)TiO3–BaTiO3 single crystals. Key Eng. Mater. 2014, 582, 96–99. [Google Scholar]
  50. Moriyoshi, C.; Hiramoto, S.; Ohkubo, H.; Kuroiwa, Y.; Osawa, H.; Sugimoto, K.; Kimura, S.; Takata, M.; Kitanaka, Y.; Noguchi, Y.; et al. Synchrotron Radiation study on time-resolved tetragonal lattice strain of BaTiO3 under electric field. Jpn. J. Appl. Phys. 2011, 50. [Google Scholar] [CrossRef]
  51. Kitanaka, Y.; Yanai, K.; Noguchi, Y.; Miyayama, M.; Kagawa, Y.; Moriyoshi, C.; Kuroiwa, Y. Non-180° polarization rotation of ferroelectric (Bi0.5Na0.5)TiO3 single crystals under electric field. Phys. Rev. B 2014, 89. [Google Scholar] [CrossRef]
  52. Yanai, K.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M.; Moriyoshi, C.; Kuroiwa, Y.; Kurushima, K.; Mori, S.; Kagawa, Y. Enhanced polarization switching in ferroelectric Bi0.5Na0.5TiO3 single crystals by defect control. Phys. Status Solidi 2013, 443, 791–795. [Google Scholar]
  53. Kitanaka, Y.; Noguchi, Y.; Miyayama, M.; Kagawa, Y.; Moriyoshi, C.; Kuroiwa, Y. Synchrotron radiation analyses of domain switching and lattice strain behaviors for ferroelectric (Bi0.5Na0.5)TiO3 single crystals under electric fields. Ferroelectrics 2013, 443, 1–7. [Google Scholar] [CrossRef]
  54. Zhang, Q.; Zhang, Y.; Wang, F.; Wang, Y.; Lin, D.; Zhao, X.; Luo, H.; Ge, W.; Viehland, D. Enhanced piezoelectric and ferroelectric properties in Mn-doped Na0.5Bi0.5TiO3–BaTiO3 single crystals. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
  55. Aksel, E.; Forrester, J.S.; Nino, J.C.; Page, K.; Shoemaker, D.P.; Jones, J.L. Local atomic structure deviation from average structure of Na0.5Bi0.5TiO3: Combined X-ray and neutron total scattering study. Phys. Rev. B 2013, 87. [Google Scholar] [CrossRef]
  56. Langreth, D.; Perdew, J. Theory of nonuniform electronic systems. I. Analysis of the gradient approximation and a generalization that works. Phys. Rev. B 1980, 21, 5469–5493. [Google Scholar] [CrossRef]
  57. Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
  58. Perdew, J.; Ruzsinszky, A.; Csonka, G.; Vydrov, O.; Scuseria, G.; Constantin, L.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100. [Google Scholar] [CrossRef]
  59. Grüning, M.; Marini, A.; Gonze, X. Implementation and testing of Lanczos-based algorithms for random-phase approximation eigenproblems. Comput. Mater. Sci. 2011, 50, 2148–2156. [Google Scholar] [CrossRef]
  60. Glazer, A.M. The classification of tilted octahedra in perovskites. Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem. 1972, 28, 3384–3392. [Google Scholar] [CrossRef]
  61. Stokes, H.T.; Kisi, E.H.; Hatch, D.M.; Howard, C.J. Group-theoretical analysis of octahedral tilting in ferroelectric perovskites. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 934–938. [Google Scholar] [CrossRef]
  62. Bubesh Babu, J.; He, M.; Zhang, D.F.; Chen, X.L.; Dhanasekaran, R. Enhancement of ferroelectric properties of Na1/2Bi1/2TiO3–BaTiO3 single crystals by Ce dopings. Appl. Phys. Lett. 2007, 90. [Google Scholar] [CrossRef]
  63. Ge, W.; Liu, H.; Zhao, X.; Fang, B.; Li, X.; Wang, F.; Zhou, D.; Yu, P.; Pan, X.; Lin, D.; et al. Crystal growth and high piezoelectric performance of 0.95Na0.5Bi0.5TiO3–0.05BaTiO3 lead-free ferroelectric materials. J. Phys. D Appl. Phys. 2008, 41. [Google Scholar] [CrossRef]
  64. Suzuki, M.; Morishita, A.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M. Polarization and piezoelectric properties of high performance bismuth sodium titanate single crystals grown by high-oxygen-pressure flux method. Jpn. J. Appl. Phys. 2010, 49. [Google Scholar] [CrossRef]
  65. Bethe, K.; Welz, F. Preparation and properties of (Ba,Sr)TiO3 single crystals. Mater. Res. Bull. 1971, 6, 209–217. [Google Scholar] [CrossRef]
  66. Bell, A.J. Phenomenologically derived electric field-temperature phase diagrams and piezoelectric coefficients for single crystal barium titanate under fields along different axes. J. Appl. Phys. 2001, 89. [Google Scholar] [CrossRef]
  67. Li, Y.L.; Cross, L.E.; Chen, L.Q. A phenomenological thermodynamic potential for BaTiO3 single crystals. J. Appl. Phys. 2005, 98. [Google Scholar] [CrossRef]
  68. Uesu, Y.; Matsuda, M.; Yamada, Y.; Fujishiro, K.; Cox, D.E.; Noheda, B.; Shirane, G. Symmetry of high-piezoelectric pb-based complex perovskites at the morphotropic phase boundary: I. Neutron diffraction study on Pb(Zn1/3Nb2/3)O3–9%PbTiO3. J. Phys. Soc. Jpn. 2002, 71, 960–965. [Google Scholar] [CrossRef]
  69. Yamada, Y.; Uesu, Y.; Matsuda, M.; Fujishiro, K.; Cox, D.E.; Noheda, B.; Shirane, G. Symmetry of high-piezoelectric pb based complex perovskites at the morphotropic phase boundary: II. Theoretical treatment. J. Phys. Soc. Jpn. 2002, 71, 966–970. [Google Scholar] [CrossRef]
  70. Ohwada, K.; Hirota, K.; Rehrig, P.; Fujii, Y.; Shirane, G. Neutron diffraction study of field-cooling effects on the relaxor ferroelectric Pb[(Zn1/3Nb2/3)0.92Ti0.08]O3. Phys. Rev. B 2003, 67. [Google Scholar] [CrossRef]
  71. Rajan, K.K.; Shanthi, M.; Chang, W.S.; Jin, J.; Lim, L.C. Dielectric and piezoelectric properties of [001] and [011]-poled relaxor ferroelectric PZN–PT and PMN–PT single crystals. Sens. Actuators A Phys. 2007, 133, 110–116. [Google Scholar] [CrossRef]
  72. Brown, I.D.; Altermatt, D. Bond-valence parameters obtained from a systematic analysis of the Inorganic Crystal Structure Database. Acta Crystallogr. Sect. B Struct. Sci. 1985, 41, 244–247. [Google Scholar] [CrossRef]
  73. Sayers, D.; Stern, E.; Lytle, F. New Technique for Investigating noncrystalline structures: Fourier analysis of the extended X-ray—Absorption fine structure. Phys. Rev. Lett. 1971, 27, 1204–1207. [Google Scholar] [CrossRef]
  74. Zhao, X.; Vanderbilt, D. Phonons and lattice dielectric properties of zirconia. Phys. Rev. B 2002, 65. [Google Scholar] [CrossRef]
  75. Zhong, W.; Vanderbilt, D. Phase transitions in BaTiO3 from first principles. Phys. Rev. Lett. 1994, 73, 1861–1864. [Google Scholar] [CrossRef]
  76. Bagayoko, D.; Zhao, G.L.; Fan, J.D.; Wang, J.T. Ab initio calculations of the electronic structure and optical properties of ferroelectric tetragonal. J. Phys. Condens. Matter 1998, 10, 5645–5655. [Google Scholar] [CrossRef]
  77. Gou, G.Y.; Bennett, J.W.; Takenaka, H.; Rappe, A.M. Post density functional theoretical studies of highly polar semiconductive Pb(Ti1−xNix)O3−x solid solutions: Effects of cation arrangement on band gap. Phys. Rev. B 2011, 83. [Google Scholar] [CrossRef]
  78. Miyazawa, H.; Natori, E.; Miyashita, S.; Shimoda, T.; Ishii, F.; Oguchi, T. Electronic states of perovskite-type oxides and ferroelectricity. Jpn. J. Appl. Phys. 2000, 39, 5679–5682. [Google Scholar] [CrossRef]
  79. Kitanaka, Y.; Ogino, M.; Hirano, K.; Noguchi, Y.; Miyayama, M.; Kagawa, Y.; Moriyoshi, C.; Kuroiwa, Y.; Torii, S.; Kamiyama, T. Crystal Structural analyses of ferrielectric tetragonal (Bi1/2Na1/2)TiO3–7%BaTiO3 powders and single crystals. Jpn. J. Appl. Phys. 2013, 52. [Google Scholar] [CrossRef]

Share and Cite

MDPI and ACS Style

Ogino, M.; Noguchi, Y.; Kitanaka, Y.; Miyayama, M.; Moriyoshi, C.; Kuroiwa, Y. Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3–BaTiO3 Single Crystals under Electric Fields. Crystals 2014, 4, 273-295. https://doi.org/10.3390/cryst4030273

AMA Style

Ogino M, Noguchi Y, Kitanaka Y, Miyayama M, Moriyoshi C, Kuroiwa Y. Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3–BaTiO3 Single Crystals under Electric Fields. Crystals. 2014; 4(3):273-295. https://doi.org/10.3390/cryst4030273

Chicago/Turabian Style

Ogino, Motohiro, Yuji Noguchi, Yuuki Kitanaka, Masaru Miyayama, Chikako Moriyoshi, and Yoshihiro Kuroiwa. 2014. "Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3–BaTiO3 Single Crystals under Electric Fields" Crystals 4, no. 3: 273-295. https://doi.org/10.3390/cryst4030273

APA Style

Ogino, M., Noguchi, Y., Kitanaka, Y., Miyayama, M., Moriyoshi, C., & Kuroiwa, Y. (2014). Polarization Rotation and Monoclinic Distortion in Ferroelectric (Bi0.5Na0.5)TiO3–BaTiO3 Single Crystals under Electric Fields. Crystals, 4(3), 273-295. https://doi.org/10.3390/cryst4030273

Article Metrics

Back to TopTop