Soft Elasticity in Main Chain Liquid Crystal Elastomers
Abstract
:1. Introduction



2. Nematic Liquid Crystal Elastomer (NLCE)


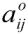 is the step length tensor at the time of crosslinking the network and
is the step length tensor at the time of crosslinking the network and 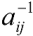 is the inverse of the step length tensor under any general deformation. The above free energy density FLCE incorporates the effect of polymer chain conformation via the step length tensors which carry the information about the nematic order, which was missing from FE. This form of the elastic free energy is useful in discussions of soft elasticity, later in this article. Considering a uniaxial strain geometry similar to the previous section, the expression of free energy now becomes [15]:
is the inverse of the step length tensor under any general deformation. The above free energy density FLCE incorporates the effect of polymer chain conformation via the step length tensors which carry the information about the nematic order, which was missing from FE. This form of the elastic free energy is useful in discussions of soft elasticity, later in this article. Considering a uniaxial strain geometry similar to the previous section, the expression of free energy now becomes [15]:

 . This form of FLCE for nematic elastomers incorporates the anisotropy of the polymer and leads to the expression of true stress of NLCEs:
. This form of FLCE for nematic elastomers incorporates the anisotropy of the polymer and leads to the expression of true stress of NLCEs:



2.1. Soft Elasticity of Nematic Liquid Crystal Elastomers
 and aij, respectively, in Equation (1). The deformation tensor λij determines how the final state is reached. Generally, macroscopic deformations cause a distortion of the polymer chain conformation. However, there exist deformations in which the shape of the polymer chain conformation is not altered; but rotated in a continuous manner until the nematic director and the stretch direction become parallel without affecting S. Such soft modes of deformations are also called Goldstone modes [11]. Generally, for any deformation, one can find a frame of reference in which the deformation appears as shear and can be separated into symmetric and anti-symmetric components [26]. For example, uniaxial elongation of a monodomain NLCE accompanied by contraction in the perpendicular directions can be viewed as pure shears in a rotated frame of reference. Pure shear is symmetric and does not contain a rotational component while an anti-symmetric part contains rotations. An ideal elastomer matrix is defined by the position of the cross-linkers. During soft deformation, they move in such a way that their overall distribution remains unchanged [11] but the polymer conformation between the cross-linked points rotates towards the stretch direction. The presence of finite-size rod like cross-linkers [48] and/or compositional fluctuation of the polymer strands [49] lead to deviation from this ideal behavior and towards “semi-soft elasticity” [45].
and aij, respectively, in Equation (1). The deformation tensor λij determines how the final state is reached. Generally, macroscopic deformations cause a distortion of the polymer chain conformation. However, there exist deformations in which the shape of the polymer chain conformation is not altered; but rotated in a continuous manner until the nematic director and the stretch direction become parallel without affecting S. Such soft modes of deformations are also called Goldstone modes [11]. Generally, for any deformation, one can find a frame of reference in which the deformation appears as shear and can be separated into symmetric and anti-symmetric components [26]. For example, uniaxial elongation of a monodomain NLCE accompanied by contraction in the perpendicular directions can be viewed as pure shears in a rotated frame of reference. Pure shear is symmetric and does not contain a rotational component while an anti-symmetric part contains rotations. An ideal elastomer matrix is defined by the position of the cross-linkers. During soft deformation, they move in such a way that their overall distribution remains unchanged [11] but the polymer conformation between the cross-linked points rotates towards the stretch direction. The presence of finite-size rod like cross-linkers [48] and/or compositional fluctuation of the polymer strands [49] lead to deviation from this ideal behavior and towards “semi-soft elasticity” [45]. 
3. Smectic Liquid Crystal Elastomers (SmLCE)
3.1. Soft Elasticity and the Shape Memory Effect in Smectic Liquid Crystal Elastomers
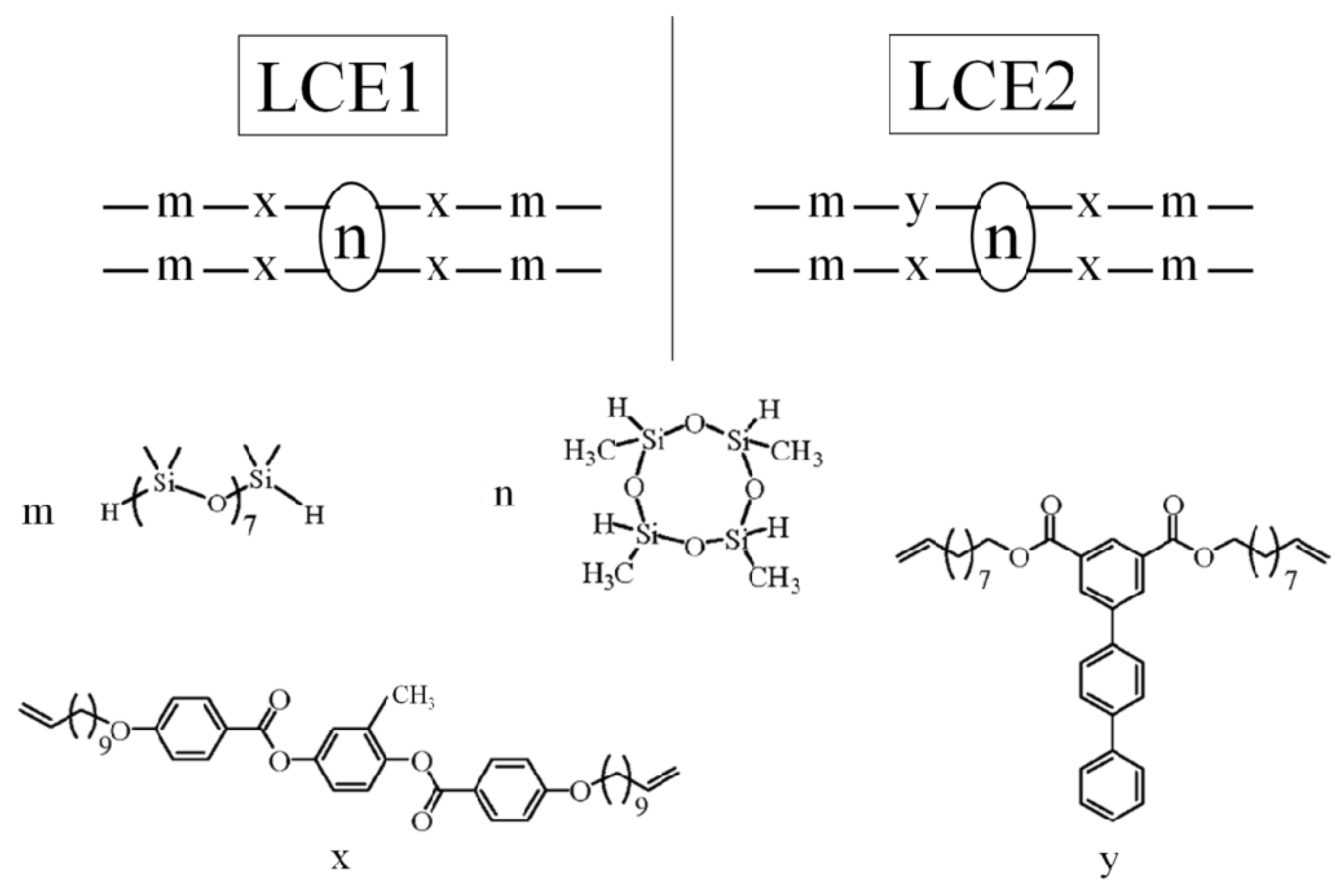
3.2. Transverse Rod Incorporation for Auxetic Effect Material
3.3. Polydomain Smectic-C Main Chain Liquid Crystal Elastomers
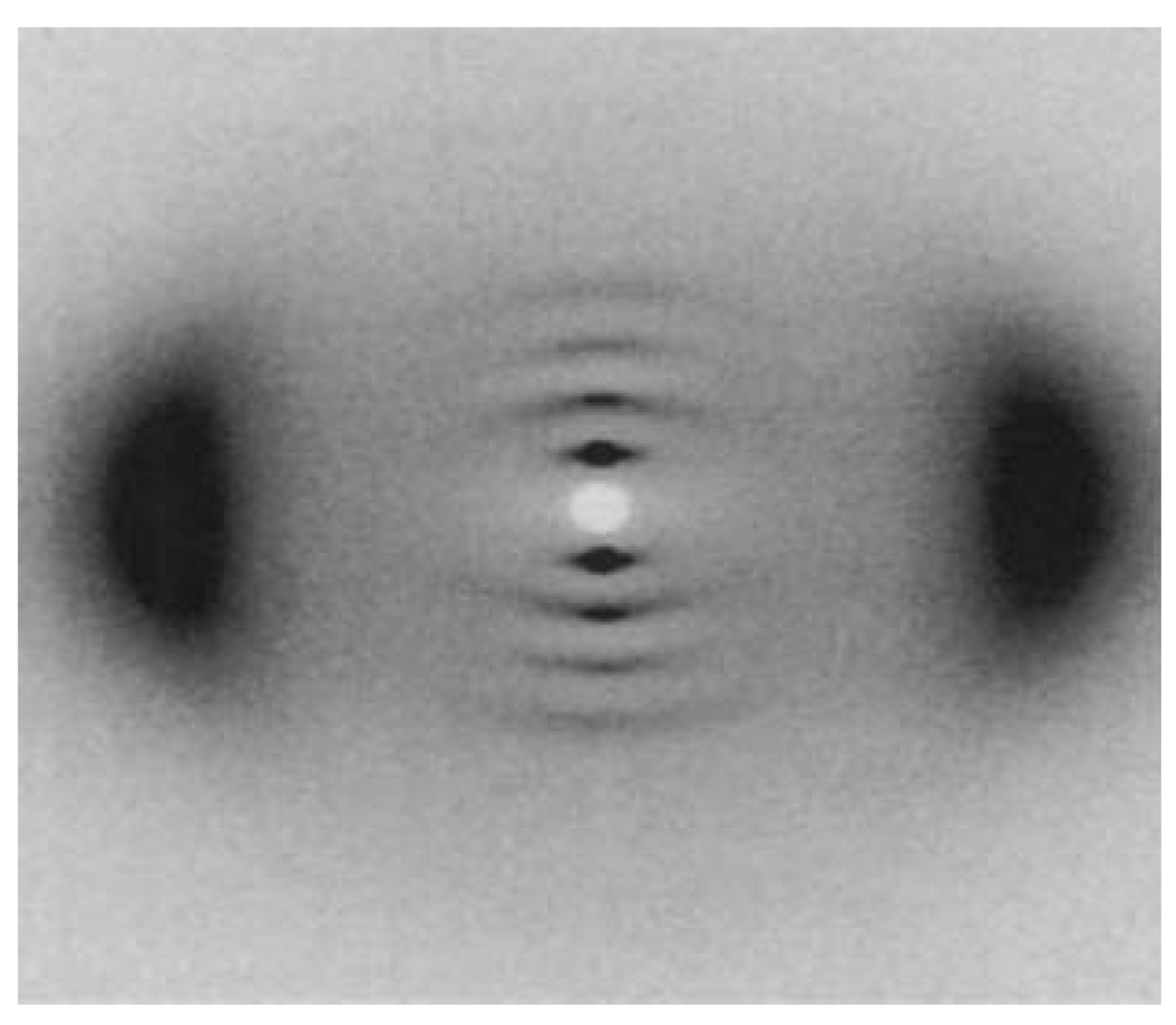
 is predominantly aligned along the stretch direction. A monodomain state such as this can again be stretched, both parallel and perpendicular to
is predominantly aligned along the stretch direction. A monodomain state such as this can again be stretched, both parallel and perpendicular to  , to study the effect on the elongated monodomain state.
, to study the effect on the elongated monodomain state.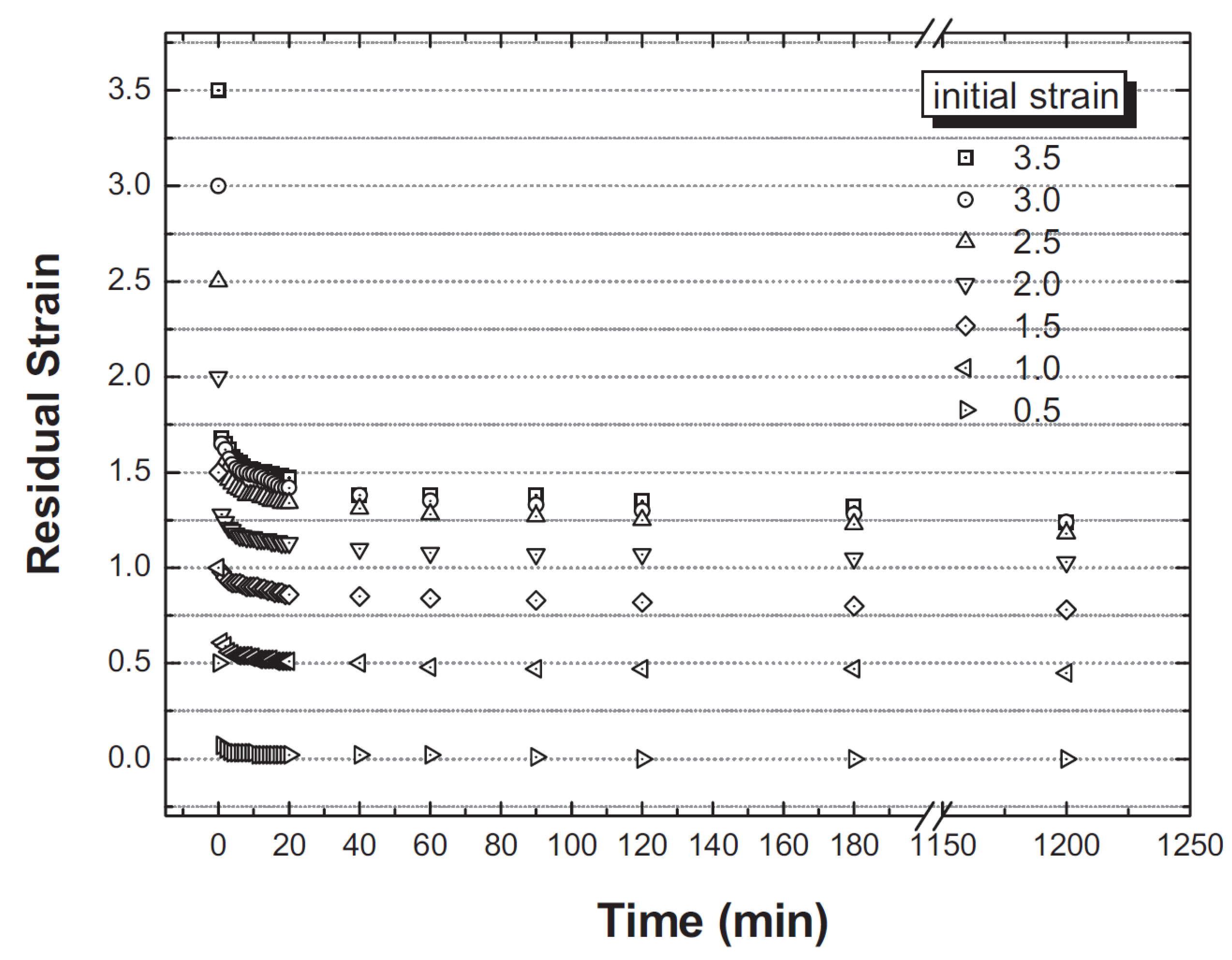
 , and also in the initially polydomain state. The value of the elastic modulus is higher when stretched parallel to
, and also in the initially polydomain state. The value of the elastic modulus is higher when stretched parallel to  than in one in the perpendicular direction. Also, the width of the plateau region is considerably reduced when stretched parallel to
than in one in the perpendicular direction. Also, the width of the plateau region is considerably reduced when stretched parallel to  . For stretching in the direction perpendicular to
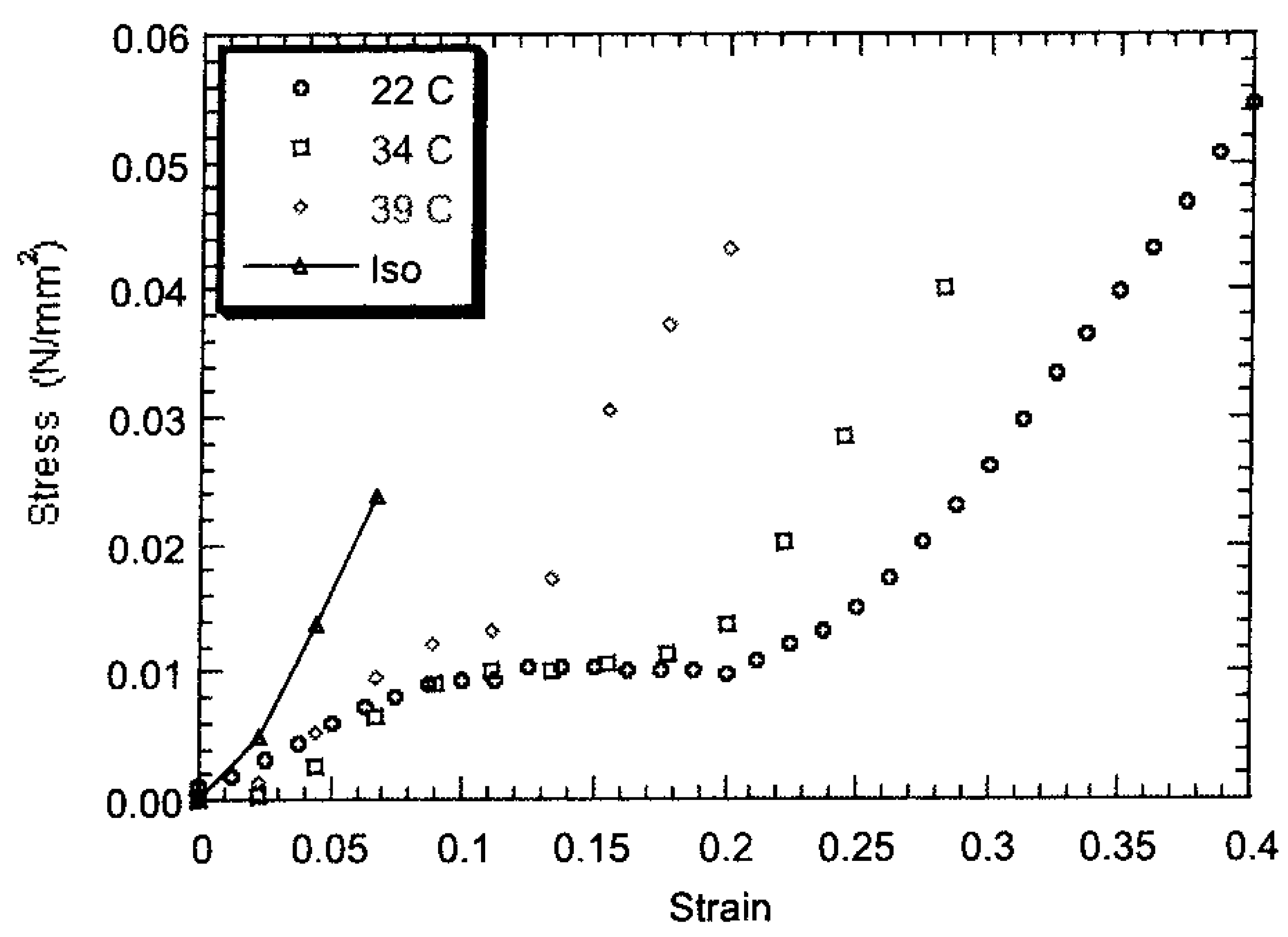
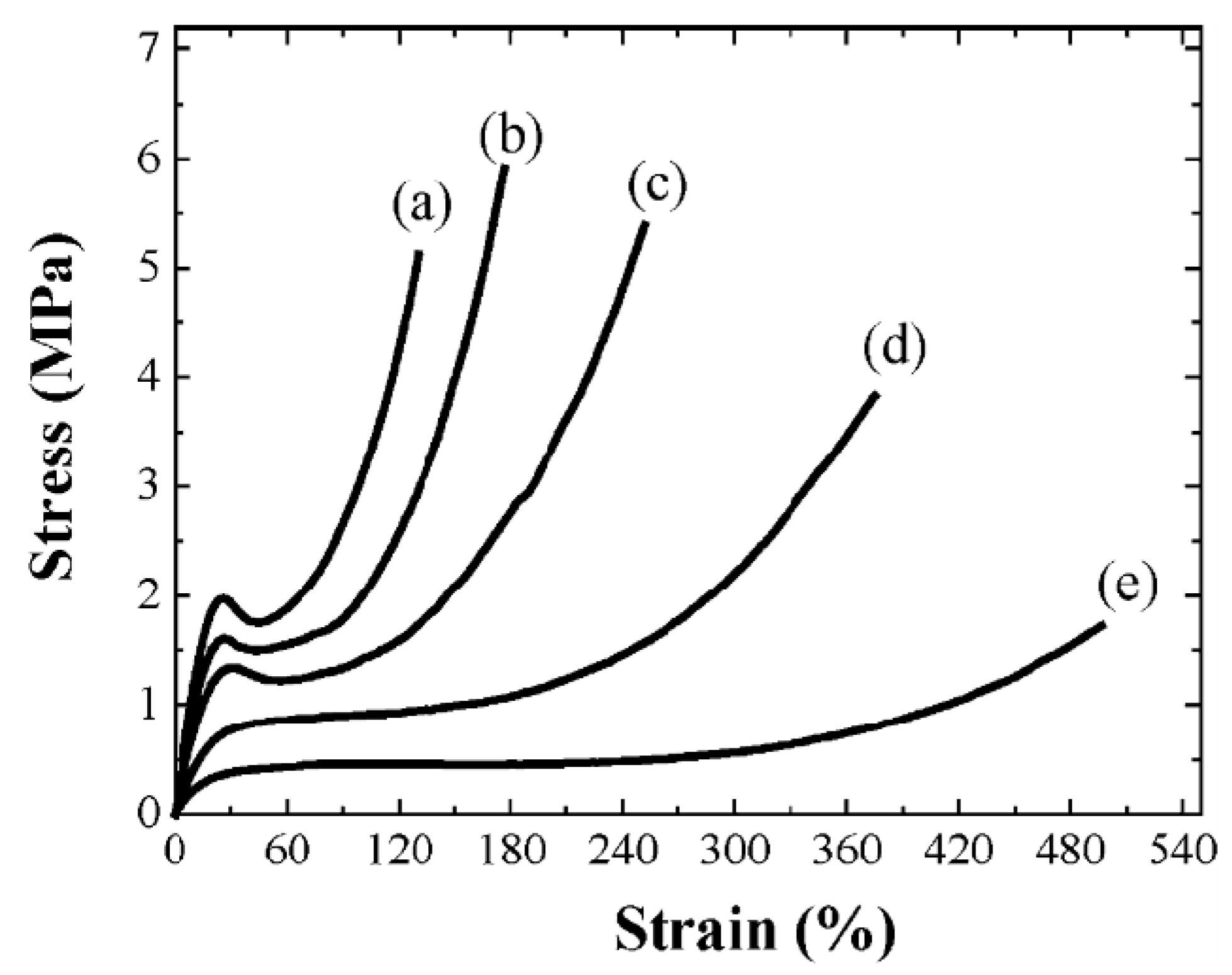
. For stretching in the direction perpendicular to  the stress-strain plateau extends up to a large strain (of ~500%) until the film breaks [65]. A volume preserving narrowing of the width is observed as the film is elongated [50]. To study this effect as a function of cross-linking density, several samples were prepared with cross-linking concentrations from 5% to 25%. Increasing crosslinkage density gave rise to higher rigidity and an increase in glass transition temperature [60]. Also, the P–M plateau became shorter with increasing crosslinker content, and at higher concentrations, a yield point was observed, Figure 8.
the stress-strain plateau extends up to a large strain (of ~500%) until the film breaks [65]. A volume preserving narrowing of the width is observed as the film is elongated [50]. To study this effect as a function of cross-linking density, several samples were prepared with cross-linking concentrations from 5% to 25%. Increasing crosslinkage density gave rise to higher rigidity and an increase in glass transition temperature [60]. Also, the P–M plateau became shorter with increasing crosslinker content, and at higher concentrations, a yield point was observed, Figure 8.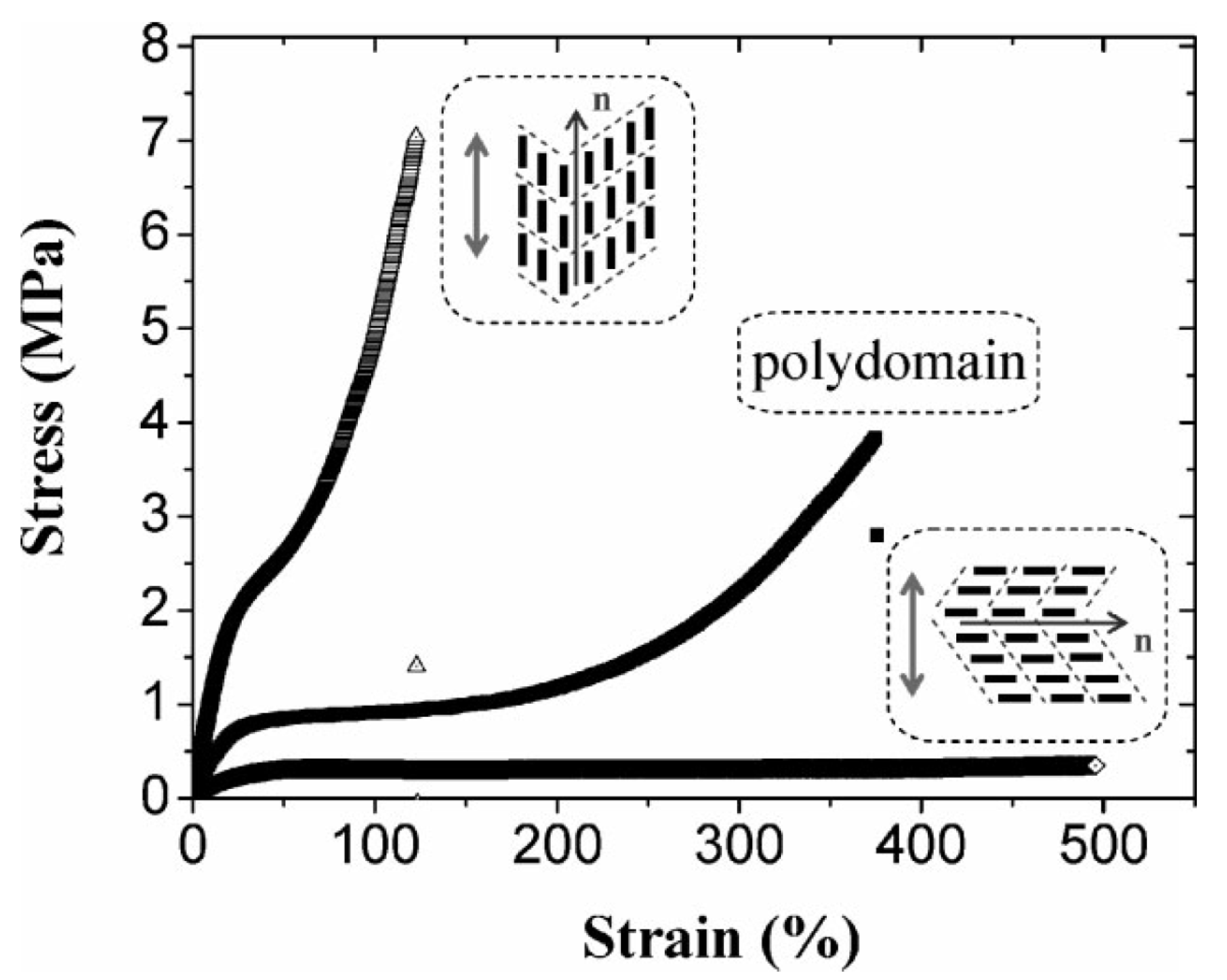
3.4. Polydomain—Monodomain Transition under Uniaxial Strain
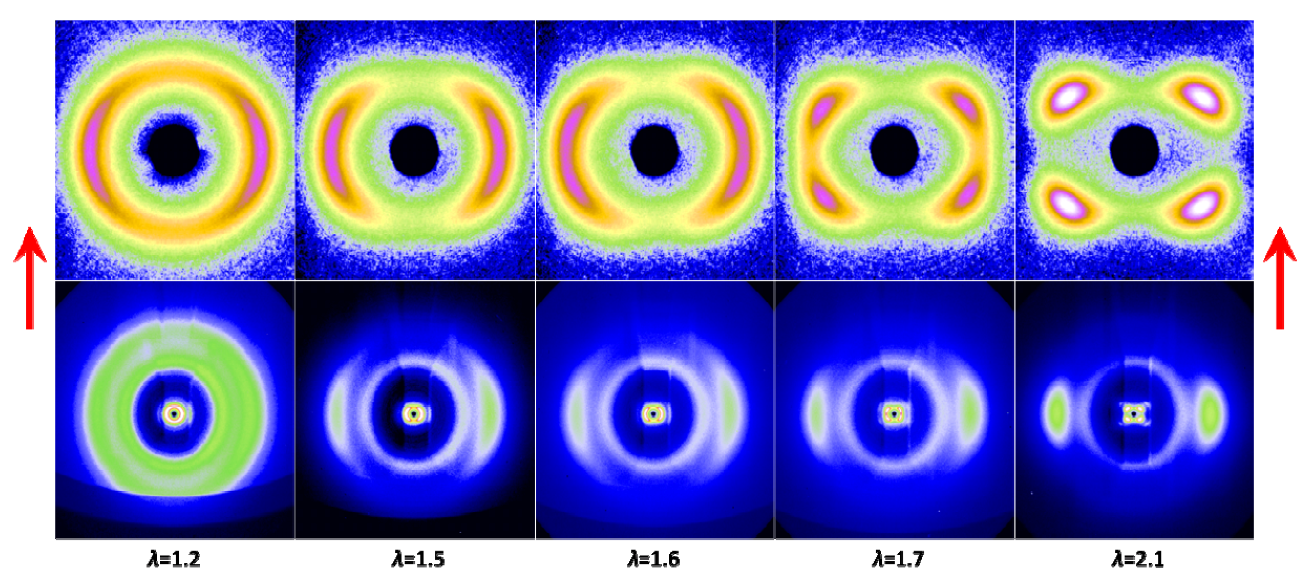
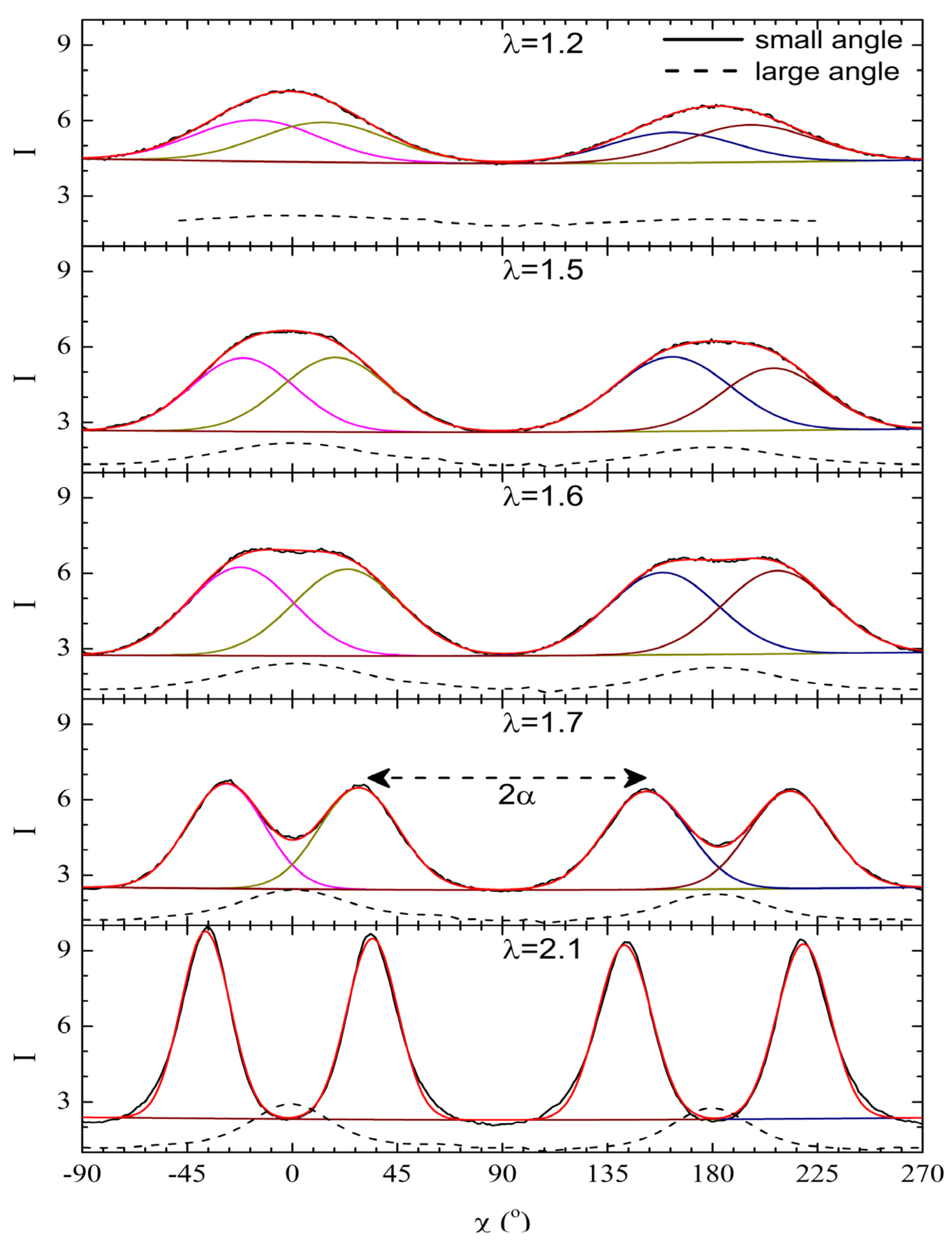
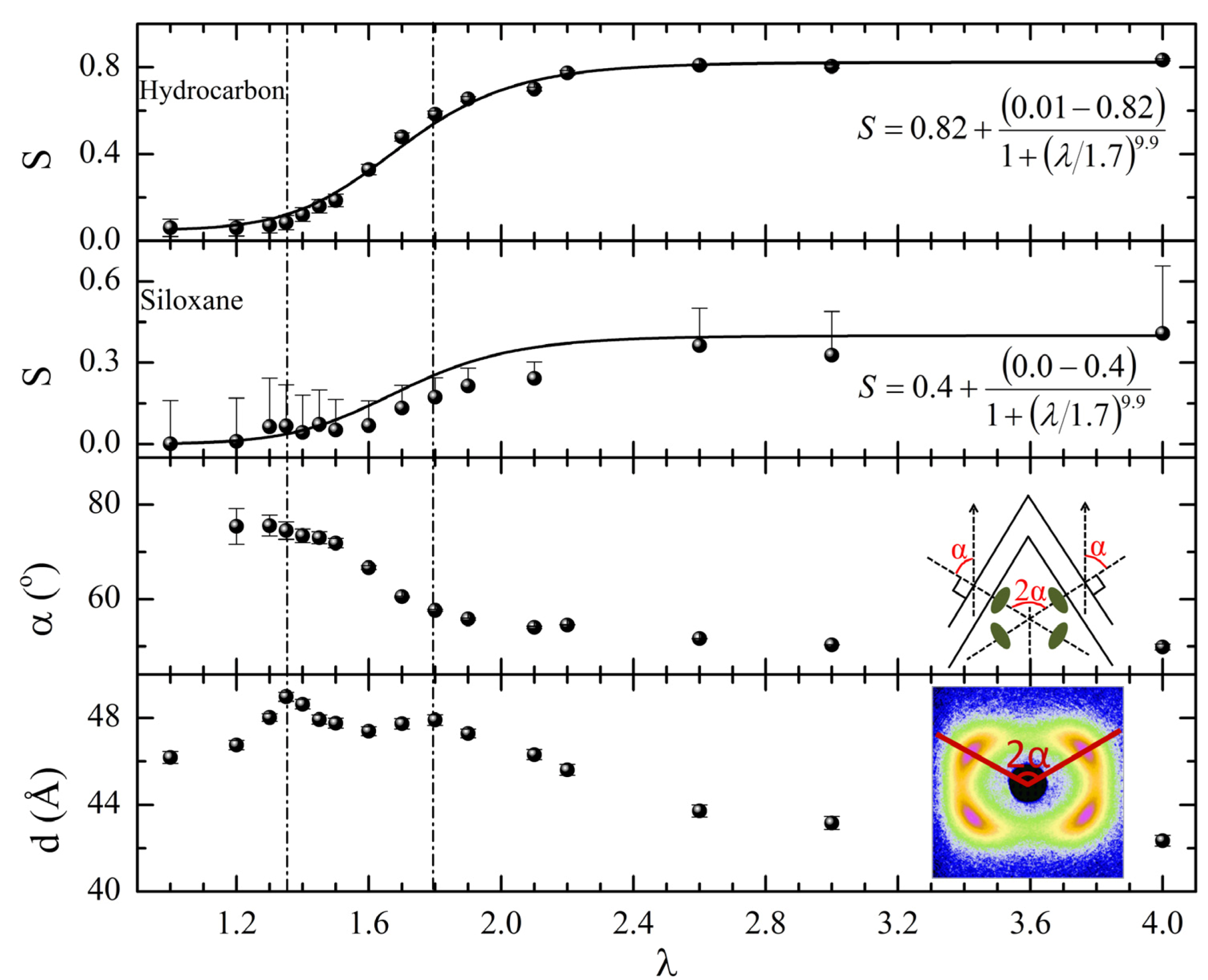
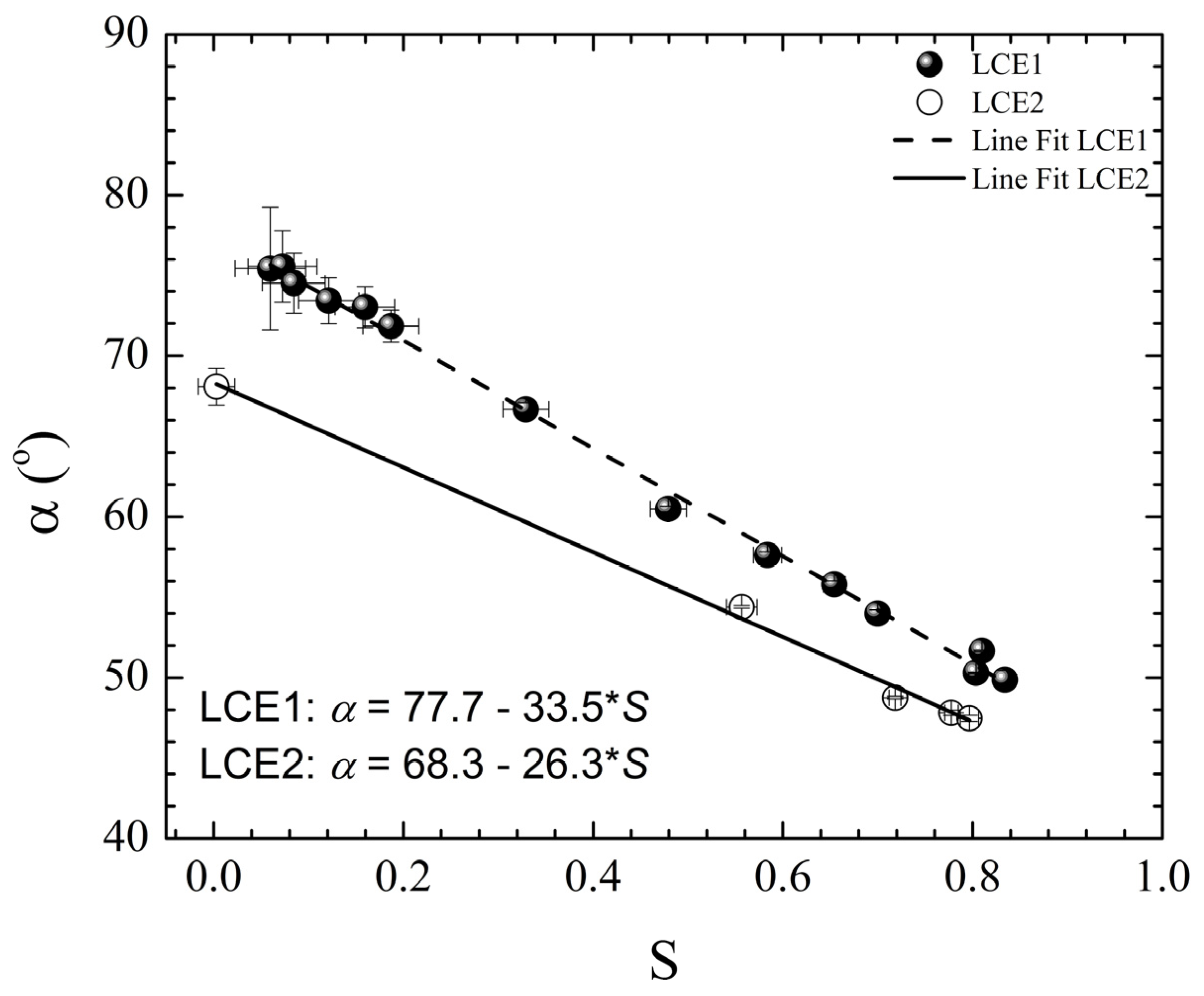
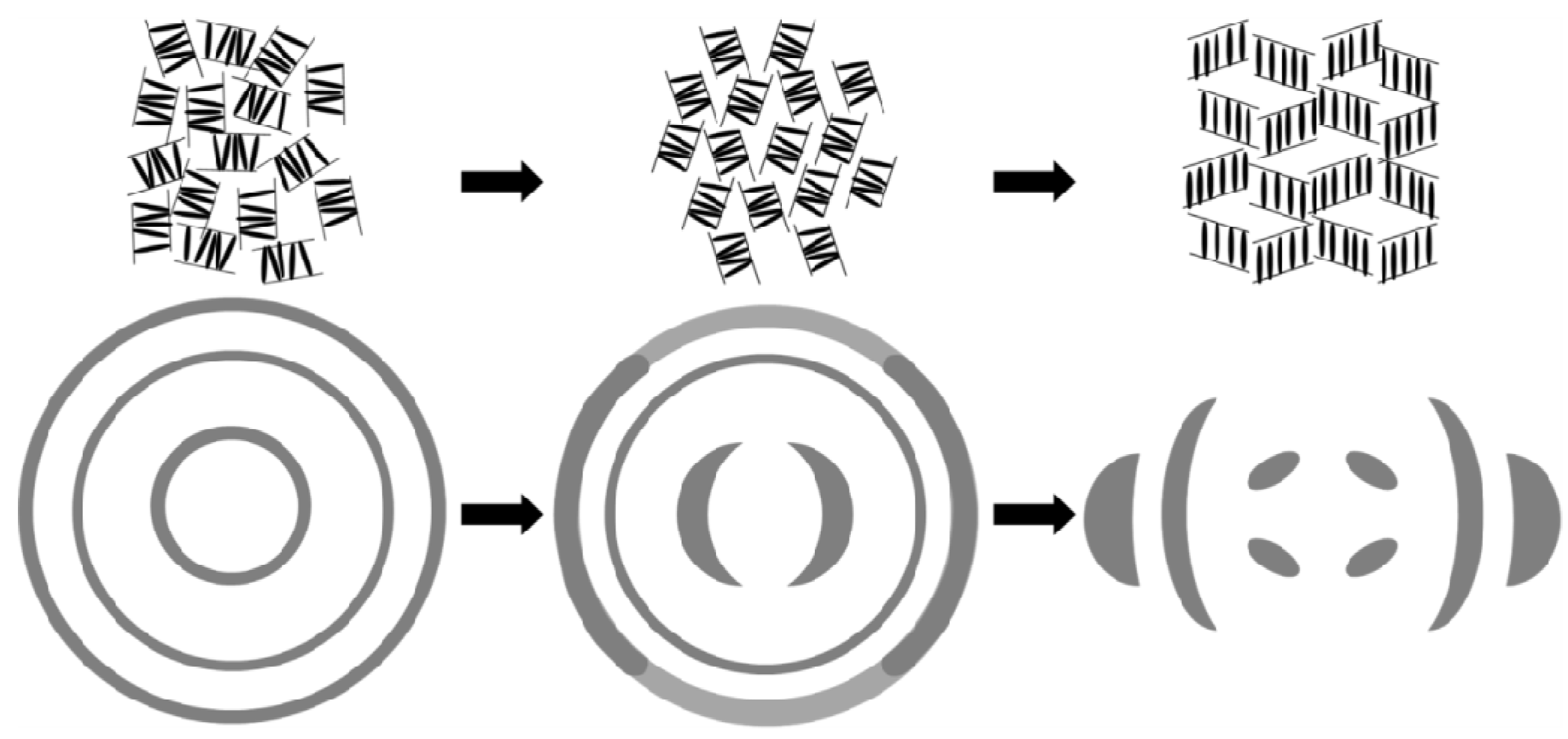
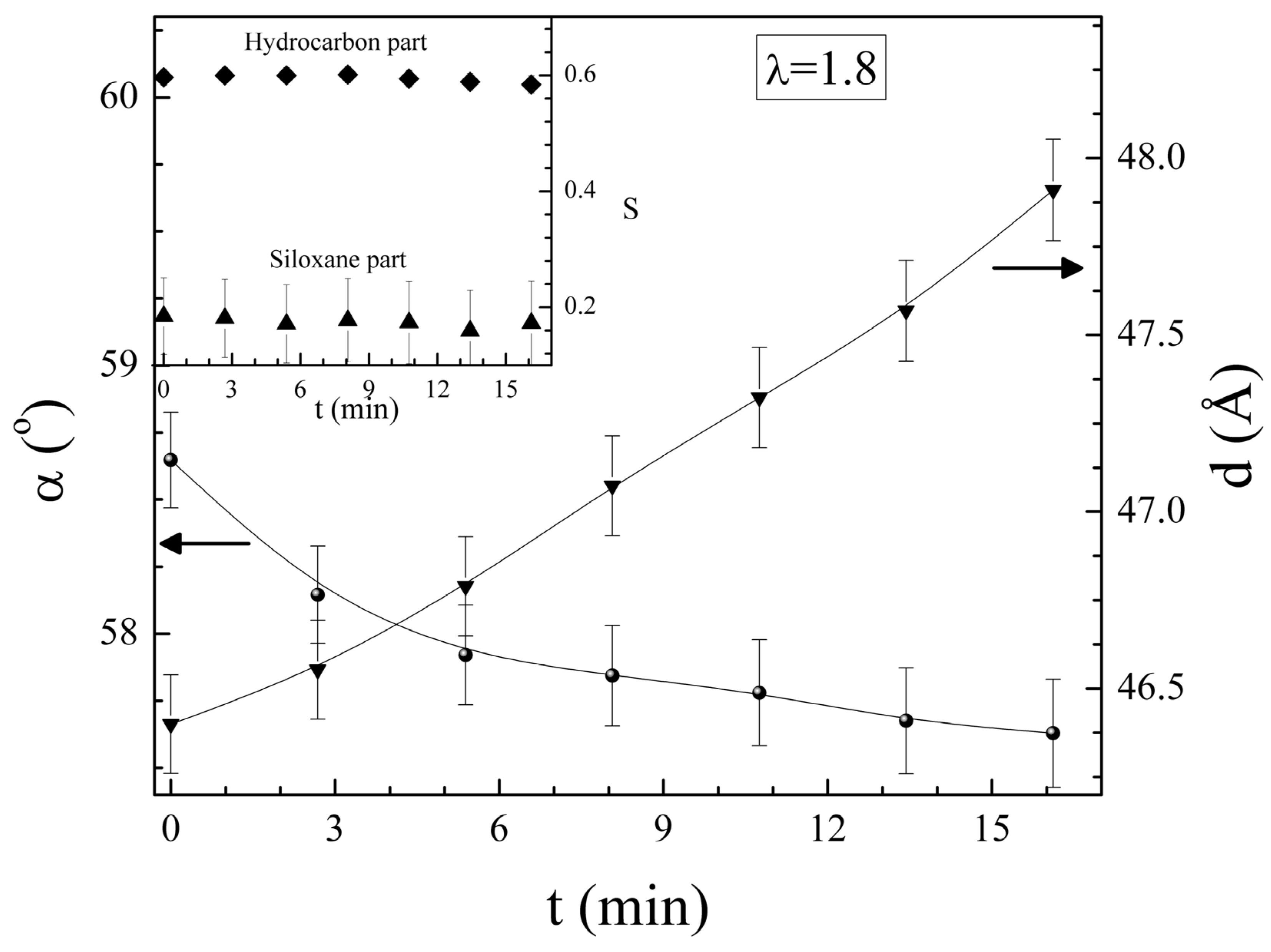
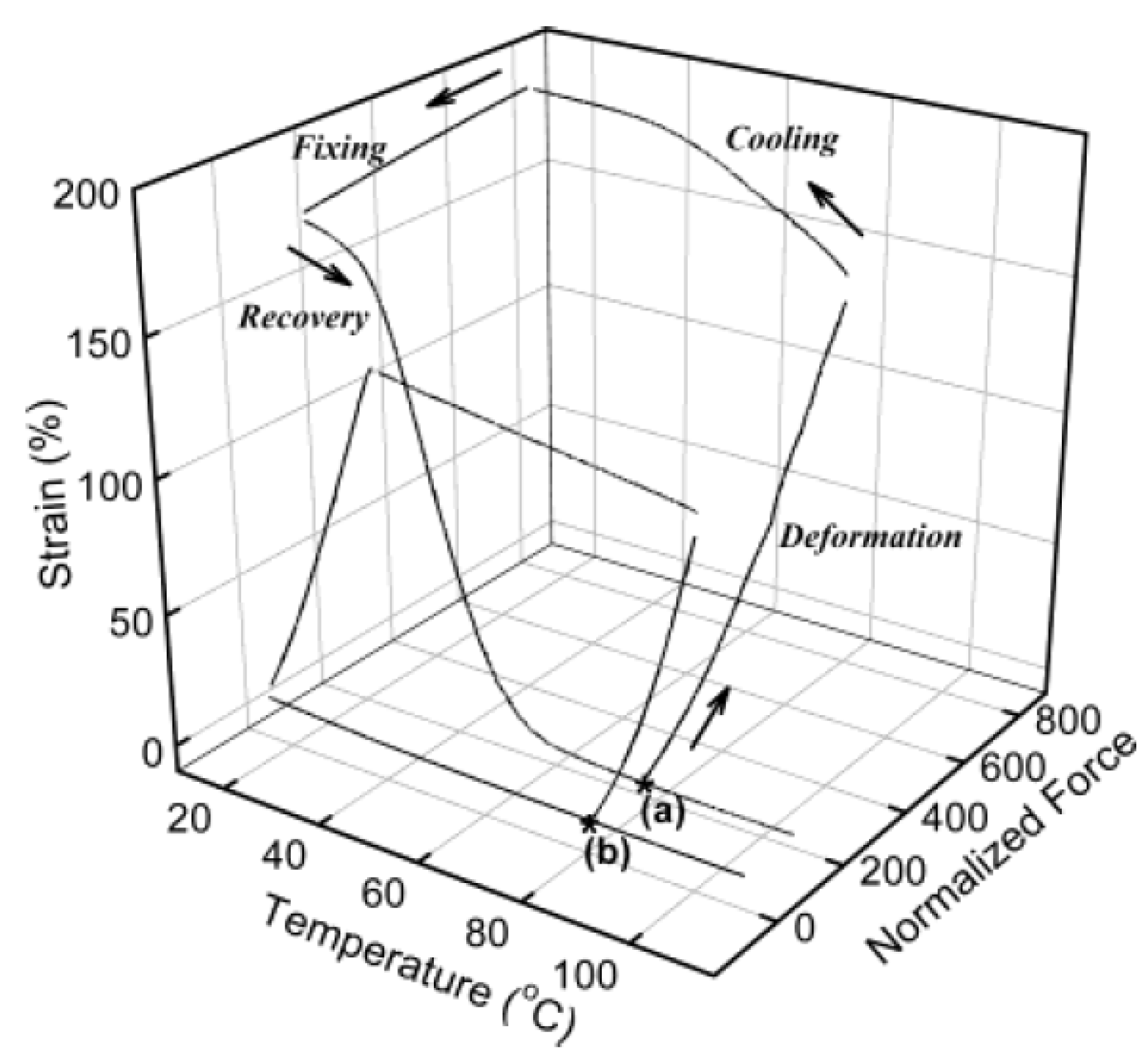
3.5. Strain Retention


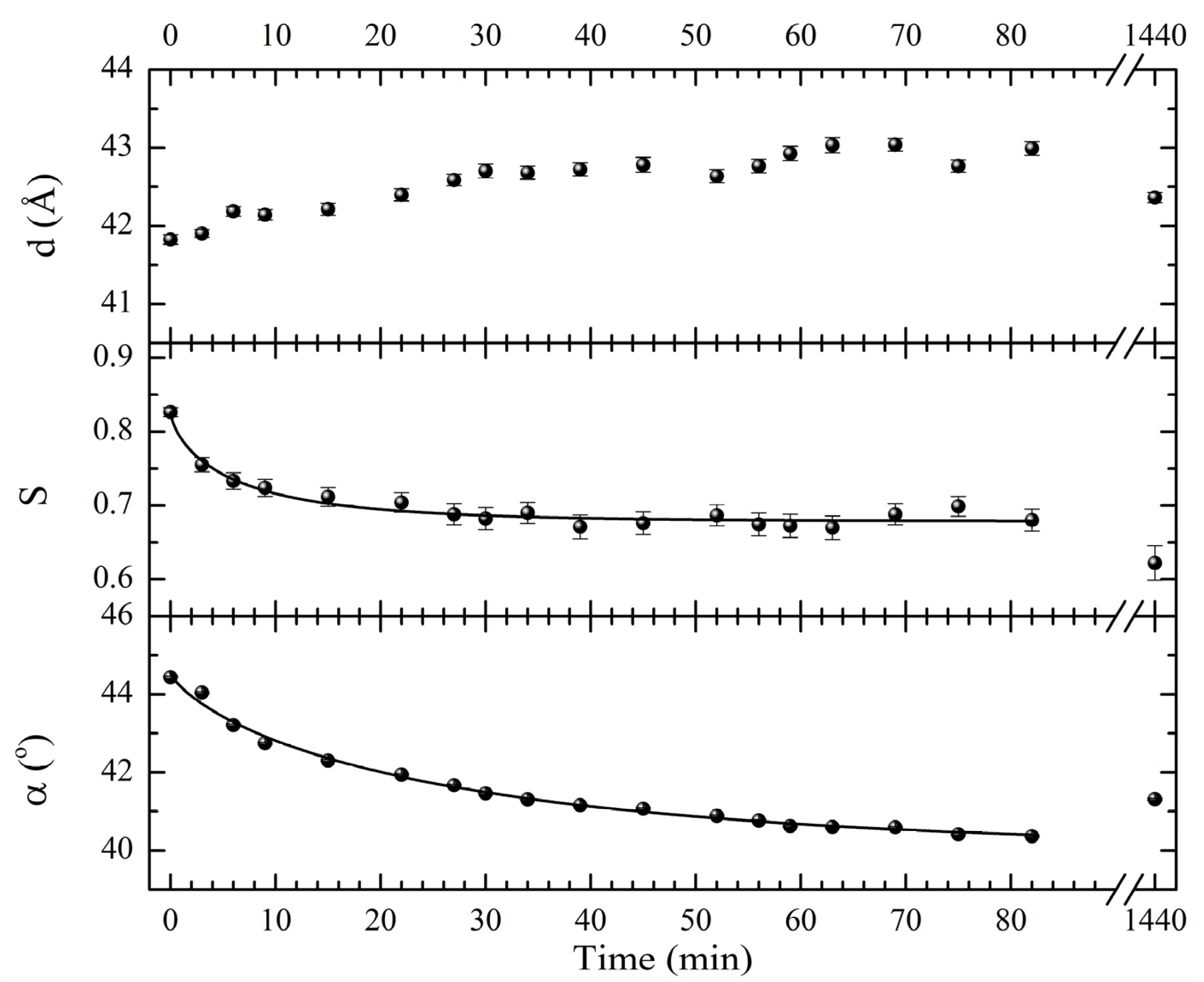
3.6. Thermal Length Recovery
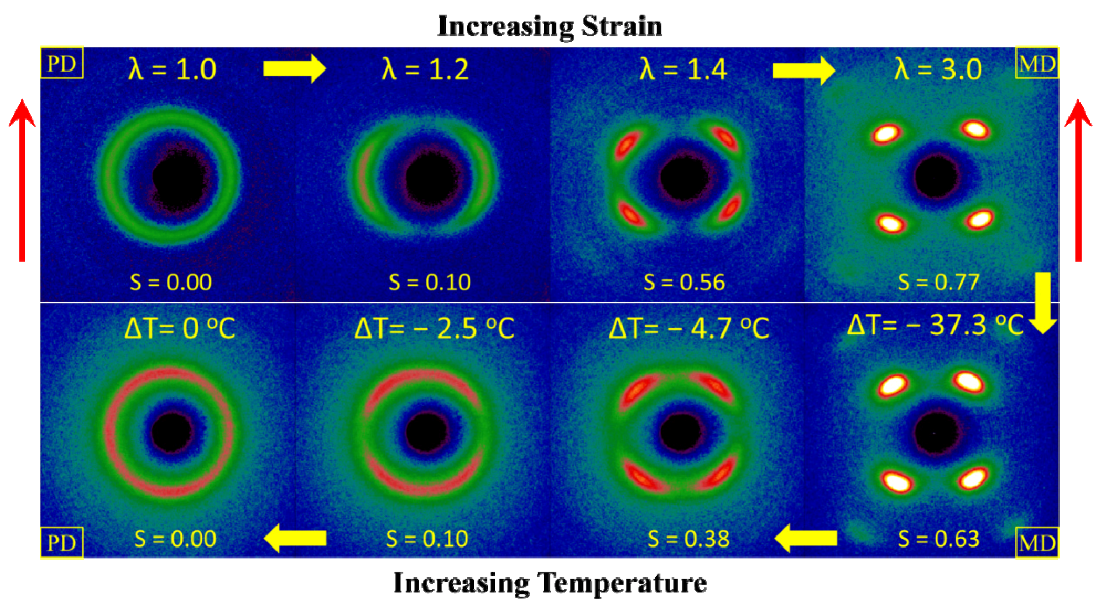
 gradually become parallel to the stretch direction and deplete the population of perpendicularly oriented mesogens. The smectic layers are oriented symmetrically with respect to the mesogens’ long axis (i.e., the stretch direction) and form smectic layers in a manner that will statistically resemble chevron-like geometry. As the mesogen distribution becomes increasingly parallel to the strain direction in the SmC phase, the chevron angle decreases ultimately saturating below 45° in the secondary monodomain state with the apex of the chevron pointing in the direction of stretch (Figure 13). During the thermally driven recovery, the distribution of polymer chains and the mesogens become increasingly random, and the chevrons begin to relax back to a polydomain state. The smectic layers continue to exhibit an orientational preference perpendicular to the stretch direction. Naturally, the remnant chevrons re-merge forming poorly defined layers that are statistically perpendicular to the stretch direction which give rise to horizontal arcs in the diffraction pattern until the system enters the isotropic phase at TI. So, these elastomers do not quite follow an entirely reverse path.
gradually become parallel to the stretch direction and deplete the population of perpendicularly oriented mesogens. The smectic layers are oriented symmetrically with respect to the mesogens’ long axis (i.e., the stretch direction) and form smectic layers in a manner that will statistically resemble chevron-like geometry. As the mesogen distribution becomes increasingly parallel to the strain direction in the SmC phase, the chevron angle decreases ultimately saturating below 45° in the secondary monodomain state with the apex of the chevron pointing in the direction of stretch (Figure 13). During the thermally driven recovery, the distribution of polymer chains and the mesogens become increasingly random, and the chevrons begin to relax back to a polydomain state. The smectic layers continue to exhibit an orientational preference perpendicular to the stretch direction. Naturally, the remnant chevrons re-merge forming poorly defined layers that are statistically perpendicular to the stretch direction which give rise to horizontal arcs in the diffraction pattern until the system enters the isotropic phase at TI. So, these elastomers do not quite follow an entirely reverse path. 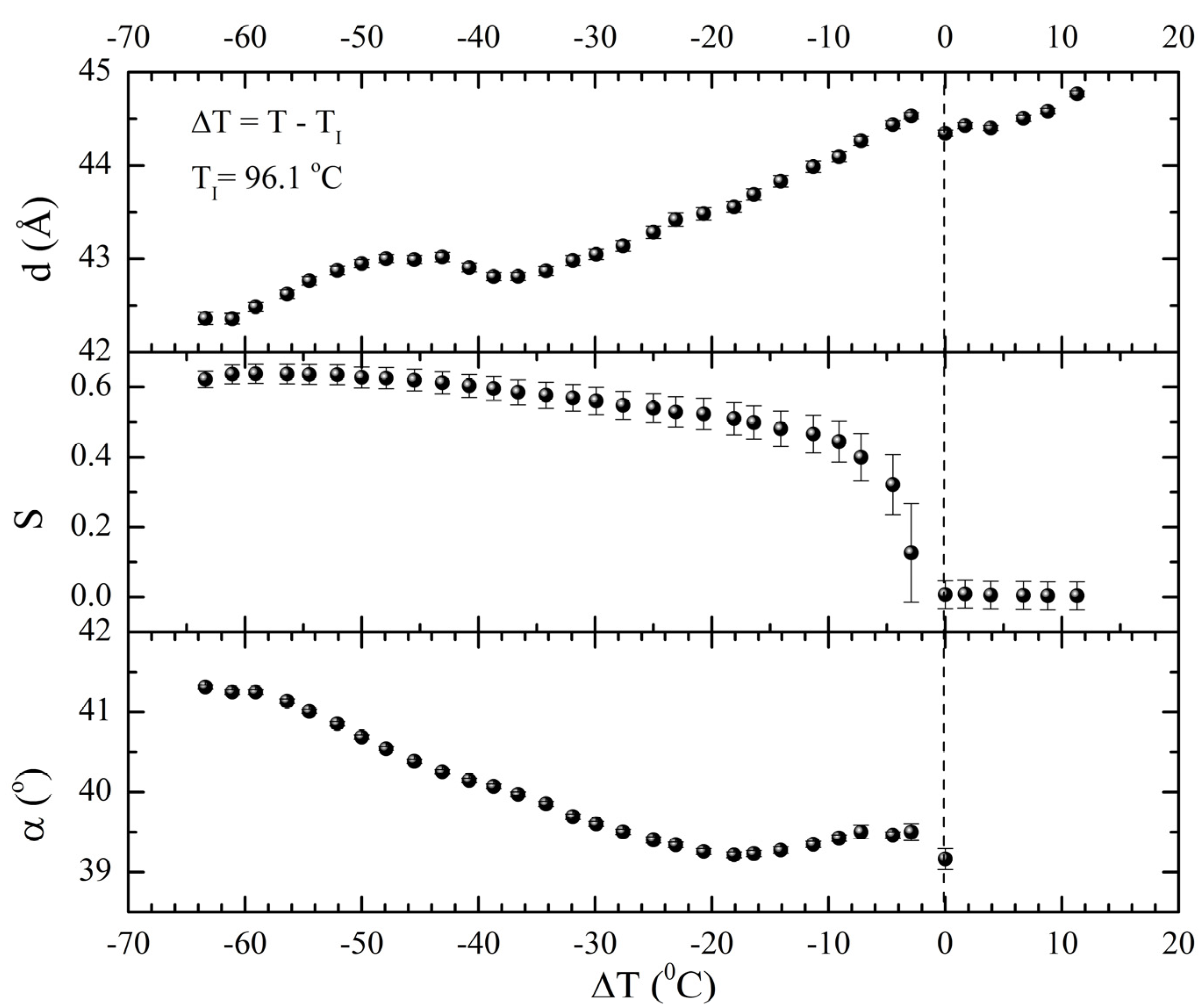
4. Conclusions
Acknowledgments
Conflict of Interest
References and Notes
- Thomsen, D.L.; Keller, P.; Naciri, J.; Pink, R.; Jeon, H.; Shenoy, D.; Ratna, B.R. Liquid crystal elastomers with mechanical properties of a muscle. Macromolecules 2001, 34, 5868–5875. [Google Scholar] [CrossRef]
- Buguin, A.; Li, M.H.; Silberzan, P.; Ladoux, B.; Keller, P. Micro-actuators: When artificial muscles made of nematic liquid crystal elastomers meet soft lithography. J. Am. Chem. Soc. 2006, 128, 1088–1089. [Google Scholar]
- Li, M.H.; Keller, P. Artificial muscles based on liquid crystal elastomers. Philos. Trans. R. Soc. Lond. Ser. A 2006, 364, 2763–2777. [Google Scholar] [CrossRef]
- Wermter, H.; Finkelmann, H. Liquid crystalline elastomers as artificial muscles. e-Polymers 2001, 013:1–013:13. [Google Scholar]
- Davis, K.A.; Burke, K.A.; Mather, P.T.; Henderson, J.H. Dynamic cell behavior on shape memory polymer substrates. Biomaterials 2011, 32, 2285–2293. [Google Scholar] [CrossRef]
- Liu, C.; Qin, H.; Mather, P.T. Review of progress in shape-memory polymers. J. Mater. Chem. 2007, 17, 1543–1558. [Google Scholar] [CrossRef]
- Rousseau, I.A.; Mather, P.T. Shape memory effect exhibited by smectic-C liquid crystalline elastomers. J. Am. Chem. Soc. 2003, 125, 15300–15301. [Google Scholar] [CrossRef]
- Burke, K.A.; Mather, P.T. Soft shape memory in main-chain liquid crystalline elastomers. J. Mater. Chem. 2010, 20, 3449–3457. [Google Scholar] [CrossRef]
- Warner, M.; Bladon, P.; Terentjev, E.M. Soft elasticity—Deformation without resistance in liquid-crystal elastomers. J. Phys. II 1994, 4, 93–102. [Google Scholar] [CrossRef]
- Verwey, G.C.; Warner, M. Soft rubber elasticity. Macromolecules 1995, 28, 4303–4306. [Google Scholar] [CrossRef]
- Olmsted, P.D. Rotational invariance and goldstone modes in nematic elastomers and gels. J. Phys. II 1994, 4, 2215–2230. [Google Scholar] [CrossRef]
- Finkelmann, H.; Greve, A.; Warner, M. The elastic anisotropy of nematic elastomers. Eur. Phys. J. E 2001, 5, 281–293. [Google Scholar] [CrossRef]
- Tajbakhsh, A.R.; Terentjev, E.M. Spontaneous thermal expansion of nematic elastomers. Eur. Phys. J. E 2001, 6, 181–188. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Scalia, G. A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-, bio- and microtechnology. Curr. Appl. Phys. 2012, 12, 1387–1412. [Google Scholar] [CrossRef]
- Warner, M.; Terentjev, E.M. Liquid Crystal Elastomers; Oxford University Press Inc.: New York, NY, USA, 2007. [Google Scholar]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar] [CrossRef]
- Brehmer, M.; Brommel, F.; Cordoyiannis, G.; Finkelmann, H.; Kramer, D.; Kutnjak, Z.; Lebar, A.; Ohm, C.; Ostrovskii, B.I.; Palffy-Muhoray, P.; et al. Liquid Crystal Elastomers: Materials and Applications; de Jeu, W.H., Ed.; Springer: Berlin and Heidelberg, Germany, 2010; Volume 250. [Google Scholar]
- Sanchez-Ferrer, A.; Fischl, T.; Stubenrauch, M.; Albrecht, A.; Wurmus, H.; Hoffmann, M.; Finkelmann, H. Liquid-crystalline elastomer microvalve for microfluidics. Adv. Mater. 2011, 23, 4526–4530. [Google Scholar] [CrossRef]
- Ping, X.; Rongben, Z. Liquid crystal elastomers, networks and gels: Advanced smart materials. J. Mater. Chem. 2005, 15, 2529–2550. [Google Scholar] [CrossRef]
- Ren, W.; Griffin, A.C. Mechanism of strain retention and shape memory in main chain liquid crystalline networks. Phys. Status Solidi B 2012, 249, 1379–1385. [Google Scholar] [CrossRef]
- Finkelmann, H.; Kock, H.J.; Rehage, G. Investigations on liquid-crystalline polysiloxanes. 3. Liquid-crystalline elastomers—A new type of liquid-crystalline material. Makromol. Chem. Rapid Commun. 1981, 2, 317–322. [Google Scholar] [CrossRef]
- Finkelmann, H.; Rehage, G. Liquid-crystal side-chain polymers. Adv. Polym. Sci. 1984, 60–61, 99–172. [Google Scholar] [CrossRef]
- Finkelmann, H.; Gleim, W.; Hammerschmidt, K.; Schatzle, J. Liquid-crystal elastomers. Makromol. Chem. Macromol. Symp. 1989, 26, 67. [Google Scholar] [CrossRef]
- Zentel, R. Liquid-crystalline elastomers. Angew. Chem. Int. Ed. 1989, 28, 1407–1415. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Oxford University Press Inc.: New York, NY, USA, 2005. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Theory of Elasticity, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2007; Volume 7. [Google Scholar]
- Spiegel, M.R. Schaum’s Outline of Theory and Problems of Vector Analysis and an Introduction to Tensor Analysis; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Wang, X.J.; Warner, M. Theory of nematic backbone polymer phases and conformations. J. Phys. A Math. Gen. 1986, 19, 2215–2227. [Google Scholar] [CrossRef]
- Wang, X.J.; Warner, M. Theory of nematic comb-like polymers. J. Phys. A Math. Gen. 1987, 20, 713–731. [Google Scholar] [CrossRef]
- Warner, M.; Gelling, K.P.; Vilgis, T.A. Theory of nematic networks. J. Chem. Phys. 1988, 88, 4008–4013. [Google Scholar] [CrossRef]
- Abramchuk, S.S.; Khokhlov, A.R. Molecular theory of high elasticite of the polymer networks taking into account the orientational ordering of links. Dokl. Akad. Nauk 1987, 297, 385–389. [Google Scholar]
- Camacho-Lopez, M.; Finkelmann, H.; Palffy-Muhoray, P.; Shelley, M. Fast liquid-crystal elastomer swims into the dark. Nat. Mater. 2004, 3, 307–310. [Google Scholar] [CrossRef]
- Sanchez-Ferrer, A.; Merekalov, A.; Finkelmann, H. Opto-mechanical effect in photoactive nematic side-chain liquid-crystalline elastomers. Macromol. Rapid Commun. 2011, 32, 671–678. [Google Scholar] [CrossRef]
- Finkelmann, H.; Nishikawa, E.; Pereira, G.G.; Warner, M. A new opto-mechanical effect in solids. Phys. Rev. Lett. 2001, 87, 015501:1–015501:4. [Google Scholar] [CrossRef]
- Corbett, D.; Warner, M. Changing liquid crystal elastomer ordering with light—A route to opto-mechanically responsive materials. Liq. Cryst. 2009, 36, 1263–1280. [Google Scholar] [CrossRef]
- Dawson, N.J.; Kuzyk, M.G.; Neal, J.; Luchette, P.; Palffy-Muhoray, P. Cascading of liquid crystal elastomer photomechanical optical devices. Opt. Commun. 2011, 284, 991–993. [Google Scholar] [CrossRef]
- Garcia-Amoros, J.; Piñol, A.; Finkelmann, H.; Velasco, D. Azophenol-based liquid−crystalline elastomers for light-driven actuators. Org. Lett. 2011, 13, 2282–2285. [Google Scholar] [CrossRef]
- Camargo, C.J.; Campanella, H.; Marshall, J.E.; Torras, N.; Zinoviev, K.; Terentjev, E.M.; Esteve, J. Batch fabrication of optical actuators using nanotube-elastomer composites towards refreshable braille displays. J. Micromech. Microeng. 2012, 22, 075009:1–075009:9. [Google Scholar] [CrossRef]
- Gregorc, M.; Hui, L.; Domenici, V.; Ambrożič, G.; Čopič, M.; Drevenšek-Olenik, I. Kinetics of holographic recording and spontaneous erasure processes in light-sensitive liquid crystal elastomers. Materials 2012, 5, 741–753. [Google Scholar] [CrossRef]
- Lin, Y.; Jin, L.; Huo, Y. Quasi-soft opto-mechanical behavior of photochromic liquid crystal elastomer: Linearized stress–strain relations and finite element simulations. Int. J. Solids Struct. 2012, 49, 2668–2680. [Google Scholar] [CrossRef]
- Sun, Y.; Evans, J.S.; Lee, T.; Senyuk, B.; Keller, P.; He, S.; Smalyukh, I.I. Optical manipulation of shape-morphing elastomeric liquid crystal microparticles doped with gold nanocrystals. Appl. Phys. Lett. 2012, 100, 241901:1–241901:5. [Google Scholar]
- Yusuf, Y.; Kai, S. Electro-opto-mechanical effects in swollen polydomain side chain liquid crystal elastomers. AIP Conf. Proc. 2012, 1454, 290–293. [Google Scholar] [CrossRef]
- Kupfer, J.; Finkelmann, H. Liquid-crystal elastomers—Influence of the orientational distribution of the cross-links on the phase-behavior and reorientation processes. Macromol. Chem. Phys. 1994, 195, 1353–1367. [Google Scholar] [CrossRef]
- Clarke, S.M.; Terentjev, E.M.; Kundler, I.; Finkelmann, H. Texture evolution during the polydomain-monodomain transition in nematic elastomers. Macromolecules 1998, 31, 4862–4872. [Google Scholar] [CrossRef]
- Biggins, J.S.; Terentjev, E.M.; Warner, M. Semisoft elastic response of nematic elastomers to complex deformations. Phys. Rev. E 2008, 78, 041704:1–041704:9. [Google Scholar] [CrossRef]
- Fridrikh, S.V.; Terentjev, E.M. Polydomain-monodomain transition in nematic elastomers. Phys. Rev. E 1999, 60, 1847–1857. [Google Scholar] [CrossRef]
- Bladon, P.; Terentjev, E.M.; Warner, M. Deformation-induced orientational transitions in liquid-crystals elastomer. J. Phys. II 1994, 4, 75–91. [Google Scholar] [CrossRef]
- Verwey, G.C.; Warner, M. Nematic elastomers cross-linked by rigid rod linkers. Macromolecules 1997, 30, 4196–4204. [Google Scholar] [CrossRef]
- Verwey, G.C.; Warner, M. Compositional fluctuations and semisoftness in nematic elastomers. Macromolecules 1997, 30, 4189–4195. [Google Scholar] [CrossRef]
- Ren, W. Structure-property relations in siloxane-based main chain liquid crystalline elastomers and related linear polymers. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2007. [Google Scholar]
- Kundler, I.; Nishikawa, E.; Finkelmann, H. Nematic and smectic liquid single crystal elastomers: Influence of external stress parallel and perpendicular to the director. Macromol. Symp. 1997, 117, 11–19. [Google Scholar] [CrossRef]
- Nishikawa, E.; Finkelmann, H.; Brand, H.R. Smectic-A liquid single crystal elastomers showing macroscopic in-plane fluidity. Macromol. Rapid Commun. 1997, 18, 65–71. [Google Scholar] [CrossRef]
- Nishikawa, E.; Finkelmann, H. Smectic-A liquid single crystal elastomers—Strain induced break-down of smectic layers. Macromol. Chem. Phys. 1999, 200, 312–322. [Google Scholar] [CrossRef]
- Adams, J.M.; Warner, M. Elasticity of smectic-A elastomers. Phys. Rev. E 2005, 71, 021708:1–021708:15. [Google Scholar] [CrossRef]
- Adams, J.M.; Warner, M. Soft elasticity in smectic elastomers. Phys. Rev. E 2005, 72, 011703:1–011703:8. [Google Scholar] [CrossRef]
- Ortiz, C.; Wagner, M.; Bhargava, N.; Ober, C.K.; Kramer, E.J. Deformation of a polydomain, smectic liquid crystalline elastomer. Macromolecules 1998, 31, 8531–8539. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafstrom, S. Negative poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative poissons ratio. Science 1987, 235, 1038–1040. [Google Scholar]
- He, C.B.; Liu, P.W.; Griffin, A.C. Toward negative poisson ratio polymers through molecular design. Macromolecules 1998, 31, 3145–3147. [Google Scholar] [CrossRef]
- Ren, W.T.; McMullan, P.J.; Griffin, A.C. Stress-strain behavior in main chain liquid crystalline elastomers: Effect of crosslinking density and transverse rod incorporation on “Poisson’s ratio”. Phys. Status Solidi B 2009, 246, 2124–2130. [Google Scholar] [CrossRef]
- Sanchez-Ferrer, A.; Finkelmann, H. Uniaxial and shear deformations in smectic-C main-chain liquid-crystalline elastomers. Macromolecules 2008, 41, 970–980. [Google Scholar] [CrossRef]
- Cordoyiannis, G.; Sanchez-Ferrer, A.; Finkelmann, H.; Rozic, B.; Zumer, S.; Kutnjak, Z. Thermal study of the isotropic to smectic-C phase transition in main-chain liquid-crystalline elastomers. Liq. Cryst. 2010, 37, 349–353. [Google Scholar] [CrossRef]
- Sanchez-Ferrer, A.; Finkelmann, H. Thermal and mechanical properties of new main-chain liquid-crystalline elastomers. Solid State Sci. 2010, 12, 1849–1852. [Google Scholar] [CrossRef]
- Sanchez-Ferrer, A.; Finkelmann, H. Polydomain-monodomain orientational process in smectic-C main-chain liquid-crystalline elastomers. Macromol. Rapid Commun. 2011, 32, 309–315. [Google Scholar] [CrossRef]
- Ren, W.; McMullan, P.J.; Griffin, A.C. Poisson’s ratio of monodomain liquid crystalline elastomers. Macromol. Chem. Phys. 2008, 209, 1896–1899. [Google Scholar] [CrossRef]
- Ren, W.; McMullan, P.J.; Guo, H.; Kumar, S.; Griffin, A.C. A liquid crystalline elastomer with a p-pentaphenyl transverse rod laterally attached to the main chain. Macromol. Chem. Phys. 2008, 209, 272–278. [Google Scholar] [CrossRef]
- Ren, W.T.; Kline, W.M.; McMullan, P.J.; Griffin, A.C. Thermal strain recovery of anelastic monodomain liquid crystalline networks: Mechanically induced strains ratios. Phys. Status Solidi B 2011, 248, 105–110. [Google Scholar] [CrossRef]
- Heinze, P.; Finkelmann, H. Shear deformation and ferroelectricity in chiral SmC* main-chain elastomers. Macromolecules 2010, 43, 6655–6665. [Google Scholar] [CrossRef]
- Ricco, T.; Pegoretti, A. Energy storage and strain-recovery processes in highly deformed semicrystalline poly(butylene terephthalate). J. Polym. Sci. B Polym. Phys. 2002, 40, 236–243. [Google Scholar] [CrossRef]
- Clarke, S.M.; Terentjev, E.M. Slow stress relaxation in liquid crystal elastomers and gels. Faraday Discuss. 1999, 112, 325–333. [Google Scholar] [CrossRef]
- Ngai, K.L. Relaxation and Diffusion in Complex Systems, 1st ed.; Springer: New York, NY, USA, 2011. [Google Scholar]
- Ortiz, C.; Ober, C.K.; Kramer, E.J. Stress relaxation of a main-chain, smectic, polydomain liquid crystalline elastomer. Polymer 1998, 39, 3713–3718. [Google Scholar] [CrossRef]
- Povolo, F.; Schwartz, G.; Hermida, E.B. Stress relaxation of PVC below the yield point. J. Polym. Sci. B Polym. Phys. 1996, 34, 1257–1267. [Google Scholar] [CrossRef]
- Wortmann, F.J.; Schulz, K.V. Nonlinear viscoelastic performance of nomex, kevlar and polypropylene fibers in a single-step stress-relaxation test. 2. Moduli, viscosities and isochronal stress-strain curves. Polymer 1995, 36, 2363–2369. [Google Scholar] [CrossRef]
- Wortmann, F.J.; Schulz, K.V. Stress-relaxation and time-temperature superposition of polypropylene fibers. Polymer 1995, 36, 315–321. [Google Scholar] [CrossRef]
- Kumar, S. Liquid Crystals: Experimental Study of Physical Properties and Phase Transitions; Cambridge University Press: Cambridge, NY, USA, 2001. [Google Scholar]
- Davidson, P.; Petermann, D.; Levelut, A.M. The measurement of the nematic order-parameter by X-ray-scattering reconsidered. J. Phys. II 1995, 5, 113–131. [Google Scholar] [CrossRef]
- Tsoularis, A.; Wallace, J. Analysis of logistic growth models. Math. Biosci. 2002, 179, 21–55. [Google Scholar] [CrossRef]
- Ishige, R.; Naito, Y.; Kang, S.M.; Tokita, M.; Watanabe, J. Regular formation of chain folding in smectic phase of main-chain bb-3(2-ph) polymer followed by columnar association of phenyl side group in propane spacer. Macromolecules 2009, 42, 2557–2562. [Google Scholar] [CrossRef]
- Ishige, R.; Osada, K.; Tagawa, H.; Niwano, H.; Tokita, M.; Watanabe, J. Elongation behavior of a main-chain smectic liquid crystalline elastomer. Macromolecules 2008, 41, 7566–7570. [Google Scholar] [CrossRef]
- Hotta, A.; Clarke, S.M.; Terentjev, E.M. Stress relaxation in transient networks of symmetric triblock styrene-isoprene-styrene copolymer. Macromolecules 2002, 35, 271–277. [Google Scholar] [CrossRef]
- Adams, J.; Conti, S.; DeSimone, A. Soft elasticity and microstructure in smectic-C elastomers. Contin. Mech. Thermodyn. 2007, 18, 319–334. [Google Scholar] [CrossRef]
- Biggins, J.S.; Warner, M.; Bhattacharya, K. Elasticity of polydomain liquid crystal elastomers. J. Mech. Phys. Solids 2012, 60, 573–590. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dey, S.; Agra-Kooijman, D.M.; Ren, W.; McMullan, P.J.; Griffin, A.C.; Kumar, S. Soft Elasticity in Main Chain Liquid Crystal Elastomers. Crystals 2013, 3, 363-390. https://doi.org/10.3390/cryst3020363
Dey S, Agra-Kooijman DM, Ren W, McMullan PJ, Griffin AC, Kumar S. Soft Elasticity in Main Chain Liquid Crystal Elastomers. Crystals. 2013; 3(2):363-390. https://doi.org/10.3390/cryst3020363
Chicago/Turabian StyleDey, Sonal, Dena M. Agra-Kooijman, Wanting Ren, Philip J. McMullan, Anselm C. Griffin, and Satyendra Kumar. 2013. "Soft Elasticity in Main Chain Liquid Crystal Elastomers" Crystals 3, no. 2: 363-390. https://doi.org/10.3390/cryst3020363
APA StyleDey, S., Agra-Kooijman, D. M., Ren, W., McMullan, P. J., Griffin, A. C., & Kumar, S. (2013). Soft Elasticity in Main Chain Liquid Crystal Elastomers. Crystals, 3(2), 363-390. https://doi.org/10.3390/cryst3020363




