Effects of Strain on Notched Zigzag Graphene Nanoribbons
Abstract
:1. Introduction

2. Theoretical Method

 is the Fermion creation(destruction) operator, which creates(destroys) an electron with spin σ = {↑, ↓} at site i(j), and niσ = 1 or 0 is the spin-dependent number operator, where ni−σ refers to the number operator corresponding to the opposite spin, −σ. The hopping term tij is taken up to third-nearest-neighbor and corresponds to the energy required for a spin to hop between sites i and j. H.c. refers to the Hermitian conjugate. The parameter U denotes the strength of the local Coulomb interaction energy between opposite spins—the so-called Hubbard-U [40]—which has been linearized using the mean-field approximation
is the Fermion creation(destruction) operator, which creates(destroys) an electron with spin σ = {↑, ↓} at site i(j), and niσ = 1 or 0 is the spin-dependent number operator, where ni−σ refers to the number operator corresponding to the opposite spin, −σ. The hopping term tij is taken up to third-nearest-neighbor and corresponds to the energy required for a spin to hop between sites i and j. H.c. refers to the Hermitian conjugate. The parameter U denotes the strength of the local Coulomb interaction energy between opposite spins—the so-called Hubbard-U [40]—which has been linearized using the mean-field approximation




 are the retarded/advanced Green’s functions. The ΓL/Rσ (E) matrices are calculated from
are the retarded/advanced Green’s functions. The ΓL/Rσ (E) matrices are calculated from


 (E) are the retarded/advanced surface Green’s functions for the leads, which have been obtained using the decimation iteration method [43].
(E) are the retarded/advanced surface Green’s functions for the leads, which have been obtained using the decimation iteration method [43].
 are the unstrained and strained hopping parameters connecting sites i and j, and r0 and r are the unstrained and strained bond lengths respectively. The strain ∈ is calculated using
are the unstrained and strained hopping parameters connecting sites i and j, and r0 and r are the unstrained and strained bond lengths respectively. The strain ∈ is calculated using


3. Results and Discussion



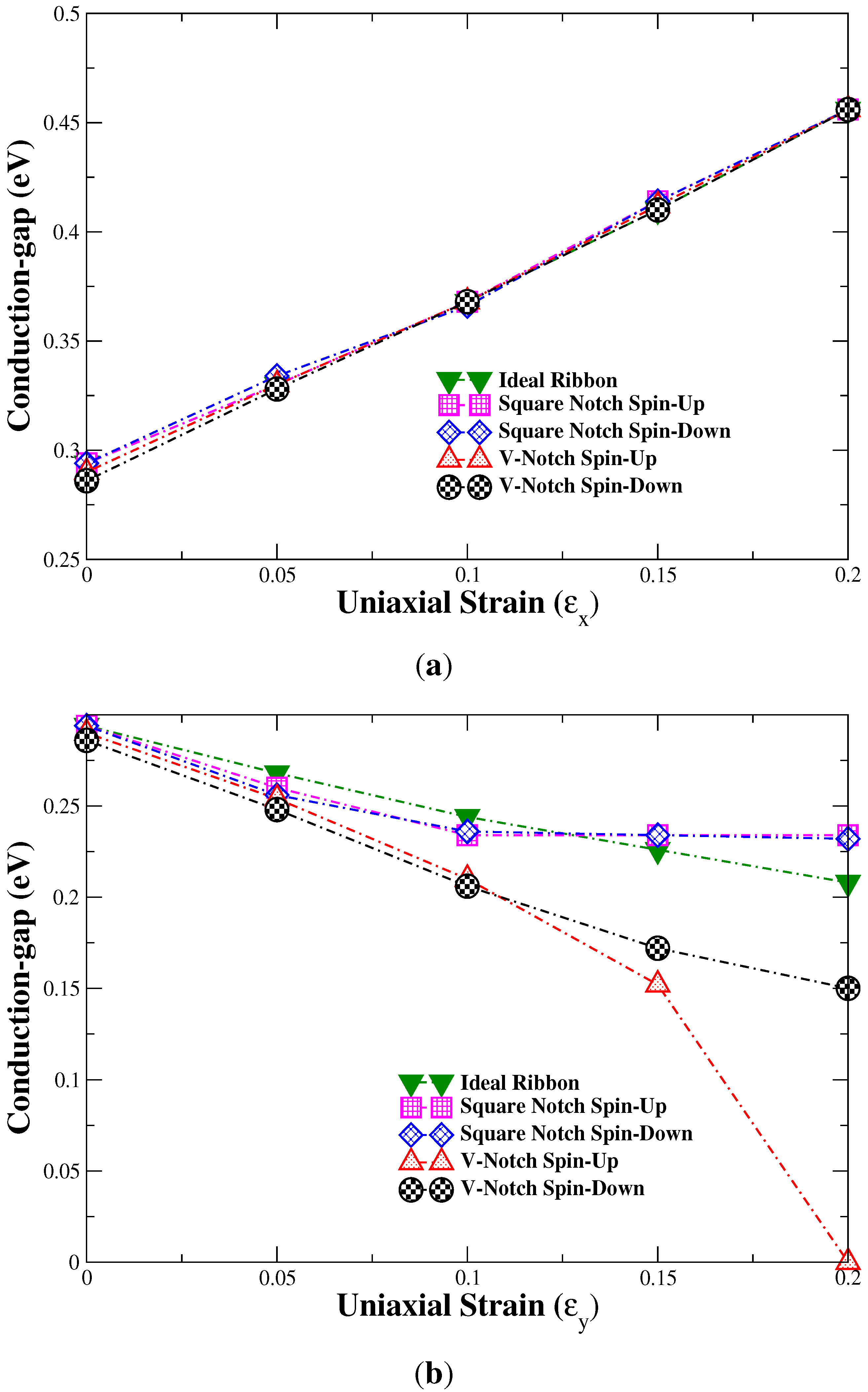
4. Conclusions
Acknowledgements
References
- Huang, B.; Liu, F.; Wu, J.; Gu, B.L.; Duan, W. Suppression of spin polarization in graphene nanoribbons by edge defects and impurities. Phys. Rev. B 2008, 77, 153411:1–153411:10. [Google Scholar]
- Areshkin, D.A.; Gunlycke, D.; White, C.T. Ballistic transport in graphene nanostrips in the presence of disorder: Importance of edge effects. Nano Lett. 2007, 7, 204–210. [Google Scholar] [CrossRef]
- Li, T.C.; Lu, S.P. Quantum conductance of graphene nanoribbons with edge defects. Phys. Rev. B 2008, 77, 085408:1–085408:8. [Google Scholar]
- Mucciolo, E.R.; Neto, A.H.C.; Lewenkopf, C.H. Conductance quantization and transport gaps in disordered graphene nanoribbons. Phys. Rev. B 2009, 79, 075407:1–075407:5. [Google Scholar]
- Cresti, A.; Nemec, N.; Biel, B.; Niebler, G.; Triozon, F.; Cuniberti, G.; Roche, S. Charge transport in disordered graphene-based low dimensional materials. Nano Res. 2008, 1, 361–394. [Google Scholar] [CrossRef]
- Cresti, A.; Roche, S. Range and correlation effects in edge disordered graphene nanoribbons. NewJ. Phys. 2009, 11, 095004:1–095004:11. [Google Scholar]
- Saloriutta, K.; Hancock, Y.; Kӓrkkӓinen, A.; Kӓrkkӓinen, L.; Puska, M.J.; Jauho, A-P. Electron transport in edge-disordered graphene nanoribbons. Phys. Rev. B 2011, 83, 205125:1–205125:6. [Google Scholar]
- Wimmer, M.; Adagideli, I.; Berber, S.; Tománek, D.; Richter, K. Spin currents in rough graphene nanoribbons: Universal fluctuations and spin injection. Phys. Rev. Lett. 2008, 100, 177207:1–177207:4. [Google Scholar]
- Zhang, X.J.; Chen, K.Q.; Tang, L.M.; Long, M.Q. Electronic transport properties on V-shaped-notched zigzag graphene nanoribbons junctions. Phys. Lett. A. 2011, 375, 3319–3324. [Google Scholar]
- Niimi, Y.; Matsui, T.; Kambara, H.; Tagami, K.; Tsukada, M.; Fukuyama, H. Scanning tunneling microscopy and spectroscopy of the electronic local density of states of graphite surfaces near monoatomic step edges. Phys. Rev. B 2006, 73, 085421:1–085421:20. [Google Scholar]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961. [Google Scholar]
- Dutta, S.; Pati, S.K. Edge reconstructions induce magnetic and metallic behavior in zigzag graphene nanoribbons. Carbon 2010, 48, 4409–4413. [Google Scholar] [CrossRef]
- Hancock, Y.; Uppstu, A.; Saloriutta, K.; Harju, A.; Puska, M.J. Generalized tight-binding transport model for graphene nanoribbon-based systems. Phys. Rev. B 2010, 81, 245402:1–245402:6. [Google Scholar]
- Hancock, Y.; Saloriutta, K.; Uppstu, A.; Harju, A.; Puska, M.J. Spin-dependence in asymmetric, v-shaped-notched graphene nanoribbons. J. Low Temp. Phys. 2008, 153, 393–398. [Google Scholar] [CrossRef]
- Lian, C.; Tahy, K.; Fang, T.; Li, G.; Xing, H.G.; Jena, D. Quantum transport in graphene nanoribbons patterned by metal masks. Appl. Phys. Lett. 2010, 96, 103109:1–103109:3. [Google Scholar]
- Berger, C.; Song, Z.; Li, X.; Wu, X.; Brown, N.; Naud, C.; Mayou, D.; Li, T.; Hass, J.; Marchenkov, A.N.; et al. Electronic confinement and coherence in patterned epitaxial graphene. Science 2006, 312, 1191–1196. [Google Scholar]
- Fischbein, M.D.; Drndic, M. Electron beam nanosculpting of suspended graphene sheets. Appl.Phys. Lett. 2008, 93, 113107:1–113107:3. [Google Scholar]
- Pereira, V.M.; Neto, A.H.C. Strain engineering of graphene’s electronic structure. Phys. Rev. Lett. 2009, 103, 046801–046801:4. [Google Scholar] [CrossRef]
- Sun, L.; Li, Q.; Ren, H.; Su, H.; Shi, Q.W.; Yang, J. Strain effect on electronic structures of graphene nanoribbons: A first-principles study. J. Chem. Phys. 2008, 129, 074704:1–074704:6. [Google Scholar]
- Poetschke, M.; Rocha, C.G.; Torres, L.E.F.F.; Roche, S.; Cuniberti, G. Modeling graphene-based nanoelectromechanical devices. Phys. Rev. B 2010, 81, 193404:1–193404:4. [Google Scholar]
- Ni, Z.H.; Yu, T.; Lu, Y.H.; Wang, Y.Y.; Feng, Y.P.; Shen, Z.X. Uniaxial strain on graphene: Raman spectroscopy study and band-gap opening. ACS Nano 2008, 2, 2301–2305. [Google Scholar] [CrossRef]
- Han, M.; Zhang, Y.; Zheng, H-B. Effect of uniaxial strain on band gap of armchair-edge graphene nanoribbons. Chin. Phys. Lett. 2010, 27, 266–269. [Google Scholar]
- Lu, Y.; Guo, J. Band gap of strained graphene nanoribbons. Nano Res. 2010, 3, 189–199. [Google Scholar]
- Su, W.S.; Wu, B.R.; Leung, T.C. A first-principles study on the electromechanical effect of graphene nanoribbon. Comput. Phys. Commun. 2011, 182, 99–102. [Google Scholar] [CrossRef]
- Viana-Gomes, J.; Pereira, V.M.; Peres, N.M.R. Magnetism in strained graphene dots. Phys. Rev. B 2009, 80, 245436:1–245436:11. [Google Scholar]
- Pellegrino, F.M.D.; Angilella, G.G.N.; Pucci, R. Dynamical polarization of graphene under strain. Phys. Rev. B 2010, 82, 115434:1–115434:9. [Google Scholar]
- Lee, S.H.; Chiu, C.W.; Ho, Y.H.; Lin, M.F. Uniaxial-stress effects on electronic structures of monolayer and bilayer graphenes. Synth. Met. 2010, 160, 2435–2441. [Google Scholar] [CrossRef]
- Zhang, X.H. Coherent transport in strained zigzag graphene nanoconstriction. Eur. Phys. J. B 2012, 85, 228–234. [Google Scholar] [CrossRef]
- Pereira, V.M.; Neto, A.H.C.; Peres, N.M.R. Tight-binding approach to uniaxial strain in graphene. Phys. Rev. B. 2009, 80, 045401:1–045401:8. [Google Scholar]
- Rostami, H.; Asgari, R. Electronic ground-state properties of strained graphene. Phys. Rev. B 2012, 86, 155435:1–155435:7. [Google Scholar]
- Bruna, M.; Vaira, A.; Battiato, A.; Vittone, E.; Borini, S. Graphene strain tuning by control of the substrate surface chemistry. Appl. Phys. Lett. 2010, 97, 021911:1–021911:3. [Google Scholar]
- Tsoukleri, G.; Parthenios, J.; Papagelis, K.; Jalil, R.; Ferrari, A.C.; Geim, A.K.; Novoselov, K.S.; Galiotis, C. Subjecting a graphene monolayer to tension and compression. Small 2009, 5, 2397–2402. [Google Scholar] [CrossRef]
- Liu, F.; Ming, P.; Li, J. Ab initio calculation of ideal strength and phonon instability of graphene under tension. Phys. Rev. B. 2007, 76, 064120:1–064120:7. [Google Scholar]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385–388. [Google Scholar] [CrossRef]
- Xu, P.; Yang, Y.; Barber, S.D.; Ackerman, M.L.; Schoelz, J.K.; Qi, D.; Kornev, I.A.; Dong, L.; Bellaiche, L.; Barraza-Lopez, S.; Thibado, P.M. Atomic control of strain in freestanding graphene. Phys. Rev. B. 2012, 85, 121406:1–121416:5. [Google Scholar]
- Frank, I.W.; Tanenbaum, D.M.; van der Zande, A.M.; McEuen, P.L. Mechanical properties of suspended graphene sheets. J. Vac. Sci. Technol. B 2007, 25, 2558–2561. [Google Scholar] [CrossRef]
- Palacios, T.; Hsu, A.; Wang, H. Applications of graphene devices in RF communications. IEEE Commun. Mag. 2010, 48, 122–128. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.H.; Kim, P.; Choi, J.Y.; Hong, B.H. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef]
- Geim, A.K. Graphene: Status and prospects. Science 2009, 324, 1530–1534. [Google Scholar] [CrossRef]
- Hubbard, J. Electron correlations in narrow energy bands. Proc. R. Soc. A 1963, 276, 238–257. [Google Scholar] [CrossRef]
- Hancock, Y.; Smith, A.E. Local and interfacial magnetic properties of inhomogeneous finite linear chains. Phys. E 2003, 18, 383–392. [Google Scholar] [CrossRef]
- Datta, S. Electronic Transport in Mesoscopic Systems; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Guinea, F.; Tejedor, C.; Flores, F.; Louis, E. Effective two-dimensional Hamiltonian at surfaces. Phys. Rev. B 1983, 28, 4397–4402. [Google Scholar]
- Brandbyge, M.; Mozos, J.L.; Ordejón, P.; Taylor, J.; Stokbro, K. Density-functional method for nonequilibrium electron transport. Phys. Rev. B 2002, 65, 165401:1–165401:17. [Google Scholar]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Ordejón, P.; Artacho, E.; Soler, J.M. Self-consistent order-N density-functional calculations for very large systems. Phys. Rev. B 1996, 53, R10441–R10444. [Google Scholar] [CrossRef]
- Ashcroft, N.; Mermin, M. Solid State Physics; Holt, Rinehart and Winston: New York, NY, USA, 1976. [Google Scholar]
- Son, Y.W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803:1–216803:4. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Baldwin, J.; Hancock, Y. Effects of Strain on Notched Zigzag Graphene Nanoribbons. Crystals 2013, 3, 38-48. https://doi.org/10.3390/cryst3010038
Baldwin J, Hancock Y. Effects of Strain on Notched Zigzag Graphene Nanoribbons. Crystals. 2013; 3(1):38-48. https://doi.org/10.3390/cryst3010038
Chicago/Turabian StyleBaldwin, Jack, and Y. Hancock. 2013. "Effects of Strain on Notched Zigzag Graphene Nanoribbons" Crystals 3, no. 1: 38-48. https://doi.org/10.3390/cryst3010038
APA StyleBaldwin, J., & Hancock, Y. (2013). Effects of Strain on Notched Zigzag Graphene Nanoribbons. Crystals, 3(1), 38-48. https://doi.org/10.3390/cryst3010038



