Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations
Abstract
:1. Introduction
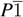 ) while Cu(dmdt)2 and Zn(tmdt)2 belonging to the second one have the crystal with the base-centered monoclinic symmetry (C2/c). The molecular shape therein is planar for the former while it is twisted for the latter. Recently, a new member Cu(tmdt)2 has been synthesized [6], whose crystal structure is similar to those of Ni(tmdt)2 and Au(tmdt)2 with its molecular shape being planar. It is quite interesting that Cu(dmdt)2 and Cu(tmdt)2 show different crystal structures and molecular shapes therein in spite of their chemical similarities. In Figure 1, chemical structural formulae of Cu(dmdt)2 and Cu(tmdt)2 and three-dimensional views (drawn with VESTA [7]) of a Cu(tmdt)2 molecule as well as the Cu(tmdt)2 crystal are shown. Magnetic susceptibility measurements imply that Cu(tmdt)2 is a one-dimensional antiferromagnetic Heisenberg system with the antiferromagnetic ordering temperature of 13 K [6].
) while Cu(dmdt)2 and Zn(tmdt)2 belonging to the second one have the crystal with the base-centered monoclinic symmetry (C2/c). The molecular shape therein is planar for the former while it is twisted for the latter. Recently, a new member Cu(tmdt)2 has been synthesized [6], whose crystal structure is similar to those of Ni(tmdt)2 and Au(tmdt)2 with its molecular shape being planar. It is quite interesting that Cu(dmdt)2 and Cu(tmdt)2 show different crystal structures and molecular shapes therein in spite of their chemical similarities. In Figure 1, chemical structural formulae of Cu(dmdt)2 and Cu(tmdt)2 and three-dimensional views (drawn with VESTA [7]) of a Cu(tmdt)2 molecule as well as the Cu(tmdt)2 crystal are shown. Magnetic susceptibility measurements imply that Cu(tmdt)2 is a one-dimensional antiferromagnetic Heisenberg system with the antiferromagnetic ordering temperature of 13 K [6].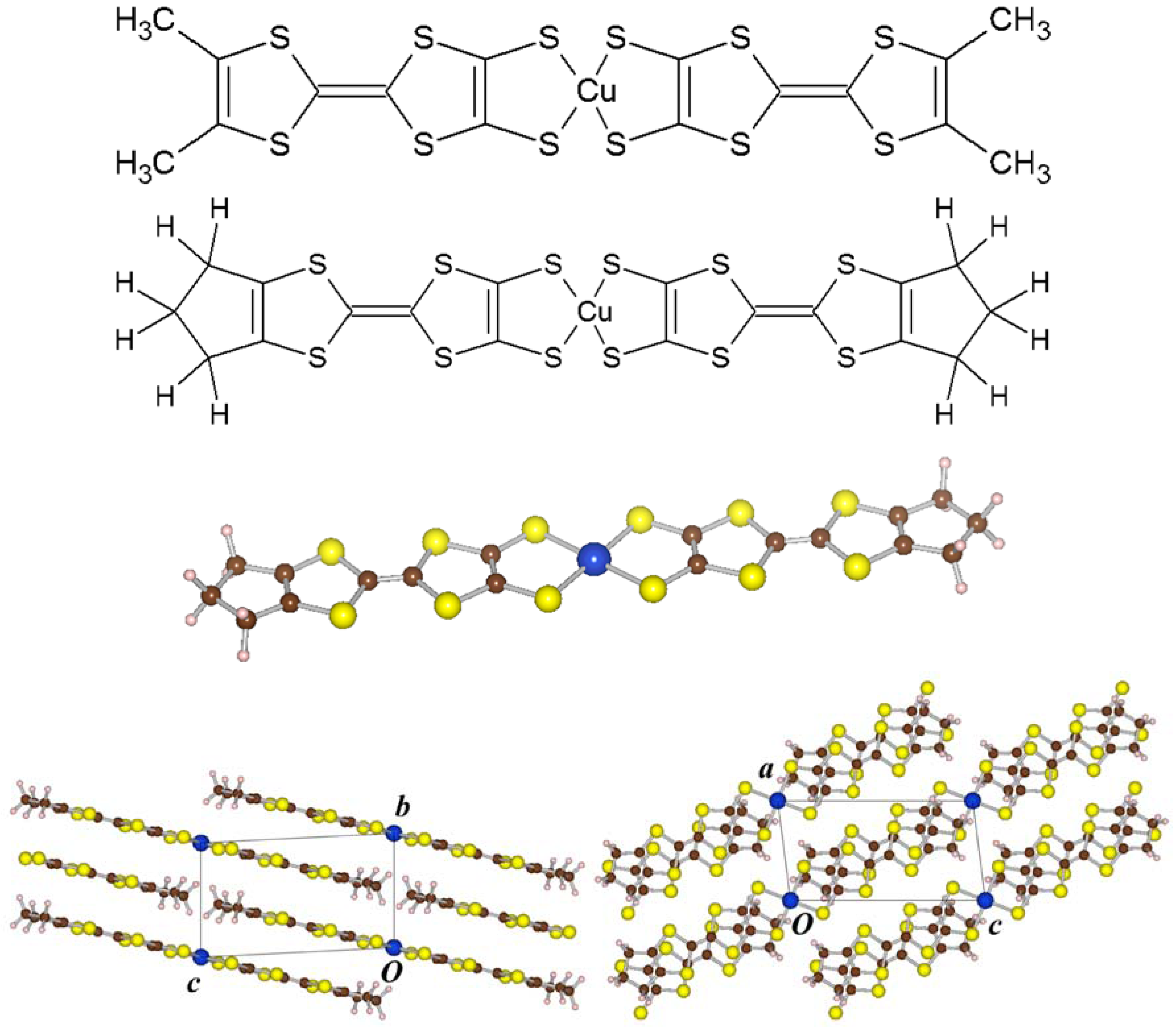
2. Method
3. Results and Discussion
3.1. Isolated Molecule
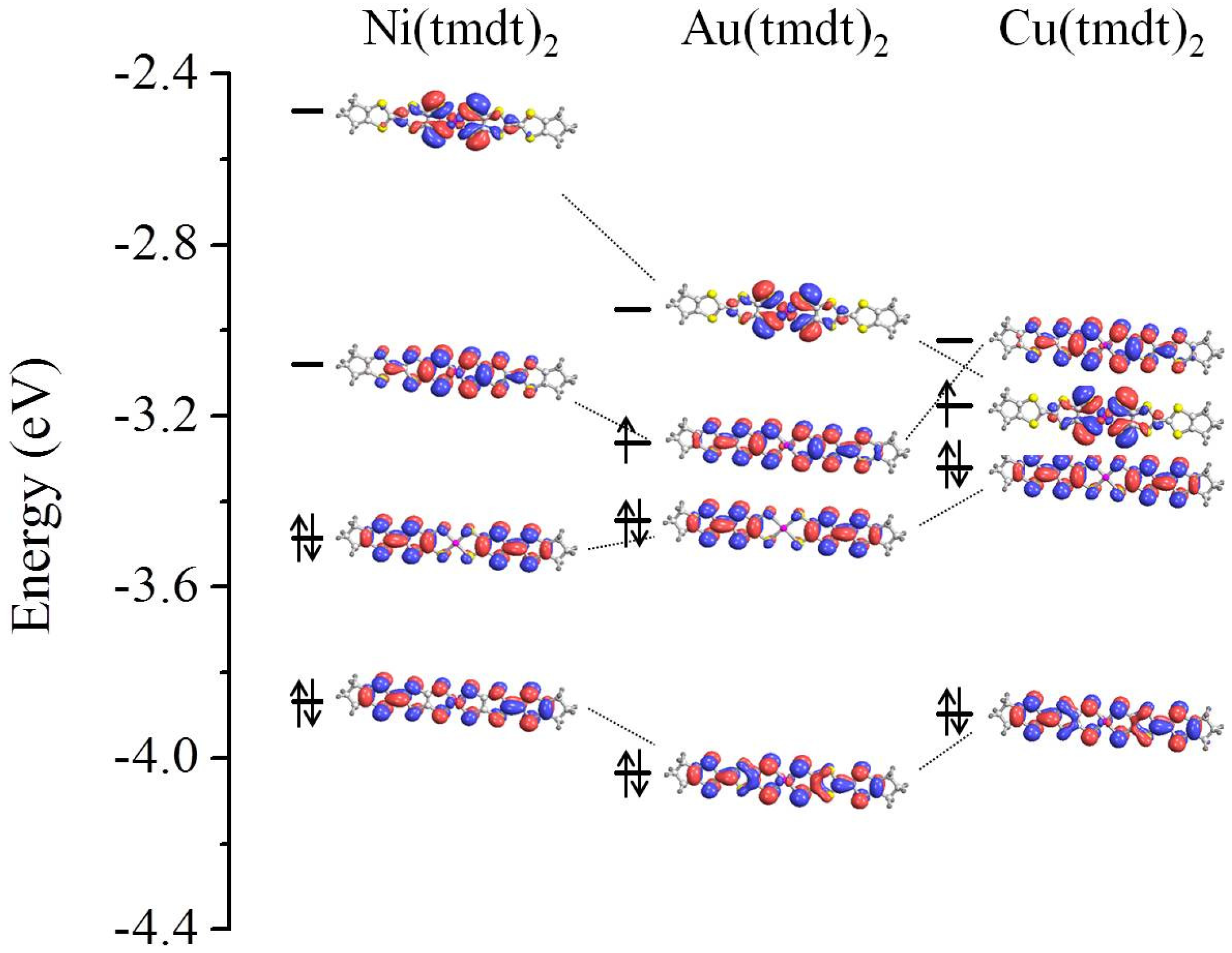
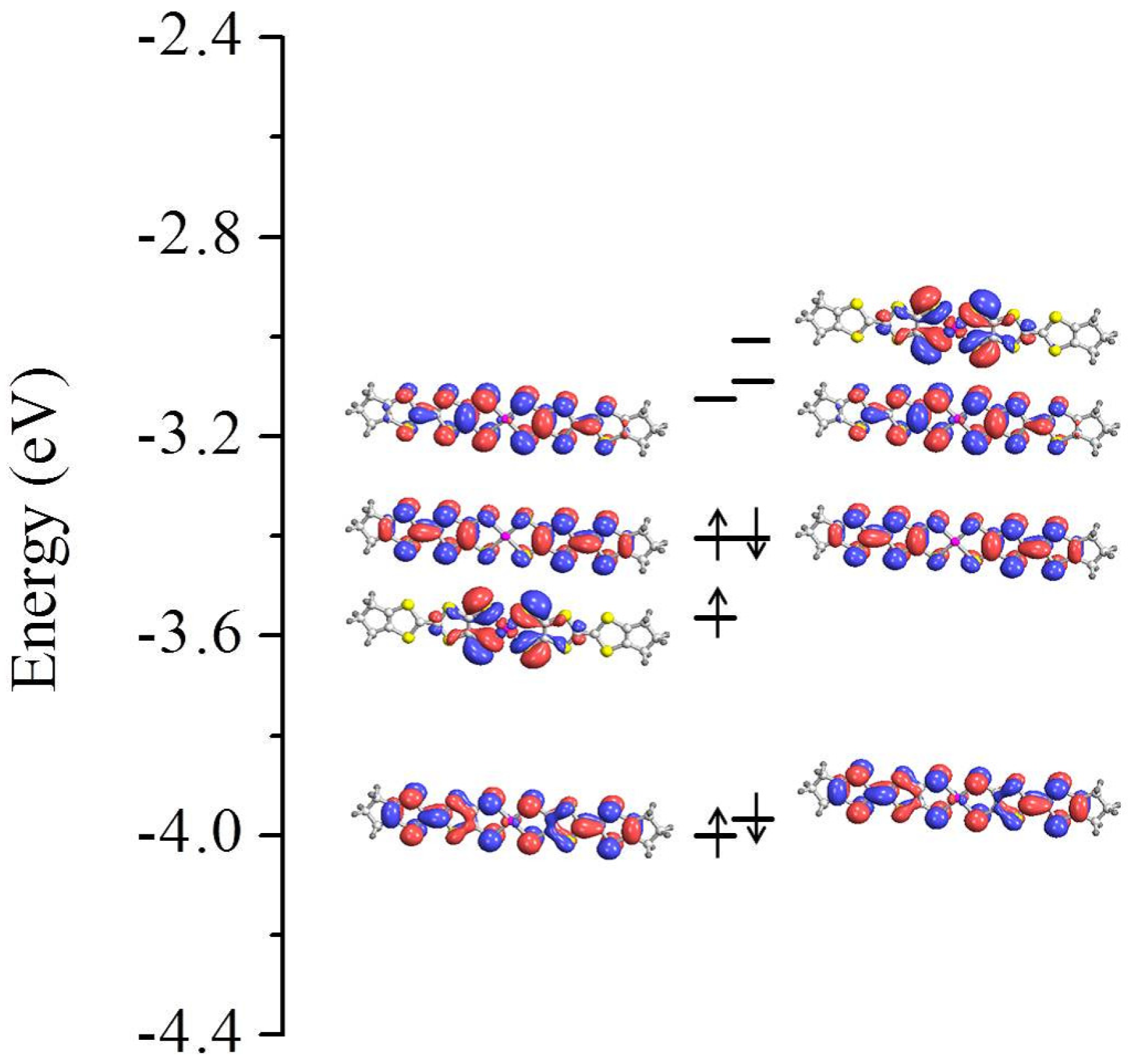
3.2. Solid State
3.2.1. Non-Magnetic Results
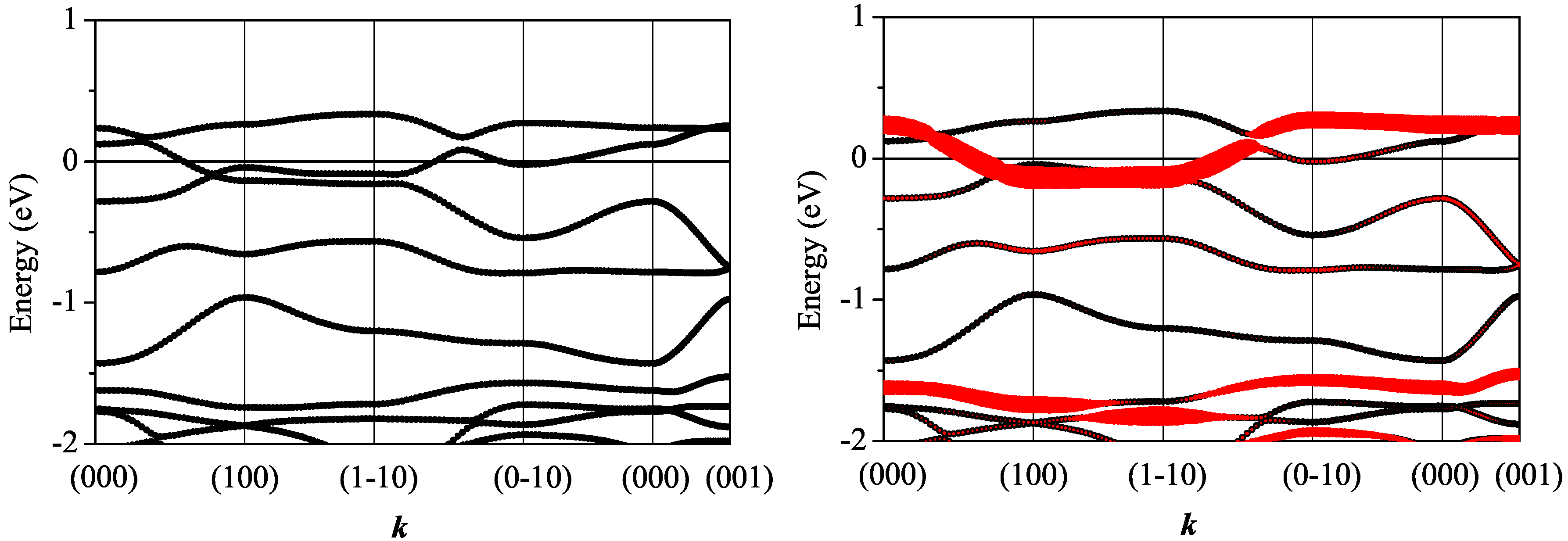
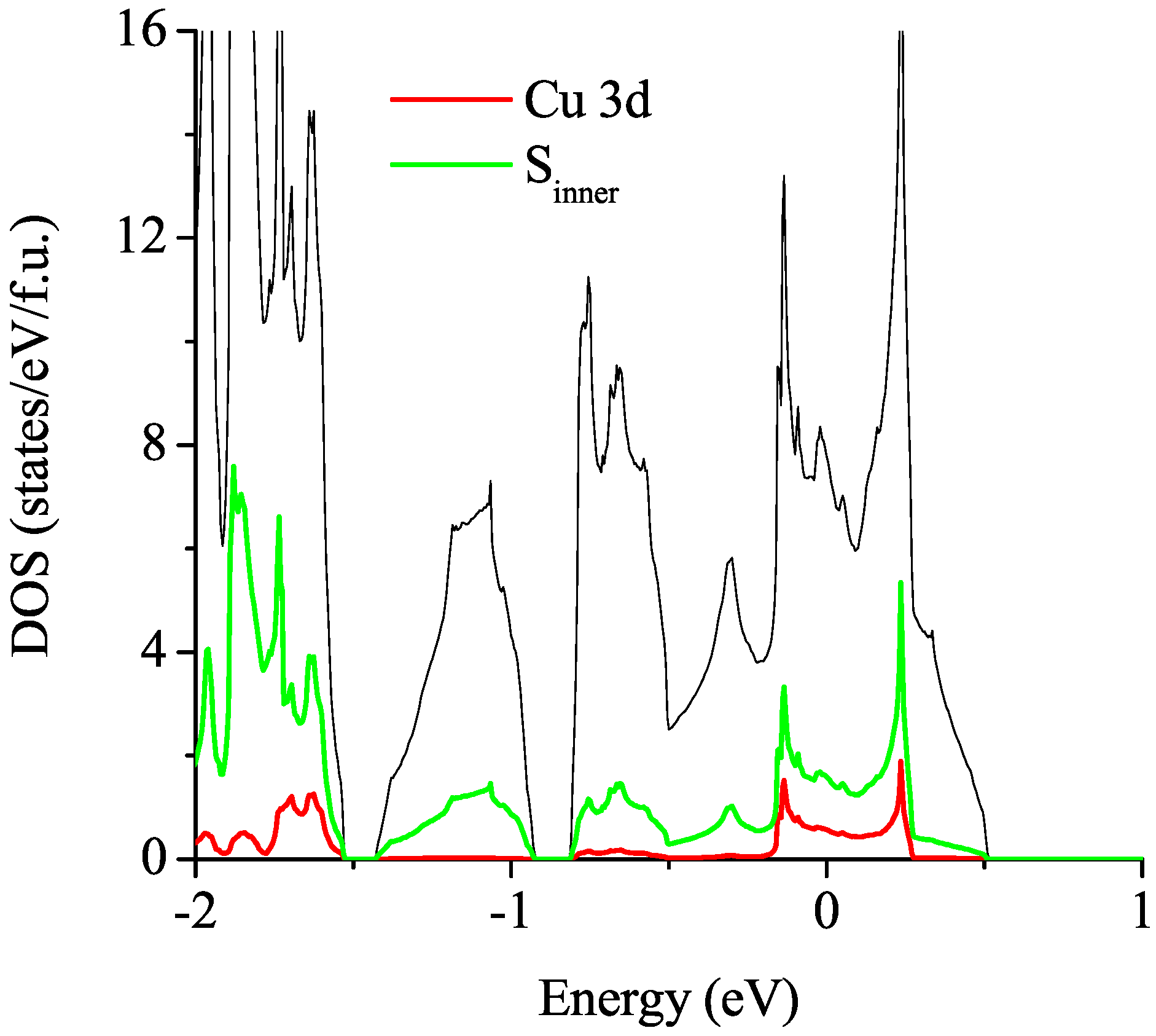
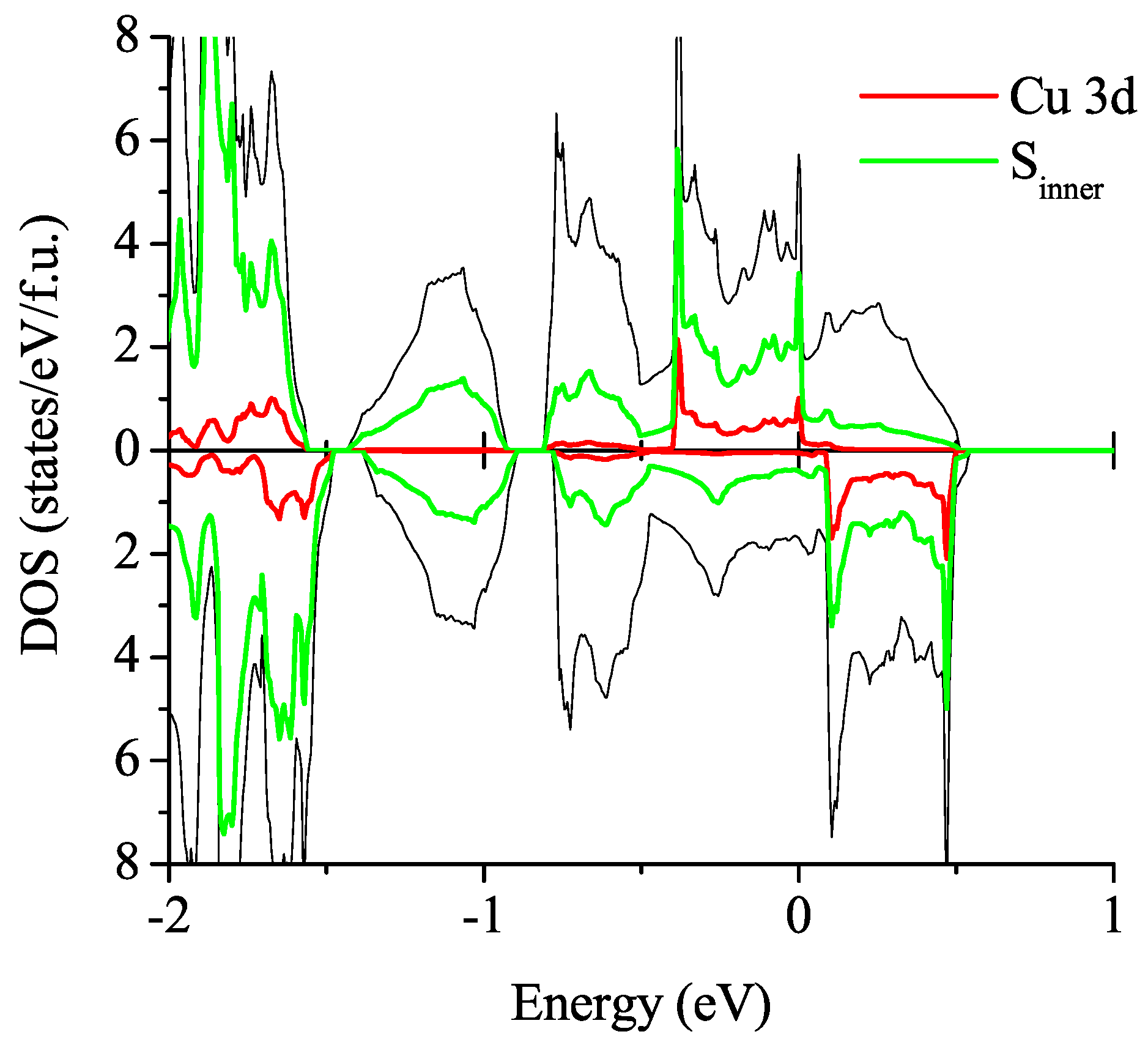
3.2.2. Spin-Polarized Results

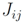 is the exchange coupling and C is the energy gain due to spin polarization. As the exchange couplings, we consider the following six contributions: three parameters for the first neighbors along each of the crystal axis,
is the exchange coupling and C is the energy gain due to spin polarization. As the exchange couplings, we consider the following six contributions: three parameters for the first neighbors along each of the crystal axis,  ,
, 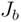 and
and 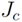 ; three parameters for the second neighbors in each crystal plane,
; three parameters for the second neighbors in each crystal plane,  ,
, 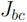 and
and  . Using the relative energies listed in Table 1, we can determine these six exchange couplings and the results are as follows:
. Using the relative energies listed in Table 1, we can determine these six exchange couplings and the results are as follows:  meV,
meV, 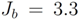 meV,
meV, 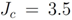 meV,
meV, 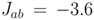 meV,
meV,  meV, and
meV, and  meV. Clearly the AFM exchange coupling along the a-axis dominates. Other coupling parameters are about one order magnitude smaller than
meV. Clearly the AFM exchange coupling along the a-axis dominates. Other coupling parameters are about one order magnitude smaller than  . Anyway, they cooperatively stabilize the AFM ordering along a by ferromagnetically coupling the neighboring AFM chains. From the temperature dependence of magnetic susceptibility, Zhou et al. [6] obtained 117 cm−1 (14.5 meV) as the AFM exchange coupling along the chain. Our value of
. Anyway, they cooperatively stabilize the AFM ordering along a by ferromagnetically coupling the neighboring AFM chains. From the temperature dependence of magnetic susceptibility, Zhou et al. [6] obtained 117 cm−1 (14.5 meV) as the AFM exchange coupling along the chain. Our value of  is about three times larger than this experimental value. Perhaps, for the present system, Coulomb corrected version like LDA+U may be better suited than simple GGA used in the present calculation. Then the exchange splitting will be enhanced and the superexchange coupling will be suppressed through the increase of energy denominator. Anyway, agreement within a numerical factor may be rather satisfactory.
is about three times larger than this experimental value. Perhaps, for the present system, Coulomb corrected version like LDA+U may be better suited than simple GGA used in the present calculation. Then the exchange splitting will be enhanced and the superexchange coupling will be suppressed through the increase of energy denominator. Anyway, agreement within a numerical factor may be rather satisfactory.| Magneticorder | Unitcell | Relative energy (meV/molecule) |
|---|---|---|
| FM | (a, b, c) | −9:3 |
| AFM | (2a, b, c) | −35:8 |
| AFM | (a, 2b, c) | −10:0 |
| AFM | (a, b, 2c) | −10:0 |
| AFM | (a, b−c, b+c) | −9:6 |
| AFM | (c+a, b, c−a) | −32:7 |
| AFM | (a−b, a+b, c) | −32:9 |
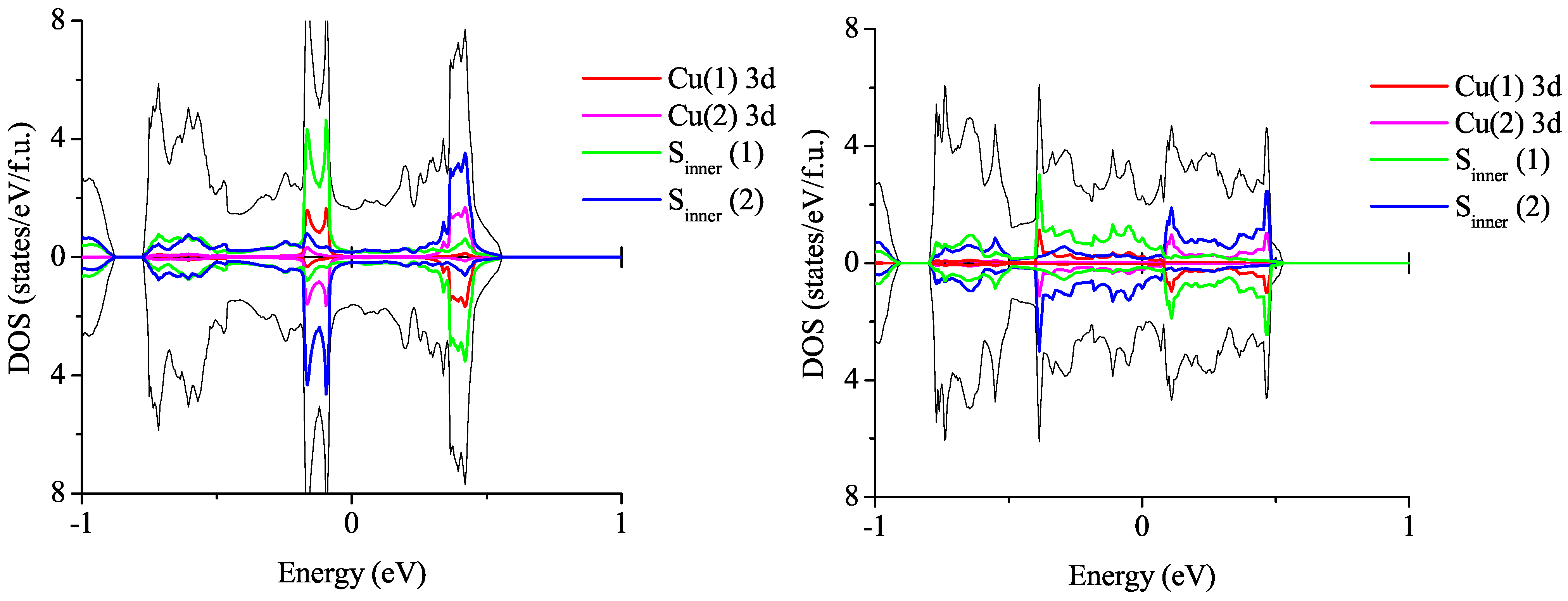
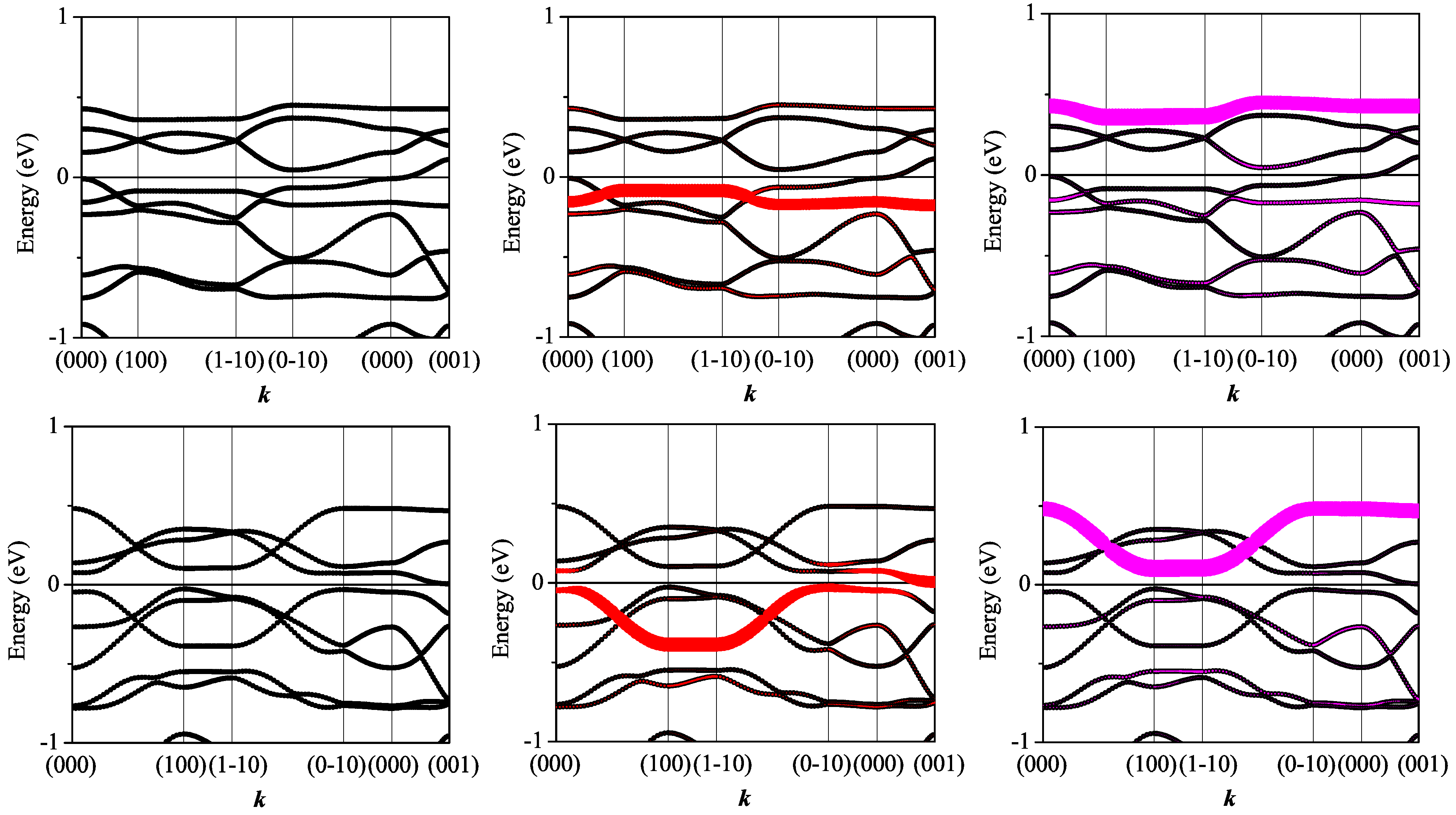
3.3. On the Qualitative Difference between Cu(tmdt)2 and Cu(dmdt)2
4. Conclusions
Acknowledgments
References
- Tanaka, H.; Okano, Y.; Kobayashi, H.; Suzuki, W.; Kobayashi, A. A three-dimensional synthetic metallic crystal composed of single-component molecules. Science 2001, 291, 285–287. [Google Scholar]
- Suzuki, W.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Takata, M.; Sakata, M.; Fujiwara, H.; Kobayashi, H. Highly conducting crystals based on single-component gold complexes with extended-TTF dithiolateligands. J. Am. Chem. Soc. 2003, 125, 1486–1487. [Google Scholar]
- Tanaka, H.; Kobayashi, H.; Kobayashi, A. A conducting crystal based on a single-component paramagnetic molecule, [Cu(dmdt)2] (dmdt = Dimethyltetrathiafulvalenedithiolate). J. Am. Chem. Soc. 2002, 124, 10002–10003. [Google Scholar] [CrossRef]
- Yamamoto, K.; Fujiwara, E.; Kobayashi, A.; Fujishiro, Y.; Nishibori, E.; Sakata, M.; Takata, M.; Tanaka, H.; Okano, Y.; Kobayashi, H. Single-component molecular conductor [Zn(tmdt)2] and related Zn complexes. Chem. Lett. 2005, 34, 1090–1091. [Google Scholar] [CrossRef]
- Tanaka, H.; Hara, S.; Tokumoto, M.; Kobayashi, A.; Kobayashi, H. Resistance measurements of microcrystals of single-component molecular metals using finely patterned interdigitated electrodes. Chem. Lett. 2007, 36, 1006–1007. [Google Scholar] [CrossRef]
- Zhou, B.; Yajima, H.; Kobayashi, A.; Okano, Y.; Tanaka, H.; Kumashiro, T.; Nishibori, E.; Sawa, H.; Kobayashi, H. Single-component molecular conductor [Cu(tmdt)2] containing an antiferromagnetic heisenberg chain. Inorg. Chem. 2010, 49, 6740–6747. [Google Scholar]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
- Ishibashi, S.; Tanaka, H.; Kohyama, M.; Tokumoto, M.; Kobayashi, A.; Kobayashi, H.; Terakura, K. Ab initio electronic structure calculation for single-component molecular conductors Au(tmdt)2 (tmdt = trimethylenetetrathiafulvalenedithiolate). J. Phys. Soc. Jpn. 2005, 74, 843–846, 1879. [Google Scholar] [CrossRef]
- Ishibashi, S.; Terakura, K.; Kobayashi, A. Electronic structures of single component molecular metals based on Ab initio calculation. J. Phys. Soc. Jpn. 2008, 77, 024702:1–024702:7. [Google Scholar]
- Seo, H.; Ishibashi, S.; Okano, Y.; Kobayashi, H.; Kobayashi, A.; Fukuyama, H.; Terakura, K. Single-component molecular metals as multiband π-d systems. J. Phys. Soc. Jpn. 2008, 77, 023714:1–023714:4. [Google Scholar]
- QMAS (Quantum MAterials Simulator). Available online: http://www.qmas.jp (accessed on 17 August 2012).
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Holzwarth, N.A.W.; Matthews, G.E.; Dunning, R.B.; Tackett, A.R.; Zeng, Y. Comparison of the projector augmented-wave, pseudopotential, and linearized augmented-plane-wave formalisms for density-functional calculations of solids. Phys. Rev. B 1997, 55, 2005–2017. [Google Scholar]
- Kresse, G.; Joubert, D. From ultrasoftpseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Seo, H. Private communication. The Institute of Physical and Chemical Research (RIKEN): Japan, 2012. [Google Scholar]
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ishibashi, S.; Terakura, K. Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals 2012, 2, 1210-1221. https://doi.org/10.3390/cryst2031210
Ishibashi S, Terakura K. Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals. 2012; 2(3):1210-1221. https://doi.org/10.3390/cryst2031210
Chicago/Turabian StyleIshibashi, Shoji, and Kiyoyuki Terakura. 2012. "Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations" Crystals 2, no. 3: 1210-1221. https://doi.org/10.3390/cryst2031210
APA StyleIshibashi, S., & Terakura, K. (2012). Electronic Structure of Cu(tmdt)2 Studied with First-Principles Calculations. Crystals, 2(3), 1210-1221. https://doi.org/10.3390/cryst2031210




