Growth and Atomic-Scale Characterization of 2D Gallium Selenide Crystals via STEM and EELS

Abstract

The advent of graphene has catalyzed extensive exploration into two-dimensional (2D) materials, among which gallium selenide (GaSe)—a layered semiconductor—stands out for its promise in optoelectronic and nanoscale device applications. To elucidate the intricate correlation between structure and electronic properties, and to enable performance optimization at the atomic scale, we employ advanced characterization methodologies. In this work, atomic-resolution Scanning Transmission Electron Microscopy (STEM) and Electron Energy Loss Spectroscopy (EELS) are utilized to investigate the structural and electronic characteristics of GaSe. STEM imaging confirms the atomic-level uniformity and verifies the β-GaSe phase, while EELS measurements reveal a thickness-dependent, tunable bandgap that decreases from 3.8 eV to 2.4 eV as the crystal thickness increases from approximately 1 nm to 30 nm—a trend attributable to quantum confinement effects.

1. Introduction

The discovery of graphene in 2004 by Geim and Novoselov [1] marked a turning point in the field of two-dimensional (2D) materials, leading to extensive research into layered van der Waals structures with remarkable electrical, optical, and mechanical properties [2,3]. These materials exhibit pronounced quantum confinement, tunable band structures, and strong light-matter interactions, making them attractive candidates for next-generation technologies [4,5]. Alongside graphene, transition metal dichalcogenides (TMDs), black phosphorus, and indium-gallium chalcogenides have attracted much attention for their optoelectronic applications [6,7,8]. Notably, recent studies on perovskites and other layered semiconductors have revealed exceptional dielectric and optical properties, such as high carrier mobility, versatile bandgap engineering, and strong dielectric response. Compared to perovskites, GaSe and similar layered compounds offer superior environmental stability and mechanical flexibility, as well as highly tunable electronic and optical behavior through thickness and stacking modulation [9].

GaSe, a layered semiconductor with a thickness-dependent bandgap, stands out for potential use in photodetectors, nonlinear optics [10], and flexible electronics [11]. However, successful device integration relies on its stability under ambient conditions, including resistance to oxidation, temperature changes, and light exposure—issues still under investigation [12]. Initial studies on few-layer GaSe transistors [13] and photodetectors [14] have highlighted their promise. Photoluminescence measurements on GaSe nanosheets [15] show strong preservation of photon polarization between absorption and emission, indicating potential for spintronic applications. Monolayer GaSe is especially attractive for nanoscale electronic, spintronic, and optoelectronic devices [16], with strain engineering providing further tunability. Theoretical work also suggests carrier-induced magnetism in single-layer GaSe [17].

GaSe’s distinctive properties arise from its anisotropic structure: covalently bonded atomic planes held together by weak vdW forces allow mechanical exfoliation and thin-film fabrication. Each layer consists of four atomic planes (Se-Ga-Ga-Se) stacked along the c-axis. Bulk GaSe forms four polytypes—β (2H), ε (2H′), γ (3R), and δ (2H–3R)—each with different stacking and unique optical and electronic characteristics [18]. Accurate identification of these polytypes is essential for application-specific use. This study focuses on the stable and widely investigated β-GaSe polytype, allowing us to isolate thickness-dependent effects from stacking order and establish clear correlations between structure and electronic properties [19].

Thickness-driven modulation of optical properties presents opportunities for functional optoelectronic devices [20]. The link between thickness, polytype, and electronic behavior highlights the need for detailed characterization. Advanced electron microscopy is revolutionizing the study of 2D materials like GaSe, enabling precise analysis of their structure and electronic properties. Aberration-corrected scanning transmission electron microscopy (STEM) provides atomic-resolution imaging, crucial for distinguishing GaSe polytypes and detecting thickness-related changes [21]. Combined electron energy loss spectroscopy (EELS) and STEM allow exploration of local electronic properties with nanometric resolution, revealing changes in the electronic density of states with layer number and polytype [22]. Unlike traditional ensemble optical measurements, our approach yields spatially resolved insight into band structure evolution across individual flakes. Only structurally pristine sample regions were analyzed, excluding those with defects or distortions, to ensure reliable correlation between EELS spectra and atomic layer number.

The integration of advanced characterization methods with theoretical modeling and atomistic simulations enables the design of GaSe-based devices optimized for optoelectronics, plasmonics, and nonlinear optics. In this study, STEM and EELS were employed to investigate GaSe’s properties. High-angle annular dark-field (HAADF) imaging in STEM mode delivers subatomic spatial resolution, facilitating accurate atomic structure determination and confirmation of the β-GaSe polytype. While density functional theory (DFT) and ab initio molecular dynamics (AIMD) are valuable for interpreting atomic-scale features of group IIIA binary compounds [23], multislice image simulations were strategically used to validate STEM and HRTEM data and confirm GaSe polytype structure. Preliminary photodetector measurements under 600 nm irradiation have also been performed, and the results are reported in the Supplementary Information.

2. Materials and Methods

High-purity gallium (99.999%) and selenium (99.999%) from Sigma Aldrich (Sigma Aldrich Merck SpA KGaA, Darmstadt, Germany) were used as starting materials. These elements were weighed in a stoichiometric 1:1 molar ratio and loaded into a cleaned quartz ampoule. The ampoule was thoroughly cleaned and evacuated to a pressure of approximately 10⁻⁵ Torr using a rotary and diffusion pump, then sealed under vacuum to prevent contamination during the crystal growth process. The selection of growth parameters adheres to established protocols for Bridgman growth of GaSe single crystals, further refined through the expertise and experimental optimization developed within our research group, with slight modifications optimized through preliminary trials to maximize the crystalline quality and phase purity of the β-GaSe ingots [24].

To promote initial reaction and homogenization, the sealed ampoule was optionally pre-reacted in a rocking furnace at 600 °C for 24 to 48 h. Both 24 and 48 h yielded comparable results in terms of phase purity and crystalline quality. After this step, the ampoule was placed vertically into a Bridgman-type furnace comprising a high-temperature zone (around 950–1000 °C), a low-temperature zone (approximately 400–500 °C), and a narrow intermediate region to establish a sharp thermal gradient. The schematic of the furnace used for the deposition, along with the corresponding thermal gradient between the different zones, is shown in Figure 1.

The ampoule was held in the high-temperature zone until the GaSe charge was fully molten, typically for 6–8 h, then, it was slowly lowered through the thermal gradient at a rate of 0.5 mm per hour. The translation rate and temperature gradient were monitored and maintained using calibrated thermocouples. As the ampoule passed into the cooler region, directional solidification occurred from the pointed bottom of the ampoule upward, encouraging the growth of a single crystal along the direction of movement.

Once the crystallization was complete, the furnace was cooled to room temperature at a controlled rate of 10 °C/h to minimize thermal stress and avoid cracking of the crystal.

The quartz ampoule was then broken open, and the GaSe ingot was extracted. Bulk pieces of the material were initially mechanically exfoliated using a scalpel blade approximately 20 microns thick from the high-quality GaSe ingots synthesized and deposited in our laboratory according to the procedures detailed above. Subsequently, a top-down process was employed to exfoliate progressively thinner GaSe fragments down to single layers. This thinning method thoroughly preserves the structural integrity of the material. The resulting thin flakes were then mounted onto TEM grids for all TEM characterizations.

Scanning Transmission Electron Microscopy (STEM) and Electron Energy Loss Spectroscopy (EELS) were performed by a Jeol JEM-ARM 200F NEOARM (JEOL Ltd., Musashino Akishima, Tokyo, Japan) operated at 200 kV to correlative morphological and electronic structure analysis. For all STEM/EELS measurements, the beam current was set to approximately 20 pA, with a probe size of ~1.0 Å (corresponding to a convergence semi-angle of 30 mrad). The estimated total electron dose during spectral imaging was on the order of 2 × 10⁶ e⁻/Ų, which was carefully optimized to minimize beam-induced damage on GaSe while maintaining sufficient signal-to-noise ratio.

To investigate the structural order of GaSe, high-angle annular dark field (HAADF) imaging was performed in scanning transmission electron microscopy (STEM) mode using an annular dark field detector. In this technique, a focused electron beam is scanned across the sample, and elastically scattered electrons at high angles (>50 mrad) are collected by the detector. The resulting signal intensity is approximately proportional to the square of the atomic number (Z²) of the scattering atoms, providing atomic number-sensitive contrast (Z-contrast). HAADF imaging minimizes contributions from diffraction effects, enabling high spatial resolution and direct compositional information at the atomic scale. For optimal imaging conditions, the convergence semi-angle of the electron probe was set to 30 mrad, and the detector’s collection angle range was set between 50 and 100 mrad. Data acquisition was performed with a pixel dwell time of 20 μs and the images were processed using Digital Micrograph (DM 3.52.3932.0) software to enhance contrast and reduce noise.

Energy-filtered transmission electron microscopy (EF-TEM) was employed to acquire energy-filtered images for improved contrast and detailed analysis of material composition at atomic resolution. Zero-loss filtering was utilized to enhance image contrast by excluding inelastically scattered electrons, while core-loss edge filtering allowed the generation of compositional maps with high spatial resolution.

Spectral imaging in scanning transmission electron microscopy (SI-STEM) was performed to analyze the electronic structure of our samples. In this technique, a focused electron beam was scanned across the sample in a raster pattern, and at each scan position, a spectrum was collected using an electron energy loss spectrometer (EELS). This method enables the simultaneous acquisition of spatial and spectral information, producing a hyperspectral data cube with two spatial dimensions and one spectral dimension. EELS spectra were recorded with an energy resolution of 50 meV over the 0–50 eV range to capture low-energy electronic transitions. To achieve a sufficient signal-to-noise ratio, a pixel dwell time of 2 ms was used during acquisition. The low-loss EELS spectrum (VEELS) provides critical information about valence electron excitations in the material. This spectral range includes key features such as:

■

Zero-Loss Peak (ZLP): A dominant peak at 0 eV, representing electrons that have not undergone inelastic scattering.

■

Plasmonic Excitations: Collective oscillations of free or weakly bound electrons, typically appearing as broad peaks at intermediate energy losses.

■

Interband Transitions: Features associated with electronic transitions between the valence and conduction bands, providing insight into the material’s electronic structure.

■

Bandgap Characteristics: The onset of energy loss intensity at specific energies, which allows estimation of the material’s bandgap and its dependence on thickness.

Data processing was performed using Digital Micrograph (DM) software.

3. Results

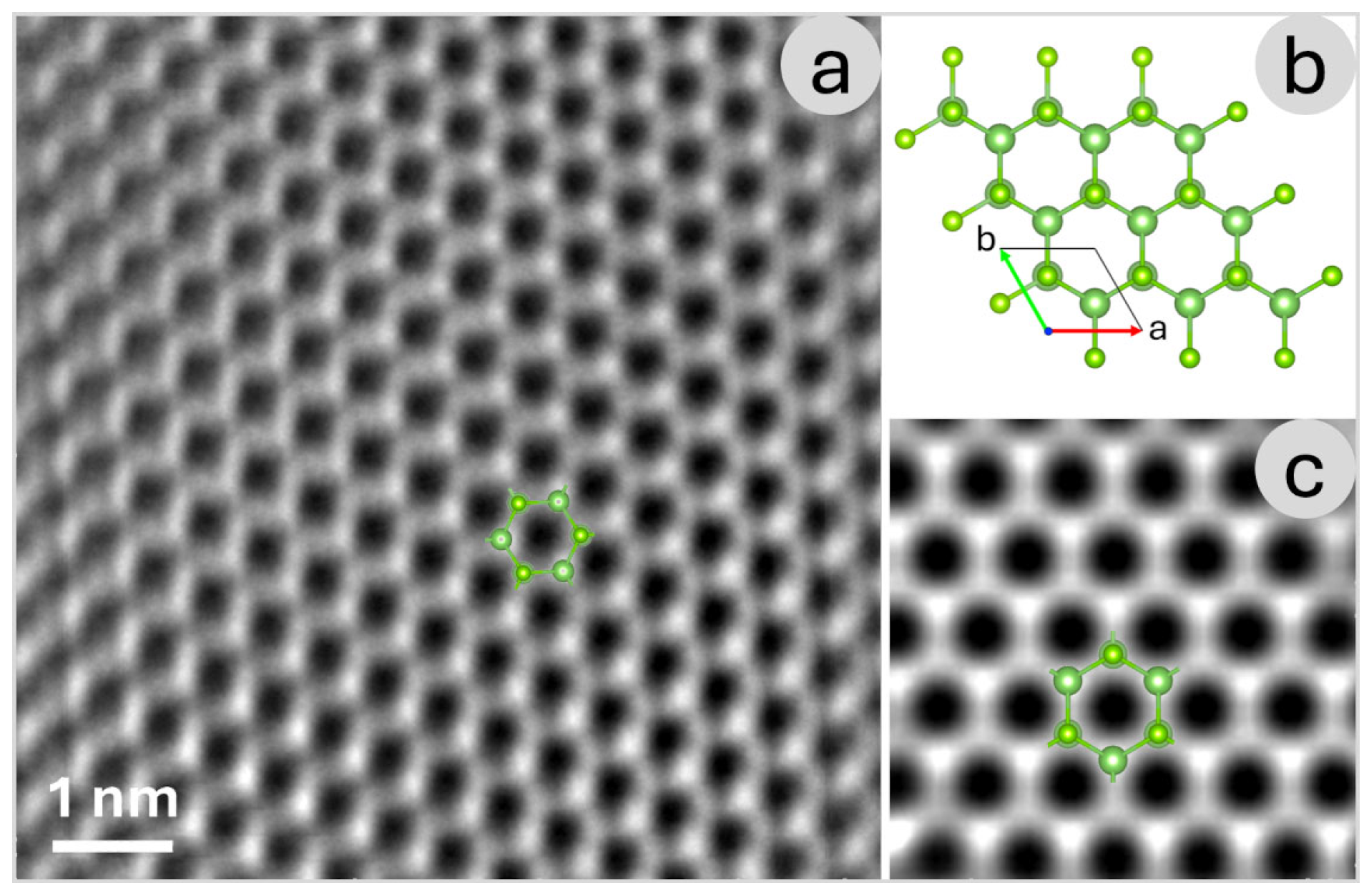
Figure 2a presents a High-Angle Annular Dark Field (HAADF) image acquired from a very thin region of the GaSe sample, providing a direct visualization of the lattice structure. HAADF imaging, a scanning transmission electron microscopy (STEM) technique, exploits the Z-contrast effect, where heavier atoms scatter electrons more strongly than lighter ones. This results in brighter spots corresponding to regions with heavier elements, enabling a clear distinction between different atomic species based on their atomic number. In the case of GaSe, this contrast mechanism is particularly useful for identifying gallium (Ga) and selenium (Se) within the lattice and analyzing structural variations at the atomic scale. The Z-contrast observed in the HAADF image is fundamental in determining the arrangement of atomic columns, allowing for a detailed study of material properties such as stacking order, local defects, and layer thickness variations. Since GaSe is a layered van der Waals material, understanding its atomic structure is crucial for evaluating its electronic and optical properties. The high-resolution imaging provided by HAADF-STEM, combined with computational simulations, enables a comprehensive investigation of different structural modifications of the monolayer.

To further aid in the interpretation of the atomic arrangements, Figure 2b displays the simulated crystal structure of the β-GaSe structural modification, generated using VESTA 2.1 [25]. VESTA is widely used for visualizing crystallographic structures and for analyzing interatomic distances, coordination environments, and bonding configurations. The inclusion of this theoretical model enables a direct comparison between expected and observed structural features, bridging the gap between computational predictions and experimental observations.

Figure 2c presents high-resolution simulated image of the GaSe monolayer, corresponding to the β-GaSe structural modification. The simulation performed using SIMULATEM 2001 [26], provides a powerful tool for generating STEM image simulations based on experimental parameters. By comparing these simulated images with experimental data, it is possible to validate structural models, identify potential distortions or defects, and gain deeper insight into the material’s behavior under different conditions.

These analyses are essential for exploring the polymorphism of GaSe, as structural variations can significantly impact its electronic band structure, carrier mobility, and optical properties. The ability to distinguish different GaSe modifications at the atomic scale provides valuable insights for tailoring the material’s characteristics for specific applications, such as in optoelectronic devices, photodetectors, and nanoscale transistors. The integration of HAADF imaging with multislice simulations proved essential for unambiguously characterizing the atomic structure of GaSe. This combined approach not only validated the polytype assignments but also demonstrated the effectiveness of correlating experimental imaging with theoretical modeling to accurately interpret local structural features in two-dimensional materials.

Figure 3a,b present a zero-loss high-resolution transmission electron microscopy (HRTEM) image of an ultrathin gallium selenide (GaSe) sheet obtained using energy-filtered transmission electron microscopy (EF-TEM), and a corresponding enlargement of the circled region, respectively. The zero-loss filtering technique selectively removes inelastically scattered electrons, which typically contribute to background noise and reduce image contrast. By filtering out these electrons, the resulting image provides improved structural clarity, allowing for a more precise visualization of atomic arrangements within the material. This technique is particularly valuable for examining delicate, nanoscale materials like GaSe, where maintaining high contrast and resolution is crucial for accurate structural characterization.

In this context, the zero-loss HRTEM image offers a contrast mechanism like the HAADF image discussed earlier. Both techniques enhance the visibility of atomic features, albeit through different mechanisms HAADF imaging relies on atomic number (Z-contrast) variations, while EF-TEM selectively removes energy-loss contributions to refine structural details. The improved contrast in the zero-loss image enables better distinction between individual GaSe layers, facilitating the analysis of structural defects, layer stacking, and local thickness variations.

To complement the structural imaging, Figure 3c,d present the corresponding composite elemental map, illustrating the spatial distribution of gallium (Ga) and selenium (Se) within the thin film, and a corresponding enlargement of the circled region, respectively. This map was generated by selecting the characteristic energy absorption edges of Se M_4,5 and Ga M_2,3, ensuring precise elemental differentiation. In the composite representation, selenium is depicted in red, while gallium appears in green, providing an intuitive visualization of the material’s composition.

The elemental mapping technique employed here is particularly useful for identifying inhomogeneities, defects, and potential segregation of elements within the sample. Given that GaSe is a van der Waals material with strong in-plane bonding and weak interlayer interactions, slight variations in stoichiometry or elemental distribution can significantly influence its electronic and optical properties. The detailed spatial distribution of gallium and selenium observed in Figure 2b provides valuable insight into the material’s uniformity, structural integrity, and potential deviations from ideal stoichiometry, which could affect device performance in optoelectronic applications.

By combining zero-loss HRTEM imaging with energy-filtered elemental mapping, this analysis provides a comprehensive characterization of the GaSe thin film at the nanoscale. The synergy between these techniques allows researchers to establish a direct link between the structural and compositional properties of the material, paving the way for a deeper understanding of its physical behavior and potential technological applications in nanodevices and photonic systems.

At medium magnification, the GaSe sample reveals its characteristic terraced structure, as shown in Figure 4a. These terraces arise due to the layered nature of GaSe, a van der Waals material composed of weakly bonded atomic sheets. The step-like morphology plays a significant role in influencing the electronic behavior of the material, as variations in layer thickness can modify local electronic states. Understanding these structural variations is crucial for applications in optoelectronics and nanodevices, where precise control over electronic properties is required.

The terraced structure serves as an ideal system for studying the correlation between morphology and electronic properties using Electron Energy Loss Spectroscopy (EELS). EELS provides detailed information on energy loss mechanisms as electrons interact with the sample, making it a powerful tool for probing local electronic structure, bandgap variations, and plasmonic excitations. Since electronic properties in GaSe are highly sensitive to thickness, EELS measurements across different terrace levels allow for the identification of trends in bandgap energy, electronic transitions, and dielectric response.

Figure 4 highlights the relationship between the morphological features (Figure 4b) observed in the HAADF mode and the quantitative electronic structure analysis performed via EELS (Figure 4c). The HAADF mode, which is sensitive to atomic number (Z-contrast), helps in distinguishing regions of different thicknesses within the sample. By selecting specific areas in the HAADF image for EELS measurements, one can extract precise spectral data corresponding to varying structural configurations. This correlation enables a deeper understanding of how morphological characteristics—such as terrace height, strain effects, and local defects—influence the electronic response of GaSe.

In the analyzed sample, multiple distinct terraces are observed, with a representative region shown in Figure 4. The terraces exhibit varying step heights, with an average value adjusted to ensure consistency with the overall thickness range of 4 to 30 nm. Each terrace measures approximately 5 nm in height and 20 nm in lateral dimension, corresponding to 1000 image points in the dataset. This well-defined thickness modulation provides a robust platform for systematically investigating the evolution of electronic properties in GaSe as a function of layer thickness. By averaging the Electron Energy Loss Spectroscopy (EELS) spectra collected from individual terraces, statistically significant trends in the thickness-dependent electronic behavior of GaSe are revealed. Additional data from other sample regions examined during this study are included in the Supplementary Information.

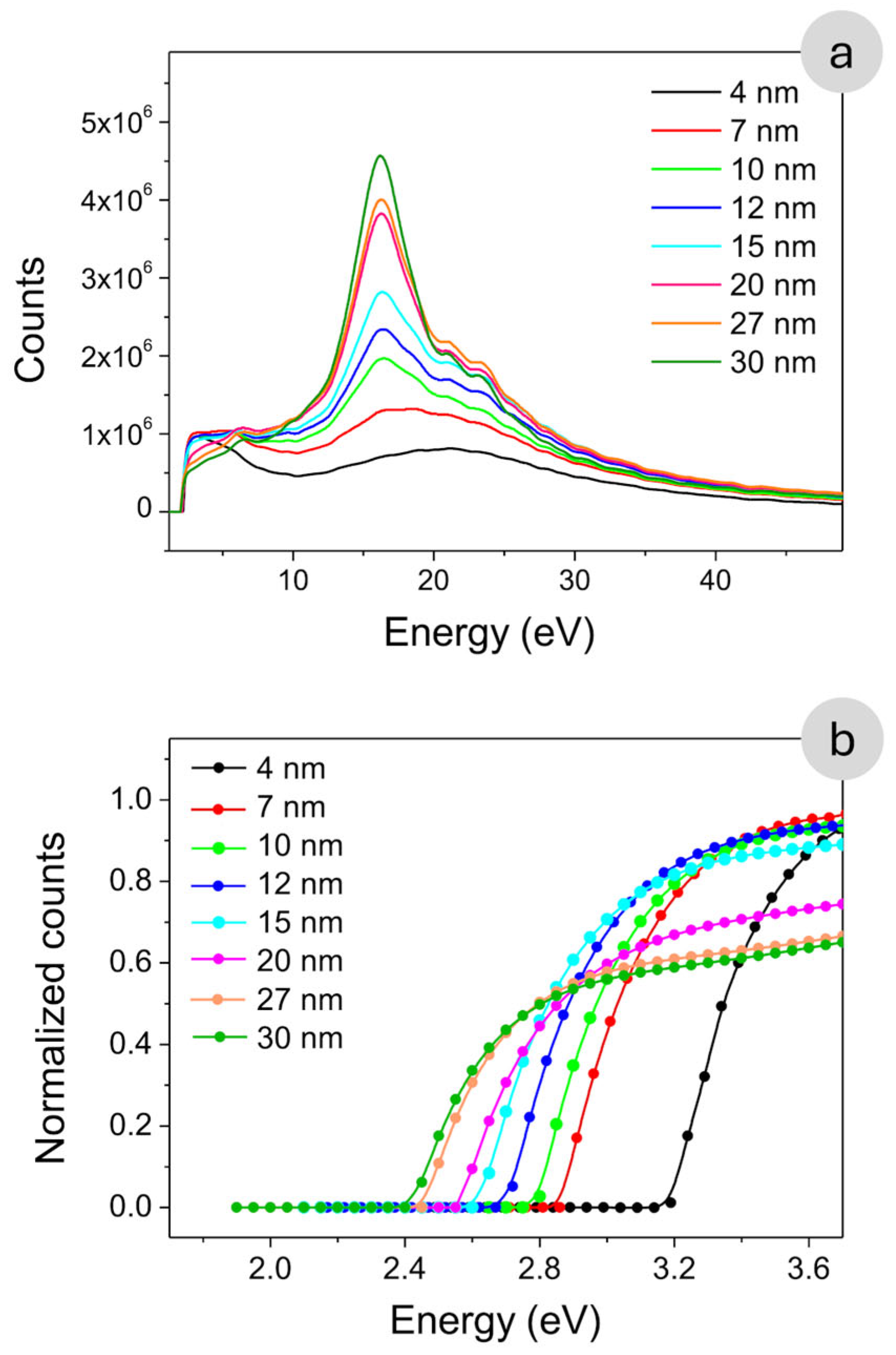
To accurately analyze the valence electron region, the zero-loss peak was subtracted (for detail see Supplementary Materials). Figure 5a presents the EELS spectra obtained from the different regions identified in Figure 4, highlighting thickness-dependent variations in low-energy electronic excitations. The intensity modulation observed in the low-loss EELS spectrum reveals distinct features corresponding to electron energy loss events due to interactions within the GaSe sample.

The EELS spectra exhibit two well-defined features centered at approximately 6 eV and 16 eV, which provide key insights into the electronic excitations in GaSe. According to previous studies, the feature near 6 eV is primarily associated with interband transitions and low-energy plasmonic resonances originating from collective oscillations of valence electrons [20]. In our measurements, this peak shows a marked increase in intensity in regions where the local thickness exceeds ~20 nm, indicating a reduced influence of quantum confinement and an enhanced contribution from bulk-like electronic states. This trend suggests that, as thickness increases, more delocalized carriers participate in excitation processes due to a higher density of available states. Conversely, the peak at ~16 eV appears consistently across all thicknesses analyzed, with minimal variation in energy or intensity. This robustness suggests that the 16 eV feature corresponds to a fundamental bulk plasmon excitation intrinsic to GaSe, largely independent of quantum size effects or local morphology [20].

These observations underline the capability of EELS to probe both surface-sensitive and bulk-sensitive excitations in layered materials, while also highlighting the critical role of sample thickness in modulating spectral response.

Figure 5b presents a zoomed-in view of the absorption edge region, revealing a clear thickness-dependent behavior. As the GaSe layer becomes thicker, the onset of the absorption edge progressively shifts toward lower energies. This redshift is attributed to the gradual suppression of quantum confinement effects, which significantly affect the electronic structure in ultrathin layers [27].

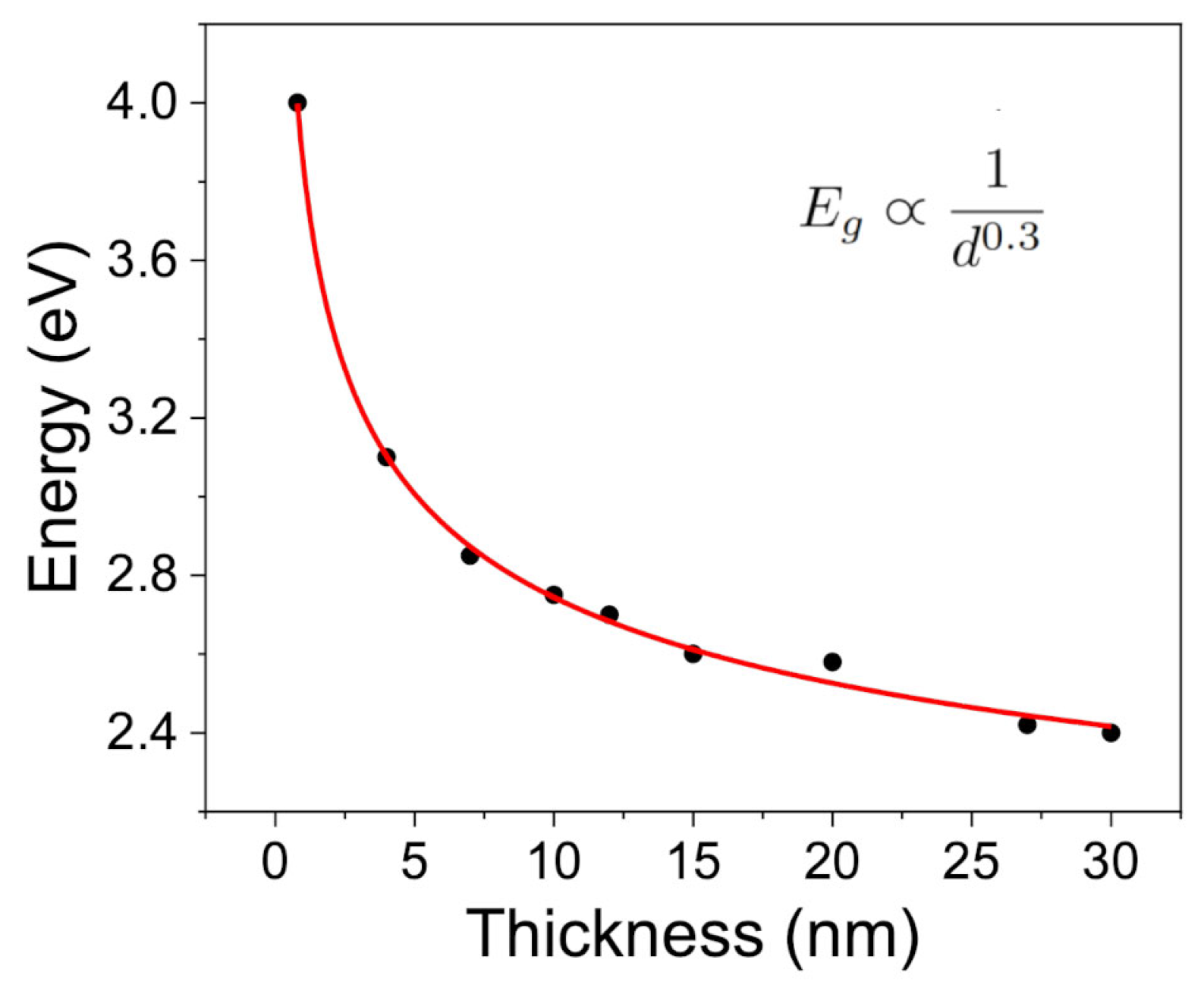
The experimental data points corresponding to the optical absorption edge are highlighted in Figure 5b and plotted as a function of material thickness in Figure 6. The observed trend suggests a possible dependence of the energy band gap on thickness of the form:

$$E_g(d)=\left[{1+\left({\displaystyle \frac{A}{d}}\right)}^n\right]E_0$$

where E₀ denotes the band gap in the bulk limit, and A and n are fitting parameters that account for the strength and dimensionality of the confinement effects. This phenomenological expression has been widely adopted in the literature to describe confinement-induced shifts in the energy gap of layered semiconductors [28,29].

However, this empirical model is too simplified to fully capture the complexity of the underlying physical phenomena. Typically, the exponent n is close to 2; however, our experimental data yield a value near 0.3. Although the 1/dⁿ dependence captures the general trend of gap widening with decreasing thickness, the fitted n deviates markedly from the ideal value of 2 predicted by the infinite square quantum well model within the effective mass approximation [30], where the confinement-induced energy shift follows:

$$∆E\propto {\displaystyle \frac{1}{d^2}}\left({\displaystyle \frac{1}{m_e^{*}}}+{\displaystyle \frac{1}{m_h^{*}}}\right)$$

where m_e^∗ and m_h^∗ are the effective masses of electrons and holes, respectively. The deviation from this ideal behavior suggests that simple quantum confinement cannot fully account for the experimental observations in few-layer GaSe. Rather, the reduced exponent likely reflects a more complex interplay of physical mechanisms beyond particle-in-a-box quantization.

Interestingly, the fitted exponent n ≈ 0.3 is numerically close to the reported in-plane effective mass ratio m^∗/m₀ ≈ 0.3 for carriers in GaSe [31]. However, this numerical similarity should not be overinterpreted as a direct physical correspondence. In the absence of a rigorous theoretical model that explicitly links the exponent n to the effective mass, such parallels remain speculative and primarily serve to indicate the presence of strong quantum size effects in the system.

Density functional theory (DFT) calculations support the interpretation of a thickness-dependent band structure evolution in GaSe, with a predicted widening of the band gap in the few-layer limit due to dimensional confinement [32]. As the number of layers decreases, the out-of-plane carrier motion becomes restricted, resulting in the discretization of energy levels and a shift in the conduction and valence band edges. This behavior is consistent with what has been observed in other van der Waals materials such as MoS₂, where a monolayer exhibits a direct band gap, while bulk MoS₂ exhibits an indirect gap due to altered electronic band dispersion [33].

Beyond quantum confinement, additional factors contribute to the modulation of the band gap with thickness. One such mechanism is the variation in dielectric screening. In ultrathin GaSe, the reduced dimensionality weakens the ability of the material to screen Coulomb interactions, leading to enhanced exciton binding energies and a concomitant increase in the optical gap [34,35]. As thickness increases, dielectric screening becomes more effective, lowering exciton binding energies and contributing to a redshift in the absorption edge.

Moreover, interlayer coupling plays a significant role in the electronic structure of GaSe. Although the layers are bound by van der Waals forces, their interaction is non-negligible and can lead to hybridization of electronic states, especially in thicker samples. This coupling alters band dispersion and contributes to the observed narrowing of the gap with increasing layer number [36]. Similar effects have been reported in layered InSe, where the optical band gap is highly sensitive to the number of layers due to strong interlayer interactions [37].

To more accurately describe the experimental trends and account for the multifaceted nature of thickness-dependent band gap evolution in GaSe, it is necessary to go beyond the simple confinement model. A refined description that incorporates additional physical effects—including dielectric screening and interlayer electronic coupling—can be formulated as:

$$E_g(d)=E_0\left[{\left({\displaystyle \frac{A}{d}}\right)}^n+B{e}^{-d/\lambda }-{\displaystyle \frac{C}{{\epsilon }^2\left(d\right)}}+1\right]$$

In this model, the first term represents quantum confinement, the second captures interlayer coupling effects (which decay exponentially with increasing thickness), and the third accounts for dielectric screening, with ε(d) describing the thickness-dependent dielectric environment [38].

The thickness-dependent dielectric permittivity of GaSe can be described using a phenomenological model of the form:

$$\epsilon (d)={\epsilon }_{\infty }\left(1-\alpha e^{-d/d_0}\right)$$

where ε(d) is the effective dielectric constant as a function of thickness d, ε_∞ is the bulk dielectric constant, α is a dimensionless parameter describing the suppression of screening at low thickness, and d₀ is a characteristic screening length scale.

Using this expression, the relative dielectric constant for a monolayer (d → 0) is estimated as:

$$\epsilon \left(0\right) \approx {\epsilon }_{\infty }(1-\alpha )\approx 4.0$$

while in the bulk limit (d → ∞), it converges to ε_∞ ≈ 8.0, in good agreement with both DFT calculations and optical spectroscopy data. Based on available literature, it is reasonable to assume that α ≈ 0, accounting for the reduced dielectric screening in atomically thin layers. The characteristic screening length is estimated as d₀ ≈ 3.2 nm, which corresponds approximately to four GaSe layers [39].

Here, the parameter λ represents a characteristic decay length associated with interlayer coupling. In layered van der Waals materials such as GaSe, although the individual layers are primarily held together by weak non-covalent forces, their electronic states can still hybridize across adjacent layers. This interlayer interaction modifies the band dispersion and becomes increasingly significant in thicker samples. The effect of such coupling on the electronic structure typically diminishes with increasing thickness and is well described by an exponential decay. The parameter λ therefore quantifies the spatial range over which interlayer electronic interactions remain effective. Physically, it reflects the extent to which electronic wavefunctions from adjacent layers overlap in the out-of-plane direction. A small λ implies that interlayer coupling is strongly localized, while a larger λ indicates more delocalized interlayer interactions [40]. For GaSe and related semiconductors, typical values of λ lie in the range of a few nanometers, corresponding to several atomic layers. Figure 7 shows the energy gap as a function of thickness, where, in addition to the experimental data for thin layers obtained from EELS measurements, we have included the bulk energy gap values derived from optical measurements using UV-Vis-NIR spectroscopy [41]. Further details on these measurements are provided in the Supplementary Materials of the paper. The equation accurately fits the experimental data across the entire thickness range, capturing both the quantum confinement effects at low thickness and the asymptotic behavior in the bulk limit. The corresponding fitting parameters are summarized in

Table 1. Fitting parameters.

Parameters	Values	Standard Error
E0	1.9 eV	0.2
A	2.6	0.3
B	0.20	0.05
C	21	4
λ	6 nm	1
n	0.39	0.01

.

4. Conclusions

In this work, we have conducted a comprehensive structural and electronic investigation of gallium selenide (GaSe) thin films across a wide thickness range, revealing several key findings:

Direct Atomic-Scale Characterization: Using HAADF-STEM and zero-loss HRTEM, we directly visualized the stacking sequences, terraced morphologies, and local structural imperfections in ultrathin GaSe. The identification of specific polymorphs was validated by simulated HAADF images and atomistic models, confirming the predominance of the β-GaSe polytype in our samples.

-

Compositional Uniformity: Energy-filtered TEM elemental mapping verified the uniform distribution of gallium and selenium, supporting the high chemical homogeneity of the synthesized films.

-

Thickness-Dependent Electronic Response: EELS analyses revealed a clear evolution of the electronic structure with increasing layer thickness. Notably, the intensity of the low-loss feature at ~6 eV increased systematically with thickness, indicating enhanced plasmonic and interband excitation contributions in thicker layers. The shift from quantum-confined to bulk-like electronic regimes was quantitatively mapped.

-

Deviation from Conventional Models: The measured optical bandgap as a function of thickness showed significant deviations from the traditional inverse-square quantum confinement model. Instead, our data are well described by an extended model that incorporates quantum confinement, thickness-dependent dielectric screening, and interlayer coupling. Key extracted parameters (confinement exponent n ≈ 0.3, dielectric screening length d₀ ≈ 3.2 nm, and interlayer coupling decay constant λ) are in excellent agreement with literature, providing a refined understanding of electronic screening and interlayer effects.

-

Methodological Impact: The integrated approach—combining advanced microscopy, spectroscopy, and modeling—proved essential for disentangling the contributions of structure, thickness, and electronic interactions in GaSe. This enabled not only the identification of critical features at the atomic scale but also the precise mapping of thickness-dependent electronic and optical properties.

-

Device-Relevant Performance: Preliminary photoresponse measurements (see Supplementary Information) demonstrated the potential of these high-quality GaSe films for photodetector applications, highlighting their environmental stability and tunable optoelectronic properties.

Altogether, our findings provide a robust framework for understanding and engineering the thickness-dependent properties of GaSe. These insights are directly relevant for the design of GaSe-based optoelectronic and photonic devices, where detailed control over structure and electronic behavior is crucial. Future studies focusing on excitonic dynamics, strain modulation, and substrate interactions are expected to further advance the utility of GaSe and related layered semiconductors for next-generation technologies.