Fractional Conductances of Wires: The S-Matrix Approach
Abstract
1. Introduction
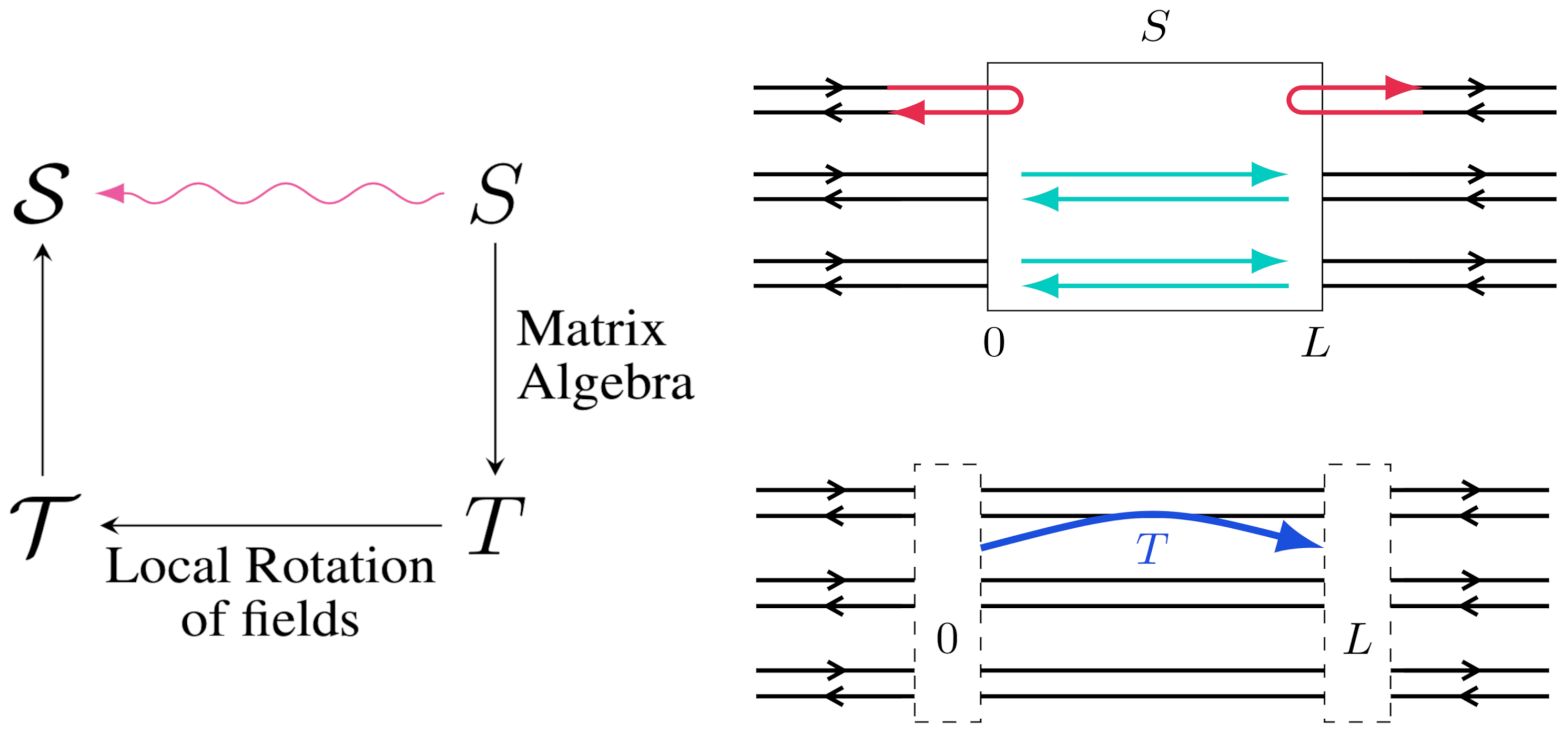
2. Model
Scattering and Transfer Matrices
3. Results
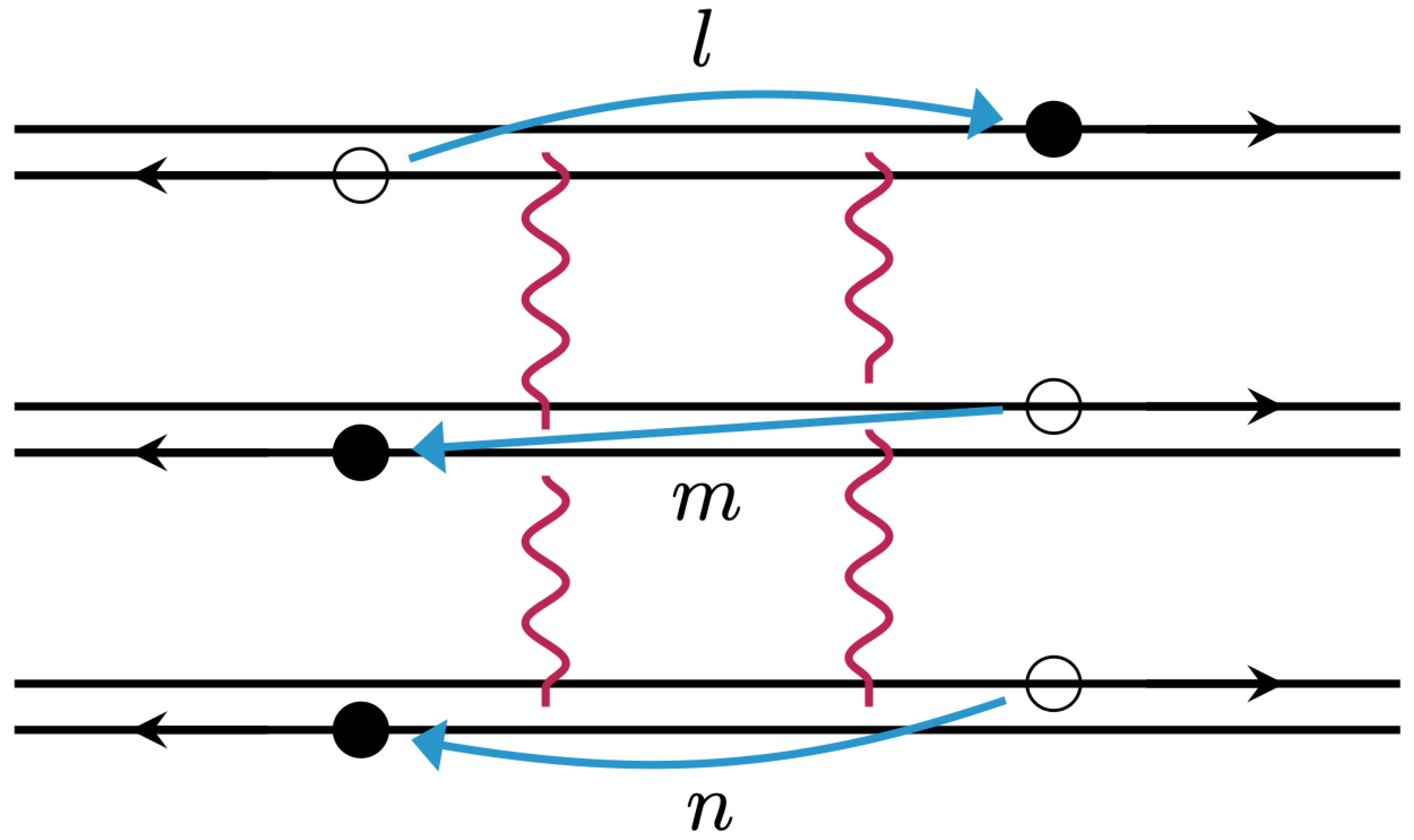
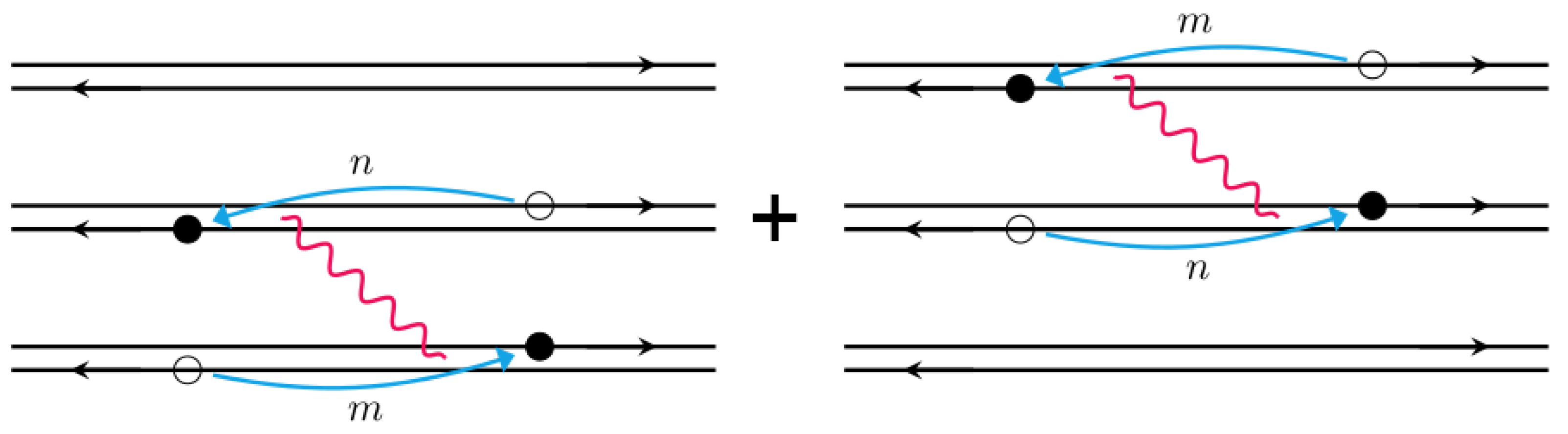
3.1. Single Backscattering Mechanism
3.2. Single Gapless Mode
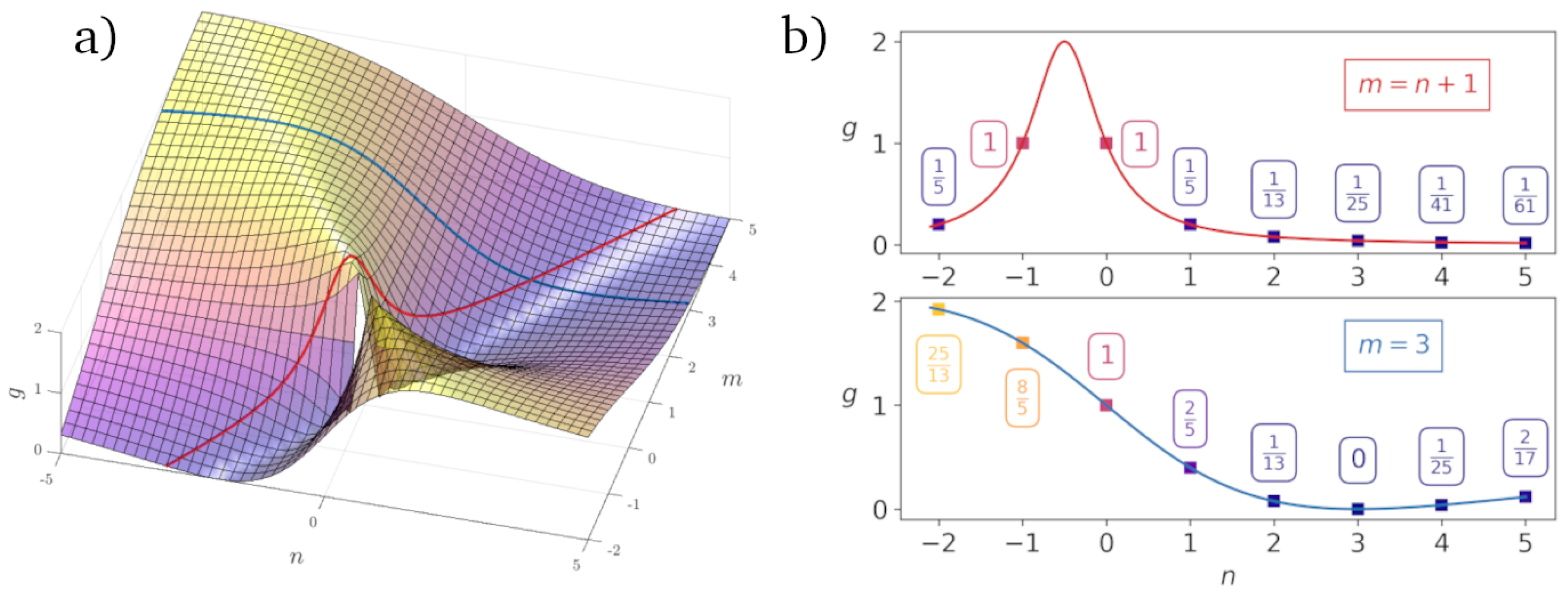
4. Finding Even Denominators
4.1. Generic Analysis
4.2. Specific Examples
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Correction Statement
References
- Haldane, F.D.M. Luttinger liquid theory of one-dimensional quantum fluids. I. Properties of the Luttinger model and their extension to the general 1D interacting spinless Fermi gas. J. Phys. C Solid State Phys. 1981, 14, 2585–2609. [Google Scholar] [CrossRef]
- Kane, C.L.; Mukhopadhyay, R.; Lubensky, T.C. Fractional Quantum Hall Effect in an Array of Quantum Wires. Phys. Rev. Lett. 2002, 88, 036401. [Google Scholar] [CrossRef] [PubMed]
- Teo, J.C.; Kane, C. From Luttinger liquid to non-Abelian quantum Hall states. Phys. Rev. B 2014, 89, 085101. [Google Scholar] [CrossRef]
- Fuji, Y.; Furusaki, A. Quantum Hall hierarchy from coupled wires. Phys. Rev. B 2019, 99, 035130. [Google Scholar] [CrossRef]
- Meng, T.; Neupert, T.; Greiter, M.; Thomale, R. Coupled-wire construction of chiral spin liquids. Phys. Rev. B 2015, 91, 241106. [Google Scholar] [CrossRef]
- Kagalovsky, V.; Chudnovskiy, A.; Yurkevich, I. Stability of a topological insulator: Interactions, disorder, and parity of Kramers doublets. Phys. Rev. B 2018, 97, 241116. [Google Scholar] [CrossRef]
- Yurkevich, I.; Kagalovsky, V. Superconducting edge states in a topological insulator. Sci. Rep. 2021, 11, 18400. [Google Scholar] [CrossRef]
- Sullivan, J.; Dua, A.; Cheng, M. Fractonic topological phases from coupled wires. Phys. Rev. Res. 2021, 3, 023123. [Google Scholar] [CrossRef]
- Fuji, Y.; Furusaki, A. Bridging three-dimensional coupled-wire models and cellular topological states: Solvable models for topological and fracton orders. Phys. Rev. Res. 2023, 5, 043108. [Google Scholar] [CrossRef]
- Kumar, S.; Pepper, M.; Holmes, S.N.; Montagu, H.; Gul, Y.; Ritchie, D.A.; Farrer, I. Zero-Magnetic Field Fractional Quantum States. Phys. Rev. Lett. 2019, 122, 086803. [Google Scholar] [CrossRef]
- Kumar, S.; Pepper, M. Interactions and non-magnetic fractional quantization in one-dimension. Appl. Phys. Lett. 2021, 119, 110502. [Google Scholar] [CrossRef]
- Villar Rodriguez, I.; Gul, Y.; Dempsey, C.P.; Dong, J.T.; Holmes, S.N.; Palmstrøm, C.J.; Pepper, M. Nonmagnetic fractional conductance in high mobility InAs quantum point contacts. Phys. Rev. B 2025, 112, 075404. [Google Scholar] [CrossRef]
- Dong, J.T.; Gul, Y.; Rodriguez, I.V.; Engel, A.N.; Dempsey, C.P.; Holmes, S.N.; Pepper, M.; Palmstrøm, C.J. Spin-orbit coupling in digital alloyed InGaAs quantum wells. arXiv 2025. [Google Scholar] [CrossRef]
- Kumar, S.; Pepper, M.; Ritchie, D.; Farrer, I. Fractional conductance quantisation in low-dimensional electrons. In Proceedings of the APS March Meeting Abstracts, Minneapolis, MN, USA & Virtual, 4–8 March 2024; p. B13.006. [Google Scholar]
- Kumar, V.; Duo, Y.; See, P.; Griffiths, J.P.; Ritchie, D.A.; Farrer, I.; Kumar, S. Correlation effects mediated by disorders in one-dimensional channels. Phys. Rev. B 2025, 112, 035404. [Google Scholar] [CrossRef]
- Kumar, S.; Pepper, M.; See, P.; Ritchie, D.; Farrer, I.; Smith, H. Spin and Charge Phases in 1D Electrons. In Proceedings of the APS March Meeting Abstracts, Chicago, IL, USA, 14–18 March 2022; p. B12.006. [Google Scholar]
- Meng, T.; Fritz, L.; Schuricht, D.; Loss, D. Low-energy properties of fractional helical Luttinger liquids. Phys. Rev. B 2014, 89, 045111. [Google Scholar] [CrossRef]
- Aseev, P.P.; Loss, D.; Klinovaja, J. Conductance of fractional Luttinger liquids at finite temperatures. Phys. Rev. B 2018, 98, 045416. [Google Scholar] [CrossRef]
- Cornfeld, E.; Neder, I.; Sela, E. Fractional shot noise in partially gapped Tomonaga-Luttinger liquids. Phys. Rev. B 2015, 91, 115427. [Google Scholar] [CrossRef]
- Shavit, G.; Oreg, Y. Fractional Conductance in Strongly Interacting 1D Systems. Phys. Rev. Lett. 2019, 123, 036803. [Google Scholar] [CrossRef]
- Sedlmayr, N.; Yurkevich, I.V.; Lerner, I.V. Tunnelling density of states at Coulomb-blockade peaks. Europhys. Lett. 2006, 76, 109. [Google Scholar] [CrossRef]
- Lesovik, R.; Glazman, L.; Khmelnitskii, D.; Shekhter, R. Reflectionless quantum transport and fundamental ballistic-resistance steps in microscopic constrictions. JETP Lett. 1988, 48, 238–241. [Google Scholar]
- Maslov, D.L.; Stone, M. Landauer conductance of Luttinger liquids with leads. Phys. Rev. B 1995, 52, R5539–R5542. [Google Scholar] [CrossRef]
- Safi, I.; Schulz, H.J. Transport in an inhomogeneous interacting one-dimensional system. Phys. Rev. B 1995, 52, R17040–R17043. [Google Scholar] [CrossRef] [PubMed]
- Ponomarenko, V.V. Renormalization of the one-dimensional conductance in the Luttinger-liquid model. Phys. Rev. B 1995, 52, R8666–R8667. [Google Scholar] [CrossRef]
- Egger, R.; Grabert, H. Applying voltage sources to a Luttinger liquid with arbitrary transmission. Phys. Rev. B 1998, 58, 10761–10768. [Google Scholar] [CrossRef]
- Oreg, Y.; Sela, E.; Stern, A. Fractional helical liquids in quantum wires. Phys. Rev. B 2014, 89, 115402. [Google Scholar] [CrossRef]
- Liu, L.; Gul, Y.; Holmes, S.; Chen, C.; Farrer, I.; Ritchie, D.; Pepper, M. Possible zero-magnetic field fractional quantization in In0. 75Ga0. 25As heterostructures. Appl. Phys. Lett. 2023, 123, 183502. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davies, R.; Kagalovsky, V.; Yurkevich, I.V. Fractional Conductances of Wires: The S-Matrix Approach. Crystals 2025, 15, 818. https://doi.org/10.3390/cryst15090818
Davies R, Kagalovsky V, Yurkevich IV. Fractional Conductances of Wires: The S-Matrix Approach. Crystals. 2025; 15(9):818. https://doi.org/10.3390/cryst15090818
Chicago/Turabian StyleDavies, Rose, Victor Kagalovsky, and Igor V. Yurkevich. 2025. "Fractional Conductances of Wires: The S-Matrix Approach" Crystals 15, no. 9: 818. https://doi.org/10.3390/cryst15090818
APA StyleDavies, R., Kagalovsky, V., & Yurkevich, I. V. (2025). Fractional Conductances of Wires: The S-Matrix Approach. Crystals, 15(9), 818. https://doi.org/10.3390/cryst15090818





