Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing
Abstract
1. Introduction
2. Materials and Methods
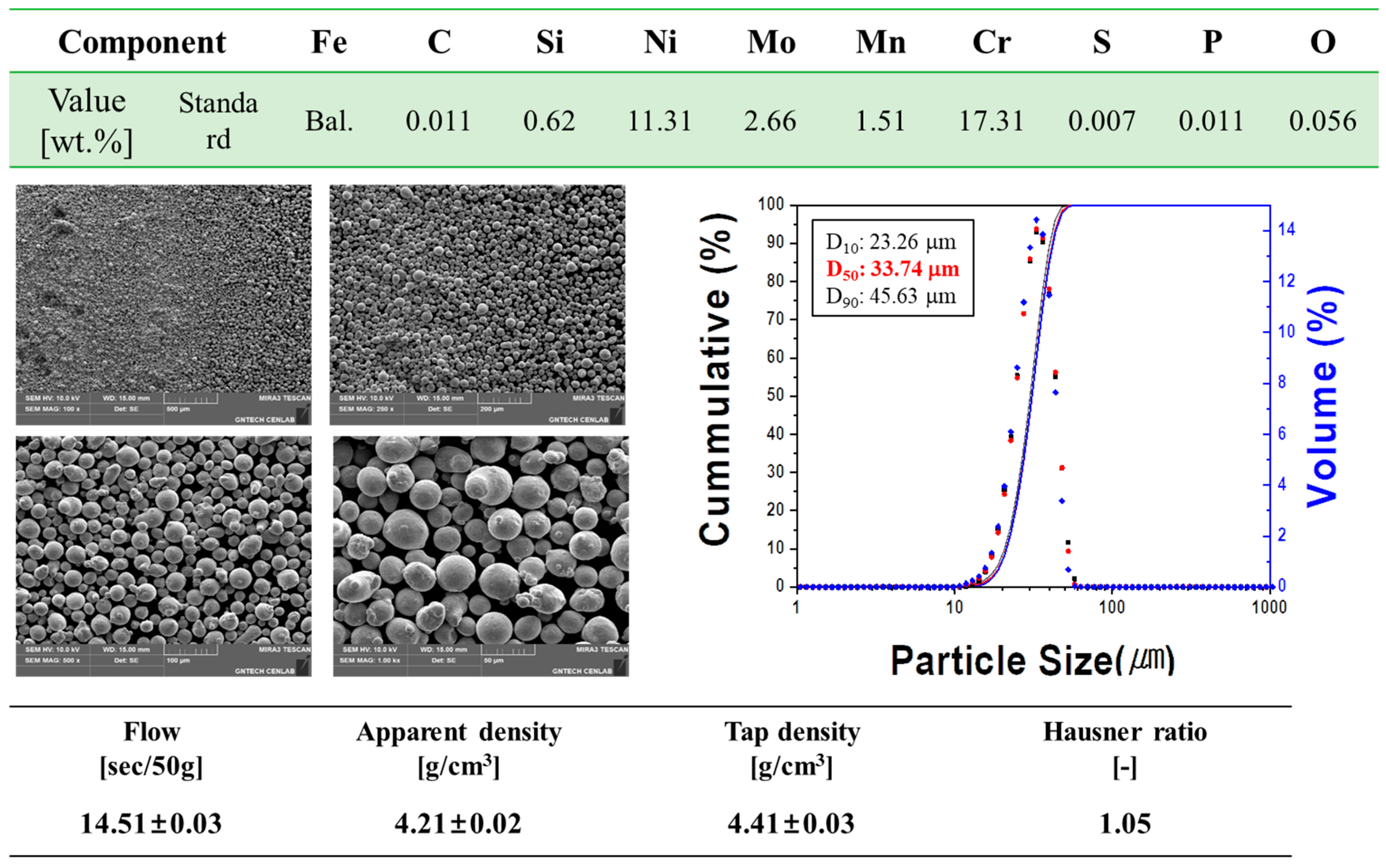
2.1. Material and Powder Characterization
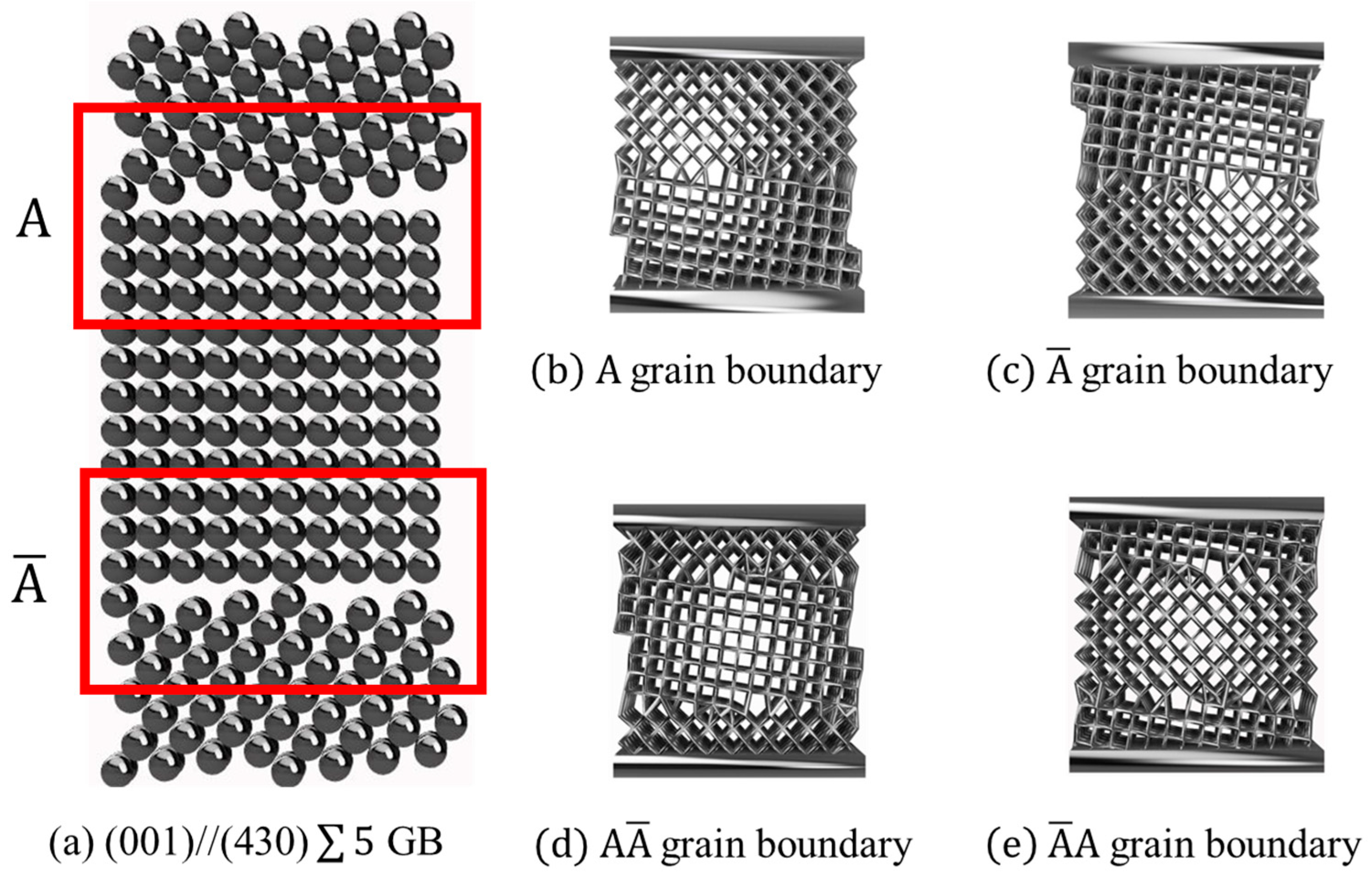
2.2. Design of Bicrystal-Inspired Structures
2.3. Fabrication and Mechanical Characterization
3. Results and Discussion
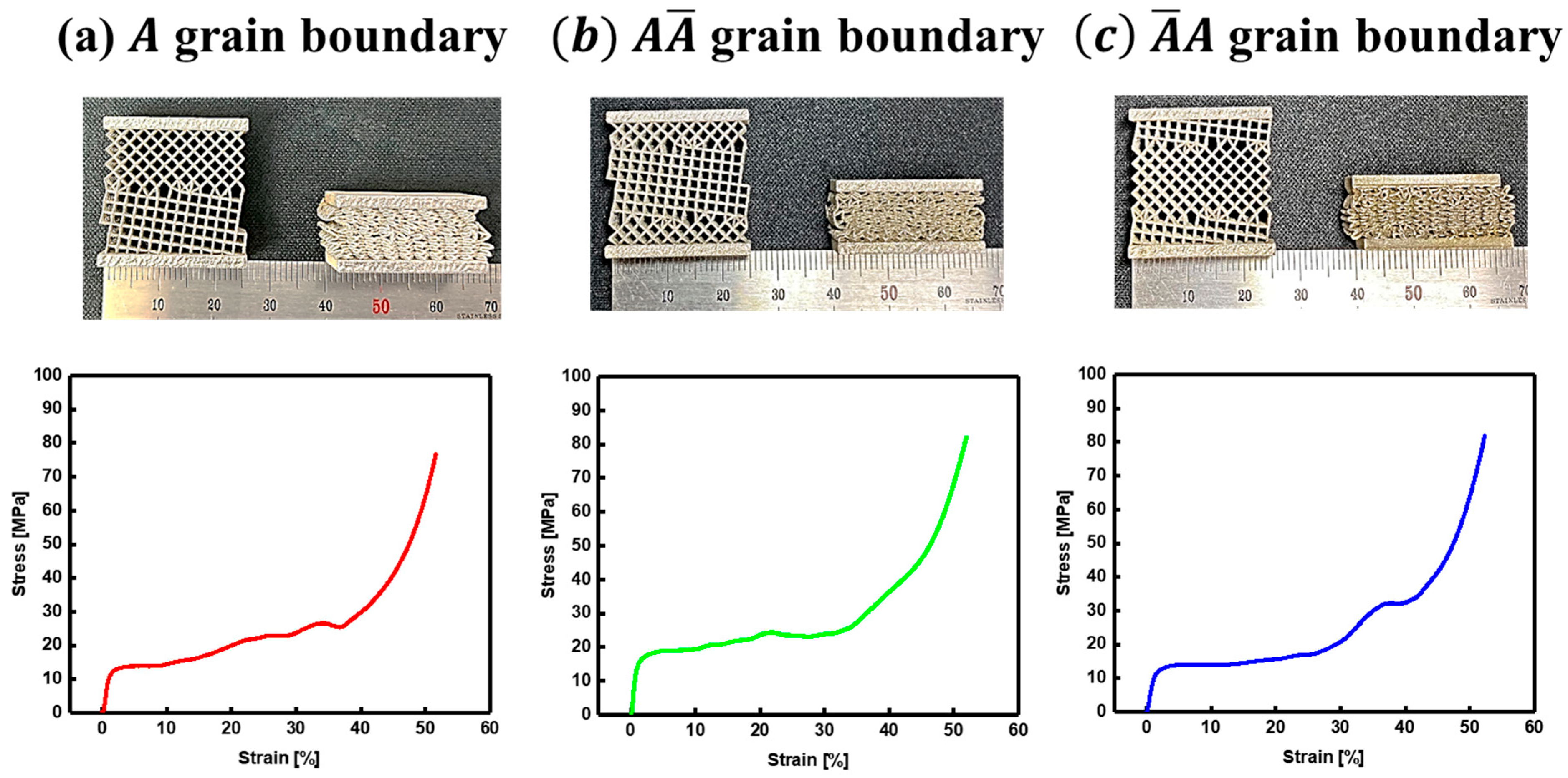
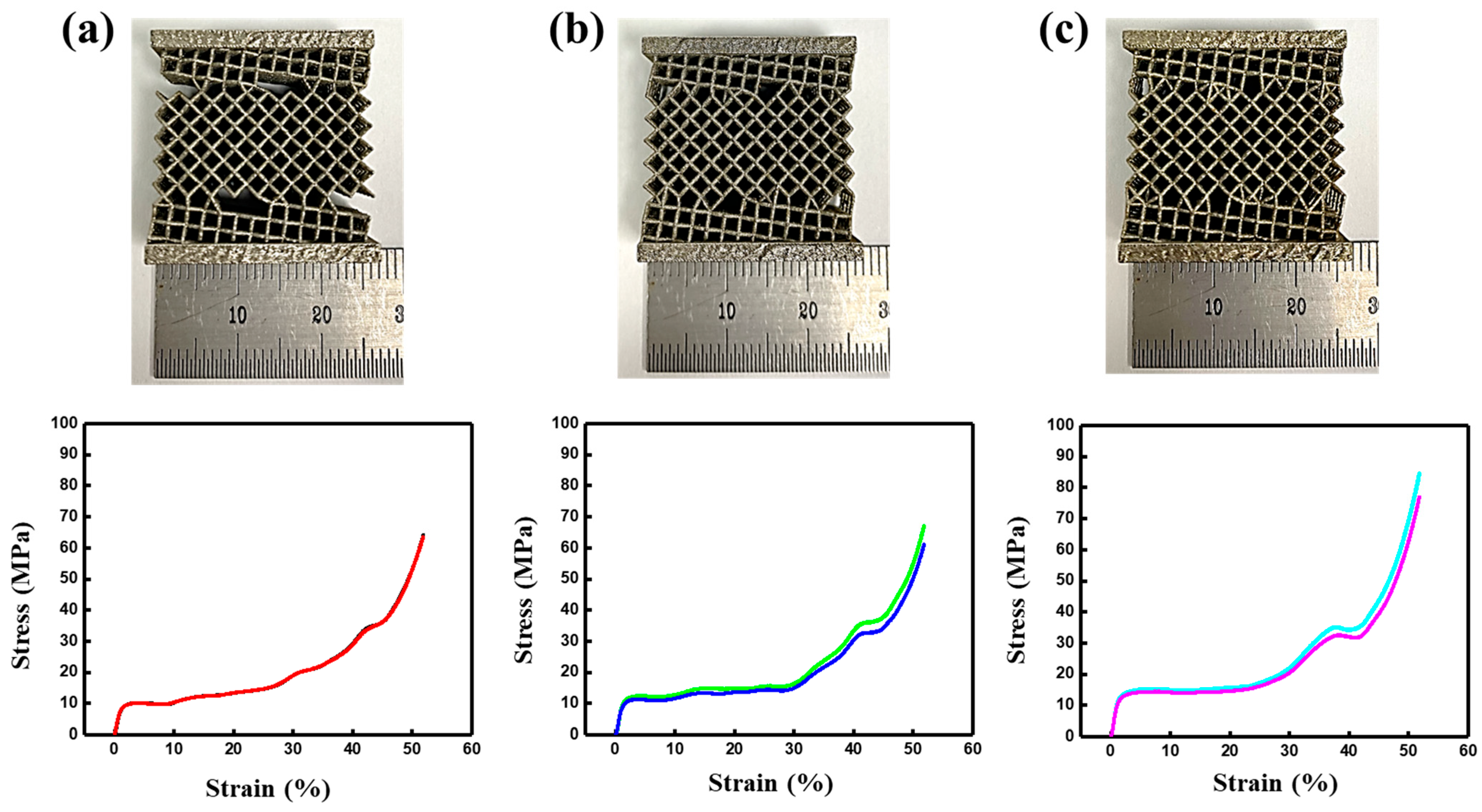
3.1. Role of Symmetry in Bicrystal Deformation
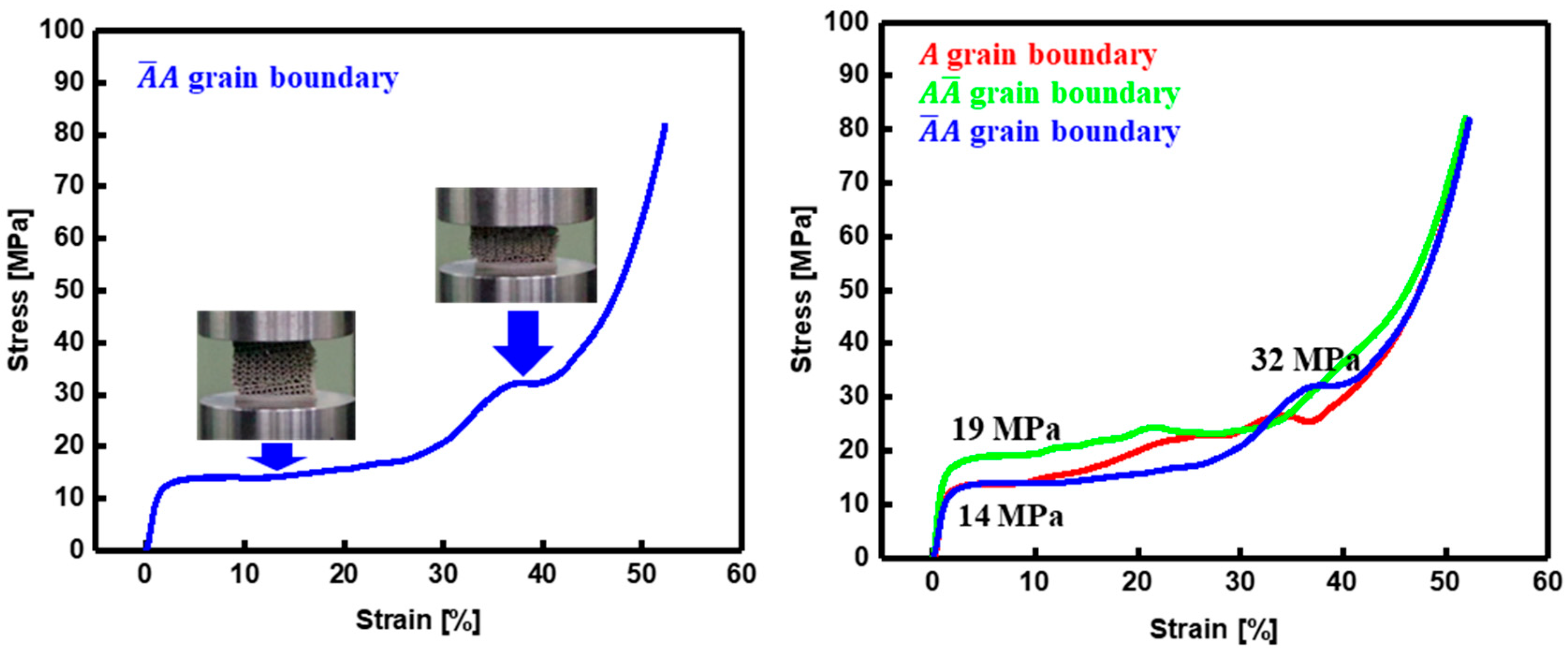
3.2. Tuning Mechanical Properties via Interfacial Bond Engineering
4. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Pham, M.-S.; Liu, C.; Todd, I.; Lertthanasarn, J. Damage-tolerant architected materials inspired by crystal microstructure. Nature 2019, 565, 305–311. [Google Scholar] [CrossRef]
- Yu, T.; Hyer, H.; Sohn, Y.; Bai, Y.; Wu, D. Structure–property relationship in high strength and lightweight AlSi10Mg microlattices fabricated by selective laser melting. Mater. Des. 2019, 182, 108062. [Google Scholar] [CrossRef]
- Li, C.; Lei, H.; Zhang, Z.; Zhang, X.; Zhou, H.; Wang, P.; Fang, D. Architecture design of periodic truss–lattice cells for additive manufacturing. Addit. Manuf. 2020, 34, 101172. [Google Scholar] [CrossRef]
- Jin, N.; Wang, F.; Wang, Y.; Zhang, B.; Cheng, H.; Zhang, H. Failure and energy absorption characteristics of four lattice structures under dynamic loading. Mater. Des. 2019, 169, 107655. [Google Scholar] [CrossRef]
- Thompson, M.K.; Moroni, G.; Vaneker, T.; Fadel, G.; Campbell, R.I.; Gibson, I.; Bernard, A.; Schulz, J.; Graf, P.; Ahuja, B.; et al. Design for additive manufacturing: Trends, opportunities, considerations, and constraints. CIRP Ann. Manuf. Technol. 2016, 65, 737–760. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef] [PubMed]
- Meza, L.R.; Das, S.; Greer, J.R. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 2014, 345, 1322–1326. [Google Scholar] [CrossRef]
- Maskery, I.; Aboulkhair, N.T.; Aremu, A.O.; Tuck, C.J.; Ashcroft, I.A. Compressive failure modes and energy absorption in additively manufactured double gyroid lattices. Addit. Manuf. 2017, 16, 24–29. [Google Scholar] [CrossRef]
- Chen, L.; Lertthanasarn, J.; Pham, M.-S. The origin of the boundary strengthening in polycrystal-inspired architected materials. Nat. Commun. 2021, 12, 4600. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Fan, H.; Bian, Y.; Yang, F. Plastic deformation and energy absorption of polycrystalline-like lattice structures. Mater. Des. 2021, 198, 109321. [Google Scholar] [CrossRef]
- Niknam, H.; Akbarzadeh, A.H. Graded lattice structures: Simultaneous enhancement in stiffness and energy absorption. Mater. Des. 2020, 196, 109129. [Google Scholar] [CrossRef]
- Yang, L.; Han, C.; Wu, H.; Hao, L.; Wei, Q.; Yan, C.; Shi, Y. Insights into unit cell size effect on mechanical responses and energy absorption capability of titanium graded porous structures manufactured by laser powder bed fusion. J. Mech. Behav. Biomed. Mater. 2020, 109, 103843. [Google Scholar] [CrossRef] [PubMed]
- EOS GmbH. EOS StainlessSteel 316L—Material Data Sheet (EOS M 290); EOS GmbH Electro Optical Systems: Krailling, Germany, 2021. [Google Scholar]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Zhai, W.; Zhou, W.; Zhu, Z.; Nai, S.M.L. Selective laser melting and mechanical properties of stainless steels. Materials 2022, 15, 7575. [Google Scholar] [CrossRef]
- Wang, X.; Yu, Z.; Liu, B.; Lin, Z.; Zhang, M. Microstructure and anisotropy of the mechanical properties of 316L stainless steel fabricated by SLM. Metals 2021, 11, 775. [Google Scholar]
- ISO/ASTM 52910:2018; Additive Manufacturing—Design—Requirements, Guidelines and Recommendations. ISO: Geneva, Switzerland; ASTM: West Conshohocken, PA, USA, 2018.
- Rosen, D.W. Design for additive manufacturing: A method to explore unexplored regions of the design space. In Proceedings of the Solid Freeform Fabrication Symposium, Austin, TX, USA, 6–8 August 2007. [Google Scholar]
- Adam, G.A.O.; Zimmer, D. Design for additive manufacturing—Element transitions and aggregated structures. CIRP J. Manuf. Sci. Technol. 2014, 7, 20–28. [Google Scholar] [CrossRef]
- Pradel, P.; Zhu, Z.; Bibb, R.; Moultrie, J. A framework for mapping DfAM knowledge for industrial and product design. J. Eng. Des. 2018, 29, 291–326. [Google Scholar] [CrossRef]
- Wiberg, A.; Persson, J.; Ölvander, J. Design for additive manufacturing—A review of available design methods. Rapid Prototyp. J. 2019, 25, 1080–1094. [Google Scholar] [CrossRef]
- Langelaar, M. An additive manufacturing filter for topology optimization of print-ready designs. Struct. Multidiscip. Optim. 2017, 55, 871–883. [Google Scholar] [CrossRef]
- Gaynor, A.T.; Guest, J.K. Topology optimization considering overhang constraints: Eliminating sacrificial support material in AM. Struct. Multidiscip. Optim. 2016, 54, 1157–1172. [Google Scholar] [CrossRef]
- Qian, X. Undercut and overhang angle control in topology optimization: A density-gradient-based integral approach. Comput. Methods Appl. Mech. Eng. 2017, 317, 224–246. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Jin, N.; Yan, Z.; Wang, Y.; Cheng, H.; Zhang, H. Effects of heat treatment on microstructure and mechanical properties of selective laser melted Ti-6Al-4V lattice materials. Int. J. Mech. Sci. 2021, 190, 106042. [Google Scholar] [CrossRef]
- ISO 13314:2011; Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals. International Organization for Standardization: Geneva, Switzerland, 2011.
- Lee, H.-S.; Mizoguchi, T.; Yamamoto, T.; Kang, S.-J.L.; Ikuhara, Y. Characterization and atomic modeling of an asymmetric grain boundary. Phys. Rev. B 2011, 84, 195319. [Google Scholar] [CrossRef]
- Lee, H.S.; Mizoguchi, T.; Mistui, J.; Yamamoto, T.; Kang, S.J.; Ikuhara, Y. Defect energetics in SrTiO3 symmetric tilt grain boundaries. Phys. Rev. B 2011, 83, 104110. [Google Scholar] [CrossRef]

| Sample ID | Structure Type | Description |
|---|---|---|
| A, Ā | Single-crystal-like | Baseline structures with a single lattice orientation. |
| ĀA, AĀ | Asymmetric Bicrystal | Two meta-grains joined at an asymmetric interface. |
| AĀ-1.3× | Tuned Asymmetric Bicrystal | AĀ structure with the lowest interfacial strut density. |
| AĀ-1.4× | Tuned Asymmetric Bicrystal | AĀ structure with medium interfacial strut density. |
| AĀ-1.5× | Tuned Asymmetric Bicrystal | AĀ structure with the highest interfacial strut density. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.-S. Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing. Crystals 2025, 15, 757. https://doi.org/10.3390/cryst15090757
Lee H-S. Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing. Crystals. 2025; 15(9):757. https://doi.org/10.3390/cryst15090757
Chicago/Turabian StyleLee, Hak-Sung. 2025. "Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing" Crystals 15, no. 9: 757. https://doi.org/10.3390/cryst15090757
APA StyleLee, H.-S. (2025). Mechanical Properties of Bicrystal-Inspired Lattice Structures Fabricated by Additive Manufacturing. Crystals, 15(9), 757. https://doi.org/10.3390/cryst15090757






