Inelastic Electron Tunneling Spectroscopy of Molecular Electronic Junctions: Recent Advances and Applications
Abstract
1. Introduction
2. Theoretical Background of IETS in Molecular Junctions
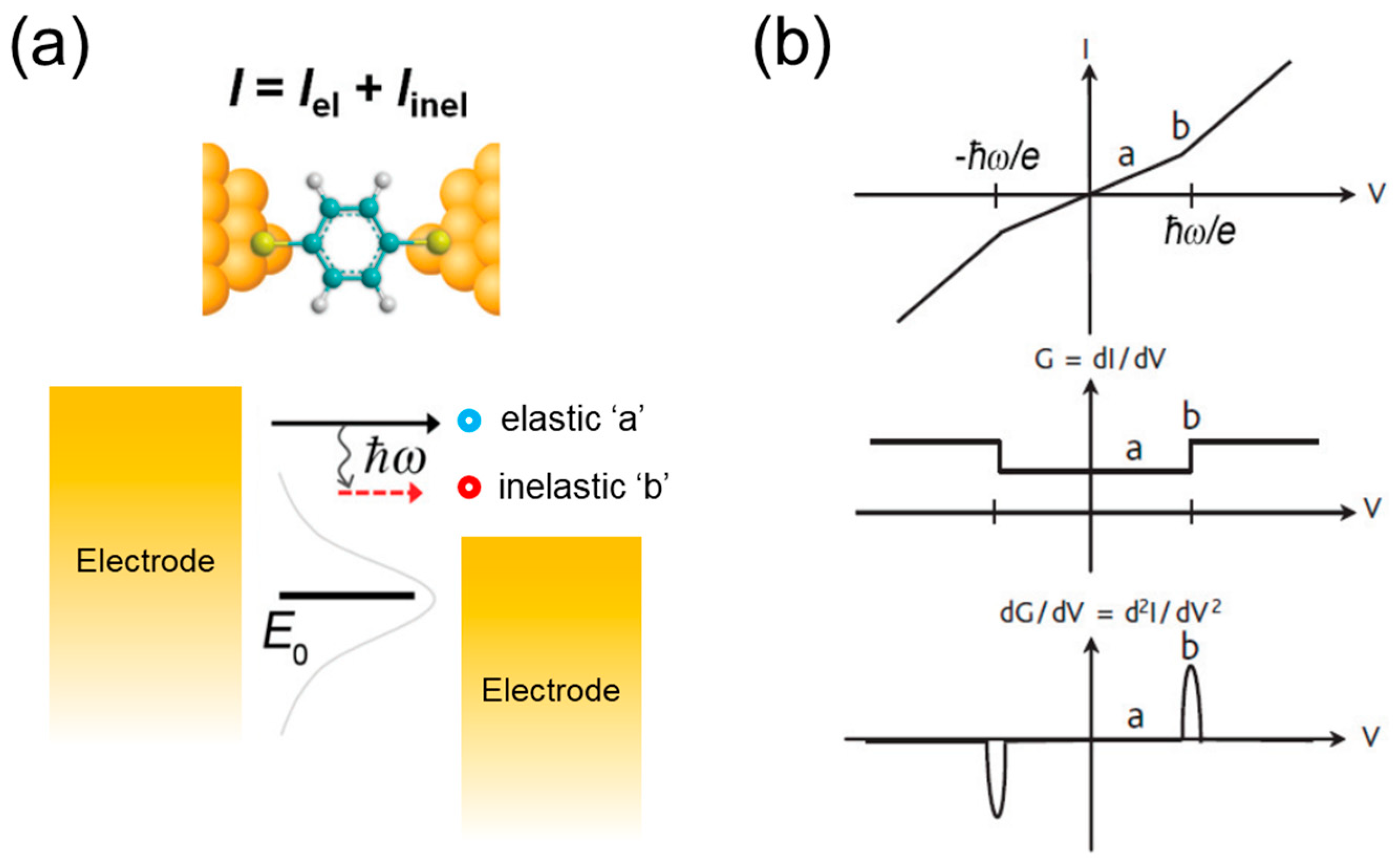
2.1. Basic Principle of IETS
2.2. Modeling and Calculation
2.3. Experimental Considerations
2.4. Scope of IETS: From Phonon to Spin
3. Advances in Methods and Materials for IETS
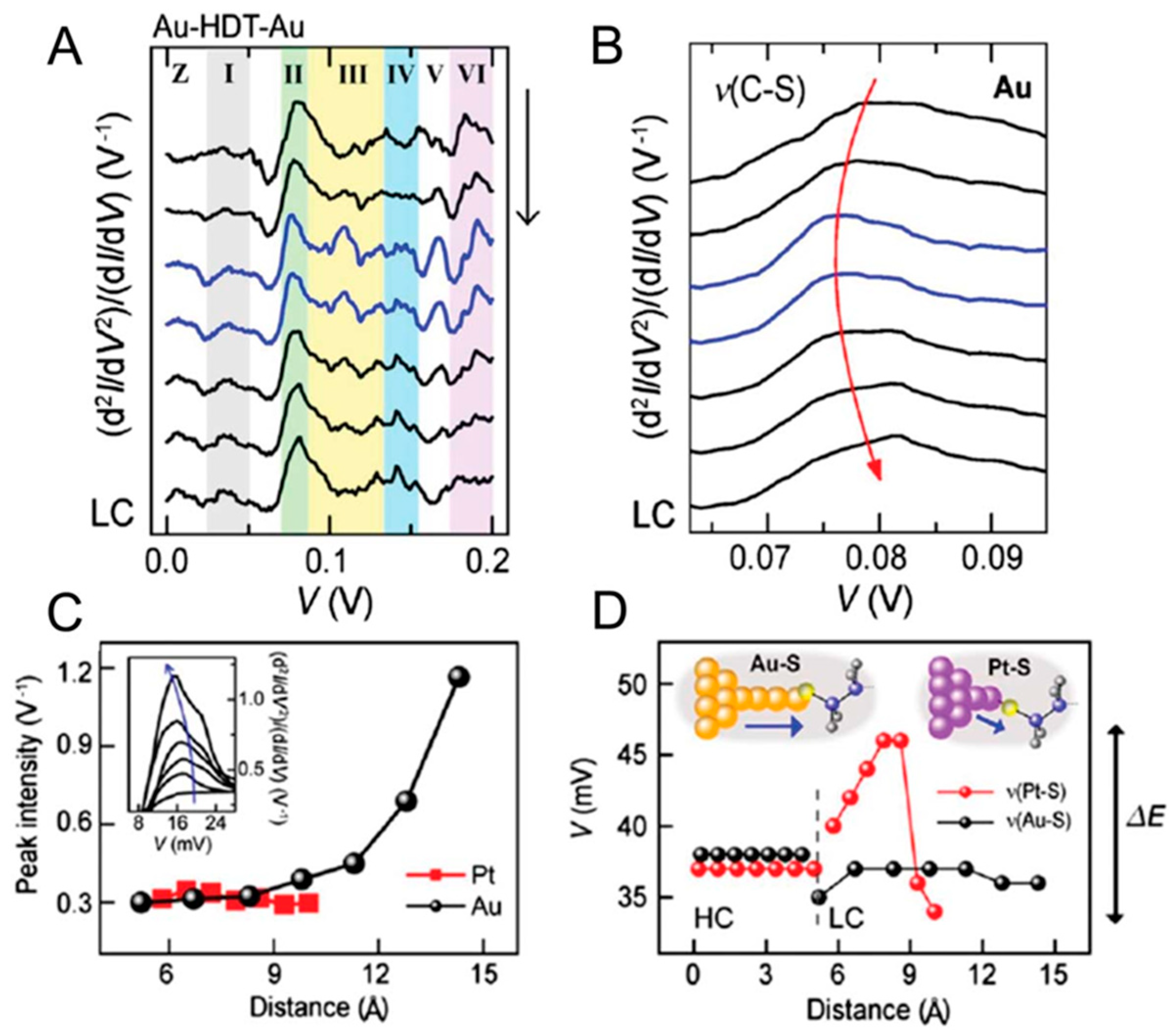
3.1. Mechanically Controlled Break Junctions
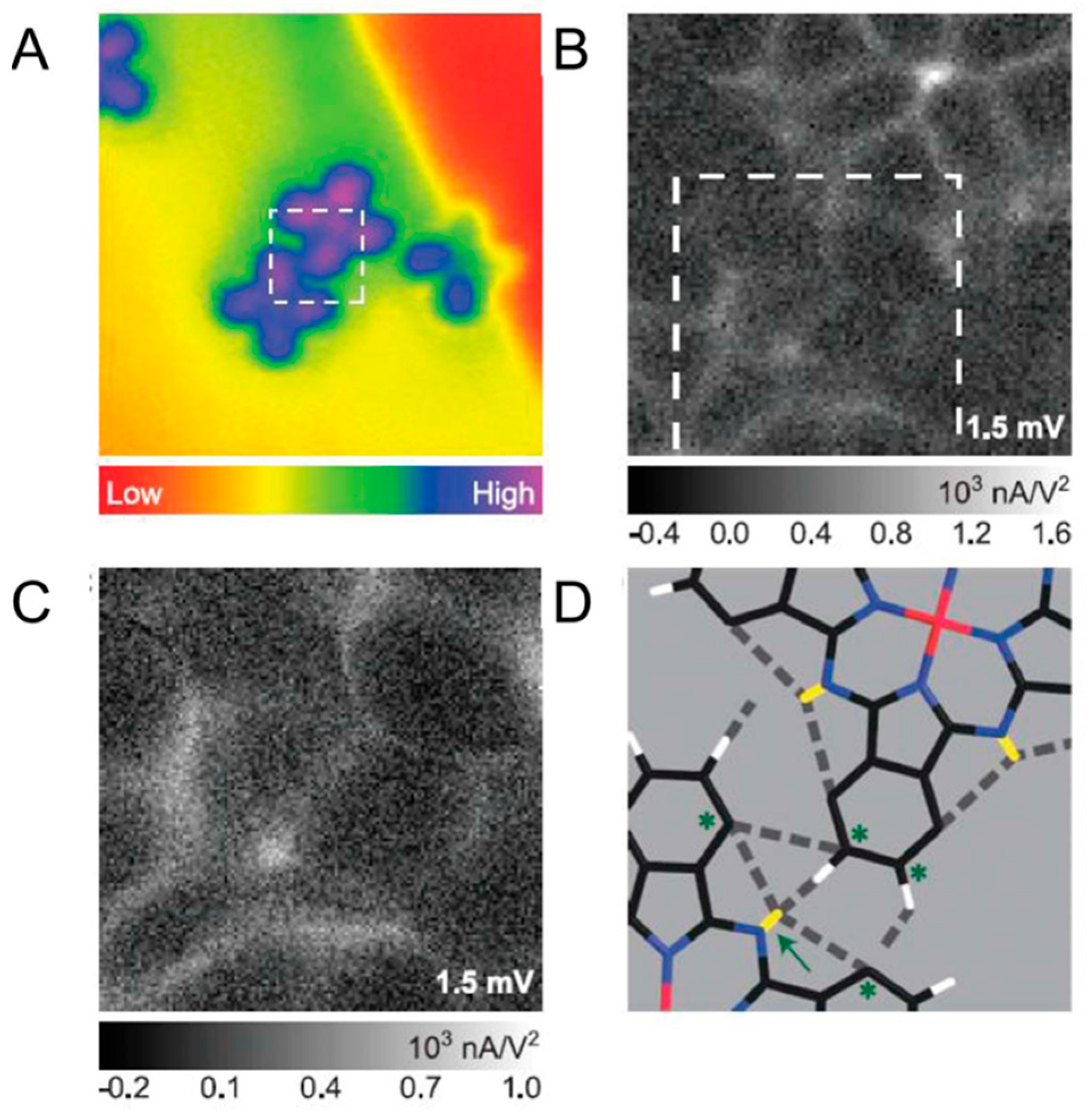
3.2. Scanning Tunneling Microscopy-Based Single-Molecule IETS
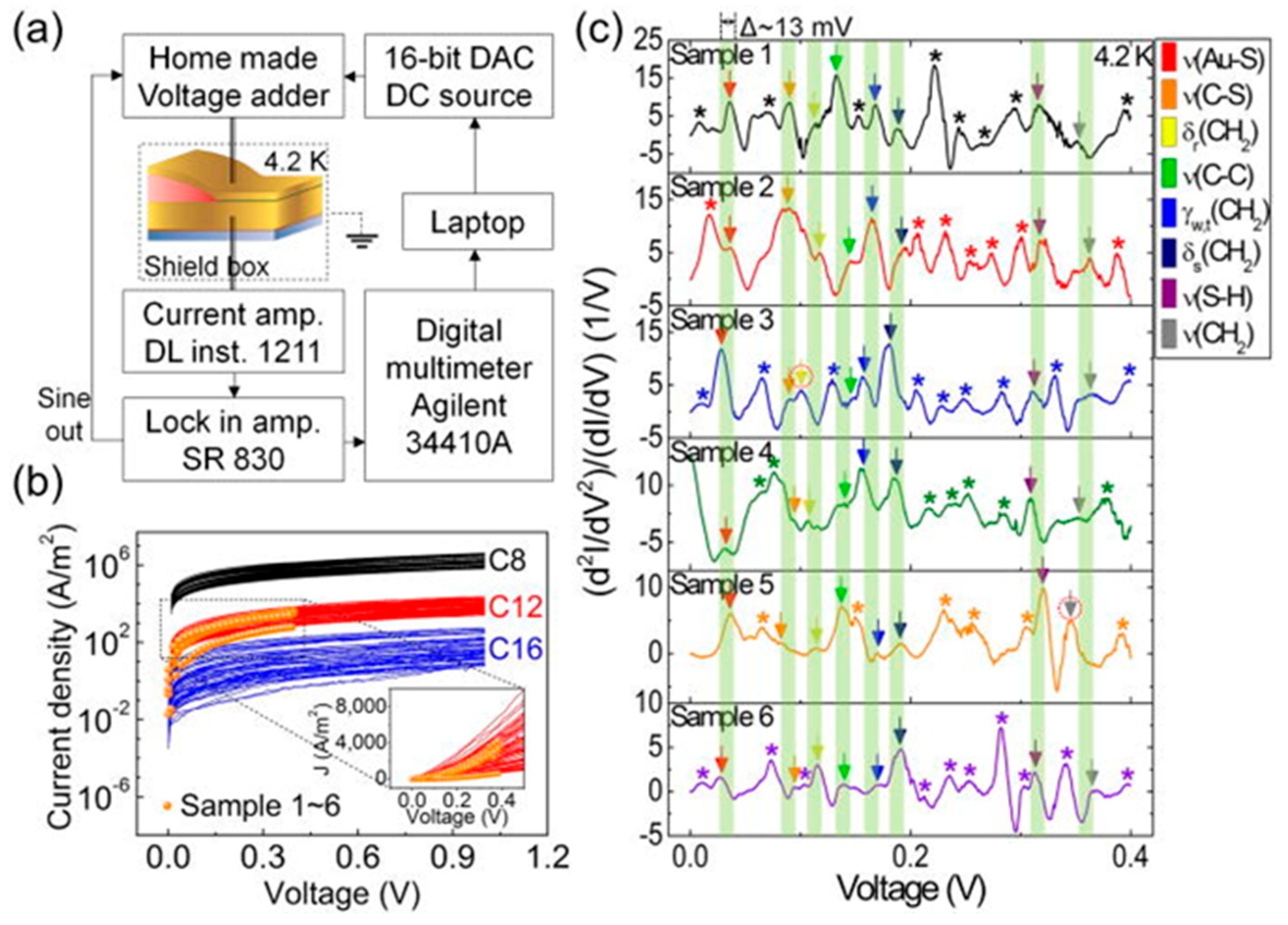
3.3. Self-Assembled Monolayer Junctions
3.4. Two-Dimensional Material Electrodes and Hybrid Junctions
3.5. High-Temperature and Low-Noise Techniques
3.6. Improved Theoretical and Computational Tools
4. Applications of IETS in Molecular Junctions
4.1. Molecular Sensors and Chemical Identification
4.2. Thermoelectric Energy Conversion and Phonon Effects
4.3. Quantum Interference Effects
4.4. Spintronic Applications of IETS
4.5. Data Analysis and Machine Learning
5. Conclusions and Perspectives
Funding
Data Availability Statement
Conflicts of Interest
References
- Aviram, A.; Ratner, M.A. Molecular rectifiers. Chem. Phys. Lett. 1974, 29, 277–283. [Google Scholar] [CrossRef]
- Tao, N.J. Electron transport in molecular junctions. Nat. Nanotechnol. 2006, 1, 173–181. [Google Scholar] [CrossRef]
- Al-Owaedi, O.A.; Najeeb, H.N.; Aldulaimi, A.K.O.; Alwan, N.H.; Ali, M.S.; Dwech, M.H.; AL-Da’amy, M.A. Thermoelectric signature of d-orbitals in tripod-based molecular junctions. Mater. Adv. 2024, 5, 9781–9791. [Google Scholar] [CrossRef]
- Song, H.; Reed, M.A.; Lee, T. Single molecule electronic device. Adv. Mat. 2011, 23, 1583–1608. [Google Scholar] [CrossRef]
- Yuan, M.; Qiu, Y.; Gao, H.; Feng, J.; Jiang, L.; Wu, Y. Molecular electronics: From nanostructure assembly to device integration. J. Am. Chem. Soc. 2024, 146, 7885–7904. [Google Scholar] [CrossRef]
- Moreno-Pineda, E.; Wernsdorfer, W. Measuring molecular magnets for quantum technologies. Nat. Rev. Phys. 2021, 3, 645–659. [Google Scholar] [CrossRef]
- Yu, C.J.; Von Kugelgen, S.; Laorenza, D.W.; Freedman, D.E. A molecular approach to quantum sensing. ACS Cent. Sci. 2021, 7, 712–723. [Google Scholar] [CrossRef]
- Xiang, D.; Wang, X.; Jia, C.; Lee, T.; Guo, X. Molecular-Scale Electronics: From Concept to Function. Chem. Rev. 2016, 116, 4318–4440. [Google Scholar] [CrossRef]
- McCreery, R.L.; Yan, H.; Bergren, A.J. A Critical Perspective on Molecular Electronic Junctions: There Is Plenty of Room in the Middle. Phys. Chem. Chem. Phys. 2013, 15, 1065–1081. [Google Scholar] [CrossRef]
- Chen, H.; Stoddart, J.F. From Molecular to Supramolecular Electronics. Nat. Rev. Mater. 2021, 6, 804–828. [Google Scholar] [CrossRef]
- Perrin, M.L.; Burzurı, E.; van der Zant, H.S.J. Single-Molecule Transistors. Chem. Soc. Rev. 2015, 44, 902–919. [Google Scholar] [CrossRef]
- Ratner, M. A Brief History of Molecular Electronics. Nat. Nanotechnol. 2013, 8, 378–381. [Google Scholar] [CrossRef]
- Cuevas, J.C.; Scheer, E. Molecular Electronics: An Introduction to Theory and Experiment; World Scientific: Singapore, 2009. [Google Scholar]
- Song, H.; Kim, Y.; Jang, Y.H.; Jeong, H.; Reed, M.A.; Lee, T. Observation of molecular orbital gating. Nature 2009, 462, 1039–1043. [Google Scholar] [CrossRef]
- Aradhya, S.V.; Venkataraman, L. Single-molecule junctions beyond electronic transport. Nat. Nanotechnol. 2013, 8, 399–410. [Google Scholar] [CrossRef]
- Vilan, A.; Aswal, D.; Cahen, D. Large-Area, Ensemble Molecular Electronics: Motivation and Challenges. Chem. Rev. 2017, 117, 4248–4286. [Google Scholar] [CrossRef]
- Reed, M.A.; Zhou, C.; Muller, C.J.; Burgin, T.P.; Tour, J.M. Conductance of a molecular junction. Science 1997, 278, 252–254. [Google Scholar] [CrossRef]
- Li, L.; Low, J.Z.; Wilhelm, J.; Liao, G.; Gunasekaran, S.; Prindle, C.R.; Starr, R.L.; Golze, D.; Nuckolls, C.; Steigerwald, M.L.; et al. Highly conducting single-molecule topological insulators based on mono- and di-radical cations. Nat. Chem. 2022, 14, 1061–1067. [Google Scholar] [CrossRef]
- Haiss, W.; Nichols, R.J.; van Zalinge, H.; Higgins, S.J.; Bethell, D.; Schiffrin, D.J. Measurement of single molecule conductivity using the spontaneous formation of molecular wires. Phys. Chem. Chem. Phys. 2004, 6, 4330–4337. [Google Scholar] [CrossRef]
- Wang, W.; Lee, T.; Reed, M.A. Mechanism of electron conduction in self-assembled alkanethiol monolayer devices. Phys. Rev. B 2003, 68, 035416. [Google Scholar] [CrossRef]
- Hines, T.; Diez-Perez, I.; Hihath, J.; Liu, H.; Wang, Z.S.; Zhao, J.; Zhou, G.; Müllen, K.; Tao, N. Transition from Tunneling to Hopping in Single Molecular Junctions by Measuring Length and Temperature Dependence. J. Am. Chem. Soc. 2010, 132, 11658. [Google Scholar] [CrossRef]
- Leary, E.; Limburg, B.; Alanazy, A.; Sangtarash, S.; Grace, I.; Swada, K.; Esdaile, L.J.; Noori, M.; Teresa Gonzalez, M.; Rubio-Bollinger, G.; et al. Bias-Driven Conductance Increase with Length in Porphyrin Tapes. J. Am. Chem. Soc. 2018, 140, 12877. [Google Scholar] [CrossRef]
- Brooke, C.; Vezzoli, A.; Higgins, S.J.; Zotti, L.A.; Palacios, J.J.; Nichols, R.J. Resonant transport and electrostatic effects in single-molecule electrical junctions. Phys. Rev. B 2015, 91, 195438. [Google Scholar] [CrossRef]
- Evers, F.; Korytar, R.; Tewari, S.; van Ruitenbeek, J.M. Advances and challenges in single-molecule electron transport. Rev. Mod. Phys. 2020, 92, 035001. [Google Scholar] [CrossRef]
- He, C.; Zhang, Q.; Fan, Y.; Zhao, C.Z.; Zhao, C.; Ye, J.; Dappe, Y.J.; Nichols, R.J.; Yang, L. Effect of Asymmetric Anchoring Groups on Electronic Transport in Hybrid Metal/Molecule/Graphene Single Molecule Junctions. Chem. Phys. Chem. 2019, 20, 1830. [Google Scholar] [CrossRef]
- Tao, S.; Zhang, Q.; He, C.; Lin, X.; Xie, R.; Zhao, C.Z.; Zhao, C.; Smogunov, A.; Dappe, Y.J.; Nichols, R.J.; et al. Graphene-Contacted Single Molecular Junctions with Conjugated Molecular Wires. ACS Appl. Nano Mater. 2019, 2, 12. [Google Scholar] [CrossRef]
- Baghernejad, M.; Van Dyck, C.; Bergfield, J.; Levine, D.R.; Gubicza, A.; Tovar, J.D.; Calame, M.; Broekmann, P.; Hong, W. Quantum interference enhanced chemical responsivity in single-molecule dithienoborepin junctions. Chem. Eur. J. 2019, 25, 15141–15146. [Google Scholar] [CrossRef]
- Li, Y.H.; Artes, J.M.; Demir, B.; Gokce, S.; Mohammad, H.M.; Alangari, M.; Anantram, M.P.; Oren, E.E.; Hihath, J. Detection and identification of genetic material via single-molecule conductance. Nat. Nanotechnol. 2018, 13, 1167–1173. [Google Scholar] [CrossRef]
- Li, X.M.; Wang, Y.H.; Seng, J.W.; Zheng, J.F.; Cao, R.; Shao, Y.; Chen, J.Z.; Li, J.F.; Zhou, X.S.; Mao, B.W. Z-Piezo pulse-modulated STM Break Junction: Toward single-molecule rectifiers with dissimilar metal electrodes. ACS Appl. Mater. Interfaces 2021, 13, 8656–8663. [Google Scholar] [CrossRef]
- Wang, Y.H.; Huang, H.; Yu, Z.; Zheng, J.F.; Shao, Y.; Zhou, X.S.; Chen, J.Z.; Li, J.F. Modulating electron transport through single-molecule junctions by heteroatom substitution. J. Mater. Chem. C 2020, 8, 6826–6831. [Google Scholar] [CrossRef]
- Kay, N.J.; Higgins, S.J.; Jeppesen, J.O.; Leary, E.; Lycoops, J.; Ulstrup, J.; Nichols, R.J. Single-molecule electrochemical gating in ionic liquids. J. Am. Chem. Soc. 2012, 134, 16817–16826. [Google Scholar] [CrossRef]
- Seng, J.W.; Tong, L.; Peng, X.Q.; Chang, W.Y.; Xie, W.; Wang, Y.H.; Zheng, J.F.; Shao, Y.; Chen, J.Z.; Jin, S.; et al. Influence of a coordinated metal center on charge transport through a Series of porphyrin molecular junctions. J. Phys. Chem. C 2022, 126, 1168–1175. [Google Scholar] [CrossRef]
- Wang, W.; Lee, T.; Kretzschmar, I.; Reed, M.A. Inelastic electron tunneling spectroscopy of an alkanedithiol self-assembled monolayer. Nano Lett. 2004, 4, 643–646. [Google Scholar] [CrossRef]
- Reed, M.A. Inelastic electron tunneling spectroscopy. Mater. Today 2008, 11, 46–50. [Google Scholar] [CrossRef]
- Cao, Y.; Austin, D.; Switzer, E.D.; Rowen, J.F.; Sander, W.; Rahman, T.S.; Morgenstern, K. Inelastic electron tunneling spectroscopy as a probe of electronic coupling at a molecule-metal interface. Phys. Rev. B 2025, 111, 115426. [Google Scholar] [CrossRef]
- Jaklevic, R.C.; Gaerttner, M.R. Inelastic electron tunneling spectroscopy. experiments on external doping of tunnel junctions by an infusion technique. Appl. Surf. Sci. 1978, 1, 479–502. [Google Scholar] [CrossRef]
- Kushmerick, J.G.; Lazorcik, J.; Patterson, C.H.; Shashidhar, R.; Seferos, D.S.; Bazan, G.C. Vibronic contributions to charge transport across molecular junctions. Nano Lett. 2004, 4, 639–642. [Google Scholar] [CrossRef]
- Lambe, J.; Jaklevic, R.C. Molecular vibration spectra by inelastic electron tunneling. Phys. Rev. 1968, 165, 821. [Google Scholar] [CrossRef]
- Jaklevic, R.C.; Lambe, J. Molecular vibration spectra by electron tunneling. Phys. Rev. Lett. 1966, 17, 1139. [Google Scholar] [CrossRef]
- Song, H.; Kim, Y.; Ku, J.; Jang, Y.H.; Jeong, H.; Lee, T. Vibrational spectra of metal-molecule-metal junctions in electromigrated nanogap electrodes by inelastic electron tunneling. Appl. Phys. Lett. 2009, 94, 103110. [Google Scholar] [CrossRef]
- Tal, O.; Krieger, M.; Leerink, B.; van Ruitenbeek, J.M. Electron-vibration interaction in single-molecule junctions: From contact to tunneling regimes. Phys. Rev. Lett. 2008, 100, 196804. [Google Scholar] [CrossRef]
- Kim, Y.; Song, H.; Strigl, F.; Pernau, H.F.; Lee, T.; Scheer, E. Conductance and vibrational states of single-molecule junctions controlled by mechanical stretching and material variation. Phys. Rev. Lett. 2011, 106, 196804. [Google Scholar] [CrossRef]
- Kim, Y.; Hellmuth, T.J.; Burkle, M.; Pauly, F.; Scheer, E. Characteristics of amine-ended and thiol-ended alkane single-molecule junctions revealed by inelastic electron tunneling spectroscopy. ACS Nano 2011, 5, 4104–4111. [Google Scholar] [CrossRef]
- Vuillaume, D. Molecular Electronics: From Single-Molecule to Large-Area Devices. Chempluschem 2019, 84, 1215–1221. [Google Scholar] [CrossRef]
- Ngabonziza, P.; Wang, Y.; van Aken, P.A.; Maier, J.; Mannhart, J. Inelastic electron tunneling spectroscopy at high-temperatures. Adv. Mater. 2021, 33, 2007299. [Google Scholar] [CrossRef]
- Hansma, P.K. Inelastic electron tunneling. Phys. Rep. 1977, 30, 145–206. [Google Scholar] [CrossRef]
- Horiuchi, T.; Ebisawa, F.; Tabei, H. New inelastic electron tunneling spectrometer with an absolute peak intensity. Rev. Sci. Instrum. 1989, 60, 993–996. [Google Scholar] [CrossRef]
- Troisi, A.; Beebe, J.M.; Picraux, L.B.; van Zee, R.D.; Stewart, D.R.; Ratner, M.A.; Kushmerick, J.G. Tracing electronic pathways in molecules by using inelastic tunneling spectroscopy. Proc. Natl. Acad. Sci. USA 2007, 104, 14255–14259. [Google Scholar] [CrossRef]
- Stipe, B.C.; Rezaei, M.A.; Ho, W. Single-molecule vibrational spectroscopy and microscopy. Science 1998, 280, 1732–1735. [Google Scholar] [CrossRef]
- Kushmerick, J.G.; Holt, D.B.; Yang, J.C.; Naciri, J.; Moore, M.H.; Shashidhar, R. Metal-molecule contacts and charge transport across monomolecular layers:measurement and theory. Phys. Rev. Lett. 2002, 89, 086802. [Google Scholar] [CrossRef]
- Troisi, A.; Ratner, M.A.; Nitzan, A. Vibronic effects in off-resonant molecular wire conduction. J. Chem. Phys. 2003, 118, 6072–6082. [Google Scholar] [CrossRef]
- Beebe, J.M.; Moore, H.J.; Lee, T.R.; Kushmerick, J.G. Vibronic coupling in semifluorinated alkanethiol junctions: Implications for selection rules in inelastic electron tunneling spectroscopy. Nano Lett. 2007, 7, 1364–1368. [Google Scholar] [CrossRef]
- Lauhon, L.J.; Ho, W. Effects of temperature and other experimental variables on single molecule vibrational spectroscopy with the scanning tunneling microscope. Rev. Sci. Instrum. 2001, 72, 216–223. [Google Scholar] [CrossRef]
- Galperin, M.; Ratner, M.A.; Nitzan, A.; Troisi, A. Nuclear coupling and polarization in molecular transport junctions: Beyond tunneling to function. Science 2008, 319, 1056–1060. [Google Scholar] [CrossRef]
- Paulsson, M.; Frederiksen, T.; Ueba, H.; Lorente, N.; Brandbyge, M. Unified description of inelastic propensity rules for electron transport through nanoscale junctions. Phys. Rev. Lett. 2008, 100, 226604. [Google Scholar] [CrossRef]
- Galperin, M.; Ratner, M.A.; Nitzan, A. Inelastic electron tunneling spectroscopy in molecular junctions: Peaks and dips. J. Chem. Phys. 2004, 121, 11965–11979. [Google Scholar] [CrossRef]
- Persson, B.N.J.; Baratoff, A. Inelastic electron-tunneling from a metal tip—The contribution from resonant processes. Phys. Rev. Lett. 1987, 59, 339–342. [Google Scholar] [CrossRef]
- Kirtley, J.; Scalapino, D.J.; Hansma, P.K. Theory of vibrational mode intensities in inelastic electron tunneling spectroscopy. Phys. Rev. B 1976, 14, 3177. [Google Scholar] [CrossRef]
- Song, H. Inelastic Electron Tunneling Spectroscopy of Aryl Alkane Molecular Junction Devices with Graphene Electrodes. Crystals 2025, 15, 433. [Google Scholar] [CrossRef]
- Kesarwani, S.; Misra, S.; Saha, D.; Della Rocca, M.L.; Roy, I.; Ganguly, S.; Mahajan, A. Simplified inelastic electron tunneling spectroscopy based on low-noise derivatives. Sci. Rep. 2022, 12, 19216. [Google Scholar] [CrossRef]
- Singh, A.K.; Martin, K.; Mastropasqua Talamo, M.; Houssin, A.; Vanthuyne, N.; Avarvari, N.; Tal, O. Single-molecule junctions map the interplay between electrons and chirality. Nat. Commun. 2025, 16, 1759. [Google Scholar] [CrossRef]
- Agrait, N.; Yeyati, A.L.; van Ruitenbeek, J.M. Quantum properties of atomic-sized conductors. Phys. Rep. 2003, 377, 81–279. [Google Scholar] [CrossRef]
- Gooding, J.J.; Gaus, K. Single-molecule sensors: Challenges and opportunities for quantitative analysis. Angew. Chem. Int. Ed. 2016, 55, 11354–11366. [Google Scholar] [CrossRef]
- Holzmeister, P.; Acuna, G.P.; Grohmann, D.; Tinnefeld, P. Breaking the concentration limit of optical single-molecule detection. Chem. Soc. Rev. 2014, 43, 1014–1028. [Google Scholar] [CrossRef]
- Venkataraman, L.; Klare, J.E.; Nuckolls, C.; Hybertsen, M.S.; Steigerwald, M.L. Dependence of single-molecule junction conductance on molecular conformation. Nature 2006, 442, 904–907. [Google Scholar] [CrossRef]
- Tam, E.S.; Parks, J.J.; Shum, W.W.; Zhong, Y.W.; Santiago-Berríos, M.E.B.; Zheng, X.; Yang, W.; Chan, G.K.L.; Abruña, H.D.; Ralph, D.C. Single-molecule conductance of pyridine-terminated dithienylethene switch molecules. ACS Nano 2011, 5, 5115–5123. [Google Scholar] [CrossRef]
- Nichols, R.J.; Higgins, S.J. Single molecule nanoelectrochemistry in electrical junctions. Acc. Chem. Res. 2016, 49, 2640–2648. [Google Scholar] [CrossRef]
- Xiao, B.; Liang, F.; Liu, S.; Im, J.; Li, Y.; Liu, J.; Zhang, B.; Zhou, J.; He, J.; Chang, S. Cucurbituril mediated single molecule detection and identification via recognition tunneling. Nanotechnology 2018, 29, 365501. [Google Scholar] [CrossRef]
- Ahn, S.; Aradhya, S.V.; Klausen, R.S.; Capozzi, B.; Roy, X.; Steigerwald, M.L.; Nuckolls, C.; Venkataraman, L. Electronic transport and mechanical stability of carboxyl linked single-molecule junctions. Phys. Chem. Chem. Phys. 2012, 14, 13841–13845. [Google Scholar] [CrossRef]
- Xiao, X.; Xu, B.; Tao, N. Changes in the conductance of single peptide molecules upon metal-ion binding. Angew. Chem. Int. Ed. 2004, 43, 6148–6152. [Google Scholar] [CrossRef]
- Kiguchi, M.; Ohto, T.; Fujii, S.; Sugiyasu, K.; Nakajima, S.; Takeuchi, M.; Nakamura, H. Single Molecular Resistive Switch Obtained via Sliding Multiple Anchoring Points and Varying Effective Wire Length. J. Am. Chem. Soc. 2014, 136, 7327–7332. [Google Scholar] [CrossRef]
- Su, T.A.; Li, H.; Steigerwald, M.L.; Venkataraman, L.; Nuckolls, C. Stereoelectronic switching in single-molecule junctions. Nat. Chem. 2015, 7, 215–220. [Google Scholar] [CrossRef]
- Kiguchi, M.; Nakashima, S.; Tada, T.; Watanabe, S.; Tsuda, S.; Tsuji, Y.; Terao, J. Single-Molecule Conductance of π-Conjugated Rotaxane: New Method for Measuring Stipulated Electric Conductance of π-Conjugated Molecular Wire Using STM Break Junction. Small 2012, 8, 726–730. [Google Scholar] [CrossRef]
- Kim, Y.; Pietsch, T.; Erbe, A.; Belzig, W.; Scheer, E. Benzenedithiol: A Broad-Range Single-Channel Molecular Conductor. Nano Lett. 2011, 11, 3734–3738. [Google Scholar] [CrossRef]
- Chiang, C.L.; Xu, C.; Han, Z.M.; Ho, W. Real-space imaging of molecular structure and chemical bonding by single-molecule inelastic tunneling probe. Science 2014, 344, 885–888. [Google Scholar] [CrossRef]
- Smit, R.H.M.; Noat, Y.; Untiedt, C.; Lang, N.D.; van Hemert, M.C.; van Ruitenbeek, J.M. Measurement of the conductance of a hydrogen molecule. Nature 2002, 419, 906–909. [Google Scholar] [CrossRef]
- Kiguchi, M.; Stadler, R.; Kristensen, I.S.; Djukic, D.; van Ruitenbeek, J.M. Evidence for a single hydrogen molecule connected by an atomic chain. Phys. Rev. Lett. 2007, 98, 146802. [Google Scholar] [CrossRef]
- Jeong, H.; Hwang, W.T.; Kim, P.; Kim, D.; Jang, Y.; Min, M.; Xiang, D.; Song, H.; Park, Y.D.; Jeong, H.; et al. Investigation of inelastic electron tunneling spectra of metal-molecule-metal junctions fabricated using direct metal transfer method. Appl. Phys. Lett. 2015, 106, 063110. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, J.; Hamill, J.M.; Xu, B. Measurement and understanding of single-molecule break junction rectification caused by asymmetric contacts. J. Chem. Phys. 2014, 141, 054712. [Google Scholar] [CrossRef]
- Tomfohr, J.K.; Sankey, O.F. Complex band structure, decay lengths, and Fermi level alignment in simple molecular electronic systems. Phys. Rev. B 2002, 65, 245105. [Google Scholar] [CrossRef]
- Quek, S.Y.; Choi, H.J.; Louie, S.G.; Neaton, J.B. Length Dependence of Conductance in Aromatic Single-Molecule Junctions. Nano Lett. 2009, 9, 3949–3953. [Google Scholar] [CrossRef]
- Dappe, Y.J.; González, C.; Cuevas, J.C. Carbon tips for all-carbon single-molecule electronics. Nanoscale 2014, 6, 6953. [Google Scholar] [CrossRef]
- Li, X.; He, J.; Hihath, J.; Xu, B.; Lindsay, S.M.; Tao, N. Conductance of Single Alkanedithiols: Conduction Mechanism and Effect of Molecule-Electrode Contacts. J. Am. Chem. Soc. 2006, 128, 2138. [Google Scholar] [CrossRef]
- Lee, Y.; Yuan, S.; Sanchez, A.; Yu, L. Charge transport mediated by d-orbitals in transition metal complexes. Chem. Commun. 2008, 247–249. [Google Scholar] [CrossRef]
- Lo, W.Y.; Zhang, N.; Cai, Z.; Li, L.; Yu, L. Beyond Molecular Wires: Design Molecular Electronic Functions Based on Dipolar Effect. Acc. Chem. Res. 2016, 49, 1852–1863. [Google Scholar] [CrossRef]
- Pollack, S.K.; Naciri, J.; Mastrangelo, J.; Patterson, C.H.; Torres, J.; Moore, M.; Shashidhar, R.; Kushmerick, J.G. Sequential Deprotection for Control of Orientation in the Self-Assembly of Asymmetric Molecules for Molecular Electronic Devices. Langmuir 2004, 20, 1838–1842. [Google Scholar] [CrossRef]
- Guo, C.; Wang, K.; Zerah-Harush, E.; Hamill, J.; Wang, B.; Dubi, Y.; Xu, B. Molecular rectifier composed of DNA with high rectification ratio enabled by intercalation. Nat. Chem. 2016, 8, 484–490. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, L.; Tao, S.; Wang, C.; Zhao, C.; González, C.; Dappe, Y.J.; Nichols, R.J.; Yang, L. Graphene as a promising electrode for low-current attenuation in nonsymmetric molecular junctions. Nano Lett. 2016, 16, 6534–6540. [Google Scholar] [CrossRef]
- McCreery, R.L.; Bergren, A.J. Progress with molecular electronic junctions: Meeting experimental challenges in design and fabrication. Adv. Mater. 2009, 21, 4303–4322. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.; Jiang, D.; Zhang, Y.; Dubonos, S.A.; Grigorieva, I.; Firsov, A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Morozov, S.; Novoselov, K.; Katsnelson, M.; Schedin, F.; Elias, D.C.; Jaszczak, J.A.; Geim, A. Giant intrinsic carrier mobilities in graphene and its bilayer. Phys. Rev. Lett. 2008, 100, 016602. [Google Scholar] [CrossRef]
- Balandin, A.A.; Ghosh, S.; Bao, W.; Calizo, I.; Teweldebrhan, D.; Miao, F.; Lau, C.N. Superior thermal conductivity of single-layer graphene. Nano Lett. 2008, 8, 902–907. [Google Scholar] [CrossRef]
- Kim, K.S.; Zhao, Y.; Jang, H.; Lee, S.Y.; Kim, J.M.; Kim, K.S.; Ahn, J.-H.; Kim, P.; Choi, J.-Y.; Hong, B. Large-scale pattern growth of graphene films for stretchable transparent electrodes. Nature 2009, 457, 706–710. [Google Scholar] [CrossRef]
- Lin, Y.-M.; Valdes-Garcia, A.; Han, S.-J.; Farmer, D.B.; Meric, I.; Sun, Y.; Wu, Y.; Dimitrakopoulos, C.; Grill, A.; Avouris, P. Wafer-scale graphene integrated circuit. Science 2011, 332, 1294–1297. [Google Scholar] [CrossRef]
- Li, W.; Cheng, G.; Liang, Y.; Tian, B.; Liang, X.; Peng, L.; Walker, A.H.; Gundlach, D.J.; Nguyen, N. Broadband optical properties of graphene by spectroscopic ellipsometry. Carbon 2016, 99, 348–353. [Google Scholar] [CrossRef]
- Giannazzo, F.; Schilirò, E.; Lo Nigro, R.; Roccaforte, F.; Yakimova, R. Atomic layer deposition of high-k insulators on epitaxial graphene: A review. Appl. Sci. 2020, 10, 2440. [Google Scholar] [CrossRef]
- Wang, L.; Ye, X.; Zhu, Y.; Jiang, H.; Xia, J.; Yue, Z.; Wan, Z.; Jia, C.; Yao, X. Conjugated molecule functionalized graphene films for energy storage devices with high energy density. Electrochimica. Acta 2020, 340, 135804. [Google Scholar] [CrossRef]
- Porfarzollah, A.; Mohammad-Rezaei, R.; Bagheri, M. Ionic liquid-functionalized graphene quantum dots as an efficient quasi-solid-state electrolyte for dye-sensitized solar cells. J. Mater. Sci. Mater. Electron. 2020, 31, 2288–2297. [Google Scholar] [CrossRef]
- Shin, D.; Kim, H.R.; Hong, B. Gold nanoparticle-mediated non-covalent functionalization of graphene for field-effect transistors. Nanoscale Adv. 2021, 3, 1404–1412. [Google Scholar] [CrossRef]
- De La Rie, J.; Enache, M.; Wang, Q.; Lu, W.; Kivala, M.; Stöhr, M. Self-Assembly of a Triphenylene-Based Electron Donor Molecule on Graphene: Structural and Electronic Properties. J. Phys. Chem. C 2022, 126, 9855–9861. [Google Scholar] [CrossRef]
- Zhan, J.; Lei, Z.D.; Zhang, Y. Non-covalent interactions of graphene surface: Mechanisms and applications. Chemistry 2022, 8, 947–979. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.Y.; Cheng, Z.W.; Chen, A.X.; Wang, P.D.; Wang, X.Y.; Lei, X.X.; Bian, Q.; Li, S.J.; Yuan, B.K.; et al. Large-scale 2D heterostructures from hydrogen-bonded organic frameworks and graphene with distinct Dirac and flat bands. Nat. Commun. 2024, 15, 5934. [Google Scholar] [CrossRef]
- Sinha, S.; Ghosal, S.; Jana, D. Electronic and optical properties of PTCDI adsorbed graphene heterostructure: A first principles study. J. Phys. Chem. Solids 2021, 155, 110109. [Google Scholar] [CrossRef]
- Pham, V.K.; Kato, M.; Uesaka, J.; Tsubouchi, R.; Go, K.; Choi, Y.J.; Noda, T.; Sawada, K.; Takahashi, K. Fabrication and characterization of strain-induced graphene for chemisorption-based graphene resonant mass sensors. Appl. Phys. Express 2024, 17, 127001. [Google Scholar] [CrossRef]
- Li, Z.; Guo, K.; Yin, C.; Li, Y.; Mertens, S.F.L. Fabricating Graphene-Based Molecular Electronics via Surface Modification by Physisorption and Chemisorption. Molecules 2025, 30, 926. [Google Scholar] [CrossRef]
- Tan, C.; Cao, X.; Wu, X.-J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.-H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef]
- Liao, M.; Nicolini, P.; Du, L.; Yuan, J.; Wang, S.; Yu, H.; Tang, J.; Cheng, P.; Watanabe, K.; Taniguchi, T.; et al. UItra-low friction and edge-pinning effect in large-lattice-mismatch van der Waals heterostructures. Nat. Mater. 2022, 21, 47–53. [Google Scholar] [CrossRef]
- Liao, M.; Wei, Z.; Du, L.; Wang, Q.; Tang, J.; Yu, H.; Wu, F.; Zhao, J.; Xu, X.; Han, B.; et al. Precise control of the interlayer twist angle in large scale MoS2 homostructures. Nat. Commun. 2020, 11, 2153. [Google Scholar] [CrossRef]
- Zhang, Q.; Hou, Y.; Zhang, T.; Xu, Z.; Huang, Z.; Yuan, P.; Jia, L.; Yang, H.; Huang, Y.; Ji, W.; et al. Visualizing Spatial Evolution of Electron-Correlated Interface in Two-Dimensional Heterostructures. ACS Nano 2021, 15, 16589–16596. [Google Scholar] [CrossRef]
- Liu, Y.-W.; Hao, C.-Y.; He, L. Tailoring the Energy Landscape of Graphene Nanostructures on Graphene and Manipulating Them Using Tilt Grain Boundaries. Phys. Rev. Appl. 2022, 17, 034013. [Google Scholar] [CrossRef]
- Gao, F.; Li, D.; Barreteau, C.; Brandbyge, M. Proposal for All-Electrical Spin Manipulation and Detection for a Single Molecule on Boron-Substituted Graphene. Phys. Rev. Lett. 2022, 129, 027201. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Y.; Huang, Z.-P.; Jia, L.-G.; Liu, L.-W.; Yang, H.-X.; Zhang, T.; He, L.; Zhou, J.-D.; Huang, Y.; et al. Visualization of Macroscopic Ising Superconducting State in Superconductor-Graphene Junctions. Adv. Quantum Technol. 2023, 6, 2300087. [Google Scholar] [CrossRef]
- Chen, Y.; Dai, Y.-X.; Zhang, Y.; Zhang, C.; Zhou, L.; Jia, L.; Wang, W.; Han, X.; Yang, H.X.; Liu, L.; et al. Nanoscale Polymorph Engineering of Metal-Correlated Insulator Junctions in Monolayer NbSe2. ACS Nano 2025, 19, 14808–14816. [Google Scholar] [CrossRef]
- Hayat, A.; Sohail, M.; Hamdy, M.S.; Taha, T.A.; AlSalem, H.S.; Alenad, A.M.; Amin, M.A.; Shah, R.; Palamanit, A.; Khan, J.; et al. Fabrication, characteristics, and applications of boron nitride and their composite nanomaterials. Surf. Interfaces 2022, 29, 101725. [Google Scholar] [CrossRef]
- Cai, X.; Liu, X.; Wei, X.; Lin, R. Effect of nitrogen-doped carbon support on the performance of catalysts for the oxygen reduction reaction. ACS Appl. Energy Mater. 2024, 7, 8705–8714. [Google Scholar] [CrossRef]
- Yang, T.; Liu, Z.; Chu, J.; Peng, X.; Kong, A. Mesoporous carbon-doped boron nitrides for cathodic and anodic hydrogen peroxide electrosynthesis. Carbon 2024, 228, 119383. [Google Scholar] [CrossRef]
- Sun, D.; Sun, Z.; Yang, D.; Jiang, X.; Tang, J.; Wang, X. Advances in boron nitride-based materials for electrochemical energy storage and conversion. Eco Energy 2023, 1, 375–404. [Google Scholar] [CrossRef]
- Harameen, H.M.A.; Akay, R.G. Investigation into the influence of boron nitride addition on the properties of SPEEK/PBI based electrolyte membrane. Int. J. Hydrogen Energy 2024, 54, 189–199. [Google Scholar] [CrossRef]
- Songfeng, E.; Liu, J.; Zhao, R.; Ning, D.; Lu, Z. Formation mechanisms of hexagonal boron nitride nanosheets in solvothermal exfoliation. Langmuir 2023, 39, 1619–1628. [Google Scholar] [CrossRef]
- Dini, D. Nanostructured metal oxide thin films as photoactive cathodes of p-type dye-sensitised solar cells. Phys. Chem. Commun. 2016, 3, 14–51. [Google Scholar]
- Powar, S.; Bhargava, R.; Daeneke, T.; Götz, G.; Bäuerle, P.; Geiger, T.; Kuster, S.; Nüesch, F.A.; Spiccia, L.; Bach, U. Thiolate/disulfide based electrolytes for p-type and tandem dye-sensitized solar cells. Electrochim. Acta 2015, 182, 458–463. [Google Scholar] [CrossRef]
- Adam, G.; Aslan, F.; Portenkirchner, E.; Stadler, P.; Scharber, M.C.; Sariciftci, N.S. Electrocatalytic reduction of carbon dioxide using sol-gel processed copper indium sulfide (CIS) immobilized on ITO-coated glass electrode. Electrocatalysis 2015, 6, 405–413. [Google Scholar] [CrossRef]
- Devi, K.P.; Goswami, P.; Chaturvedi, H. Fabrication of nanocrystalline TiO2 thin films using Sol-Gel spin coating technology and investigation of its structural, morphology and optical characteristics. Appl. Surf. Sci. 2022, 591, 153226. [Google Scholar] [CrossRef]
- Nie, S.; Li, J.; Tao, L.; He, Y.; Dastan, D.; Meng, X.; Poldorn, P.; Yin, X. Insights into selective mechanism of NiO-TiO2 heterojunction to H2 and CO. ACS Sens. 2023, 8, 4121–4131. [Google Scholar] [CrossRef]
- Ge, S.; Sang, D.; Zou, L.; Li, C.; Wang, G.; Fan, J.; Wang, Q. High-temperature photoelectronic transport behavior of n-TiO2 nanorod clusters/p-degenerated boron-doped diamond heterojunction. Diam. Relat. Mater. 2024, 144, 110962. [Google Scholar] [CrossRef]
- Ge, S.; Sang, D.; Li, C.; Shi, Y.; Wang, Q.; Xiao, D. Research Progress and Future Perspectives on Photonic and Optoelectronic Devices Based on p-Type Boron-Doped Diamond/n-Type Titanium Dioxide Heterojunctions: A Mini Review. Nanomaterials 2025, 15, 1003. [Google Scholar] [CrossRef]
- Komoto, Y.; Ryu, J.; Taniguchi, M. Machine learning and analytical methods for single-molecule conductance measurements. Chem. Commun. 2023, 59, 6796–6810. [Google Scholar] [CrossRef]
- Lv, S.-L.; Zeng, C.; Yu, Z.; Zheng, J.-F.; Wang, Y.-H.; Shao, Y.; Zhou, X.-S. Recent Advances in Single-Molecule Sensors Based on STM Break Junction Measurements. Biosensors 2022, 12, 565. [Google Scholar] [CrossRef]
- Turin, L. A Spectroscopic Mechanism for Primary Olfactory Reception. Chem. Senses 1996, 21, 773–791. [Google Scholar] [CrossRef]
- Bommisetty, V.; Bhandari, S.; Karmacharya, R.L.; Rislov, D.A.; Mileham, R.D.; Galipeau, D. Gas Sensing Based on Inelastic Electron Tunneling Spectroscopy. IEEE Sens. J. 2008, 8, 983–988. [Google Scholar] [CrossRef]
- Fereiro, J.A.; Pecht, I.; Sheves, M.; Cahen, D. Inelastic Electron Tunneling Spectroscopic Analysis of Bias-Induced Structural Changes in a Solid-State Protein Junction. Small 2021, 17, 2008218. [Google Scholar] [CrossRef]
- Sun, M.; Li, Z.; Mao, Q.; Shen, D. Thermoelectric percolation phenomenon in carbon fiber-reinforced concrete. Cem. Concr. Res. 1998, 28, 1707–1712. [Google Scholar] [CrossRef]
- Ghosh, S.; Harish, S.; Rocky, K.A.; Ohtaki, M.; Saha, B.B. Graphene enhanced thermoelectric properties of cement based composites for building energy harvesting. Energy Build. 2019, 202, 109419. [Google Scholar] [CrossRef]
- Pichanusakorn, P.; Bandaru, P. Nanostructured thermoelectrics. Mater. Sci. Eng. R Rep. 2010, 67, 19–63. [Google Scholar] [CrossRef]
- Lan, Y.; Minnich, A.J.; Chen, G.; Ahn, J.P.; Sung, Y.M. Enhancement of thermoelectric figure-of-merit by a bulk nanostructuring approach. Adv. Funct. Mater. 2010, 20, 357–376. [Google Scholar] [CrossRef]
- He, J.; Tritt, T.M. Advances in thermoelectric materials research: Looking back and moving forward. Science 2017, 357, 1369. [Google Scholar] [CrossRef]
- Sootsman, J.R.; Chung, D.Y.; Kanatzidis, M.G. New and old concepts in thermoelectric materials. Angew. Chem. Int. Ed. Engl. 2009, 48, 8616–8639. [Google Scholar] [CrossRef]
- Akasaka, M.; Iida, T.; Nemoto, T.; Soga, J.; Sato, J.; Makino, K.; Fukano, M.; Takanashi, Y. Non-wetting crystal growth of Mg2Si by vertical Bridgman method and thermoelectric characteristics. J. Cryst. Growth 2007, 304, 196. [Google Scholar] [CrossRef]
- Liu, W.; Tan, X.; Yin, K.; Liu, H.; Tang, X.; Shi, J.; Zhang, Q.; Uher, C. Convergence of conduction bands as a means of enhancing thermoelectric performance of n-type Mg2Si1−xSnx solid solutions. Phys. Rev. Lett. 2012, 108, 166601. [Google Scholar] [CrossRef]
- Bhandari, C.M.; Rowe, D.M. CRC Handbook of Thermoelectrics; CRC Press: Boca Raton, FL, USA, 1995; p. 43. [Google Scholar]
- Sevinçli, H.; Sevik, C.; Çağin, T.; Cuniberti, G. A bottom-up route to enhance thermoelectric figures of merit in graphene nanoribbons. Sci. Rep. 2013, 3, 1228. [Google Scholar]
- Kawata, T.; Iguchi, Y.; Itoh, T.; Takahata, K.; Terasaki, I. Na-site substitution effects on the thermoelectric properties of NaCo2O4. Phys. Rev. B 1999, 60, 10584–10587. [Google Scholar] [CrossRef]
- Zhao, L.-D.; Zhang, B.-P.; Li, J.-F.; Zhou, M.; Liu, W.-S.; Liu, J. Thermoelectric and mechanical properties of nano-SiC-dispersed Bi2Te3 fabricated by mechanical alloying and spark plasma sintering. J. Alloys Compd. 2008, 455, 259–264. [Google Scholar] [CrossRef]
- He, P.; Jang, J.; Kang, H.; Yoon, H.J. Thermoelectricity in molecular tunnel junctions. Chem. Rev. 2025, 125, 2953–3004. [Google Scholar] [CrossRef]
- Kim, Y.; Jeong, W.; Kim, K.; Lee, W.; Reddy, P. Electrostatic control of thermoelectricity in molecular junctions. Nat. Nanotechnol. 2014, 9, 881–885. [Google Scholar] [CrossRef]
- Guedon, C.M.; Valkenier, H.; Markussen, T.; Thygesen, K.S.; Hummelen, J.C.; van der Molen, S.J. Observation of quantum interference in molecular charge transport. Nat. Nanotechnol. 2012, 7, 304–308. [Google Scholar] [CrossRef]
- Hartle, R.; Butzin, M.; Rubio-Pons, O.; Thoss, M. Quantum interference and decoherence in single-molecule junctions: How vibrations induce electrical current. Phys. Rev. Lett. 2011, 107, 046802. [Google Scholar] [CrossRef]
- Salhani, C.; Lambert, J.; Mlack, J.; Ramos, R. Inelastic electron tunneling spectroscopy in molecular junctions showing quantum interference. Phys. Rev. B 2017, 95, 165431. [Google Scholar] [CrossRef]
- Zhao, C.; Yang, L.; Henriques, J.C.G. Spin excitations in nanographene-based antiferromagnetic spin-1/2 Heisenberg chains. Nat. Mater. 2025, 24, 722–727. [Google Scholar] [CrossRef]
- Gu, G.; Zhao, G.; Lin, C.; Li, Y.; Jin, C.; Xiang, G. Asperomagnetic order in diluted magnetic semiconductor (Ba, Na)(Zn, Mn)2As2. Appl. Phys. Lett. 2018, 112, 032402. [Google Scholar] [CrossRef]
- Surmach, M.A.; Chen, B.J.; Deng, Z.; Jin, C.Q.; Glasbrenner, J.K.; Mazin, I.I.; Ivanov, A.; Inosov, D.S. Weak doping dependence of the antiferromagnetic coupling between nearest-neighbor mn2+ spins in (ba1−xkx)(zn1−ymny)2as2. Phys. Rev. B 2018, 97, 104418. [Google Scholar] [CrossRef]
- Suzuki, H.; Zhao, G.; Okamoto, J.; Sakamoto, S.; Chen, Z.-Y.; Nonaka, Y.; Shibata, G.; Zhao, K.; Chen, B.; Wu, W.-B.; et al. Magnetic properties and electronic configurations of mn ions in the diluted magnetic semiconductor ba1−xkx(zn1−ymny)2as2 studied by x-ray magnetic circular dichroism and resonant inelastic x-ray scattering. J. Phys. Soc. Jpn. 2022, 91, 064710. [Google Scholar] [CrossRef]
- Zhao, X.; Dong, J.; Fu, L.; Gu, Y.; Zhang, R.; Yang, Q.; Xie, L.; Tang, Y.; Ning, F. (ba1−xnax)f(zn1−xmnx)sb: A novel fluoride-antimonide magnetic semiconductor with decoupled charge and spin doping. J. Semicond. 2022, 43, 112501. [Google Scholar] [CrossRef]
- Seo, J.; De, C.; Ha, H.; Lee, J.E.; Park, S.; Park, J.; Skourski, Y.; Choi, E.S.; Kim, B.; Cho, G.Y.; et al. Colossal angular magnetoresistance in ferrimagnetic nodal-line semiconductors. Nature 2021, 599, 576–581. [Google Scholar] [CrossRef]
- Zhao, G.; Cai, Y.; Kojima, K.M.; Sheng, Q.; Beare, J.; Luke, G.; Li, X.; Peng, Y.; Ziman, T.; Zhao, K.; et al. Magnetic evolution of carrier doping and spin dynamics in diluted magnetic semiconductors (ba, na)(zn, mn)2as2. Condens. Matter 2025, 10, 30. [Google Scholar] [CrossRef]
- Van Vreumingen, D.; Tewari, S.; Verbeek, F.; Van Ruitenbeek, J.M. Towards Controlled Single-Molecule Manipulation Using “Real-Time” Molecular Dynamics Simulation: A GPU Implementation. Micromachines 2018, 9, 270. [Google Scholar] [CrossRef]
- Rascón-Ramos, H.; Artés, J.M.; Li, Y.; Hihath, J. Binding configurations and intramolecular strain in single-molecule devices. Nat. Mater. 2015, 14, 517–522. [Google Scholar] [CrossRef]
- Kuroda, Y.; Suenaga, A.; Sato, Y.; Kosuda, S.; Taiji, M. All-atom molecular dynamics analysis of multi-peptide systems reproduces peptide solubility in line with experimental observations. Sci. Rep. 2016, 6, 19479. [Google Scholar] [CrossRef]
- Ofarim, A.; Kopp, B.; Möller, T.; Martin, L.; Boneberg, J.; Leiderer, P.; Scheer, E. Thermo-voltage measurements of atomic contacts at low temperature. Beilstein J. Nanotechnol. 2016, 7, 767–775. [Google Scholar] [CrossRef]
- Rocha, A.R.; Garcia-Suarez, V.M.; Bailey, S.W.; Lambert, C.J.; Ferrer, J.; Sanvito, S. Towards molecular spintronics. Nat. Mater. 2005, 4, 335–339. [Google Scholar] [CrossRef]
- Taylor, J.; Guo, H.; Wang, J. Ab initio modeling of quantum transport properties of molecular electronic devices. Phys. Rev. B 2001, 63, 245407. [Google Scholar] [CrossRef]
- Liu, R.; Ke, S.; Baranger, H.U.; Yang, W. Negative differential resistance and hysteresis through an organometallic molecule from molecular-level crossing. J. Am. Chem. Soc. 2006, 128, 6274–6275. [Google Scholar] [CrossRef]
- Matsuura, Y. Current rectification in nickelocenylferrocene sandwiched between two gold electrodes. J. Chem. Phys. 2013, 138, 014311. [Google Scholar] [CrossRef]
- Xu, B.; Tao, N.J. Measurement of single-molecule resistance by repeated formation of molecular junctions. Science 2003, 301, 1221–1223. [Google Scholar] [CrossRef]
- Lafferentz, L.; Ample, F.; Yu, H.; Hecht, S.; Joachim, C.; Grill, L. Conductance of a single conjugated polymer as a continuous function of its length. Science 2009, 323, 1193–1197. [Google Scholar] [CrossRef]
- Jia, C.; Migliore, A.; Xin, N.; Huang, S.; Wang, J.; Yang, Q.; Wang, S.; Chen, H.; Wang, D.; Feng, B.; et al. Covalently bonded single-molecule junctions with stable and reversible photoswitched conductivity. Science 2016, 352, 1443–1445. [Google Scholar] [CrossRef]
- Tsutsui, M.; Rahong, S.; Iizumi, Y.; Okazaki, T.; Taniguchi, M.; Kawai, T. Single-molecule sensing electrode embedded in-plane nanopore. Sci. Rep. 2011, 1, 46. [Google Scholar] [CrossRef]
- Xiang, L.; Palma, J.L.; Li, Y.; Mujica, V.; Ratner, M.A.; Tao, N. Gate-controlled conductance switching in DNA. Nat. Commun. 2017, 8, 14471. [Google Scholar] [CrossRef]
- Kaneko, S.; Murai, D.; Marques-Gonzalez, S.; Nakamura, H.; Komoto, Y.; Fujii, S.; Nishino, T.; Ikeda, K.; Tsukagoshi, K.; Kiguchi, M. Site-selection in single-molecule junction for highly reproducible molecular electronics. J. Am. Chem. Soc. 2016, 138, 1294–1300. [Google Scholar] [CrossRef]
- Lee, S.K.; Ohto, T.; Yamada, R.; Tada, H. Thermopower of benzenedithiol and C60 molecular junctions with Ni and Au electrodes. Nano Lett. 2014, 14, 5276–5280. [Google Scholar] [CrossRef]
- Fuechsle, M.; Miwa, J.A.; Mahapatra, S.; Ryu, H.; Lee, S.; Warschkow, O.; Hollenberg, L.C.L.; Klimeck, G.; Simmons, M.Y. A single-atom transistor. Nat. Nanotechnol. 2012, 7, 242–246. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, Z.B.; Liu, J.Y.; Lu, M.; Yang, D.Z.; Yang, F.Z.; Tian, Z.Q. An electrochemically assisted mechanically controllable break junction approach for single molecule junction conductance measurements. Nano Res. 2011, 4, 1199–1207. [Google Scholar] [CrossRef]
- Smith, C.E.; Xie, Z.; Baldea, I.; Frisbie, C.D. Work function and temperature dependence of electron tunneling through an n-type perylene diimide molecular junction with isocyanide surface linkers. Nanoscale 2018, 10, 964–975. [Google Scholar] [CrossRef]
- Sun, L.; Diaz-Fernandez, Y.A.; Gschneidtner, T.A.; Westerlund, F.; Lara-Avila, S.; Moth-Poulsen, K. Single-molecule electronics: From chemical design to functional devices. Chem. Soc. Rev. 2014, 43, 7378–7411. [Google Scholar] [CrossRef]
- Gao, J.; Yan, N.; Nie, K.; Gao, Z.; Xu, J. A 2.44 μs row conversion time 12-bit high-speed differential single-slope ADC with TDC applied to CMOS image sensor. Microelectron. J. 2022, 102, 105322. [Google Scholar] [CrossRef]
- Molaei, H.; Hajsadeghi, K. A 5.3-ps, 8-b Time to Digital Converter Using a New Gain-Reconfigurable Time Amplifier. IEEE Trans. Circuits Syst. 2019, 66, 352–356. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Z. A Time-to-Digital Converter for Low-Power Consumption Single Slope Analog-to-Digital Converters in a High-Speed CMOS Image Sensor. Micromachines 2024, 15, 578. [Google Scholar] [CrossRef]
- Bazaka, K.; Jacob, M. Implantable Devices: Issues and Challenges. Electronics 2012, 2, 1–34. [Google Scholar] [CrossRef]
- Jiang, L.; Yang, Y.; Chen, Y.; Zhou, Q. Ultrasound-Induced Wireless Energy Harvesting: From Materials Strategies to Functional Applications. Nano Energy 2020, 77, 105131. [Google Scholar] [CrossRef]
- Wu, C. Research on reliability of complementary metal oxide semiconductor integrated circuit. Appl. Comput. Eng. 2023, 7, 8–13. [Google Scholar] [CrossRef]
- Hussain, A.M.; Hussain, M.M. CMOS-technology enabled flexible and stretchable electronics for internet of everything applications. Adv. Mater. 2016, 28, 4219–4249. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, Z.; Wang, R.; Huang, R. Investigation of Sheet Width Dependence on Hot Carrier Degradation in GAA Nanosheet Transistors. In Proceedings of the IEEE Silicon Nanoelectronics Workshop (SNW), Honolulu, HI, USA, 15–16 June 2024; pp. 49–50. [Google Scholar]
- Mahapatra, S.; Sharma, U. A Review of Hot Carrier Degradation in n-Channel MOSFETs—Part I: Physical Mechanism. IEEE Trans. Electron. Devices 2020, 67, 2660–2671. [Google Scholar] [CrossRef]
- Moreno, E.; Villada, M.P.; Ruiz, F.G.; Roldán, J.B.; Marin, E.G. A new explicit and analytical model for square Gate-All-Around MOSFETs with rounded corners. Solid. State Electron. 2015, 111, 180–187. [Google Scholar] [CrossRef]
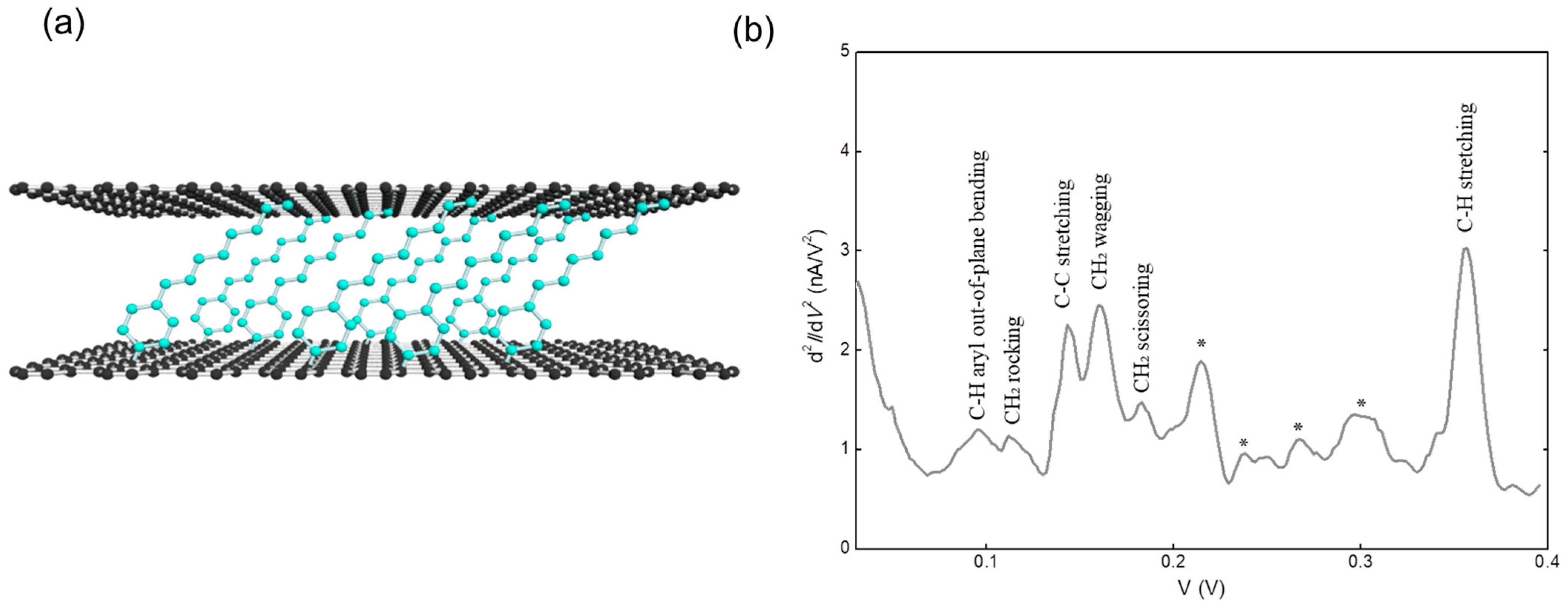
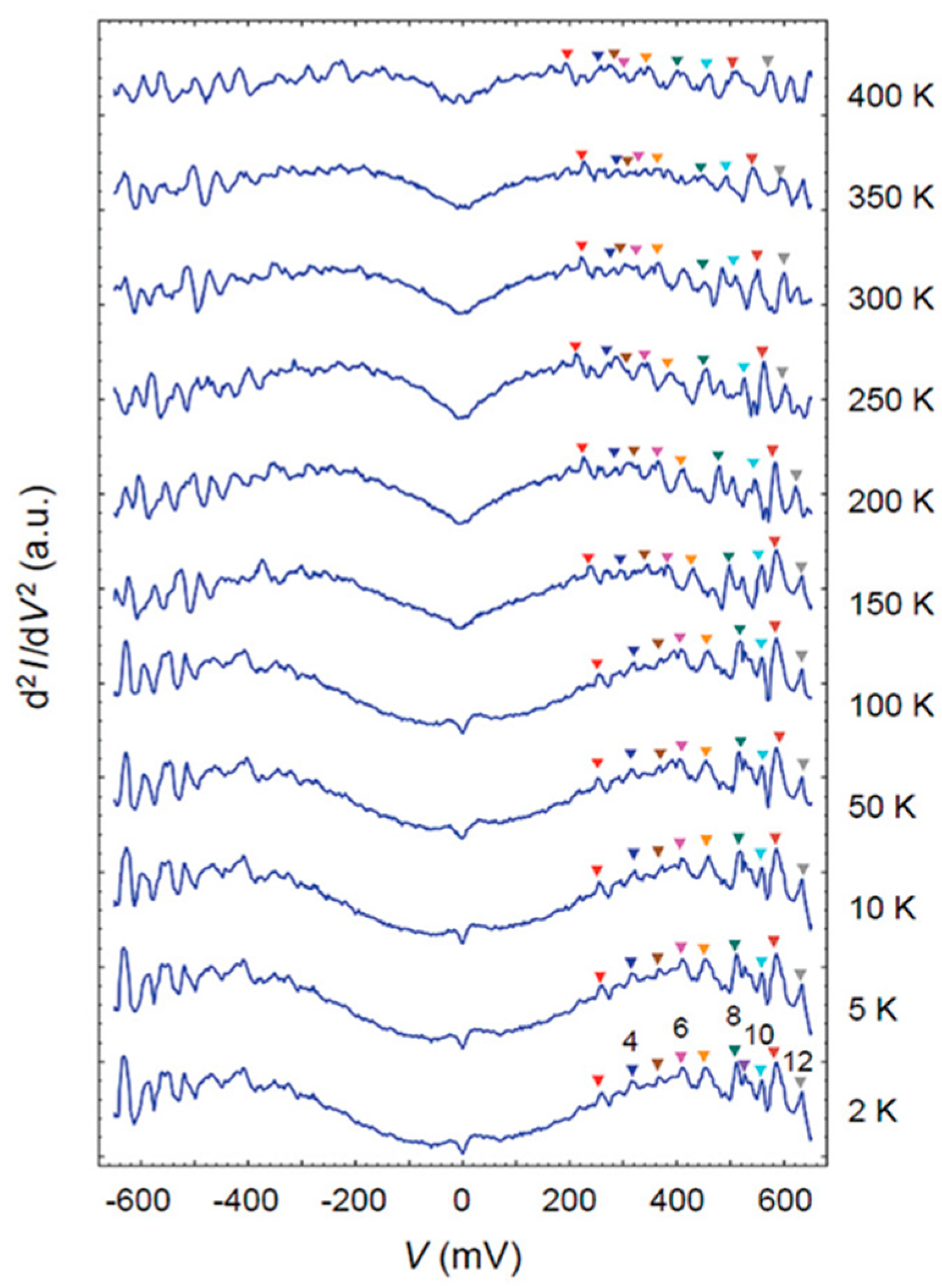
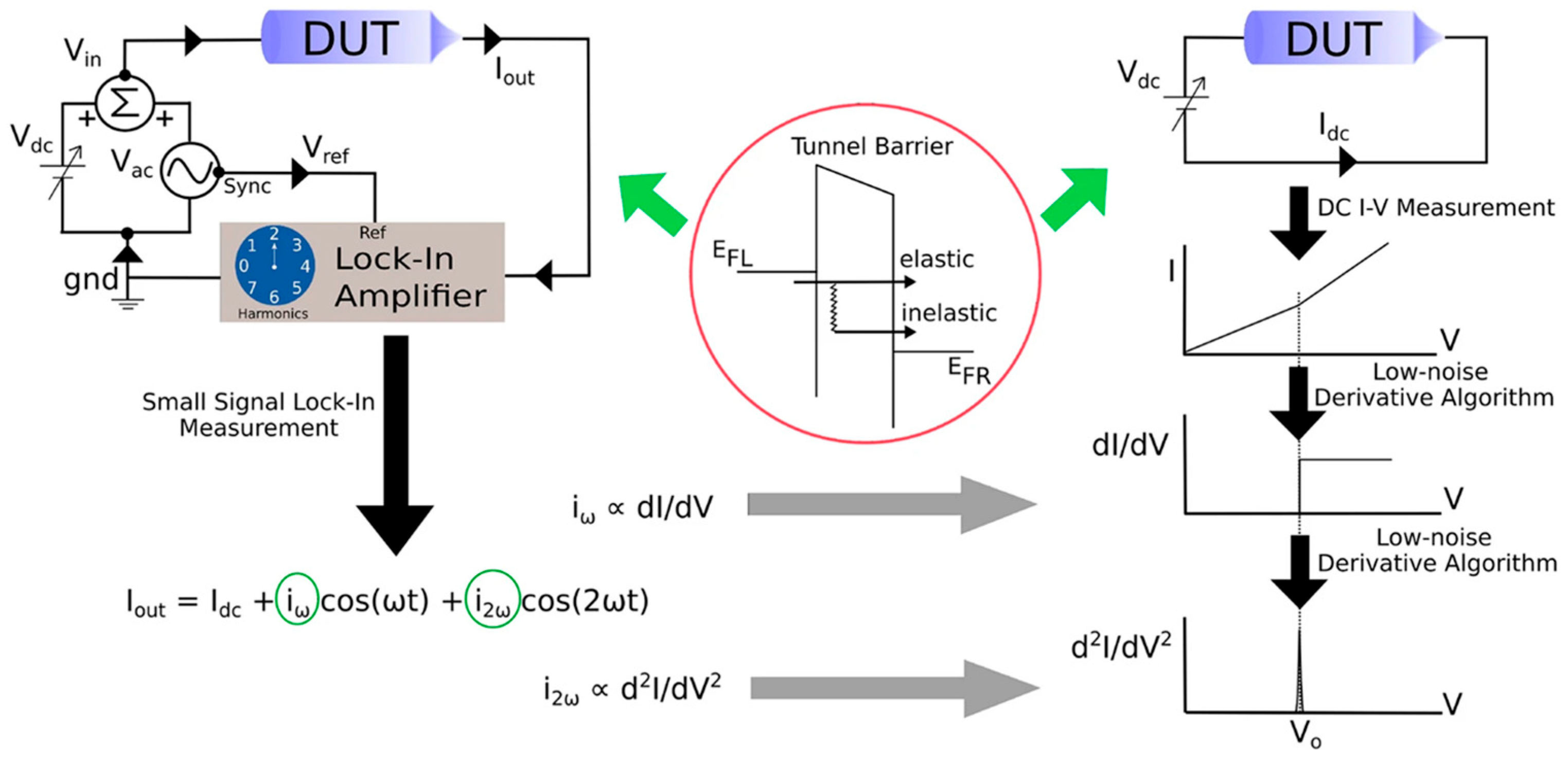
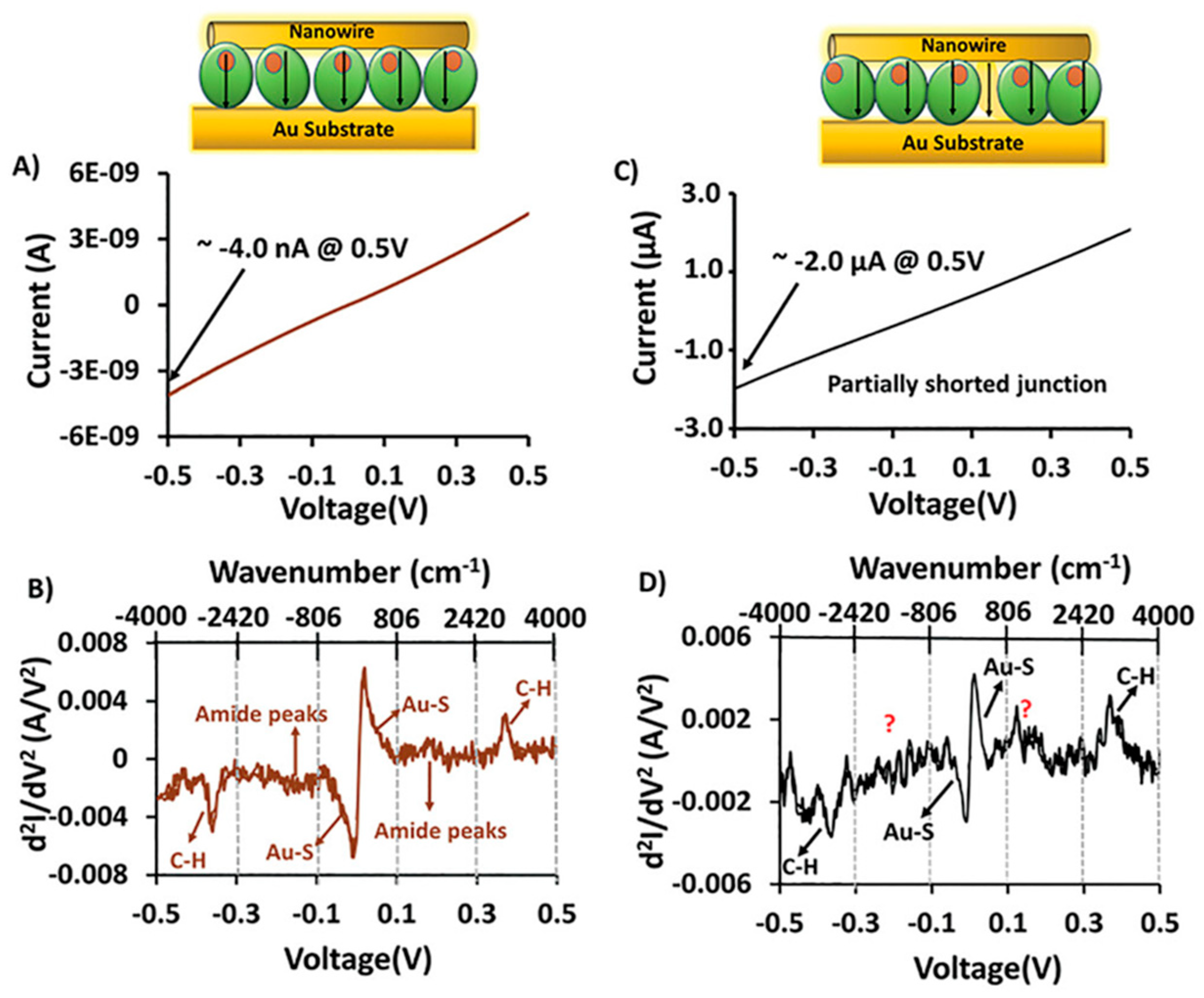
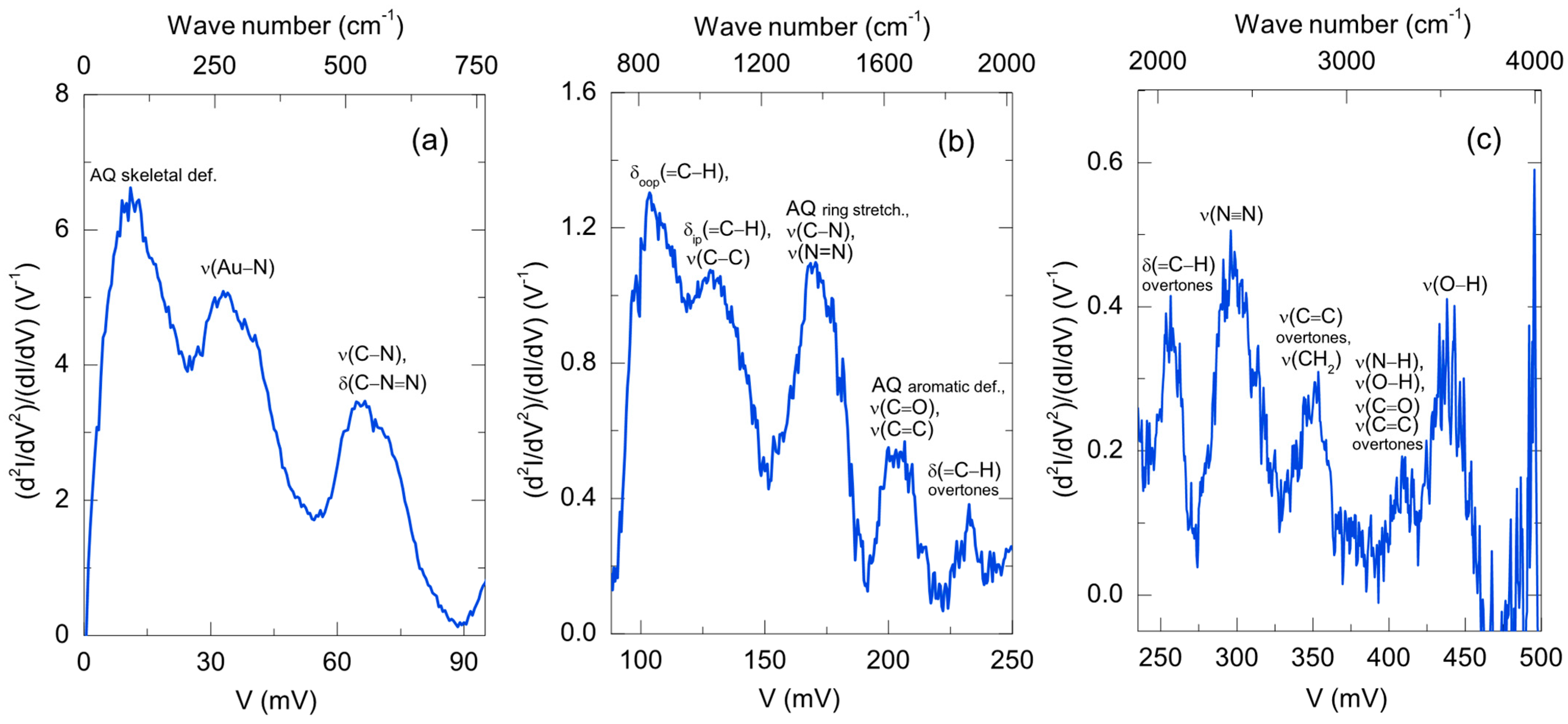
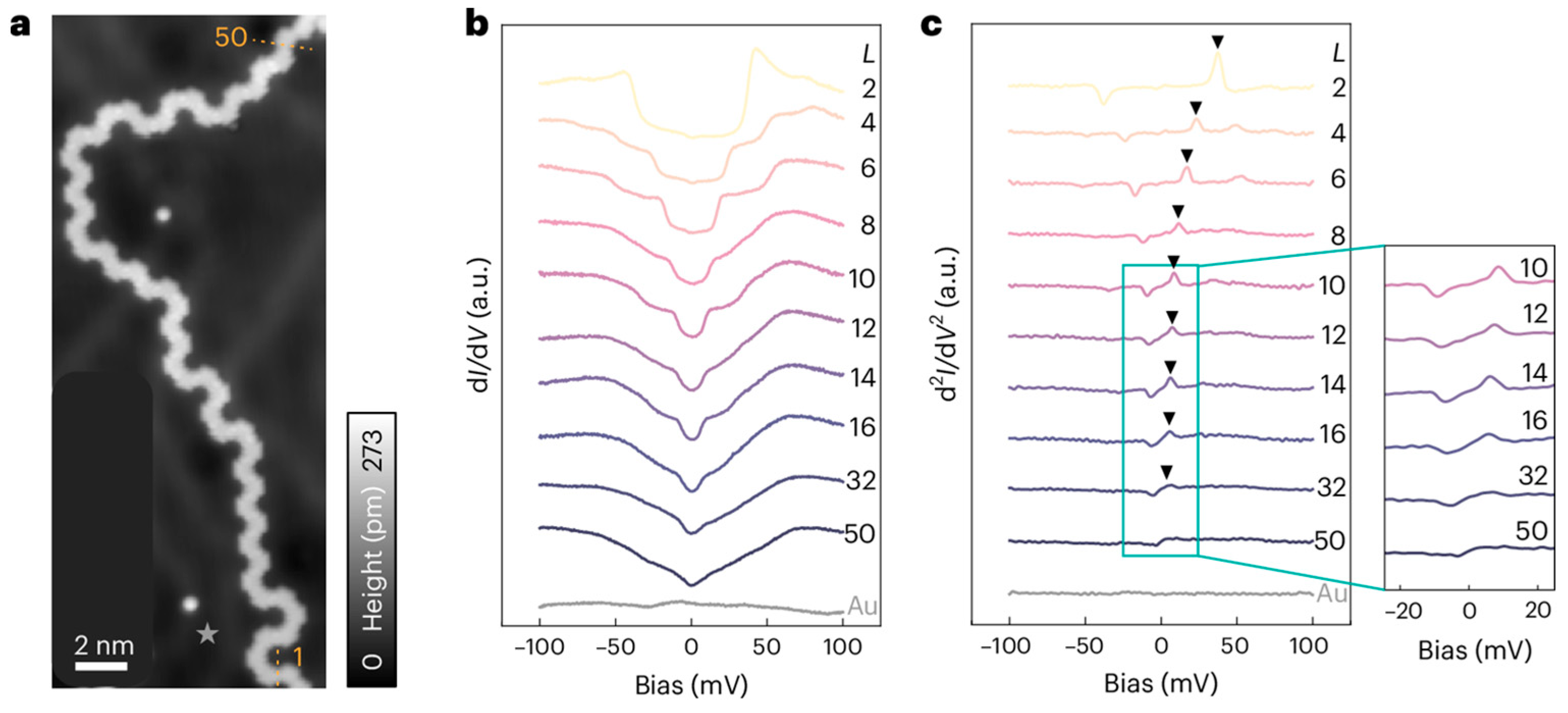
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H. Inelastic Electron Tunneling Spectroscopy of Molecular Electronic Junctions: Recent Advances and Applications. Crystals 2025, 15, 681. https://doi.org/10.3390/cryst15080681
Song H. Inelastic Electron Tunneling Spectroscopy of Molecular Electronic Junctions: Recent Advances and Applications. Crystals. 2025; 15(8):681. https://doi.org/10.3390/cryst15080681
Chicago/Turabian StyleSong, Hyunwook. 2025. "Inelastic Electron Tunneling Spectroscopy of Molecular Electronic Junctions: Recent Advances and Applications" Crystals 15, no. 8: 681. https://doi.org/10.3390/cryst15080681
APA StyleSong, H. (2025). Inelastic Electron Tunneling Spectroscopy of Molecular Electronic Junctions: Recent Advances and Applications. Crystals, 15(8), 681. https://doi.org/10.3390/cryst15080681




