A Single-Phase Aluminum-Based Chiral Metamaterial with Simultaneous Negative Mass Density and Bulk Modulus
Abstract
1. Introduction
2. Methods
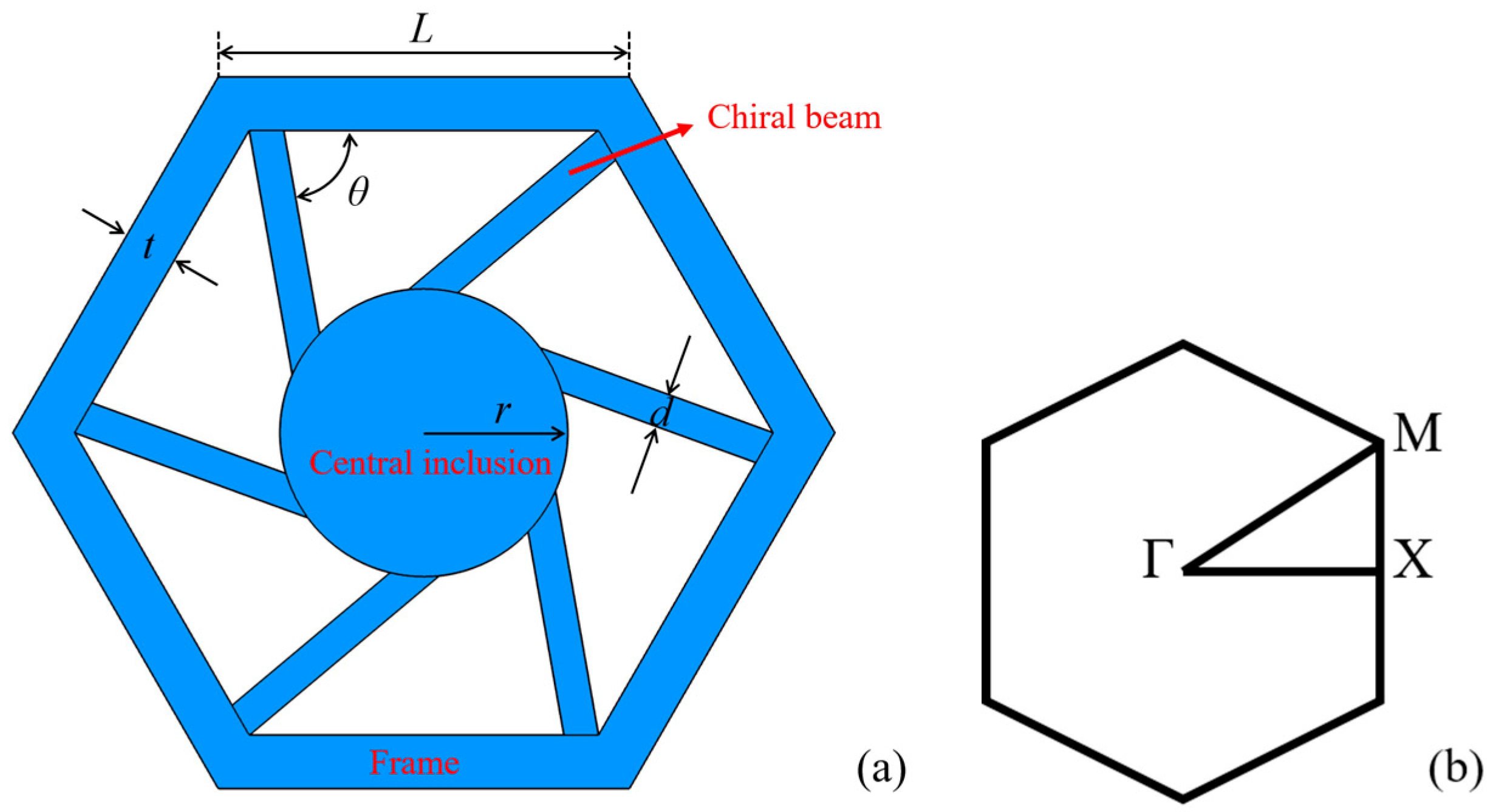
2.1. Metamaterial Design
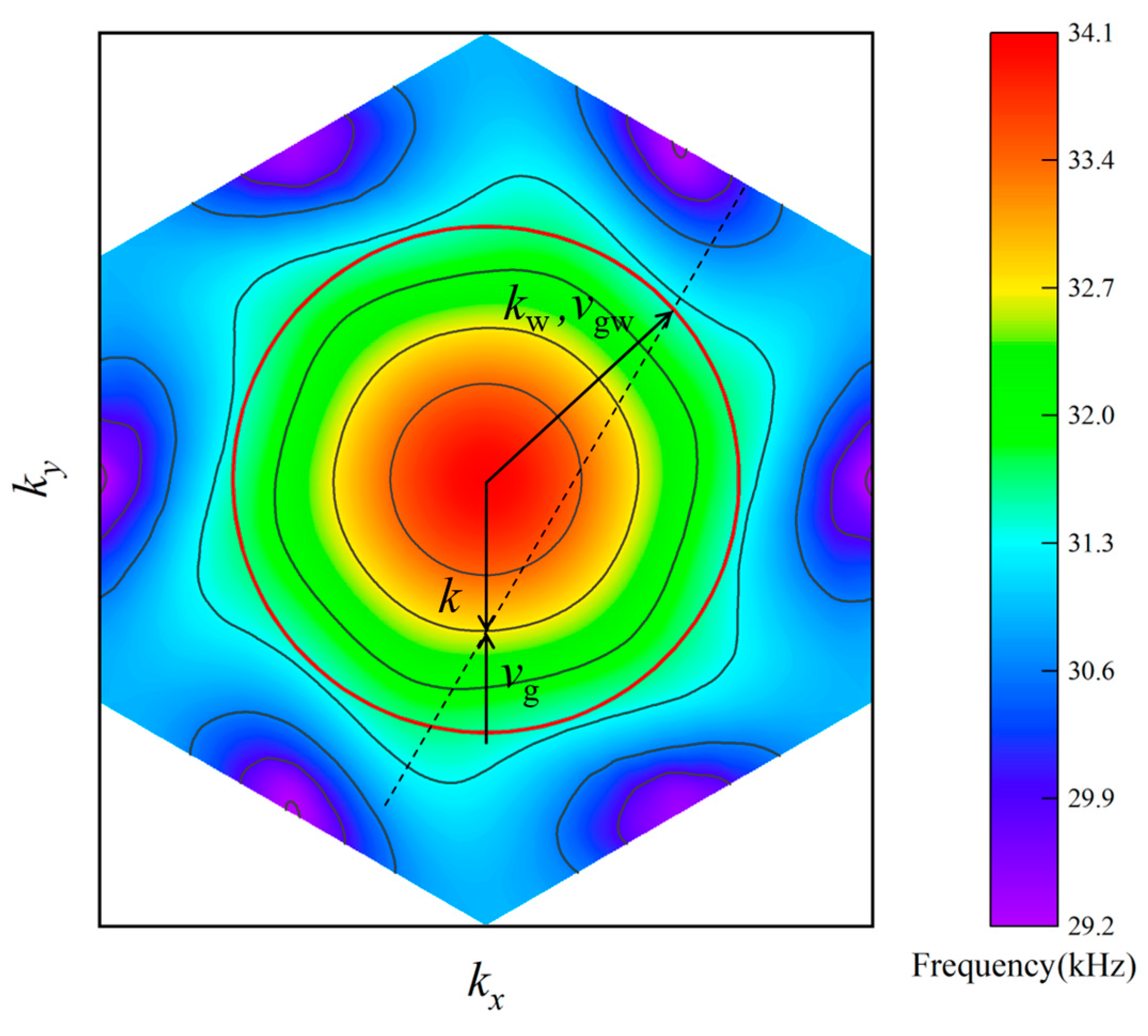
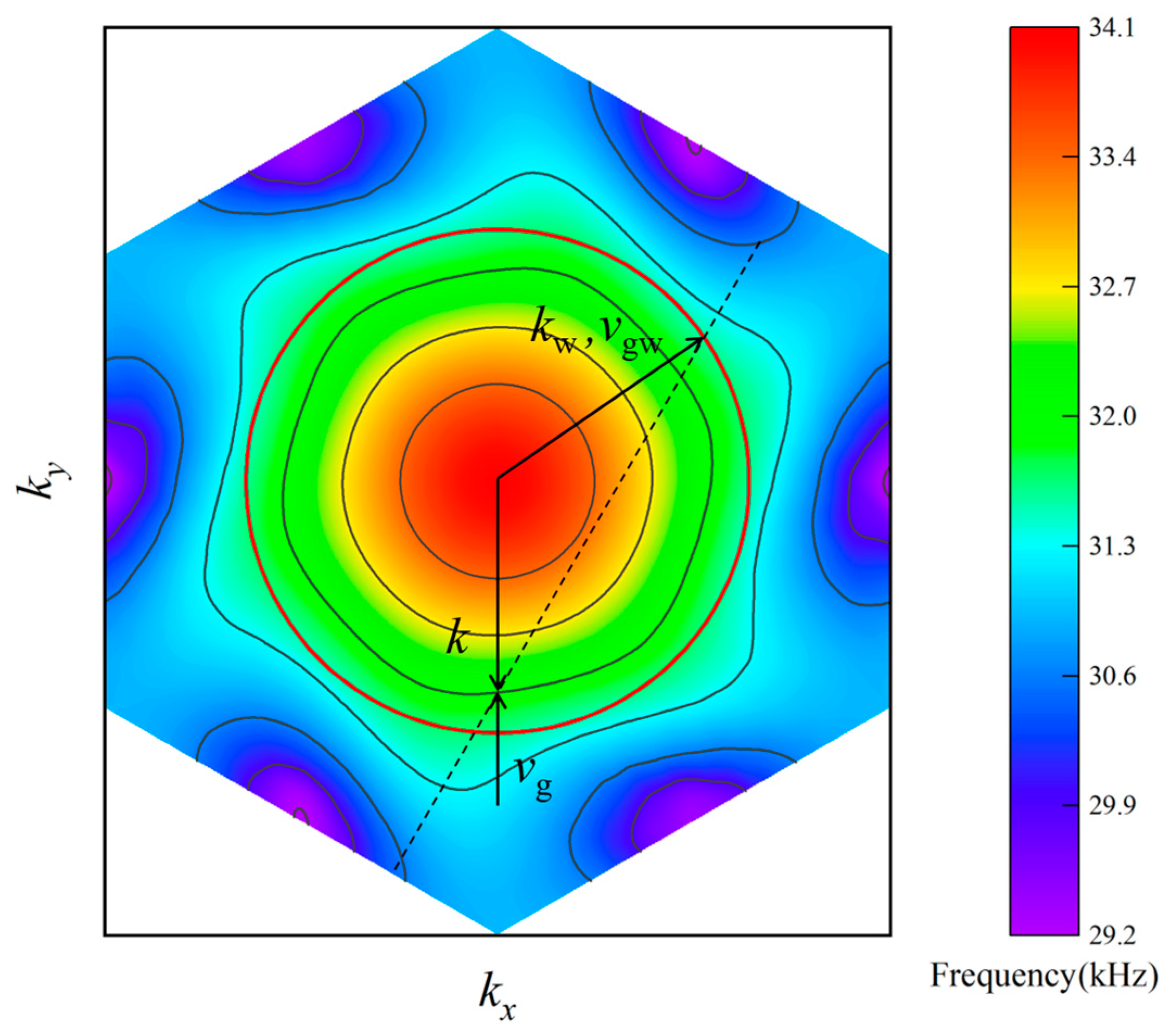
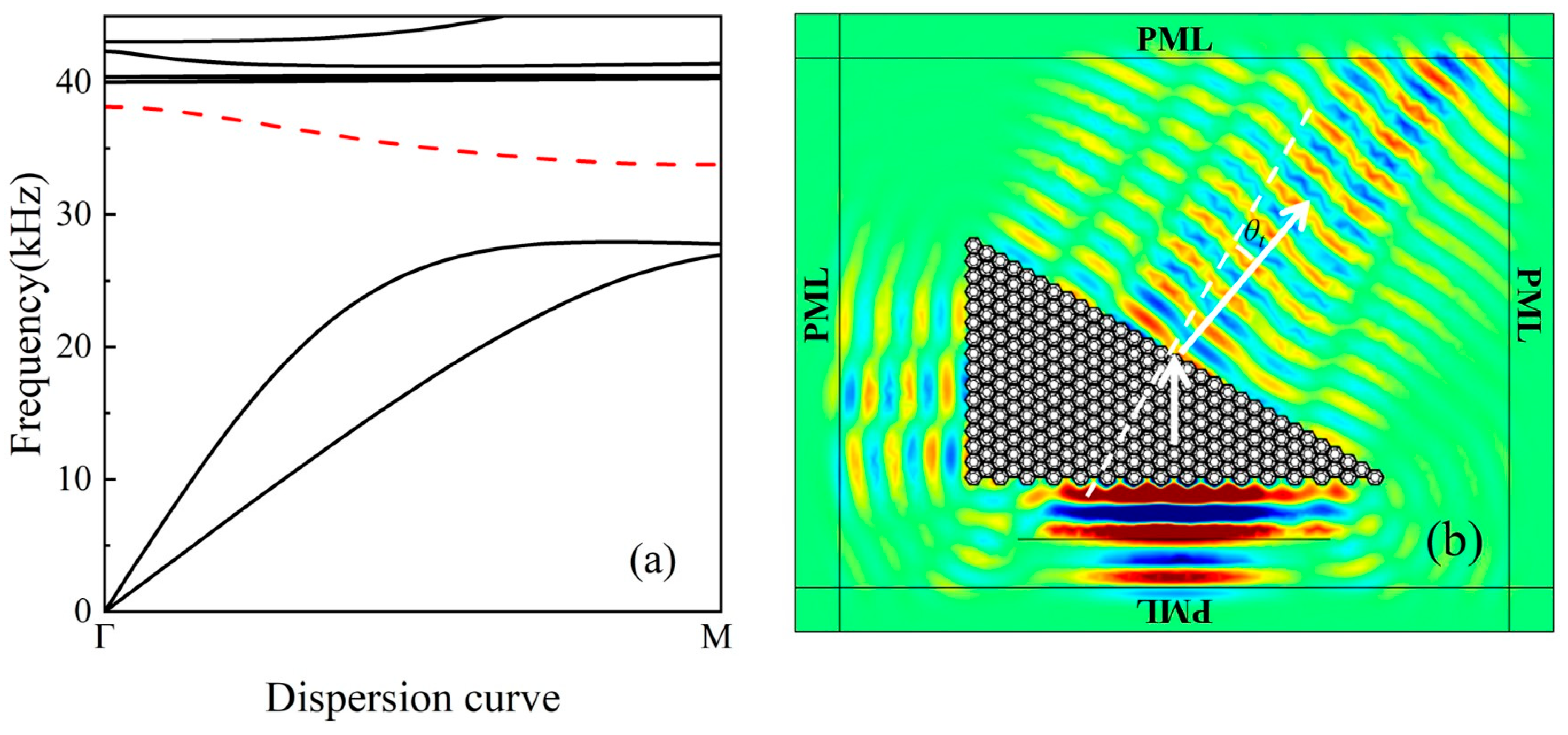
2.2. Dispersion Analysis
2.3. Effective Parameter Extraction and Modal Analysis
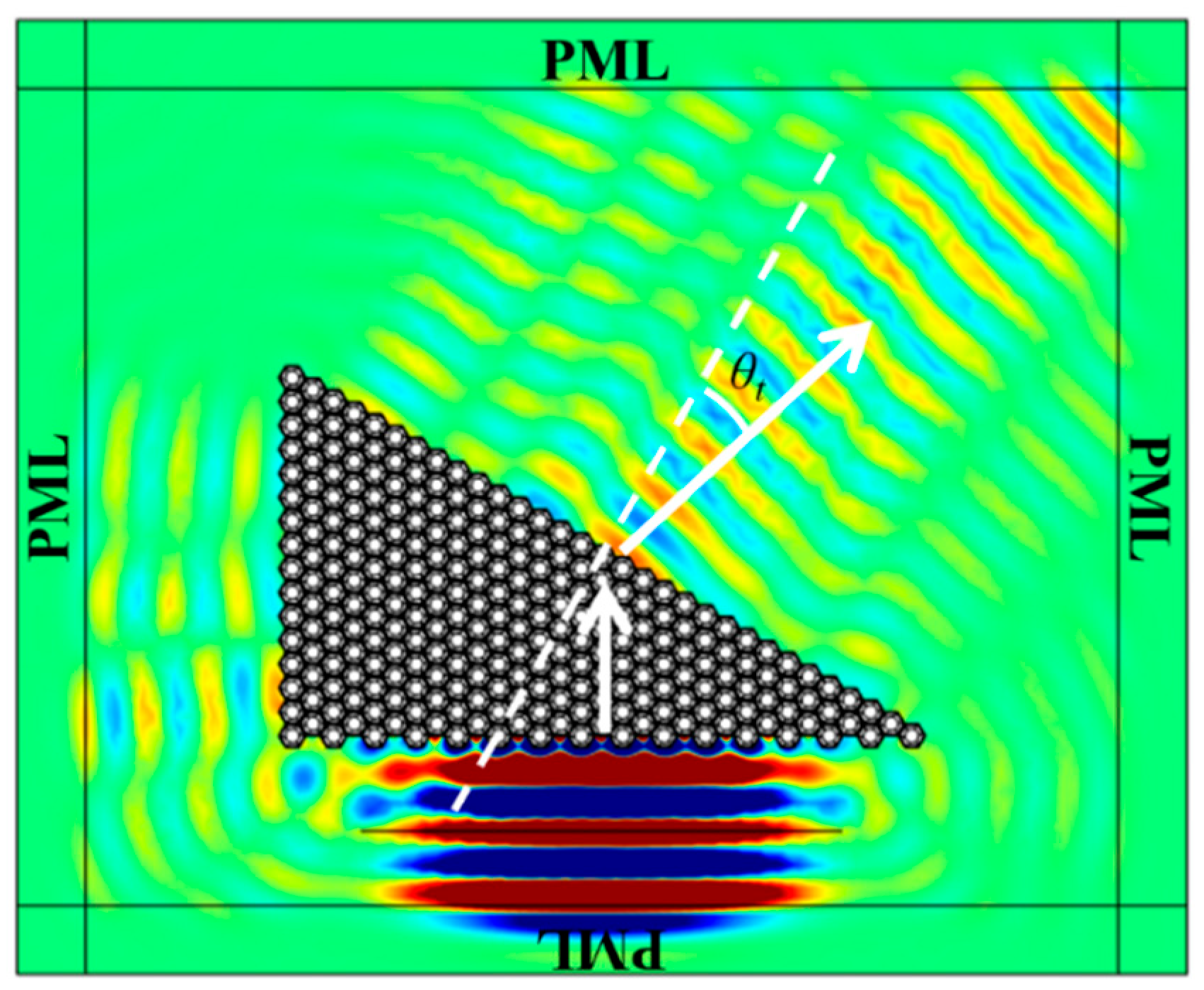
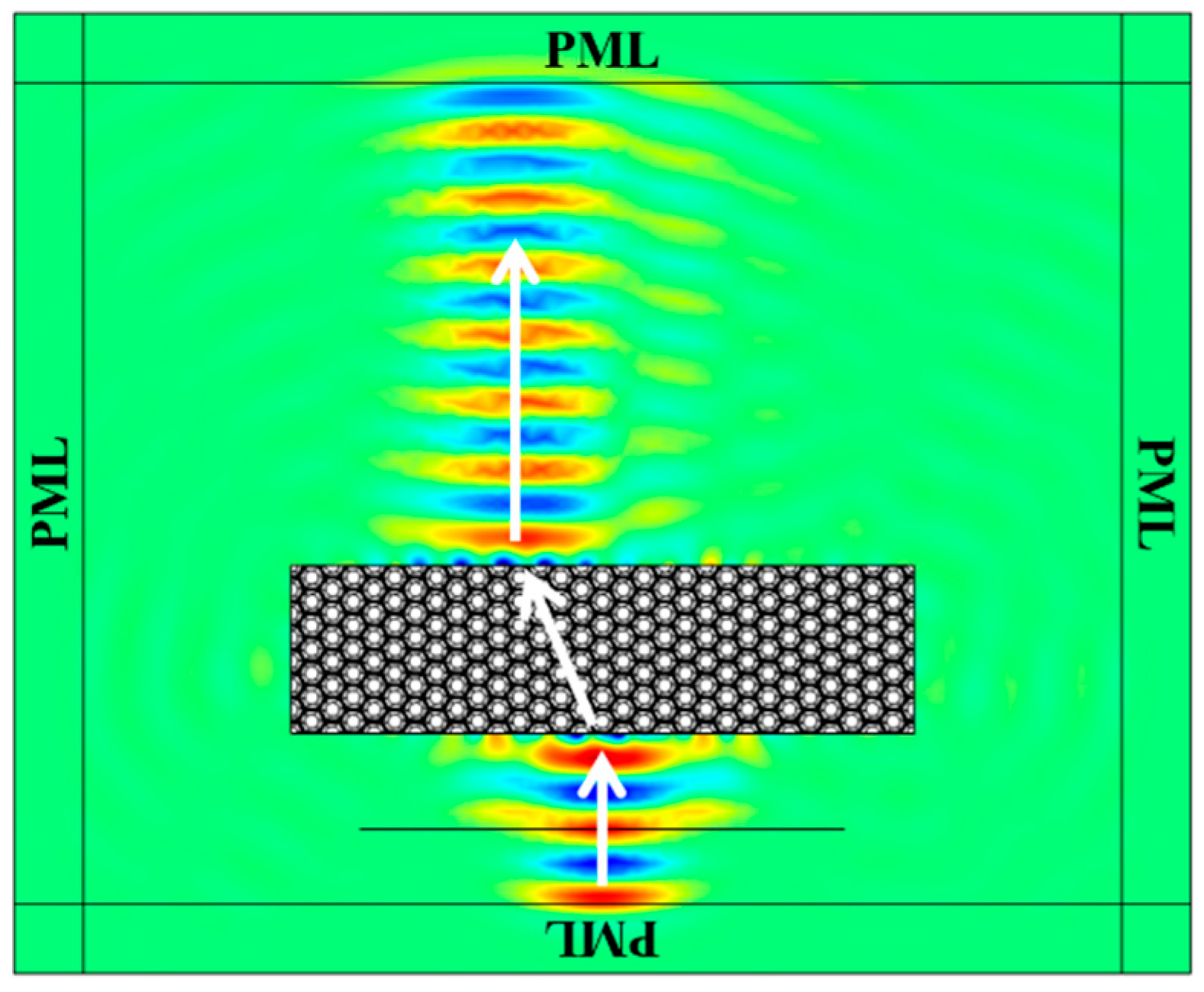
2.4. Finite Element Validation of Negative Refraction
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Detailed Procedure for Effective Parameter Retrieval
Appendix A.1. Homogenization Framework
Appendix A.2. Boundary Conditions and Loading Scenarios
- (a)
- Effective Mass Density:
- (b)
- Effective Bulk Modulus
- (c)
- Effective Shear Modulus
Appendix A.3. Numerical Implementation
Appendix A.4. Validation
Appendix B. Modal Analysis Setup for Figure 3
References
- Pendry, J.B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Sigalas, M.M.; Economou, E.N. Elastic and Acoustic Wave Band Structure. J. Sound Vib. 1992, 158, 377–382. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Foteinopoulou, S.; Economou, E.N.; Soukoulis, C.M. Refraction at Media with Negative Refractive Index. Phys. Rev. Lett. 2003, 90, 107402. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Kafesaki, M.; Economou, E.N. Negative-Index Materials: New Frontiers in Optics. Adv. Mater. 2006, 18, 1941–1952. [Google Scholar] [CrossRef]
- Dong, H.-W.; Zhao, S.-D.; Wei, P.; Cheng, L.; Wang, Y.-S.; Zhang, C. Systematic Design and Realization of Double-Negative Acoustic Metamaterials by Topology Optimization. Acta Mater. 2019, 172, 102–120. [Google Scholar] [CrossRef]
- Christensen, J.; De Abajo, F.J.G. Anisotropic Metamaterials for Full Control of Acoustic Waves. Phys. Rev. Lett. 2012, 108, 124301. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Effective Medium Theory for Elastic Metamaterials in Two Dimensions. Phys. Rev. B 2007, 76, 205313. [Google Scholar] [CrossRef]
- Milton, G.W.; Willis, J.R. On Modifications of Newton’s Second Law and Linear Continuum Elastodynamics. Proc. R. Soc. A 2007, 463, 855–880. [Google Scholar] [CrossRef]
- Huang, H.H.; Sun, C.T.; Huang, G.L. On the Negative Effective Mass Density in Acoustic Metamaterials. Int. J. Eng. Sci. 2009, 47, 610–617. [Google Scholar] [CrossRef]
- Chan, C.T.; Li, J.; Fung, K.H. On Extending the Concept of Double Negativity to Acoustic Waves. J. Zhejiang Univ.-Sci. A 2006, 7, 24–28. [Google Scholar] [CrossRef]
- Zhang, S.; Park, Y.-S.; Li, J.; Lu, X.; Zhang, W.; Zhang, X. Negative Refractive Index in Chiral Metamaterials. Phys. Rev. Lett. 2009, 102, 023901. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Koschny, T.; Kafesaki, M.; Economou, E.N.; Pendry, J.B.; Soukoulis, C.M. Saturation of the Magnetic Response of Split-Ring Resonators at Optical Frequencies. Phys. Rev. Lett. 2005, 95, 223902. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chan, C.T. Double-Negative Acoustic Metamaterial. Phys. Rev. E 2004, 70, 055602. [Google Scholar] [CrossRef] [PubMed]
- Kafesaki, M.; Penciu, R.S.; Economou, E.N. Air Bubbles in Water: A Strongly Multiple Scattering Medium for Acoustic Waves. Phys. Rev. Lett. 2000, 84, 6050–6053. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of Topological Valley Transport of Sound in Sonic Crystals. Nat. Phys. 2017, 13, 369–374. [Google Scholar] [CrossRef]
- Liu, T.; Lei, Z. Low-Frequency Bandgap and Tension-Compression to Twist Mode Transition of a Novel Pull-Rotation Chiral Structure. J. Phys. D Appl. Phys. 2025, 58, 225301. [Google Scholar] [CrossRef]
- Lemkalli, B.; Kadic, M.; El Badri, Y.; Guenneau, S.; Mir, A.; Achaoui, Y. The Emergence of Low-Frequency Dual Fano Resonances in Chiral Twisting Metamaterials. Wave Motion 2024, 127, 103302. [Google Scholar] [CrossRef]
- Oudich, M.; Djafari-Rouhani, B.; Pennec, Y.; Assouar, M.B.; Bonello, B. Negative Effective Mass Density of Acoustic Metamaterial Plate Decorated with Low Frequency Resonant Pillars. J. Appl. Phys. 2014, 116. [Google Scholar] [CrossRef]
- Torrent, D.; Sánchez-Dehesa, J. Acoustic Metamaterials for New Two-Dimensional Sonic Devices. New J. Phys. 2007, 9, 323. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic Metamaterials: From Local Resonances to Broad Horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef] [PubMed]
- Kadic, M.; Milton, G.W.; van Hecke, M.; Wegener, M. 3D Metamaterials. Nat. Rev. Phys. 2019, 1, 198–210. [Google Scholar] [CrossRef]
- Frenzel, T.; Kadic, M.; Wegener, M. Three-Dimensional Mechanical Metamaterials with a Twist. Science 2017, 358, 1072–1074. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.N.; Hu, G.K.; Huang, G.L.; Sun, C.T. An Elastic Metamaterial with Simultaneously Negative Mass Density and Bulk Modulus. Appl. Phys. Lett. 2011, 98, 251907. [Google Scholar] [CrossRef]
- Zhu, R.; Liu, X.N.; Hu, G.K.; Sun, C.T.; Huang, G.L. Negative Refraction of Elastic Waves at the Deep-Subwavelength Scale in a Single-Phase Metamaterial. Nat. Commun. 2014, 5, 5510. [Google Scholar] [CrossRef] [PubMed]
- Benedetti, A.; Alam, B.; Esposito, M.; Tasco, V.; Leahu, G.; Belardini, A.; Li Voti, R.; Passaseo, A.; Sibilia, C. Precise Detection of Circular Dichroism in a Cluster of Nano-Helices by Photoacoustic Measurements. Sci. Rep. 2017, 7, 5257. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.L.; Gao, N.; Chen, W.Q.; Bao, R.H. Extension/Compression-Controlled Complete Band Gaps in 2D Chiral Square-Lattice-Like Structures. Acta Mech. Solida Sin. 2018, 31, 51–65. [Google Scholar] [CrossRef]
- Petronijevic, E.; Leahu, G.; Belardini, A.; Centini, M.; Li Voti, R.; Hakkarainen, T.; Koivusalo, E.; Rizzo Piton, M.; Suomalainen, S.; Guina, M.; et al. Photo-Acoustic Spectroscopy Reveals Extrinsic Optical Chirality in GaAs-Based Nanowires Partially Covered with Gold. Int. J. Thermophys. 2018, 39, 46. [Google Scholar] [CrossRef]
- Usta, F.; Türkmen, H.S.; Scarpa, F. Low-Velocity Impact Resistance of Composite Sandwich Panels with Various Types of Auxetic and Non-Auxetic Core Structures. Thin-Walled Struct. 2021, 163, 107738. [Google Scholar] [CrossRef]
- Tallon, B.; Kovalenko, A.; Poncelet, O.; Aristégui, C.; Mondain-Monval, O.; Brunet, T. Experimental Demonstration of Negative Refraction with 3D Locally Resonant Acoustic Metafluids. Sci. Rep. 2021, 11, 4627. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zeng, T.; Ni, H.; Hou, Y.; Pan, G. A New Local Resonance Metamaterial for Flat and Cylindrical Structures Depended on Elastic Chiral Spiral Beams. Sci. China Technol. Sci. 2024, 67, 3597–3611. [Google Scholar] [CrossRef]
- Ding, W.; Chen, T.; Yu, D.; Chen, C.; Zhang, R.; Zhu, J.; Assouar, B. Isotacticity in Chiral Phononic Crystals for Low-Frequency Bandgap. Int. J. Mech. Sci. 2024, 261, 108678. [Google Scholar] [CrossRef]
- Petronijevic, E.; Cesca, T.; Scian, C.; Mattei, G.; Li Voti, R.; Sibilia, C.; Belardini, A. Extrinsic Chirality Tailors Stokes Parameters in Simple Asymmetric Metasurfaces. Nanoscale 2024, 16, 16477–16484. [Google Scholar] [CrossRef] [PubMed]
- Wen, X.-D.; Gao, S.-Q.; Kang, L.; Li, Y.-X. Study on Band-Gap Characteristics and Formation Mechanism of Four-Ligament Chiral Elastic Metamaterials. J. Phys. D Appl. Phys. 2025, 58, 075302. [Google Scholar] [CrossRef]
- Ding, W.; Zhang, R.; Chen, T.; Qu, S.; Yu, D.; Dong, L.; Zhu, J.; Yang, Y.; Assouar, B. Origin and Tuning of Bandgap in Chiral Phononic Crystals. Commun. Phys. 2024, 7, 272. [Google Scholar] [CrossRef]
- Bergamini, A.; Miniaci, M.; Delpero, T.; Tallarico, D.; Van Damme, B.; Hannema, G.; Leibacher, I.; Zemp, A. Tacticity in Chiral Phononic Crystals. Nat. Commun. 2019, 10, 4525. [Google Scholar] [CrossRef] [PubMed]
- Pancella, C.; D’Annibale, F. A Timoshenko-like Equivalent Beam Model for the Static Analysis of a Chiral Metamaterial. Contin. Mech. Thermodyn. 2025, 37, 59. [Google Scholar] [CrossRef]
- Lin, X.Y.; Li, E.; He, Z.C.; Wu, Y.; Li, Q.Q. Design of Single-Phase Chiral Metamaterials for Broadband Double Negativity via Shape Optimization. Appl. Math. Model. 2021, 91, 335–357. [Google Scholar] [CrossRef]
- Sun, F.; Zhang, X.; Zhang, S.; Wu, H.; Yang, S. Low-Frequency Bandgap and Anomalous Refraction of Elastic Waves in Tetra-Chiral Metamaterial. Mech. Adv. Mater. Struct. 2025. [Google Scholar] [CrossRef]
- Band, Y.B.; Kuzmenko, I.; Trippenbach, M. Negative Refraction in Isotropic Achiral and Chiral Materials. Phys. Rev. A 2024, 109, 063514. [Google Scholar] [CrossRef]
- Sang, S.; Sandgren, E.; Wang, Z. Wave Attenuation and Negative Refraction of Elastic Waves in a Single-Phase Elastic Metamaterial. Acta Mech. 2018, 229, 2561–2569. [Google Scholar] [CrossRef]
- Wang, J.; Xiang, J.; Xuan, D.; Chen, Z.; Wang, R.; Liu, Q.; Zhou, X. Study on the Double Negativity in Deformed Single-Phase Chiral Metamaterials under Tensile Loads. J. Appl. Phys. 2024, 135, 123103. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, F.; Shen, Z.; Cheng, Y.; Zhao, H. A Single-Phase Aluminum-Based Chiral Metamaterial with Simultaneous Negative Mass Density and Bulk Modulus. Crystals 2025, 15, 679. https://doi.org/10.3390/cryst15080679
Zhao F, Shen Z, Cheng Y, Zhao H. A Single-Phase Aluminum-Based Chiral Metamaterial with Simultaneous Negative Mass Density and Bulk Modulus. Crystals. 2025; 15(8):679. https://doi.org/10.3390/cryst15080679
Chicago/Turabian StyleZhao, Fanglei, Zhenxing Shen, Yong Cheng, and Huichuan Zhao. 2025. "A Single-Phase Aluminum-Based Chiral Metamaterial with Simultaneous Negative Mass Density and Bulk Modulus" Crystals 15, no. 8: 679. https://doi.org/10.3390/cryst15080679
APA StyleZhao, F., Shen, Z., Cheng, Y., & Zhao, H. (2025). A Single-Phase Aluminum-Based Chiral Metamaterial with Simultaneous Negative Mass Density and Bulk Modulus. Crystals, 15(8), 679. https://doi.org/10.3390/cryst15080679





