Crystal Plasticity Finite Element Analysis of Spherical Nanoindentation Stress–Strain Curve of Single-Crystal Copper
Abstract
1. Introduction
2. Materials and Methods
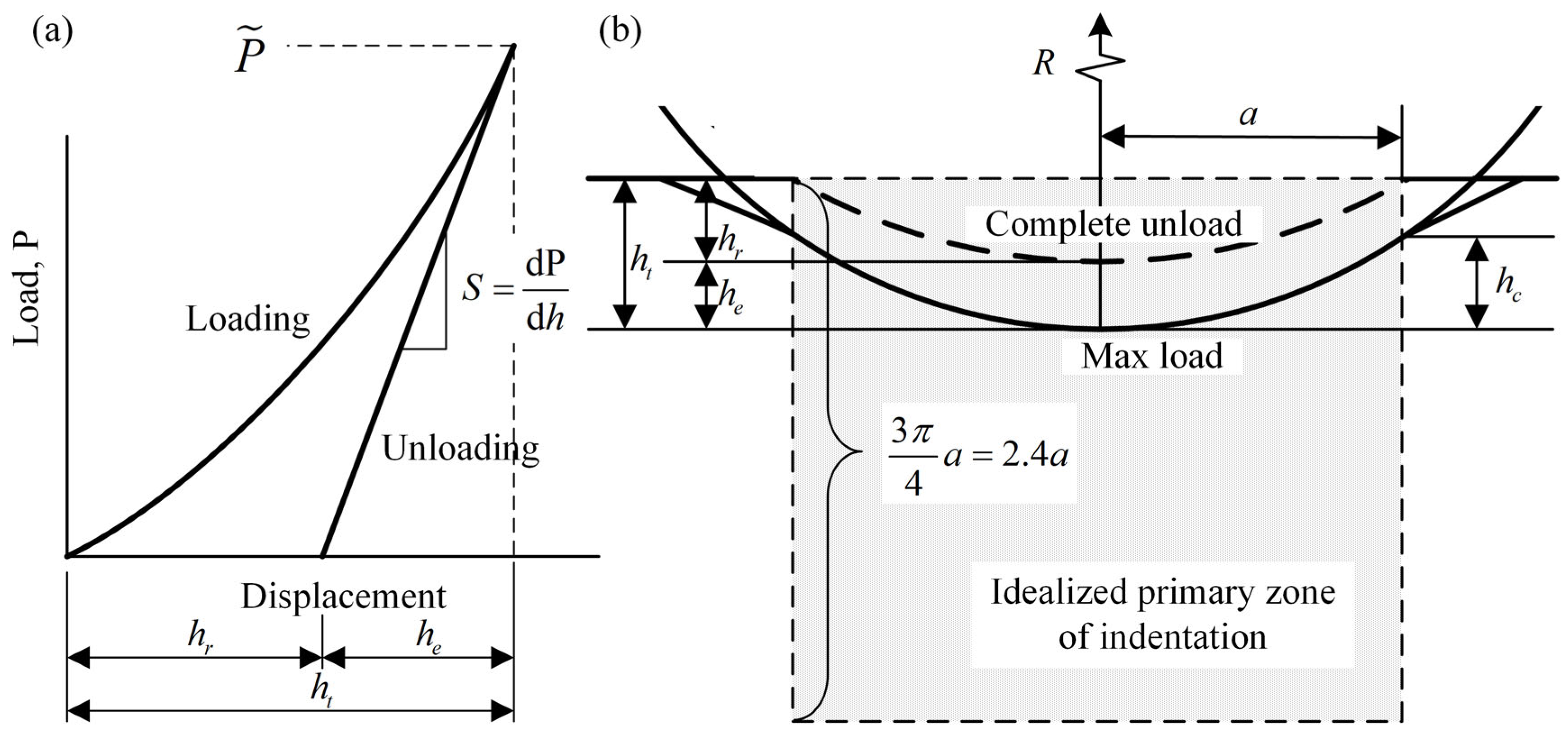
2.1. Spherical Indentation Process
2.2. ISS Curve
3. CPFEM Model of Nanoindentation
3.1. Setup of Nanoindentation
3.2. Crystal Plasticity
4. Results and Discussion
4.1. Mechanical Properties
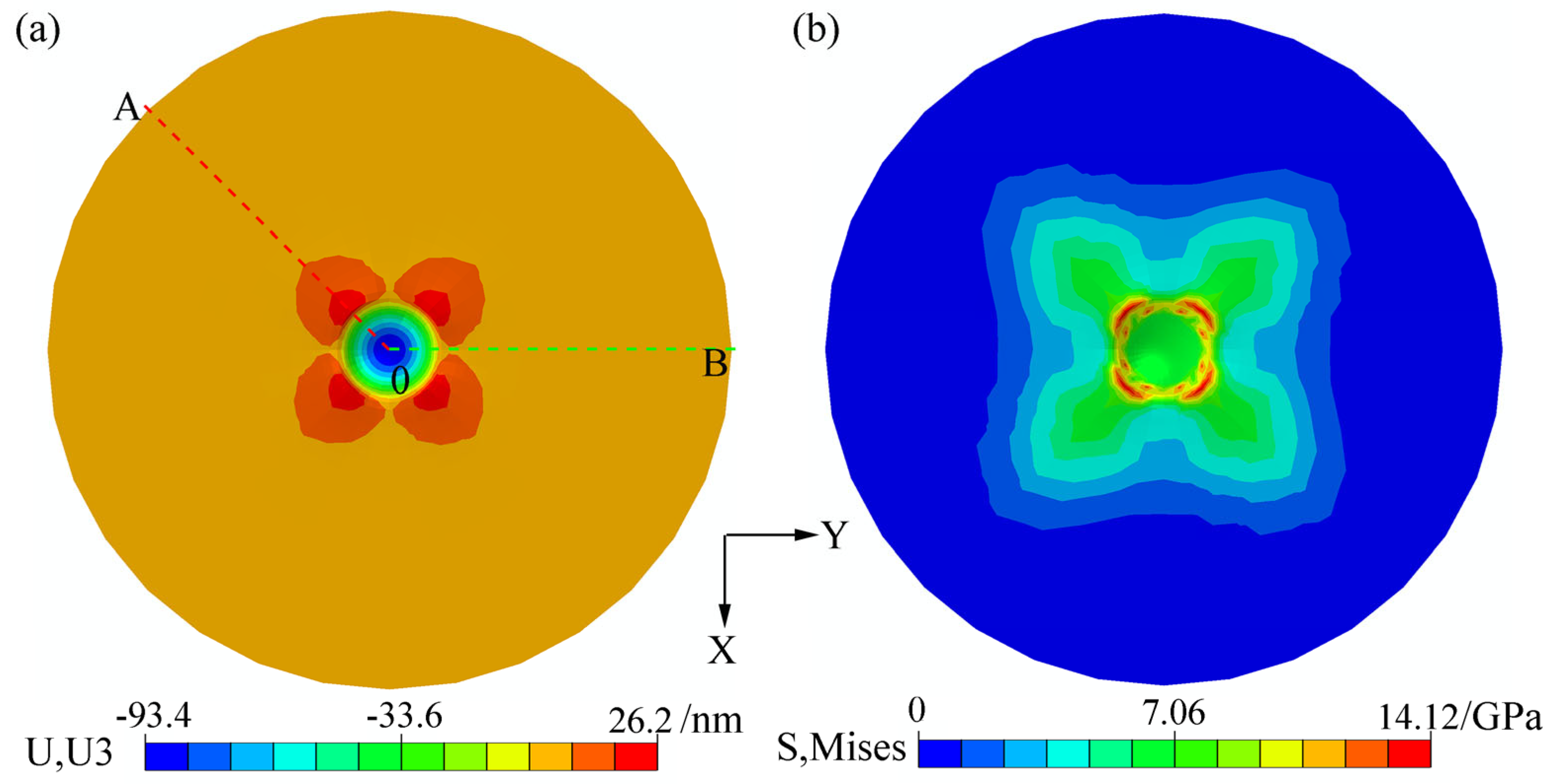
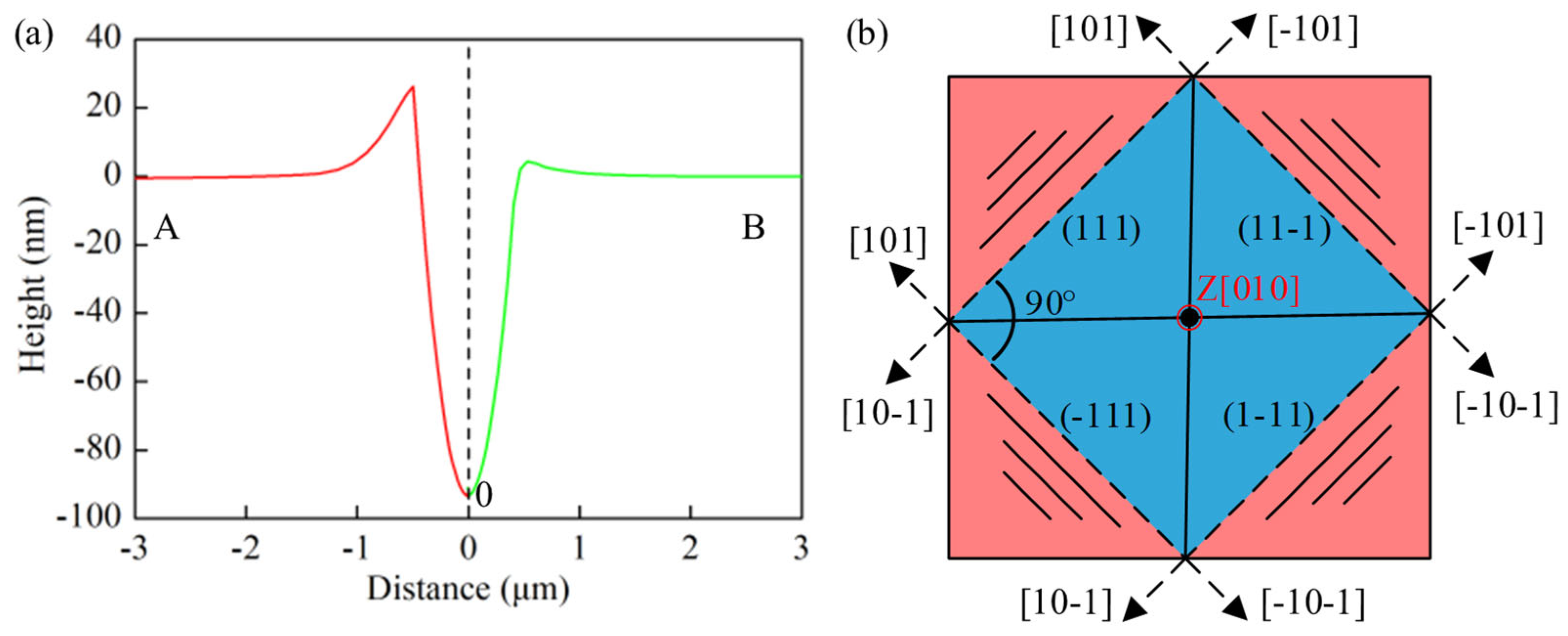
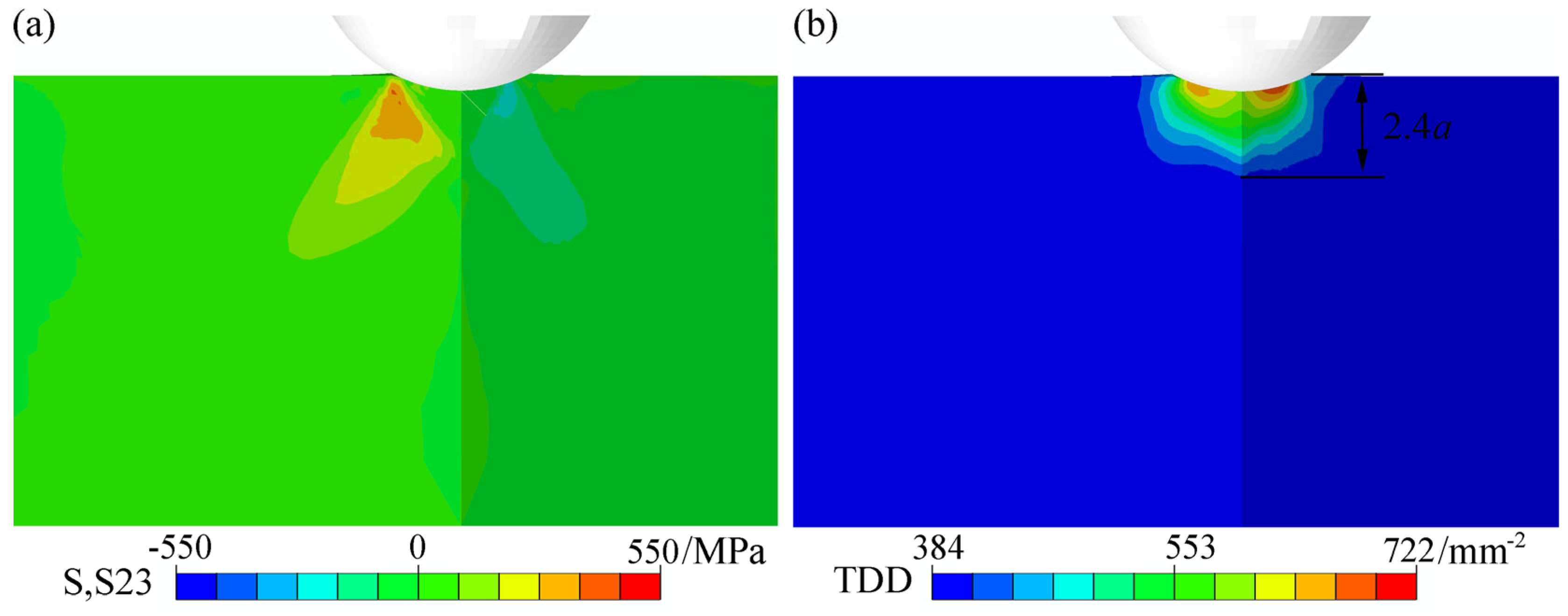
4.2. Surface Pile-Up
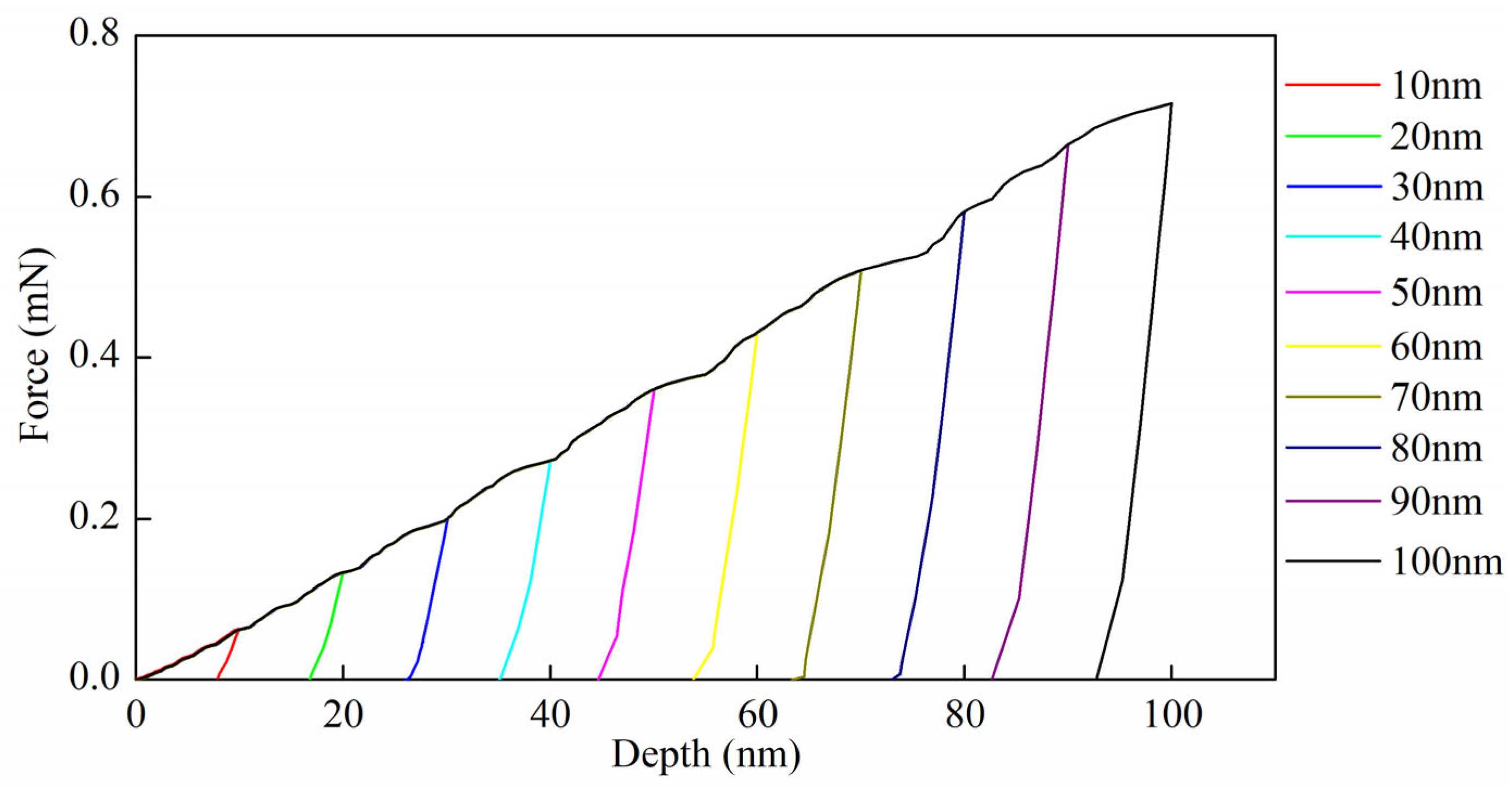
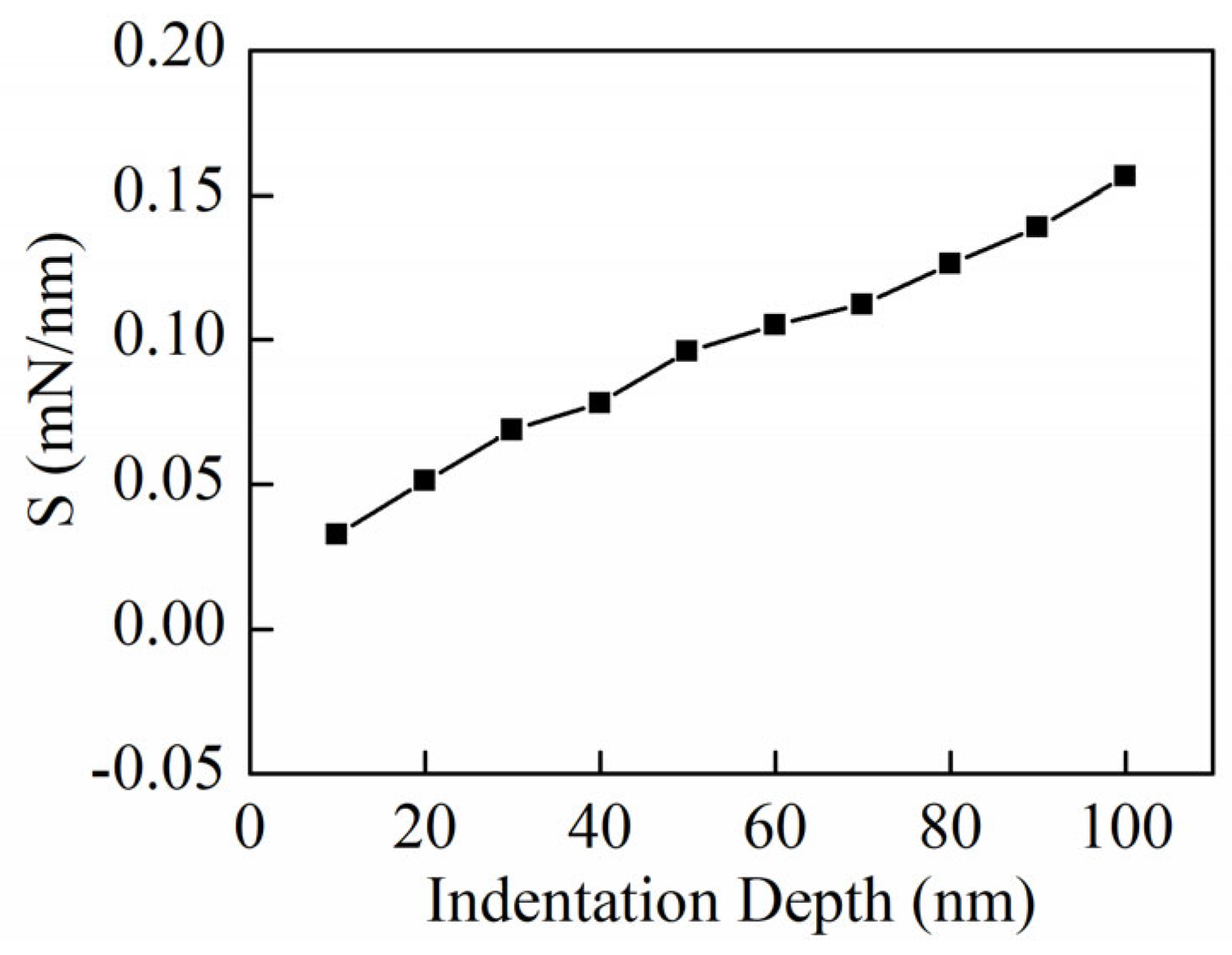
4.3. Effect of Indentation Depth
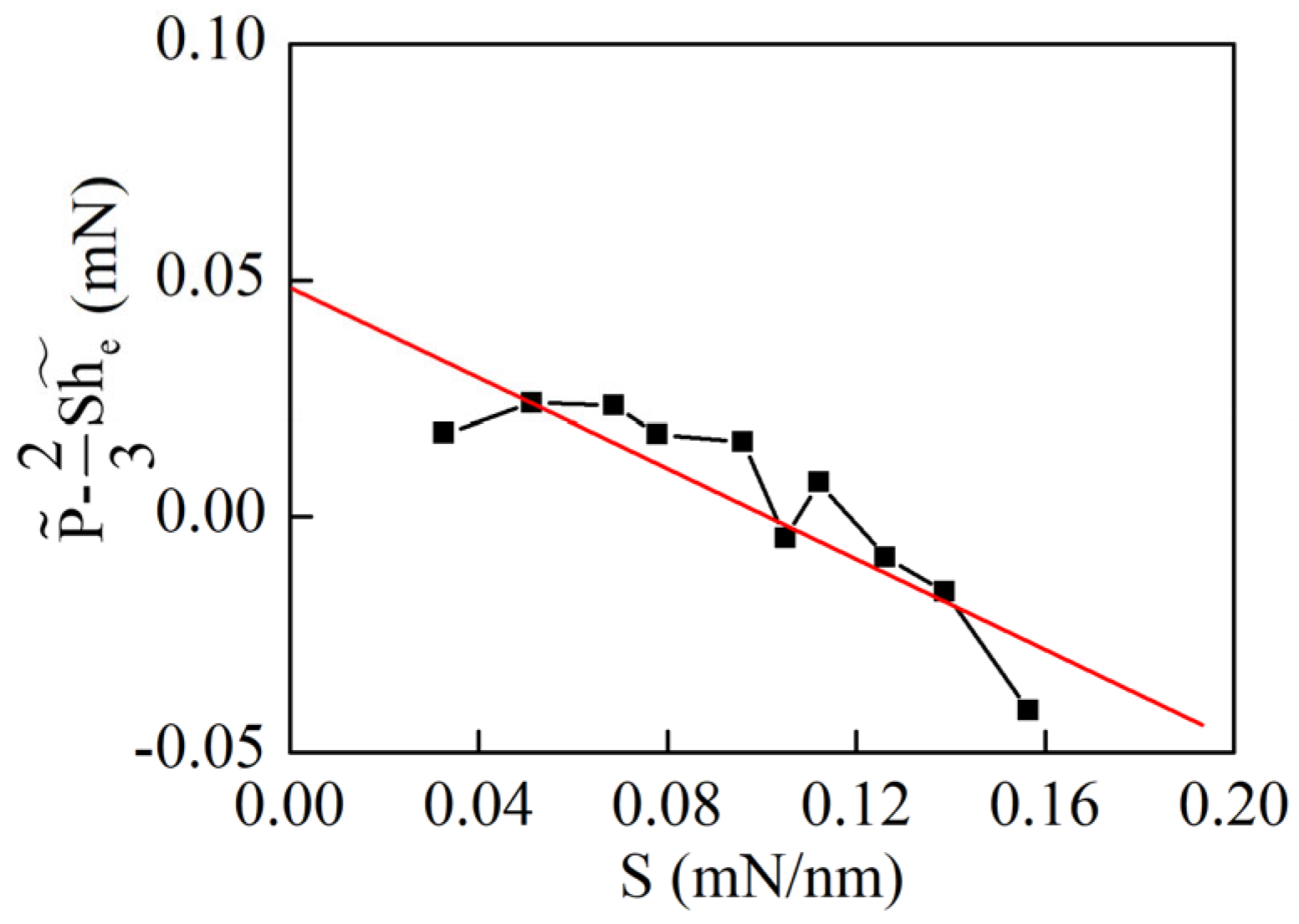
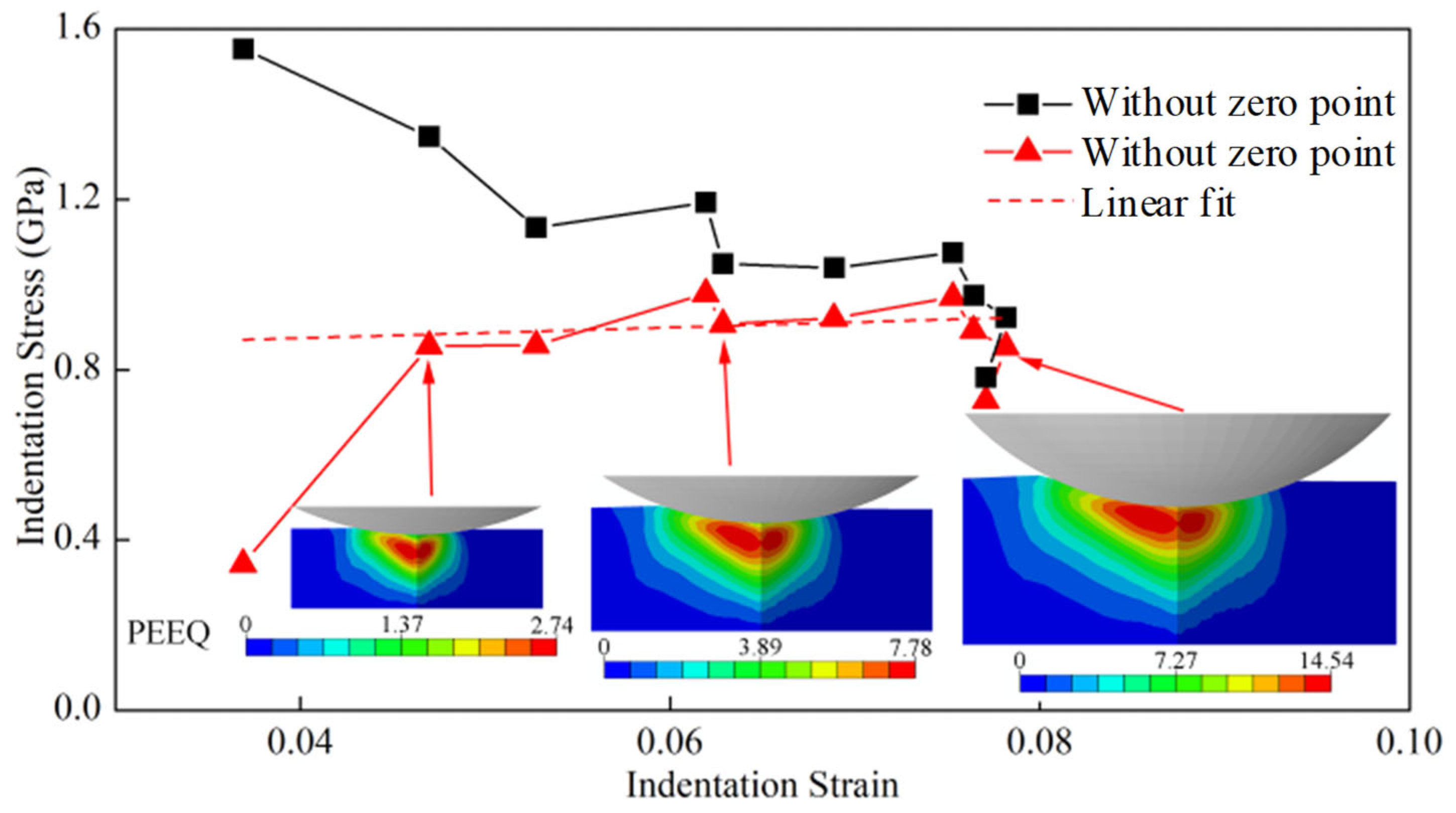
4.4. Indentation Stress–Strain Curve
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Stelmashenko, N.A.; Walls, M.G.; Brown, L.M.; Milma, Y.V. Microindentations on W and Mo oriented single crystals: An STM study. Acta Metall. Mater. 1993, 41, 2855–2865. [Google Scholar] [CrossRef]
- Wang, X.; Li, H.; Chandrashekhara, K.; Rummel, S.; Lekakh, S.; Van Aken, D.; O’mAlley, R. Inverse finite element modeling of the barreling effect on experimental stress-strain curve for high temperature steel compression test. J. Mater. Process. Technol. 2017, 243, 465–473. [Google Scholar] [CrossRef]
- Paramatmuni, C.; Kanjarla, A.K. A crystal plasticity FFT based study of deformation twinning, anisotropy and micromechanics in HCP materials: Application to AZ31 alloy. Int. J. Plast. 2019, 113, 269–290. [Google Scholar] [CrossRef]
- Lyu, H.; Hamid, M.; Ruimi, A.; Zbib, H.M. Stress/strain gradient plasticity model for size effects in heterogeneous nano-microstructures. Int. J. Plast. 2017, 97, 46–63. [Google Scholar] [CrossRef]
- Delaire, F.; Raphanel, J.L.; Rey, C. Plastic heterogeneities of a copper multicrystal deformed in uniaxial tension: Experimental study and finite element simulations. Acta Mater. 2000, 48, 1075–1087. [Google Scholar] [CrossRef]
- Wang, H.; Clausen, B.; Tomé, C.; Wu, P. Studying the effect of stress relaxation and creep on lattice strain evolution of stainless steel under tension. Acta Mater. 2013, 61, 1179–1188. [Google Scholar] [CrossRef]
- Wei, P.; Lu, C.; Tieu, K.; Su, L.; Deng, G.; Huang, W. A study on the texture evolution mechanism of nickel single crystal deformed by high pressure torsion. Mater. Sci. Eng. A 2017, 684, 239–248. [Google Scholar] [CrossRef]
- Kumar, M.A.; Mahesh, S. Subdivision and microtexture development in fcc grains during plane strain compression. Int. J. Plast. 2013, 44, 95–110. [Google Scholar] [CrossRef]
- Li, L.; Shen, L.; Proust, G.; Moy, C.K.; Ranzi, G. Three-dimensional crystal plasticity finite element simulation of nanoindentation on aluminium alloy 2024. Mater. Sci. Eng. A 2013, 579, 41–49. [Google Scholar] [CrossRef]
- Li, D.; Nielsen, M.H.; Lee, J.R.I.; Frandsen, C.; Banfield, J.F.; De Yoreo, J.J. Direction-specific interactions control crystal growth by oriented attachment. Science 2012, 336, 1014–1018. [Google Scholar] [CrossRef] [PubMed]
- Tian, M.; Wang, J.; Kurtz, J.; Mallouk, T.E.; Chan, M.H.W. Electrochemical growth of single-crystal metal nanowires via a two-dimensional nucleation and growth mechanism. Nano Lett. 2003, 3, 919–923. [Google Scholar] [CrossRef] [PubMed]
- Romano-Rodríguez, A.; Hernández-Ramírez, F. Dual-beam focused ion beam (FIB): A prototyping tool for micro and nanofabrication. Microelectron. Eng. 2007, 84, 789–792. [Google Scholar] [CrossRef]
- Shim, S.; Bei, H.; Miller, M.; Pharr, G.; George, E. Effects of focused ion beam milling on the compressive behavior of directionally solidified micropillars and the nanoindentation response of an electropolished surface. Acta Mater. 2009, 57, 503–510. [Google Scholar] [CrossRef]
- Doerner, M.F.; Nix, W.D. A method for interpreting the data from depth-sensing indentation instruments. J. Mater. Res. 1986, 1, 601–609. [Google Scholar] [CrossRef]
- Oliver, W.C.; Pharr, G.M. Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 2004, 19, 3–20. [Google Scholar] [CrossRef]
- Tabor, D. The Hardness of Metals; Clarendon Press: Oxford, UK, 1951. [Google Scholar]
- Bouzakis, K.-D.; Michailidis, N.; Hadjiyiannis, S.; Skordaris, G.; Erkens, G. The effect of specimen roughness and indenter tip geometry on the determination accuracy of thin hard coatings stress–strain laws by nanoindentation. Mater. Charact. 2002, 49, 149–156. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Pathak, S. Determination of the effective zero-point and the extraction of spherical nanoindentation stress–strain curves. Acta Mater. 2008, 56, 3523–3532. [Google Scholar] [CrossRef]
- Pathak, S.; Kalidindi, S.R. Spherical nanoindentation stress–strain curves. Mater. Sci. Eng. R Rep. 2015, 91, 1–36. [Google Scholar] [CrossRef]
- Hertz, H.; Jones, D.E.; Schott, G.A. Miscellaneous Papers; Macmillan and Company: New York, NY, USA, 1896. [Google Scholar]
- Johnson, K.L. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Hill, R.; Rice, J.R. Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 1972, 20, 401–413. [Google Scholar] [CrossRef]
- Rice, J.R. Inelastic constitutive relations for solids: An internal-variable theory and its application to metal plasticity. J. Mech. Phys. Solids 1971, 19, 433–455. [Google Scholar] [CrossRef]
- Pan, J.; Rice, J.R. Rate sensitivity of plastic flow and implications for yield-surface vertices. Int. J. Solids Struct. 1983, 19, 973–987. [Google Scholar] [CrossRef]
- Bassani, J.L.; Wu, T.Y. Latent hardening in single crystals. II. Analytical characterization and predictions. Proc. R. Soc. A 1991, 435, 21–41. [Google Scholar]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, J.; Hassan, H.U.; Zhang, J.; Yan, Y.; Hartmaier, A.; Sun, T. Coupled effect of crystallographic orientation and indenter geometry on nanoindentation of single crystalline copper. Int. J. Mech. Sci. 2018, 148, 531–539. [Google Scholar] [CrossRef]
- Eidel, B. Crystal plasticity finite-element analysis versus experimental results of pyramidal indentation into (001) fcc single crystal. Acta Mater. 2011, 59, 1761–1771. [Google Scholar] [CrossRef]
- Kucharski, S.; Maj, M.; Ryś, M.; Petryk, H. Size effects in spherical indentation of single crystal copper. Int. J. Mech. Sci. 2024, 272, 109138. [Google Scholar] [CrossRef]
- Paliwal, D.; Basantia, S.K.; Yadava, M.; Gurao, N.P. A finite element method and fast Fourier transform based crystal plasticity simulations study on the evolution of microstructure and mechanical properties of gradient structure copper. Mater. Sci. Eng. A 2025, 919, 147472. [Google Scholar] [CrossRef]
- Kucharski, S.; Jarząbek, D. Depth dependence of nanoindentation pile-up patterns in copper single crystals. Metall. Mater. Trans. A 2014, 45, 4997–5008. [Google Scholar] [CrossRef]
- Yao, W.Z.; You, J.H. Berkovich nanoindentation study of monocrystalline tungsten: A crystal plasticity study of surface pile-up deformation. Philos. Mag. 2017, 97, 1418–1435. [Google Scholar] [CrossRef]
- Liu, M.; Lu, C.; Tieu, K.A.; Peng, C.-T.; Kong, C. A combined experimental-numerical approach for determining mechanical properties of aluminum subjects to nanoindentation. Sci. Rep. 2015, 5, 15072. [Google Scholar] [CrossRef] [PubMed]
- Leitner, A.; Maier-Kiener, V.; Kiener, D. Essential refinements of spherical nanoindentation protocols for the reliable determination of mechanical flow curves. Mater. Des. 2018, 146, 69–80. [Google Scholar] [CrossRef]


| Parameter | Lattice Structure | Density (gm/cc) | Hardness (GPa) | Young’s Modulus (GPa) |
|---|---|---|---|---|
| value | FCC | 8.33 | 1.33 | 125.6 |
| Parameter | C11 | C12 | C44 | Nslip | m | n | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| value | 168.4 d3 | 121.4 d3 | 75.4 d3 | 12 | 13 | 1 × 10−9 | 110 | 32 | 100 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, H.; Wang, Z.; Qu, S.; Shan, W.; Tan, R. Crystal Plasticity Finite Element Analysis of Spherical Nanoindentation Stress–Strain Curve of Single-Crystal Copper. Crystals 2025, 15, 561. https://doi.org/10.3390/cryst15060561
Xia H, Wang Z, Qu S, Shan W, Tan R. Crystal Plasticity Finite Element Analysis of Spherical Nanoindentation Stress–Strain Curve of Single-Crystal Copper. Crystals. 2025; 15(6):561. https://doi.org/10.3390/cryst15060561
Chicago/Turabian StyleXia, Haoming, Zhanfeng Wang, Shichao Qu, Weijie Shan, and Rongkai Tan. 2025. "Crystal Plasticity Finite Element Analysis of Spherical Nanoindentation Stress–Strain Curve of Single-Crystal Copper" Crystals 15, no. 6: 561. https://doi.org/10.3390/cryst15060561
APA StyleXia, H., Wang, Z., Qu, S., Shan, W., & Tan, R. (2025). Crystal Plasticity Finite Element Analysis of Spherical Nanoindentation Stress–Strain Curve of Single-Crystal Copper. Crystals, 15(6), 561. https://doi.org/10.3390/cryst15060561





