Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation
Abstract
:1. Introduction
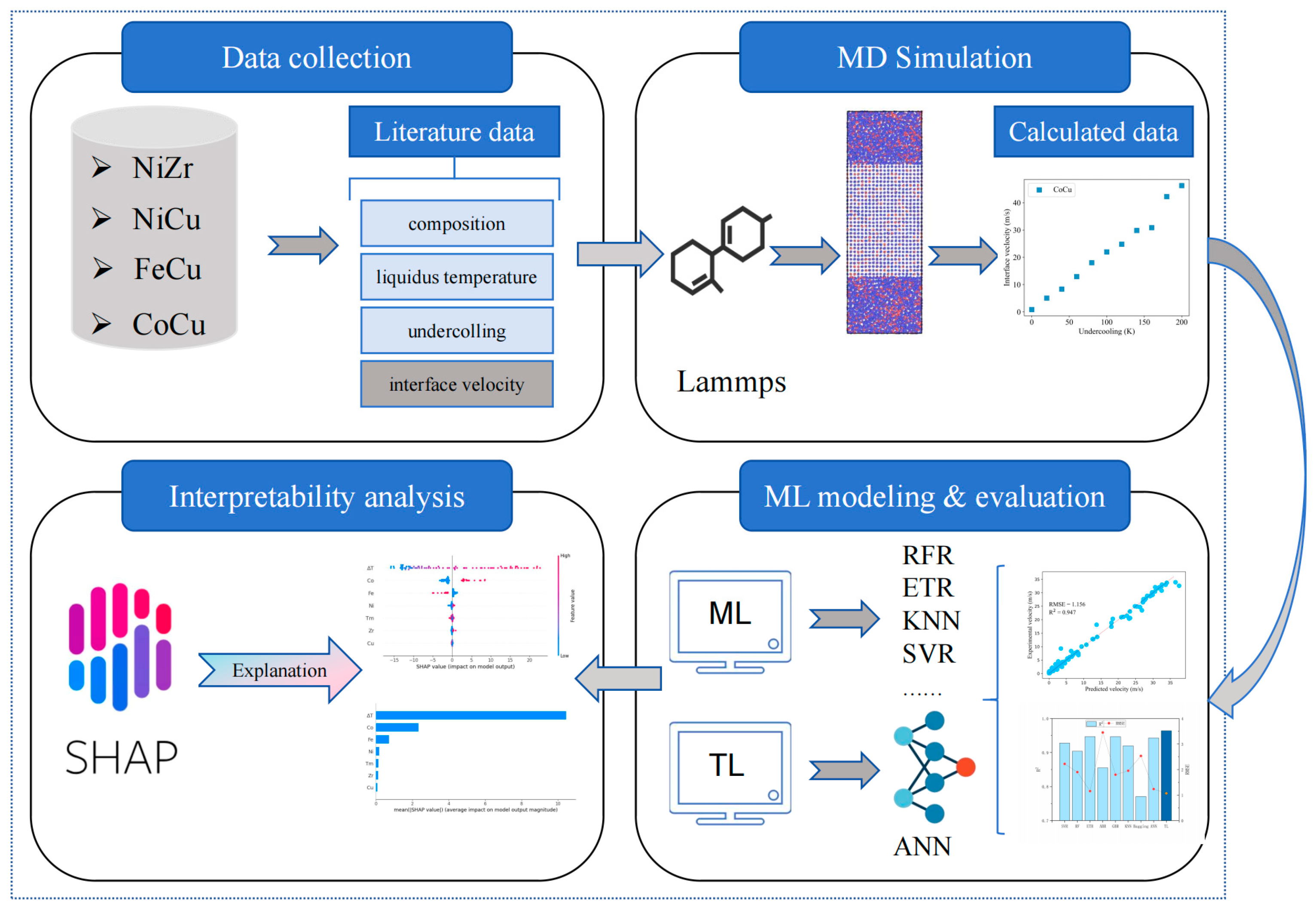
2. Materials and Methods
2.1. Dataset Briefing
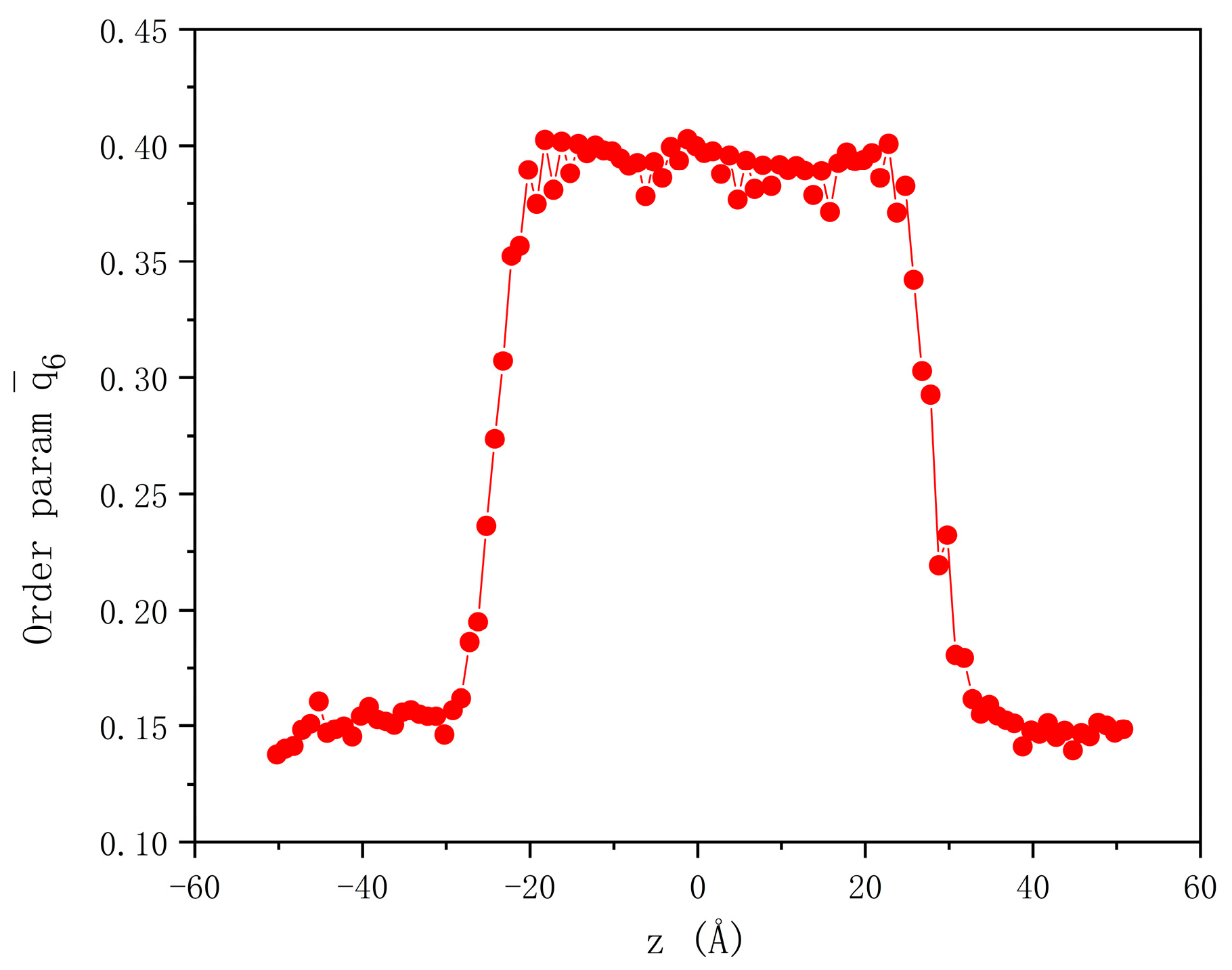
2.2. MD Simulation
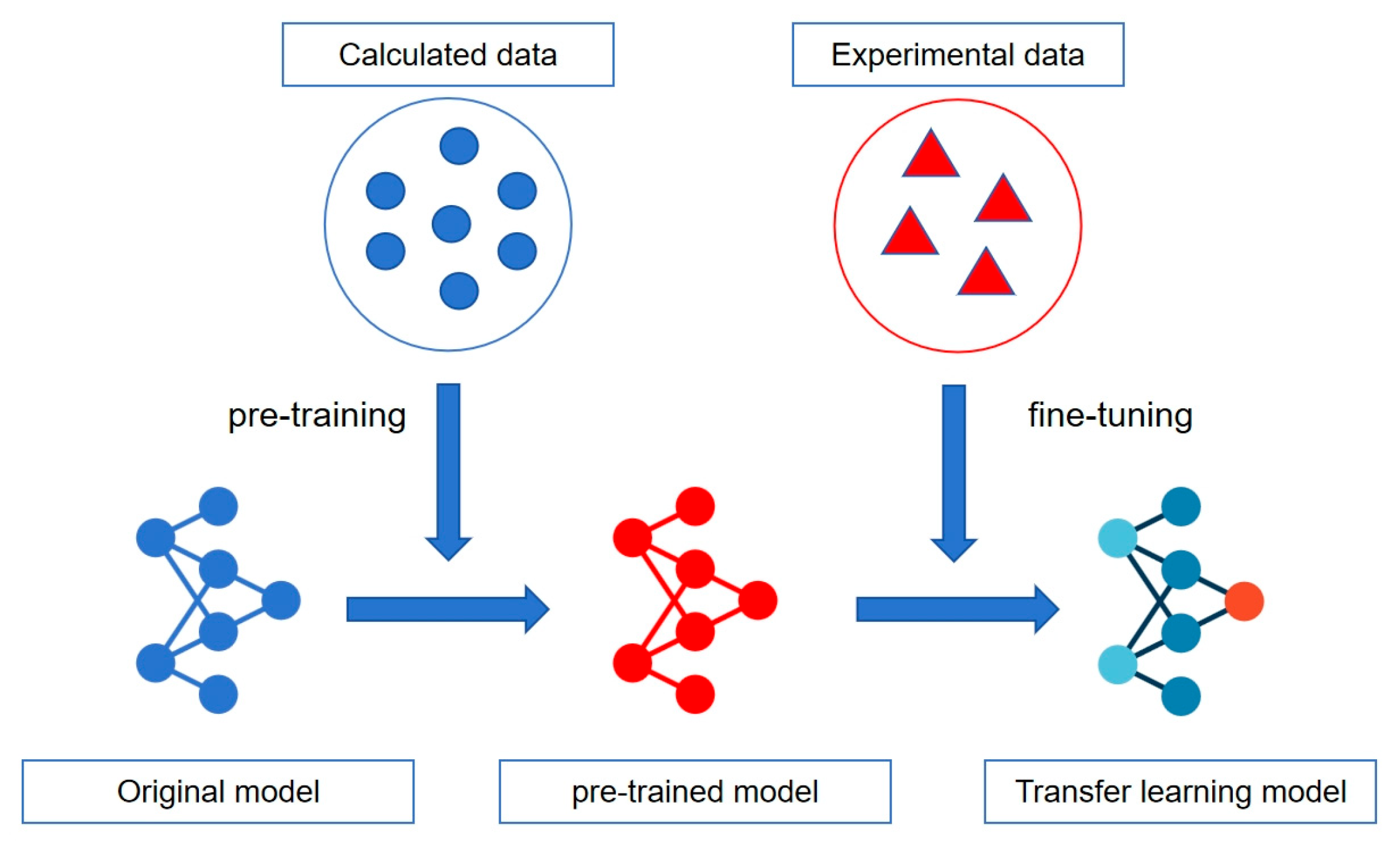
2.3. Transfer Learning Strategy
3. Results and Discussion
3.1. Interface Velocity Calculation by MD
3.2. Interpolation Ability
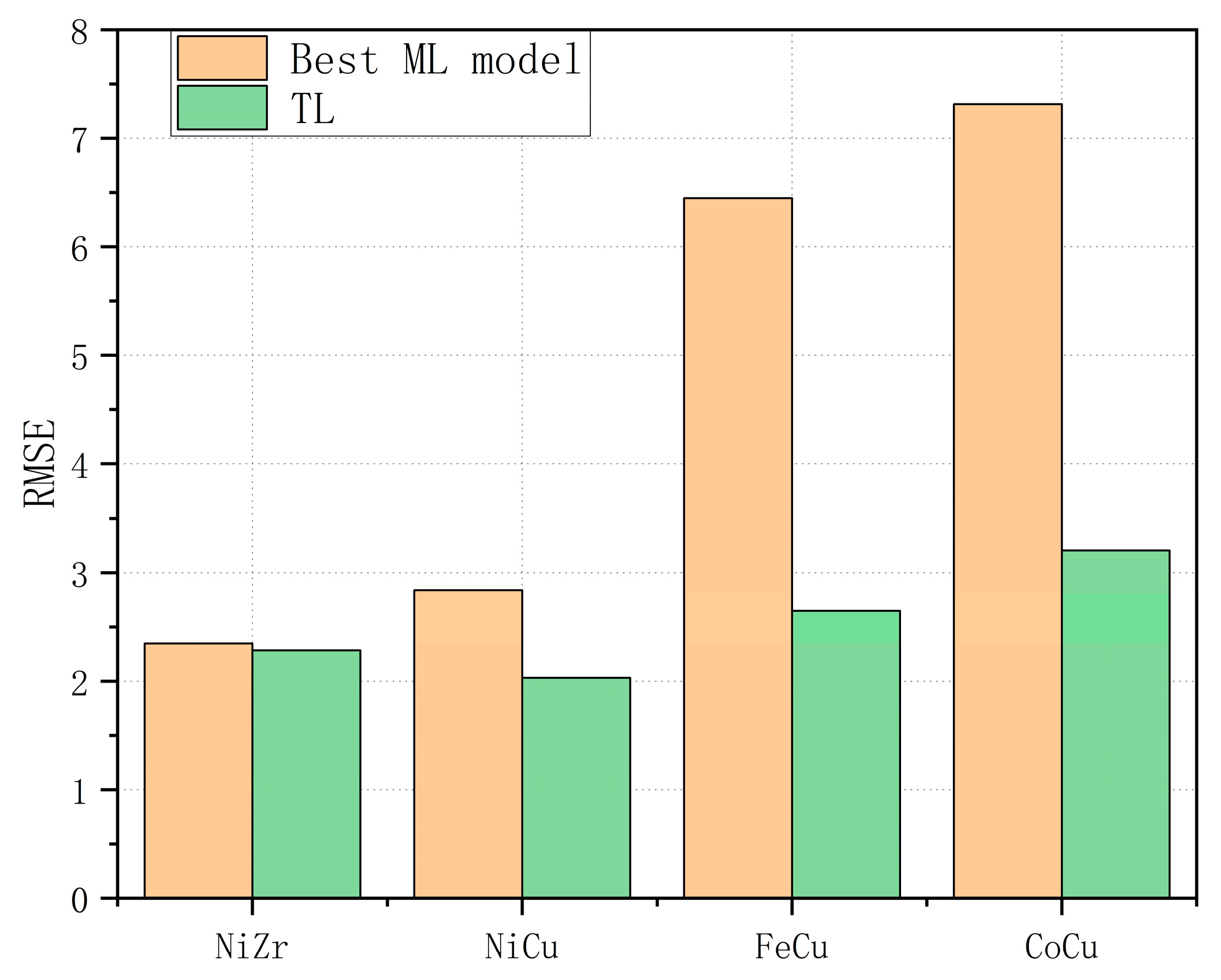
3.3. Extrapolation Ability
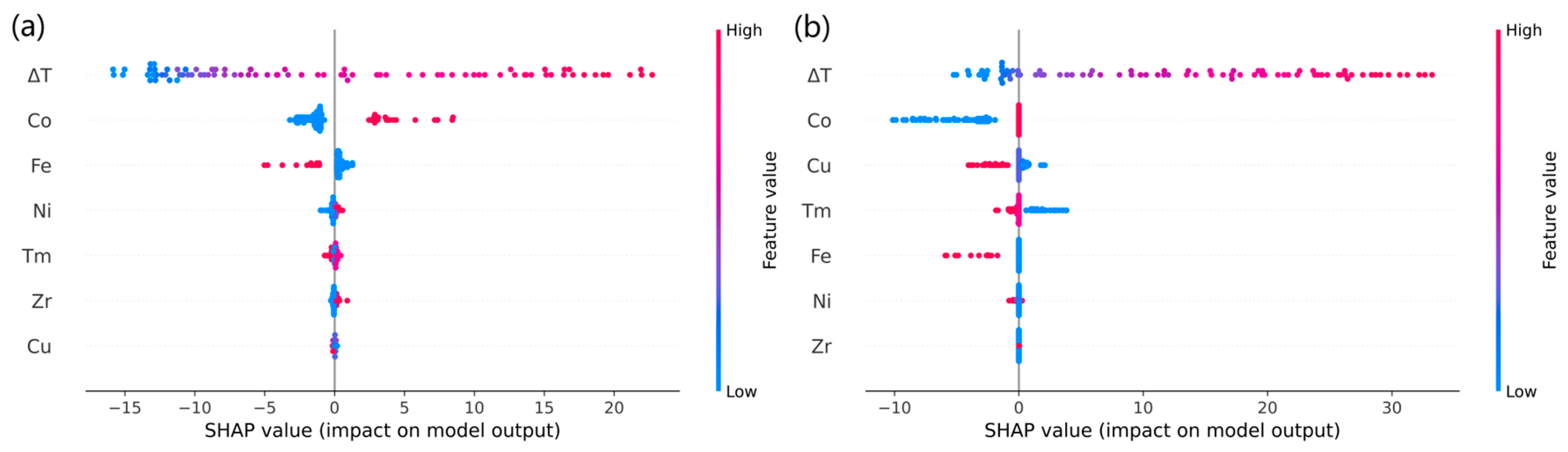
3.4. Interpretability Analysis
4. Conclusions
- The solidification process of the four alloy systems was simulated via MD, and the corresponding interface velocity results demonstrated a similar trend to the collected experimental data.
- For both interpolation and extrapolation, the TL model, which is driven by both physical information and experimental data, demonstrates superior performance compared to the ML models, which rely solely on experimental data. Especially for the extrapolation prediction of an alloy system, its constituent elements are not fully included in the experimental data used to train the ML models.
- Interpretability analysis revealed the importance ranking of features and demonstrated the way in which features affect the model prediction. By comparing the interpretability analyses of the ML models only driven by experimental data and the TL model, it is concluded that the data calculated by MD improve the way features work in the TL model by introducing physical information indirectly.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kurz, W.; Rappaz, M.; Trivedi, R. Progress in modelling solidification microstructures in metals and alloys. Part II: Dendrites from 2001 to 2018. Int. Mater. Rev. 2021, 66, 30–76. [Google Scholar] [CrossRef]
- Alexandrov, D.V.; Galenko, P.K. A review on the theory of stable dendritic growth. Phil. Trans. A 2021, 379, 20200325. [Google Scholar] [CrossRef] [PubMed]
- Alexandrov, D.V.; Galenko, P.K. The Mullins–Sekerka theory: 60 years of morphological stability. J. Appl. Phys. 2024, 136, 055103. [Google Scholar] [CrossRef]
- Mullins, W.W.; Sekerka, R.F. Stability of a planar interface during solidification of a dilute binary alloy. J. Appl. Phys. 1964, 35, 444–451. [Google Scholar] [CrossRef]
- Galenko, P.K.; Phanikumar, G.; Funke, O.; Chernova, L.; Reutzel, S.; Kolbe, M.; Herlach, D.M. Dendritic solidification and fragmentation in undercooled Ni–Zr alloys. Mater. Sci. Eng. 2007, 449, 649–653. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M. Atomistic computation of liquid diffusivity, solid-liquid interfacial free energy, and kinetic coefficient in Au and Ag. Phys. Rev. B 2002, 65, 214106. [Google Scholar] [CrossRef]
- Sun, D.Y.; Asta, M.; Hoyt, J.J. Kinetic coefficient of Ni solid-liquid interfaces from molecular-dynamics simulations. Phys. Rev. B 2004, 69, 024108. [Google Scholar] [CrossRef]
- Sun, D.Y.; Asta, M.; Hoyt, J.J. Crystal-melt interfacial free energies and mobilities in fcc and bcc Fe. Phys. Rev. B 2004, 69, 174103. [Google Scholar] [CrossRef]
- Hoyt, J.J.; Asta, M.; Sun, D.Y. Molecular dynamics simulations of the crystal–melt interfacial free energy and mobility in Mo and V. Philos. Mag. 2006, 86, 3651–3664. [Google Scholar] [CrossRef]
- Ashkenazy, Y.; Averback, R.S. Atomic mechanisms controlling crystallization behaviour in metals at deep undercoolings. Europhys. Lett. 2007, 79, 26005. [Google Scholar] [CrossRef]
- Xia, Z.G.; Sun, D.Y.; Asta, M.; Hoyt, J.J. Molecular dynamics calculations of the crystal-melt interfacial mobility for hexagonal close-packed Mg. Phys. Rev. B—Condens. Matter Mater. Phys. 2007, 75, 012103. [Google Scholar] [CrossRef]
- Ashkenazy, Y.; Averback, R.S. Kinetic stages in the crystallization of deeply undercooled body-centered-cubic and face-centered-cubic metals. Acta Mater. 2010, 58, 524–530. [Google Scholar] [CrossRef]
- Fang, T.; Wang, L.; Qi, Y. Molecular dynamics simulation of crystal growth of undercooled liquid Co. Phys. B Condens. Matter. 2013, 423, 6–9. [Google Scholar] [CrossRef]
- Sun, G.; Xu, J.; Harrowell, P. The mechanism of the ultrafast crystal growth of pure metals from their melts. Nat. Mater. 2018, 17, 881–886. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Y.; Wang, H.; Li, M. Crystal–melt interface kinetic behaviors of iron. AIP Adv. 2021, 11, 035241. [Google Scholar] [CrossRef]
- Hu, G.; Wu, L.; Ren, Z.; Shi, J.; Li, Y.; Xu, B.; Luo, C. olecular dynamic calculation of solidification kinetic coefficient of metallic γ metallic uranium. J. Nucl. Mater. 2022, 559, 153369. [Google Scholar] [CrossRef]
- Zhao, Y. Understanding and design of metallic alloys guided by phase-field simulations. npj Comput. Mater. 2023, 9, 94. [Google Scholar] [CrossRef]
- Reuther, K.; Rettenmayr, M. Perspectives for cellular automata for the simulation of dendritic solidification–A review. Comput. Mater. Sci. 2014, 95, 213–220. [Google Scholar] [CrossRef]
- Pal, P.; Abhishek, G.S.; Karagadde, S. A Monte Carlo approach to simulate dendritic microstructures during binary alloy solidification. Modell. Simul. Mater. Sci. Eng. 2020, 28, 085001. [Google Scholar] [CrossRef]
- Chan, W.L.; Averback, R.S.; Cahill, D.G.; Ashkenazy, Y. Solidification velocities in deeply undercooled silver. Phys. Rev. Lett. 2009, 102, 095701. [Google Scholar] [CrossRef]
- Mendelev, M.I.; Rahman, M.J.; Hoyt, J.J.; Asta, M. Molecular-dynamics study of solid–liquid interface migration in fcc metals. Modell. Simul. Mater. Sci. Eng. 2010, 18, 074002. [Google Scholar] [CrossRef]
- Ramakrishnan, R.; Phanikumar, G.; Sankarasubramanian, R. Crystal–Melt Interface Growth Velocity of Ni–Zr Alloys Through Molecular Dynamics Simulations. Trans. Ind. Inst. Met. 2015, 68, 1113–1117. [Google Scholar] [CrossRef]
- Kavousi, S.; Novak, B.R.; Zaeem, M.A.; Moldovan, D. Combined molecular dynamics and phase field simulation investigations of crystal-melt interfacial properties and dendritic solidification of highly undercooled titanium. Comp. Mater. Sci. 2019, 163, 218–229. [Google Scholar] [CrossRef]
- Rozas, R.E.; Orrego, J.L.; Toledo, P.G. Interfacial properties and crystal growth of Ni and Ni50Al50 from molecular dynamics simulations. J. Appl. Phys. 2023, 133, 214701. [Google Scholar] [CrossRef]
- Cui, D.; Zhang, J.; Li, X.; Liang, Z.; Zhang, X.; Yang, Y.; Wang, H. Atomistic insights into sluggish crystal growth in an undercooled CoNiCrFe multi-principal element alloy. J. Alloys Compd. 2023, 941, 168881. [Google Scholar] [CrossRef]
- Han, X.J.; Chen, M.; Guo, Z.Y. A molecular dynamics study for the thermophysical properties of liquid Ti–Al alloys. Int. J. Thermophys. 2005, 26, 869–880. [Google Scholar] [CrossRef]
- Wang, X.L.; Dong, Y.; Mohr, M.; Fecht, H.J.; Wang, X.D.; Cao, Q.P.; Zhang, D.X.; Dai, Z.W.; Jiang, J.Z. Correlation between viscosity and local atomic structure in liquid Zr56Co28Al16 alloy. Microgravity Sci. Technol. 2022, 34, 10. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. Apl Mater. 2016, 4, 053208. [Google Scholar] [CrossRef]
- Johnston, D.C. The puzzle of high temperature superconductivity in layered iron pnictides and chalcogenides. Adv. Phys. 2010, 59, 803–1061. [Google Scholar] [CrossRef]
- Saal, J.E.; Kirklin, S.; Aykol, M.; Meredig, B.; Wolverton, C. Materials design and discovery with high-throughput density functional theory: The open quantum materials database (OQMD). JOM 2013, 65, 1501–1509. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Liu, D.; Zou, R.; Yang, Z. Hardness prediction of high entropy alloys with machine learning and material descriptors selection by improved genetic algorithm. Comp. Mater. Sci. 2022, 205, 111185. [Google Scholar] [CrossRef]
- Yang, Z.; Li, S.; Li, S.; Yang, J.; Liu, D. A two-step data augmentation method based on generative adversarial network for hardness prediction of high entropy alloy. Comp. Mater. Sci. 2023, 220, 112064. [Google Scholar] [CrossRef]
- Li, S.; Li, S.; Liu, D.; Yang, J.; Zhang, M. Hardness prediction of high entropy alloys with periodic table representation of composition, processing, structure and physical parameters. J. Alloys Compd. 2023, 967, 171735. [Google Scholar] [CrossRef]
- Li, J.; Xie, B.; Fang, Q.; Liu, B.; Liu, Y.; Liaw, P.K. High-throughput simulation combined machine learning search for optimum elemental composition in medium entropy alloy. J. Mater. Sci. Technol. 2021, 68, 70–75. [Google Scholar] [CrossRef]
- Huang, W.; Martin, P.; Zhuang, H.L. Machine-learning phase prediction of high-entropy alloys. Acta Mater. 2019, 169, 225–236. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Li, S.; Chen, M. Prediction, interpretation and extrapolation for shear modulus and bulk modulus of solid-state electrolytes based on machine learning. Mater. Today Commun. 2024, 38, 108294. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Li, S.; Li, S.; Chen, M. Interpretable Machine Learning Prediction of Voltage and Specific Capacity for Electrode Materials. Adv. Theory Simul. 2024, 7, 2400227. [Google Scholar] [CrossRef]
- Goud, V.S.; Rahul, M.R.; Phanikumar, G. Prediction of growth velocity of undercooled multicomponent metallic alloys using a machine learning approach. Scr. Mater. 2022, 207, 114309. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Liu, F. Modeling for free dendrite growth based on physically-informed machine learning method. Scr. Mater. 2024, 242, 115918. [Google Scholar] [CrossRef]
- Galenko, P.K.; Danilov, D.A. Local nonequilibrium effect on rapid dendritic growth in a binary alloy melt. Phys. Lett. A 1977, 235, 271–280. [Google Scholar] [CrossRef]
- Galenko, P.K.; Danilov, D.A. Model for free dendritic alloy growth under interfacial and bulk phase nonequilibrium conditions. J. Cryst. Growth 1999, 197, 992–1002. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, Z.; Hu, H.; He, X.; Fu, H.; Xie, J. A rapid and effective method for alloy materials design via sample data transfer machine learning. npj Comput. Mater. 2023, 9, 26. [Google Scholar] [CrossRef]
- Zhou, C.; Yuan, R.; Su, B.; Fan, J.; Tang, B.; Zhang, P.; Li, J. Creep rupture life prediction of high-temperature titanium alloy using cross-material transfer learning. J. Mater. Sci. Technol. 2024, 178, 39–47. [Google Scholar] [CrossRef]
- Galenko, P.K.; Kolbe, M.; Herlach, D.M.; Rettenmayr, M. Kinetics of dendrite growth and dendritic fragmentation in theundercooled Co81. 2Cu18. 8 alloy’smelt. Metall. Res. Technol. 2014, 111, 295–303. [Google Scholar] [CrossRef]
- Galenko, P.K.; Reutzel, S.; Herlach, D.M.; Danilov, D.; Nestler, B. Modelling of dendritic solidification in undercooled dilute Ni–Zr melts. Acta Mater. 2007, 55, 6834–6842. [Google Scholar] [CrossRef]
- Herlach, D.M. Non-equilibrium solidification of undercooled metallic metls. Mater. Sci. Eng. R Rep. 1994, 12, 177–272. [Google Scholar] [CrossRef]
- Xia, Z.C.; Wang, W.L.; Luo, S.B.; Wei, B. Specific heat capacity and dendritic growth kinetics of liquid peritectic Fe-Cu alloys. Chem. Phys. Lett. 2016, 658, 220–223. [Google Scholar] [CrossRef]
- Rahul, M.R.; Samal, S.; Phanikumar, G. Metastable microstructures in the solidification of undercooled high entropy alloys. J. Alloys Compd. 2020, 821, 153488. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Wilson, S.R.; Mendelev, M.I. Anisotropy of the solid–liquid interface properties of the Ni–Zr B33 phase from molecular dynamics simulation. Philos. Mag. 2015, 95, 224–241. [Google Scholar] [CrossRef]
- Howells, C.A.; Mishin, Y. Angular-dependent interatomic potential for the binary Ni–Cr system. Modell. Simul. Mater. Sci. Eng. 2018, 26, 085008. [Google Scholar] [CrossRef]
- Lee, B.J.; Wirth, B.D.; Shim, J.H.; Kwon, J.; Kwon, S.C.; Hong, J.H. Modified embedded-atom method interatomic potential for the Fe-Cu alloy system and cascade simulations on pure Fe and Fe-Cu alloys. Phys. Rev. B 2005, 71, 184205. [Google Scholar] [CrossRef]
- Wang, J.; Oh, S.H.; Lee, B.J. Second-nearest-neighbor modified embedded-atom method interatomic potential for Cu-M (M=Co, Mo) binary systems. Comput. Mater. Sci. 2020, 178, 109627. [Google Scholar] [CrossRef]
- Steinhardt, P.J.; Nelson, D.R.; Ronchetti, M. Bond-orientational order in liquids and glasses. Phys. Rev. B 1983, 28, 784. [Google Scholar] [CrossRef]
- Lechner, W.; Dellago, C. Accurate determination of crystal structures based on averaged local bond order parameters. J. Chem. Phys. 2008, 129, 114707. [Google Scholar] [CrossRef]
- Hosna, A.; Merry, E.; Gyalmo, J.; Alom, Z.; Aung, Z.; Azim, M.A. Transfer learning: A friendly introduction. J. Big Data 2022, 9, 102. [Google Scholar] [CrossRef]
- Perez, M. Gibbs–Thomson effects in phase transformations. Scr. Mater. 2005, 52, 709. [Google Scholar] [CrossRef]




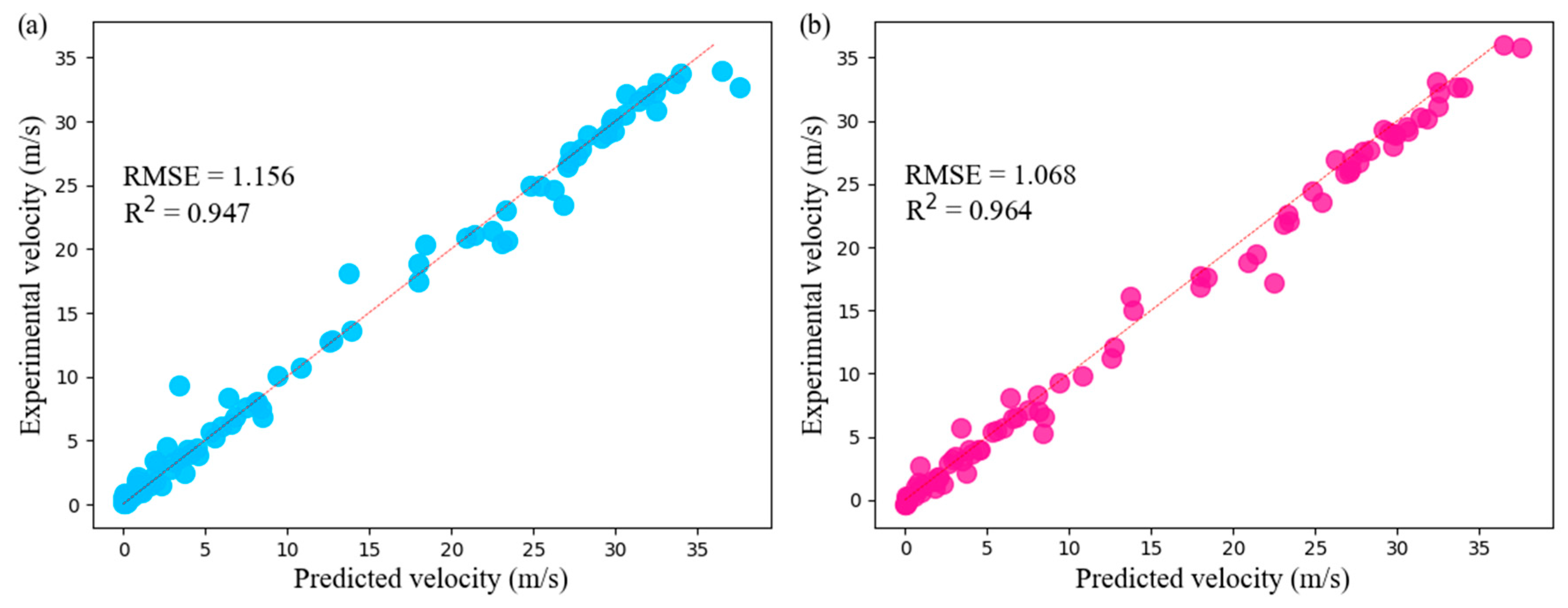

| SVR | RF | ETR | ABR | GBR | KNN | Bagging | ANN | TL | |
|---|---|---|---|---|---|---|---|---|---|
| R2 | 0.928 | 0.904 | 0.947 | 0.855 | 0.947 | 0.920 | 0.771 | 0.943 | 0.964 |
| RMSE | 2.222 | 1.901 | 1.156 | 3.453 | 1.800 | 1.954 | 2.534 | 1.236 | 1.068 |
| NiZr | NiCu | FeCu | CoCu | |
|---|---|---|---|---|
| SVR | 0.508 (7.704) | −2.839 (11.636) | 0.034 (13.224) | 0.598 (7.684) |
| RF | 0.950 (2.448) | 0.801 (5.180) | 0.580 (8.716) | 0.390 (9.467) |
| ETR | 0.907 (3.342) | 0.940 (2.839) | 0.707 (7.285) | 0.566 (7.982) |
| ABR | 0.887 (3.687) | 0.755 (5.758) | 0.658 (7.870) | 0.535 (8.265) |
| GBR | 0.954 (2.349) | 0.851 (4.488) | 0.562 (8.901) | 0.278 (10.297) |
| KNN | 0.418 (8.378) | 0.519 (8.065) | 0.770 (6.447) | 0.628 (7.391) |
| Bagging | 0.919 (3.115) | 0.793 (5.290) | 0.562 (8.901) | 0.508 (8.501) |
| ANN | 0.938 (2.716) | 0.879 (4.036) | 0.623 (8.257) | 0.635 (7.315) |
| TL | 0.956 (2.286) | 0.969 (2.032) | 0.961 (2.649) | 0.930 (3.205) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Zhang, M.; Li, S.; Li, S. Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation. Crystals 2025, 15, 484. https://doi.org/10.3390/cryst15050484
Wei J, Zhang M, Li S, Li S. Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation. Crystals. 2025; 15(5):484. https://doi.org/10.3390/cryst15050484
Chicago/Turabian StyleWei, Jia, Mingyu Zhang, Shuai Li, and Shu Li. 2025. "Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation" Crystals 15, no. 5: 484. https://doi.org/10.3390/cryst15050484
APA StyleWei, J., Zhang, M., Li, S., & Li, S. (2025). Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation. Crystals, 15(5), 484. https://doi.org/10.3390/cryst15050484







