Next Article in Journal
Growth and Characterization of High Doping Concentration (2.1 at%) Ytterbium (Yb) Doped Lithium Niobate (LiNbO3) Crystal: An Electrically Tunable Lasing Medium
Previous Article in Journal
Prediction of Dendrite Growth Velocity in Undercooled Binary Alloys Based on Transfer Learning and Molecular Dynamics Simulation
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Crystals
Volume 15
Issue 5
10.3390/cryst15050485
crystals-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dilute Paramagnetism and Non-Trivial Topology in Quasicrystal Approximant Fe4Al13

by
Keenan E. Avers
1,†,
Jarryd A. Horn
1,†,
Ram Kumar
1,
Shanta R. Saha
1,
Peter Zavalij
2,
Yuanfeng Xu
3,4,
Bogdan Andrei Bernevig
3 and
Johnpierre Paglione
1,5,*
1
Maryland Quantum Materials Center and Department of Physics, University of Maryland, College Park, MD 20742, USA
2
Department of Chemistry, University of Maryland, College Park, MD 20742, USA
3
Department of Physics, Princeton University, Princeton, NJ 08544, USA
4
Center for Correlated Matter and School of Physics, Zhejiang University, Hangzhou 310058, China
5
Canadian Institute for Advanced Research, Toronto, ON M5G 1Z8, Canada
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Crystals 2025, 15(5), 485; https://doi.org/10.3390/cryst15050485
Submission received: 25 April 2025 / Revised: 15 May 2025 / Accepted: 17 May 2025 / Published: 21 May 2025
(This article belongs to the Section Crystalline Metals and Alloys)
Browse Figures
Versions Notes

Abstract

:
A very fundamental property of both weakly and strongly interacting materials is the nature of their magnetic response. In this work, we detail the growth of crystals of the quasicrystal approximant Fe4Al13 with an Al flux solvent method. We characterize our samples using electrical transport and heat capacity, yielding results consistent with a simple non-magnetic metal. However, magnetization measurements portray an extremely unusual response for a dilute paramagnet and do not exhibit the characteristic Curie behavior expected for a weakly interacting material at high temperature. Electronic structure calculations confirm metallic behavior but also indicate that each isolated band near the Fermi energy hosts non-trivial topologies, including strong, weak, and nodal components, with resultant topological surface states distinguishable from bulk states on the (001) surface. With half-filled flat bands apparent in the calculation, but an absence of long-range magnetic order, the unusual quasi-paramagnetic response suggests the dilute paramagnetic behavior in this quasicrystal approximant is surprising and may serve as a test of the fundamental assumptions that are taken for granted for the magnetic response of weakly interacting systems.

1. Introduction

The magnetic response of a material is among one of the most fundamental properties used to understand the physics of a many-body system. Many strongly interacting materials have exotic magnetic states and behaviors at low temperatures, such as frustrated antiferromagnetism in triangular lattices [1,2,3,4,5], quantum criticality in heavy Fermion systems [6,7,8,9,10], and Skrymions in broken inversion symmetric lattices [11,12,13,14]. In contrast, especially for weakly correlated/interacting systems at sufficiently high temperatures, all of these systems should end up as a paramagnet and obey the Curie law [15].
In this work, we draw attention to our crystals of Al flux-grown Fe4Al13 and its characterization as an example of a weakly interacting system. The material exhibits very simple electrical transport consistent with a non-magnetic metal and heat capacity contributions of only conduction electrons and lattice phonons, with no indication of any electronic or structural phase transitions. The material does, however, have a complicated monoclinic crystal structure with a large unit cell that hosts off-stoichiometric paramagnetic Fe impurities. Although the Curie law should be valid for such a dilute paramagnet, to our surprise, the magnetic response of the material exhibits a complicated temperature and field dependence. Our results conflict with the basic assumptions of a weakly interacting dilute paramagnet.
As Fe and Al are extremely common and inexpensive elements, it is no surprise that Fe-Al binaries have been extensively investigated [16,17,18,19,20,21,22]. It is important to note that Fe4Al13 borders on the formation of a quasicrystal [23]: a crystal lattice with a nominally forbidden long-range arrangement of atoms that exhibits no discrete translational symmetries and lacking an underlying unique unit cell [24]. However, quasicrsytals still maintain a global sense of discrete rotational symmetries [25,26] in contrast to fully disordered glassy solids [27]. A fundamental assumption in condensed matter physics is the notion that a material exhibits rotational and translational symmetries of a crystalline structure. These, in turn, allow a symmetry-based starting point for understanding electrical and magnetic properties from a microscopic level [28]. It is an open question as to what electronic and magnetic [29,30,31] physics are permissible when such fundamental assumptions are relaxed. While the Fe4Al13 crystal structure is the subject of interest for the aforementioned reasons, here, we focus on unreported properties of Fe4Al13 as a result of using this system for a simple demonstration of flux crystal growth [32,33].

2. Materials and Methods

Crystals of Fe4Al13 were grown as part of a practical training session for the University of Maryland’s 2024 Fundamentals of Quantum Materials Winter School (FQM2024), with basic yields and the systematic approach shown in Figure 1. The synthesis of this Fe-Al compound was carried out using an Al “self-flux technique”, which allows crystals to nucleate in an excess of solvent composed of intrinsic elements in the flux (in this case, Al). The Fe4Al13 composition itself was selected for training because of its wide liquidus region and quick crystal growth. This allows a pragmatic hands-on educational introduction to the flux growth technique that demonstrates the ability to vary the relative Fe-Al composition over the liquidus range and still obtain the correct stoichiometric crystal formation. The approach also allows for systematically investigating how the morphology of the yielded crystals may change with the starting Fe:Al ratio. Elemental Fe granules (Thermo Scientific 99.98%, Waltham, MA, USA) and Al shot (Alfa Aesar 99.999%, Haverhill, MA, USA) were loaded into 2 mL alumina crucibles and flame-sealed in quartz ampoules with Ar gas. The ampoules were heated to 1100 °C and held at that temperature for 6 h. The temperature was then decreased to 750 °C over 6 h and held at that temperature until removal from the furnace and centrifugation of the excess Al. Examples of three groups with different trial stoichiometries—labeled 1a, 3a, and 2b—are shown in Figure 1a on a section of the Fe-Al binary alloy phase diagram. The a c -plane of the monoclinic crystal structure is shown in Figure 1b and exemplifies its nature as bordering on the formation of a decagonal quasicrystal. In contrast, the b c -plane view of the unit cell is a bit more regular, consistent with the b-axis being much shorter than the a- and c-axis. Photographs of the resultant Fe4Al13 crystals are shown in Figure 1d–f. Depending on the exact molar ratio of Fe to Al, the crystals changed size and morphology, with one example crystal reaching a length of 7 mm, which exemplifies the simplicity and relative speed of growth of this material that lends itself well to educational and demonstrative purposes. A general trend was observed from this study, where a too dilute Fe to Al molar ratio (Figure 1d) does not allow for a sufficient cooling time below the liquidus curve to yield larger crystals nor decent mass yield, while in contrast, an Fe-rich ratio can result in incomplete dissolution and formation of polycrystalline lumps (Figure 1e).
While the systematic relation between the starting Fe:Al ratio and crystal yield and size is relatively simple to understand, interpreting how the Fe:Al ratio impacts a sample’s electrical and magnetic properties is not straightforward, as regions of the Fe-Al binary phase diagram host many alloys and compounds with wide stoichiometry ranges and degrees of metastability [34]. To this end, additional crystals of Fe4Al13 were grown with Fe:Al ratios of 1:5, 1:10, and 1:20 using a similar recipe as the FQM2024 students, but over a longer time frame; the temperature of 1100 °C was held for 24 h, and the temperature was slowly decreased by 3 °C per hour to 800 °C at which the centrifuging occurred. All further results in this manuscript are from these samples. A similar trend to the size and morphology was observed with the Fe:Al = 1:20 crystals being small needles and Fe:Al = 1:5 yielding larger plates limited only by the size of the crucible.
Electrical transport was measured in a commercial cryostat using a standard 4-wire configuration with electrical contact conducted with Ag paint and Au wires. Magnetization measurements were performed with a commercial SQUID magnetometer using a quartz rod and GE varnish in order to minimize the diamagnetic background. Heat capacity was measured on a commercial cryostat with the two-tau relaxation method. The orientation of the single crystals was determined using Laue X-ray diffraction and powder X-ray diffractometer to identify facet orientations. To further characterize the crystallographic structure, single-crystal X-ray diffraction using Bruker D8Venture w/PhotonIII diffractometer was performed on a sample from the Fe:Al = 1:10 batch at several temperatures (T).

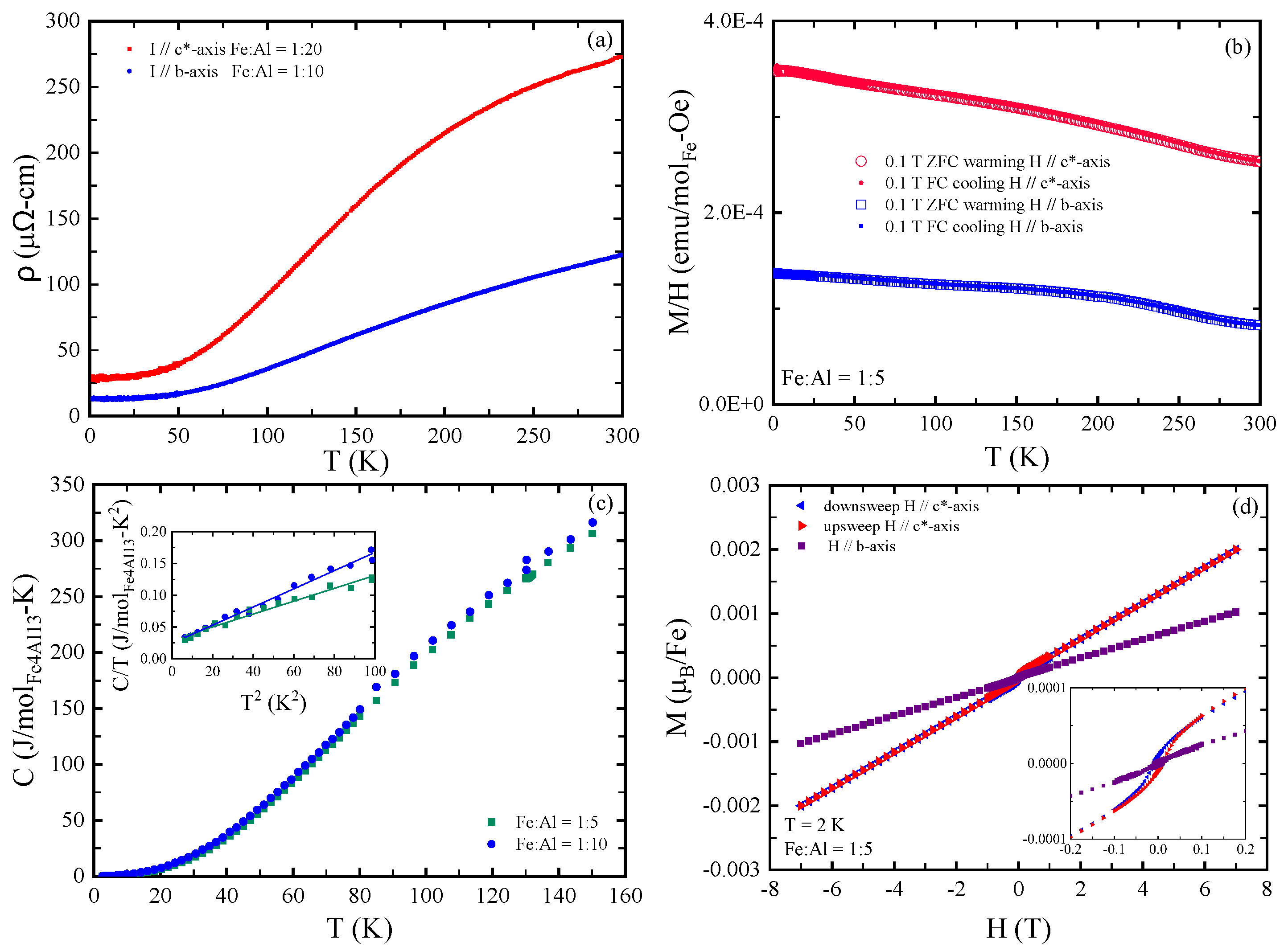
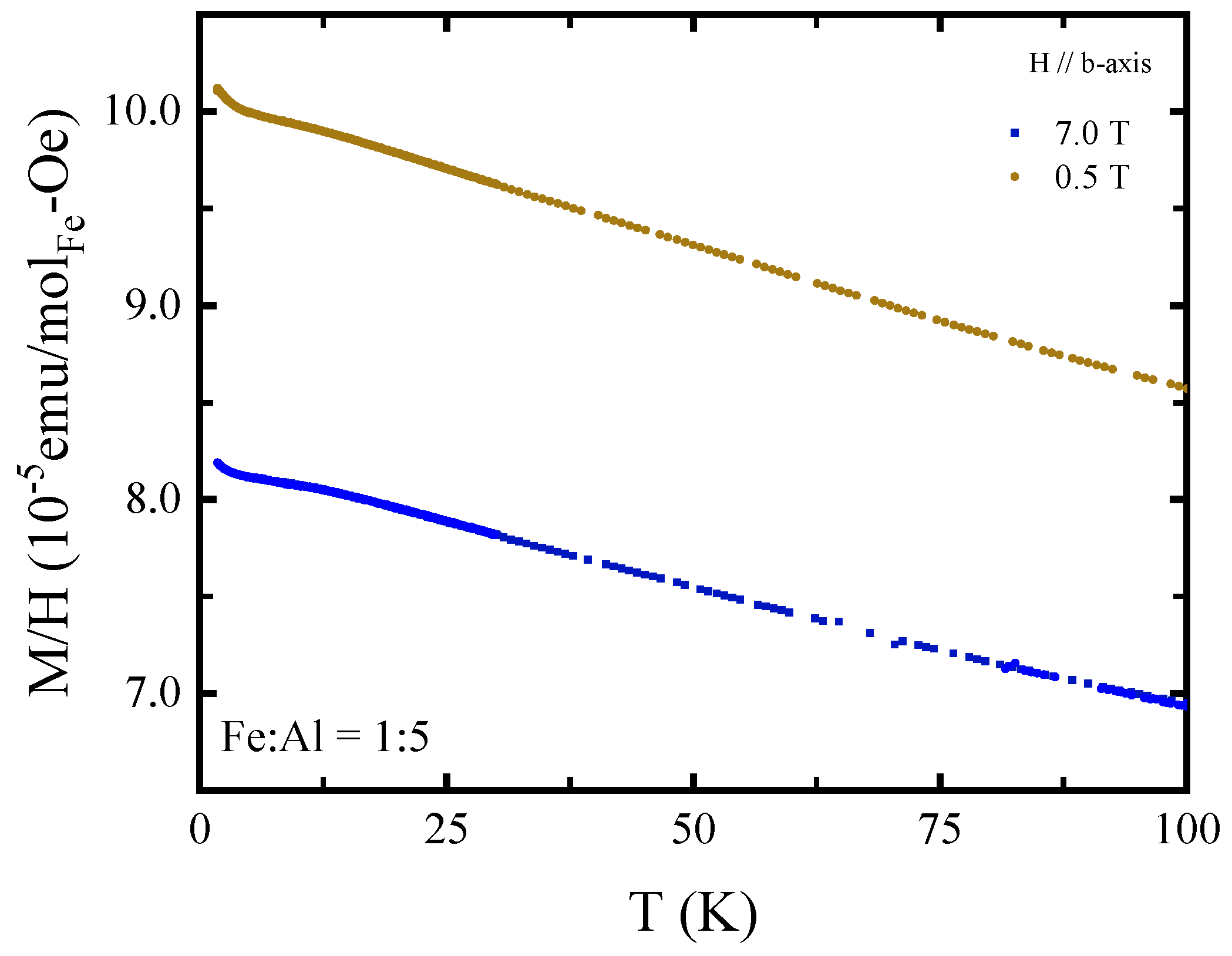
3. Results

Single-crystal X-ray diffraction yielded a refined structure consistent with the monoclinic C2/m space group with six formula units per unit cell with additional details in Table 1 and is consistent with previous results [17,35]. We performed temperature-dependent diffraction scans to characterize the crystal structure down to 100 K, finding no evidence of any phase transition nor anomalous structural behavior, with a unit cell volume decreasing monotonically and eventually saturating at approximately 1477 Å3. Refer to Table 1 for parameters.
The resistivity ( ρ ) vs. temperature (T) of Fe4Al13 crystals for Fe:Al = 1:20 and 1:10 with current (I) parallel to the reciprocal lattice c*-axis (i.e., perpendicular to a b -plane) and parallel to the b-axis, respectively, is shown in Figure 2a. The electrical transport is typical of a paramagnetic metal, with decreasing resistivity on cooling. The magnitude of ρ ( T ) is much smaller for the I ‖ b -axis, which may be a reflection of the electronic structure and mobility anisotropy. The magnetoresistance is small for both samples, at most +10 percent, even at a magnetic field (H) of 9 T and 2 K perhaps expected for a system prone to disorder owing to the complicated unit cell of low symmetry and off-stoichiometric tendencies. The Hall effect was measured for the Fe:Al = 1:20 sample (H parallel a-axis) between 2 K and 50 K and shows a single band hole-like response with a temperature-independent Hall coefficient of R H ∼ +1.4 × 10−7  Ω -cm/T, which corresponds to a carrier density of ∼+4.4 × 1021 cm−3.
The Magnetization (M) behavior is shown in Figure 2b and demonstrates a significant departure from the expected behavior of both magnetic and non-magnetic metals. A comparison of M / H vs. T for Fe:Al = 1:5 at 0.1 T shows minimal qualitative anisotropy for fields along the b-axis and along the c*-axis, although given the large size of the crystals, part of this anisotropy could be due to the difference in the filling fraction of the pick-up coil that complicates the normalization of the data and qualitative comparisons. Regardless, the low field magnetic response is noticeably larger for fields along the c*-axis compared to the b-axis, but there is a hump feature at ∼225 K for both field directions, which suggests that the unusual physics present is not bound to a particular crystallographic direction. At colder T, the M / H begins to increase linearly in T, or perhaps slightly sublinearly, until at the coldest T measured, there is a minor asymmetry between zero field cooled (ZFC) and field cooled (FC) data. This behavior of M / H vs. T is extraordinarily unusual and does not match anything close to the expected behavior of the local moment nor the itinerant magnetic response of materials [15]. We shall call this behavior a quasi-paramagnet in order to distinguish it from a traditional paramagnet.
The heat capacity, shown in Figure 2c, is again typical of a weakly correlated metal, with a small T-linear component at low temperatures consistent with a nearly free electron mass uncomplicated by correlations or other sources of entropy enhancement. A fit with the standard conduction electron Sommerfeld ( γ T ) and phonon Debye ( B T 3 ) terms below 10 K is shown in the inset with the 1:10 sample having slightly smaller γ than the 1:5 sample, consistent with a minor change in the density of states at the Fermi energy. The values of γ for the Fe:Al = 1:5 and 1:10 samples are 7.5 ± 0.6 mJ/mol-K2 and 6.1 ± 0.6 mJ/mol-K2, respectively. In contrast, the 1:5 sample has a larger Debye temperature θ D , which suggests changes in stoichiometry that alter the phonon spectrum. The values of θ D for the Fe:Al = 1:5 and 1:10 samples are 319 ± 5 K and 284 ± 3 K, respectively. The stoichiometry also alters the higher temperature behavior with the 1:10 having more heat capacity than the 1:5 sample, even up to 150 K. There are no indications of magnetic contributions to heat capacity.
The M vs. H behavior at 2 K in Figure 2d is again suggestive of paramagnetism of dilute Fe moments, rather than the quasi-paramagnetic temperature scaling. The anisotropy is consistent with the results in Figure 2b with a larger response with H along the c*-axis compared to the b-axis. The initial low H behavior is due to a small amount of ferromagnetic or superparamagnetic naturally occurring Fe oxide on the surface of the crystal. The difference in apparent hysteretic behavior between the two field directions may point to something subtle involving both the aforementioned coil filling fraction, as well as geometric demagnetization effects, which could be non-trivial for a weak paramagnet coated with a ferromagnetic layer.
The M / H vs. T behavior at larger field strengths after the surface ferromagnetic contaminants are polarized exhibits minimal qualitative change as shown in Figure 3. The linear in T behavior remains prominent, which suggests that the Zeeman energy scale is the dominant contribution to the thermodynamics. All of the above experimental results are consistent with a weakly interacting system, except the M / H vs. T quasi-paramagnetic scaling, and motivate a closer look at the band structure.

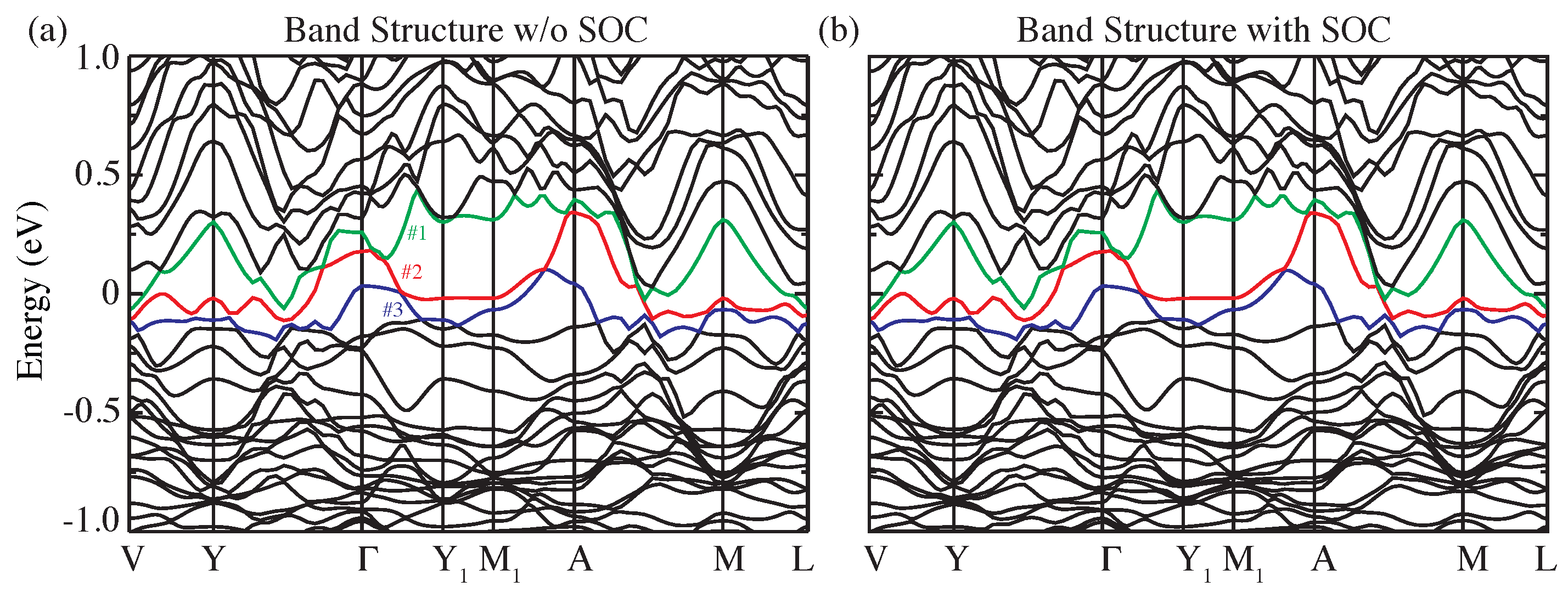
4. Density Functional Theory Calculations

Although previous calculations assume a ferromagnetic ground state [39], we do not observe experimental signatures of a bulk ferromagnetic ground state in the aforementioned results. This motivated another attempt to perform density functional theory (DFT) calculations [40,41] with the results shown in Figure 4. The results without (a) and with (b) spin-orbit coupling (SOC) show minimal apparent difference owing to the light elements involved in the system. As expected, Fe4Al13 is a metal with an odd number of electrons per primitive cell. There are three bands at the Fermi level that we refer to as bands # 1, # 2, and # 3. Band # 2 contributes the most at the Fermi level and is half-filled. We further calculated the band representations at the high-symmetry points in the Brillouin zone and identified the corresponding band topologies for each band [42]. In the absence of SOC, none of the three bands (# 1∼3) are isolated because their associated band representations do not satisfy the compatibility relations of this group. Consequently, symmetry-protected nodal points (or lines) must exist between these bands and those above and below them. Detailed analysis reveals that a mirror-symmetry-protected nodal line is present between bands # 2 and # 3 (as well as between bands # 2 and # 1) on the G-A-M-Y plane. With SOC included, the nodal lines become gapped, and all three bands are isolated. For each gap, we consider all bands below it as occupied and calculate the corresponding topological indices. The results indicate that the gap between bands # 1 and # 2 is topologically nontrivial with indices ( z 2 , 1 , z 2 , 2 , z 2 , 3 , z 4 ) = ( 0003 ) , while the gap between bands # 2 and # 3 is also topologically nontrivial with indices ( z 2 , 1 , z 2 , 2 , z 2 , 3 , z 4 ) = ( 1101 ) . Both of the above indices indicate a strong topological insulator phase. However, the presence of a multitude of bands (due to the large number of atoms per unit cell and the low symmetry group) gives rise to a complicated “spaghetti-like” band structure, with a strong metallic character. As such, the topological indices should be interpreted as indices of the bands rather than those of the Fermi level, which again, is metallic. We point out that the red band, which is stoichiometrically half-filled, is much flatter than many of its neighbors, with a bandwidth of less than 100 meV for most momenta. Half-filled flat bands have a strong tendency to magnetize, shown both experimentally and theoretically. Hence experimental observation of a lack of magnetism in this compound is surprising.
We computed the surface states along the (001) direction using the Green’s function method [43]. Figure 5a displays the first Brillouin zone with labeled high-symmetry points, along with an illustration of how these points map from the bulk to the (001) surface Brillouin zone. Figure 5b,c present the dispersion of the surface states along high-symmetry points and the Fermi surface on the (001) surface (with Al termination), respectively, clearly distinguishing the topological surface states from the bulk states along X ¯ − Γ ¯ . Similar results were obtained for the Fe-terminated surface in Figure 5d,e.

5. Discussion

This work demonstrated the utility of Fe4Al13 crystal growth for educational purposes with an Al flux growth method, revealing a surprising lack of magnetism and an unusual magnetic susceptibility behavior. The electrical transport and heat capacity suggest a weakly correlated non-magnetically ordered metal. The magnetization, however, demonstrates anomalous temperature dependence that is inconsistent with local moment Curie behavior and itinerant Pauli paramagnetism, which we refer to as quasi-paramagnetism for now. A comparison of our results with Czochralski-grown Fe4Al13 crystals [35,44] shows similar transport and heat capacity, although their magnetization results are, at first glance, more suggestive of Curie-like behavior. This suggests that Fe4Al13 crystals, by slow cooling Al flux, create an interesting collection of dilute Fe moments that break conventional weakly correlated paramagnetic behavior. Although Fe4Al13 is crystalline, it is very close to being a decahedral quasicrystal and is described as a quasicrystal approximant [45]. As we observe no indication of single ion Kondo behavior [46], the local Fe impurity moment coupling with the conduction electrons must be very weak. As the band structure is suggested to be complicated due to the Hall and thermopower response [35], it can be expected that the Ruderman–Kittel–Kasuya–Yosida (RKKY) [47] conduction electron-mediated interaction among the dilute Fe moments is non-trivial. In fact, it has already been confirmed that tuning the RKKY interaction in quasicrystal approximant Au-Ga-Tb systems can change the ground state from ferromagnetic-like to antiferromagnetic-like [29]. It is conceivable that our Fe4Al13 is a more dilute version of this in which we have random antiferromagnetic and ferromagnetic RKKY mediated interactions among Fe impurities, which leads to frustration and breakdown in Curie behavior. It suggests that future examinations of dilute paramagnetic behavior in metallic quasicrystals and quasicrystal approximants could be worthwhile in order to test for breakdowns in the very fundamental Curie law, although we note the even J. H Van Vleck himself pointed out the limits of the Curie law [48].

Author Contributions

Conceptualization, K.E.A. and J.A.H.; methodology, K.E.A.; validation, K.E.A., J.A.H., and J.P.; formal analysis, K.E.A., Y.X., and B.A.B.; investigation, K.E.A., J.A.H., R.K., S.R.S., and P.Z.; resources, S.R.S.; data curation, K.E.A.; writing—original draft preparation, K.E.A.; writing—review and editing, K.E.A. and J.P.; visualization, K.E.A.; supervision, J.P.; project administration, J.P.; funding acquisition, J.P. All authors have read and agreed to the published version of the manuscript.

Funding

Research at the University of Maryland and funding for the Fundamentals of Quantum Materials Winter School was provided by the Gordon and Betty Moore Foundation’s EPiQS Initiative, the U.S. National Science Foundation (NSF) Grant No. DMR2310428, the Institute for Complex Adaptive Matter (workshop No. 8881), the Canadian Institute for Advanced Research, and the Maryland Quantum Materials Center. B.A.B. was supported by the Office of Basic Energy Sciences, Material Sciences, and Engineering Division, U.S. Department of Energy (DOE) under Contract No. DE-SC0016239.

Data Availability Statement

Dataset available on request from the authors.

Acknowledgments

The authors acknowledge the generous continued support from funders of the FQM Winter School, in particular, the Gordon and Betty Moore Foundation. We also thank the students of the January 2024 Fundamentals of Quantum Materials Winter School who synthesized a significant quantity of Fe4Al13 crystals as part of their hands-on module training.

Conflicts of Interest

The authors declare no conflicts of interest.

Abbreviations

The following abbreviations are used in this manuscript:
FQM2024Fundamentals of Quantum Materials Winter School
FeIron
AlAluminum
ρ Resistivity
HMagnetic field
TTemperature
CHeat capacity
MMagnetization
DFTDensity functional theory

References

  1. Khatua, J.; Pregelj, M.; Elghandour, A.; Jagličic, Z.; Klingeler, R.; Zorko, A.; Khuntia, P. Magnetic properties of the triangular-lattice antiferromagnets Ba3RB9O18 (R = Yb, Er). Phys. Rev. B 2022, 106, 104408. [Google Scholar] [CrossRef]
  2. Avers, K.E.; Maksimov, P.A.; Rosa, P.F.S.; Thomas, S.M.; Thompson, J.D.; Halperin, W.P.; Movshovich, R.; Chernyshev, A.L. Fingerprinting triangular-lattice antiferromagnet by excitation gaps. Phys. Rev. B 2021, 103, L180406. [Google Scholar] [CrossRef]
  3. Ogunbunmi, M.O.; Strydom, A.M. Physical and magnetic properties of frustrated triangular-lattice antiferromagnets R3Cu (R = Ce, Pr). J. Alloys Compd. 2022, 895, 162545. [Google Scholar] [CrossRef]
  4. Zhong, R.; Guo, S.; Cava, R.J. Frustrated magnetism in the layered triangular lattice materials K2Co(SeO3)2 and Rb2Co(SeO3)2. Phys. Rev. Mater. 2020, 4, 084406. [Google Scholar] [CrossRef]
  5. Deswal, S.; Kumar, D.; Rout, D.; Singh, S.; Kumar, P. Quasi-two-dimensional frustrated spin-1 triangular lattice antiferromagnet Ca3NiNb2O9: A proximate spin liquid. Phys. Rev. B 2024, 110, 024430. [Google Scholar] [CrossRef]
  6. Kumar, A.; Hu, N.C.; MacDonald, A.H.; Potter, A.C. Gate-tunable heavy fermion quantum criticality in a moiré Kondo lattice. Phys. Rev. B 2022, 106, L041116. [Google Scholar] [CrossRef]
  7. Si, Q.; Steglich, F. Heavy Fermions and Quantum Phase Transitions. Science 2010, 329, 1161–1166. [Google Scholar] [CrossRef]
  8. Wang, J.; Yang, Y.f. Nonlocal Kondo effect and quantum critical phase in heavy-fermion metals. Phys. Rev. B 2021, 104, 165120. [Google Scholar] [CrossRef]
  9. Shrestha, K.; Zhang, S.; Greene, L.H.; Lai, Y.; Baumbach, R.E.; Sasmal, K.; Maple, M.B.; Park, W.K. Spectroscopic evidence for the direct involvement of local moments in the pairing process of the heavy-fermion superconductor CeCoIn5. Phys. Rev. B 2021, 103, 224515. [Google Scholar] [CrossRef]
  10. Asaba, T.; Lee, S.; Seo, S.; Avers, K.E.; Thomas, S.M.; Movshovich, R.; Thompson, J.D.; Rosa, P.F.S.; Bauer, E.D.; Ronning, F. Physical properties of YbFe5P3 with a quasi-one-dimensional crystal structure. Phys. Rev. B 2021, 104, 195140. [Google Scholar] [CrossRef]
  11. Münzer, W.; Neubauer, A.; Adams, T.; Mühlbauer, S.; Franz, C.; Jonietz, F.; Georgii, R.; Böni, P.; Pedersen, B.; Schmidt, M.; et al. Skyrmion lattice in the doped semiconductor Fe1−xCoxSi. Phys. Rev. B 2010, 81, 041203. [Google Scholar] [CrossRef]
  12. Brearton, R.; Burn, D.M.; Haghighirad, A.A.; van der Laan, G.; Hesjedal, T. Three-dimensional structure of magnetic skyrmions. Phys. Rev. B 2022, 106, 214404. [Google Scholar] [CrossRef]
  13. Yang, S.; Zhao, Y.; Zhang, X.; Xing, X.; Du, H.; Li, X.; Mochizuki, M.; Xu, X.; Åkerman, J.; Zhou, Y. Fundamentals and applications of the skyrmion Hall effect. Appl. Phys. Rev. 2024, 11, 041335. [Google Scholar] [CrossRef]
  14. Divic, S.; Ling, H.; Pereg-Barnea, T.; Paramekanti, A. Magnetic skyrmion crystal at a topological insulator surface. Phys. Rev. B 2022, 105, 035156. [Google Scholar] [CrossRef]
  15. Mugiraneza, S.; Hallal, A.M. Tutorial: A beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law. Commun. Phys. 2022, 5, 95. [Google Scholar] [CrossRef]
  16. Liu, C.; Fan, C. Crystal structure of the λ-Al13Fe4-type intermetallic (Al,Cu)13(Fe,Cu)4. IUCrData 2018, 3, x180363. [Google Scholar] [CrossRef]
  17. Grin, J.; Burkhardt, U.; Ellner, M.; Peters, K. Refinement of the Fe4Al13 structure and its relationship to the quasihomological structure homotypical structures. Z. Krist. 1994, 209, 479–487. [Google Scholar]
  18. Ding, L.; Sapanathan, T.; Schryvers, D.; Simar, A.; Idrissi, H. On the formation of antiphase boundaries in Fe4Al13 intermetallics during a high temperature treatment. Scr. Mater. 2022, 215, 114726. [Google Scholar] [CrossRef]
  19. Ellner, M. Polymorphic phase transformation of Fe4Al13 causing multiple twinning with decagonal pseudo-symmetry. Acta Crystallogr. Sect. B 1995, 51, 31–36. [Google Scholar] [CrossRef]
  20. Zienert, T.; Leineweber, A.; Fabrichnaya, O. Heat capacity of Fe-Al intermetallics: B2-FeAl, FeAl2, Fe2Al5 and Fe4Al13. J. Alloys Compd. 2017, 725, 848–859. [Google Scholar] [CrossRef]
  21. Tobita, K.; Sato, N.; Kitahara, K.; Takagiwa, Y.; Kimura, K. Effect of Anomalous Crystal Structure of Iron Aluminides Fe2Al5 and Fe4Al13: Low Phonon Thermal Conductivity and Potentiality as Thermoelectric Materials. Mater. Trans. 2016, 57, 1045–1049. [Google Scholar] [CrossRef]
  22. Mingjian, H.; Chunzhi, L.; Minggao, Y.; Yan, J. The multiple twinning of Fe4Al13 as a heterogeneous phase in commercial AlZnMgCu alloys. Mater. Sci. Eng. 1988, 100, L23–L25. [Google Scholar] [CrossRef]
  23. Agrosi, G.; Manzari, P.; Mele, D.; Tempesta, G.; Rizzo, F.; Catelani, T.; Bindi, L. A naturally occurring Al-Cu-Fe-Si quasicrystal in a micrometeorite from southern Italy. Commun. Earth Environ. 2024, 5, 67. [Google Scholar] [CrossRef]
  24. Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
  25. He, Z.; Ma, H.; Li, H.; Li, X.; Ma, X. New type of Al-based decagonal quasicrystal in Al60Cr20Fe10Si10 alloy. Sci. Rep. 2016, 6, 22337. [Google Scholar] [CrossRef] [PubMed]
  26. Mihalkovič, M.; Widom, M. Spontaneous formation of thermodynamically stable Al-Cu-Fe icosahedral quasicrystal from realistic atomistic simulations. Phys. Rev. Res. 2020, 2, 013196. [Google Scholar] [CrossRef]
  27. Sun, B.; Pan, M.; Zhao, D.; Wang, W.; Xi, X.; Sandor, M.; Wu, Y. Aluminum-rich bulk metallic glasses. Scr. Mater. 2008, 59, 1159–1162. [Google Scholar] [CrossRef]
  28. Dresselhaus, M.; Dresselhaus, G.; Jorio, A. Group Theory: Application to the Physics of Condensed Matter; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
  29. Labib, F.; Nawa, K.; Suzuki, S.; Wu, H.C.; Ishikawa, A.; Inagaki, K.; Fujii, T.; Kinjo, K.; Sato, T.J.; Tamura, R. Unveiling exotic magnetic phase diagram of a non-Heisenberg quasicrystal approximant. Mater. Today Phys. 2024, 40, 101321. [Google Scholar] [CrossRef]
  30. Nawa, K.; Avdeev, M.; Ishikawa, A.; Takakura, H.; Wang, C.W.; Okuyama, D.; Murasaki, R.; Tamura, R.; Sato, T.J. Magnetic properties of the quasicrystal approximant Au65Ga21Tb14. Phys. Rev. Mater. 2023, 7, 054412. [Google Scholar] [CrossRef]
  31. Deguchi, K.; Matsukawa, S.; Sato, N.K.; Hattori, T.; Ishida, K.; Takakura, H.; Ishimasa, T. Quantum critical state in a magnetic quasicrystal. Nat. Mater. 2012, 11, 1013. [Google Scholar] [CrossRef]
  32. Paglione, J.; Butch, N.P.; Rodriguez, E.E. Fundamentals of Quantum Materials; World Scientific: Singapore, 2021. [Google Scholar]
  33. Canfield, P.C.; Fisk, Z. Growth of single crystals from metallic fluxes. Philos. Mag. Part B 1992, 65, 1117–1123. [Google Scholar] [CrossRef]
  34. Shang, S.; Sun, H.; Pan, B.; Wang, Y.; Krajewski, A.M.; Banu, M.; Li, J.; Liu, Z. Forming mechanism of equilibrium and non-equilibrium metallurgical phases in dissimilar aluminum/steel (Al–Fe) joints. Sci. Rep. 2021, 11, 24251. [Google Scholar] [CrossRef] [PubMed]
  35. Popčević, P.; Smontara, A.; Ivkov, J.; Wencka, M.; Komelj, M.; Jeglič, P.; Vrtnik, S.; Bobnar, M.; Jagličić, Z.; Bauer, B.; et al. Anisotropic physical properties of the Al13Fe4 complex intermetallic and its ternary derivative Al13(Fe,Ni)4. Phys. Rev. B 2010, 81, 184203. [Google Scholar] [CrossRef]
  36. Krause, L.; Herbst-Irmer, R.; Sheldrick, G.M.; Stalke, D. Comparison of silver and molybdenum microfocus X-ray sources for single-crystal structure determination. J. Appl. Crystallogr. 2015, 48, 3–10. [Google Scholar] [CrossRef] [PubMed]
  37. Sheldrick, G.M. SHELXT—Integrated space-group and crystal-structure determination. Acta Crystallogr. Sect. 2015, 71, 3–8. [Google Scholar] [CrossRef]
  38. Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. Sect. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
  39. Ullah, I.; Mehmood, S.; Ali, Z.; Rehman, G.; Khan, I.; Ahmad, I. Theoretical studies of the electronic structure and magnetic properties of aluminum-rich intermetallic alloy Al13Fe4. Int. J. Mod. Phys. B 2018, 32, 1850201. [Google Scholar] [CrossRef]
  40. Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
  41. Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
  42. Bradlyn, B.; Cano, J.; Wang, Z.; Bernevig, B.A. Topological quantum chemistry. Nature 2017, 547, 298–305. [Google Scholar] [CrossRef]
  43. Wu, Q.; Zhang, S.; Song, H.F.; Troyer, M.; Soluyanov, A.A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 2018, 224, 405–416. [Google Scholar] [CrossRef]
  44. Gille, P.; Bauer, B. Single crystal growth of Al13Co4 and Al13Fe4 from Al-rich solutions by the Czochralski method. Cryst. Res. Technol. 2008, 43, 1161–1167. [Google Scholar] [CrossRef]
  45. Liu, Y.; Fan, C.; Xu, Z.; Fu, R.; Wen, B.; Zhang, L. Orientation Relationship of the Intergrowth Al13Fe3 and Al13Fe4 Intermetallics Determined by Single-Crystal X-ray Diffraction. Metals 2024, 14, 463. [Google Scholar] [CrossRef]
  46. Hewson, A.C. The Kondo Problem to Heavy Fermions; Cambridge Studies in Magnetism; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
  47. Xin, Y.; Stolt, I.; Song, Y.; Dai, P.; Halperin, W.P. RKKY coupled local-moment magnetism in NaFe1−xCuxAs. Phys. Rev. B 2021, 104, 144421. [Google Scholar] [CrossRef]
  48. Van Vleck, J. χ = C/(T + δ), the most overworked formula in the history of paramagnetism. Physica 1973, 69, 177–192. [Google Scholar] [CrossRef]
Crystals 15 00485 g001
Figure 1. Systematic study of molten Al flux growth of Fe4Al13 crystals produced by students of the 2024 Fundamentals of Quantum Materials winter school. (a) Alloy phase diagram representation of three synthesis batches with approximately 1:20, 1:10, and 1:5 Fe:Al molar ratios for batches 1a, 3a, and 2b, respectively. (b,c) Unit cell of Fe4Al13 from single crystal X-ray refinement projected onto the a–c and b–c planes. (d–f) Photographs of the resulting crystal yield from batches 1a, 2b, and 3a.
Figure 1. Systematic study of molten Al flux growth of Fe4Al13 crystals produced by students of the 2024 Fundamentals of Quantum Materials winter school. (a) Alloy phase diagram representation of three synthesis batches with approximately 1:20, 1:10, and 1:5 Fe:Al molar ratios for batches 1a, 3a, and 2b, respectively. (b,c) Unit cell of Fe4Al13 from single crystal X-ray refinement projected onto the a–c and b–c planes. (d–f) Photographs of the resulting crystal yield from batches 1a, 2b, and 3a.
Crystals 15 00485 g001
Crystals 15 00485 g002
Figure 2. (a) Resistivity ( ρ ) vs. temperature (T) of Al flux- grown single crystals of Fe4Al13 for current (I) along the c*-axis (red, Fe:Al = 1:20) and b-axis (blue, Fe:Al = 1:10). The overall transport behavior is typical of a metal, although anisotropic owing to the low symmetry of crystal structure. (b) Magnetization temperature dependence of a single crystal for growth ratio of Fe:Al = 1:5 taken at 0.1 T along the b-axis and the c*-axis. There is a change in magnitude by changing the field direction, but results are qualitatively similar. Although the magnitude of the magnetization is small, its linear temperature dependence is extremely unusual in that it does not obey Curie behavior of localized magnetic moments, nor the constant in T Pauli susceptibility of conduction electrons. The slight asymmetry between ZFC and FC at low H and low T suggests a minor contribution from a naturally occurring Fe oxide surface layer. (c) Heat capacity (C) vs. T of Al flux-grown Fe4Al13 crystals for Fe:Al = 1:5 (green) and Fe:Al = 1:10 (blue). The insert shows a low-T inset C / T vs. T 2 with fits to the standard electronic and phonon terms. Low Sommerfeld coefficients γ indicate a weakly correlated electronic state. There is also a slight difference in the phonon behaviors reflected in the different Debye temperatures between the two samples, which suggests that changes in stoichiometry and growth conditions can alter the phonon spectrum. (d) Magnetization field dependence of single crystals for Fe:Al = 1:5 measured at 2 K. The crystalline anisotropy is minimal between fields along the c*-axis and the b-axis. The inset emphasizes a minor hysteretic contribution from a surface oxide.
Figure 2. (a) Resistivity ( ρ ) vs. temperature (T) of Al flux- grown single crystals of Fe4Al13 for current (I) along the c*-axis (red, Fe:Al = 1:20) and b-axis (blue, Fe:Al = 1:10). The overall transport behavior is typical of a metal, although anisotropic owing to the low symmetry of crystal structure. (b) Magnetization temperature dependence of a single crystal for growth ratio of Fe:Al = 1:5 taken at 0.1 T along the b-axis and the c*-axis. There is a change in magnitude by changing the field direction, but results are qualitatively similar. Although the magnitude of the magnetization is small, its linear temperature dependence is extremely unusual in that it does not obey Curie behavior of localized magnetic moments, nor the constant in T Pauli susceptibility of conduction electrons. The slight asymmetry between ZFC and FC at low H and low T suggests a minor contribution from a naturally occurring Fe oxide surface layer. (c) Heat capacity (C) vs. T of Al flux-grown Fe4Al13 crystals for Fe:Al = 1:5 (green) and Fe:Al = 1:10 (blue). The insert shows a low-T inset C / T vs. T 2 with fits to the standard electronic and phonon terms. Low Sommerfeld coefficients γ indicate a weakly correlated electronic state. There is also a slight difference in the phonon behaviors reflected in the different Debye temperatures between the two samples, which suggests that changes in stoichiometry and growth conditions can alter the phonon spectrum. (d) Magnetization field dependence of single crystals for Fe:Al = 1:5 measured at 2 K. The crystalline anisotropy is minimal between fields along the c*-axis and the b-axis. The inset emphasizes a minor hysteretic contribution from a surface oxide.
Crystals 15 00485 g002
Crystals 15 00485 g003
Figure 3. Low temperature view of M / H vs. T for stronger magnetic fields parallel to the b-axis. The linear T behavior persists in the highest fields measured.
Figure 3. Low temperature view of M / H vs. T for stronger magnetic fields parallel to the b-axis. The linear T behavior persists in the highest fields measured.
Crystals 15 00485 g003
Crystals 15 00485 g004
Figure 4. Band structure calculations (a) without and (b) with spin-orbit coupling. The three bands #1∼3 are indicated with green, red, and blue lines. We note the rather flat half-filled band (red) hugging the Fermi level.
Figure 4. Band structure calculations (a) without and (b) with spin-orbit coupling. The three bands #1∼3 are indicated with green, red, and blue lines. We note the rather flat half-filled band (red) hugging the Fermi level.
Crystals 15 00485 g004
Crystals 15 00485 g005
Figure 5. Surface state (SS) calculations. (a) The bulk Brillouin zone (BZ) with high-symmetry points labeled is shown, with the (001) surface BZ highlighted in magenta. Below, an illustration demonstrates how the high-symmetry points are mapped from the bulk to the (001) surface. The three reciprocal lattice vectors are defined as ( k 1 , k 2 , k 3 ) = 2 π Ω ( b × c , c × a , a × b ) , where (a, b, c) represent the three lattice vectors shown in Figure 1, and Ω denotes the volume of the unit cell. Band dispersion (b) and Fermi surface (FS) (c) on the (001) surface with Al termination are displayed, with topological surface states (TSSs) along the X ¯ − Γ ¯ path clearly indicated in both plots. Panels (d,e) show similar results for the Fe-terminated (001) surface.
Figure 5. Surface state (SS) calculations. (a) The bulk Brillouin zone (BZ) with high-symmetry points labeled is shown, with the (001) surface BZ highlighted in magenta. Below, an illustration demonstrates how the high-symmetry points are mapped from the bulk to the (001) surface. The three reciprocal lattice vectors are defined as ( k 1 , k 2 , k 3 ) = 2 π Ω ( b × c , c × a , a × b ) , where (a, b, c) represent the three lattice vectors shown in Figure 1, and Ω denotes the volume of the unit cell. Band dispersion (b) and Fermi surface (FS) (c) on the (001) surface with Al termination are displayed, with topological surface states (TSSs) along the X ¯ − Γ ¯ path clearly indicated in both plots. Panels (d,e) show similar results for the Fe-terminated (001) surface.
Crystals 15 00485 g005
Table 1. Single-crystal X-ray refinement parameters for Fe4Al13 measured on a Bruker D8Venture w/PhotonIII diffractometer. Integral intensity was corrected for absorption using SADABS-2016/2 software [36] and the multi-scan method. Structures were solved with the ShelXT [37] program and refined with the ShelXL program [38] using least-square minimization. All results are consistent with monoclinic space group C2/m with 6 formula units per unit cell.
Table 1. Single-crystal X-ray refinement parameters for Fe4Al13 measured on a Bruker D8Venture w/PhotonIII diffractometer. Integral intensity was corrected for absorption using SADABS-2016/2 software [36] and the multi-scan method. Structures were solved with the ShelXT [37] program and refined with the ShelXL program [38] using least-square minimization. All results are consistent with monoclinic space group C2/m with 6 formula units per unit cell.
T (K)250150100
a (Å)15.4659(9)15.440(5)15.447(2)
b (Å)8.0759(5)8.067(2)8.0677(12)
c (Å)12.4618(7)12.452(4)12.4458(18)
β (°)107.7041(9)107.728(4)107.701(2)
V (Å3)1482.78(15)1477.3(8)1477.6(4)
ρ (g/cm3)3.8583.8723.871
R10.02170.02190.0218
wR20.04940.05040.0490
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Avers, K.E.; Horn, J.A.; Kumar, R.; Saha, S.R.; Zavalij, P.; Xu, Y.; Bernevig, B.A.; Paglione, J. Dilute Paramagnetism and Non-Trivial Topology in Quasicrystal Approximant Fe4Al13. Crystals 2025, 15, 485. https://doi.org/10.3390/cryst15050485

AMA Style

Avers KE, Horn JA, Kumar R, Saha SR, Zavalij P, Xu Y, Bernevig BA, Paglione J. Dilute Paramagnetism and Non-Trivial Topology in Quasicrystal Approximant Fe4Al13. Crystals. 2025; 15(5):485. https://doi.org/10.3390/cryst15050485

Chicago/Turabian Style

Avers, Keenan E., Jarryd A. Horn, Ram Kumar, Shanta R. Saha, Peter Zavalij, Yuanfeng Xu, Bogdan Andrei Bernevig, and Johnpierre Paglione. 2025. "Dilute Paramagnetism and Non-Trivial Topology in Quasicrystal Approximant Fe4Al13" Crystals 15, no. 5: 485. https://doi.org/10.3390/cryst15050485

APA Style

Avers, K. E., Horn, J. A., Kumar, R., Saha, S. R., Zavalij, P., Xu, Y., Bernevig, B. A., & Paglione, J. (2025). Dilute Paramagnetism and Non-Trivial Topology in Quasicrystal Approximant Fe4Al13. Crystals, 15(5), 485. https://doi.org/10.3390/cryst15050485

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop