Inspection of Bulk Crystals for Quality Control in Crystal Growth: Assessment of High-Energy X-Ray Transmission Topography and Back-Reflection Topography Pinpointed for Physical Vapor Transport-Grown Aluminum Nitride
Abstract
1. Introduction
2. Materials and Methods
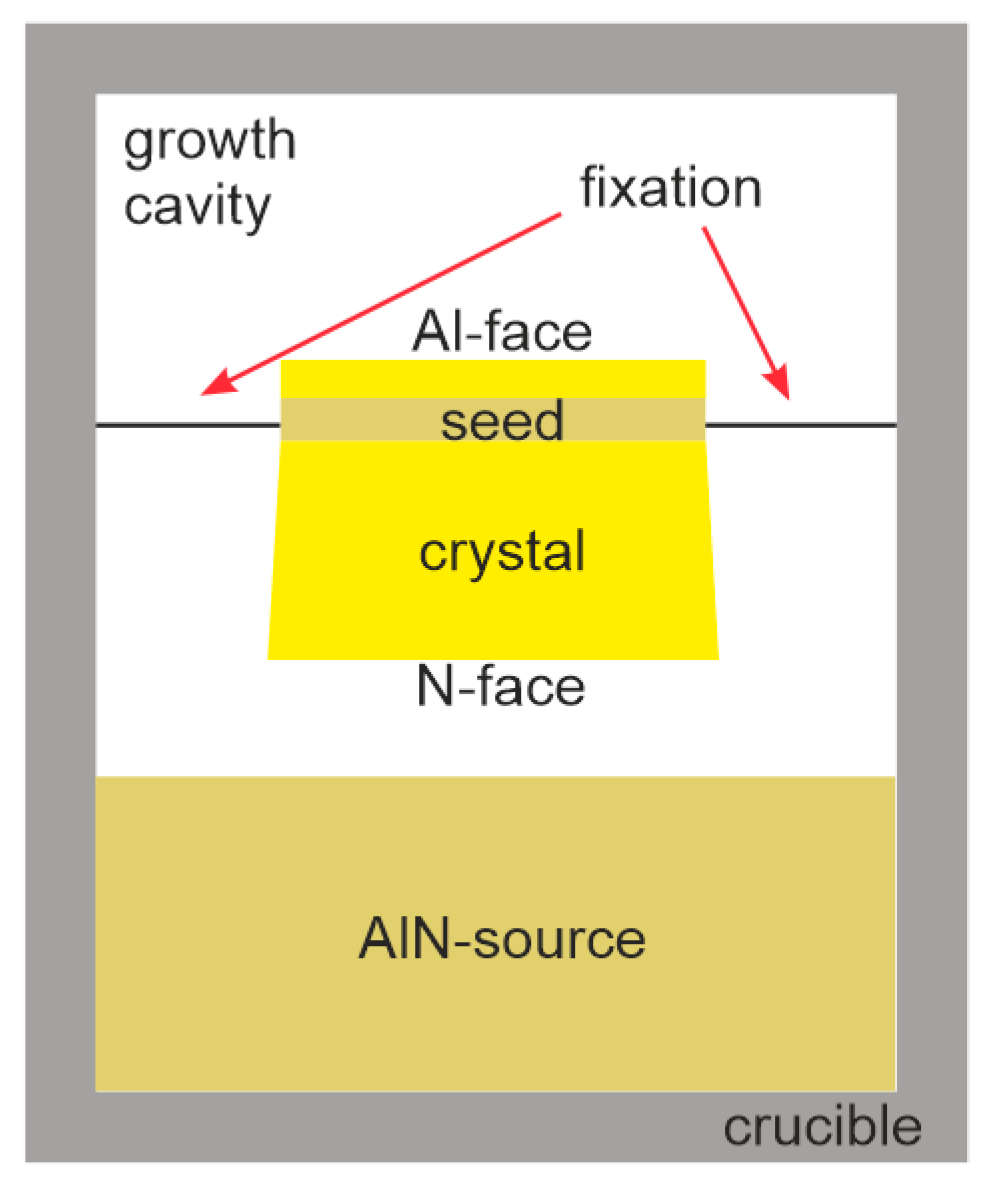
2.1. Aluminum Nitride PVT Growth
2.2. Experimental Measurement Setups
2.2.1. Surface Inspection Tool
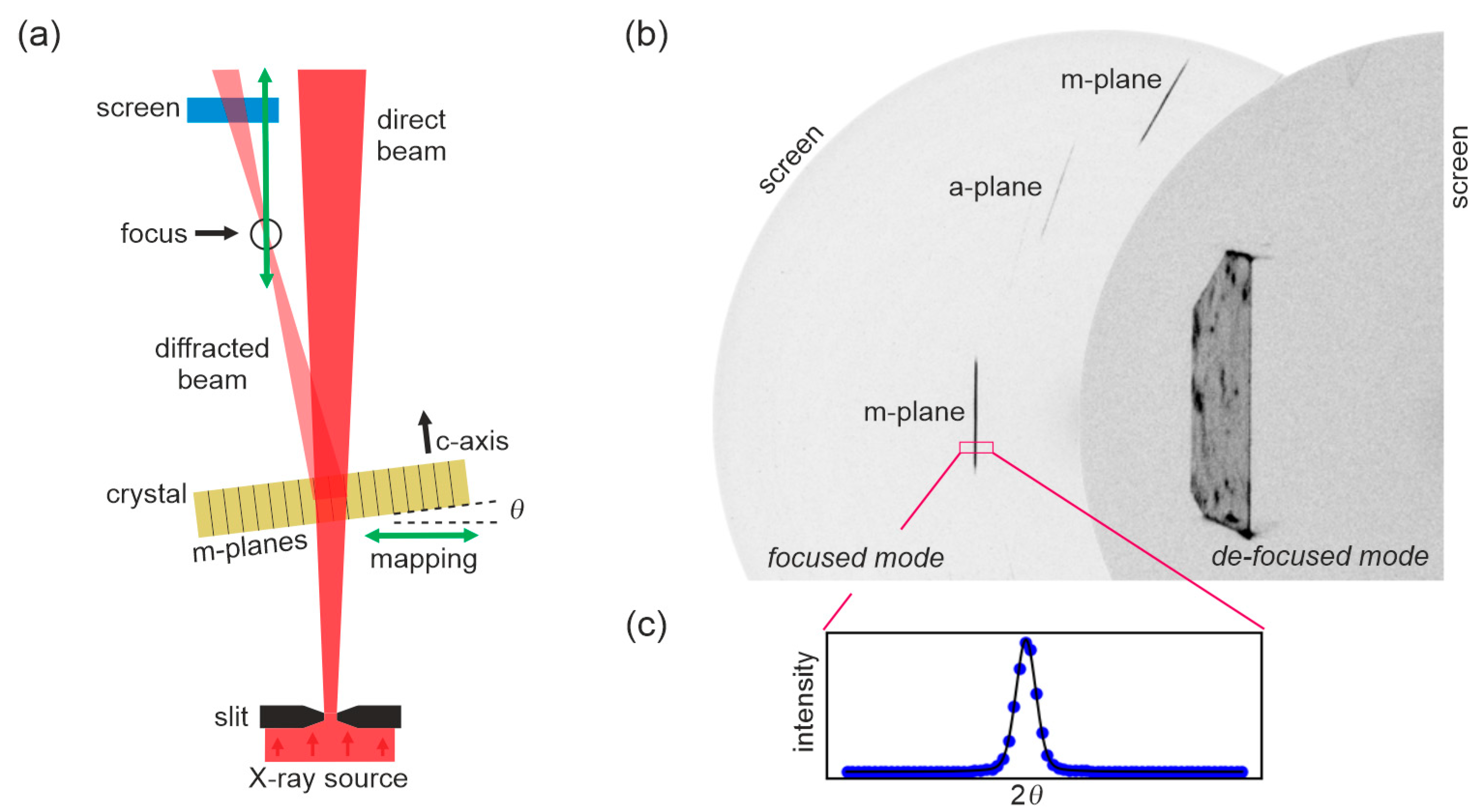
2.2.2. X-Ray Topography Setups (Back-Reflection and Lang Transmission)
2.2.3. High Energy X-Ray Laue Topography Setup
2.3. X-Ray Measurement Procedures
2.3.1. X-Ray Topography in Reflection Geometry
2.3.2. X-Ray Topography in Transmission Geometry (Lang)
2.3.3. High-Energy Laue Topography in Transmission Geometry
2.3.4. Three-Dimensional Section Topography
3. Results and Discussion
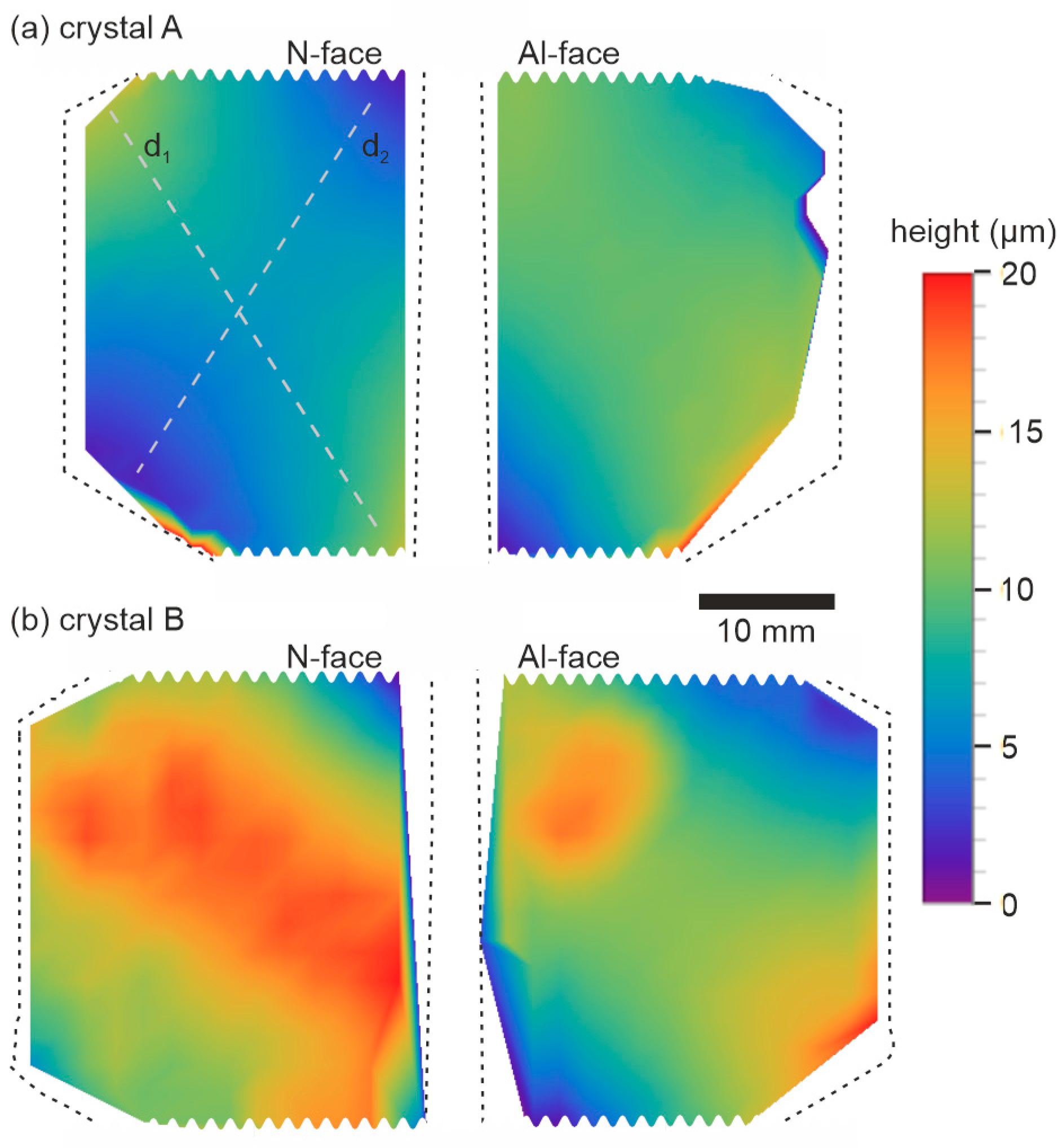
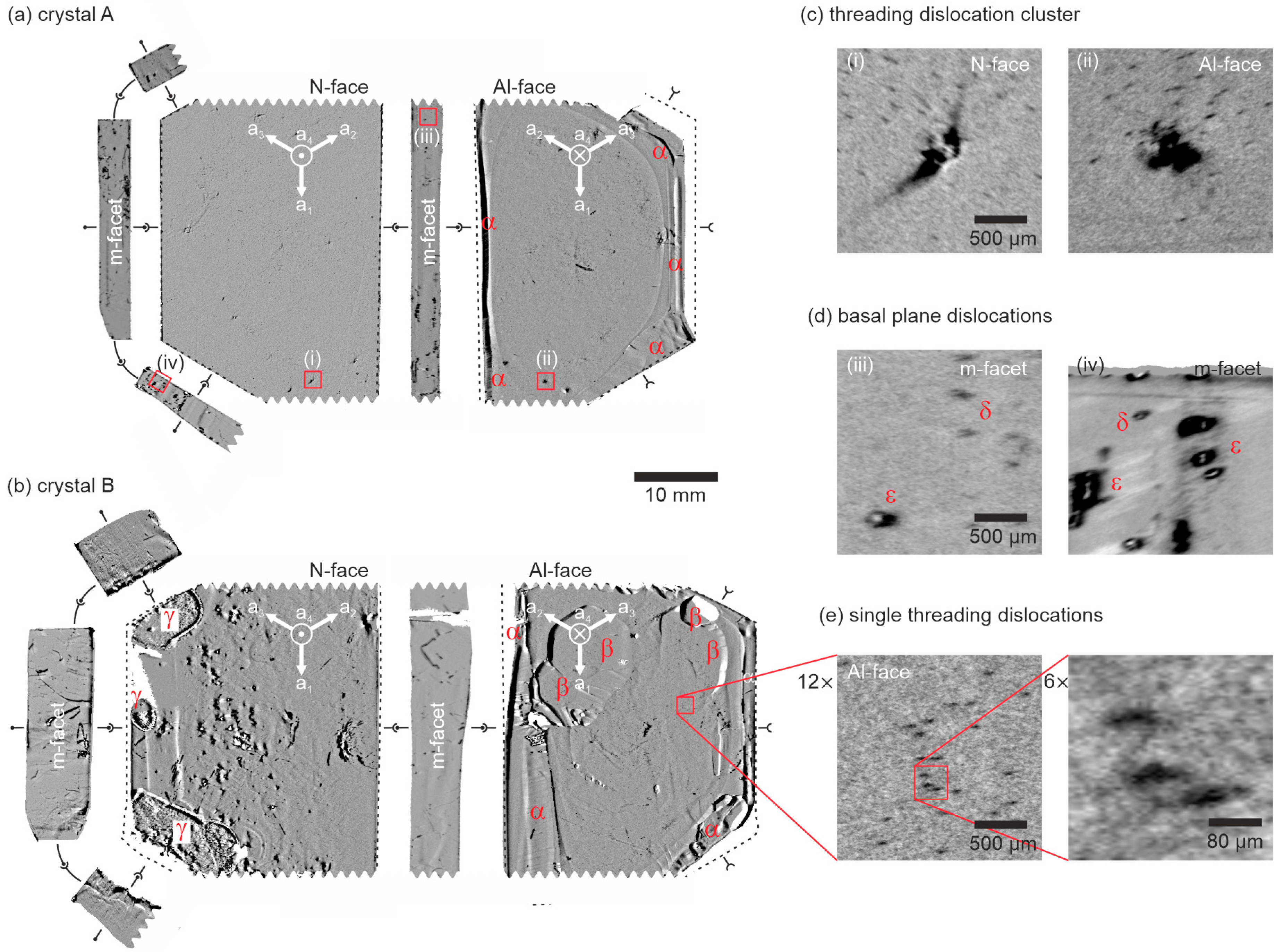
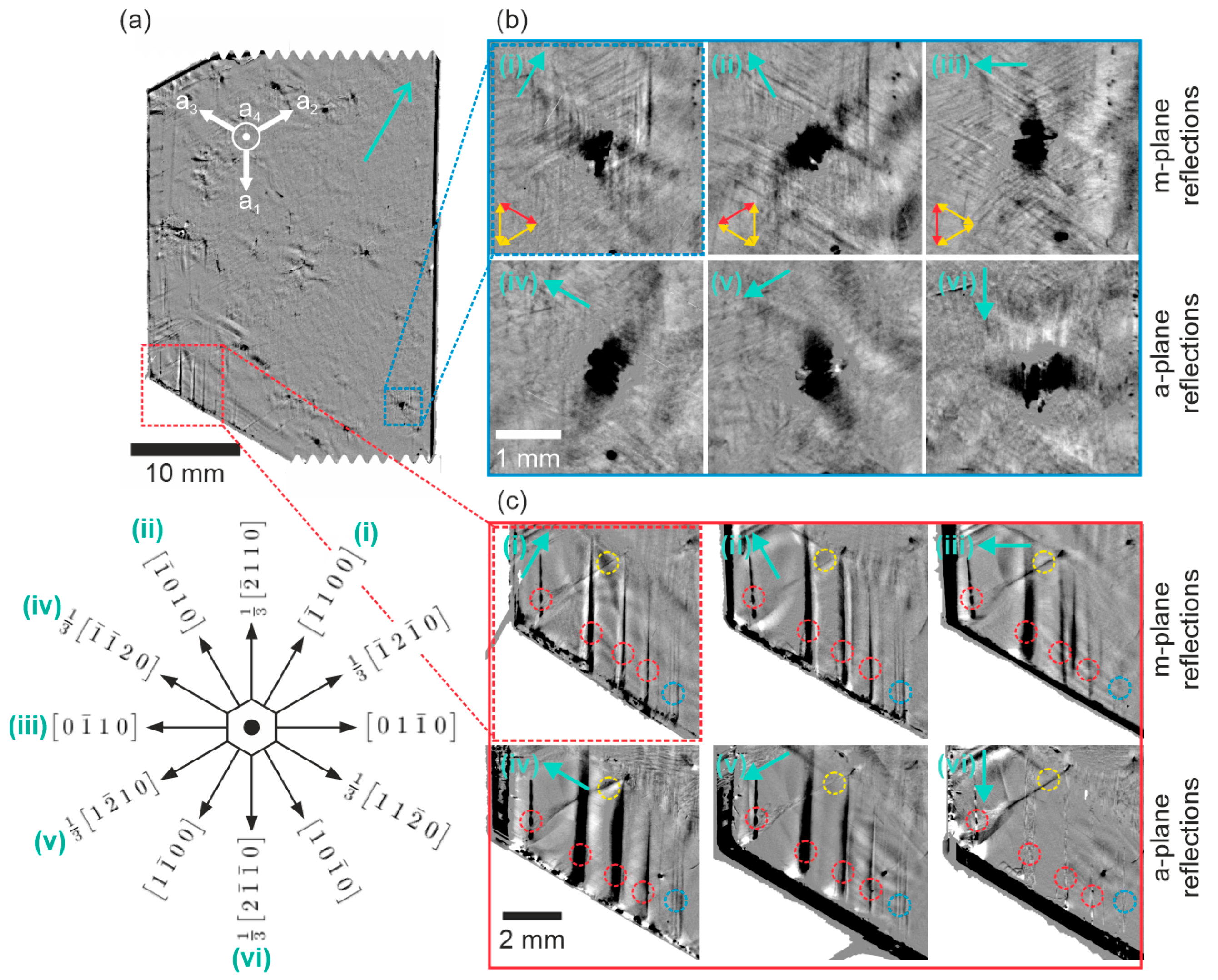
3.1. Crystal Habit, Lattice Curvature, and Facet Identification
3.2. X-Ray Topography in Back-Reflection Geometry of the Crystal Surface
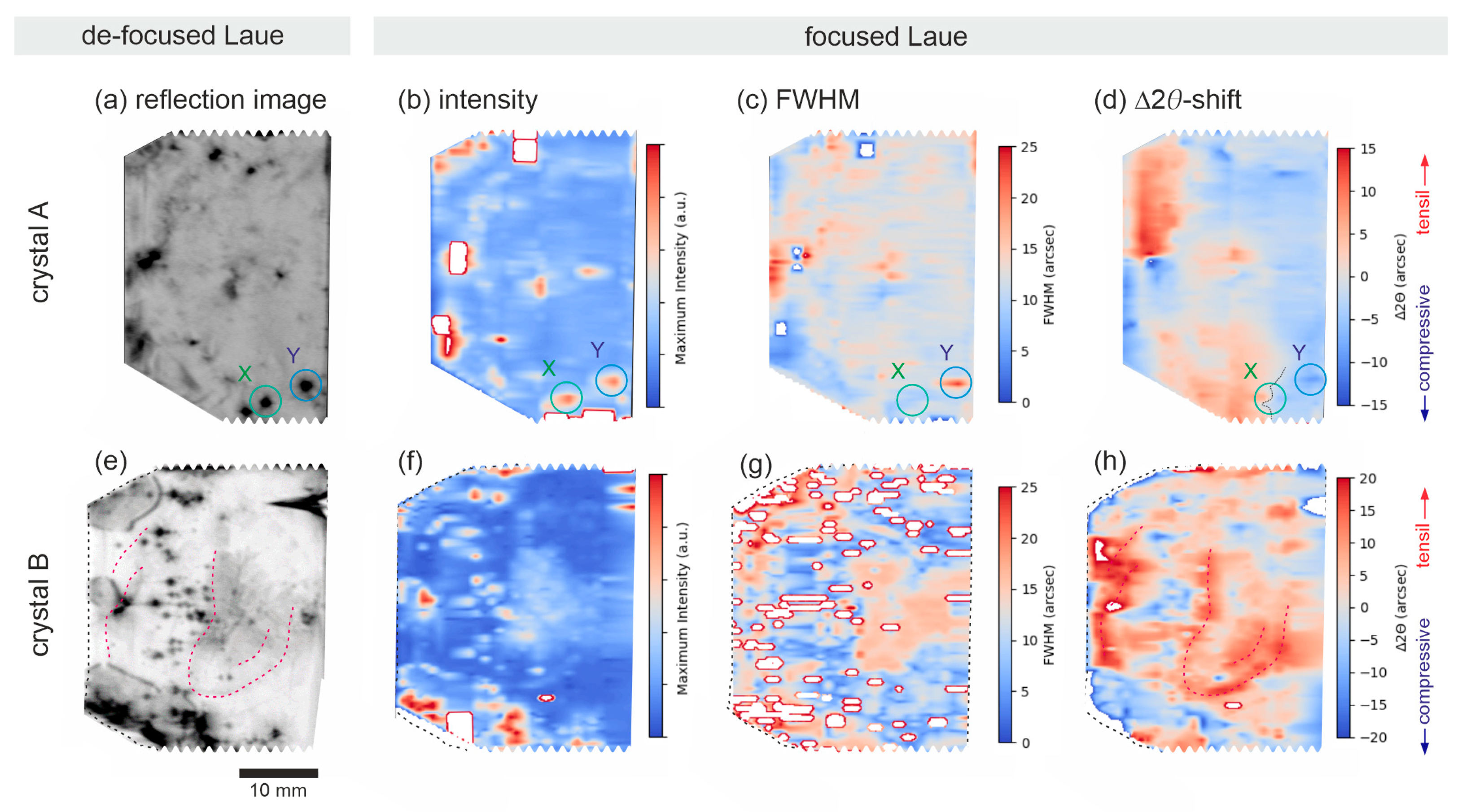
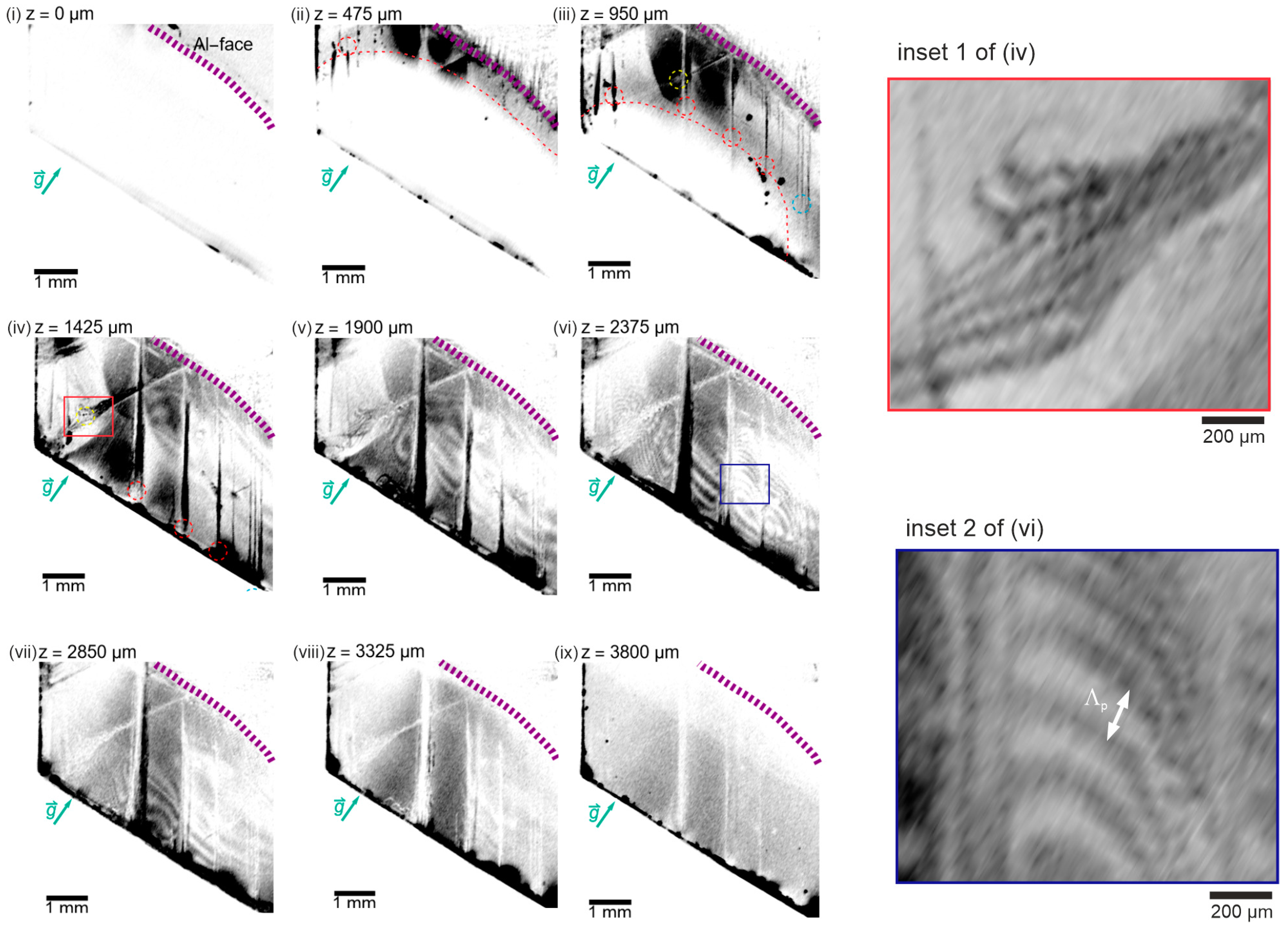
3.3. Integrated Bulk Characterization
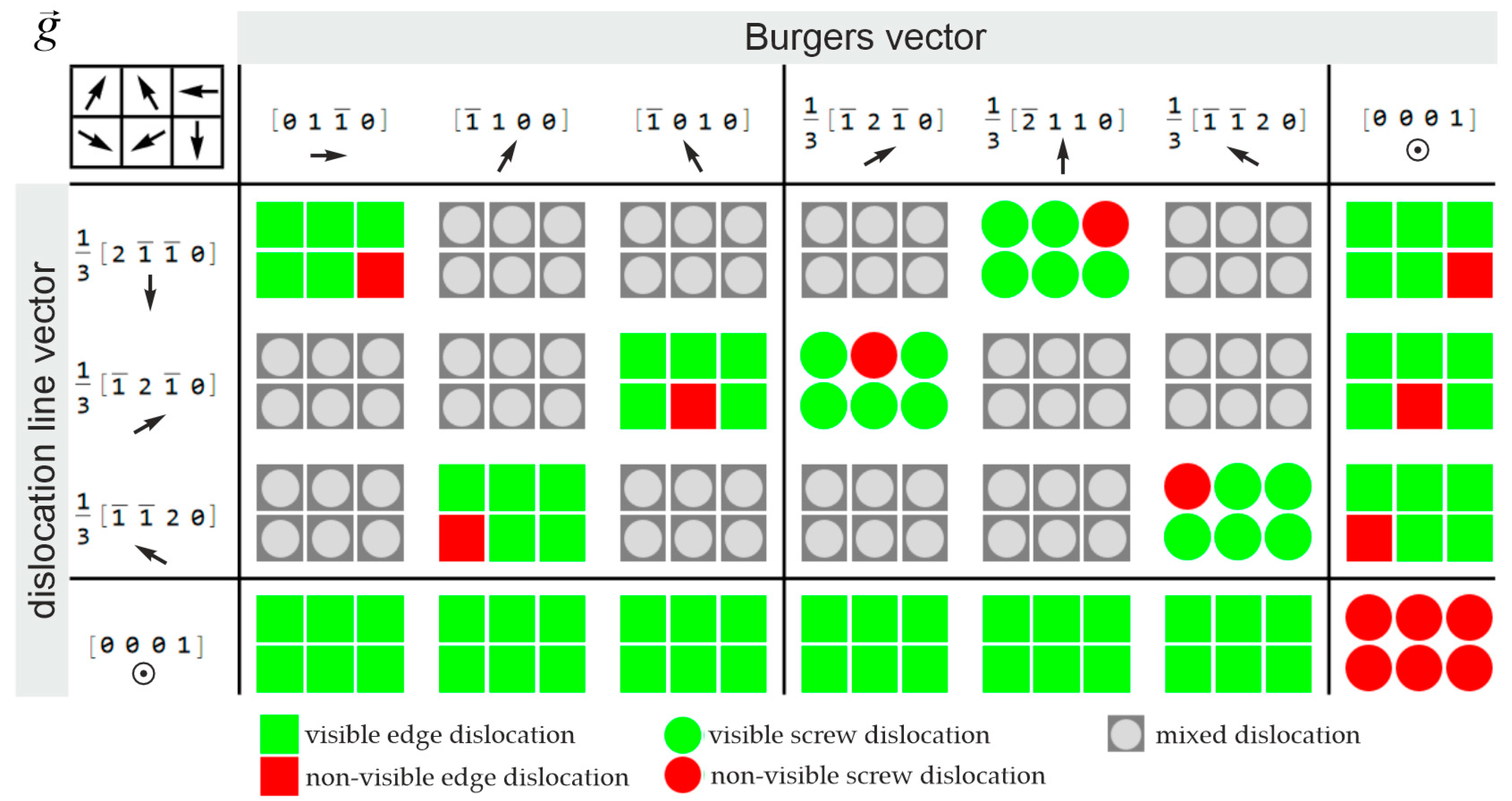
3.4. Three-Dimensional Dislocation Modeling—Revealing the Borrmann Effect
4. Conclusions: Assessment of Methods
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Measurement Procedure for X-Ray Topography
References
- Doolittle, W.A.; Matthews, C.M.; Ahmad, H.; Motoki, K.; Lee, S.; Ghosh, A.; Marshall, E.N.; Tang, A.L.; Manocha, P.; Yoder, P.D. Prospectives for AlN electronics and optoelectronics and the important role of alternative synthesis. Appl. Phys. Lett. 2023, 123, 070501. [Google Scholar] [CrossRef]
- Glenn Zorpette. The New, New Transistor. Available online: https://spectrum.ieee.org/aluminum-nitride (accessed on 8 May 2025).
- Semiconductor Today. HexaTech Investment Accelerates 100 mm AlN Substrate Program. Available online: https://www.semiconductor-today.com/news_items/2022/oct/hexatech-061022.shtml (accessed on 8 May 2025).
- Bondokov, R.T.; Hogan, K.; Norbury, G.Q.; Mark, J.; Branagan, S.P.; Ishigami, N.; Grandusky, J.; Chen, J. (Invited) Development of 3-inch AlN Single Crystal Substrates. ECS Trans. 2022, 109, 13–19. [Google Scholar] [CrossRef]
- Chen, W.-H.; Qin, Z.-Y.; Tian, X.-Y.; Zhong, X.-H.; Sun, Z.-H.; Li, B.-K.; Zheng, R.-S.; Guo, Y.; Wu, H.-L. The Physical Vapor Transport Method for Bulk AlN Crystal Growth. Molecules 2019, 24, 1562. [Google Scholar] [CrossRef]
- Dalmau, R.; Sitar, Z. AlN Bulk Crystal Growth by Physical Vapor Transport. In Springer Handbook of Crystal Growth; Dhanaraj, G., Byrappa, K., Prasad, V., Dudley, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 821–843. ISBN 978-3-540-74182-4. [Google Scholar]
- Sumathi, R.R. Review—Status and Challenges in Hetero-epitaxial Growth Approach for Large Diameter AlN Single Crystalline Substrates. ECS J. Solid State Sci. Technol. 2021, 10, 35001. [Google Scholar] [CrossRef]
- Amano, H.; Collazo, R.; de Santi, C.; Einfeldt, S.; Funato, M.; Glaab, J.; Hagedorn, S.; Hirano, A.; Hirayama, H.; Ishii, R.; et al. The 2020 UV emitter roadmap. J. Phys. D Appl. Phys. 2020, 53, 503001. [Google Scholar] [CrossRef]
- Hartmann, C.; Kabukcuoglu, M.P.; Richter, C.; Klump, A.; Schulz, D.; Juda, U.; Bickermann, M.; Hänschke, D.; Schröder, T.; Straubinger, T. Efficient diameter enlargement of bulk AlN single crystals with high structural quality. Appl. Phys. Express 2023, 16, 75502. [Google Scholar] [CrossRef]
- Lider, V.V. X-Ray Diffraction Topography Methods (Review). Phys. Solid State 2021, 63, 189–214. [Google Scholar] [CrossRef]
- Danilewsky, A.N. X-Ray Topography—More than Nice Pictures. Cryst. Res. Technol. 2020, 55, 2000012. [Google Scholar] [CrossRef]
- Dalmau, R.; Britt, J.; Fang, H.Y.; Raghothamachar, B.; Dudley, M.; Schlesser, R. X-Ray Topography Characterization of Large Diameter AlN Single Crystal Substrates. MSF 2020, 1004, 63–68. [Google Scholar] [CrossRef]
- Yao, Y.; Sugawara, Y.; Ishikawa, Y.; Okada, N.; Tadatomo, K. Crystallinity Evaluation and Dislocation Observation for an Aluminum Nitride Single-Crystal Substrate on a Wafer Scale. J. Electron. Mater. 2020, 49, 5144–5153. [Google Scholar] [CrossRef]
- Yao, Y.; Tsusaka, Y.; Ishikawa, Y.; Sugawara, Y.; Fujita, Y.; Matsui, J.; Okada, N.; Tadatomo, K. Study of dislocations in AlN single-crystal using bright-field synchrotron x-ray topography under a multiple-beam diffraction condition. Appl. Phys. Lett. 2020, 117, 092102. [Google Scholar] [CrossRef]
- Zhou, T.; Raghothamachar, B.; Wu, F.; Dalmau, R.; Moody, B.; Craft, S.; Schlesser, R.; Dudley, M.; Sitar, Z. Characterization of Threading Dislocations in PVT-Grown AlN Substrates via x-Ray Topography and Ray Tracing Simulation. J. Electron. Mater. 2014, 43, 838–842. [Google Scholar] [CrossRef]
- Raghothamachar, B.; Dudley, M.; Rojo, J.C.; Morgan, K.; Schowalter, L.J. X-ray characterization of bulk AIN single crystals grown by the sublimation technique. J. Cryst. Growth 2003, 250, 244–250. [Google Scholar] [CrossRef]
- Wicht, T.; Müller, S.; Weingärtner, R.; Epelbaum, B.; Besendörfer, S.; Bläß, U.; Weisser, M.; Unruh, T.; Meissner, E. X-ray characterization of physical-vapor-transport-grown bulk AlN single crystals. J. Appl. Crystallogr. 2020, 53, 1080–1086. [Google Scholar] [CrossRef] [PubMed]
- Straubinger, T.; Hartmann, C.; Kabukcuoglu, M.P.; Albrecht, M.; Bickermann, M.; Klump, A.; Bode, S.; Hamann, E.; Haaga, S.; Hurst, M.; et al. Dislocation Climb in AlN Crystals Grown at Low-Temperature Gradients Revealed by 3D X-ray Diffraction Imaging. Cryst. Growth Des. 2023, 23, 1538–1546. [Google Scholar] [CrossRef]
- Soukhojak, A.; Stannard, T.; Manning, I.; Lee, C.; Chung, G.; Gave, M.; Sanchez, E. Measurement of Dislocation Density in SiC Wafers Using Production XRT. MSF 2022, 1062, 304–308. [Google Scholar] [CrossRef]
- Christian Kranert, Christian Reimann, Shintaro Kobayashi, Yoshinoro Ueji, Kenta Shimamoto, Kazuhiko Omote. Scrutinising SiC with X-ray topography. Compd. Semicond. 2023, 29, 18–23. [Google Scholar]
- Kirste, L.; Grabianska, K.; Kucharski, R.; Sochacki, T.; Lucznik, B.; Bockowski, M. Structural Analysis of Low Defect Ammonothermally Grown GaN Wafers by Borrmann Effect X-ray Topography. Materials 2021, 14, 5472. [Google Scholar] [CrossRef] [PubMed]
- Kranert, C.; Wimmer, P.; Drouin, A.; Reimann, C.; Friedrich, J. Comparative study of methods for counting of dislocations in 4H-SiC. Mater. Sci. Semicond. Process. 2024, 170, 107948. [Google Scholar] [CrossRef]
- Bergmann, C.; Will, J.; Gröschel, A.; Weisser, M.; Magerl, A. Radial oxygen precipitation of a 12” CZ silicon crystal studied in-situ with high energy X-ray diffraction. Phys. Status Solidi A 2014, 211, 2450–2454. [Google Scholar] [CrossRef]
- Stockmeier, M.; Magerl, A. A focusing Laue diffractometer for the investigation of bulk crystals. J. Appl. Crystallogr. 2008, 41, 754–760. [Google Scholar] [CrossRef]
- Shul’pina, I.L.; Suvorov, E.V.; Smirnova, I.A.; Argunova, T.S. Section Methods of X-Ray Diffraction Topography. Tech. Phys. 2023, 68, 778–798. [Google Scholar] [CrossRef]
- Bearden, J.A. X-Ray Wavelengths. Rev. Mod. Phys. 1967, 39, 78–124. [Google Scholar] [CrossRef]
- Hubbell, J.; Seltzer, S. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients 1 keV to 20 MeV for Elements Z = 1 to 92 and 48 Additional Substances of Dosimetric Interest. Available online: http://physics.nist.gov/PhysRefData/XrayMassCoef/cover.html (accessed on 8 May 2025).
- Wikipedia. Kapton. Available online: https://en.wikipedia.org/wiki/Kapton (accessed on 8 May 2025).
- Nilsson, D.; Janzén, E.; Kakanakova-Georgieva, A. Lattice parameters of AlN bulk, homoepitaxial and heteroepitaxial material. J. Phys. D Appl. Phys. 2016, 49, 175108. [Google Scholar] [CrossRef]
- Bickermann, M.; Epelbaum, B.M.; Filip, O.; Tautz, B.; Heimann, P.; Winnacker, A. Faceting in AlN bulk crystal growth and its impact on optical properties of the crystals. Phys. Status Solidi C 2012, 9, 449–452. [Google Scholar] [CrossRef]
- Cui, Y.; Hu, X.; Xie, X.; Wang, R.; Xu, X. Spatial variation of lattice plane bending of 4H-SiC substrates. CrystEngComm 2017, 19, 3844–3849. [Google Scholar] [CrossRef]
- Yang, X.; Yu, J.; Chen, X.; Peng, Y.; Hu, X.; Xu, X.; Yang, X.; Song, Y.; Wang, R. Basal plane bending of 4H-SiC single crystals grown by sublimation method with different seed attachment methods. CrystEngComm 2018, 20, 6957–6962. [Google Scholar] [CrossRef]
- Ishiji, K.; Kawado, S.; Hirai, Y.; Nagamachi, S. Determination of observable depth of dislocations in 4H-SiC by X-ray topography in back reflection. Jpn. J. Appl. Phys. 2017, 56, 106601. [Google Scholar] [CrossRef]
- Bowen, D.K.; Tanner, B.K. High Resolution X-Ray Diffractometry and Topography; Taylor & Francis: London, UK, 1998; ISBN 0-8506-6758-5. [Google Scholar]
- Authier, A. Dynamical Theory of X-Ray Diffraction; Oxford University Press: Oxford, UK, 2001; ISBN 9780198559603. [Google Scholar]
- Fujie, F.; Peng, H.; Ailihumaer, T.; Raghothamachar, B.; Dudley, M.; Harada, S.; Tagawa, M.; Ujihara, T. Synchrotron X-ray topographic image contrast variation of screw-type basal plane dislocations located at different depths below the crystal surface in 4H-SiC. Acta Mater. 2021, 208, 116746. [Google Scholar] [CrossRef]
- Ailihumaer, T.; Peng, H.; Fujie, F.; Raghothamachar, B.; Dudley, M.; Harada, S.; Ujihara, T. Surface relaxation and photoelectric absorption effects on synchrotron X-ray topographic images of dislocations lying on the basal plane in off-axis 4H-SiC crystals. Mater. Sci. Eng. B 2021, 271, 115281. [Google Scholar] [CrossRef]
- Lübbert, D.; Baumbach, T.; Mikulík, P.; Pernot, P.; Helfen, L.; Köhler, R.; Katona, T.M.; Keller, S.; DenBaars, S.P. Local wing tilt analysis of laterally overgrown GaN by X-ray rocking curve imaging. J. Phys. D Appl. Phys. 2005, 38, A50–A54. [Google Scholar] [CrossRef]
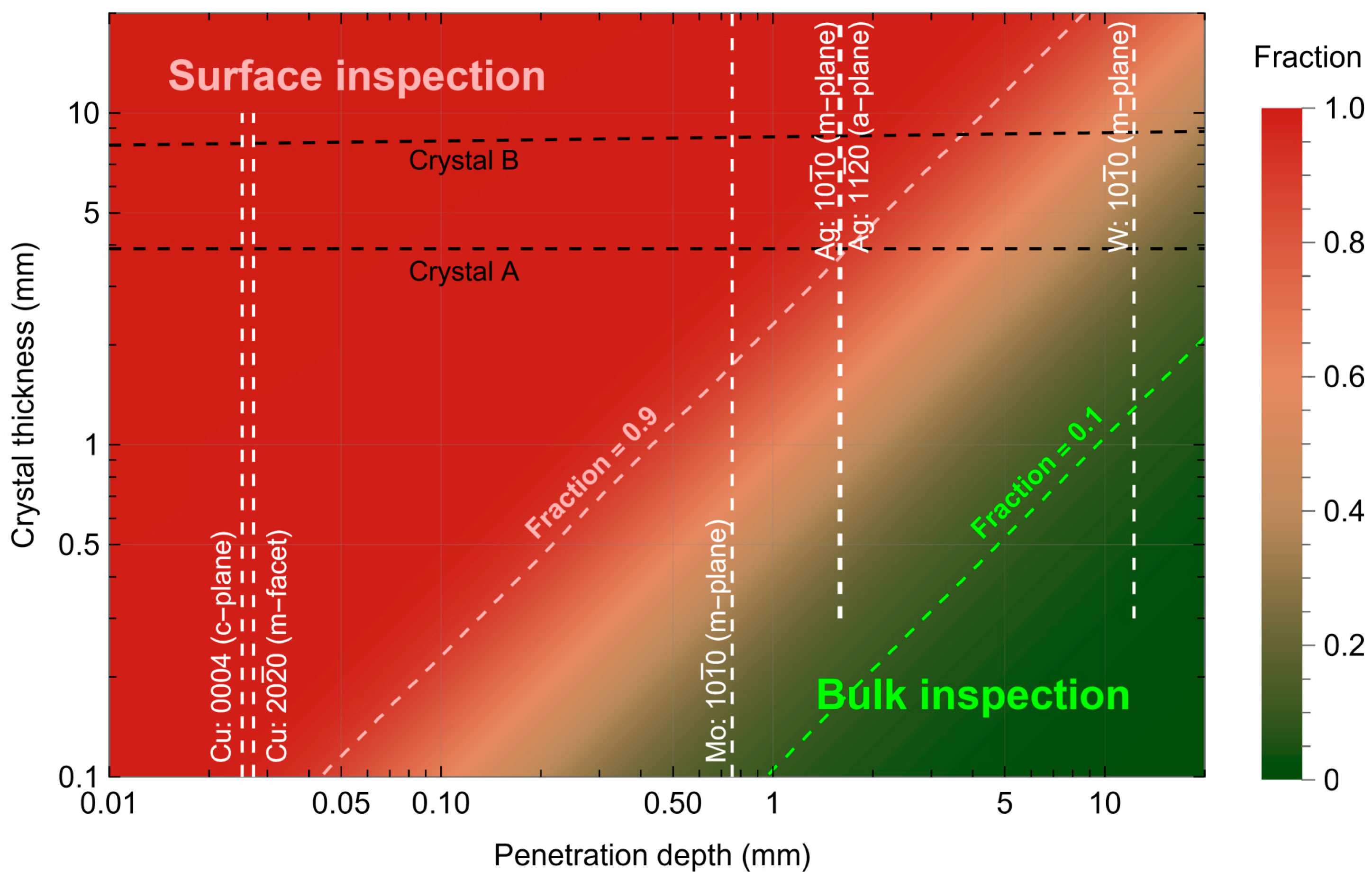


| Ambient Pressure | Growth Temperature | Axial Temp Gradient | Growth Rate | Growth Time | Crystal Thickness | |
|---|---|---|---|---|---|---|
| crystal A | ~850 mbar | ~2500 K | low | 37 µm/h | 92 h | 3.9 mm |
| crystal B | high | 119 µm/h | 63 h | 8 mm |
| Anode Material | X-Ray Power | Characteristic Wavelength 1 | Absorption Coefficient 2 | Penetration Depth 3 |
|---|---|---|---|---|
| Copper (Cu) | 1200 W | 1.54056 Å | 114.0 cm−1 | 88 µm |
| Molybdenum (Mo) | 1200 W | 0.70930 Å | 13.2 cm−1 | 760 µm |
| Silver (Ag) | 780 W | 0.55941 Å | 6.2 cm−1 | 1610 µm |
| Tungsten (W) | 500 W | 0.20901 Å | 0.8 cm−1 | 12,260 µm |
| Surface | Lattice Plane | Reflection Index | Bragg Angle | Anode |
|---|---|---|---|---|
| Surface inspection (back-reflection geometry) | ||||
| N-face/Al-face | c-plane | 38.2212° | Cu | |
| m-facets | m-plane | 34.8891° | Cu | |
| a-facets | a-plane | 29.6933° | Cu | |
| Bulk inspection (transmission geometry) | ||||
| N-face up | m-plane | 5.9609° | Ag | |
| N-face up | a-plane | 10.3624° | Ag | |
| N-face up | m-plane | 2.23° | W | |
| N-Face | Al-Face | |||
|---|---|---|---|---|
| crystal A | m | m | m | m |
| crystal B | − | m | m | m |
| Qualifiers | Surface Inspection | Bulk Inspection | |
|---|---|---|---|
| Integrated Bulk | 3D Section Topography | ||
| performance | fast | time-consuming | very time-consuming |
| crystal thickness | independent | energy dependent | energy dependent |
| dislocation content | only at surface, threading screw dislocations | full dislocation networks | full trajectory of line dislocation |
| topograph resolution | camera dependent | camera dependent | in expense of time |
| mappings | full crystal | full crystal | small parts |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weingärtner, R.; Epelbaum, B.; Lesnik, A.; Lukin, G.; Müller, S.; Schiller, L.; Meissner, E.; Weisser, M.; Besendörfer, S. Inspection of Bulk Crystals for Quality Control in Crystal Growth: Assessment of High-Energy X-Ray Transmission Topography and Back-Reflection Topography Pinpointed for Physical Vapor Transport-Grown Aluminum Nitride. Crystals 2025, 15, 449. https://doi.org/10.3390/cryst15050449
Weingärtner R, Epelbaum B, Lesnik A, Lukin G, Müller S, Schiller L, Meissner E, Weisser M, Besendörfer S. Inspection of Bulk Crystals for Quality Control in Crystal Growth: Assessment of High-Energy X-Ray Transmission Topography and Back-Reflection Topography Pinpointed for Physical Vapor Transport-Grown Aluminum Nitride. Crystals. 2025; 15(5):449. https://doi.org/10.3390/cryst15050449
Chicago/Turabian StyleWeingärtner, Roland, Boris Epelbaum, Andreas Lesnik, Gleb Lukin, Stephan Müller, Leon Schiller, Elke Meissner, Matthias Weisser, and Sven Besendörfer. 2025. "Inspection of Bulk Crystals for Quality Control in Crystal Growth: Assessment of High-Energy X-Ray Transmission Topography and Back-Reflection Topography Pinpointed for Physical Vapor Transport-Grown Aluminum Nitride" Crystals 15, no. 5: 449. https://doi.org/10.3390/cryst15050449
APA StyleWeingärtner, R., Epelbaum, B., Lesnik, A., Lukin, G., Müller, S., Schiller, L., Meissner, E., Weisser, M., & Besendörfer, S. (2025). Inspection of Bulk Crystals for Quality Control in Crystal Growth: Assessment of High-Energy X-Ray Transmission Topography and Back-Reflection Topography Pinpointed for Physical Vapor Transport-Grown Aluminum Nitride. Crystals, 15(5), 449. https://doi.org/10.3390/cryst15050449







