Delicate Competition Between Different Excitonic Orderings in Ta₂NiSe₅

Abstract

We investigate the energetics of the quasi-one-dimensional layered compound ${\mathrm{Ta}}_2{\mathrm{NiSe}}_5$ in the excitonic phase within the six-band model using Hartree–Fock calculations. We calculate energies of states with different kinds of excitonic order and show that they differ by less than meV and depend sensitively on precise values of interchain hopping matrix elements.

1. Introduction

${\mathrm{Ta}}_2{\mathrm{NiSe}}_5$ (TNS) is a layered transition metal dichalcogenide compound that undergoes a semi-metal to semi-conductor phase transition followed by a structural transition from a high-temperature orthorhombic phase to a low-temperature monoclinic phase at $T_c=325$ K [1,2]. A gap of 0.15 eV opens across the Fermi level between the valence and conduction band due to this transition [3]. In the monoclinic phase, the Ta and Se atoms undergo a shear-like displacement, and the reflection symmetries are broken [4], but the magnitude of the displacement is moderate with the monoclinic angle being small (0.7 degrees only) [1]. The size of the gap exceeds what one finds in standard LDA calculations in monoclinic phase [5] (see, however, [4,6]). The large gap and peculiar two-hump shape of the valence band inspired the interpretations [7,8,9] that the dominant instability is of electronic origin and the low-temperature state was proposed to be thought as an excitonic insulator [10,11,12,13,14]. Additionally, short time scales and peculiar fluence dependences observed in pump–probe time-resolved studies [15,16,17,18,19] as well as the vanishing of thermopower at low temperatures [20] have been interpreted in terms of electronic degrees of freedom and argued to point to the excitonic ground state.

In its purest form, as relevant in heterostructure/bilayer systems [21,22,23,24,25,26], the excitonic phase transition results in the spontaneous breaking of the U(1) symmetry associated with the separate conservation of charge in valence/conduction orbital (or layer) subspaces coupled by Coulomb repulsion. Recent theoretical work [27] clarified the nature of symmetry breaking in the putative excitonic phase and pointed out that in the case of TNS, excitonic condensation leads to spontaneous hybridization terms that break mirror symmetries only.

A different line of research has emphasized the existence of structural instabilities [4,6] without explicit reference to excitonic ordering. Notably, the monoclinic structure possesses lower energy, and its deformation aligns with the freezing of an unstable ${\mathrm{B}}_{2g}$ mode. Theoretical work in Ref. [28] also concludes that ${\mathrm{Ta}}_2{\mathrm{NiS}}_5$ and ${\mathrm{Ta}}_2{\mathrm{NiSe}}_5$ are not fundamentally dissimilar, suggesting that many properties might be shared. Consistent with this line of thought, some experimental pump–probe ARPES (Angle-Resolved Photoemission Spectroscopy) studies [29] argue against the presence of excitonic effects. This is challenged by a recent nonequilibrium Raman study [30] that found a nonequilibrium state without a gap but with monoclinic distortion.

In our previous work [31], we studied the collective modes in TNS using a realistic model that treat the electronic and lattice instability on an equal footing within the Hartree–Fock treatment. In the excitonic phase, we saw the signature of a massive phase mode due to the breaking of discrete lattice symmetries, and we studied the interplay with the electron–phonon interaction that led to the increased mass of the phase mode, which also stabilized excitonic ordering.

In this paper, we inspect the excitonic ordering in the absence of electron–phonon interaction more closely. We find that within the Hartree–Fock approximation, one can stabilize excitonic ordering distinct from the one that is compatible with structural distortions in the monoclinic phase. We evaluate the energies of those ordered states and find that their energies are close (the energy differences are less than meV). Depending on precise values of the overall interchain hopping amplitude (that are all compatible with the orthorhombic symmetry), two different kinds of excitonic ordering may be found in the ground state. For the choice of hopping matrix elements exploited in Refs. [27,31], the ordering compatible with monoclinic distortion is found.

2. Model and Methods

TNS is a layered compound where the different layers stack up in the ‘b’ direction and a single layer lies in the ‘ac’ plane. In each ‘ac’ plane layer one finds Ta-Ni-Ta chains running along a direction and that are weakly hybridized in the c-direction and these chains within a 2D layer make TNS a quasi-one-dimensional-layered compound. The unit cell contains 4 Ta and 2 Ni atoms that constitute elements of two Ta-Ni-Ta chains. We consider a realistic minimal model of a 2D layer of TNS following Ref. [27]. We consider low-energy bands spanned by one Wannier d-orbital per each Ta and Ni atom using the 6-atom unit cell (see Figure 1). In the unit cell, the four Ta atoms are labeled 1 to 4, and the two Ni atoms are labeled 5 and 6. The 6 atoms are distributed in two chains as (1, 2, 5) and (3, 4, 6) as marked by green lines in Figure 1. In the high-temperature orthorhombic structure (Cmcm space group), the symmetry group contains inversion $\mathcal{I}$ and four reflection symmetries for planes parallel and perpendicular to the Ta-Ni-Ta chain (${\sigma }_{\Vert ,\perp }^{A/B}$) as marked in Figure 1. The reflection symmetries are broken as we enter the monoclinic phase (C2/c space group) due to the shear displacement of the Ta atoms, but the inversion symmetry and the product of the reflection symmetries are preserved [6,27].

The six bands of TNS are given by Hamiltonian

$${\widehat{H}}_{\mathrm{kin}}=\sum _{\mathbf{R}\delta }{\widehat{\Psi }}_{\mathbf{R}+\delta \sigma }^{†}T\left(\delta \right){\widehat{\Psi }}_{\mathbf{R}\sigma },$$

(1)

where the sum is taken over all unit cells $\mathbf{R}$ and neighboring cells $\delta$ as parametrized by the matrix of tight-binding hopping elements T. We have introduced the spinor ${\widehat{\Psi }}_{\mathbf{R}\sigma }=\{{\widehat{c}}_{1\sigma \mathbf{R}},\dots ,{\widehat{c}}_{6\sigma \mathbf{R}}\}$ and ${\widehat{c}}_{i\sigma \mathbf{R}}$ is the annihilation operator in unit cell $\mathbf{R}$, orbital i and spin $\sigma$. In Figure 1, the crystalline structure and unit cell are depicted.

The matrix elements of the kinetic energy $T\left(\delta \right)$ obtained using density-functional theory and Wannierization technique [27,32] are given in

Table 1. Elements of the hopping matrix $T\left(\delta \right)$ taken from Ref. [27].

Cases	Hopping Matrix Elements t($\mathit{\delta }$)
Intra-chain Ta-Ta	${\mathrm{T}}_{ii}$ (${\mathrm{a}}_x$, 0) = ${\mathrm{T}}_{ii}$ (${-\mathrm{a}}_x$, 0) = −0.72 eV
	${\mathrm{T}}_{ii}$ (0, 0) = 1.35 eV, i = 1,...,4
Intra-chain Ni-Ni	${\mathrm{T}}_{ii}$ (${\mathrm{a}}_x$, 0) = ${\mathrm{T}}_{ii}$ (${-\mathrm{a}}_x$, 0) = 0.30 eV,
	${\mathrm{T}}_{ii}$ (0, 0) = −0.36 eV, i = 5, 6
Intra-chain Ta-Ni	${\mathrm{T}}_{15}$ (${\mathrm{a}}_x$, 0) = ${\mathrm{T}}_{25}$ (${\mathrm{a}}_x$, 0) = ${-\mathrm{T}}_{25}$ (0) = ${-\mathrm{T}}_{15}$ (0)
	= ${-\mathrm{T}}_{36}$ (0) = ${-\mathrm{T}}_{46}$ (0) = ${\mathrm{T}}_{36}$ (${-\mathrm{a}}_x$, 0), ${\mathrm{T}}_{46}$ (${-\mathrm{a}}_x$, 0) = −0.035 eV
Inter-chain Ta-Ni	${\mathrm{T}}_{35}$ (${\mathrm{a}}_x$, 0) = ${-\mathrm{T}}_{35}$ (${-\mathrm{a}}_x$, 0), ${\mathrm{T}}_{45}$ (${\mathrm{a}}_x$, ${\mathrm{a}}_y$) =
	${-\mathrm{T}}_{45}$ (${-\mathrm{a}}_x$, ${\mathrm{a}}_y$) = −0.04 eV,
	${\mathrm{T}}_{26}$ (${\mathrm{a}}_x$, 0) = ${-\mathrm{T}}_{26}$ (${-\mathrm{a}}_x$, 0) =
	${\mathrm{T}}_{16}$ (${\mathrm{a}}_x$, ${-\mathrm{a}}_y$) = ${-\mathrm{T}}_{16}$ (${-\mathrm{a}}_x$, ${-\mathrm{a}}_y$) = ${\mathrm{T}}_{45}$ (${-\mathrm{a}}_x$, ${\mathrm{a}}_y$)
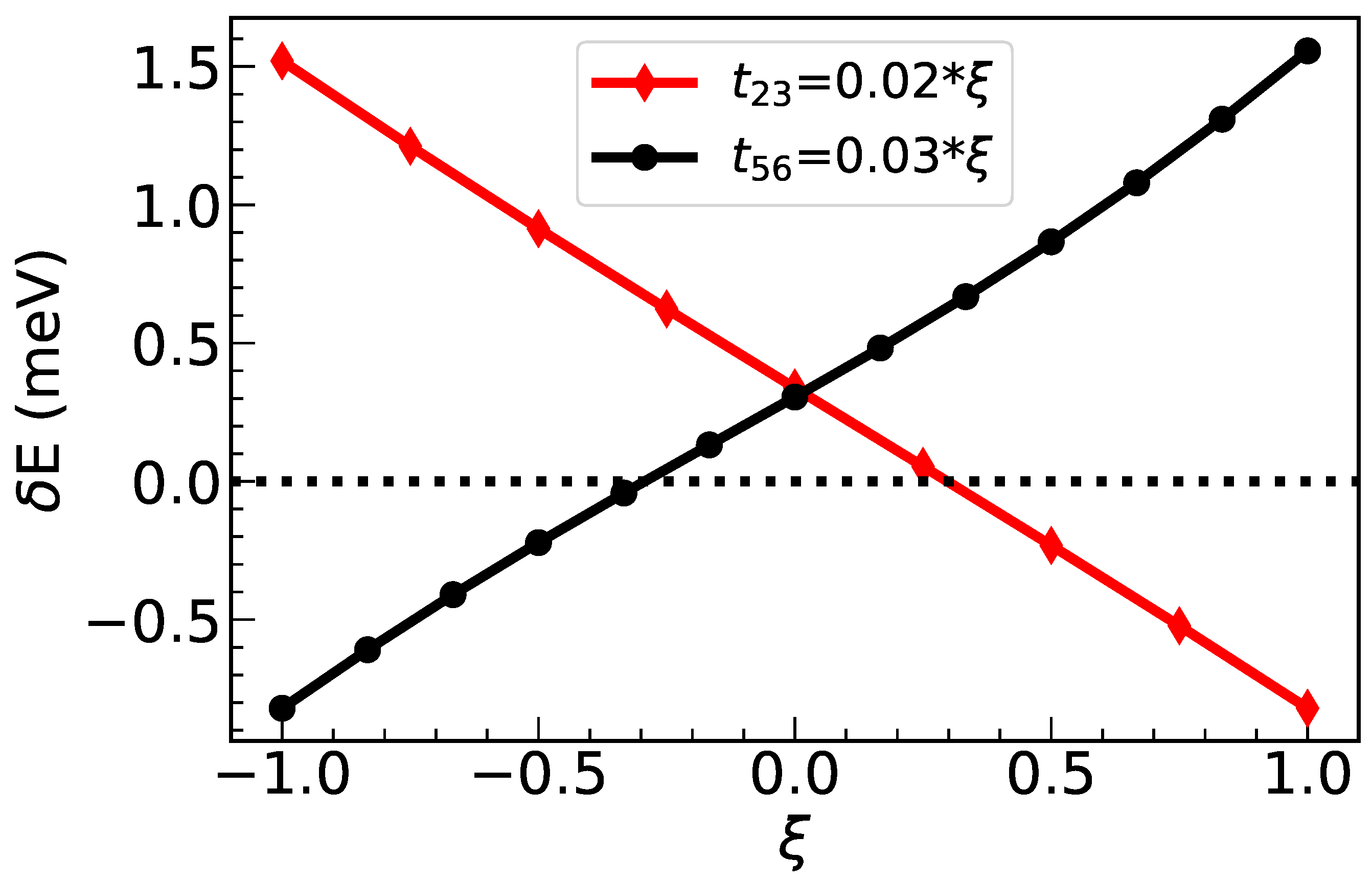
Inter-chain Ta-Ta	${\mathrm{T}}_{23}$ (0) = ${\mathrm{T}}_{23}$ (${\mathrm{a}}_x$, 0) = ${\mathrm{T}}_{41}$ (${-\mathrm{a}}_x$, ${\mathrm{a}}_y$) =
	${\mathrm{T}}_{41}$ (0, ${\mathrm{a}}_y$) = 0.02 eV
Inter-chain Ni-Ni	${\mathrm{T}}_{65}$ (0) = ${\mathrm{T}}_{65}$ (${\mathrm{a}}_x$, 0) = ${\mathrm{T}}_{65}$ (${\mathrm{a}}_x$, ${\mathrm{a}}_y$) =
	${\mathrm{T}}_{65}$ (0, ${\mathrm{a}}_y$) = −0.03 eV

We note that in the above notation ${\mathrm{T}}_{ij}$ (0, 0) indicates hopping within the unit cell, ${\mathrm{T}}_{ij}$ (${\mathrm{a}}_x$, 0) or ${\mathrm{T}}_{ij}$ (${-\mathrm{a}}_x$, 0) indicates horizontal hopping (along ‘a’ direction) to the right or left in the nearest neighbour unit cell. ${\mathrm{T}}_{ij}$ (${\mathrm{a}}_y$, 0) or ${\mathrm{T}}_{ij}$ (${-\mathrm{a}}_y$, 0) indicates vertical hopping (along ‘c’ direction) to up or down in the nearest neighbour unit cell. A detailed pictorial representation is available in Ref. [27].

. We note that nearest neighbour hopping is considered in the vertical and horizontal directions. Hopping within one Ta-Ni-Ta chain is denoted as “intra-chain” while hopping between chains is denoted as ‘inter-chain’.

The electronic interaction energy is given by

$$\begin{array}{ccc}\hfill {\widehat{H}}_{\mathrm{int}}& =& U\sum _{\mathbf{R}i}{\widehat{n}}_{i\uparrow \mathbf{R}}{\widehat{n}}_{i\downarrow \mathbf{R}}+V\sum _{\begin{array}{c}{\delta }_i\in \{1,2\}\\ \mathbf{R}\sigma {\sigma }^{\prime }\end{array}}{\widehat{n}}_{i\sigma \mathbf{R}+{\delta }_i}{\widehat{n}}_{5{\sigma }^{\prime }\mathbf{R}}\hfill \\ & +& V\sum _{\begin{array}{c}{\delta }_i\in \{3,4\}\\ \mathbf{R}\sigma {\sigma }^{\prime }\end{array}}{\widehat{n}}_{i\sigma \mathbf{R}+{\delta }_i}{\widehat{n}}_{6{\sigma }^{\prime }\mathbf{R}},\hfill \end{array}$$

(2)

where the first term represents the on-site Hubbard interaction for all atoms. The second and third terms describe the repulsion between nearest neighbours, where ${\delta }_i$ sums over all nearest neighbours of both Ni atoms. In momentum space, the interaction reads

$${\widehat{H}}_{\mathrm{int}}=\sum _{\mathbf{k},\mathbf{q}}{V}_{\mathbf{q}}^{ij}{\widehat{n}}_{i\mathbf{k}}{\widehat{n}}_{j\mathbf{k}+\mathbf{q}},$$

where we have introduced the full density operator at momentum $\mathbf{k}$ for orbital i as ${\widehat{n}}_{i\mathbf{k}}={\sum }_{\mathbf{q}\sigma }{\widehat{c}}_{i\sigma \mathbf{k}+\mathbf{q}}^{†}{\widehat{c}}_{i\sigma \mathbf{q}}.$ The interaction vertex matrix is given by

$$V_{\mathbf{k}}=\left(\begin{array}{cccccc}U/2& 0& 0& 0& V_1\left(\mathbf{k}\right)& 0\\ 0& U/2& 0& 0& V_1\left(\mathbf{k}\right)& 0\\ 0& 0& U/2& 0& 0& V_2\left(\mathbf{k}\right)\\ 0& 0& 0& U/2& 0& V_2\left(\mathbf{k}\right)\\ V_1^{*}\left(\mathbf{k}\right)& V_1^{*}\left(\mathbf{k}\right)& 0& 0& U/2& 0\\ 0& 0& V_2^{*}\left(\mathbf{k}\right)& V_2^{*}\left(\mathbf{k}\right)& 0& U/2\end{array}\right),$$

(3)

with $V_1=V(1+{exp}^{\mathrm{i}{k}_x})$ and $V_2=V(1+{exp}^{-\mathrm{i}{k}_x})$.

We solve the problem using the Hartree Fock method as used in Refs. [27,31]. The Hartree contribution to the self-energy is given by

$${\Sigma }_{ii}^H\left(t\right)=\left\{\begin{array}{c}{V}_{\mathbf{k}=0}^{ii}{n}_i\left(t\right)\mathrm{intraorbital}\hfill \\ 2V_{\mathbf{k}=0}^{ij}{n}_j\left(t\right)\mathrm{interorbital},\hfill \end{array}\right.$$

(4)

where we have assumed the translational invariance $n_{i,\mathbf{R}}=n_i$ and employed the Einstein notation. The Fock term is given as

$${\Sigma }_{ij,\mathbf{k}}^F\left(t\right)=-\sum _{\mathbf{q}}{V}_{\mathbf{q}}^{ij}\langle {\widehat{\varphi }}_{ij,\mathbf{k}-\mathbf{q}}\rangle \left(t\right).$$

(5)

Excitonic order is given by nonvanishing expectation value of ${\widehat{\varphi }}_{\mathbf{R}}=\{{\widehat{\varphi }}_{15\mathbf{R}},{\widehat{\varphi }}_{25\mathbf{R}},{\widehat{\varphi }}_{36\mathbf{R}},{\widehat{\varphi }}_{46\mathbf{R}}\}.$ Here ${\widehat{\varphi }}_{ij\mathbf{R}}={\sum }_{\sigma }{\widehat{c}}_{i\sigma \mathbf{R}}^{†}{\widehat{c}}_{j\sigma \mathbf{R}}+{\widehat{c}}_{i\sigma \mathbf{R}\pm a}^{†}{\widehat{c}}_{j\sigma \mathbf{R}},$ and a is a shift in the x direction. We choose $+(-)$ for $\left\{ij\right\}=15,25(36,46)$, respectively. In the ground state, the components of the order parameter ${\varphi }_{\mathbf{R}}=\langle {\widehat{\varphi }}_{\mathbf{R}}\rangle$ are real. Their signs (total $2^4=16$ choices of which subset (1111), (1-1-11), (1-11-1), and (1-111) corresponds to physically different cases) determine distinct excitonic orderings. Among these, the ordering that is described by ${\varphi }_{\mathbf{R}}={\varphi }_0\{1,-1,-1,1\}$ breaks ${\sigma }_{\Vert ,\perp }^{A/B}$ symmetries consistent with the monoclinic distortion [6,27]. We investigate if (and when) this ordering has the lowest energy.

3. Results

We set the intra-band interaction $U=2.5$ eV and the inter-band interaction V = 0.785 eV, which leads to the excitonic phase with a gap that agrees with the experimental band gap. In practice, our calculations were performed at $\beta =1/T=100$, but we checked that to the reported number of digits, the energies do not change upon further cooling down, so the results are characteristic of the ground state. When we do not write out the unit of energy explicitly, we have eV in mind.

We calculate the energies of distinct symmetry broken states for parameters in Table 1, and we find three distinct energies corresponding to phases (1-1-11), (11-1-1), and (1-111) with non-degenerate energies as presented in

Table 2. The non-degenerate total energies (${\mathrm{E}}_{\mathrm{tot}}$), bare band gap ${\mathrm{E}}_{\mathrm{gap}}$, energy difference between the maximally hybridized band ${\mathrm{E}}_{\mathrm{ex}}$ for different orderings and hoppings given in Table 1 ${\mathrm{E}}_{\mathrm{G}}$ denote the ground state energy. All energies are in eV.

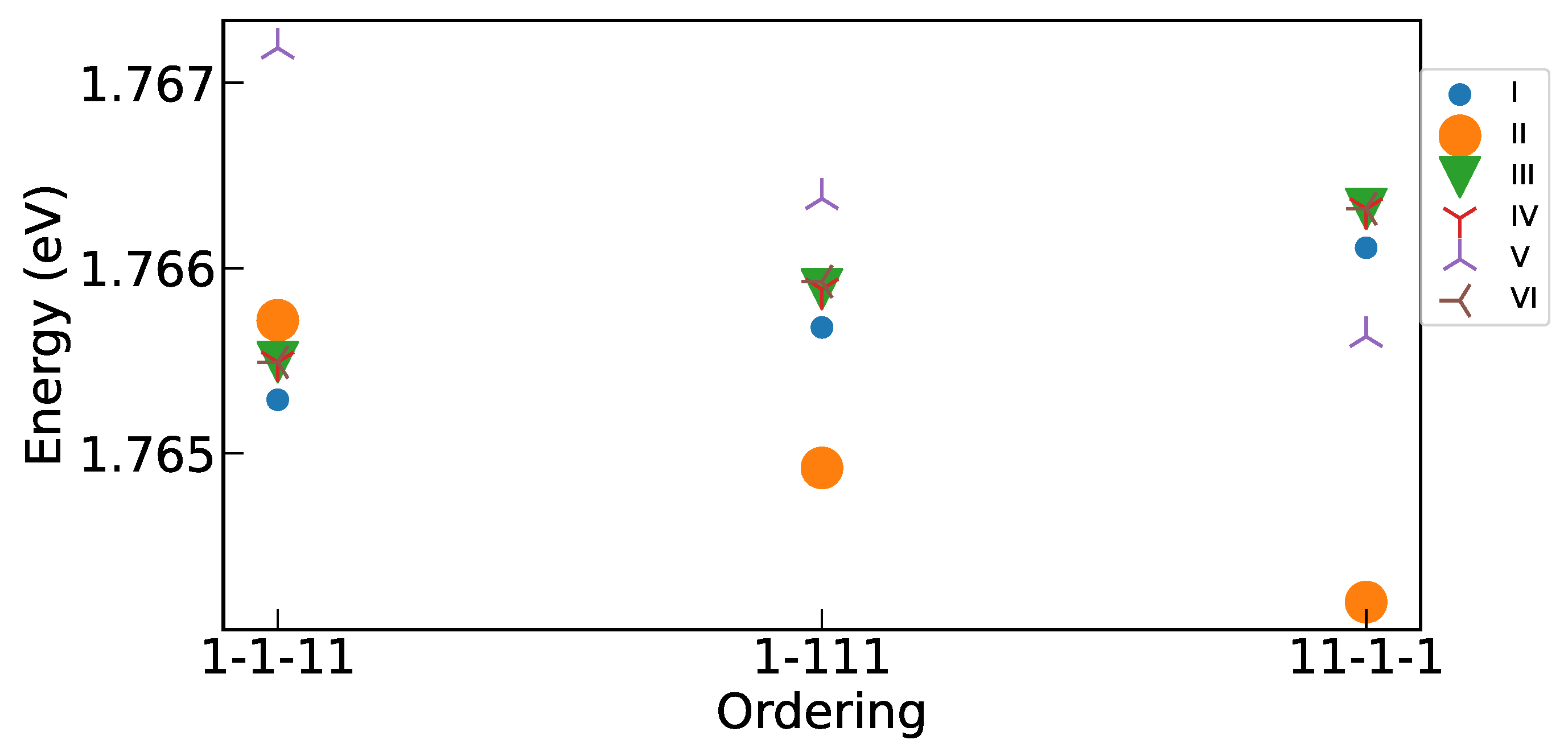
Ordering	${\mathrm{E}}_{\mathbf{tot}}$	${\mathrm{E}}_{\mathbf{gap}}$	${\mathrm{E}}_{\mathbf{ex}}$	Comment
(1-1-11)	1.765289	0.138	0.308	${\mathrm{E}}_{\mathrm{G}}$
(11-1-1)	1.766109	0.133	0.328	${\mathrm{E}}_{\mathrm{G}}$ + $8\times {10}^{-4}$
(1-111)	1.765679	0.139	0.340	${\mathrm{E}}_{\mathrm{G}}$ + $3.9\times {10}^{-4}$

. The symmetry broken phases of the different excitonic orderings in Table 2 are pictorially represented in Figure 2. Phases (1111) and (1-1-11) are degenerate. If one investigates a single Ta-Ni-Ta chain, orderings 1-1 and 11 are degenerate, and only the relative signs of interchain hybridization affect the energetics. While all components of the order parameter have the same magnitude in the case of orderings (1-1-11), (11-1-1) with value ${\varphi }_0=0.1476$, two distinct magnitudes are found for the ordering (1-111) with components $|{\varphi }_{15}|=|{\varphi }_{46}|=0.1514$, and $|{\varphi }_{25}|=|{\varphi }_{36}|=0.1387$.

For our chosen model in Table 1, we indeed see that the monoclinic phase (1, −1, −1, 1) is the ground state. However, the energy of other symmetry-broken phases is larger by less than a meV. We further show in Figure 3a–c the band structure corresponding to the different phases. All symmetry-broken phases show the excitonic gap with nominal changes in the bandgap (around 0.6 per cent) at the ‘$\Gamma$’ point as presented in Table 2. The orbital weights of Ta (in blue) and Ni (in red) show that the maximum hybridization occurs along the ‘Z-$\Gamma$-X’ path and affects the higher conduction bands of Ta. Moreover, the energy gap between the maximally hybridized bands (${\mathrm{E}}_{\mathrm{ex}}$) is more than twice the bare band gap ${\mathrm{E}}_{\mathrm{gap}}$ as shown in Table 2. The behavior of excitonic hybridization is similar for the different phases.

We investigated why energy differs for various phases. If we decouple the two chains, i.e., switch off the interchain matrix elements, all energies would be degenerate, and therefore the inter-chain hoppings determine the ground state configuration. The degeneracy of energy for a decoupled chain can be explained analytically by a simple three-chain model as in Ref. [33].

The monoclinic phase (1-1-11) is the ground state for the choice of model in Table 1. We comment here that while the different hopping parameters in the orthorhombic phase should respect the crystal symmetry, which restrains the choice of their relative phases, it is still possible to have different choices of overall signs of the hopping amplitude (+/−) in Table 1 without disturbing the crystal symmetry. The precise magnitude of the hoppings (including the overall sign) relies on the details of the first-principle calculation and Wannier construction, e.g., choice and the orientation of the Wannier orbitals.

It turns out that the ground state ordering varies with the precise choice of the overall interchain hopping amplitudes. To demonstrate this, we first varied the signs of the interchain hoppings and presented the energies for the different orderings and hopping sign configurations in

Table 3. Dependence of ground state ordering on interchain hopping signs. The hoppings are expressed in eV. Configuration I corresponds to the case presented in Table 1 and is taken as the reference configuration. In the last column, we mention which of the hopping signs differ from those of configuration I. Column GS indicates the ordering in the ground state. $\Delta$E shows the energy difference (in ${10}^{-4}$ eV) between the ground state ordering and the lowest excited ordered state of the same configuration.

Config *	${\mathbf{T}}_{15}\left(0\right)$	${\mathbf{T}}_{35}({\mathbf{a}}_{\mathbf{x}},0)$	${\mathbf{T}}_{23}\left(0\right)$	${\mathbf{T}}_{65}\left(0\right)$	GS	$\mathbf{\Delta }$E	Comment
I	$0.035$	$-0.04$	$0.02$	$-0.03$	(1-1-11)	3.9	-
II	$0.035$	$-0.04$	$-0.02$	$-0.03$	(11-1-1)	7.2	Ta-Ta interchain
III	$-0.035$	$-0.04$	$0.02$	$-0.03$	(1-1-11)	3.9	Ta-Ni intrachain
IV	$0.035$	$0.04$	$0.02$	$-0.03$	(1-1-11)	3.9	Ta-Ni interchain
V	$0.035$	$-0.04$	$0.02$	$0.03$	(11-1-1)	7.4	Ni-Ni interchain
VI	$0.035$	$-0.04$	$-0.02$	$0.03$	(1-1-11)	4.3	Ta-Ta, Ni-Ni interchain

* Config refers to configuration.

. To avoid confusion, we again stress the nomenclature: we refer to the different symmetry broken phases as different orderings (or different “kinds” of ordering), and a certain combination of the overall hopping sign as a configuration. Hence, for each configuration, we explore several different orderings. We find two different ground state orderings, namely (1-1-11) and (11-1-1), that vary as the signs of the hoppings are varied.

One may also present the results graphically. In Figure 4, we plot the energies for different orderings and indicate the configuration by different symbols. We see that configurations II and V behave oppositely to the others. In II and V, (11-1-1) has a lower energy than the ordering (1-1-11), whereas for the other configurations, the opposite statement holds.

Since Ta-Ta ($t_{23}$) and Ni-Ni ($t_{65}$) interchain hopping strength determines the ground state of the system, we tune these parameters around those corresponding to configuration I and plot the resulting dependence of $\delta E=E(1-1-11)-E(11-1-1)$ in Figure 5. We vary $t_{23}$ by tuning a parameter $\xi$ as $t_{23}=0.02\mathrm{eV}\xi$ and show the data in red (keeping all the other parameters as in configuration I). The same exercise is repeated by varying instead $t_{56}=0.03\xi$ and the data is shown in black. We see a roughly linear dependence of $\delta E$ with the hopping strength and the crossing of the zero line clearly indicates that for a certain hopping the ground state energy flips from (1-1-11) to (11-1-1) in both the cases. Notice that the ground state flips at a nonvanishing value of the respective hopping, i.e., not only the signs of the hoppings but their precise magnitudes set the ground state.

In Figure 6, we show the dependence of the magnitude of the order parameter ${\varphi }_0$ with $\xi$ for the ordering (1-1-11) (in solid line) and (11-1-1) (in dashed line) when $t_{23}$ is varied (left in red) and $t_{56}$ is varied (right in black). We see that for a constant Ni-Ni interchain hopping $t_{56}=0.03$, the value of the order parameter increases for (1-1-11) (and decreases for (11-1-1)) with increasing Ta-Ta interchain hopping, while for a constant Ta-Ta interchain hopping $t_{23}=0.02$, the behavior is rather opposite.

Our results point out that different orderings are energetically close. The smallness of energy differences stems from the smallness of interchain hybridization matrix elements, and this follows physically from the fact that associated Wannier orbitals are far in the real space. From that point of view, it is clear that our finding of small energy differences between distinct orderings may be robust to the changes in other parameters of calculations, provided one remains in the excitonic phase and the interchain matrix elements remain small. We explicitly checked that changing intra-chain hopping for 10meV leads to an overall energy change of 10 meV, but the energy balance between the phases that is determined by the interchain parameters remained unchanged.

4. Conclusions

We explored how energies of symmetry inequivalent excitonic insulator ordering vary with interchain hopping magnitude within Hartree–Fock calculations. We find that symmetry inequivalent orderings have energies that differ by only a small value of order less than meV and that the precise ordering pattern depends sensitively on the value of the interchain hopping amplitudes. The presence of such a sensitive balance in energy between different orders hints that other degrees of freedom should have an important role in stabilizing the ground state observed in the actual material. This agrees with previous work, suggesting that the intertwined orders with both electronic and lattice should be considered to understand the nature of the ground state [31]. Finally, the situation opens the possibility of using external stimuli, e.g., strain engineering or laser excitations, to manipulate the state of matter.

Our method could be further used to study the energy balance between different excitonic orderings in another promising excitonic insulator candidate ${\mathrm{Ta}}_2{\mathrm{Pd}}_3{\mathrm{Te}}_5$, which is also a quasi-one-dimensional layered compound with Ta-Pd-Ta chains in the ’bc’ plane [34,35].