Learning Self-Supervised Representations of Powder-Diffraction Patterns
Abstract
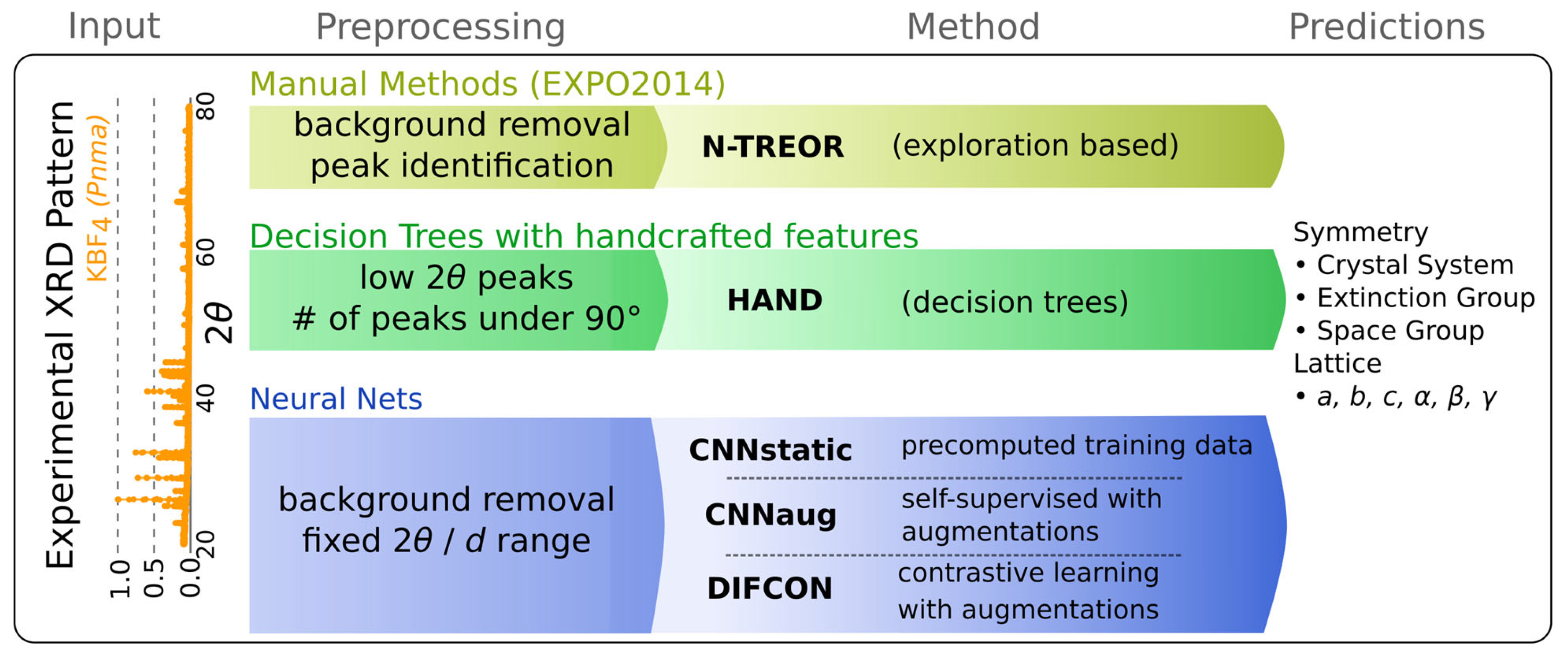
1. Introduction
2. Previous Works
3. Crystallographic and Diffraction Data
4. Computational Experiments
4.1. NTREOR
4.2. HAND
4.3. CNN Static-Supervised
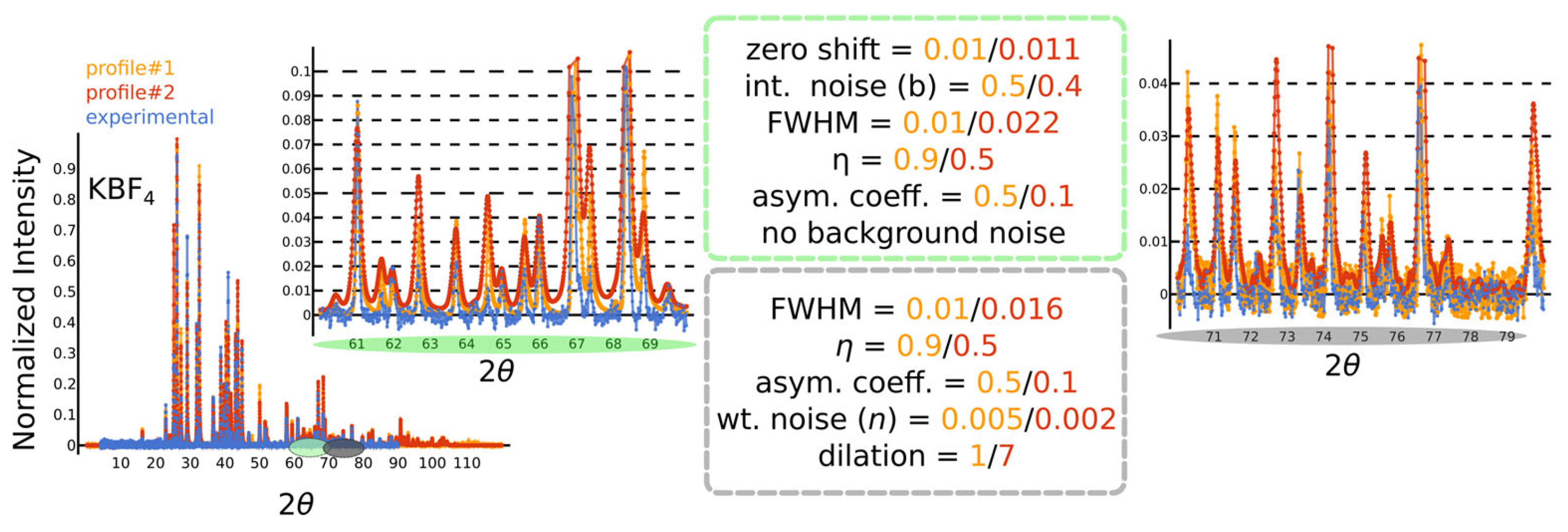
- We begin with a simple zero shift, shifting the entire pattern along the axis by a small (maximally ) amount, simulating errors commonly introduced by improper calibration of the instrument.
- Next, we add a very small amount of random-like x-axis white noise to each peak position ().
- Peak cropping and padding: the peaks at the tails (high and low ) are randomly cropped; i.e., the are replaced with zeros.
- Noise to the integrated intensities is also introduced, simulating all sorts of effects, e.g., of non-ideal detectors. Operations that simultaneously vary the position and integrated intensity effectively model variations due to different experimental effects. For example, changes in integrated intensities can at least partly represent the impact of micro-strain anisotropies, preferred orientations in the powder sample, wavelength fluctuations, as well as Lorentz and polarization factors.
- Binning is performed over the = 0–120 range using a fixed bin width and a copper radiation wavelength of . While this might seem trivial, it requires careful consideration. The peak positions depend on the radiation wavelength via Bragg’s law, and the choice of binning affects intensity values. To enable the model to generalize across different radiation wavelengths, one could use the -spacing for peak positions. Due to the non-linear relationship between -spacing and , however, variations in the binned intensities become highly pronounced and cannot be sufficiently accounted for by adding noise to the integrated intensities before binning. Our investigation shows that the variation over the binned intensities is more reasonable when binning over for a specific being equivalent to the wavelength used for training. For inputs with a different radiation wavelength , the measured value can be easily converted to the corresponding of the training wavelength via the d-spacing, namely, . Please note that this might truncate high values for the case < .
- Small impurity peaks: small amounts of random-like impurity peaks whose intensities are smaller or comparable to the smallest Bragg reflection, but higher than the noise level in a diffraction pattern, are added. This acts as a type of compositional noise in the XRD profile.
- Convolving a peak profile (): a pseudo-Voigt profile with peak asymmetry is convolved across the binned diffraction pattern. This is inspired by the profile used by the CW-XRD refinement program in GSAS-II [23,24], although here we are simply interested in a function form that offers reasonable variations of the profile and not its precise fitting capabilities. The full-width-at-half-maximum (FWHM) is inspired by the Caglioti [12] functional form and is presented in Table 1; here, the parameters are sampled using Latin-Hypercube sampling [27]; the pseudo-Voigt profile is a linear combination of a Gaussian and a Lorentzian using the same (FWHM) weighted by the mixing parameter η; asymmetry is introduced by an error function applied over the pseudo-Voigt profile.
- Overall noise: a background noise is added to the XRD profile. This contains a combination of white noise and intensity-dependent noise. The pattern is then re-normalized.
- Cropping and Padding: Finally, the edges of the XRD profile are cropped randomly and padded with zeros. This is to facilitate generalizability over cases where the edges of the XRD pattern need to be cropped due to extreme background radiation.
4.4. CNN with Augmentations
- Supervised Learning: both inputs and outputs are fully labeled for all instances in the dataset.
- Unsupervised Learning: outputs are entirely unlabeled, and the model discovers patterns or structures in the data without explicit guidance.
- Semi-Supervised Learning: a portion of the data is labeled, while the rest remains unlabeled.
- Self-Supervised Learning: partial relationships between inputs and outputs are leveraged during different stages of the training pipeline. Self-supervised models generate pseudo-labels or pretext tasks to aid in learning meaningful representations.
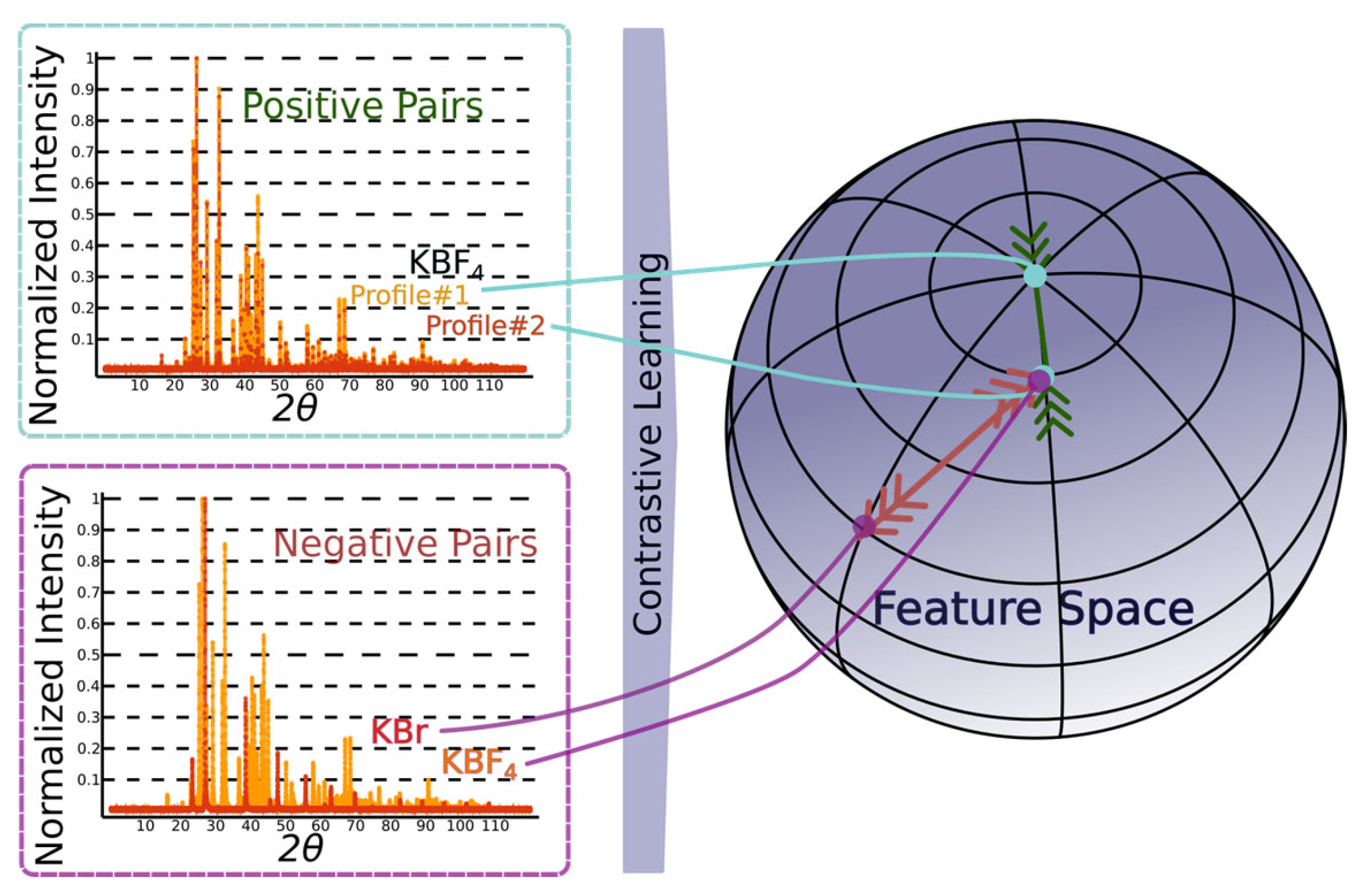
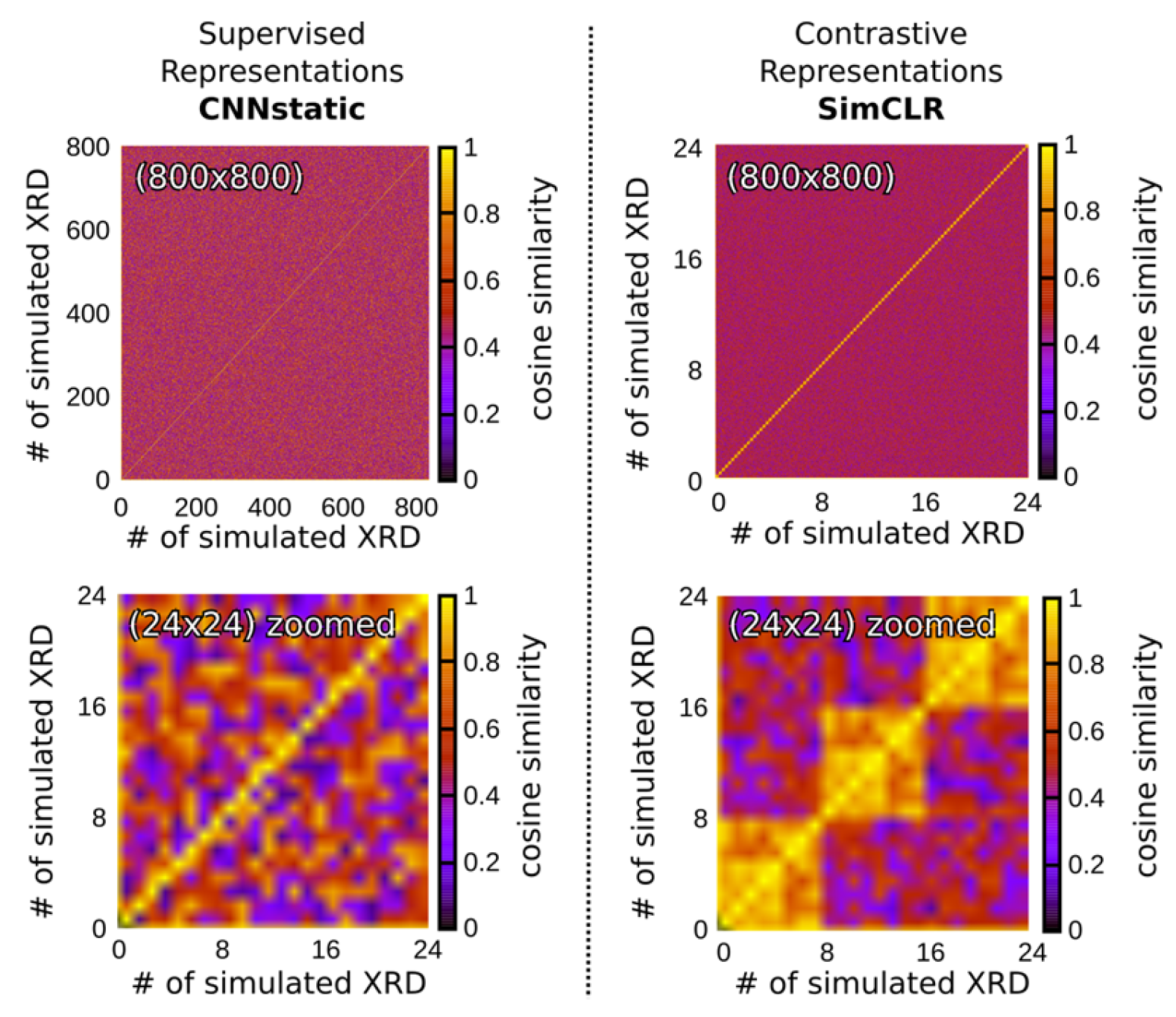
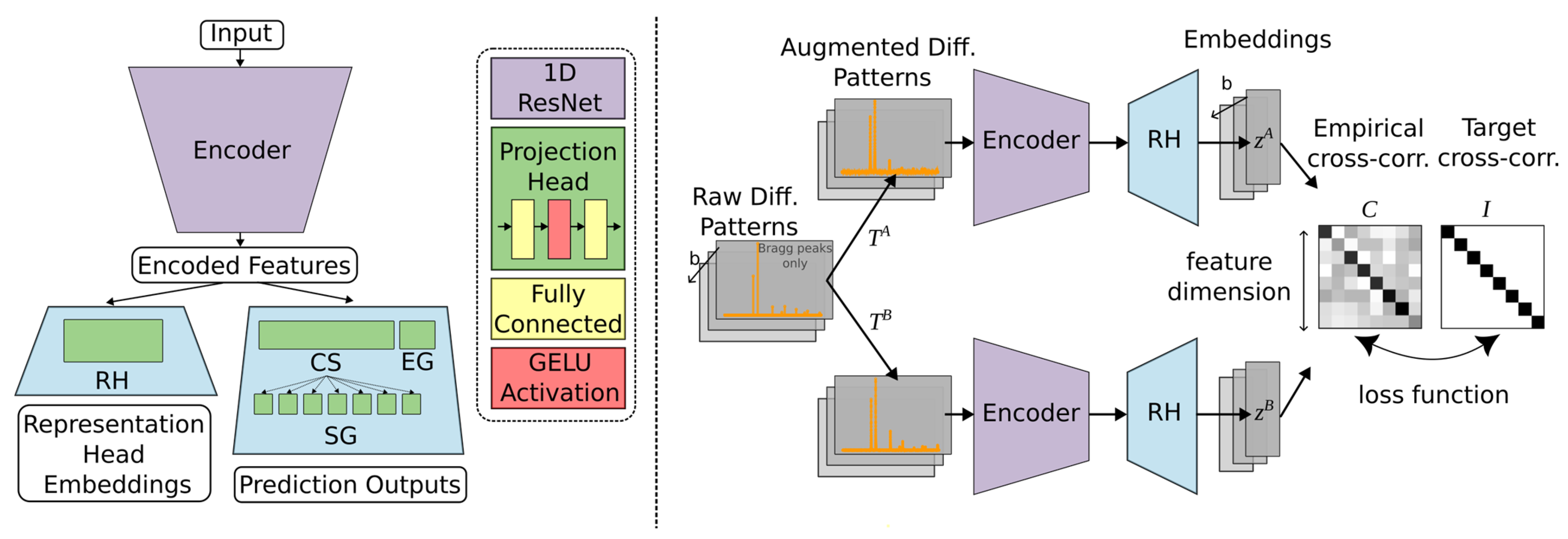
4.5. Self-Supervised Contrastive Representation Learning
- By leveraging contrastive representation learning, the RH generates embeddings that capture essential features of the input diffraction patterns, which are subsequently passed to the downstream classification heads for CS, EG, and SG predictions. This approach not only strengthens the model’s ability to generalize across simulated and real-world data but also facilitates more accurate indexing by learning a feature space that mirrors the underlying crystallographic distinctions. We consider two distinct contrastive learning approaches for DIFCON: SimCLR [28] and Barlow Twins [29]. Both approaches aim to learn robust representations but differ significantly in their objectives and optimization strategies, which we highlight below: SimCLR relies on a contrastive loss function called NT-Xent (Normalized Temperature-scaled Cross Entropy Loss). It uses positive pairs (augmented views of the same sample) and negative pairs (views of different samples) to define the loss. In the context of XRD, we adapt the SimCLR approach by using diffraction-specific augmentations, such as noise injection, random peak shifting, and impurity peak addition, to create positive pairs. Negative pairs are generated using diffraction patterns from different crystal structures.
- The Barlow Twins method, in contrast, eliminates the need for explicit negative pairs. It introduces a redundancy-reduction loss that aligns positive pairs while discouraging redundancy in the feature space. Specifically, the method aims to make the cross-correlation matrix of embeddings from positive pairs as close to the identity matrix as possible. By reducing redundancy, Barlow Twins ensures that each dimension of the learned representation captures unique information. A notable advantage of this method is its computational efficiency, as it does not rely on large batch sizes or negative samples. It does, however, require a much higher dimensional feature vector.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Giacovazzo, C.; Monaco, H.L.; Artioli, G.; Viterbo, D.; Milanesio, M.; Gilli, G.; Gilli, P.; Zanotti, G.; Ferraris, G.; Catti, M. Fundamentals of Crystallography; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Giacovazzo, C. Direct Phasing in Crystallography: Fundamentals and Applications; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Brunger, A.T. Simulated annealing in crystallography. Annu. Rev. Phys. Chem. 1991, 42, 197–223. [Google Scholar] [CrossRef]
- Kariuki, B.M.; Serrano-González, H.; Johnston, R.L.; Harris, K.D. The application of a genetic algorithm for solving crystal structures from powder diffraction data. Chem. Phys. Lett. 1997, 280, 189–195. [Google Scholar] [CrossRef]
- Oszlányi, G.; Sütő, A. The Charge Flipping Algorithm. Acta Crystallogr. A 2007, 64, 123–134. [Google Scholar] [CrossRef]
- Hendrycks, D.; Zhao, K.; Basart, S.; Steinhardt, J.; Song, D. Natural Adversarial Examples. arXiv 2019, arXiv:1907.07174. [Google Scholar]
- Jumper, J.; Evans, R.; Pritzel, A.; Green, T.; Figurnov, M.; Ronneberger, O.; Tunyasuvunakool, K.; Bates, R.; Žídek, A.; Potapenko, A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. [Google Scholar] [CrossRef]
- Altomare, A.; Giacovazzo, C.; Guagliardi, A.; Moliterni, A.G.G.; Rizzi, R.; Werner, P.-E. New Techniques for Indexing: N-TREOR in EXPO. J. Appl. Cryst. 2000, 33, 1180–1186. [Google Scholar] [CrossRef]
- Gasparotto, P.; Barba, L.; Stadler, H.-C.; Assmann, G.; Mendonça, H.; Ashton, A.W.; Janousch, M.; Leonarski, F.; Béjar, B. TORO Indexer: A PyTorch-based indexing algorithm for kilohertz serial crystallography. J. Appl. Crystallogr. 2024, 57, 931–944. [Google Scholar] [CrossRef]
- Suzuki, Y.; Hino, H.; Hawai, T.; Saito, K.; Kotsugi, M.; Ono, K. Symmetry prediction and knowledge discovery from X-ray diffraction patterns using an interpretable machine learning approach. Sci. Rep. 2020, 10, 21790. [Google Scholar] [CrossRef]
- Park, W.B.; Chung, J.; Jung, J.; Sohn, K.; Singh, S.P.; Pyo, M.; Shin, N.; Sohn, K.-S. Classification of crystal structure using a convolutional neural network. IUCrJ 2017, 4, 486–494. [Google Scholar] [CrossRef]
- Caglioti, G.; Paoletti, A.; Ricci, F. Choice of collimators for a crystal spectrometer for neutron diffraction. Nucl. Instrum. 1958, 3, 223–228. [Google Scholar] [CrossRef]
- Lee, B.D.; Lee, J.-W.; Park, W.B.; Park, J.; Cho, M.-Y.; Singh, S.P.; Pyo, M.; Sohn, K.-S. Powder X-Ray Diffraction Pattern Is All You Need for Machine-Learning-Based Symmetry Identification and Property Prediction. Adv. Intell. Syst. 2022, 4, 2200042. [Google Scholar] [CrossRef]
- Oviedo, F.; Ren, Z.; Sun, S.; Settens, C.; Liu, Z.; Hartono, N.T.P.; Ramasamy, S.; DeCost, B.L.; Tian, S.I.P.; Romano, G.; et al. Fast and interpretable classification of small X-ray diffraction datasets using data augmentation and deep neural networks. npj Comput. Mater. 2019, 5, 60. [Google Scholar] [CrossRef]
- Salgado, J.E.; Lerman, S.; Du, Z.; Xu, C.; Abdolrahim, N. Automated classification of big X-ray diffraction data using deep learning models. npj Comput. Mater. 2023, 9, 214. [Google Scholar] [CrossRef]
- Lolla, S.; Liang, H.; Kusne, A.G.; Takeuchi, I.; Ratcliff, W. A semi-supervised deep-learning approach for automatic crystal structure classification. J. Appl. Crystallogr. 2022, 55, 882–889. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Lange, J.; Komissarov, L.; Lang, R.; Enkelmann, D.D.; Anelli, A. Automatic Solid Form Classification in Pharmaceutical Drug Development. arXiv 2024, arXiv:2411.03308. [Google Scholar]
- Schulte, H.; Hoffmann, F.; Mikut, R. Siamese Netwroks for 1D Signal Identification. In Proceedings of the 30th Workshop Computational Intelligence, Berlin, Germany, 26–27 November 2020. [Google Scholar]
- Lai, Q.; Xu, F.; Yao, L.; Gao, Z.; Liu, S.; Wang, H.; Lu, S.; He, D.; Wang, L.; Zhang, L.; et al. End-to-End Crystal Structure Prediction from Powder X-Ray Diffraction. Adv. Sci. 2025, 12, 2410722. [Google Scholar] [CrossRef]
- Sohl-Dickstein, J.; Weiss, E.A.; Maheswaranathan, N.; Ganguli, S. Deep Unsupervised Learning Using Nonequilibrium Thermodynamics. arXiv 2015, arXiv:1503.03585. [Google Scholar]
- Ho, J.; Jain, A.; Abbeel, P. Denoising Diffusion Probabilistic Models. arXiv 2020, arXiv:2006.11239. [Google Scholar]
- Toby, B.H.; Von Dreele, R.B. GSAS-II: The Genesis of a Modern Open-Source All Purpose Crystallography Software Package. J. Appl. Cryst. 2013, 46, 544–549. [Google Scholar] [CrossRef]
- O’Donnell, J.H.; Von Dreele, R.B.; Chan, M.K.Y.; Toby, B.H. A scripting interface for GSAS-II. J. Appl. Crystallogr. 2018, 51, 1244–1250. [Google Scholar] [CrossRef]
- Altomare, A.; Cuocci, C.; Giacovazzo, C.; Moliterni, A.; Rizzi, R.; Corriero, N.; Falcicchio, A. EXPO2013: A kit of tools for phasing crystal structures from powder data. J. Appl. Crystallogr. 2013, 46, 1231–1235. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- McKay, M.D.; Beckman, R.J.; Conover, W.J. Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code. Technometrics 1979, 21, 239–245. [Google Scholar] [CrossRef]
- Chen, T.; Kornblith, S.; Norouzi, M.; Hinton, G. A Simple Framework for Contrastive Learning of Visual Representations. arXiv 2020, arXiv:2002.05709. [Google Scholar]
- Zbontar, J.; Jing, L.; Misra, I.; LeCun, Y.; Deny, S. Barlow Twins: Self-Supervised Learning via Redundancy Reduction. Proc. Mach. Learn. Res. 2021, 139, 12310–12320. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian Error Linear Units (GELUS). arXiv 2016, arXiv:1606.08415. [Google Scholar]
| Operation | Functional Form/Random Variable(s) |
|---|---|
| zero shift | |
| x-axis white noise | |
| peak cropping and padding | |
| intensity noise | , |
| Binning (no random variables) | , |
| impurity peaks | |
| profile | , |
| background noise | |
| cropping and padding |
| Equivariance Test | Invariance Test | Experimental Test | |||||||
|---|---|---|---|---|---|---|---|---|---|
| CS | EG | SG | CS | EG | SG | CS | EG | SG | |
| NTREOR | – | – | – | – | – | – | 49% | – | – |
| HAND | 94% | 91% | 87% | – | – | – | 55% | 32% | 39% |
| CNNstatic | 89% | 82% | 79% | 40% | 33% | 24% | 22% | 15% | 13% |
| CNNaug | 90% | 83% | 81% | 45% | 35% | 28% | 23% | 16% | 13% |
| DIFCON | 88% | 80% | 78% | 79% | 71% | 66% | 74% | 48% | 41% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Das, S.; Vorholt, M.; Houben, A.; Dronskowski, R. Learning Self-Supervised Representations of Powder-Diffraction Patterns. Crystals 2025, 15, 393. https://doi.org/10.3390/cryst15050393
Das S, Vorholt M, Houben A, Dronskowski R. Learning Self-Supervised Representations of Powder-Diffraction Patterns. Crystals. 2025; 15(5):393. https://doi.org/10.3390/cryst15050393
Chicago/Turabian StyleDas, Shubhayu, Markus Vorholt, Andreas Houben, and Richard Dronskowski. 2025. "Learning Self-Supervised Representations of Powder-Diffraction Patterns" Crystals 15, no. 5: 393. https://doi.org/10.3390/cryst15050393
APA StyleDas, S., Vorholt, M., Houben, A., & Dronskowski, R. (2025). Learning Self-Supervised Representations of Powder-Diffraction Patterns. Crystals, 15(5), 393. https://doi.org/10.3390/cryst15050393








