Quantitative Analysis of Shear Texture Evolution in Accumulative Roll Bonded AA 1060 Aluminum Alloy
Abstract
1. Introduction
2. Experimental Procedure
3. Results and Discussion
4. Conclusions
- (1)
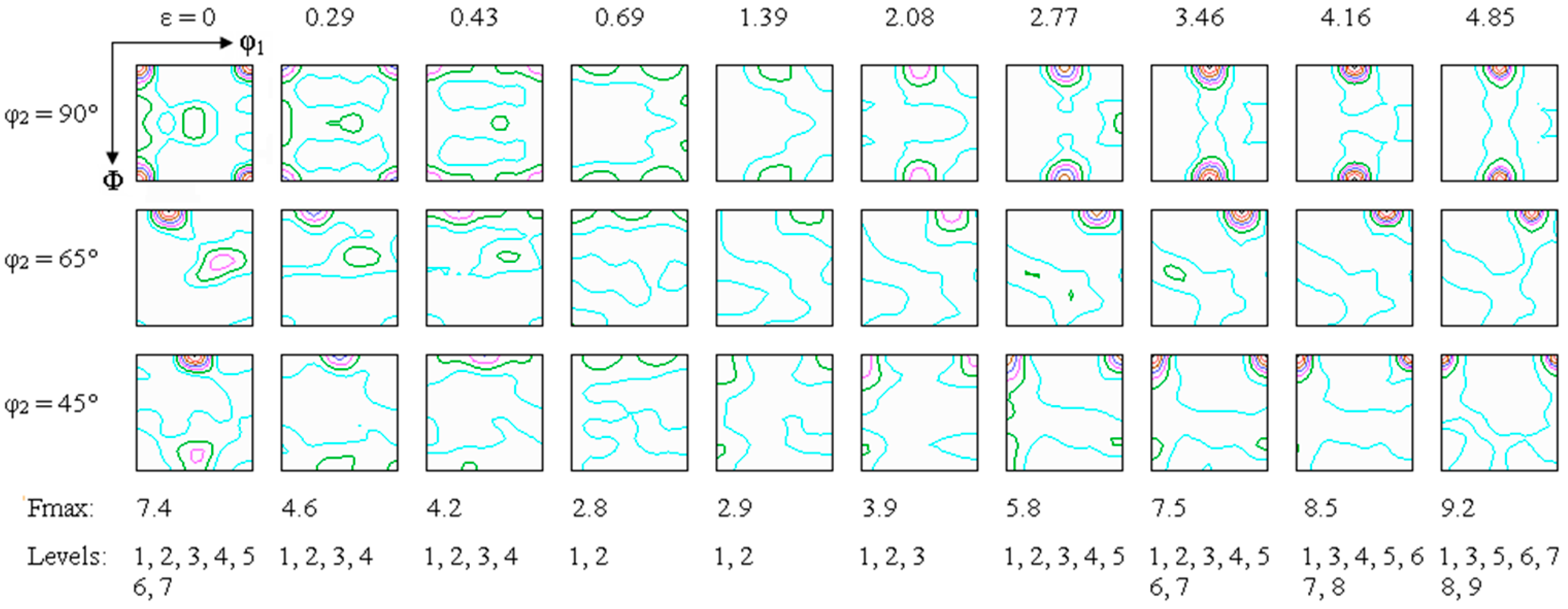
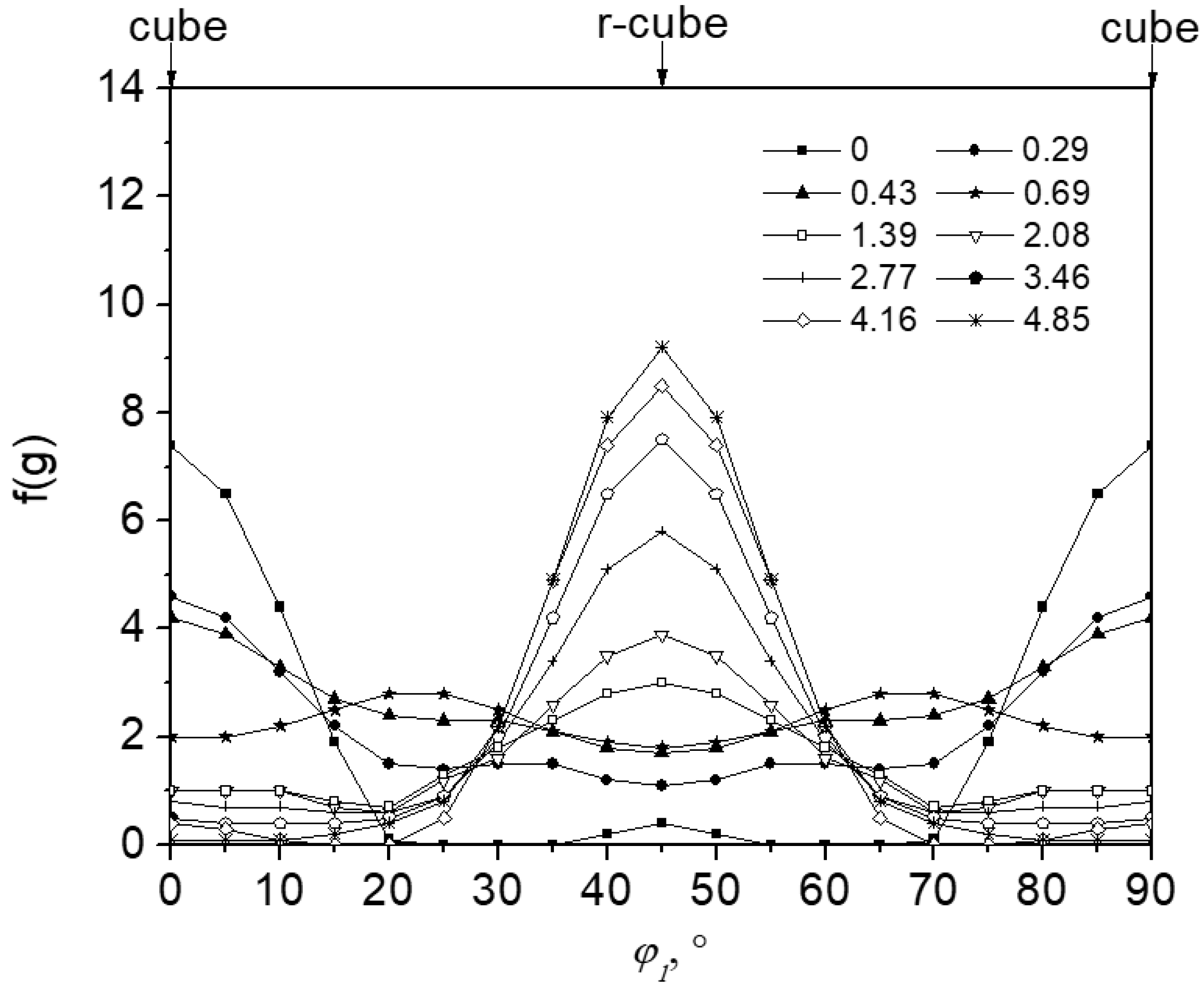
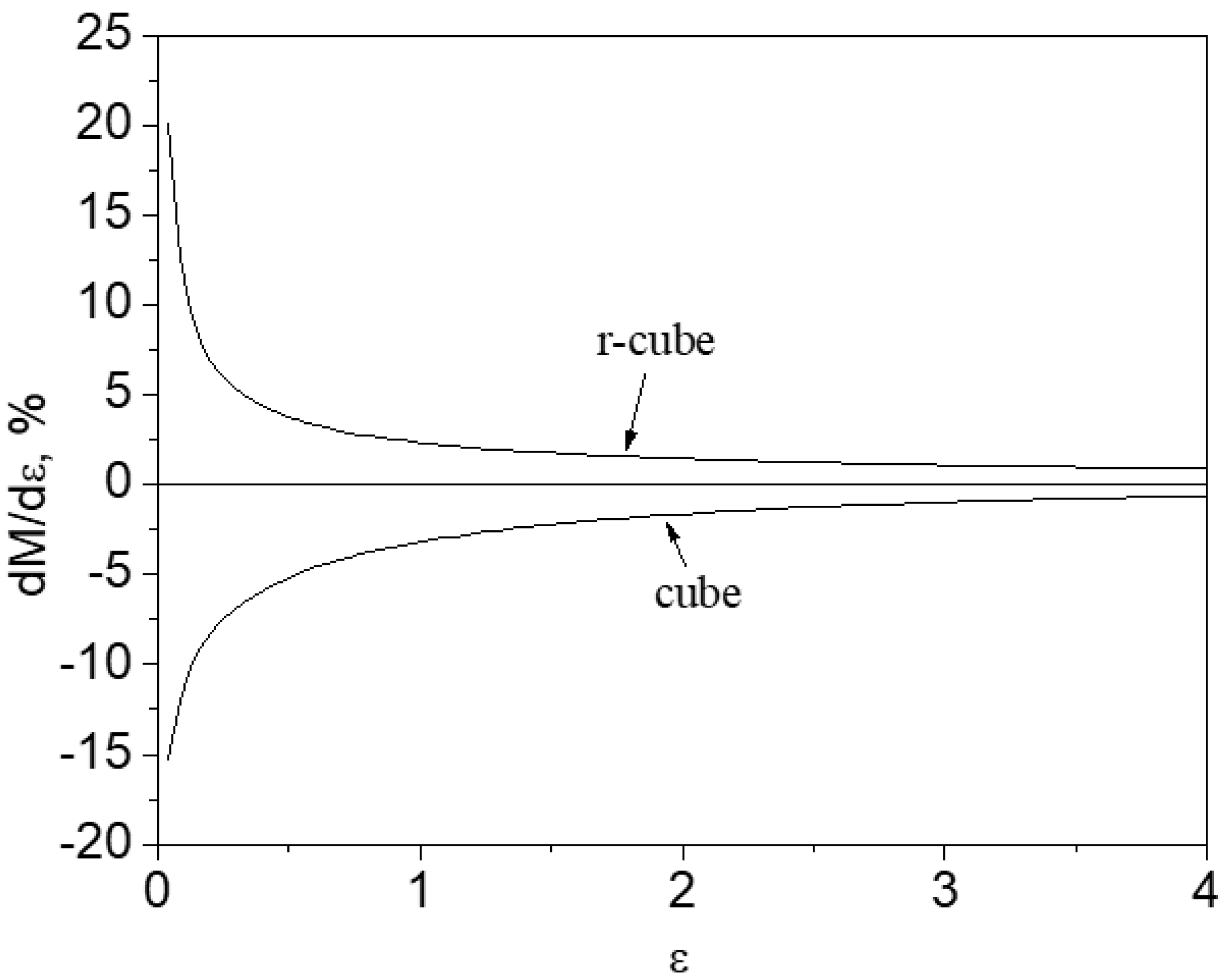
- During the ARB process, the initial cube texture at the surface layer progressively transformed into a r-cube texture. As the accumulated true strain increased, the intensity of the cube texture diminished while the intensity of the r-cube texture was enhanced. At an accumulated true strain of 4.85, a pronounced r-cube texture was observed at the surface layer.
- (2)
- The development of shear texture at the surface layer was described using mathematical models relating texture volume fractions to accumulated true strain. The rate at which the cube component diminished and the r-cube component formed initially decreased rapidly with increasing strain, and subsequently the rates of change slowed down.
- (3)
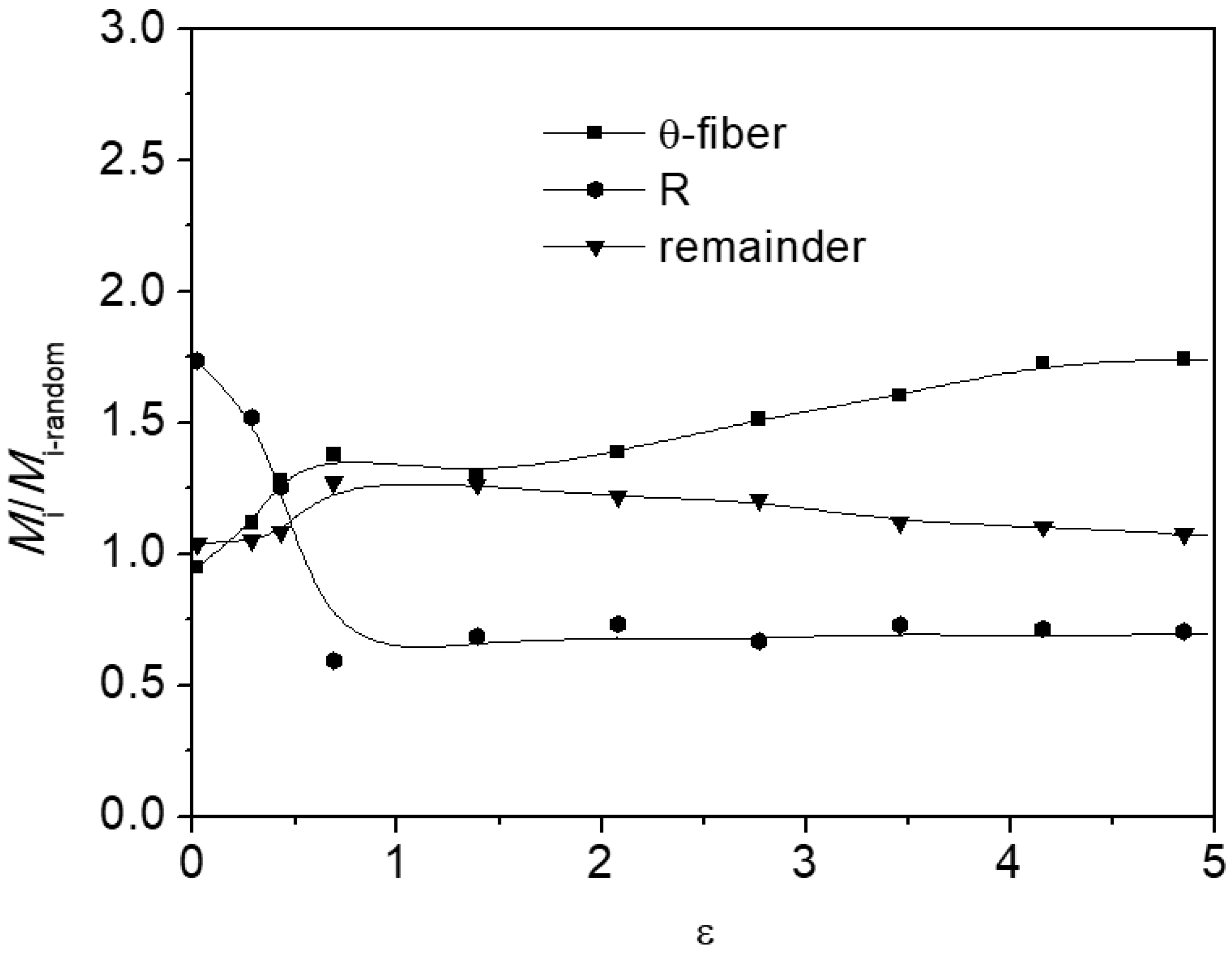
- The strength of the R component at the surface layer decreased sharply to a value of 0.69 with increasing true strain and then stabilized. Conversely, the strength of the remaining component increased initially before decreasing slowly. This indicates that the R orientation transitions toward the r-cube orientation through the residual texture region during the ARB process.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Houtte, P.V. On the equivalence of the relaxed Taylor theory and the Bishop-Hill theory for partially constrained plastic deformation of crystals. Mater. Sci. Eng. 1982, 55, 69–77. [Google Scholar] [CrossRef]
- Hirsch, J.; Lücke, K. Overview no. 76: Mechanism of deformation and development of rolling textures in polycrystalline f.c.c. metals-II. Simulation and interpretation of experiments on the basis of Taylor-type theories. Acta Metall. Mater. 1988, 36, 2883–2904. [Google Scholar] [CrossRef]
- Delannay, L.; Kalidindi, S.R.; Houtte, P.V. Quantitative prediction of textures in aluminium cold rolled to moderate strains. Mater. Sci. Eng. A 2002, 336, 233–244. [Google Scholar] [CrossRef]
- Liu, W.C.; Zhai, T.; Man, C.-S.; Radhakrishnan, B.; Morris, J.G. Effect of initial texture on texture evolution in cold-rolled AA 5182 aluminium alloy. Philos. Mag. 2004, 84, 3305–3321. [Google Scholar] [CrossRef]
- Liu, W.C.; Li, Z.; Man, C.-S.; Raabe, D.; Morris, J.G. Effect of precipitation on rolling texture evolution in continuous cast AA 3105 aluminum alloy. Mater. Sci. Eng. A 2006, 434, 105–113. [Google Scholar] [CrossRef]
- Zhang, J.X.; Liu, C.; Liu, W.C.; Man, C.-S. Effect of precipitation state on texture evolution in cold-rolled continuous cast AA 2037 aluminum alloy. J. Alloys Compd. 2017, 728, 1199–1208. [Google Scholar] [CrossRef]
- Liu, W.C.; Man, C.-S.; Raabe, D. Effect of strain hardening on texture development in cold rolled Al-Mg alloy. Mater. Sci. Eng. A 2010, 527, 1249–1254. [Google Scholar] [CrossRef]
- Fattah-Alhosseini, A.; Gashti, S.O. Corrosion behavior of ultra-fine grained 1050 aluminum alloy fabricated by ARB process in a buffer borate solution. J. Mater. Eng. Perform. 2015, 24, 3386–3393. [Google Scholar] [CrossRef]
- Jamaati, R.; Toroghinejad, M.R.; Mohtadi-Bonab, M.A.; Edris, H.; Szpunar, J.A.; Salmani, M.R. Texture development of ARB-processed steel-based nanocomposite. J. Mater. Eng. Perform. 2014, 23, 4436–4445. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Mishin, O.V.; Godfrey, A. Analysis of through-thickness heterogeneities of microstructure and texture in nickel after accumulative roll bonding. J. Mater. Sci. 2014, 49, 287–293. [Google Scholar] [CrossRef]
- Toroghinejad, M.R.; Jamaati, R.; Hoseini, M.; Szpunar, J.A.; Dutkiewicz, J. Texture evolution of nanostructured aluminum/copper composite produced by the accumulative roll bonding and folding process. Metall. Mater. Trans. A 2013, 44, 1587–1598. [Google Scholar] [CrossRef]
- Wang, Z.J.; Ma, M.; Qiu, Z.X.; Zhang, J.X.; Liu, W.C. Microstructure, texture and mechanical properties of AA 1060 aluminum alloy processed by cryogenic accumulative roll bonding. Mater. Charact. 2018, 139, 269–278. [Google Scholar] [CrossRef]
- Kim, H.W.; Kang, S.B.; Tsuji, N.; Minamino, Y. Deformation textures of AA8011 aluminum alloy sheets severely deformed by accumulative roll bonding. Metall. Mater. Trans. A 2005, 36A, 3151–3163. [Google Scholar] [CrossRef]
- Su, L.H.; Lu, C.; Gazder, A.A.; Saleh, A.A.; Deng, G.Y.; Tieu, K.; Li, H.J. Shear texture gradient in AA6061 aluminum alloy processed by accumulative roll bonding with high roll roughness. J. Alloys Compd. 2014, 594, 12–22. [Google Scholar] [CrossRef]
- Li, S.; Sun, F.; Li, H. Observation and modeling of the through-thickness texture gradient in commercial-purity aluminum sheets processed by accumulative roll-bonding. Acta Mater. 2010, 58, 1317–1331. [Google Scholar] [CrossRef]
- Jamaati, R.; Toroghinejad, M.R.; Hoseini, M.; Szpunar, J.A. Texture development in Al/Al2O3 MMCs produced by anodizing and ARB processes. Mater. Sci. Eng. A 2011, 528, 3573–3580. [Google Scholar] [CrossRef]
- Sun, H.Y.; Wang, Z.J.; Du, P.; Zhang, J.X.; Liu, W.C. Effect of rolling reduction and heat treatment on the microstructure and mechanical properties of Al1060/Al6061-0.5 SiC/Al1060 laminates. Mater. Sci. Eng. A 2022, 830, 142328. [Google Scholar] [CrossRef]
- Zhou, Y.L.; Yang, Y.; Tan, Y.B.; Xiang, S.; Ma, M.; Zhao, F.; Yang, M. Recrystallization behavior and texture evolution during annealing of cryogenic-rolled 3003 aluminum alloy. J. Alloys Compd. 2024, 997, 174818. [Google Scholar] [CrossRef]
- Bunge, H.J. Texture Analysis in Materials Science; Elsevier: Amsterdam, The Netherlands, 1982. [Google Scholar]
- Liu, W.C.; Morris, J.G. Kinetics of the formation of the β fiber rolling texture in continuous cast AA 5xxx series aluminum alloys. Scr. Mater. 2002, 47, 743–748. [Google Scholar] [CrossRef]
- Liu, W.C.; Morris, J.G. Comparison of the texture evolution in cold rolled DC and SC AA 5182 aluminum alloys. Mater. Sci. Eng. A 2003, 339, 183–193. [Google Scholar] [CrossRef]
- Liu, W.C.; Morris, J.G. Quantitative analysis of texture evolution in cold-rolled, continuous-cast AA 5xxx-series aluminum alloys. Metall. Trans. A 2004, 35A, 265–277. [Google Scholar] [CrossRef]
- Wang, W.X.; Zhang, J.X.; Wang, Z.J.; Liu, W.C. A comparative study of the transformation kinetics of recrystallization texture of CC and DC 3003 aluminum alloys. Mater. Charact. 2018, 141, 412–422. [Google Scholar] [CrossRef]
- Miszczyk, M.M.; Paul, H.; Driver, J.H.; Poplewska, J. The influence of deformation texture on nucleation and growth of cube grains during primary recrystallization of AA1050 alloy. Acta Mater. 2017, 129, 378–387. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Liu, W.C.; Morris, J.G. Comparison of texture evolution during cold rolling between direct chill and continuous cast aluminium alloy 5052. Mater. Sic. Technol. 2003, 19, 1379–1385. [Google Scholar] [CrossRef]

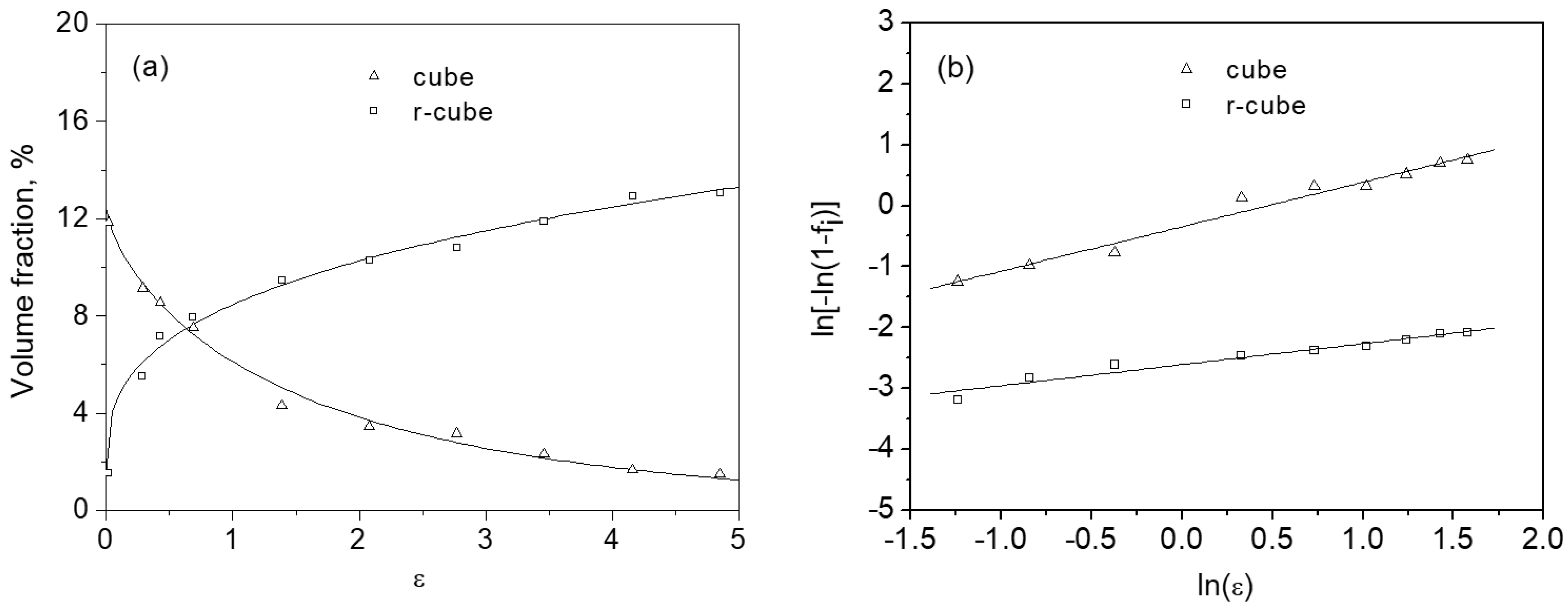
| Texture Component | Mi0 (%) | ki | ni | r |
|---|---|---|---|---|
| cube | 12.44 | 0.71 (0.68 ~ 0.74) | 0.84 ± 0.04 | 0.955 |
| r-cube | 1.53 | 0.073 (0.071 ~ 0.076) | 0.35 ± 0.03 | 0.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, P.; Li, C.; Liu, L.; Chen, B.; Li, M.; Wang, Z.; Liu, S. Quantitative Analysis of Shear Texture Evolution in Accumulative Roll Bonded AA 1060 Aluminum Alloy. Crystals 2025, 15, 369. https://doi.org/10.3390/cryst15040369
Du P, Li C, Liu L, Chen B, Li M, Wang Z, Liu S. Quantitative Analysis of Shear Texture Evolution in Accumulative Roll Bonded AA 1060 Aluminum Alloy. Crystals. 2025; 15(4):369. https://doi.org/10.3390/cryst15040369
Chicago/Turabian StyleDu, Peng, Chao Li, Lei Liu, Bao Chen, Mingyu Li, Zhijie Wang, and Sha Liu. 2025. "Quantitative Analysis of Shear Texture Evolution in Accumulative Roll Bonded AA 1060 Aluminum Alloy" Crystals 15, no. 4: 369. https://doi.org/10.3390/cryst15040369
APA StyleDu, P., Li, C., Liu, L., Chen, B., Li, M., Wang, Z., & Liu, S. (2025). Quantitative Analysis of Shear Texture Evolution in Accumulative Roll Bonded AA 1060 Aluminum Alloy. Crystals, 15(4), 369. https://doi.org/10.3390/cryst15040369







