A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals
Abstract
1. Introduction
2. Structural Design
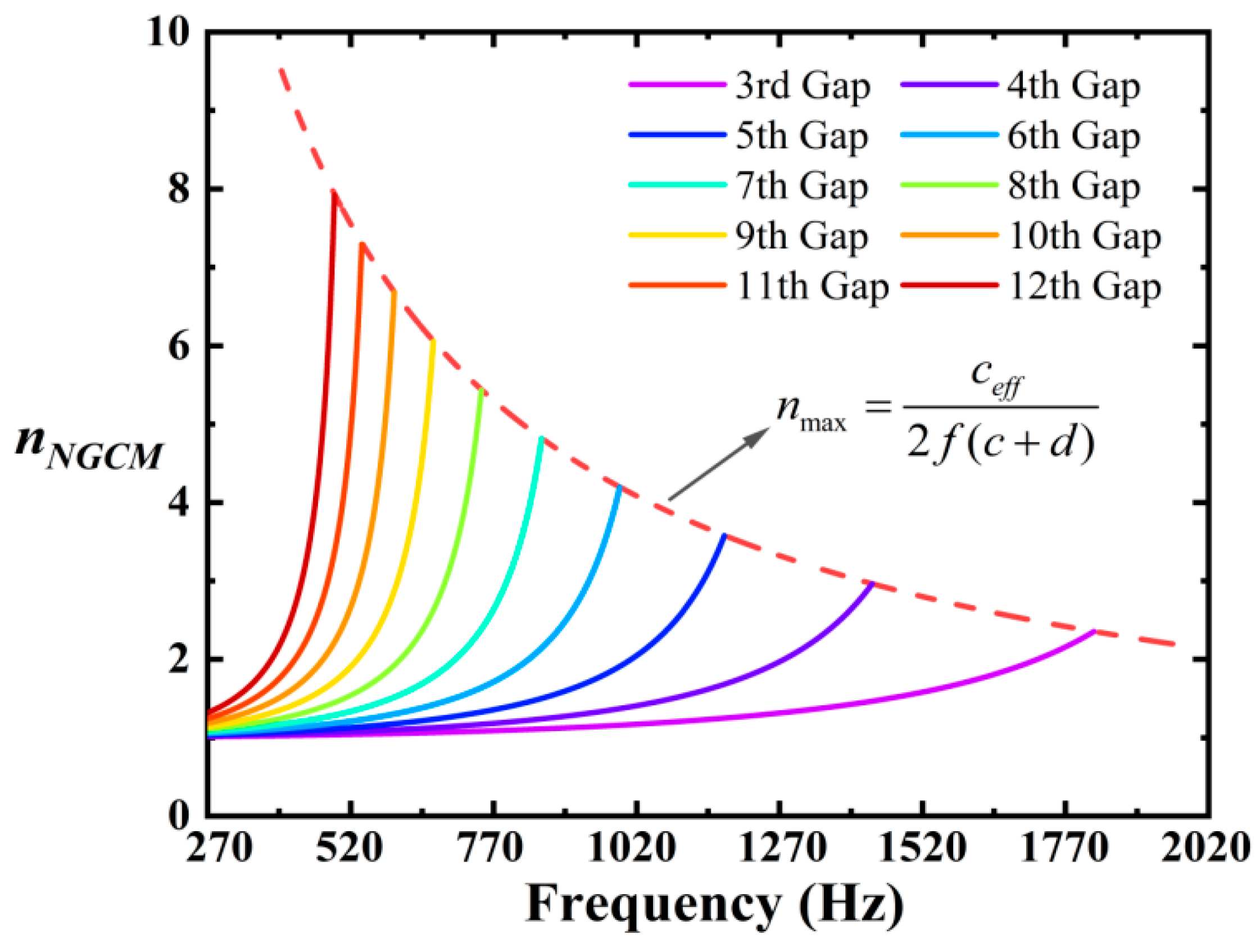
3. Theoretical Derivation and Calculations
4. Simulation Analysis
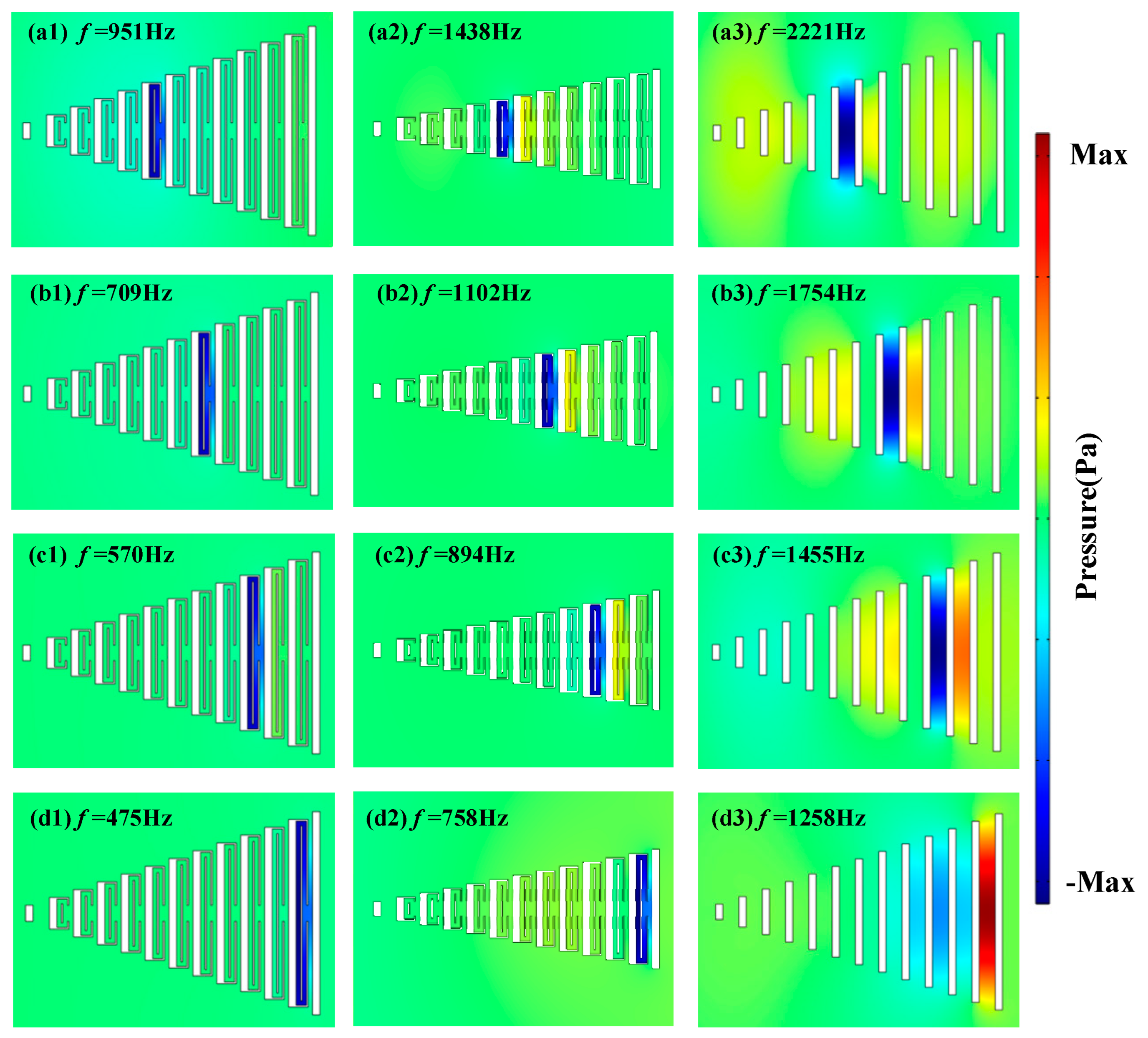
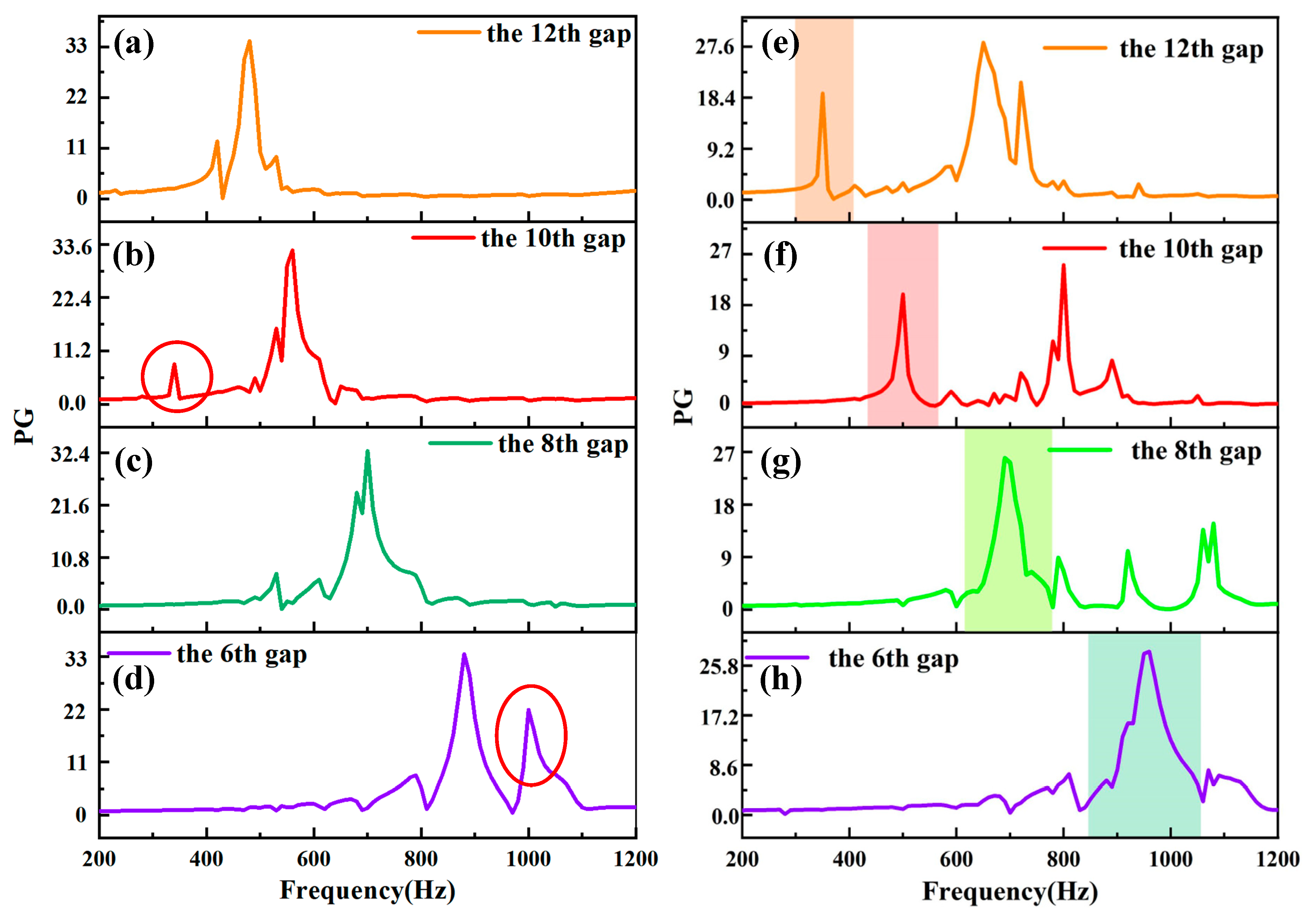
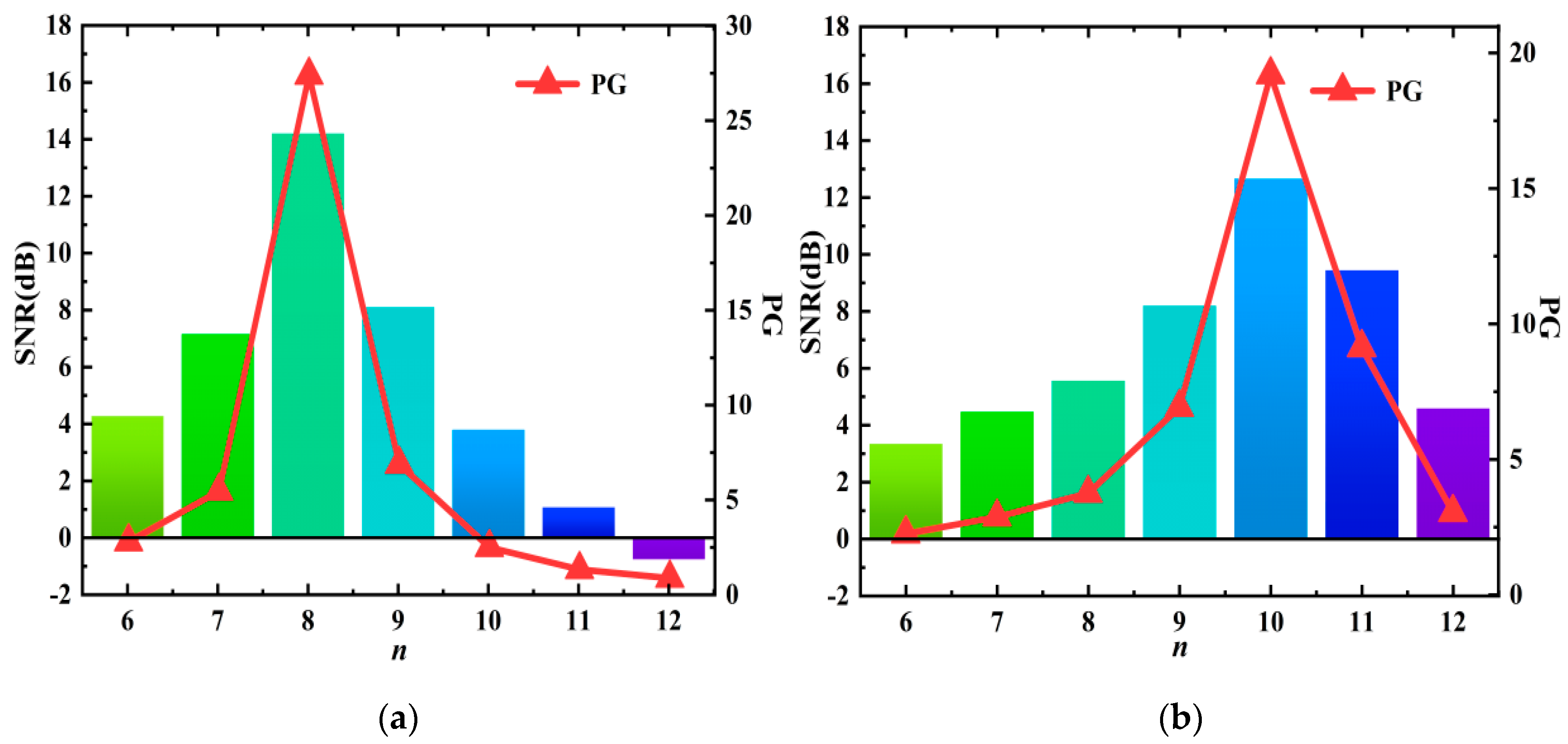
4.1. Study on the Acoustic Response of ZCGM Structures Under Thermo-Viscous Loss Conditions
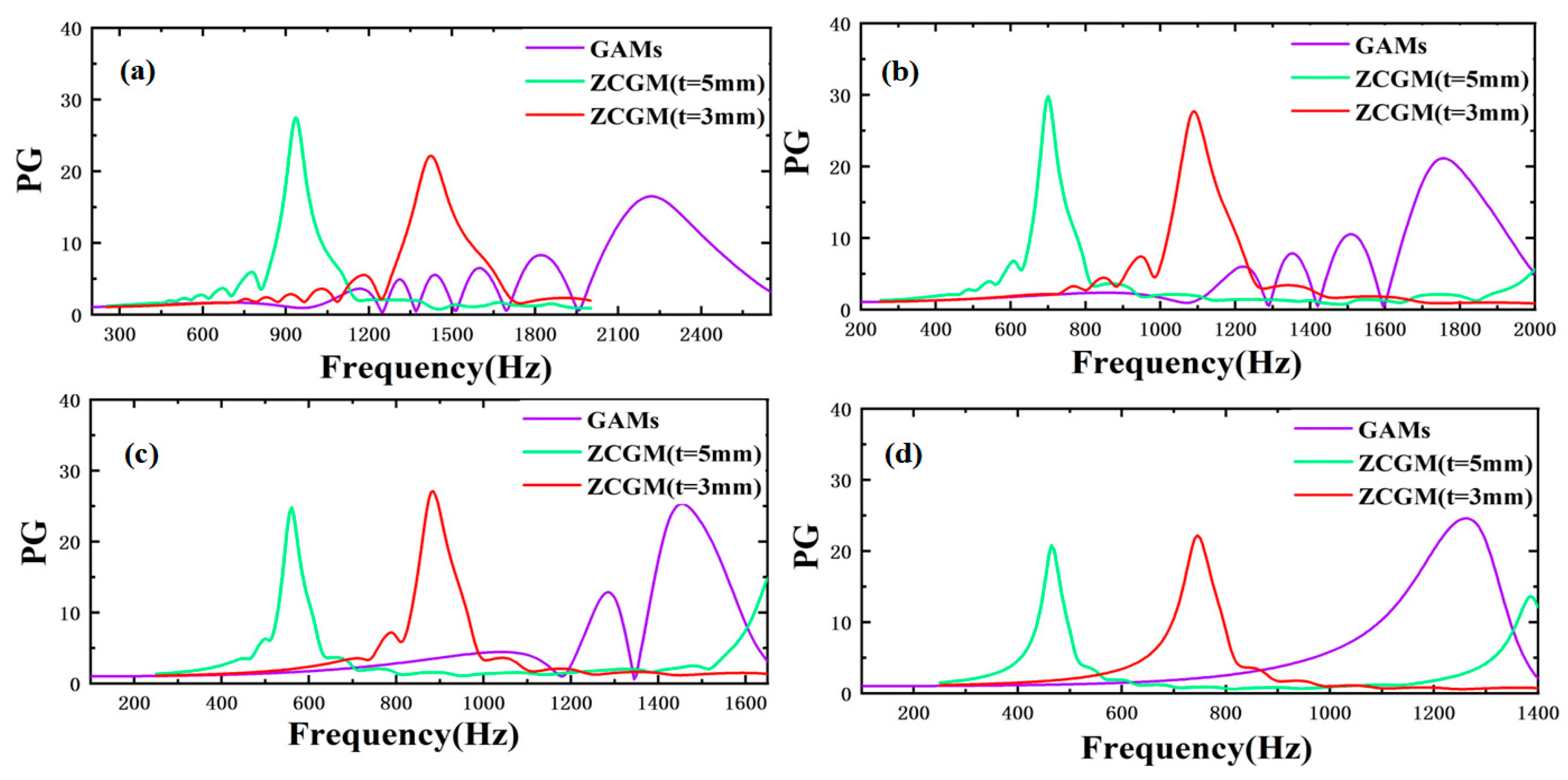
4.2. Acoustic Response of ZCGM Structures of Different Material Acoustic-Structural Coupling Conditions
5. Experimental Validations
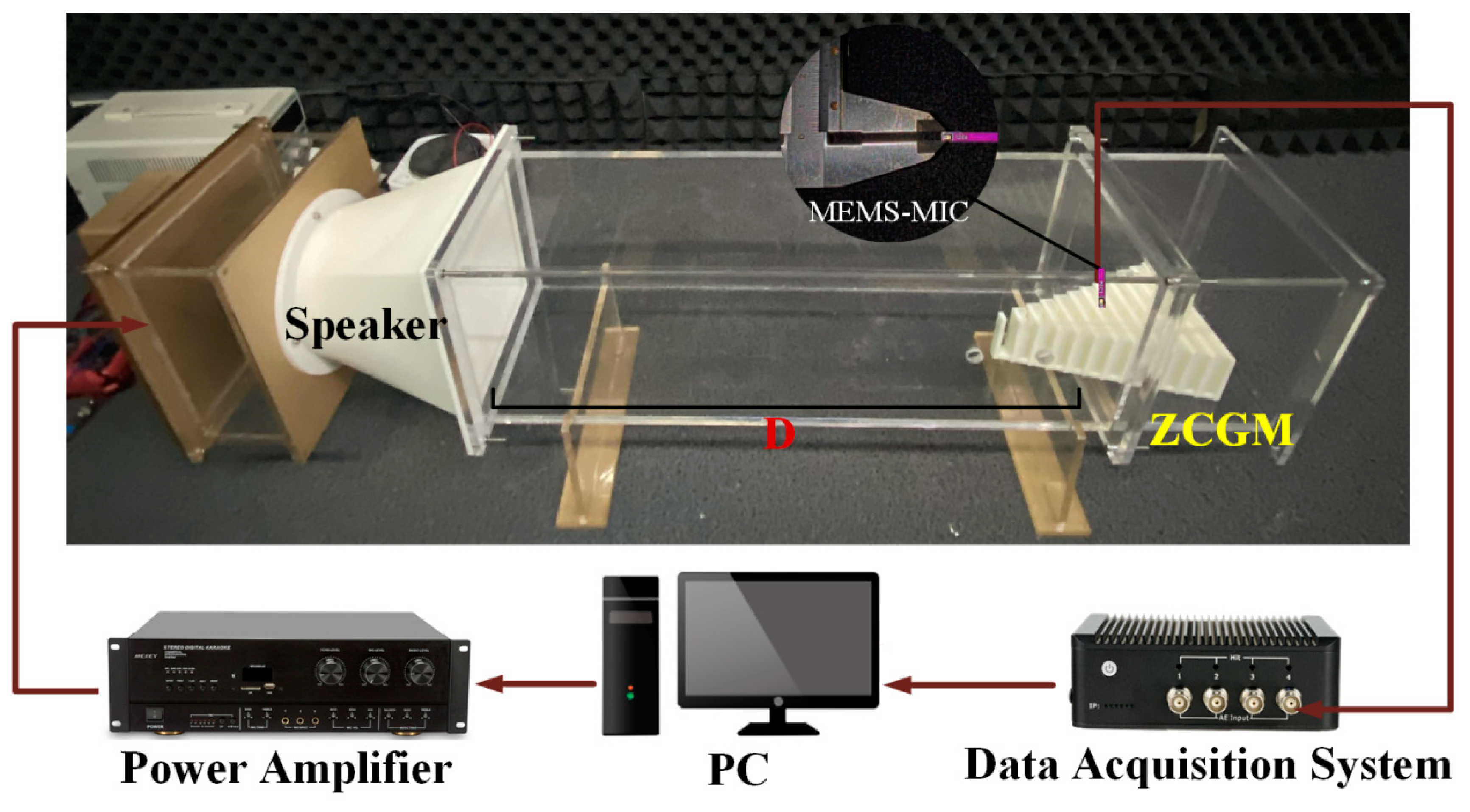
5.1. Experimental System
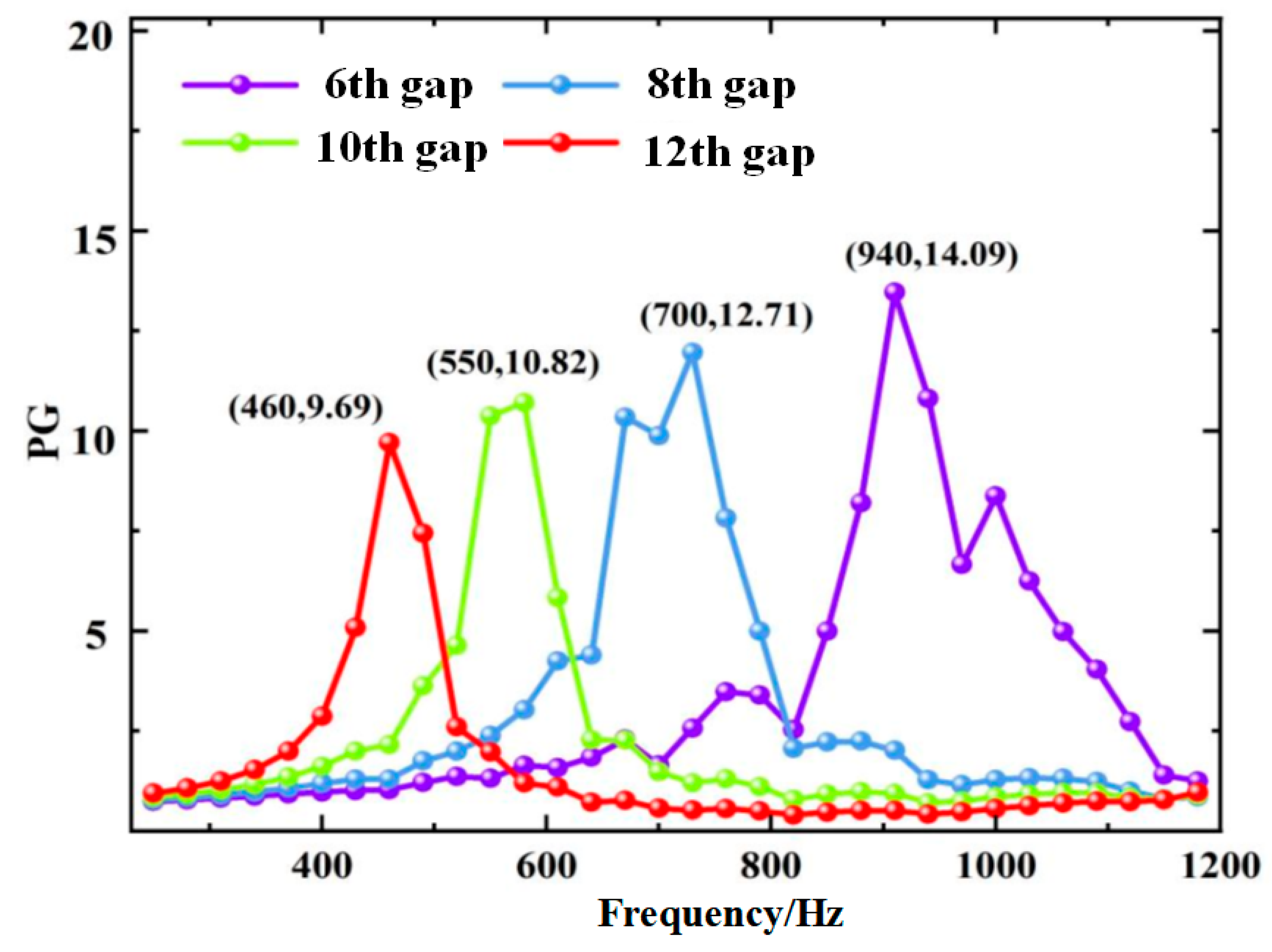
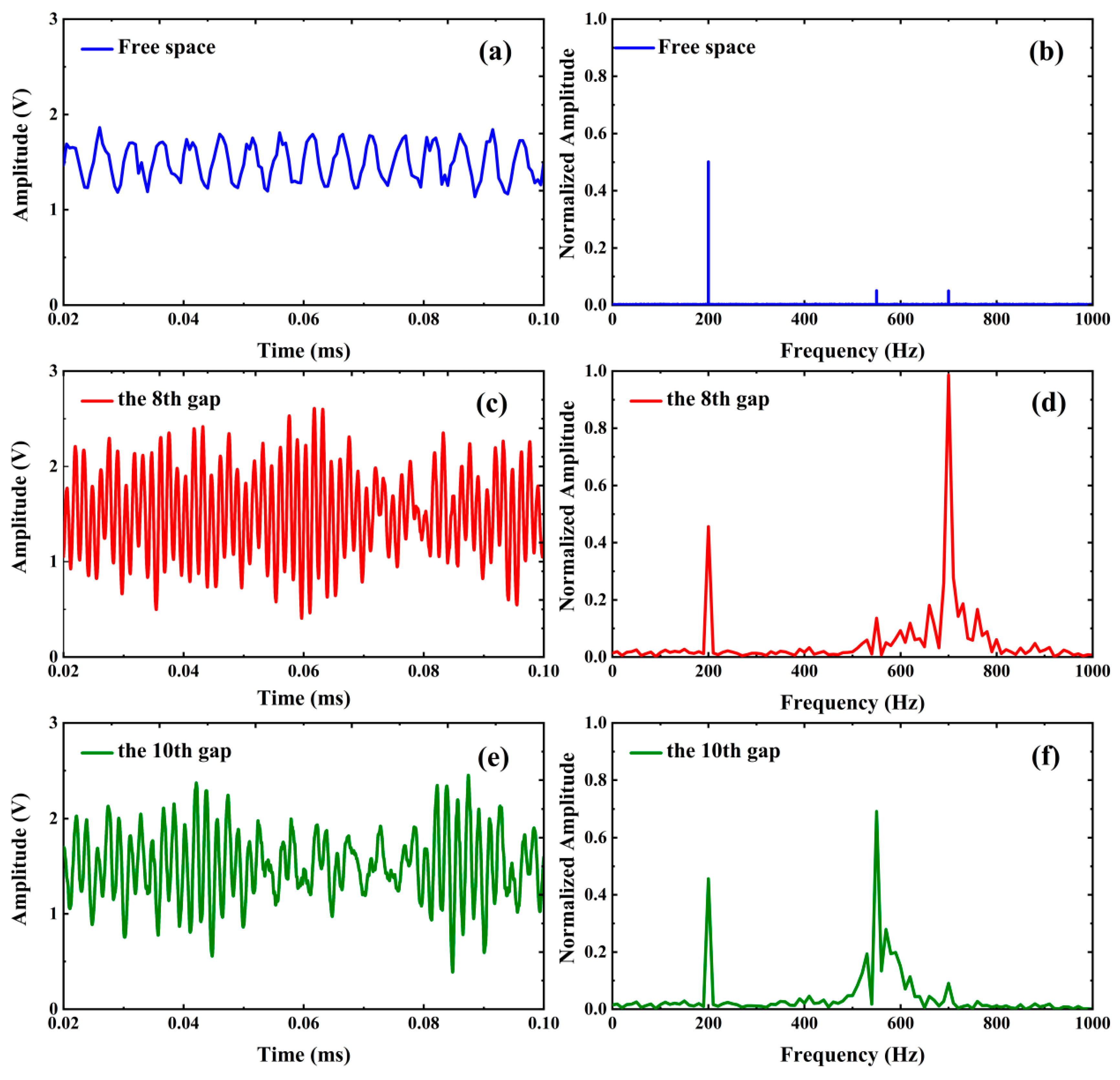
5.2. Sweep Frequency Signal Testing Based on the ZCGM Structure
5.3. Acoustic Sensing of Harmonic Signals Based on the ZCGM Structure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mahapatra, C.; Mohanty, A.R. Optimization of number of microphones and microphone spacing using time delay based multilateration approach for explosive sound source localization. Appl. Acoust. 2022, 198, 108998. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, D.; You, W.; Li, J.; Du, M. Two-dimensional planar sound source localization based on microphone array. J. Phys. Conf. Ser. 2022, 2232, 012006. [Google Scholar] [CrossRef]
- Kaneko, S.; Ozawa, Y.; Nakai, K.; Saito, Y.; Asai, K.; Nonomura, T.; Ura, H. High-efficiency sound source localization using data-driven sparse sampling with validation using monopole laser sound source. AIP Adv. 2024, 14, 065025. [Google Scholar] [CrossRef]
- He, P.; Shen, L.; Henson, B.; Zakharov, Y.V. Coarse-to-Fine Localization of Underwater Acoustic Communication Receivers. Sensors 2022, 22, 6968. [Google Scholar] [CrossRef] [PubMed]
- Miller, A.; Miller, B.; Miller, G. On AUV Control with the Aid of Position Estimation Algorithms Based on Acoustic Seabed Sensing and DOA Measurements. Sensors 2019, 19, 5520. [Google Scholar] [CrossRef]
- Otero, P.; Hernández-Romero, Á.; Luque-Nieto, M.-Á.; Ariza, A. Underwater Positioning System Based on Drifting Buoys and Acoustic Modems. J. Mar. Sci. Eng. 2023, 11, 682. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, L.; Jin, S.; Zhao, J.; Huang, C.; Yu, Y. AUV-Based Side-Scan Sonar Real-Time Method for Underwater-Target Detection. J. Mar. Sci. Eng. 2023, 11, 690. [Google Scholar] [CrossRef]
- Viegas, R.; Zabel, F.; Silva, A. In-Lab Demonstration of an Underwater Acoustic Spiral Source. Sensors 2023, 23, 4931. [Google Scholar] [CrossRef]
- Chen, Q.; Wang, P.; Wei, H. An algorithm for multi-target tracking in low-signal-to-clutter-ratio underwater acoustic scenes. AIP Adv. 2024, 14, 105121. [Google Scholar] [CrossRef]
- Zhang, T.; Zhang, W.; Shao, X.; Yang, Y.; Wu, Y.; Lei, M.; Wang, Z. Compressed sensing approach for CMUT sparse array in multi-element synthetic transmit aperture. Sens. Actuators A Phys. 2023, 349, 113965. [Google Scholar] [CrossRef]
- Chun-Di, S.I.; Chen, E.L.; Yang, S.P.; Wang, C.Y. Experimental on vehicle noise source identification. Noise Vib. Control 2010, 2, 40–43. [Google Scholar]
- Tian, H.; Peng, W.; Gao, K.; Jin, M.; Wu, T. High-resolution acoustic imaging method based on block sparsity constraint. AIP Adv. 2024, 14, 105230. [Google Scholar] [CrossRef]
- Zhao, W.; Yu, H.; Wen, Y.; Li, P.; Wang, X.; Wang, F.; Yang, Y.; Liu, L.; Li, W.J. Improving photoacoustic-imaging axial positioning accuracy and signal-to-noise ratio using acoustic echo effect. Sens. Actuators A Phys. 2021, 329, 112788. [Google Scholar] [CrossRef]
- Pascual, S.; Bonafonte, A.; Serrà, J. SEGAN: Speech Enhancement Generative Adversarial Network. In Proceedings of the Interspeech 2017, Stockholm, Sweden, 20–24 August 2017. [Google Scholar]
- Donahue, C.; Li, B.; Prabhavalkar, R. Exploring Speech Enhancement with Generative Adversarial Networks for Robust Speech Recognition. In Proceedings of the 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15–20 April 2018; pp. 5024–5028. [Google Scholar]
- Hao, X.; Su, X.; Wang, Z.; Zhang, H.; Batushiren. UNetGAN: A Robust Speech Enhancement Approach in Time Domain for Extremely Low Signal-to-Noise Ratio Condition. In Proceedings of the Interspeech 2019, Graz, Austria, 15–19 September 2019; pp. 1786–1790. [Google Scholar]
- Hu, P.; Zhao, J.-B.; Liu, H.; Zhang, X.; Yao, H.; Zhang, G.-j. Low-frequency acoustic isolation performance of Helmholtz cavity acoustic metamaterials with bilateral single openings. AIP Adv. 2024, 14, 045325. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Lu, W.; Hu, G.; Xu, B.-q.; Cao, W. Low-frequency forbidden bandgap engineering via a cascade of multiple 1D superlattices. J. Appl. Phys. 2018, 124, 155102. [Google Scholar] [CrossRef]
- Chen, D.-C.; Zhu, X.-F.; Wei, Q.; Yao, J.; Wu, D.-J. Broadband tunable focusing lenses by acoustic coding metasurfaces. J. Phys. D Appl. Phys. 2020, 53, 255501. [Google Scholar] [CrossRef]
- Chen, D.-C.; Zhu, X.-F.; Wei, Q.; Wu, D.-J. Bidirectional asymmetric acoustic focusing with two flat acoustic metasurfaces. Chin. Phys. B 2018, 27, 124302. [Google Scholar] [CrossRef]
- Gao, X.-y.; Cui, X.-b.; Zhang, Y.; Zhu, J.-j.; Huang, C.-p. Acoustoelectric conversion and deep-subwavelength acoustic focusing based on Fresnel zone plates. AIP Adv. 2023, 13, 035336. [Google Scholar] [CrossRef]
- Zangeneh-Nejad, F.; Fleury, R. Acoustic Analogues of High-Index Optical Waveguide Devices. Sci. Rep. 2018, 8, 10401. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.-q.; Wu, J.; Lu, W.; Gu, X.; Zhang, L.-j.; Zhang, S.; Zhang, Y. Transmission and rainbow trapping of acoustic waves in a fluid medium using gradient-index superlattices. J. Appl. Phys. 2021, 129, 154501. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, H.; Reilly, M.; Bae, H.; Yu, M. Enhanced acoustic sensing through wave compression and pressure amplification in anisotropic metamaterials. Nat. Commun. 2014, 5, 5247. [Google Scholar] [CrossRef] [PubMed]
- Xinjing, H.; Yutian, Y.; Jinyu, M.; Jian, L.; Xiaobo, R. An Acoustic Metamaterial-Based Sensor Capable of Multiband Filtering and Amplification. IEEE Sens. J. 2020, 20, 4413–4419. [Google Scholar] [CrossRef]
- Han, J.; Yang, P.; Tang, S. Local acoustic field enhancement of single cell photoacoustic signal detection based on metamaterial structure. AIP Adv. 2019, 9, 095064. [Google Scholar] [CrossRef]
- Chen, T.; Jiao, J.; Yu, D. Enhanced broadband acoustic sensing in gradient coiled metamaterials. J. Phys. D Appl. Phys. 2021, 54, 085501. [Google Scholar] [CrossRef]
- Chen, T.; Wang, C.; Yu, D. Pressure amplification and directional acoustic sensing based on a gradient metamaterial coupled with space-coiling structure. Mech. Syst. Signal Process. 2022, 181, 109499. [Google Scholar] [CrossRef]
- Birir, J.K.; Gatari, M.J.; Rajagopal, P. Structured channel metamaterials for deep sub-wavelength resolution in guided ultrasonics. AIP Adv. 2020, 10, 065027. [Google Scholar] [CrossRef]
- Cummer, S.A.; Christensen, J.; Alù, A. Controlling sound with acoustic metamaterials. Nat. Rev. Mater. 2016, 1, 16001. [Google Scholar] [CrossRef]
- Zhu, X.; Liang, B.; Kan, W.; Peng, Y.-G.; Cheng, J. Deep-Subwavelength-Scale Directional Sensing Based on Highly Localized Dipolar Mie Resonances. Phys. Rev. Appl. 2016, 5, 054015. [Google Scholar] [CrossRef]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic metamaterials. Nat. Photonics 2013, 7, 948–957. [Google Scholar] [CrossRef]
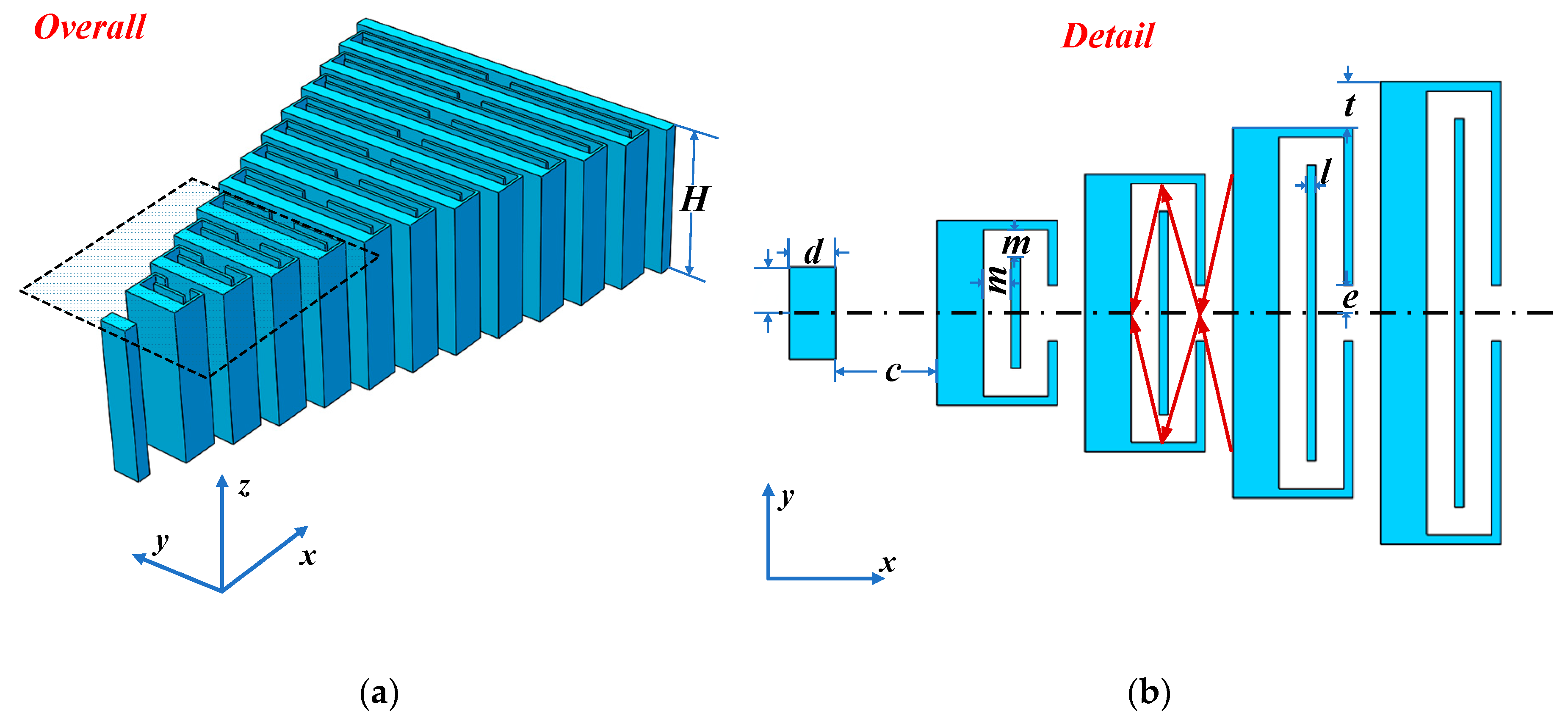

| Parameters | L1 | D | m | l | c | t | H | e |
|---|---|---|---|---|---|---|---|---|
| Values (mm) | 5 | 5 | 3 | 1 | 11 | 5 | 55 | 3 |
| Air Gaps | fnum (Hz) | Air Gaps | fnum (Hz) |
|---|---|---|---|
| 3rd | 1885 | 8th | 708 |
| 4th | 1430 | 9th | 628 |
| 5th | 1141 | 10th | 570 |
| 6th | 951 | 11th | 517 |
| 7th | 808 | 12th | 475 |
| Air Gaps | f1 (Hz) | f2 (Hz) | F (Hz) | Air Gaps | f1 (Hz) | f2 (Hz) | F (Hz) |
|---|---|---|---|---|---|---|---|
| 3rd | 1910 | 2610 | 3543 | 8th | 709 | 1102 | 1754 |
| 4th | 1430 | 2056 | 3007 | 9th | 628 | 986 | 1588 |
| 5th | 1142 | 1692 | 2561 | 10th | 570 | 894 | 1455 |
| 6th | 951 | 1438 | 2221 | 11th | 518 | 818 | 1338 |
| 7th | 809 | 1248 | 1958 | 12th | 475 | 758 | 1258 |
| Air Gaps | Simulated Gain (t = 5 mm) | Actual Gain | Actual Gain/Simulated Gain (%) |
|---|---|---|---|
| 6th | 27.5 | 14.09 | 51.2% |
| 8th | 29.8 | 12.71 | 42.6% |
| 10th | 24.7 | 10.82 | 43.8% |
| 12th | 20.75 | 9.69 | 46.6% |
| Method | Sound Pressure Gain Multiple | Frequency Range |
|---|---|---|
| ZCGM | 20 | Low frequency (475–1910 Hz) |
| Traditional GAM | 15 | High frequency (1258–3543 Hz) |
| Huang’s [25] | >10 | Underwater mid-high frequencies |
| John K. Birir’s [29] | Unspecified | Ultra-high frequency (guided wave ultrasound) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ren, Y.; Hao, G.; Zhao, X.; Han, J. A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals. Crystals 2025, 15, 216. https://doi.org/10.3390/cryst15030216
Ren Y, Hao G, Zhao X, Han J. A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals. Crystals. 2025; 15(3):216. https://doi.org/10.3390/cryst15030216
Chicago/Turabian StyleRen, Yulin, Guodong Hao, Xinsa Zhao, and Jianning Han. 2025. "A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals" Crystals 15, no. 3: 216. https://doi.org/10.3390/cryst15030216
APA StyleRen, Y., Hao, G., Zhao, X., & Han, J. (2025). A Tunable Z-Shaped Channel Gradient Metamaterial for Enhanced Detection of Weak Acoustic Signals. Crystals, 15(3), 216. https://doi.org/10.3390/cryst15030216






